Analysis of the Precision, Robustness, and Speed of Elastic Resonator Interference Stress Microscopy

Abstract

Localization-microscopy-based methods are widely used to map the forces that cells apply to their substrates and to study important questions of cellular biomechanics. By contrast, elastic resonator interference stress microscopy (ERISM) uses an interference-based approach, which requires low light intensity and facilitates imaging of cellular forces with extreme precision (down to pN forces) and robustness (e.g., for continuous force monitoring over weeks). Here, the measurement trade-offs and numerical considerations required to optimize the performance of ERISM are described. The crucial parts of the fitting algorithm and the computational tools used to evaluate the data are explained in detail, and the precision and accuracy achievable with ERISM are analyzed. Additional features that can improve the robustness of ERISM further are discussed. The implementation of the analysis algorithm is verified with simulated test data and with experimental data. In addition, an approach to increase the acquisition speed of ERISM by a factor of four compared to the original implementation is described. In combination, these strategies allow us to measure the forces generated by a neural growth cone with high temporal resolution and continuously over several hours.

Introduction

The mechanical forces cells exert on their environment are critical in many biological processes, e.g., during cell migration, immune response, morphogenesis, wound healing, tumor metastasis, and extracellular matrix deposition (1, 2, 3, 4, 5, 6). A number of methods have been developed to measure and image cellular forces, which have been recently reviewed in (7). These techniques have made extremely valuable contributions to our understanding of cell-substrate and cell-cell interactions (8, 9, 10). The currently most widely used methods are arguably traction force microscopy (TFM) (11, 12, 13, 14, 15, 16) and the use of micromachined elastic micropillars (1, 17, 18). Both methods use localization microscopy to track the movement of microscopic markers (located within or on top of a test substrate) that occurs in response to the force pattern cells exert onto the substrate. A global translation field is then extrapolated from these local displacement measurements. Displacements in-plane can be tracked easily with conventional microscopy, but recording vertical, out-of-plane displacements is more challenging and in general less accurate, as most microscopy modalities provide lower axial than lateral resolution. Therefore, existing force-sensing techniques sometimes struggle to resolve and accurately quantify small forces that cells apply perpendicular to their substrate, even though these out-of-plane forces are assumed to be crucially important in many processes (14, 19, 20). In addition, most currently used techniques require fluorescence imaging, which can lead to phototoxic effects, in particular if high frame rates or long time-lapse series are required. Finally, many methods require detaching of cells after the measurement. This prevents measuring the same cells repeatedly or performing immunostaining at the end of a measurement, which in many cases would otherwise be the most adequate method to link biomechanical observations to the biochemical context in the cell.

We recently introduced elastic resonator interference stress microscopy (ERISM) as a novel technique to measure forces exerted by cells on planar substrates (21). By using optical interference instead of localization microscopy, ERISM can in principle measure cell-induced displacements with higher accuracy and provides a more direct measure of displacement, in particular for vertical forces. In comparison to most existing techniques, it also allows long-term measurements to be performed more easily, e.g., to continuously monitor cell division over several generations or to track cell differentiation occurring over the course of more than a week. In addition, there is no need to detach the cells after a measurement, which facilitates immunostaining of cells immediately after an ERISM measurement. The original publication on ERISM explained the measurement concept and illustrated the potential of ERISM through several examples of applications. However, a description of the measurement trade-offs and numerical considerations required to optimize the performance of ERISM and details on the computational tools used to evaluate the data have not yet been reported.

Here, we provide detailed information on the implementation of the ERISM analysis at a level of detail that should allow other scientists to implement this method for their own measurements. We begin by giving a short summary of the working principle of ERISM and the related calculations. We then provide in-depth information about how to calculate cell-induced substrate deformations from the measured data, which then forms the basis for calculating the stress that cells apply to an ERISM substrate. Furthermore, we explain the crucial parts of the fitting algorithm—including a detailed discussion of its precision and accuracy—link it to optical limitations of the technique, and verify the implementation of the analysis algorithm with simulated test data and experimental data. In addition, we present an approach to increase the acquisition speed of ERISM by a factor of four compared to the original implementation, which may prove important for the investigation of fast biological processes or to follow a large number of cells in parallel. As an important example of the capability of ERISM, we show measurements of the force generated by a neural growth cone. The high temporal resolution, exquisite force sensitivity, and long-term capability (continuous measurement over several hours) allow observation of features in the activity of the growth cone that one may otherwise miss.

Materials and Methods

The computations described in the following were performed on a standard desktop computer with an IntelCore i7 3770K at 3.5 GHz (quad core), 8 GB of RAM, and a Windows 7 operating system.

The experimental setup used for the measurements described here is similar to the setup described in (21) with differences pointed out where relevant in the Results.

For the neuronal growth cone experiments, dorsal root ganglia (DRG) were extracted from 2-day-old mouse pups. After preparing a cell suspension, DRG were seeded at a density of 5000 cells per square centimeter on an ERISM microcavity with apparent stiffness of 3.2 kPa. Before cell seeding, the microcavity was coated with poly-D-lysine (5 μgmL⁻¹ in H₂O) for 2 h and then with laminin (10 μg mL⁻¹, in phosphate-buffered saline) for 2 h. Cells were seeded in Neurobasal medium (Gibco, Gaithersburg, MD) supplemented with 2 mmol GlutaMAX-I and 2 vol% B-27. After seeding, DRG were incubated on the ERISM microcavity for 4 days. ERISM measurements were performed in an on-stage incubator (Okolab, San Francisco, CA) at 5% CO₂, 37°C, and 100% humidity.

Results and Discussion

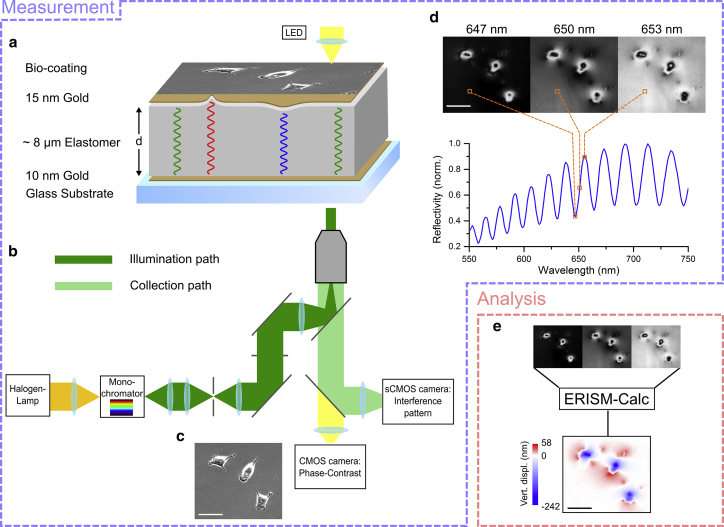
The general concept of ERISM is summarized in Fig. 1. The main element of ERISM is an elastic, optical microcavity that consists of two semitransparent gold mirrors and an elastic spacer material in between (in the present implementation, a siloxane-based elastomer). Using a microscope objective underneath the microcavity substrate, the structure is illuminated with monochromatic light from a monochromator coupled to a halogen lamp. When the reflection of the cavity is imaged with the same microscope objective, an interference fringe pattern is observed (Fig. 1, b and d). In this image, dark areas correspond to positions where light couples to resonant modes of the microcavity. This occurs if the wavelength of the incident light is

$$\lambda =\frac{2dn\left(\lambda \right)}{m}\text{,}$$ (1)

where d is the local thickness of the microcavity, n(λ) is the wavelength-dependent refractive index of the elastic spacer material, and m is the order of interference or mode number. A perfectly flat microcavity (with homogeneous thickness) will show the same reflectance at every point in the image. However, if a localized force is applied to the surface of the microcavity, the cavity thickness d at this position, and hence the resonance wavelength, will change. As the whole field of view is illuminated at once, any changes in cavity thickness across the field of view are directly apparent from a reflectance image recorded at a single wavelength of illumination (cf. Fig. 1 d). To obtain more precise information on the local cavity thickness, we generally record reflectance images for a range of illumination wavelengths that is large enough to capture multiple minima. (This will be explained in more detail below.) By recording one such stack of images, reflectance spectra are acquired for each point within the field of view (cf. Fig. 1 d for an example of a representative single pixel from a typical image stack that contains images for 201 wavelengths with over 1 million pixels each). The minima in these spectra, which represent the resonance wavelengths of the microcavity, can then be used to calculate the local thickness of the cavity for every pixel in the image.

Figure 1.

Overview of the working principle of ERISM. (a) A microcavity with a cell attached to the functionalized top gold layer is depicted. (b) The microcavity is illuminated from underneath, and the reflectivity is recorded by an sCMOS camera. (c) In parallel, a dia-illumination phase-contrast image is recorded on a separate CMOS camera using a different spectral channel. Shown is the image obtained for a microcavity on which 3t3 fibroblast cells are cultured. (d) Representative reflectance images for illumination at 647, 650, and 653 nm and reflectivity versus wavelength for a single pixel from the recorded image stack are shown. (e) A schematic illustration of the ERISM image analysis process is given. Using the reflection spectra extracted from the image stack for each pixel, the “ERISM-Calc” software derives the cell-induced vertical displacement. Data are shown for the same cells shown in (c) and (d). All scale bars, 50 μm. To see this figure in color, go online.

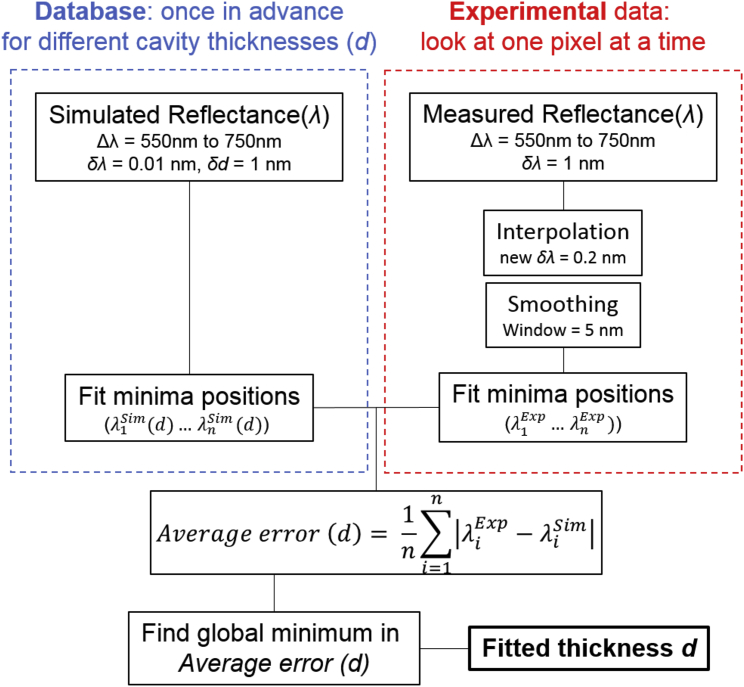
Fig. 2 visualizes the overall data flow from data acquisition to the fitted cavity thickness at each position across the image. In the following, we briefly summarize the involved steps; each part is then explained in detail in the next section. If the gold layers had perfect and wavelength-independent reflection, and there were no other layers except the elastomer present in the cavity, one could use Eq. 1 to calculate the thickness, provided two or more wavelengths at which the reflectance spectrum has a local minimum are known (in the following, we refer to these wavelengths as the “minima positions”). However, for real microcavities, the reflectivity of the mirrors is wavelength-dependent, and there is a nonideal phase shift upon reflection. Furthermore, the elastomer in the cavity is a dispersive medium, and in addition to the elastomer, there is a thin adhesion layer of SiO₂ present on the bottom gold mirror. We therefore use a transfer matrix algorithm to calculate the expected reflectance spectrum of our microcavity structure for different microcavity thicknesses. This transfer matrix calculation is performed in advance for every possible microcavity thickness, and a database is created that links each cavity thickness to a set of minima positions. (Performing the transfer matrix calculation during analysis of reflectance images would dramatically increase the time required to compute ERISM maps without any benefit.) Using this database, we then fit the cavity thickness by simply comparing the minima positions extracted from the experimental data to the minima positions in the database to find the thickness for which the difference is minimal. The use of an optimized algorithm is crucial, as—depending on image size—the thickness for more than 1 million pixels has to be fitted for each field of view that is analyzed.

Figure 2.

Data flow of the algorithm used to fit the cavity thickness for each pixel within the field of view, i.e., for each reflectance-over-wavelength dataset (measured reflectance (λ)). The values listed for the wavelength range (Δλ), the wavelength step size (δλ), the thickness step size (δd), and the smoothing window are the standard values, but these are adjusted as needed, which is described later. The left-hand side (blue box) illustrates how the database containing sets of resonance wavelength $\left({\mathit{\lambda }}_1^{\mathbf{S}\mathbf{i}\mathbf{m}}\left(\mathit{d}\right),{\mathit{\lambda }}_2^{\mathbf{S}\mathbf{i}\mathbf{m}}\left(\mathit{d}\right),\dots ,{\mathit{\lambda }}_{\mathit{n}}^{\mathbf{S}\mathbf{i}\mathbf{m}}\left(\mathit{d}\right)\right)$ is created, which is only done once. The right-hand side (red box) describes how the measured reflectance data is preconditioned and analyzed. The average error is calculated for each pixel and is given by the sum of the differences between experimental and simulated wavelength for each of the observed resonance wavelengths $\left({\mathit{\lambda }}_1,{\mathit{\lambda }}_2,\dots ,{\mathit{\lambda }}_{\mathit{n}}\right)$. To see this figure in color, go online.

Thickness fitting algorithm

The code used for the transfer matrix simulations shown in this study is based on an open-source Python code by Yuffa et al. (22). The core part of transfer matrix calculations in optics is to calculate the Fresnel coefficients at every material interface to determine how much light is transmitted or reflected at each interface. These coefficients are then combined by matrix multiplication to yield the total transmission and reflectance of the structure.

The layer structure we used for the devices discussed in this study is 500 μm glass, 0.5 nm chromium, 10 nm gold, 50 nm SiO₂, 8000 nm elastomer, and 15 nm gold. The chosen thickness of the gold layers represents a trade-off between high Q-factor, high mechanical sensitivity, and sufficient transmittance of light through the cavity to allow combination with phase-contrast and fluorescence imaging. A thicker top mirror on top of the elastomer would allow increasing the Q-factor but would increase the effective stiffness and thus make the device less sensitive to stress exerted by cells. The mechanical characteristics of the microcavity were discussed in more detail in (21).

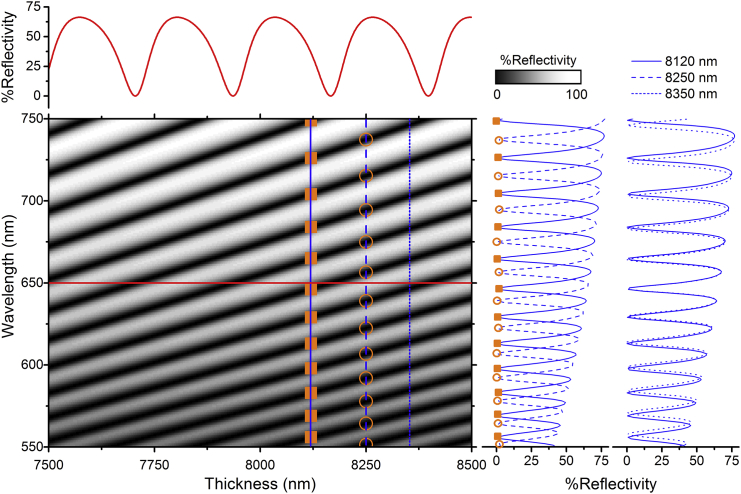
The reflectance spectrum of this layered structure is simulated at normal incidence for a wavelength range from 550–750 nm and for elastomer thicknesses between 7500 and 8500 nm (Fig. 3; we find that cells normally do not deform the microcavity by more than ±500 nm, but the simulation range can be expanded if necessary). From Fig. 3, it is clear that for a constant wavelength of illumination, one will see multiple dark areas (fringes) if the cavity thickness changes by more than 225 nm across the field of view. This is beneficial, as it provides a real-time estimate of thickness differences across the field of view. On the other hand, it also shows that one cannot determine the absolute thickness at each position across the microcavity from knowing just a single resonance wavelength at each position. In principle, the free spectral range (FSR), i.e., the spectral separation between two reflectance minima, can be used to extract the absolute thickness,

$$\text{FSR}\left(\mathit{\nu }\right)=\frac{c}{2n\left(\mathit{\nu }\right)d}\text{.}$$ (2)

Figure 3.

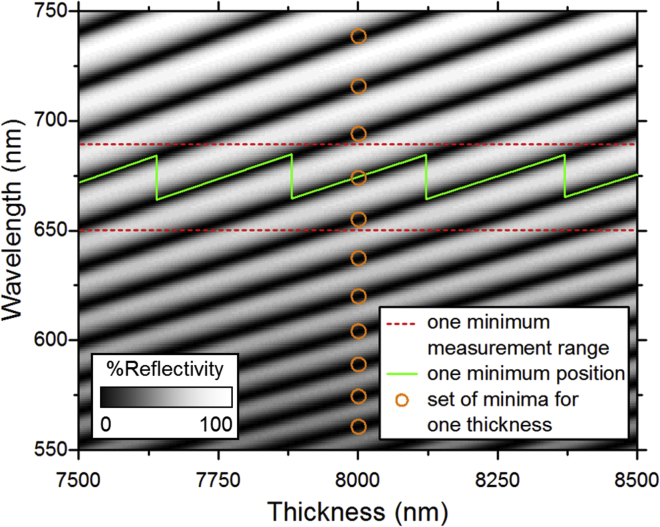
Two-dimensional (2D) map of the simulated reflectivity for a wavelength range of 550–750 nm and a cavity thickness range of 7500–8500 nm. The data above and to the right of the 2D map represent profiles of the reflectivity over cavity thickness and wavelength, respectively (taken at the positions indicated by the respective lines in the 2D map). The reflectivity-over-wavelength profiles (blue lines) correspond to the type of data that is obtained for each pixel during an experiment. The orange squares and circles mark two exemplary sets of minima positions corresponding to cavity thicknesses of 8120 and 8250 nm, respectively. The reflectivity-over-wavelength profiles at the very right represent profiles at 8120 and 8350 nm, i.e., reflectivity spectra which are one mode apart. To see this figure in color, go online.

Here, ν and c are the frequency and speed of light in vacuum. However, because we do not have a perfect Fabry-Pérot resonator, the FSR depends on the frequency/wavelength of the light, i.e., there is no single FSR for our microcavity. Therefore, to fit the cavity thickness, we instead use the positions of all minima in the measurement range; this means we include the information about the FSR as well as the absolute position of each minimum. As illustrated on the right-hand side of Fig. 3, this set of minima positions is unique for each cavity thickness, even when comparing two thicknesses that differ by exactly one interference order m.

The minima positions for all cavity thicknesses are extracted from the transfer-matrix simulations using a standard peak-finding procedure, and the wavelengths are then stored for each cavity thickness d as (${\lambda }_1^{\text{Sim}}\left(d\right),{\lambda }_2^{\text{Sim}}\left(d\right),\dots ,{\lambda }_n^{\text{Sim}}\left(d\right)$), where n is the number of minima in the spectral range considered. The transfer-matrix calculation and peak finding have to be performed only once for any given layer structure to populate the database linking cavity thicknesses to minima positions (blue box in Fig. 2).

The peak-finding procedure used in the current implementation of the algorithm checks from smaller to larger wavelengths, whether the next reflectivity value is larger or smaller than the one at the current wavelength. If it is smaller, the algorithm will continue to search for smaller values; if the next value is larger, the program checks whether any smaller values can be found within a predefined range, e.g., in the next 5 nm, to avoid false fits because of numerical errors or noise from the experimentally determined refractive index data. If not, a minimum is found, and its wavelength is stored as ${\lambda }_i^{\text{Sim}}$. The algorithm continues to search for the next minimum using the procedure above until the end of the wavelength range is reached.

A similar procedure is applied to determine the experimental minima positions from the measured data. The set of experimentally measured and fitted minima $\left({\lambda }_1^{\text{Exp}},{\lambda }_2^{\text{Exp}},\dots ,{\lambda }_n^{\text{Exp}}\right)$ is then compared to the previously compiled database of cavity thickness d and minima positions $\left({\lambda }_1^{\text{Sim}}\left(d\right),{\lambda }_2^{\text{Sim}}\left(d\right),\dots ,{\lambda }_n^{\text{Sim}}\left(d\right)\right)$ by calculating—for each thickness d—the average error between the experimental and simulated minima positions:

$$Averageerror\left(d\right)=\frac{1}{n}\sum _{i=1}^n\left|{\lambda }_i^{\text{Exp}}-{\lambda }_i^{\text{Sim}}\left(d\right)\right|\text{.}$$ (3)

Here, n is the number of minima found in the experimentally obtained reflectance profile. We use the average error rather than the total error to have a measure of the deviation that is independent of the number of minima in the analyzed spectrum.

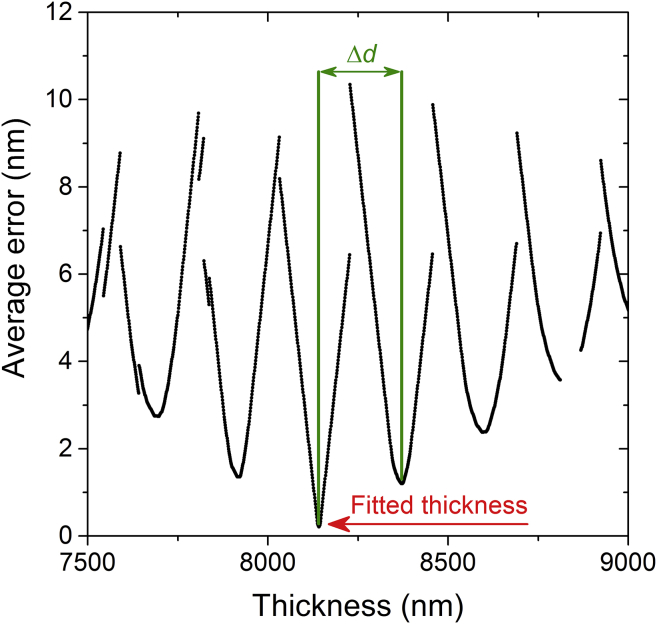
Fig. 4 shows a typical example of how the average error changes with d. There are several local minima, which correspond to different cavity modes m (and thus different cavity thicknesses), that are separated by intervals of approximately $\mathit{\Delta }d\left(\lambda \right)=\lambda /2n\left(\lambda \right)$ (cf. Eq. 1). Because Δd depends on wavelength, the distance between local minima represents an average value.

Figure 4.

Average error as defined in Eq. 3 between experimentally obtained minima and simulated minima positions for different microcavity thicknesses. Δd represents the spacing between two minima. The thickness at the global minimum of the average error is assumed to be the actual thickness of the microcavity (indicated by red arrow). To see this figure in color, go online.

However, the figure also shows that there is only one global minimum, i.e., one thickness, for which the deviation between the simulated and experimental minima positions is the smallest. (Also, note that this minimum is the steepest of all observed local minima.) The thickness associated with this global minimum is taken as the best fit for the local thickness of the cavity at this position of the field of view. If the signal quality decreases or the cavity thickness changes during one scan—e.g., because of the very fast movement of a cell—the reflectivity minima positions may change such that the differences in the average error between different cavity modes become smaller. In extreme cases, even a wrong mode number m might be fitted. This issue and ways for its mitigation will be discussed later (cf. Fig. 8).

Figure 8.

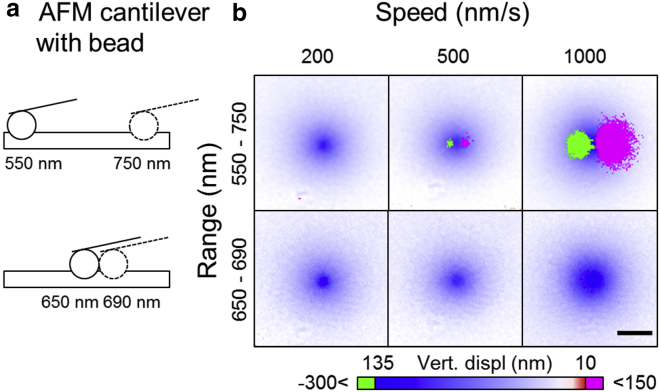
Comparison of the ability of ERISM to measure the deformation induced by a moving AFM cantilever indented into the microcavity when using either the conventional scheme that fits all minima in a range of 550–750 nm or the one-minimum tracking scheme, which only scans the 650–690 nm range. (a) A schematic of the AFM cantilever positions at the start and end of one ERISM scan is given. (b) The fitted vertical displacement for different cantilever speeds and fitting ranges is given. Green and magenta represent pixels for which unphysical values were fitted (green, <−300 nm and magenta, >150 nm). Scale bars, 5 μm. All images show a section of the full field of view that is centered on the maximal indentation. To see this figure in color, go online.

Testing the accuracy and precision with simulated data

The finite spectral bandwidth of the light used to illuminate the microcavity and the desire to perform the measurement quickly limit the smallest possible wavelength step size during acquisition to ∼1 nm. However, by interpolating and smoothing, we can localize the position of the reflectance minimum with an accuracy beyond 1 nm, as illustrated in Fig. 5 a. This is analogous to particle localization measurements in superresolution imaging (e.g., PALM and STORM) (23, 24) and does not represent a violation of Nyquist’s theorem.

Figure 5.

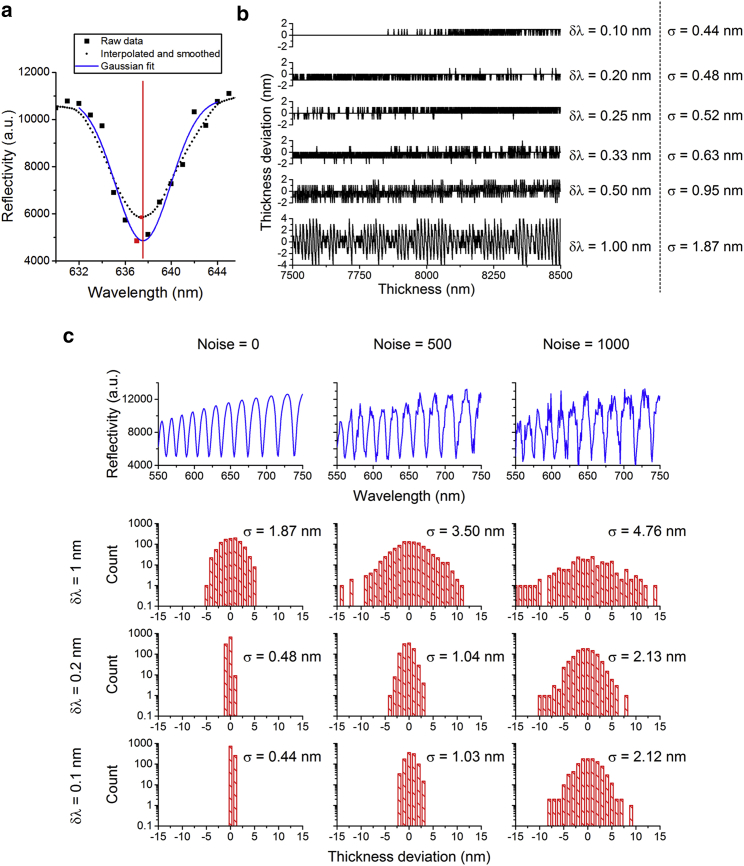
Testing the precision of the thickness fitting algorithm with reflectance data produced by transfer matrix calculations. Different interpolation conditions and different amounts of Gaussian noise added to the data are compared. (a) A comparison of typical raw data (with Noise = 500, see below), interpolated and smoothed data, and a Gaussian peak fit to the raw data is shown. Red symbols mark the minima in each corresponding data set. The red line indicates the minimum of the Gaussian fit. (b) The difference between nominal and fitted thickness for different increments of wavelength interpolation δλ is shown. σ is the standard deviation of the difference between nominal cavity thickness and fitted thickness. (c) The difference in thickness for different δλ and different amounts of Gaussian noise added to the transfer matrix calculations (standard deviation of noise 0, 500, and 1000) is given. The blue profiles (top) illustrate how the added noise affects the reflectance spectra (cavity thickness, 8000 nm). Note that for noise = 1000 and δλ = 1 nm, the total fraction of pixels in the image that can be fitted at all is only 20%. To see this figure in color, go online.

To investigate the precision of the cavity thickness measurement, we first test our code against simulated test data, i.e., theoretical reflectance spectra obtained by a transfer-matrix calculation are used for the procedure stated in the red box in Fig. 2. This is done using the entire data set from Fig. 3, i.e., the full reflectance profiles in a wavelength range for 550–750 nm in 1-nm-wavelength steps and for thickness values between 7500 and 8500 nm in 1-nm-thickness steps. These reflectivity profiles are then used to fit the thickness as described above. For this test as well as for our calculations on measured data, the precompiled database with the minima positions for each cavity thickness is calculated in wavelength steps of 0.01 nm to ensure that the precision of the database is not the limiting factor.

The results of these calculations are shown in Fig. 5 b, which plots the difference between the cavity thickness predicted by the algorithm and the nominal thickness. The difference is shown for different interpolation increments δλ. This analysis shows that interpolating and smoothing the experimental data indeed improves the precision of the calculation. Without any interpolation, the standard deviation and peak-to-peak deviation of the difference are σ = 1.87 nm and σ_peak-to-peak = 8 nm, respectively. Both values decrease significantly when the data is interpolated at increments of δλ = 0.2 nm and smoothed with a 5-nm moving average filter. However, we do not observe a further significant improvement by interpolating the data at δλ = 0.1 nm increments versus δλ = 0.2 nm.

Next, we investigate the influence of noise on the precision of the thickness fitting. Gaussian noise with different standard deviations (stated as “Noise =” in Fig. 5 c) is added to the reflectance spectra before the thickness fitting is performed. The results are summarized in Fig. 5 c; the blue profiles show the reflectivity spectra for a microcavity thickness of 8000 nm with different amounts of noise added; the histograms summarize the deviation between nominal and fitted thickness for the entire 7500–8500 nm thickness range. In Fig. 5 c, the column in the middle (Noise = 500) represents a scenario similar to experimental noise under standard conditions. The results show that interpolating and smoothing the data greatly improves the precision of the thickness fitting: the standard deviation of the deviation between nominal thickness and fitted thickness is reduced from 3.50 to 1.04 nm (for Noise = 500) by interpolating in δλ = 0.2 nm steps. We see this improvement for all three noise levels but again see no significant further improvement for any of the noise levels when using δλ = 0.1 nm. Therefore, δλ = 0.2 nm will be used to prevent unnecessary use of computation time. We attribute the fact that we do not see a further improvement in precision to the statistical effect of actually fitting multiple minima positions so that the average error from Eq. 3 should be divided by $\sqrt{N}$.

We also test how our approach of interpolating and smoothing the data before fitting the minima positions compares to fitting each minimum with a peak function, which is often done in superresolution imaging. (We used a Gaussian here, as we find that it describes the broad and partly overlapping minima better than a Lorentzian.) For this, we take the simulated reflectivity plot for a cavity thickness of 8120 nm (blue line in Fig. 3) and, without performing any initial interpolation or smoothing of the data, fit each minimum position with a Gaussian function. Eq. 3 is then used to calculate the average error between the determined and simulated (true) minima positions. For comparison, we use the method used before (i.e., interpolating with 0.2-nm increments, smoothing with a 5-nm moving average filter, finding the minima with the simple minimum finding algorithm described above, and then applying Eq. 3). We find that the average error is 0.19 nm for the interpolation and smoothing approach and 0.18 nm for fitting the minima positions with a Gaussian function. (Fig. 5 a shows the raw data, interpolated/smoothed data, and Gaussian fit for one reflectance dip of a typical data set and compares the values for the minimal wavelength that are obtained with each approach.) We therefore conclude that fitting a Gaussian function does not lead to a more accurate fit. However, it is computationally much more demanding than our approach, as a least square fit has to be carried out for each minimum separately, and in addition, an initial guess of the approximate positions of the minima has to be made. We have not optimized the peak fitting routine but estimate that even after optimization, it would remain more than 10-fold slower than the interpolation and smoothing approach. In light of the large number of reflection spectra that need to be analyzed for each image, the interpolation and smoothing approach combined with the simple minima-finding algorithm described above is therefore more suitable.

Finally, to estimate the thickness resolution of our approach, we derive a relation between changes in the position of minima and changes in cavity thickness. The derivative of Eq. 1 is $\left(\text{d}\lambda /\text{d}d\right)=\left(2n\left(\lambda \right)/m\right)$ and provides a measure of how much one reflection minimum shifts per 1-nm change in cavity thickness. For typical values (λ = 650 nm and d = 8000 nm, Eq. 1 gives m = 34), we find that each minimum shifts by ∼0.08 nm/nm (nm change in wavelength per nm thickness change). The calculations in the previous paragraphs showed that the average error in the spectral position of the reflection minima is between 0.19 and 0.24 nm (depending on whether or not noise is considered). This would imply an error in the thickness measurement of $\left(0.24\text{nm}/\left(0.08\text{nm}/\text{nm}\right)\right)\approx 3\text{nm}$. However, as the thickness fitting algorithm considers about 10 minima across the investigated wavelength range (typically 550–750 nm), the precision of the thickness measurement improves to $\left(0.24\text{nm}/\left(0.08\text{nm}/\left(\text{nm}\times \sqrt{10}\right)\right)\right)\approx 1\text{nm}$.

Testing the precision with real data

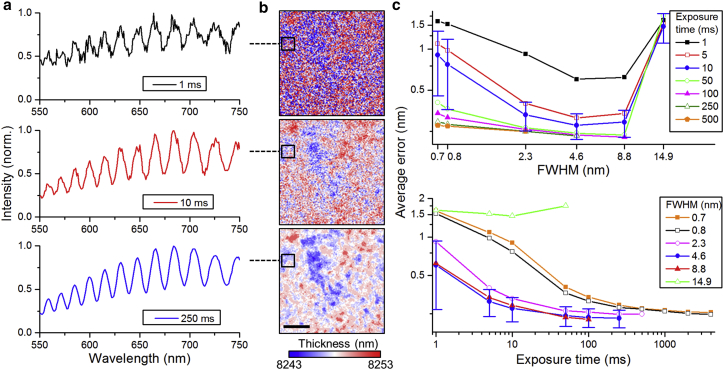
In the next section, we will investigate how the precision of thickness fitting is influenced by the spectral bandwidth of the light used to illuminate the microcavity, the camera exposure time, and the roughness of the cavity mirrors. Measurements were taken on a flat, nondeformed region of an elastic microcavity (same structure as described above) using different exposure times and bandwidths. (The bandwidth was adjusted by changing the slit widths of the monochromator used in the experimental setup for recording ERISM data. See (21) for more details on the setup.). The results of this experiment are summarized in Fig. 6. We find that higher exposure times generally lead to less noisy reflectivity profiles (Fig. 6 a) and consequently yield less noisy thickness maps (Fig. 6 b). For the longest exposure time tested (250 ms), a surface structure, which we attribute to the local roughness of the gold mirrors, is resolved. To quantify the quality of our measurement, we calculate the average error (Eq. 3) for different combinations of exposure time and bandwidths (full width at half-maximum (FWHM)), taking in each case the mean over the whole field of view of our system (in the configuration presented here, this is generally 1024 × 1280 px, corresponding to 166 × 207 μm² when a 40× microscope objective is used; cf. Fig. 6 c). When the exposure time is kept constant, the average error decreases with increasing bandwidth. The reason for this somewhat counterintuitive behavior is that at larger bandwidths, more light passes through the monochromator slits. This improves the signal/noise ratio and hence allows for a more accurate determination of the minimum position, in particular in combination with the interpolation and smoothing approach described above. However, if the bandwidth is too large (e.g., FWHM of 14.9 nm), the interference contrast reduces drastically, which then results in large average errors for all exposure times we applied. Furthermore, we find that increasing the exposure time only reduces the average error significantly for exposure times up to 10 ms (when using FWHM bandwidth ≥2.3 nm), indicating that beyond a certain signal/noise ratio, the thickness fitting does not improve by a further significant amount. The slits yielding FWHM bandwidths of 4.6 and 8.8 nm perform nearly equally well, and our data indicate that a bandwidth below 4.6 nm does not improve the precision of the fit. To minimize the overall scan time, we select a slit width yielding an FWHM bandwidth of 4.6 nm (physical width of these slits, 0.6 mm) and an exposure time of 10 ms for most measurements. The mean average error for these measurement parameters is 0.25 nm; this is comparable to the value estimated with simulated data (0.24 nm) and corresponds to a 1 nm precision for the thickness fitting. We also note that the standard deviation of the average error is typically around 20% for relevant measurement parameters; for 4.6-nm FWHM and 10-ms exposure, 95% of all pixels have an error <0.55 nm. We therefore conclude that it is sufficient to fit the cavity thickness in 1-nm steps, i.e., to use 1-nm-thickness increments in the database with simulated minima positions. Smaller thickness steps could be used if needed, but in this configuration would unnecessarily increase computation time. We note that with the fabrication process used here, ERISM microcavities have a root mean square surface roughness of approximately 2 nm (see (21)).

Figure 6.

Investigation of the influence of the spectral bandwidth of the light source (FWHM) and camera exposure time on the thickness fitting for a flat microcavity. (a) Reflectance spectra for a single pixel within the field of view for different exposure times (spectral bandwidth, 4.6 nm) are shown. (b) The thickness of the microcavity for the same exposure times as in (a) is given. Scale bars, 5 μm. The black box indicates the pixel for which spectrum is shown in (a). (c) A semi-log plot of average deviation between experimentally determined and simulated sets of minima for the fitted cavity thicknesses versus spectral bandwidth (top) and camera exposure time (bottom) is given. Error bars represent the standard deviation of the average error; for better visibility, they are only shown for 10 ms exposure time and 4.6 nm FWHM. To see this figure in color, go online.

Limitations of thickness fitting

We observed that the thickness fitting can yield inaccurate results if very short exposure times are used (<10 ms), if there are extremely steep changes in cavity thickness (large gradients), or if the observed processes is highly dynamic, causing considerable thickness changes during the wavelength scan. One of the provisions we introduced to prevent unphysical results is a “tolerance” parameter. If the average error is above the tolerance value for a pixel in the image, then the thickness for this pixel is set to “not a number” rather than to the thickness yielding the smallest average error. Typically, the tolerance is set to 1 nm, i.e., the maximal average deviation between measured and simulated resonance wavelength must be smaller than 1 nm. This corresponds to a maximal allowed deviation in thickness of 12.5 nm. We find that the average error only ever gets close to the 1-nm tolerance if deformations are >150 nm. For these large deformations, allowing pixels to be fitted with a 12.5-nm inaccuracy seems acceptable, as this corresponds to a maximal error in the measured deformation of less than 10%. For smaller deformations, the precision of the measurement is much higher (as described above), as the tolerance compliance is not reached.

Another measure to prevent unphysical results relates to the suppression of mode jumps. If the fitting algorithm fails to determine the thickness correctly, the fitted thickness most frequently corresponds to a higher or lower mode number (m) than the mode number found for the surrounding pixels. Reflectivity spectra of adjacent modes can have the same minimum position in the middle of the measurement range, but the minima positions at the edge of the measurement range would differ significantly (cf. right plot in Fig. 3). Thickness changes by one mode order between adjacent pixels are unphysical in most conditions (1 pixel corresponds to 160 nm lateral distance when using a 40× microscope objective; the approximated thickness difference between two modes is $\mathit{\Delta }d\left(\lambda \right)=\left(\lambda /2n\left(\lambda \right)\right)\approx 230\text{nm}$ at λ = 650 nm). We attribute the jumps in thickness between mode numbers to a deterioration in signal under the extreme conditions outlined above. To understand this better, we compare the minima positions for two adjacent mode numbers m₁ and m₂, with $m_2=m_1+1$ and the central minimum at the same position. The average error between these two sets of minima is 1.33 nm. A measured dataset, which jumps between these two different thicknesses, would therefore have an average error of approximately 1.33 nm/2 = 0.67 nm.

As described above, the average error between experimentally obtained and simulated minima positions is typically around 0.25 nm (we confirmed this for a range of different datasets; data not shown). This is much smaller than the minimal average error of 0.67 nm that can lead to unphysical jumps between modes. Indeed, mode jumps have not been an issue in most of the experiments we have performed so far. In rare cases, however, mode jumps are observed, and we therefore implemented an optional feature that prevents the fitting algorithm from giving out a thickness that differs by more than a certain value from the thickness of adjacent pixels (typically a maximal step height of 50 nm per pixel is used). Although this feature leads to more consistent data, it has been rarely required so far. In future, it might become more important if faster processes are investigated.

For the thickness calculations in Fig. 6, we used a tolerance of 2 nm to show how strongly the measurement parameters influence the average error. However, when using the two narrowest slit settings (FWHM, 0.7 or 0.8 nm) and an exposure time of 1 or 5 ms, or when using the widest possible slit setting (FWHM, 14.9 nm), the average error for 90–99% of the pixels was above 2 nm, and these pixels were therefore not considered in the statistic. In reality, the performance of the algorithm for these extremely unfavorable measurement conditions would therefore be even worse. On the other hand, using the standard measurement and fitting parameters introduced above, we routinely fit >99.99% of all pixels, with the few nonfitted pixels usually occurring at positions where the microcavity has microscopic defects (e.g., because of mechanical damage or because of dust particles captured during the fabrication process).

Increasing measurement speed by tracking one minimum

If fast processes are to be monitored with ERISM, or if multiple fields of view are tracked, one may want to optimize the time it takes to record the required data. In general, the time required for one measurement is a combination of the time it takes for the monochromator to switch between wavelengths and back to the starting wavelength, the exposure time of the camera, and, if required, the time needed to record a phase-contrast image of the cells on the cavity in between wavelength scans. (Usually one wants to take a phase-contrast image after each scan to link any cell movement to the calculated displacement maps.) If images are recorded in 1-nm steps over the 550–750 nm range as described above, this corresponds to the following times: switching the monochromator to 201 different wavelengths, ∼4 s; switching the monochromator back from 750 to 550 nm, ∼1 s; recording 201 images at 10-ms exposure time, at least ∼2 s; and recording one phase-contrast image, ∼0.4 s. Overall, this adds up to ∼7.4 s per scan, which agrees with the measurement achieved in our laboratory using LabView software to operate the entire setup. (In practice, 1 in 10 wavelength scans takes slightly longer, ∼8 s in total, because of time required to prepare buffers for the images and other software operations.)

Most of the measurement time is spent on the exposure time to take reflectance images and for moving the monochromator. Therefore, one possibility to speed up the measurement would be to reduce exposure time and/or increase the speed of wavelength tuning. However, substantial improvements would require a significant increase in the intensity of illumination (which can cause issues with phototoxicity and would require a substantially more expensive light source, e.g., a supercontinuum laser). In addition, recording and storing the image data may become challenging. (The implementation presented here can still run on a standard desktop PC equipped with a conventional solid-state drive but already uses a sCMOS camera that is connected via CameraLink.)

As an alternative, we suggest a scheme in which the cavity thickness is fitted by tracking the position of only one reflectance minimum. This allows a substantial reduction of the wavelength scan range (e.g., to 620–660 nm instead of the 550–750 nm range used so far) and thus results in a fourfold reduction in the time required to acquire one image stack. However, for this scheme to provide the absolute cavity thickness, the mode of interference m needs to be known, which can be achieved by performing one full wavelength scan at the beginning of a measurement series. Afterwards, changes in cavity thickness can be calculated from the spectral position of a single minimum in the reflectance spectra. In addition, thickness changes between frames need to be smaller than half the thickness difference between two adjacent modes (approximately 115 nm). Otherwise, there is ambiguity about whether the thickness increases or decreases between frames. In practice, neither of these prerequisites has been an issue so far.

The one-minimum tracking scheme is visualized in Fig. 7. The green line shows how the position of a single minimum in the 620–660 nm band changes for different cavity thicknesses, always picking the longer wavelength minimum within the investigated range and considering, as before, a thickness range between 7500 and 8500 nm. The minima positions that would be used when fitting the cavity thickness from a full-range wavelength scan are also shown for one cavity thickness.

Figure 7.

Visualization of the one-minimum tracking scheme that uses a reduced wavelength scan range (red dashed lines). The position of the longest wavelength minimum within this range is tracked (indicated by the green line). By contrast, for the standard algorithm, multiple minima across a broader wavelength range have to be tracked (indicated by orange circles for a single cavity thickness). To see this figure in color, go online.

To demonstrate the benefit of the one-minimum tracking approach for measuring a dynamic system, we performed a nanoindentation measurement with an atomic force microscope (AFM). A microbead was attached to the AFM cantilever and indented into a microcavity by ∼130 nm. The cantilever with the bead was then moved laterally across the surface of the cavity at three different speeds (200, 500, and 1000 nm/s) with the bead indented the whole time (Fig. 8). While the cantilever was moving horizontally, measurements were taken at the maximal available acquisition speed (camera exposure time, 10 ms). For the conventional 201-nm full-wavelength scan, the measurement takes 8 s under these conditions; for the one-minimum tracking scheme with a scan range of 41 nm, it takes 2 s. Consequently, for speeds of 200, 500, and 1000 nm/s, the cantilever moves a distance of 1600, 4000, and 8000 nm, respectively, during a conventional 201-nm scan; it moves by 400, 1000, and 2000 nm, respectively, for a 41-nm scan range.

If the cavity thickness changes substantially during a measurement, one expects the reflectance spectra to become distorted, as the actual cavity thickness is different for each of the reflectance images. It would then be unclear which changes are linked to the actual wavelength scan and which are linked to the change in cavity thickness. This is likely to lead to a less accurate fit. In fact, we observe that when using the conventional full-wavelength-range fitting algorithm, the thicknesses fitted to the left and right of the center of indentation take unphysical values if the cantilever moves at high speed. Although a thickness value is fitted for all these pixels, the increase in thickness during the scan increases the spacing between the minima in the reflectance spectra, which leads to a fitted thickness that corresponds to the next lower-order cavity mode. For instance, instead of 8000 nm, a thickness of 7770 nm is fitted (pixels marked in green in Fig. 8 b). On the opposite side of the center of the indentation, the cavity thickness decreases during the scan. In this case, the spacing between the minima is smaller, which results in a fitted thickness that is ∼230 nm larger than the actual value (magenta colored pixels in Fig. 8 b). This effect is somewhat analogous to the Doppler effect in acoustics, in which the frequency of sound waves emitted by a moving sound source appears higher (lower) if the source is moving toward (away from) the detector.

When we analyze our data using the one-minimum tracking scheme, the unphysical thicknesses described above are not observed. In fact, because only one minimum is used to fit the thickness, there is no possibility of encountering a mode jump. Apart from the fourfold increase in frame rate, the one-minimum tracking scheme is thus also more robust against motion-induced artifacts.

A further advantage of the one-minimum tracking scheme is that the total amount of data that needs to be stored and analyzed is reduced substantially. This is particularly beneficial for very long time-lapse measurements; ERISM has already been used to continuously record cell-induced cavity deformations for over 5 days.

A potential drawback of the one-minimum tracking scheme may be a loss in the precision of the fitted thickness compared to the multiple minima fit. To investigate this further, we apply the one-minimum algorithm to calculate the thickness for the simulated reflectance data discussed in Fig. 5 (using the Noise = 500 dataset). As before, we subtract the result from the nominal thickness to obtain the deviation between nominal thickness and experiment and then use the standard deviation of this difference as a measure of how well the fitted thickness matches the nominal thickness. Table 1 compares the results to the conventional algorithm that evaluates all minima in the 550–750 nm range. Without interpolation and smoothing (δλ = 1 nm), the standard deviation for the one-minimum algorithm is more than 7 nm. If data interpolation is added (which is the standard for the conventional algorithm), the standard deviation decreases by a factor of ∼3. (It does not make a significant difference if the signal is interpolated in 0.2 or 0.1 nm steps.) Although the standard deviation of the one-minimum algorithm (2.73 nm) is still more than double the value obtained for the multiple-minima algorithm (1.04 nm), it is comparable to the surface roughness of the microcavity. We therefore conclude that using the one-minimum algorithm does not decrease the precision of the thickness fit significantly and is therefore beneficial for increasing frame rate and reducing data volume.

Table 1.

SD of the Difference between Simulated Data and Fitted Data for the Conventional Algorithm that Considers Multiple Minima across a 550–750 nm Wavelength Range and the Algorithm That Tracks the Position of Only One Minimum

δλ/nm (Interpolation Increment)	σ/nm (Multiple-Minima Fit)	σ/nm (One-Minimum Fit)
1.0	3.50	7.34
0.2	1.05	2.73
0.1	1.03	2.64

For simulated data, please see Fig. 5, noise = 500.

Computation time and extraction of mechanical stress

With the computer hardware used in this study, we achieve computation times of approximately 1 min for 1024 × 1280 pixels when fitting multiple minima of the reflectance spectra and 20 s when using the one-minimum algorithm. Furthermore, we can run multiple instances of the program in parallel on a multicore CPU, and thus the quad-core CPU used here effectively achieves computation times down to 5 s for the one-minimum algorithm.

If necessary, the mechanical stress or force that cells apply can be calculated from the ERISM deformation maps. In our previous work, we demonstrated how this can be achieved by finite element modeling (FEM), validating our FEM results using AFM indentation measurements with a known force (21). For completeness, we briefly summarize the general strategy here. The gold and the thin oxide layers on the top side of the microcavity are stiffer than the elastomer beneath, and their presence therefore broadens the deformation of the cavity in response to a point force exerted on the top surface of the cavity. The stress field at the elastomer-gold interface is also broadened by the stiff gold/oxide layer, just like the deformation map. However, because of conservation of force, when integrating the stress field over an area around a point force, the overall force is preserved, so that the stress at the elastomer-gold interface is a useful measure for the applied stress, as long as the broadening does not lead to an unacceptable reduction in lateral resolution. In our previous study, we found that the lateral resolution of ERISM is 1.6 μm, which is similar to or better than values achieved with other commonly used force-mapping techniques. We therefore model our structure as an 8.5-μm-thick linear isotropic elastic material with a Poisson’s ratio of 0.49 and a Young’s modulus of 300 Pa (obtained by combining AFM, FEM, and ERISM, and confirmed by rheometry). The displacement map measured with ERISM is applied to the top surface of the FEM model, and the Cauchy stress tensor at the elastomer-gold interface is computed. The vertical component of this tensor is then taken as a measure for the stress applied by the cells, even though it is broadened by ∼1.6 μm as described above. (In the future, further regularization or deconvolution could be used to limit this effect, but such efforts are beyond this study on optimizing the measurement conditions and the calculation of deformation maps.) The total force applied by cells or subcellular components can be obtained by integrating over a displaced area. All stress and force calculations we have performed so far were done with COMSOL Multiphysics 5.0. Using the same hardware as described above, computing the stress for a grid with >10⁵ nodes typically takes 2 min. However, we have not optimized these calculations for computation time or memory usage.

Long-term growth-cone measurement with high temporal resolution

In our previous publication, we demonstrated the broad applicability of ERISM for a variety of different cell types (21). For this publication, we have chosen to investigate neural-growth-cone behavior. It has been challenging to measure the forces generated by neural growth cones with TFM at high frame rates because the forces involved are generally weak and the sensitivity of neurons to light can lead to retraction of growth cones (25). As shown above, ERISM is currently capable of achieving a temporal resolution down to 2 s and requires a significantly lower light intensity than the fluorescence imaging used in TFM. Here, we show that we can measure the forces applied by growth cones of primary mouse neurons continuously over several hours.

ERISM and phase-contrast images were taken every 3.5 s over more than 3 h. A linear background plane was calculated from the first ERISM image of the series using the mean values of three 10 × 10 px regions in the image in which no cells were present. This plane was then subtracted from each successive frame. In addition, the displacement at a position at which no cells applied forces was subtracted from each frame over the whole course of the experiment to further reduce changes of the calculated thickness because of any focus drift. In addition, we applied a Gaussian smoothing in lateral direction with standard deviation of four pixels to reduce the impact of surface roughness of the microcavity on the final data. This smoothing causes only a negligible reduction in peak displacements (less than 10%), as all deformations are at least 1.6-μm wide (lateral mechanical resolution of ERISM), which is 10 times larger than the effective pixel size (0.16 × 0.16 μm). We then extracted the maximal and minimal displacement over time using the ImageJ plugin MTrackJ (26). This yielded the vertical displacement and the lateral coordinates for each time point. The lateral coordinates at each time point were also used to calculate the lateral velocity of the point of maximal indentation.

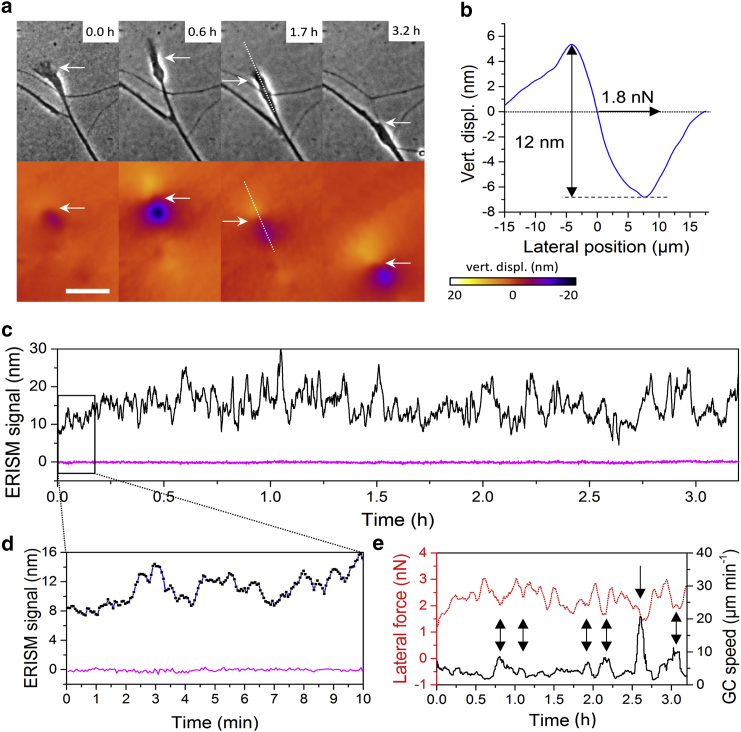
Fig. 9 a shows phase-contrast images and vertical displacement maps for four different time points. Growth cones are usually not thicker than 1 μm (27) and hence, for geometrical reasons, are unlikely to exert a significant vertical force. Indeed, a cross section of the vertical displacement (Fig. 9 b) reveals the characteristic push-pull twist that we previously observed and quantified for horizontal forces applied with an AFM (21). Using the previously established linear correlation between vertical twist (i.e., height difference between point of deepest indentation and point of maximum) and the lateral force (150 pN per nanometer of vertical twist), we find that the twist of 12 nm in Fig. 9 b corresponds to 1.8 nN of lateral force. This value is comparable to the results of Polackwich et al. (25), who measured peak forces between 2 and 5 nN when investigating the forces exerted by five different growth cones.

Figure 9.

Data summarizing the measurement of a neural growth cone with ERISM. (a) Phase-contrast images and corresponding displacement maps for four different time points are shown. Scale bar, 20 μm. The white arrows are reference points between phase-contrast images and displacement maps. (b) The profile of the vertical displacement at the position indicated by the white dotted line in (a) is given. The ERISM signal is 12 nm, calculated by subtracting the value at maximal pushing from the value at maximal pulling. The lateral force has been calculated as explained in the text. (c) The ERISM signal (black) and noise (at a position where no forces are exerted by growth cone, magenta) are shown for the 3.2 h of the experiment. (d) A close-up of ERISM signal and noise level over 10 min. Black squares indicate the actual data points, and the blue line is a guide to the eye and corresponds to the line in (c). (e) The lateral force (red dotted line) and growth cone speed over time (black line, smoothed with 5-min gliding average) are given. The arrows indicate prominent anticorrelations between lateral force and growth cone speed. To see this figure in color, go online.

In Fig. 9 c, we show all data points for the vertical twist the growth cone exerts over time. In addition, we measured the vertical displacement at a position at which no forces were applied to compare measurement-to-measurement variations (noise, magenta line) with the actual signal from the growth cone. Because of the long measurement time, the details of the ERISM signal at shorter timescales are not visible in Fig. 9 c. Therefore, we show a close-up of the ERISM signal and the noise over 10 min in Fig. 9 d. The noise alternates between 0.5 and −0.5 nm. Clearly, the ERISM signal shows changes of more than 20 nm over the whole duration of the experiment (cf. Fig. 9 d) but also shows smaller changes clearly above the noise level, e.g., ∼5 nm over 2 min or even 1–2 nm changes that happen over less than 30 s (cf. Fig. 9 d).

Fig. 9 e shows the lateral force applied by the growth cone that was obtained from the vertical twist as described above. This shows that over time, the force applied varies between ∼1 and 3 nN. Fig. 9 e also compares the lateral force to the migratory speed of the growth cone. Both curves consistently follow a similar, but mirrored, shape over the 3.2 h of the experiment. Where the lateral force shows a dip, in most cases, the speed shows a peak. This means that at higher growth-cone speeds, the exerted force is lower, consistent with earlier observations on macrophage extension (21).

Conclusions

We have given an in-depth description of the data analysis procedures used in ERISM and of the considerations involved in selecting the measurement parameters. We explained how the spectral position of reflectance minima in the experimental data is compared against a database containing calculated minima positions for all possible thicknesses of the microcavity. The average absolute difference between experimental and calculated minima positions (average error) was used as the fitting parameter that is minimized to determine the actual thickness of the cavity for each pixel in the field of view.

To improve resolution, interpolation and smoothing of the experimental data were introduced. This allowed localizing the spectral position of reflectance minima with an accuracy better than the 1-nm step size used in the experiment, analogous to localization techniques used in superresolution microscopy. Using simulated data for testing, it was found that interpolation and smoothing can improve the deviation between the fitted and the nominal thickness by approximately threefold: to σ = 0.44 nm for a noise-free case and to σ = 1.03 nm if a realistic amount of noise is added to the simulated data. Interpolation increments of δλ = 0.2 nm and smoothing by a 5-nm moving average filter were found to be the optimal combination of parameters.

We also optimized the measurement conditions, in particular the camera exposure time used when recording the reflectance of the microcavity and the spectral width of the monochromatic light used for illumination. Although a number of settings gave good results, we concluded that 10-ms exposure time and an FWHM spectral bandwidth of 4.6 nm provide near-ideal performance for most situations. To improve the robustness of the measurement and to prevent artifacts and unphysical results, we introduced a tolerance parameter that ensures that the cavity thickness is set to “not a number” if the agreement between experimental and calculated minima is poor. We also introduced a feature that suppresses the occurrence of mode jumps by limiting the maximal thickness difference allowed between neighboring pixels. We find that a tolerance and maximal thickness step of 1 and 50 nm, respectively, very effectively prevent the occurrence of artifacts. With the above measurement and fitting parameters, over 99.99% of the pixels in an ERISM map are routinely fitted with the correct cavity thickness.

We have introduced a modification of the ERISM measurement to improve acquisition speed and reduce the amount of data that needs to be stored and analyzed. By recording reflectance images over a reduced wavelength range of 41 nm instead of 201 nm and analyzing the position of only one reflectance minimum, the time needed to acquire each thickness map was reduced by fourfold to ∼2 s. We demonstrated the benefit of this approach by analyzing the deformation profile induced by an AFM indenter that is moved laterally across the ERISM substrate.

Finally, we used the high force sensitivity of ERISM to measure the forces exerted by a neural growth cone with high temporal resolution over 3 h. Despite recording over 3000 ERISM maps, we did not observe any phototoxic effects, consistent with the low light intensity used by ERISM (<150 μW cm⁻²). The growth cone applied lateral forces of ∼1–3 nN, and these were found to fluctuate by different amounts over different timescales. We also found that forces were lower when the velocity of the growth cone was high and vice versa.

The algorithm described here has been implemented in Cython/Python and is freely available to the community for noncommercial use. The data presented in this manuscript and the software to perform the Cython/Python algorithm described here can be accessed at https://doi.org/10.17630/ec95b62c-ab3e-4331-9c1d-f6af1ab69f12. We welcome feedback and further developments.

Author Contributions

P.L. performed all experiments, data analysis, and developed ERISM-Calc with input from N.M.K. and M.C.G. P.L. and M.C.G. wrote the manuscript with input from N.M.K.

Editor: Jochen Guck.