Using Machine Learning Algorithms to Predict Risk for Development of Calciphylaxis in Patients with Chronic Kidney Disease

Abstract

Calciphylaxis is a disorder that results in necrotic cutaneous lesions with a high rate of mortality. Due to its rarity and complexity, the risk factors for and the disease mechanism of calciphylaxis are not fully understood. This work focuses on the use of machine learning to both predict disease risk and model the contributing factors learned from an electronic health record data set. We present the results of four modeling approaches on several subpopulations of patients with chronic kidney disease (CKD). We find that modeling calciphylaxis risk with random forests learned from binary feature data produces strong models, and in the case of predicting calciphylaxis development among stage 4 CKD patients, we achieve an AUC-ROC of 0.8718. This ability to successfully predict calciphylaxis may provide an excellent opportunity for clinical translation of the predictive models presented in this paper.

Introduction

Calciphylaxis, also known as calcific uremic arteriolopathy, is a highly morbid disorder that presents with necrotic lesions of the skin resultant at least partially from ischemia caused by calcification of the small and medium-sized arteries¹. The mortality rate of calciphylaxis has been measured in excess of 50% within one year of initial diagnosis². One of the most commonly associated comorbidities with calciphylaxis is chronic kidney disease (CKD)¹. In particular, calciphylaxis is found most often among patients in the late stages of CKD and end-stage renal disease (ESRD)¹. While calciphylaxis was originally named by Hans Selye in 1962, there is still much that is unknown about its origin and risk factors. Known risk factors include: CKD, ESRD, mineral and bone disorders, diabetes mellitus, hyperphosphatemia, female gender, obesity, warfarin use, and ethnicity³.

Currently, calciphylaxis is identified by histological examination of excised tissue. This examination and confirmation of calciphylaxis occurs after a patient has already developed the clinical manifestations of this highly morbid disease. Currently, there are no risk assessment models used in clinical practice for identifying patients at risk for development of calciphylaxis. In this work, we aim to produce such a risk assessment model for patients with CKD. A diagnosis of CKD is accompanied by regular monitoring through frequent patient contacts with their healthcare system. The translation of a calciphylaxis risk assessment model targeted to patients with CKD could allow for intervention which may prevent the disease.

In recent years, the use of electronic health records (EHRs) has increased in healthcare systems⁴. This wealth of data has created unprecedented opportunities for computational approaches to not only augment existing knowledge of various diseases but also produce predictive models to assess patient risk. Diseases such as breast cancer⁵ and myocardial infarction⁶ have already been successfully modeled using machine learning algorithms. Machine learning, a branch of artificial intelligence, focuses on producing algorithms that learn rules or relationships about a set of variables to predict the value or outcome of an unknown variable. In the context of healthcare data, machine-learned models can be used to predict the disease risk of a patient from the information present in their health record. In some cases, the models produced by a machine learning algorithm can be manually inspected to understand which variables suggest different patient outcomes. In this paper, we present the use of two machine learning algorithms, lasso-penalized logistic regression⁷ and random forests⁸, in the context of prediction and risk factor analysis for calciphylaxis. We present these methodologies on several subpopulations of CKD and ESRD and show that they produce a strong prediction of calciphylaxis.

Experimental Methodology

Data

Our dataset is derived from patient visits to the Marshfield Clinic, a health care system that serves Northern and Central Wisconsin. Data include diagnosis codes, in the forms of both ICD-9 and ICD-10 codes, demographic information, laboratory values, vital sign readings, procedures, and medications present on patient records. Apart from age and gender, all features were initially extracted as counts, that is the number of times an event occurred on a patient record from the start of their record to the censor date which we later define. These values were gathered from patients identified as case or control patients for our experiments. Case patients were manually identified by their attending surgeon, who confirmed calciphylaxis diagnosis via inspection of patient records and histological examination of excised tissue. Control patients were required to have no diagnosis codes indicative of calciphylaxis in their records including ICD-9 codes 275.49 and 709.1, and ICD-10 codes L95.9 and E83.59. Moreover, for both case and control patients, we required a minimum of 10 unique diagnosis codes on their records. The minimum data requirement was implemented to ensure sufficient patient history for prediction.

Case-Control Matching

We present research on 5 different CKD patient populations: patients with any stage of CKD, which we refer to as “any stage”, patients with stage 3 CKD (stage 3), patients with stage 4 CKD (stage 4), patients with stage 5 CKD (stage 5), and patients with stage 5 CKD requiring chronic dialysis, which we refer to as end-stage renal disease (ESRD). In all experiments, we attempted to match up to 10 control patients for each case patient. We chose a 10-to-1 ratio based on the small number of confirmed cases. For the purposes of illustrating our case-control matching scheme consider two patients, Bob (case) and Alex (control), who will become an eventual case-control pair. Bob was manually identified as a case patient via histological examination and inspection of his patient record. Furthermore, we require Bob to have some stage of CKD and place him in the appropriate population. We then search for candidate control patients to match with Bob who have a birthdate within 30 days of Bob’s and the same gender. Let Alex be one of these candidate control patients. Alex must have the same stage of CKD as Bob on or before Bob’s calciphylaxis diagnosis date. Furthermore, Alex must have entries on his record both before and after Bob’s calciphylaxis diagnosis date. This control data straddling of the case diagnosis date allows us to ensure that the control patient was alive and present in the Marshfield system during the case patient’s diagnosis. Now that we have identified Alex as a control match for our case patient, Bob, we finally truncate both their patient records by removing all data following 30-days prior to Bob’s calciphylaxis diagnosis date. This truncation allows us to control for class-label leakage and ensure we are performing a prediction task. This case-control matching procedure was performed up to 10 times for each case patient. Details of these patient populations are in Table 1.

Table 1.

Description of the five experimental patient populations. For each population, we describe the ICD-9 and ICD-10 diagnosis codes associated. Moreover, we present the number of case and control patients for each population and the total number of non-zero features on their records that were included in the model.

	Any Stage	Stage 3	Stage 4	Stage 5	ESRD
ICD-9 Code(s)	585-585.9	585.3	585.4	585.5	585.6
ICD-10 Code(s)	N18-N18.9	N18.3	N18.4	N18.5	N18.6
# Features	9,288	5,037	6,662	5,864	6,974
# Cases	38	10	15	12	17
# Controls	363	100	148	117	165
Total Patients	401	110	163	129	182

Feature Construction

In addition to our experimentation based on the stage of chronic kidney disease, we explored the effects of binary versus continuous feature representations. The raw dataset was structured such that each non-demographic variable, e.g., a lab test, had a value for the number of times the patient had received that particular variable on their record. The counts for each variable were done from the start of the patient’s record until an experiment-specific date, e.g., their first entry of a particular stage of chronic kidney disease. One potential concern about using count data is the likelihood of chronically sick patients to have an increased number of healthcare encounters. In this way, uncorrelated variables that are recorded often such as a height measurement vital could become inappropriately correlated with disease status. This was of particular concern as calciphylaxis tends to occur in much sicker patients. For this reason, we also explored the use of binary features. We constructed these features by setting any non-demographic feature value to 1 if the patient had ever had it entered on their record, and 0 if they had never had it on their record. In the case of continuous features, we simply scaled the counts for each feature to be between 0 and 1, which was of use when comparing the relative importance of features when evaluating our models.

Model Construction Methods

We explored the predictive capacities of two different machine learning models: random forests and logistic regression. Random forest models are well known for both their strong accuracy and their resilience to high dimensional data. Furthermore, random forests can capture nonlinear interactions in data. While random forests are strong predictors, they are often difficult to interpret, and interpretation is often critical in a healthcare context. For this reason, we additionally explored logistic regression models. Because logistic regression is not inherently resilient to high dimensional data, we employed lasso-penalized logistic regression, which utilizes an L1-regularization term in the objective function of the model to penalize features that were only marginally informative and to encourage a small set of strongly predictive features in the final model. This is necessary not only to obtain comprehensible models but also to obtain accurate ones, as the patient populations we modeled included thousands of unique features and logistic regression without some form of dimensionality reduction can perform very poorly in such situations. The L1 or “lasso” penalty is a widely-used approach to dimensionality reduction in regression.

For both the random forest and the logistic regression models we performed a case-control matched leave-one-case-out cross-validation. For each experiment, we chose fc-folds, one fold for each of the k case patients and its matching controls. In this procedure, for each round of cross validation one fold was chosen to be left out and was comprised of a single case patient and the up to 10 control patients matched with it. In the case of random forests, models were constructed using the remaining k — 1 folds of training data. We built 500 decision trees for each forest and used the square root of the number of features as the number of features to consider at each split. Trees were grown to leaf purity where possible and splits were chosen via Gini gain that was calculated in a balanced fashion in that case patients were weighted more heavily such that their total combined weight equaled that of the control patients.

For logistic regression, we performed an additional layer of internal leave-one-case-out cross-validation to tune the penalty coefficient for the L1 regularization term. That is, we performed an internal k — 1 rounds of internal cross validation with 1 tuning fold and k — 2 training folds. In this tuning procedure, we consider 10 different penalty values logarithmically spaced between 10^-4 and 10⁴. Each penalty value was evaluated via an internal cross-validation layer and the optimal penalty value was chosen based on the performance of the various models as judged by a weighted accuracy measurement that ensured equal combined weights for the cases and the controls. Thus, for each external cross-validation fold, the remaining folds were used to select a penalty value and a new predictive model was trained on those folds and finally evaluated on the original held out fold. Logistic regression models were all constructed using a balanced class weight approach like that employed in the random forest models.

For each of the 20 choices of CKD population, model family, and feature type, e.g. predicting CKD stage 4 with random forests using binary features, we repeated the model construction 30 times. To account of the skew of our data, for both, random forest and logistic regression we constructed the models with the “balanced” class-weight option in the scikit-learn library. These replications were done because random forests are stochastic by nature, and logistic regression may have multiple equally good solutions to their optimization problem, both of which can produce varying results across multiple runs from the same data set. In this way, we could better estimate the predictive quality achieved under each experimental condition.

Model Evaluation Methods

Model evaluation is done quantitatively via the construction of receiver operating characteristic (ROC) curves and precision-recall (PR) curves. While we report both the area under the ROC-curve (AUC-ROC) and PR-curve (AUC-PR), we primarily use the AUC-ROC as a numerical evaluation of the quality of our models. We do this because AUC-ROC provides a metric of efficacy that is unbiased by the class skew of a dataset. Because we attempt to achieve a 10-to-1 control to case ratio this may not be representative of the true population skew, and thus we provide a fairer analysis of our results via ROC-curves⁹. For our best performing model and feature combination, we present both ROC- and PR-curves for completeness but do not use them in ranking the quality of the models. Both ROC-curves and PR-curves were constructed for each model in a similar fashion. For a single repetition of a single experiment we first produced a vector of predicted probabilities corresponding to model estimated risk for each patient. We produced this vector during the leave-one-case-out fc-fold cross validation by using the model built on the training folds to predict the labels of the test fold. Our final predicted probability vector was the union of these predictions as each patient was only in a test fold once. From these predicted probabilities and the true class labels we constructed either a ROC- or PR- curve in the typical fashion. Then across the 30 repetitions for each experiment, we performed vertical averaging of the 30 resulting curves to yield a final curve.

For each of the five experimental conditions, we wish to know which of the four models performed best. We evaluated model performance via a sign test and evaluated 12 hypotheses which were of the form: “Binary feature random forest is significantly better than binary feature logistic regression”. These twelve hypotheses were all of the unique ordered pairs of the four models drawn without replacement. For each experimental condition, we chose an experiment-wide p-value of α = 0.05 as our threshold for significance. We performed a Bonferroni correction and required $p_i\le \frac{0.05}{12}$ for an individual hypothesis to be significant. If a model was significantly better than the three other models, then we considered it to be the best model for that experimental condition.

Our p-values for each hypothesis were calculated via the aforementioned sign test, the details of which we provide now. Because the 30 repetitions of each experimental condition and model are not truly independent of one another, we cannot use bootstrapping to calculate confidence intervals on our AUCs. Instead, we use a sign test to determine if a model is correct more often than another model a statistically significant number of times. For each model, we first construct a ROC-curve in the fashion described above. To convert the probabilities from each algorithm to labels, we choose a threshold corresponding to an 80% true positive rate, or recall, for our algorithms. Because of the serious nature and high mortality rate of calciphylaxis we chose 80% recall to reflect the significant cost difference between false negatives and false positives. Thus, for each experiment, the threshold corresponding to 80% recall was used to label predictions as either positive or negative. For every patient we then checked the label assigned by both models and its true label, if both models assigned the same label, that patient was considered a tie and not counted, however, if the models differed then the first model received either a win or a loss if it was correct or incorrect respectively. Then, each hypothesis was tested by first counting n_wins, the number of times the first model predicted a patient correctly and the second model predicted that patient incorrectly, and n_loss, the converse statement. Finally, we calculate the cumulative distribution of the binomial function Binom (n_wins,n_loss, 0.5) to determine a p-value for a particular hypothesis.

We perform a qualitative evaluation of our models by inspecting the top performing features returned from our models. In the case of random forests, we used the approach detailed in Breiman 1984 to determine feature importance values via the Gini importance¹⁰.

Results

In general, we find that we achieve superior performance predicting calciphylaxis from a specific stage of CKD compared to an arbitrary stage. We present in Table 2 the precise ROC-AUC values achieved in each experiment. We note that in general random forests outperform logistic regression and that use of binary features roughly outperforms the use of continuous features. In two of the five experimental conditions, we found random forests with binary features to outperform the other three approaches with a statistically significant difference.

Table 2.

AUC-ROC, AUC-PR, Accuracy, and Precision @ Recall = 80% values for each experimental condition and algorithm. For each experimental condition, the algorithm that performed best is highlighted in bold if it is statistically significantly better than the other three algorithms as determined by a sign test. Note that just binary random forests achieved statistical significance and did so in two experimental conditions. For CKD stage 4 binary random forests outperformed its competitors with p ≤ 3.78e – 04. For ESRD stage 4 binary random forests outperformed its competitors with p ≤ 1.92e – 04.

Stage	Model	Features	AUC-ROC	AUC-PR	Accuracy	Pre. @ 80%
3	Logistic Regression	Binary	0.789	0.189	0.545	0.190
		Continuous	0.785	0.215	0.545	0.164
	Random Forest	Binary	0.846	0.261	0.545	0.212
		Continuous	0.847	0.279	0.545	0.230
4	Logistic Regression	Binary	0.791	0.190	0.515	0.188
		Continuous	0.635	0.125	0.528	0.131
	Random Forest	Binary	0.872	0.292	0.546	0.269
		Continuous	0.791	0.200	0.546	0.194
5	Logistic Regression	Binary	0.707	0.194	0.543	0.164
		Continuous	0.689	0.169	0.532	0.195
	Random Forest	Binary	0.796	0.212	0.535	0.248
		Continuous	0.770	0.184	0.535	0.213
ESRD	Logistic Regression	Binary	0.746	0.168	0.538	0.168
		Continuous	0.750	0.198	0.549	0.170
	Random Forest	Binary	0.858	0.440	0.538	0.286
		Continuous	0.838	0.425	0.538	0.244
Any	Logistic Regression	Binary	0.713	0.188	0.534	0.156
		Continuous	0.734	0.162	0.541	0.173
	Random Forest	Binary	0.738	0.199	0.536	0.151
		Continuous	0.725	0.185	0.536	0.156

Given the strong performance of random forests using binary features, we chose to visualize the ROC- and PR-curves for this model and feature engineering scheme across the five experimental conditions and present this in Figure 1. We note that the models predicting CKD at a specific stage appear to be clustered together and roughly separated from the ROC-curve representing prediction at an arbitrary stage of CKD. Additionally, there appears to be some separation between the PR-curve representing prediction of ESRD as compared to the other stages of CKD.

Figure 1.

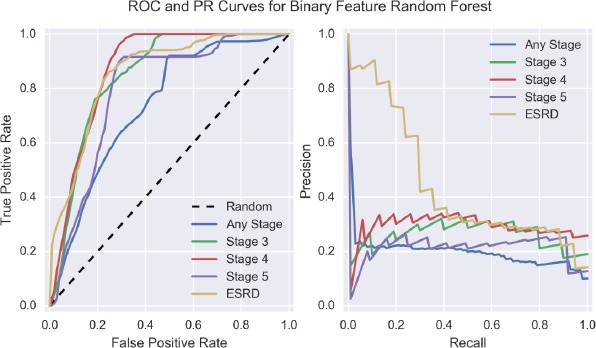
ROC- and PR-Curves for binary feature random forest across the five experimental conditions.

For each of the five experimental conditions, we present in Table 3 the top 10 features used in prediction for the binary feature random forest. We note that many of these features are strongly related to many already known risk factors for calciphylaxis. Moreover, these features are suggestive that we successfully control for CKD, as few CKD related features appear among the top features for these models. We find that there may be some temporal confounding, as the feature “Prescription transmit via erx system” is present in the top ten features for both stage 4 and stage 5 models. This particular feature can appear when a model is attempting to distinguish cases and controls temporally, as the introduction of electronic transmission of prescriptions can be used to infer if a patient’s data is from a more recent period by inspecting if this feature is present on their record.

Table 3.

Ranking of 10 top random forest model features for each of the 5 CKD experiments: any CKD stage, stage 3 CKD, stage 4 CKD, stage 5 CKD, and ESRD. For each experiment, feature importance values were averaged first across each of the k-folds for cross-validation, and then those values were averaged across the 30 repetitions completed to produce a final importance value for each feature.

Rank	Any Stage	Stage 3	Stage 4	Stage 5	ESRD
1	Hepatitis B Surface Ag	Obesity	Anemia in CKD	Obesity	Thyroxine (T4)
2	Anemia inCKD	Lactescence/Chylomicrons	Morbid Obesity	Morbid Obesity	Obesity
3	Secondary Hyper-parathyroidismof Renal Origin	Chylomicrons	Thyroid Stimulating Hormone-Reg’l C	Parathyroid Hormone (PTH),1-84	Amylase-Pancreatic
4	Direct Microscopy	ALT (GPT)	Obesity	Radiologic exam knee complete 4/more views	Age
5	Ulcer of Lower Limb, Unspecified	Differential Polychromatophili	Chylomicrons	Instrument Neutrophil #	Frac.O2Hb, Arterial
6	Iron Defic Anemia Nos	Differential Poikilocytosis	Lactescence/Chylomicrons	Age	Arthropathy, unspecified
7	Hepatitis B Surface (HBs) Ab	Uric Acid, Blood	Thyroxine (T4)	Uric Acid, Bld	Prothrombin Time(PT)
8	% O2 Saturation	Differential Activated Lymph	Secondary Hyper-parathyroidismof Renal Origin	Non-HDL Cholesterol	Abdominal Pain
9	Differential Poikilocytosis	Sodium serum plasma or whole blood	Prescription transmit via erxsystem	Prescription transmit via erxsystem	Chronic Liver DiseaseNec
10	Blood Urea Nirtrogen-Post-Dial	Platelet Estimate	Hypercholesterolemia	Skin Suture Nec	Blood count complete automated

Discussions

In this work, we explored prediction of calciphylaxis at various stages of CKD, through the use of random forest or logistic regression models and either binary or continuous features. We find that overall prediction of calciphylaxis is achievable with strong results and note that in each of the experimental conditions in which we predict calciphylaxis during a specific stage of CKD, we find at least one model with an AUC-ROC of nearly 0.8 or above. Such AUC-ROC values suggest models of a high quality capable of predicting calciphylaxis with reasonable efficacy. Given the high mortality rate of calciphylaxis, we feel that early prediction of calciphylaxis would be of great benefit for physicians who wish to monitor patient risk. In particular, we find some of our strongest results when predicting calciphylaxis using binary feature random forests for the experimental conditions of stages 3 and 4 where patients have moderate to advanced CKD.

It is worth noting that for a given task and feature type, random forests nearly always outperformed logistic regression. We feel that this is likely due to the ability for random forests to capture nonlinear interactions in data. Furthermore, for a given task and model type, binary features achieved AUC-ROC values that were typically equal to or better than those achieved with the use of continuous features. This is of interest as our constructions for binary and continuous features ensured that continuous features had strictly greater information. For every feature other than age, the binary feature could be obtained from the continuous feature by thresholding such that a continuous feature of value 0 becomes a binary feature of value 0, and a continuous feature of value anything greater than 0 becomes a binary feature of value 1. In the case of random forests, this could be expressed as splitting on a particular continuous feature, f_i, with f_i < 0 being the logical test for indicating which branch to choose. The poorer performance from continuous features suggests that there may be some overfitting occurring. By using binary features, we are limiting the expressiveness of our models, and such an action could cause improvement in the case of a model that is overfitting.

In our analysis of the top performing features for the various models and experimental conditions, we found that features could be grouped roughly into one of three categories: previously known calciphylaxis risk factors, indicators of potential confounding in the model, or potential calciphylaxis risk factors with minimal or no previous support. Of those risk factors for calciphylaxis that are previously discovered, our models pick up most strongly on obesity and its related risks, anemia/low iron, and hyperparathyroidism. It is worth noting that we see minimal use of CKD features, which suggests that our method for controlling for CKD was largely successful. There are some features which suggest either temporal confounding. In particular, the feature “Prescription transmit via erx system” is likely being used to separate patients by how recently they visited the Marshfield Clinics. Such a feature can be exploited during cases of temporal confounding as the use of an electronic prescription transmittal system is a relatively recent addition to workflows in healthcare systems. Finally, we find some of our top features are related to liver disease and/or liver function, a relationship that is not strongly established with calciphylaxis. In particular, we see both various liver function labs and testing for hepatitis B as strong features for predicting calciphylaxis.

Conclusion

Patients suffering from late-stage CKD and ESRD are known to be at a much higher risk for calciphylaxis¹, a vascular disorder with a one-year mortality rate in excess of 50%². By identifying at-risk patients, we provide an opportunity for these patients to take actions to mitigate their risk factors and avoid a potentially deadly disease. Additionally, by modeling calciphylaxis to predict patient risk, we invite the opportunity to discover more about the potential risk factors of what is a poorly understood disease. In this work, we explored prediction of calciphylaxis at various stages of CKD, through the use of random forest or logistic regression models and either binary or continuous features. From this work, we found that random forests using binary features tended to outperform other methodologies and that we could typically predict calciphylaxis with strong efficacy. Furthermore, we found that our models not only largely exploited known risk factors for calciphylaxis but also found some evidence for a previously unsupported connection to liver function and hepatitis. We note that our results show these models to be of high quality and intend to explore the potential for translating these models to a clinical setting, where they could be used to identify patients who are of higher risk for developing calciphylaxis.

Financial Support

The authors gratefully acknowledge the support of the NIH BD2K grant: U54 AI117924, the NIG NIGMS grant: R01 GM097618, the NLM training grant: 5T15LM007359, and the NIH NCATS grant: UL1 TR000427.