The Ad-Hoc Uncertainty Principle of Patient Privacy

Abstract

The Health Information Portability and Accountability Act (HIPAA) allows for the exchange of de-identified patient data, but its definition of de-identification is essentially open-ended, thus leaving the onus on dataset providers to ensure patient privacy. The Patient Centered Outcomes Research Network (PCORnet) builds a de-identification approach into queries, but we have noticed various subtle problems with this approach. We censor aggregate counts below a threshold (i.e. <11) to protect patient privacy. However, we have found that thresholded numbers can at times be inferred, and some key numbers are not thresholded at all. Furthermore, PCORnet’s approach of thresholding low counts introduces a selection bias which slants the data towards larger health care sites and their corresponding demographics. We propose a solution: instead of censoring low counts, introduce Gaussian noise to all aggregate counts. We describe this approach and the freely available tools we created for this purpose.

Introduction

Patient Privacy in “De-identified”, Aggregate Data

The Health Information Portability and Accountability Act (HIPAA) allows for the exchange of fully de-identified patient data with many fewer restrictions than data in which patient identity can be determined. Therefore, with the proliferation of large-scale clinical data research networks (e.g. in PCORnet[1] and ACT[2]), transmitting de-identified data is an ideal way to quickly assess study feasibility without being slowed down by regulatory approvals regarding patient privacy.

Unfortunately, assuring that any data set is de-identified is extremely difficult. [3] HIPAA defines 18 distinct identifiers that must be removed from data to ensure it has been de-identified. However, the 18th identifier is “other unique identifying numbers, characteristics or codes,” thus leaving the meaning of de-identification virtually open ended and defined by the ability of a clever adversary to re-identify patient data.

Therefore, even data that is presented in aggregate and not at the patient level could be identifiable if various information in the aggregate data can be combined with personal or public knowledge to re-identify a single patient. Even more insidious is when an aggregate count of patients is counting only one patient. For example, if the number of patients hospitalized greater than six times in the last three months who are black, transgender, and have AIDS equals one, then we know not only enough information to identify the patient but also various demographics about them.

In order to deal with this potential lapse in the protection of patient information, PCORnet has thus far taken a censoring, or thresholding, approach, censoring all aggregate counts in a typical query report that are < 11 to be replaced by a ‘T’. Because individual patients are difficult to identify from sufficiently large aggregate patient counts, one way to prevent patient identification is simply to censor all counts smaller than a predetermined value.

When responding to PCORnet queries, institutions are given the option to censor aggregate counts below a certain threshold. The PCORnet Data Committee has standardized this threshold to <11 patients, but the threshold can be manually adjusted by site researchers prior to submission of results. With the threshold at <11, for example, all counts between 1-10 patients are replaced by a “T”.

Inspection of the results of recent queries has revealed a number of instances where censoring to a threshold is not enough to adequately mask the small aggregate patient counts. In some cases, although small counts are properly censored by a “T”, the “T” can be easily calculated to the exact value below the threshold.

In this manuscript, we analyze situations where this occurs and propose a solution that offers advantages to all parties. This solution is what we dub “The Ad-Hoc Uncertainty Principle of Patient Privacy.”

Methods

Problems with a Censoring Approach

In some cases, although small counts are properly censored by a “T”, they can be easily calculated to the exact value using other available counts. We have seen this in two particular following situations.

Attrition Tables, in which inclusion and exclusion criteria are provided and show the exact number of patients excluded and remaining at each step of the cohort identification process [see Table 1]. In this example, by subtracting the excluded patients from the remaining patients from the previous step, the value of T can be determined. So, for example, the T in Sample1 is 100-98=2 patients.

Table 1:

Attrition Table Example, in which it is possible to infer T.

Patient Characteristics Tables, which display the demographic distribution of the base patient population [see Table 2]. Because all values in each enumerated criteria list are shown, a single T can be inferred by taking the total population count and subtracting every visible criteria count. So, for example, the T in Sample1 is 100-50-49-0=1 patient.

Table 2:

Patient Count by Characteristics, in which it is possible to infer the Ts.

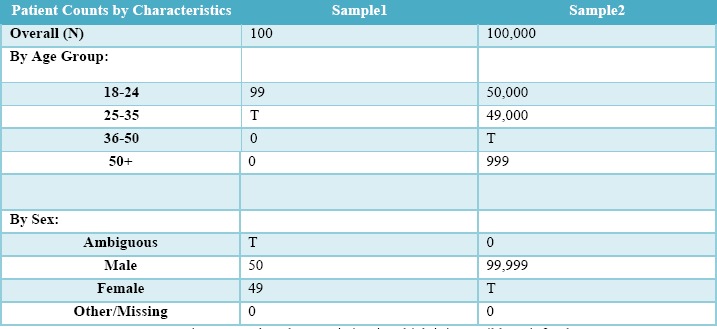
In certain query results, PCORnet query results are not obfuscated at all, as part of an attempt to understand whether variation in distributions may be due to population variability or population size. While PCORnet does not intend to use individual site results (only results aggregated across all sites), these are still sent to the PCORnet Coordinating Center without any low cell count masking, thus potentially exposing patient identity. While PCORnet’s study goals are important, protecting patient information is paramount.

Proposed Solution

Various solutions can remedy these problems while retaining the ability to study exact counts of aggregate numbers, including a round-robin data aggregation approach[4] and a homomorphic encryption approach [5]. However, since PCORnet is interested in using these queries to study population trends, rather than specific numbers, we recommend an obfuscation approach utilizing Gaussian noise [6]. This is far easier to implement (both technically and logistically) than other approaches.

Specifically, we propose that PCORnet obfuscate low aggregate counts by adding Gaussian noise to all categorical variable results – a random integer based off of the Normal Gaussian distribution with a mean of 0 and a standard deviation of 2.5 for categorical variables. Refer to Figure 1 below to see the probability distribution for possible random integers this discrete Gaussian could produce. This procedure entirely removes the need to mask low aggregate counts with a “T”

Figure 1.

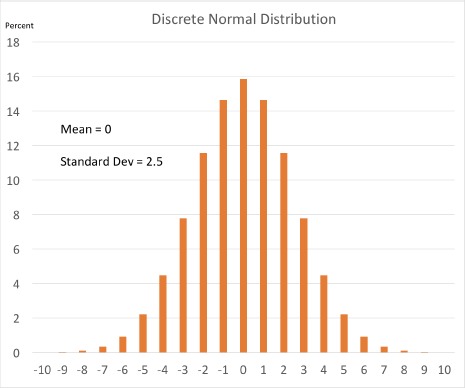
Probability distribution for the discrete normalized Gaussian that we propose to use as noise.

Gaussian noise has been previously recommended as an obfuscation technique to mask patient identities [6]. In thispaper, Murphy et al. demonstrated that a Gaussian probability distribution was superior to constant or triangular-shaped distribution being that it took longer for the running average of patient counts to converge on the true mean during their Monte Carlo simulations. These simulations represent a simulated attack, where a hacker runs the same query multiple times while taking the running average of these counts until the running average consistently stays within +/- 0.5 of the true patient count. They found that while using a standard deviation of 1.33, it took on average about 12.3 repeats before the running average converged on the true value. Using python, we repeated this simulation using varying standard deviations. We found that using a standard deviation of 2.5, an attacker would need to issue on average about 24 queries before the running average of these counts would converge on the true value. We find this to be a reasonable obstacle to prevent patient identification within PCORNet centered queries, because a query would need to be repeated on the order of 20 times before there is any likelihood of getting the true value. It is unlikely that the PCORnet Query Tool, even with multiple queries potentially interacting with the same subpopulation, will ever reach convergence. (This is especially true considering that data sets are refreshed quarterly, at which point the actual count will change.) Other applications with much higher potential query repeatability might require a different value.

There is a well-understood and standard procedure for adding numbers with associated Gaussian uncertainties. The measurement uncertainties (i.e. uncertainties due to fuzzing) must be propagated down to the aggregate sum.

Error sum propagation can be calculated as follows. For a sum f of independent counts A and B where:

$$f=A+B$$

Then the corresponding square of the uncertainty ${\sigma }_f^2$ for this sum is:

$${\sigma }_f^2={\sigma }_A^2+{\sigma }_B^2$$

Therefore, for, sites that use the same fuzzing uncertainty, the uncertainty of the sum of their counts is equal to the square root of the number of sites multiplied by the Gaussian uncertainty σ_A:

$${\sigma }_f={\sigma }_A\sqrt{x}$$

The patient count uncertainty grows with the square root of the number of sites in the final aggregate sum.

Results

We have written a SAS fuzzing script designed to be applied to SAS data sets resulting from queries to the PCORNet data marts. This script takes the following approach:

1. Low counts below a certain threshold (i.e. 11) are identified on all of the data output by a PCORnet analytic query, after the query analysis (so all of the analysis is already completed on the real counts before this occurs).

2. The low counts' corresponding distributions such as their percentile and cumulative distributions are omitted using a similar method to PCORnet's current low cell count masking (i.e. replacing the number with ‘T’). These must be omitted since the stratification of patients could narrow results to a single individual, particularly in cases of very low aggregate counts.

3. All of the remaining counts are fuzzed using the Gaussian fuzzing technique. Specifically, for each aggregate count in the data set, the computer picks a randomly-generated number based off of a Gaussian distribution with a mean of ‘0’ and a standard deviation of ‘2.5.’ That randomly generated number is rounded to the nearest integer, and then added to that aggregate count. This is repeated for each aggregate count until every aggregate count has been ‘fuzzed.’

Using this approach, no aggregate counts and only the sensitive distributions corresponding to low cell counts would be omitted. This is in contrast to the current approach, where counts <11 are omitted.

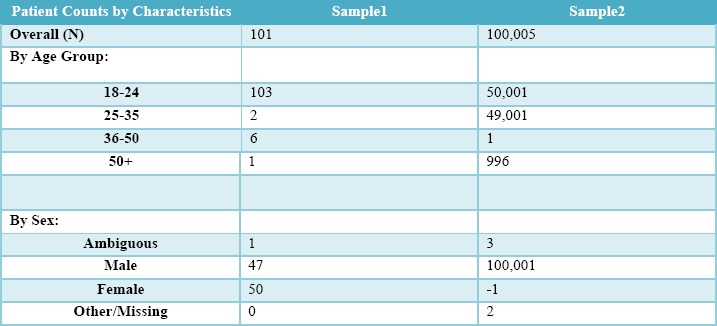
Table 3 shows a version of Table 2 that has been ‘fuzzed’ using this approach rather than thresholded. There are no thresholds because the exact count is no longer presented. Although the categories do not sum to exactly 100% of patients, the technique allows all cells to have a value without risking patient privacy and without implicitly revealing small cell counts, as was the case in Table 2.

Table 3:

Patient Count by Characteristics, from Table 2, in which Gaussian noise is applied rather than thresholds. Exact counts of small cells are no longer possible to infer, and all cells have a value.

This code is available in our GitHub repository, at https://github.com/ARCH-commons/arch-utils. [7]

Discussion

As an illustrative analogy, we will compare our ad hoc rule to the Heisenberg uncertainty principle from the field of quantum mechanics. This principle states that it is impossible to simultaneously know the exact location and exact velocity of a particle such as an electron. In this vein of thought, we propose that in all aggregate counts returned to the coordinating center, an observer should not be able to simultaneously determine a count's exact value as well as that count's exact query term information. We suggest that PCORnet queries respect this Ad Hoc Uncertainty Principle of Patient Privacy. To re-iterate, the Heisenberg Principle insists that the uncertainty in particle position multiplied by the uncertainty in particle momentum is constant, however if one is sure that the particle is in a particular position state (aka an eigenstate of position), then the uncertainty is entirely attributed to the particle's momentum. Analogously, our proposed rule requires that in order to know the exact query terms for a set of counts (namely the query is in an ‘eigenstate’ of a particular set of query terms), then an uncertainty must be attributed solely to the numeric count, and this uncertainty must be no smaller than 2.5 (the standard deviation of our Gaussian distribution).

This analogy is not perfect. In our example, the uncertainty in the patient counts is finite (2.5) whereas in the case of eigenstates in quantum mechanics the complementary variable that is not certain has an infinite uncertainty. Regardless of this nuance, it is helpful to think of our proposed technique as a way of adding uncertainty to our data so that the identities of patients cannot be discovered, analogously to how the positions of elementary particles are obscured via the Heisenberg Uncertainty Principle.

Analysis of data that has gone through our obfuscation process is akin to the analysis of data with measurement uncertainty in physical science: When a physical scientist makes a measurement, there is an associated measurement uncertainty attributed to that number. This uncertainty is also called the ‘precision’ of the measurement. If the scientist were to then gather a collection of independently measured data points measuring the same observable quantity, this collection would make up a distribution of results which could be Gaussian in shape, with a standard deviation equal to the measurement uncertainty or precision of the individual data points. While our fuzzed counts are not fuzzed due to true measurement uncertainty (and it should not be conflated as such), the aggregation of these counts utilizes a similar process to how a physical scientist would aggregate counts: this is easily accounted for, and networks would be able to accurately report aggregated results from all sites instead of only from a more limited pool of sites withlarger counts.

Advantages over Thresholding

The PCORnet Coordinating Center has recommended a solution of raising the threshold value so as not to create calculable T values. However, in order to adequately obfuscate the data, the low cell count threshold must often be increased substantially to the point of obfuscating the results of the query in their entirety. In Table 1, a threshold value of 99 is needed, and in Table 2, a threshold value of 99,999 is necessary! Our proposed solution would prevent sites from having to increase the obfuscation threshold to the point of obscuring the entire results of a query.

Masking small counts leads to under representation of small databases in studies. When thresholding hides the majority of usable data at a site, then data from small sites with unique demographic representations will be underrepresented, and this will introduce a selection bias slanted toward larger sites and their corresponding demographic pools. The Gaussian-noise obfuscation approach enables smaller sites to contribute their data, no matter how small, which in turn will enable networks to give a more complete and thorough analysis of the data across the network, and thereby providing more far-reaching and useful conclusions for researchers.

Limitations and Future Directions

In some circumstances where all sites have low counts, the current thresholding technique is superior to Gaussian noise. In particular, when the aggregate sum is less than or about equal to the aggregate uncertainty for a particular number of sites, then a thresholded censorship approach is best. This is illustrated in Figure 2 below. We plot the aggregate uncertainty (shaded area) versus the aggregate sum. The sums are represented by a set of straight lines with a slope equal to the average number of counts per site, where ‘x’ is the number of sites. When the average site reports a count of 2.5 or more for a query (i.e. slope is greater than or equal to 2.5), then the aggregate uncertainty is never greater than the aggregate sum, and therefore these cases are all well suited for our Gaussian fuzzing technique. In contrast, for smaller slopes such as 1 or 0.5, it may be better for the network to use thresholded censoring for smaller numbers of sites. When the aggregate sum is less than or about equal to the aggregate uncertainty for a particular number of sites, such as when x is less than or equal to 6 for the aggregate sum function with a slope of 1, then a thresholded censorship approach is best.

Figure 2:

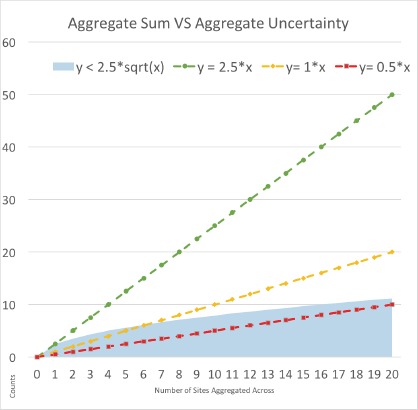
Aggregate sums represented by linear functions where the slope signifies the average number of counts per site and where x represents the number of sites. These aggregate sum functions are compared to the aggregate uncertainty (shaded area).

Using this method of Gaussian fuzzing to obfuscate our results has an interesting quirk: one needs to potentially accept negative values for counts as they may be necessary in order to preserve the correct fuzzing uncertainty from each individual site. Thus, by extension these negative values are necessary in order to assess the correct fuzzing uncertainty after error propagation. To understand this, consider a query looking for counts of patients with a rare disease. Suppose in one case, a patient count is ‘3’ before fuzzing. Our proposed method of introducing Gaussian noise would then produce a random number based off of the Gaussian distribution with a mean of ‘0’ and a standard deviation of ‘2.5,’ which could produce a negative number to be summed with the original count. This could in turn cause the fuzzed count to become a negative number, such as ‘-2.’ This negative number must be retained in order to preserve the Gaussian properties of the cumulative distribution; if it were rejected, the distributions of counts generated after fuzzing would be skewed to be larger than expected and may no longer be Gaussian, and thus the aforementioned error propagation formulas described in the Results section will no longer be valid.

Any queries that result in ‘0’ counts do not need to be fuzzed to protect patient privacy, which could be accounted for in order to reduce the aggregate uncertainties. However, this would also require an additional reference table to keep track of fuzzed versus non-fuzzed zeros.

In the future, it may be useful to examine how this technique could work in concert with a query lockout feature that would inhibit a user from issuing the same query too many times within a certain period. This could be implemented not only to prevent Gaussian convergence of the true number of patients, but also if the lockout threshold is low enough (e.g. 10), then the fuzzing uncertainty could also be decreased to an appropriate value (e.g. 1.33, which would take about 12.3 tries to converge on the mean). This could enable smaller sites or sites with small counts to undergo less fuzzing, thereby enabling their aggregate counts to surpass their aggregate uncertainties.

Conclusion

This approach of ceasing the censorship of low counts while introducing Gaussian noise to all aggregate counts will help data research networks obtain a more a complete report that more accurately reflects the data across the entire network, avoiding potential selection biases slanted towards larger healthcare sites and more prevalent demographics pools.

Funding

This work was funded through a Patient-Centered Outcomes Research Institute (PCORI) Award (CDRN-1306-04608) for development of the National Patient-Centered Clinical Research Network, known as PCORnet.

Disclaimer

The statements presented in this publication are solely the responsibility of the author(s) and do not necessarily represent the views of the Patient-Centered Outcomes Research Institute (PCORI), its Board of Governors or Methodology Committee or other participants in PCORnet.