Abstract
The pubovisceral muscles (PVM) help form the distal maternal birth canal. It is not known why 13% of vaginal deliveries end in PVM tears, so insights are needed to better prevent them because their sequelae can lead to pelvic organ prolapse later in life. In this paper we provide the first quantification of the variation in in vivo viscoelastic properties of the intact distal birth canal in healthy nulliparous women using Fung’s Quasilinear Viscoelastic Theory and a secondary analysis of data from a clinical trial of constant force birth canal dilation to 8 cm diameter in the first stage of labor in 26 nullipara. We hypothesized that no significant inter-individual variation would be found in the long time constant, τ2, which characterizes how long it takes the birth canal to be dilated by the fetal head. That hypothesis was rejected because τ2 values ranged 20-fold above and below the median value. These data were input to a biomechanical model to calculate how such variations affect the predicted length of the active second stage of labor as well as PVM tear risk. The results show there was a 100-fold change in the predicted length of active second stage for the shortest and longest τ2 values, with a noticeable increase for τ2 values over 1,000 seconds. The correlation coefficent between predicted and observed second stage durations was 0.51. We conclude that τ2 is a strong theoretical contributor to the time a mother has to push in order to deliver a fetal head larger than her birth canal, but a weak predictor of PVM tear risk.
Keywords: Levator ani, viscoelasticity, birth, second stage duration, injury
1 Introduction
During the second stage of labor, the distal birth canal soft tissues undergo remarkable deformation, typically increasing its circumference three-fold (Lien, Mooney, DeLancey, & Ashton-Miller, 2004; Lien, DeLancey, & Ashton-Miller, 2009; Zan, et al., 2010; Silva, et al., 2015). The distal portion of the birth canal is formed by the pubovisceral muscle (PVM), a subdivision of the levator ani muscles (Figure 1). The PVM originates bilaterally high on the inside aspect of the pubic symphysis to form a U-shaped loop that must be dilated and pushed downward by the fetal head during birth (Figure 1) as it partially wraps around the underside of the pelvic rami (Tracy, DeLancey, & Ashton-Miller, 2016). Due to the large degree of stretch required towards the end of the second stage of labor (Jing, Ashton-Miller, & DeLancey, 2012; Hoyte, et al., 2008; Li, Kruger, Nash, & Nielsen, 2011), the PVM tears in approximately 13% of vaginal deliveries (Shek & Dietz, 2010). These tears have been linked to the development of pelvic organ prolapse later in life in some individuals (Mant, Painter, & Vessey, 1997; DeLancey, et al., 2007; Ashton-Miller & DeLancey, 2009), a disorder for which 10% of all US women eventually require corrective surgery (Boyles, Weber, & Meyn, 2003; Ashton-Miller & DeLancey, 2009).
Figure 1.
Schematic illustration of the levator ani muscles. The subcomponents of the pubovisceral muscle (puboperineal, PPM; puboanal, PAM, and pubovaginal, PVaM) are shown. Left: Schematic view of the levator ani muscles from below after the vulvar structures and perineal membrane have been removed showing the arcus tendineus levator ani (ATLA); external anal sphincter (EAS); puboanal muscle (PAM); perineal body (PB) uniting the two ends of the puboperineal muscle (PPM); iliococcygeal muscle (ICM); puborectal muscle (PRM). Right: The LA muscle seen from above looking over the sacral promontory (SAC) showing the PVaM. The urethra, vagina, and rectum have been transected just above the pelvic floor. (The internal obturator muscles are not shown so as to reveal the origins of the levator muscle.) © DeLancey 2003.
Some women choose elective Cesarean Section because they are concerned about such complications; however, this operation carries its own immediate and delayed risks (Zelop & Heffner, 2004; Visser, 2015). It would be useful to be able to estimate the likelihood that stiff birth canal tissues might prolong the second stage of labor, because the risk of complications to mother and infant rise with second stages exceeding three hours.
We will therefore build on the geometric analysis of the fit between the fetal head and maternal birth canal described in Tracy et al. (Tracy, DeLancey, & Ashton-Miller, 2016). Specifically, we now incorporate the recently characterized viscoelastic behavior of the term pregnant human birth canal (Tracy, et al., 2018) into that model to simulate the biomechanical interaction between the fetal head and viscoelastic maternal birth canal during the active second stage of labor. Here, the predicted PVM tear outcome will be reported in the context of a PVM state parameter, based on the product of stress times strain, where a value greater than 1 indicates that a PVM tear is predicted. Tracy et al. (Tracy, et al., 2018) characterized the maternal viscoelastic behavior of the intact distal birth canal for one term-pregnant patient in the first stage of labor using a five parameter Quasilinear Viscoelastic Theory (QLV) constitutive model (Fung, 1993) which employed two elastic constants and three other constants to describe the tissue creep behavior; of these τ1 described the short time constant and τ2 the long time constant (Equation 3). Since τ2 governs how rapidly the distal birth canal will dilate if one was to distend it during the many minutes of the first stage of labor, and since that analysis did not consider inter-individual τ2 variations, we will here first test the null hypothesis that there is no significant variation in the distal birth canal τ2 behavior between 30 term-pregnant women in their first stage of labor. Then we will test the null hypothesis that the variation in τ2 will neither affect (1) the predicted length of their active second stage of labor, nor (2) the risk of a PVM tear.
2 Methods
A clinical proof-of-concept and safety trial of a new birth canal dilation device developed by Materna Medical, Inc. (Mountain View, CA 94040) was conducted at Baylor College of Medicine with institutional board approval (Orejuela, et al., 2018). The device generates an outward radial force via four pads in order to dilate the distal birth canal to 8 cm diameter in nulliparous women during their first stage of labor. Once the University of Michigan authors became aware that both the time course of the dilation force and the resulting dilation were recorded synchronously, we asked the Materna and Baylor College of Medicine authors whether they could share de-identified force and displacement data collected as a byproduct of their clinical trial. This was because these data offer the unusual opportunity to quantify the viscoelastic behavior of the distal birth canal in laboring women (see, for example, (Tracy, et al., 2018)). These biomechanical data were collected continuously while the device was powered on, and included the entire duration of birth canal dilation by the device, as well as the time required for device calibration, insertion, and removal. We could then use the force data as the input to a simulation after conversion to tensile stress values in the direction of the line-of-action of the muscle fibers. This conversion was based on an assumed average anatomic cross sectional area of the healthy female PVM equal to 1.2 cm2 (Morris, Murray, DeLancey, & Ashton-Miller, 2012). In the first part of this paper, therefore, a secondary analysis was conducted of the Orejuela et al (2018) biomechanical data by fitting the birth canal force-dilation-time data for 30 nulliparous women, ages 18 years or older with singleton pregnancies of at least 37 weeks gestation, to a five-parameter constitutive model based on QLV theory for soft tissues (Tracy, et al., 2018).
2.1 Birth Simulations
Here, we describe a model to predict the length of the second stage of labor and the risk of a PVM tear by considering the relationship between maternal birth canal capacity and fetal head demand. Stress–strain relationships were assumed to be governed by the 5-parameter QLV constitutive model that was applied to the distal vagina (Tracy, et al., 2018). This model, was chosen because it has successfully been used to describe soft tissue tensile behavior (Fung, 1993) and because we found it provided the best fit to human, squirrel monkey, and ovine tissue birth canal data (Tracy, et al., 2018).
This 5-parameter model included the following creep form:
| (1) |
Here, ε indicates strain, and σ indicates stress as defined using the following elastic function:
| (2) |
where A and B are coefficients with values of 16.1 MPa and 0.081 (unitless), respectively. In equation 1, J indicates the following creep function:
| (3) |
where and
Here, τ1 and τ2 indicate the short and long time constants, respectively, while C is a unitless relaxation coefficient. τ1 and C have values of 0.973 seconds and 13.08, respectively, while variations in the values of τ2 are discussed below.
Maternal capacity and the PVM U-shaped sling length were then calculated for the 2.3rd to the 97.7th percentile female based on the Tracy et al. (2016) geometric capacity-demand model. This considered maternal birth canal capacity to be determined by the subpubic arch angle, PVM origin location, and PVM length after examining these relationships using 3D anatomical models built from pelvic MRI scans of three healthy women who had delivered by cesarean delivery without attempting vaginal delivery. Fetal demand was represented by fetal heads ranging from the 2.3rd to the 97.7th percentile with average molding (Tracy, DeLancey, & Ashton-Miller, 2016). Birth simulations were run for each maternal capacity – to – fetal head demand pairing from the 2.3rd to the 97.7th percentile, as well as for the patient-specific measurements available from the participants in the Baylor clinical trial cohort. All simulations were run in MATLAB R2015a with a time step size of 0.1 seconds.
PVM strain, εPVM, was assumed to be related to general birth canal strain, εBC, based on the ratio between their initial circumferences, lPVM and lBC respectively (Tracy, DeLancey, & Ashton-Miller, 2016).
| (4) |
It was also estimated (and assumed), based on anatomical analysis (Tracy, et al., 2018) of the height of the PVM relative to the distension device, that 83% of the total force applied by the Materna birth canal distension device was resisted as a tensile load in the PVM. The other 17% was assumed to be resisted by fascia and other vaginal tissues not comprising the PVM.
In the modified Tracy et al. (2016) model, simulations of vaginal birth during the second stage of labor were driven by intrauterine pressure as an input, as measured in previous experiments. This included a 2.6 kPa basal intrauterine pressure, an 8.5 kPa rise during contractions, and an additional 10.5 kPa rise during each volitional push (Rempen & Kraus, 1991). Contractions and pushes were each modeled as the first half of one period of a cosine wave. Specifically, contractions were assumed to last for 90 seconds, followed by 90 second rest; three 10 second pushes were assumed per contraction with each followed by 10 seconds of rest (Rempen & Kraus, 1991; Allman, Genevler, Johnson, & Steer, 1996; Buhimschi, Buhimschi, Malinow, Kopelman, & Weiner, 2002).
Intrauterine pressure was assumed to be related to circumferential stress in the PVM U-shaped sling, based on the following calculations (Figure 2):
| (5) |
| (6) |
Figure 2.
Intrauterine pressure (blue arrow) creates an expulsion force distributed over the fetal head (grey circle). The tension (T) in the PVM (dark blue band low on head) was related to intrauterine pressure using the radius of the fetal head (light blue lines) and the angle (alpha) between the midline of the fetal head and the contact point of the PVM on the fetal head.
Balancing “Vertical” Forces:
| (7) |
Here, Piu indicates intrauterine pressure and rh indicates fetal head radius.
| (8) |
Balancing “Horizontal” Forces:
| (9) |
| (10) |
where APVM is the cross-sectional area of the PVM.
Based on image analysis of a single neonatal head photograph taken shortly post-delivery, fetal head anatomy was observed to deviate from perfectly spherical anatomy. By identifying the point at which this deviation occurred, a maximum alpha value of 0.68 radians was measured. This value then was assumed for all simulations.
Simulations of births were run for 2.5th to the 97.5th percentile maternal birth capacity and 2.5th to 97.5th fetal head circumferences for three values of τ2: the median (555 seconds), the short extreme at 1/20th the median, and the long extreme at 20 times the median. Trials that had a second stage predicted to exceed 24 hours in length were terminated because this would not be allowed clinically, and the baby would have been delivered by cesarean section.
2.2 Post analysis of Results in Microsoft Excel 2010
The cells in ‘Length of Active Second Stage’ figures (see Results) were shaded blue to indicate an exceptionally long labor when a threshold of 3 hours was exceeded because obstetrical guidelines recommend intervening at this point (Spong, Berghella, Wenstrom, Mercer, & Saade, 2012). Numerical results were reported for simulated labors with second stages lasting less than 24 hours.
Likewise, the cells in ‘PVM state parameter’ figures were shaded red in order to indicate that the threshold for injury, discussed below, had been exceeded. This threshold for injury was 2.7 MPa (PVM state parameter equal to 1), discussed below.
The soft tissue injury criterion was assumed to be the product of stress*strain. This was based on literature available for ligament failures (Chiba & Komatsu, 1993; Panjabi, Crisco, Lydon, & Dvorak, 1998; Bonner, et al., 2015), while the exact value of 2.7 MPa was based on the measured conditions for the ultimate failure of pregnant ovine tissue estimated graphically from Ulrich et al. (Ulrich, et al., 2014).
A smoothing function with a width of τ2 values spanning 100 seconds was used in Figure 7. This was done to account for heightened sensitivity to the timing of fetal head delivery during the final contraction for deliveries that require very few contractions, as addressed in the Discussion.
Figure 7.
The predicted values of the PVM state parameter for the range of τ2 values observed. Results are for simulations for a single 20th percentile maternal capacity and 50th percentile fetal demand pairing. The threshold for predicted injury (2.7 MPa) is shown as the red line.
3 Results
3.1 Measured Variations in the Long Time Constant, τ2
Of the 30 nullipara tested, variation in viscoelastic responses could be explained for 26 of them by changes in the long time constant, τ2, alone (Figure 3). The remaining four subjects showed variation in other parameters, such as parameters A and B of the elastic constitutive relationship (Equation 2) when compared with the rest of the cohort. We therefore rejected the null hypothesis that there is no significant variation between term pregnant mothers in the long time constant, τ2.
Figure 3.
Histogram of long time constant, τ2, values represented in logarithmic form.
3.2 Predicted Length of Active Second Stage
We also rejected the null hypothesis that the variation in τ2 would not affect the length of the active second stage of labor, showing that the duration of the active second stage increased with increasing values of τ2. For example, values of τ2 over 1,000 seconds result in predicted active second stages of greater than 1 hour for the 50th percentile maternal capacity and 50th percentile fetal demand (Figure 4).
Figure 4.
Predicted length of the active second stage for the range of τ2 values observed. Results are for simulations for a single 50th percentile maternal capacity and 50th percentile fetal demand pairing.
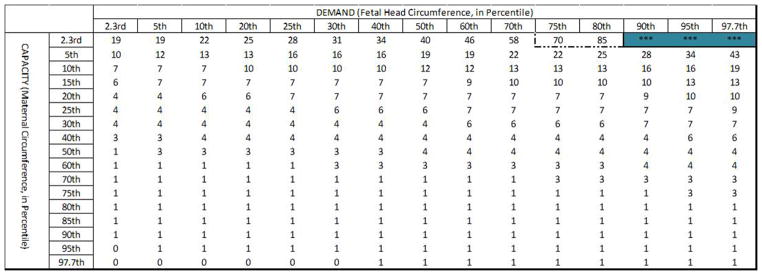
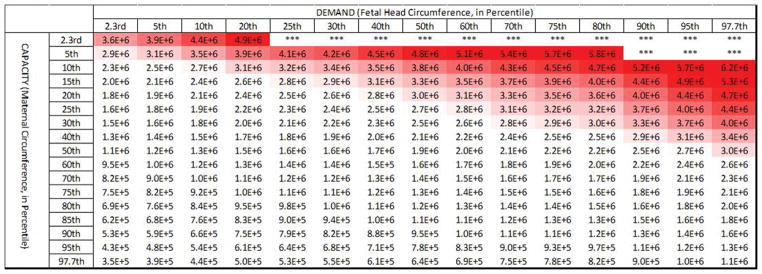
Expanding upon this further, we considered a wide range of pairings between maternal capacity and fetal head demand (Figure 5). The simulations show that for the lower bound of observed τ2 values (τ2= 27 seconds, or 1/20th of the median) only 2% of births exceeded 1 hour of active second stage. Additionally, simulations run for the median observed τ2 value (550 seconds) resulted in 26% of births exceeding 1 hour of active second stage, with none exceeding 5 hours. However, simulations run for the upper bound (20 times median) of observed τ2 values (τ2= 11,000 seconds) resulted in 89% of births being predicted to exceed 1 hour in active second stage.
Figure 5.
Predicted length of active second stage (in minutes) across the range of pairings of maternal capacity-to-fetal head demand are shown for τ2 values of 1/20th of the median (27 seconds, top panel), median (550 seconds, middle panel), and 20X the median (11,000 seconds, bottom panel). The intensity of the (blue) shading indicates the extent by which each active second stage exceeds 3 hours. The 1 hour (dot-dot-dash line), 2 hour (dot-dash line), 3 hour (dashed line) and 4 hour (solid line) cutoffs are marked in each table.
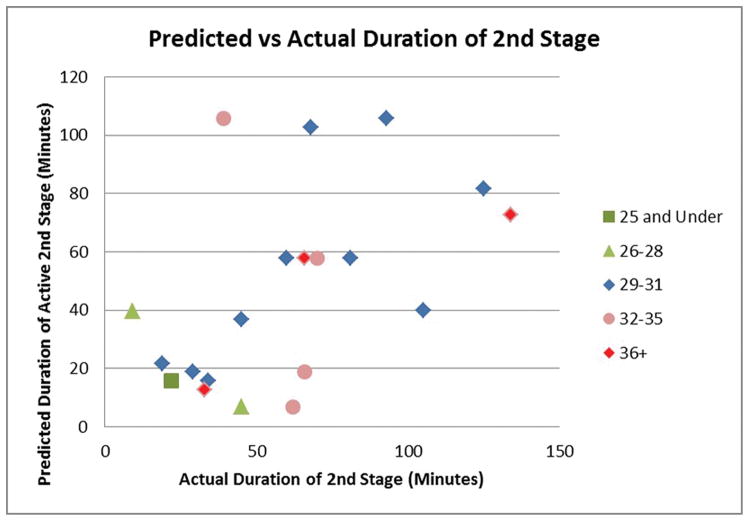
The correlation coefficient between the model-predicted and actual 2nd stage durations was 0.51 across all ages, and 0.66 for the median age group (Figure 6).
Figure 6.
Biomechanical model-predicted duration of active second stage plotted against actual duration of the second stage partitioned by maternal age group (in units of years). The correlation coefficients are 0.51 and 0.66 for the entire cohort and for the median age group, respectively.
3.3 Predicted PVM Tears
A gradual increase was found in the PVM state parameter, used in determining predicted tears, for increasing values of τ2. This was enough to change whether the 2.7 MPa predicted tear threshold was met for some patients, such as the 20th percentile maternal capacity-to-50th percentile fetal head demand case (Figure 7). Therefore, we also rejected the null hypothesis that variation in τ2 does not affect levator ani tear risk.
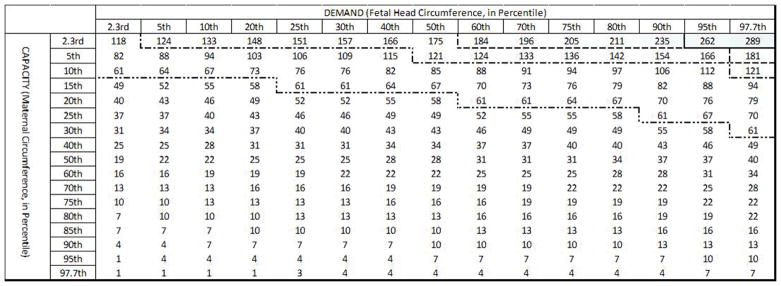
Across all maternal capacity and fetal head demand pairings, we demonstrated that for 27 seconds, 550 seconds, and 11,000 seconds τ2 values, predicted PVM tear rates were 27%, 30%, and 32%, respectively. This relatively narrow variation, represented by dashed lines added to the median table of Figure 8, serves as a confidence interval guide when using this table to evaluate the PVM tear risk of a mother for whom viscoelastic properties are unknown.
Figure 8.
Predicted PVM state parameter across the full range of pairings of maternal capacity-to-fetal head demand are shown for τ2 values of 27 seconds (top panel), 550 seconds (middle panel), and 11,000 seconds (bottom panel). The intensity of the (red) shading indicates the extent by which the predicted injury threshold of 2.7 MPa (PVM state parameter of 1) is exceeded. In the median table, the predicted PVM tear cutoffs for each of the other two tables are marked by the dashed lines.
4 Discussion
These are the first measurements of the viscoelastic behavior of the distal birth canal in women during labor. The remarkable range in maternal τ2 values, from 20-fold above to 20-fold below the median value, representing a 400-fold difference, was a surprising new finding of the secondary analysis of the Baylor birth canal dilation data (Orejuela, et al., 2018).
The finding that the predicted length of the active second stage ranged from a few minutes to tens of hours depending on the τ2 value is a second new finding. This is clinically important because long labors are linked to birth complications such as low Apgar scores, low umbilical artery pH, higher rates of resuscitation and ICU admission, higher rates of hypoxic-ischemia encephalopathy, cesarean procedures for non-reassuring fetal heart tones, as well as maternal risk for chorioamnionitis and post-partum hemorrhage (Senecal, Xiong, & Fraser, 2005; Rouse, et al., 2009; Bleich, Alexander, McIntire, & Leveon, 2012; Laughon, et al., 2014; Leveno, Nelson, & McIntire, 2016). These biomechanically-predicted second stage duration data correlated with clinically reported active second stage durations for our cohort (Orejuela, et al., 2018) with a correlation coefficient of 0.51. Our results also compare favorably with clinical results in that 61% of all active second stage simulations were predicted to take less than 1 hour: for example, a study of 21,991 nullipara, found that 62% of second stages lasted less than 1 hour (Bleich, Alexander, McIntire, & Leveon, 2012). However, for the median τ2 case, this predicted value was 74%. It should be noted that our simulations should be taken in the broader context of other factors known to influence second stage, such as poor maternal effort during the active pushing phase, whether due to lack of effort or because of a deep epidural, or occiput-posterior fetal head orientation, which can increase the length of the second stage by an average of 45 minutes in nulliparous women with epidurals (Senecal, Xiong, & Fraser, 2005).
It is of clinical interest that women who will experience an active second stage exceeding 3 hours can be identified, at least theoretically using the predictive model.
Clinically, if an impending lengthy active second stage could be predicted, interventions could be used to help alleviate fetal distress. However, when considering Figures 5 and 8, there are certain scenarios when a woman may experience a very long second stage of labor while not being at risk for a levator tear, such as a pairing at the 20th percentile for both maternal capacity and fetal head demand, for example. In cases such as these, interventions such as forceps instrumentation, chosen due to the anticipated long length of labor, could result in a levator tear in a mother that was not previously at risk.
A limitation of our birth simulations is that the birth canal stress values peak depending on when, during the contraction, the birth occurred. For instance, if a mother is near to delivery at the end of a contraction and succeeds in pushing the head out, the stress in the birth canal at birth will be higher than if her distal canal tissue can relax until the beginning of the next contraction. The effects of this can be seen in the top table of Figure 8, where births are very short, and the role of this phenomenon is non-negligible. As the length of active second stage increases, the total amount of time available for tissue relaxation increases, and the effect of adding an additional contraction for relaxation then becomes marginal.
In this study, we chose the product of stress times strain as the criterion for PVM injury. Some previous models of soft tissue injury have selected purely strain-based criteria (Li W., 2016). However, we note that literature values for soft tissue failure do show a dependence on both stress and strain (Chiba & Komatsu, 1993; Panjabi, Crisco, Lydon, & Dvorak, 1998; Ulrich, et al., 2014; Bonner, et al., 2015), hence our choice of failure criterion seems reasonable.
To address the accuracy of our predicted tear rates, let us compare our models to the approximately 15% PVM tear rates observed clinically (Guzman Rojas, Wong, Shek, & Dietz, 2014; Cassado, et al., 2014). In the present paper we demonstrate that, for a 50th percentile fetal head and the median τ2 value, mothers larger than the 20th percentile are predicted to deliver without PVM tear. Considering the variation in τ2 values, this cutoff ranges from the 15th to 25th percentile mother, close to values observed clinically. However, the clinical data do not include women who are unable to deliver without cesarean section (Harper, Stamilio, Odibo, Peipert, & Macones, 2011; Gurung, Malla, Lama, Malla, & Singh, 2017), who represent the upper right portion of the tables in Figure 8, and who are predicted to experience tears if they were able to deliver vaginally. So, the present predictions appear to be reasonable and not overly conservative.
Acknowledgments
We gratefully acknowledge financial support from the Office for Research on Women’s Health SCOR program on Sex Differences in Women’s Health (P50 HD 44406, Project 1). We thank Mark Juravic of Materna Medical, Inc., for contributing the de-identified human birth canal fo1rce-displacement-time data in the absence of any financial support. The study sponsors had no involvement in study design, data analysis, the writing of the manuscript, or in the decision to submit this manuscript for publication.
Footnotes
Conflict of Interest Statement
The authors have no conflicts of interest to disclose.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
5 Bibliography
- Allman AC, Genevler ES, Johnson MR, Steer PJ. Head-to-Cervix Force: an Important Physiological Variable in Labour. 1. The Temporal Relation Between Head-to-Cervix Force and Intrauterine Pressure During Labour. British Journal of Obstetrics and Gynaecology. 1996;103:763–768. doi: 10.1111/j.1471-0528.1996.tb09870.x. [DOI] [PubMed] [Google Scholar]
- Ashton-Miller JA, DeLancey JO. On the Biomechanics of Vaginal Birth and Common Sequelae. Annual Review of Biomedical Engineering. 2009;11:163–176. doi: 10.1146/annurev-bioeng-061008-124823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bleich AT, Alexander JM, McIntire DD, Leveon KJ. An Analysis of Second-Stage Labor beyond 3 Hours in Nulliparous Women. American Journal of Perinatology. 2012;29(9):717–722. doi: 10.1055/s-0032-1314894. [DOI] [PubMed] [Google Scholar]
- Bonner TJ, Newell N, Karunaratne A, Pullen AD, Amis AA, Bull AM, Masouros SD. Strain-rate Sensitivity of the Lateral Collateral Ligament of the Knee. Journal of the Mechanical Behavior of Biomedical Materials. 2015;41:261–70. doi: 10.1016/j.jmbbm.2014.07.004. [DOI] [PubMed] [Google Scholar]
- Boyles S, Weber A, Meyn L. Procedures for Pelvic Organ Prolapse in the United States, 1979–1997. American Journal of Obstetrics and Gynecology. 2003;188(1):108–15. doi: 10.1067/mob.2003.101. [DOI] [PubMed] [Google Scholar]
- Buhimschi CS, Buhimschi IA, Malinow AM, Kopelman JN, Weiner CP. Pushing in Labor: Performance and Not Endurance. American Journal of Obstetrics and Gynecology. 2002;186(6):1339–44. doi: 10.1067/mob.2002.122402. [DOI] [PubMed] [Google Scholar]
- Cassado J, Pessarrodona A, Rodriguez-Carballeira M, Hinojosa L, Manrique G, Marquez A, Marcias M. Does episiotomy protect against injury of the levator ani muscle in normal delivery? Neuorology and Urodynamics. 2014:1212–6. doi: 10.1002/nau.22488. [DOI] [PubMed] [Google Scholar]
- Chiba M, Komatsu K. Mechanical Responses of the Periodontal Ligament in the Transverse Section of the Rat Mandibular Incisor at Various Velocities of Loading In Vitro. Journal of Biomechanics. 1993;26(4):561–70. doi: 10.1016/0021-9290(93)90017-9. [DOI] [PubMed] [Google Scholar]
- DeLancey JO, Morgan DM, Fenner DE, Kearney R, Guire K, Miller JM, … Aston-Miller JA. Comparison of levator ani muscle defects and function in women with and without pelvic organ prolapse. Obstetrics and Gynecology. 2007;109:295–302. doi: 10.1097/01.AOG.0000250901.57095.ba. [DOI] [PubMed] [Google Scholar]
- Fung YC. Biomechanics: Mechanical Properties of Living Tissues. New York, NY: Springer-Verlag; 1993. [Google Scholar]
- Gurung P, Malla S, Lama S, Malla A, Singh A. Caesarean section during second stage of labor in a tertiary center. Journal of Nepal Health Research Council. 2017:178–81. doi: 10.3126/jnhrc.v15i2.18210. [DOI] [PubMed] [Google Scholar]
- Guzman Rojas R, Wong V, Shek K, Dietz H. Impact of levator trauma on pelvic floor muscle function. International Urogynecology Journal. 2014:375–80. doi: 10.1007/s00192-013-2226-4. [DOI] [PubMed] [Google Scholar]
- Harper L, Stamilio D, Odibo A, Peipert J, Macones G. Vaginal birth after cesarean for cephalopelvic disproportion: effect of birth weight difference on success. Obstetrics and Gynecology. 2011:343–8. doi: 10.1097/AOG.0b013e31820776fd. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoyte L, Damaser M, Warfield S, Chukkapalli G, Majumdar A, Choi D, … Krysl P. Quantity and distribution of levator ani stretch during simulated vaginal childbirth. American Journal of Obstetrics and Gynecology. 2008:198.e1–5. doi: 10.1016/j.ajog.2008.04.027. [DOI] [PubMed] [Google Scholar]
- Jing D, Ashton-Miller JA, DeLancey JO. A subject-specific anisotropic visco-hyperelastic finite element model of female pelvic floor stress and strain during the second stage of labor. Journal of Biomechanics. 2012;45:455–460. doi: 10.1016/j.jbiomech.2011.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laughon SK, Berghella V, Reddy UM, Sundaram R, Lu Z, Hoffman MK. Neonatal and Maternal Outcomes With Prolonged Second Stage of Labor. Obstetrics and Gynecology. 2014;124(1):57–67. doi: 10.1097/AOG.0000000000000278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leveno KJ, Nelson DB, McIntire DD. Second-stage labor: how long is too long? American Journal of Obstetrics and Gynecology. 2016;214(4):484–489. doi: 10.1016/j.ajog.2015.10.926. [DOI] [PubMed] [Google Scholar]
- Li W. Damage Models for Soft Tissues: A Survey. Journal of Medical and Biological Engineering. 2016;36:285–307. doi: 10.1007/s40846-016-0132-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Kruger J, Nash M, Nielsen P. Anisotropic effects of the levator ani muscle during childbirth. Biomechanics and Modeling in Mechanobiology. 2011:485–94. doi: 10.1007/s10237-010-0249-z. [DOI] [PubMed] [Google Scholar]
- Lien K, Mooney B, DeLancey J, Ashton-Miller J. Levator ani muscle stretch induced by simulated vaginal birth. Obstetrics and Gynecology. 2004;103(1):31–40. doi: 10.1097/01.AOG.0000109207.22354.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lien KC, DeLancey JO, Ashton-Miller JA. Biomechanical Analyses of the Efficacy of Patterns of Maternal Effort on Second-Stage Progress. Obstetrics & Gynecology. 2009;113(4):873–880. doi: 10.1097/AOG.0b013e31819c82e1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mant J, Painter R, Vessey M. Epidemiology of genital prolapse: observations from the Oxford Planning Association Study. British Journal of Obstetrics and Gynaecology. 1997;104(5):579–85. doi: 10.1111/j.1471-0528.1997.tb11536.x. [DOI] [PubMed] [Google Scholar]
- Morris VC, Murray MP, DeLancey JO, Ashton-Miller JA. A comparison of the effect of age on levator ani and obturator internus muscle cross-sectional areas and volumes in nulliparous women. Neurourology and Urodynamics. 2012;31(4):481–6. doi: 10.1002/nau.21208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orejuela F, Gandhi R, Mack L, Lee W, Sangi-Haghpeykar H, Dietz H, Ramin S. Prospective evaluation of the safety and feasibility of a pelvic floor dilator during active labor. International Urogynecology Journal. 2018:e1–8. doi: 10.1007/s00192-018-3555-0. [DOI] [PubMed] [Google Scholar]
- Panjabi MM, Crisco JJ, Lydon C, Dvorak J. The Mechanical Properties of Human Alar and Transverse Ligaments at Slow and Fast Extension Rates. Clinical Biomechanics. 1998;13(2):112–20. doi: 10.1016/s0268-0033(97)00053-3. [DOI] [PubMed] [Google Scholar]
- Rempen A, Kraus M. Pressures on the Fetal Head During Normal Labor. Journal of Perinatal Medicine. 1991;19(3):199–206. doi: 10.1515/jpme.1991.19.3.199. [DOI] [PubMed] [Google Scholar]
- Rouse D, Weiner S, Bloom S, Varner M, Spong C, Ramin S, … Anderson G. Second-stage Labor Duration in Nulliparous Women: Relationship to Maternal and Perinatal Outcomes. American Journal of Obstetrics and Gynecology. 2009;201(4):357e1–7. doi: 10.1016/j.ajog.2009.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senecal J, Xiong X, Fraser WD. Effect of Fetal Position on Second-Stage Duration and Labor Outcome. Obstetrics and Gynecology. 2005;105(4):763–772. doi: 10.1097/01.AOG.0000154889.47063.84. [DOI] [PubMed] [Google Scholar]
- Shek K, Dietz H. Intrapartum risk factors for levator trauma. BJOG An International Journal of Obstetrics and Gynecology. 2010;117(12):1485–1492. doi: 10.1111/j.1471-0528.2010.02704.x. [DOI] [PubMed] [Google Scholar]
- Silva ME, Oliveira DA, Roza TH, Brandao S, Parente MP, Mascarenhas T, Natal Jorge RM. Study on the influence of the fetus head molding on the biomechanical behavior of the pelvic floor muscles, during vaginal delivery. Journal of Biomechanics. 2015;48(9):1600–1605. doi: 10.1016/j.jbiomech.2015.02.032. [DOI] [PubMed] [Google Scholar]
- Spong C, Berghella V, Wenstrom K, Mercer B, Saade G. Preventing the first cesarean delivery: summary of a joint Eunice Kennedy Shriver National Institute of Child Health and Human Development, Society for Maternal-Fetal Medicine, and American College of Obstetricians and Gynecologists Workshop. Obstetrics and Gynecology. 2012;120(5):1181–93. doi: 10.1097/aog.0b013e3182704880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tracy PV, DeLancey JO, Ashton-Miller JA. A Geometric Capacity - Demand Analysis of Maternal Levator Muscle Stretch Required for Vaginal Delivery. Journal of Biomechanical Engineering. 2016:e1–e54. doi: 10.1115/1.4032424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tracy PV, Wineman AS, Orejuela FJ, Ramin SM, DeLancey JO, Ashton-Miller JA. A Constitutive Model Description of the In Vivo Material Properties of Lower Birth Canal Tissue During the First Stage of Labor. Journal of the Mechanical Behavior of Biomedical Materials. 2018;79:213–218. doi: 10.1016/j.jmbbm.2017.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulrich D, Edwards SL, Su K, White JF, Ramshaw JA, Jenkin G, … Gargett CE. Influence of Reproductive Status on Tissue Composition and Biomechanical Properties of Ovine Vagina. Public Library of Science. 2014;9(4):1–8. doi: 10.1371/journal.pone.0093172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visser GH. Women are designed to deliver vaginally and not by cesarean section: an obstetritian’s view. Neonatology. 2015;107(1):8–13. doi: 10.1159/000365164. [DOI] [PubMed] [Google Scholar]
- Zan P, Yan G, Liu H, Yang B, Zhao Y, Luo N. Biomechanical modeling of the rectum for the desing of a novel artificial anal sphincter. Biomedical Instrumentation and Technology. 2010;44(3):257–60. doi: 10.2345/0899-8205-44.3.257. [DOI] [PubMed] [Google Scholar]
- Zelop C, Heffner LJ. The downside of cesarean delivery: short- and long-term complications. Clinical Obstetrics and Gynecology. 2004;47(2):386–93. doi: 10.1097/00003081-200406000-00012. [DOI] [PubMed] [Google Scholar]