Precision spectroscopy of H¹³CN using a free-running, all-fiber dual electro-optic frequency comb system

Abstract

We demonstrate the precision molecular spectroscopy of H¹³CN using a free-running, all-fiber dual electro-optic frequency comb system. Successive interferograms, acquired at a rate of Δf_rep = 1 MHz, were phase-corrected in post-processing, averaged, and normalized to yield the complex transmission spectrum of several transitions within the 2ν₁ H¹³CN band centered near λ = 1545 nm. With spectral signal-to-noise ratios as high as 326:1 achieved in 2 ms of integration time, we report accurate measurements of H¹³CN transition intensities which will aid in the study of extreme astrophysical environments.

Precision molecular spectroscopy, performed in combination with traceable, accurate measurements of highly controlled sample conditions, enables modern remote sensing of the Earth’s atmosphere via the establishment of parameterized line list databases [1]. For a variety of astrophysical environments, however, such as exoplanetary atmospheres, comets, or dense nebula, replicating all the anticipated gas conditions in a controlled laboratory environment is simply not feasible. Therefore, extensive line lists that employ semi-empirical and ab initio computation methods to derive spectroscopic parameters are an active area of research [2]. To rigorously benchmark these computational line lists against experiments, new tools for highly accurate and precise atomic and molecular spectroscopy are required [3, 4].

Electro-optic (EO) frequency combs are one such new tool [5–14]. Capable of rapid acquisition via dual-comb spectroscopy (DCS) [15], and with a relative frequency axis defined by a radiofrequency (RF) clock, EO frequency comb spectroscopy avoids many systematic phenomena that ultimately limit even fast-scanning continuous-wave (CW) spectroscopies. In combination with an all-fiber system, including fiber-coupled reference and sample gas cells, these properties enable rapid acquisition and therefore invite deep averaging of spectroscopic parameters. Notability, our all-fiber system outperforms an earlier fiber-based comb spectrometer [16] in several key metrics: signal-to-noise ratio (4-fold), acquisition time (5-fold), and achievable resolution [14].

As a proof-of-principle demonstration, we accurately measure line intensities (S_int) of several rotational-vibrational transitions within the 2ν₁ band of H¹³CN at wavelengths ranging from 1536 nm to 1562 nm [17]. Hydrogen cyanide (HCN) and its isomer hydrogen isocyanide (HNC) are readily identified throughout the interstellar medium, in extreme astrophysical environments such as comets, interstellar clouds and star forming regions [18]. For example, the quantitative analysis of the HCN/HNC isomer ratio as well as ¹²C/¹³C and H/D isotopic ratios in comets using millimeter and submillimeter wave observations revealed fundamental chemistries of solar system formation [19, 20]. With the launch of the James Webb Space Telescope, new infrared observations of HCN throughout our solar system and beyond will become possible [21, 22]. Therefore, accurate laboratory studies of HCN infrared spectroscopic parameters are required.

A block diagram of the all-fiber, dual electro-optic frequency comb (DEOFC) system built at the National Institute of Standards and Technology (NIST) is illustrated in Fig. 1. A portion of the output of a CW external-cavity diode laser (ECDL, 50 ms line width < 200 kHz) was coupled to a high-bandwidth (100 Hz) wavelength meter (WVM) to control the absolute laser frequency f_CW to within ±1 MHz of a target molecular transition frequency f₀ via electronic feedback to the ECDL current. The remaining laser output was amplified (booster optical amplifier, BOA) and split into local oscillator (LO) and probe lasers. The probe comb was generated by a dual-drive Mach-Zehnder modulator (DDMZM) [23] driven at f_rep and injected into either a flame-sealed reference (N₂) or sample (H¹³CN) multipass cell (fiber-coupled, total path length L = 79 cm ± 1 cm). The LO laser was shifted by f_AOM=50 MHz using an acousto-optic modulator (AOM) and the subsequent LO comb was generated by a second DDMZM driven at f_rep + Δf_rep. Dual-comb interferograms were recorded using a photoreceiver (PR), high-bandwidth digital-to-analog converter (DAQ), and personal computer (PC). Importantly, all optical components were fiber-coupled, and all RF synthesizers, as well as the DAQ, were synchronized using a 10 MHz Cs clock signal.

Fig. 1.

All-fiber dual electro-optic frequency comb (DEOFC) system. Fiber optics are drawn as solid lines, and electronic signals as dashed lines. Unless otherwise indicated, fiber-optic splitters/combiners have a power ratio of 50/50. Abbreviations are ECDL, external-cavity diode laser, ISO, optical isolator, WVM, wavelength meter, BOA, booster optical amplifier, AOM, acousto-optic modulator, DDMZM, dual-drive Mach-Zehnder modulator, PR photoreceiver, DAQ digital-to-analog converter, and PC, personal computer.

The real portion of a typical interferogram, with period 1/Δf_rep = 1 μs, is plotted in the left panel of Fig. 2. The Fourier transform of 1000 consecutive interferograms is plotted vs. RF in the right panel of Fig. 2, highlighting the comb nature of the electrical signal around f_AOM.

Fig. 2.

Left panel. Representative real time-domain DEOFC system waveform. Right panel. The Fourier transform of 1000 consecutive interferograms like that plotted in the left panel, centered around f_AOM = 50 MHz.

Here we used custom post-correction software [24, 25] to coherently average the acquired interferograms. The first step of the algorithm demodulated the signal at f_AOM. This shifted it to baseband and extracted a complex analytic representation of the interferogram thus avoiding overlap with the negative spectral alias. After digital filtering, the baseband signal was down-sampled to a frequency which equaled half the bandwidth of the electrical comb, typically 20 MHz. This procedure reduced the number of points per interferogram, and thus increased algorithm speed.

With all RF synthesizers synchronized to a common clock, Δf_rep could be arbitrarily chosen such that the number of points in an interferogram remained constant and equal to an exact integer number of points, even after down-sampling. Inter-interferogram timing was thus not an issue in our DEOFC system, in contrast to DCS performed with mode-locked combs [24–26]. However, small phase corrections of successive interferograms are still required for deep averaging [10], even for our high-mutual-coherence EO combs which originated from the same CW laser. Indeed, any differential environmental perturbation between the two interferometer arms that occur at rates < Δf_rep/2 (500 kHz) will lead to measurable phase drifts, destroying the inherent mutual coherence.

Phase extraction was performed here in a manner similar to [26]: a cross-correlation was computed between the first interferogram, thereafter called “reference interferogram,” and each successive acquisition. The phase difference between the reference interferogram and the uncorrected interferogram was computed at the maximum of the cross-correlation, and a quadratic fit was performed to accurately find cross-correlation maximum. This computation yielded a unique phase difference per interferogram. The phase signal was interpolated to each interferogram sample, and the interpolated phase was used to correct interferograms before segmenting for coherent averaging.

Figure 3 illustrates the retrieved temporal phase evolution over a representative 1 ms acquisition. Because of the high mutual coherence, the phase noise was constrained to <1 rad. The Allan variance plots in the bottom panels of Fig 3 nevertheless show that coherent averaging of the uncorrected interferograms is not possible beyond a few tens of acquisitions, while corrected interferograms are averaged for at least 1 000 measurements.

Fig. 3.

Top panel. Extracted phase from the cross-correlation of consecutive interferograms for a 1 ms waveform showing small relative phase drifts. Bottom panels. Allan variance plots of the real (left) and imaginary (right) parts of the interferogram at its maximum value are shown for corrected (blue lines) and raw (black lines) waveforms.

The H¹³CN spectral acquisition procedure was as follows. We recorded 1000 consecutive interferograms at a sampling rate of 8 × 10⁸ s⁻¹ (total time of 1 ms) for the probe comb transmitted through the H¹³CN gas cell. The fiber-optic switch was then triggered, coupling the probe comb into the reference gas cell, and another 1 ms waveform was recorded. Individual interferograms comprising the waveforms were phase corrected (as previously discussed) and averaged into single probe and reference interferograms, respectively. Fourier transforms of each averaged interferogram yielded the complex RF spectrum at each RF comb tooth, and thus the normalized complex transmission spectrum.

A typical spectrum of the P24 transition (blue dots) is plotted in Fig. 4, along with the corresponding fitted model (top panels) and residuals (bottom panels). The spectrum is normalized, linear baseline corrected, and recorded in a total integration time of 2 ms. For a series of 50 individual P24 spectra like that plotted in Fig. 4, the highest observed spectroscopic SNR, defined as the maximum absorbance (αL) divided by the standard deviation of the fitted residuals (observed-minus-calculated, σ_omc,x), was 197:1. Overall, we observed SNRs for H¹³CN as high as 326:1 (R8 transition).

Fig. 4.

Complex transmission spectrum of the P24 rotational-vibrational transition of the 2ν₁ H¹³CN band with vacuum frequency f₀ = 191.973 284 280 THz [17]. Experimental data points are plotted as blue dots, the fitted model as black lines (top panels), and the residuals as black lines (bottom panels). Plotted in the top left panel is the absolute value of the complex transmission spectrum T = exp{−(α + iφ)L/2}, and the corresponding phase angles are plotted in the top right panel.

The complex sample transmission was modeled as T = exp{−(α + iφ)L/2}, where α and φ are the resonant intensity absorption and dispersion coefficients, respectively, of the sample gas. For the model, we used a complex Voigt line profile with a fixed inhomogeneous contribution from Doppler broadening and a floated homogeneous contribution from pressure broadening. To test the influence of potential systematic sources of uncertainty such as interfering hot-band transitions, sample pressure drift, or spurious etalons, we performed repeat measurements over several weeks using several absolute optical detunings δ₀ = f₀ − f_CW ≤ ± f_rep, several values of f_rep, three photoreceivers, and a range of optical powers. From these measurements, we estimate that the long-term reproducibility of our reported H¹³CN transition intensities contributed 1.5 % to the combined relative uncertainty budget.

We estimate the theoretical spectral noise limit from Newbury, Coddington and Swann to be σ_omc,t = 3.2 × 10⁻³, a value equal to the quadrature sum of detector noise, quantum shot noise, and the system dynamic range [27]. For the individual P24 spectrum in Fig. 4, the experimental spectral noises were σ_omc,x = 4.6× 10⁻³ for transmission (bottom left panel) and σ_omc,x = 6.1× 10⁻³ rad for phase (bottom right panel). Therefore, our optimum system performance was close to the theoretical limit (which assumes a normal distribution for the probe/LO comb power spectrum [27]).

The spectral acquisition and analysis presented above was performed for the following 2ν₁ H¹³CN transitions: R8, P11, P14, P16, P17, P20, P23, and P24. Because the pressure self-broadening coefficients change by more than a factor of four between these transitions, we adjusted f_rep to maintain at least four comb teeth per twice the calculated homogeneous broadening (i.e., full width) at an estimated sample pressure of p = 13.3 kPa (100 Torr) [17, 26]. This trivial flexibility highlights another advantage of our DEOFC system, namely on-demand f_rep agility over more than five orders of magnitude [5–14] and limited only by the DDMZM bandwidth.

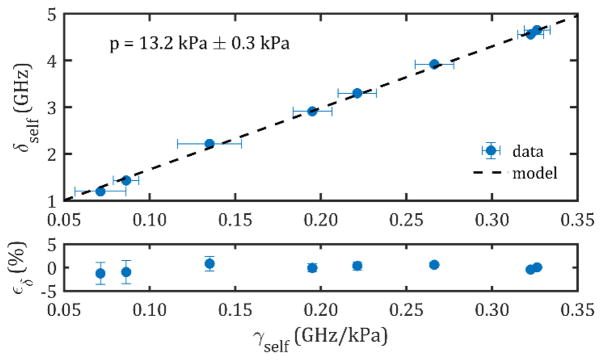
To report accurate values of S_int by measurement of the integrated line area, we required accurate knowledge of the H¹³CN sample conditions, including pressure, temperature, mole fraction, isotopic abundance, and optical path length. Because we used a commercial flame-sealed H¹³CN gas cell, we could not make a direct measurement of the sample pressure during spectral acquisition. However, the H¹³CN homogeneous broadening coefficients associated with pressure self-broadening (δ_self) are known [17, 26]. Plotted in Fig. 5 are the measured homogeneous broadenings for all isolated H¹³CN transitions investigated herein versus the known pressure self-broadening coefficients measured at NIST [17].

Fig. 5.

Top panel. Plot of the measured homogeneous contributions to the fitted Voigt profiles (δ_self) vs. the known pressure self-broadening coefficients (γ_self) [17]. Error bars represent the ± 1σ uncertainties in δ_self (statistical fit uncertainty) and γ_self [17], respectively. The linear model (black dashed line) reveals a fitted sample pressure of p = 13.2 kPa ± 0.3 kPa. Bottom panel. Fractional fitted residuals ε_δ = r_i/δ_self, where r_i = δ_{self, obs.} − δ_{self, calc.}, along with the fractional relative uncertainties (σ/δ_self).

The result of Fig. 5 is a weighted linear fit, with the sample pressure as its slope. We measure p = 13.2 kPa ± 0.3 kPa (relative uncertainty of 2.0 %), in agreement with the manufacturer’s specification of p = 13.3 kPa ± 1.3 kPa. The residuals from the fitted linear model r_i = δ_{self, obs.} − δ_{self, calc} are plotted relative to δ_self in the bottom panel of Fig. 5, where ε_δ = r_i/δ_self. Sample temperature (average value of 297.2 K ± 0.4 K) was monitored during spectral acquisition using a NIST-calibrated platinum resistance thermometer mounted in good thermal contact with the gas cell. Measured values of S_int were corrected to a reference temperature of 296 K using the known H¹³CN total partition function [1, 2], transition frequencies [2], and lower state energies [2]. Relative uncertainties in the sample temperature, mole fraction, optical path length, and isotopic abundance were 0.1 %, 0.6 %, 1.3 %, and 1.4 %, respectively. The quadrature sum of all relative uncertainties yielded an estimated combined relative uncertainty of σ_S = 3 %.

Absolute H¹³CN transition intensities at 296 K, scaled by the HITRAN natural isotopic abundance χ₁₃₄ = 0.011068 [1], are listed in Table 1, along with their combined relative uncertainties, rotational assignments, and nominal values of f_rep. For comparison of S_int with those calculated from theory, we define ε_UCL = S_UCL/S_int − 1, where S_UCL were calculated for inclusion in the ExoMol database by researchers at the University College London (UCL) using quantum chemistry methods [2]. The average deviation between theory and experiment is ε_UCL < 2 %, comparable to our reported σ_S = 3 %.

Table 1.

Measured intensities (S_int) for the 2ν₁ band of H¹³CN. Combined relative uncertainties (σ_S/S_int) and ab initio intensities [2] expressed relative to S_int (ε_UCL) are also listed.

Transition	frep (GHz)	Sint × 1023 (cm/molecule)	σS/Sint (%)	εUCL (%)
R8	2.175 23	7.63	3	4
P11	2.150 23	5.97	3	8
P14	1.775 23	4.58	3	4
P16	1.475 23	3.48	3	1
P17	1.300 23	2.85	3	3
P20	0.900 23	1.75	3	−11
P23	0.575 23	0.720	3	−1
P24	0.475 23	0.502	3	6

To the best of our knowledge, experimental values of S_int for this overtone band of H¹³CN were only reported once before using Fourier transform spectroscopy (FTS) [28]. For the eight transitions measured here, we report an average value of ε_H-P = S_H-P/S_int − 1 = −28 % ± 4 %, where S_H-P were calculated from the tabulated band intensity, spectroscopic equations, parameters, constants and appendices in [28], and where H-P denotes the author affiliations of Harvard and Princeton. The FTS study is broad in its scope, having reported parameters for 26 HCN bands. Therefore, further experimental validations are required to explore the discrepancy observed here for only a small number of rotational-vibrational 2ν₁ H¹³CN transitions.

In this letter, we demonstrate the need for, ability to, and benefit of phase correction of dual electro-optic frequency comb interferograms for up to 1 ms using custom post-processing. Beyond ~10 ms, additional intensity noises (fiber polarization noise, system etalon drifts, and modulator residual amplitude noise) rendered the post-processing algorithm less efficient. Therefore, the extension of phase coherence to longer time scales, as well as the addition of real-time post-processing hardware and software, is the focus of future work. With integration times > 1 ms per waveform, we anticipate exploring highly accurate intensity measurements of the entire 2ν₁ H¹³CN band. The incorporation of a fiber-coupled flow cell will also enable the accurate measurement of sample pressure, thus reducing the largest reported source of systematic uncertainty.