Cell expansion not cell differentiation predominantly co-ordinates veins and stomata within and among herbs and woody angiosperms grown under sun and shade

Abstract

Background and aims It has been proposed that modification of leaf size, driven by epidermal cell size, balances leaf water supply (determined by veins) with transpirational demand (generated by stomata) during acclimation to local irradiance. We aimed to determine whether this is a general pattern among plant species with contrasting growth habits.

Methods We compared observed relationships between leaf minor vein density, stomatal density, epidermal cell size and leaf size in four pairs of herbs and woody species from the same families grown under sun and shade conditions with modelled relationships assuming vein and stomatal densities respond passively to epidermal cell expansion. Leaf lignin content was also quantified to assess whether construction costs of herbaceous leaf veins differ from those of woody plants and the leaf mass fraction invested in veins.

Key Results Modelled relationships accurately described observed relationships, indicating that in all species, co-ordinated changes to the density of minor veins and stomata were mediated by a common relationship between epidermal cell size, vein density and stomatal density, with little or no impact from stomatal index. This co-ordination was independent of changes in leaf size and is likely to be an adaptive process driven by the significant proportion of biomass invested in veins (13·1 % of sun leaf dry weight and 21·7 % of shade leaf dry weight). Relative costs of venation increased in the shade, intensifying selective pressure towards economizing investment in vein density.

Conclusions Modulation of epidermal cell size appears to be a general mechanism among our experimental species to maintain a constant ratio between leaf anatomical traits that control leaf water fluxes independently of habit. We propose that this process may co-ordinate plasticity in hydraulic supply and demand in the majority of eudicot angiosperms.

INTRODUCTION

The efficiency with which the leaf vascular system distributes liquid water to the mesophyll tissue is a fundamental determinant of photosynthetic capacity because water supply imposes a limit on stomatal aperture and, as a result, the uptake of carbon dioxide (CO₂) (Meinzer and Grantz, 1990; Brodribb et al., 2005, 2007). Previous research has found a strong correlation between leaf conductances to water in liquid and vapour phase across a diversity of plant species (Sack et al., 2003, 2005; Brodribb et al., 2005). In addition, the co-ordination of these conductances during leaf acclimation to sun and shade appears to be modulated by plastic changes to minor vein density (total minor vein length per unit area) and stomatal density (total number of stomata per unit area) in a diverse range of woody angiosperm species (Brodribb and Jordan, 2011; Carins Murphy et al., 2012). In general, shade leaves of woody plants have lower densities of veins and stomata, lower conductance to water (liquid and vapour) and lower rates of CO₂ assimilation (Wylie, 1949; Abrams and Kubiske, 1990; Ashton and Berlyn, 1994; Uhl and Mosbrugger, 1999; Brodribb and Jordan, 2011). This implies that the leaf hydraulic and photosynthetic systems can acclimate to local conditions, particularly situations with different levels of light, to provide a balanced supply of water and CO₂ for transpiration and photosynthesis.

Shade leaves of woody angiosperms are often larger than sun leaves from the same species or individual (Bergen, 1904; Poole et al., 1996). This plasticity is a potential mechanism by which the balance between water supply and demand is maintained under contrasting light environments (Zwieniecki et al., 2004; Carins Murphy et al., 2012; Martins et al., 2014). Zwieniecki et al. (2004) demonstrated that vein density is linked to differential leaf expansion within Quercus rubra trees in a way that ensures the water transport system is suited to the different evaporative demands experienced at the top and bottom of the canopy. Furthermore, plasticity in leaf size in the angiosperm tree Toona ciliata (mediated by variation in epidermal cell size) was found to regulate vein density and stomatal density, suggesting that differential leaf expansion can drive co-ordinated changes to the density of veins and stomata through a ‘dilution’ effect (Carins Murphy et al., 2012). If the density of veins and stomata is passively regulated by this dilution effect, then the efficiency of water delivery to the stomata through the leaf vasculature (the leaf hydraulic conductance) and the demand for water generated at the stomata (the stomatal conductance) remain balanced during acclimation to light (Carins Murphy et al., 2012). Such acclimation allows leaves to approach a balance whereby investment in the leaf vein network is sufficient such that stomata are supplied with the minimum amount of water required to allow them to open fully under well-watered conditions. The stomata can therefore provide the CO₂ required for maximum photosynthesis, but with the minimum amount of leaf vein infrastructure. Under these circumstances, plants are thought to optimize photosynthetic gain for the energy invested in the construction and ongoing maintenance of the vascular and stomatal systems (Brodribb and Jordan, 2011; Franks et al., 2012).

The studies outlined above were primarily concerned with woody plants, and the generality of this model is unknown, particularly for herbs which may have different capacities and mechanisms for leaf acclimation to different light conditions. Although the leaves of some herbaceous species follow the same pattern as many woody species in undergoing increased expansion when grown under low light (Hughes, 1959; Willmot and Moore, 1973; Ciha and Brun, 1975; Rawson and Craven, 1975; Young and Smith, 1980; Thomas et al., 2003), sun leaves are larger than shade leaves in other species (Gay and Hurd, 1975; Dengler, 1980; Kalve et al., 2014). If increased leaf expansion acts to decrease vein and stomatal densities in unison in herbs (as observed in woody plants), then species producing large sun leaves with large epidermal cells and small shade leaves with small epidermal cells would be maladapted. This is because sun leaves would have lower densities of veins and stomata than shade leaves and, as a result, either shade leaves would be oversupplied with veins and stomata (and therefore impose energetic costs on the plant), or sun leaves would be undersupplied and susceptible to the adverse effects of high evaporative demand under high light. This suggests that the passive response of vein and stomatal densities to differential leaf expansion described above for T. ciliata (Carins Murphy et al., 2012) may be absent in herbaceous plants that produce larger leaves under sun conditions. Furthermore, recent research suggests that leaf size can be modified independently of epidermal cell size in woody species and that vein and stomatal densities are instead correlated with epidermal cell size (Brodribb et al., 2013; Carins Murphy et al., 2014). This provides a mechanism to control leaf size and vein and stomatal densities independently. Brodribb et al. (2013) demonstrated that vein and stomatal densities are correlated with epidermal cell size across woody angiosperm species from the Proteaceae family, but it is not known whether these relationships are present in herbs or whether this mechanism enables plastic changes to vein density and stomatal density in response to sun and shade.

Thus, here we sought to determine whether there are general rules linking leaf size, epidermal cell size and the density of veins and stomata in a disparate group of woody and herbaceous eudicot angiosperms grown under sun and shade conditions. Specifically we aimed to determine whether differential epidermal cell expansion under sun and shade conditions and among species regulates leaf size as well as the density of veins and stomata, thus driving co-ordinated development of veins and stomata in herbs as has been observed in woody plants. To do this, we first aimed to (1) establish whether there is a general relationship between epidermal cell size and leaf size across species before (2) determining whether the density of veins and stomata fits a geometric model whereby both are passively ‘diluted’ by differential epidermal cell expansion. Under a passive dilution model, it is predicted that no new xylem or guard cells are added during leaf expansion and both are passively diluted by epidermal cell expansion. To investigate this, we compared modelled relationships between vein density, stomatal density and epidermal cell size that assume that vein and stomatal densities respond passively to epidermal cell expansion with observed relationships across four pairs of woody and herbaceous angiosperm species (one woody and one herbaceous species from each of four families of eudicot angiosperms; Table 1). This group included some agricultural cultivars (Glycine max ‘Bunya’, Ocimum basilicum and Solanum lycopersicum ‘Rainbow’) which may not have experienced the same natural selective pressures as the other species. Lastly, we aimed to (3) combine these data with the leaf lignin content of the herbs and woody species to determine whether the construction costs of herbaceous leaf vein networks differ from those of woody plants and what proportion of leaf weight can be attributed to the veins.

Table 1.

Family and habit of the experimental species

Family	Woody species	Herbaceous species
Asteraceae	Bedfordia salicina (Labill.) DC.	Senecio minimus Poir.
Fabaceae	Bauhinia purpurea L.	Glycine max (L.) Merr. ‘Bunya’
Lamiaceae	Prostanthera lasianthos Labill.	Ocimum basilicum L.
Solanaceae	Solanum laciniatum Aiton	Solanum lycopersicum L. ‘Rainbow’

Assuming that vein and stomatal densities change due to a common dilution by epidermal cells, then geometrically it would be expected to find strong positive relationships between vein density and 1/√epidermal cell size, stomatal density and 1/epidermal cell size, and vein density and √stomatal density under a passive dilution model (i.e. where no new xylem or guard cells are added during leaf expansion, xylem cells expand in unison with epidermal cells and both are passively diluted by epidermal cell expansion). It follows that these relationships in the experimental species should be explained by modelled relationships that make these assumptions. Positive relationships were also predicted between lignin per unit area and minor vein volume per unit area because lignin is a major component of plant veins, and between leaf hydraulic conductance and vein density because leaf hydraulic conductance is limited by the distance liquid water travels between the vein tips and evaporative surfaces near the stomata, which is inversely proportional to vein density (Brodribb et al., 2007).

MATERIALS AND METHODS

Plant material and experimental conditions

Eight angiosperm species were selected to provide a woody and herbaceous representative from each of four plant families (Table 1). Five plants of each species were grown under either sun or shade conditions in a mixture of 76 % composted pine bark and 24 % coarse potting sand. All plants received weekly applications of liquid fertilizer (Aquasol, Hortico). As a result of mortality, four Bauhinia purpurea plants in the shade treatment, four Bedfordia salicina plants in the sun treatment, three B. salicina plants in the shade treatment and four G. max plants in both treatments were available for analysis. Furthermore, only two B. salicina shade plants were measured for leaf hydraulic conductance. Four additional T. ciliata plants were grown under sun and shade conditions to determine lignin content, leaf mass per unit area (LMA) and minor vein volume per unit area of this species. These data were compared with previously published data from T. ciliata grown under similar sun and shade conditions (Carins Murphy et al., 2012). All plants were grown in a glasshouse under controlled conditions. Woody species were less than a year old at the time of the experiment and were allowed to acclimate to experimental conditions for approx. 3 months so a new cohort of leaves could initiate and expand. Herbaceous species were grown from seed under experimental conditions and were 1–2 months old at the time of the experiment. All plants experienced day and night temperatures of 15 and 25 ºC, respectively, and ambient relative humidity. Natural light was supplemented by sodium vapour lamps in the morning and evening to maintain a 14 h photoperiod. Plants grown in the sun treatment received a maximum photosynthetic photon flux density (PPFD) of approx. 1800 μmol m^–2 s^–1, while plants in the shade treatment were grown under 90 % shade cloth and received a maximum PPFD of approx. 200 μmol m^–2 s^–1 (preliminary tests showed that lower light intensities caused mortality in several species).

Leaf hydraulic conductance

Two healthy, mature leaves from the most recently expanded cohort per plant were used to determine maximum leaf hydraulic conductance (Table 2). Leaves were measured between 1000 and 1300 h using the evaporative flux method (Sack et al., 2002; Brodribb and Holbrook, 2006). Plants were transferred to the laboratory where leaves to be measured were acclimated to humid, low CO₂ conditions in plastic zip lock bags for approx. 1 h to ensure stomata were fully open (Brodribb et al., 2009). Leaves were excised under water and attached to a flow meter (Brodribb and Holbrook, 2006) (for construction details see http://prometheuswiki.publish.csiro.au/tiki-index.php?page=Constructing+and+operating+a+hydraulics+flow+meter). Leaves were then placed in conditions suitable for transpiration (i.e. under a light source providing an approximate PPFD of 600 μmol m^–2 s^–1 and heated evenly by a stream of warm air maintaining leaf temperature between 25 and 30 ºC). Transpiration was allowed to reach a steady state (<10 % variation over 240 s) and the resulting flux of water into the leaf was recorded. Leaves were detached from the flow meter and leaf water potential was measured immediately after using a pressure chamber. Leaf hydraulic conductance (K_L) was calculated using the following equation:

$$K_{\mathrm{L}}=F/{\Psi }_{\mathrm{L}}$$ (1)

where F is the rate of water flow into the leaf and Ψ_L is the leaf water potential at steady state. Leaves were scanned and leaf size determined using an image analysis program (ImageJ; National Institutes of Health, Bethesda, MD, USA). Leaf hydraulic conductance was normalized to leaf size and the viscosity of water at 20 ºC using an empirical function based on data from Korson et al. (1969) to account for variation in leaf size and the temperature response of water viscosity.

Table 2.

A list of measured traits and their units

Variable	Unit
Epidermal cell density	mm–2
Epidermal cell size	mm2
Leaf hydraulic conductance	mmol m–2 s–1 MPa–1
Leaf mass per unit area	mg mm–2
Leaf size	cm2
Lignin per unit area	mg mm–2
Lignin per unit dry weight	mg g–1
Midday leaf water potential	MPa
Minor vein diameter	mm
Minor vein volume per unit area	mm3 mm–2
Stomatal density	mm–2
Stomatal index	Unitless
Stomatal size	mm2
Vein density	mm mm–2

Midday leaf water potential

An additional two healthy, mature leaves from the most recently expanded cohort per plant were used to determine midday leaf water potential (Table 2) using a pressure chamber.

Anatomical traits and leaf size

The same two leaves per plant used to determine leaf hydraulic conductance were scanned at 300 pixels per inch to measure leaf size (Table 2) using ImageJ. Vein density, minor vein diameter and minor vein volume per unit area of these leaves (Table 2) were then quantified using paradermal sections. To prepare the paradermal sections, two approx. 100 mm² sections of lamina were taken at random from each leaf (one from near the leaf margin and the other from the middle of the lamina avoiding the midrib), and the adaxial epidermis and palisade tissue were removed with a sharp razor. Sections were placed in commercial household bleach (50 g L^–1 sodium hypochlorite and 13 g L^–1 sodium hydroxide) until all pigment was removed. Sections were rinsed, stained with 1 % toluidine blue and mounted on microscope slides in phenol glycerine jelly. Five fields of view (FOVs) at × 10 magnification (FOV area 0·56 mm²) were photographed from each section using a camera (Digital Sight DS-L1; Nikon, Melville, NY, USA) mounted on a microscope (DM 1000; Leica, Nussloch, Germany). A lower ×4 magnification (FOV area 3·47 mm²) was used when photographing the shade leaves of Bedfordia salicina, O. basilicum, Senecio minimus and S. lycopersicum to ensure that at least three entire areoles were included in each FOV. This protocol was simplified in some cases because the removal of epidermis and palisade tissue was unnecessary for the thinner herbaceous leaves and the shade leaves of woody species. Vein density was measured as the total length of leaf vascular tissue per mm² of leaf area using ImageJ. The diameters of the three highest order veins per FOV were measured to determine minor vein diameter. This equated to 30 measurements of minor vein diameter per leaf. Minor vein volume per unit area (V_V) was then calculated as:

$$V_{\mathrm{V}}=\pi r^{2}L/\text{FOV} \text{area}$$ (2)

where r is the minor vein radius (half the minor vein diameter) and L is the total vein length per FOV.

Stomatal density, stomatal size (the combined area of a pair of guard cells), stomatal index, epidermal cell size and epidermal cell density (Table 2) were determined from cuticles taken from the same leaves. Two 6 mm discs were taken from each leaf and placed in commercial household bleach until the cuticle and mesophyll could be separated. One section was taken near the leaf margin and the other from the middle of the lamina (avoiding the midrib). Cuticles were rinsed, stained with 1 % crystal violet and mounted on microscope slides in phenol glycerine jelly. Five FOVs at × 20 magnification (FOV area 0·14 mm²) were photographed from all cuticles using the same microscope set-up described above [except for those of Bauhinia purpurea, where five FOVs at × 20 magnification through a × 2·5 tube (FOV area 0·025 mm²) were photographed]. Partial stomata and epidermal cells were included in density counts if visible along the top and right-hand edge of photomicrographs and discarded if visible along the bottom and left-hand edge. Stomatal size was determined for five stomata per FOV using ImageJ. Epidermal cell size (S_EC) was subsequently calculated as:

$$S_{\text{EC}}=[1 – (D_{\mathrm{S}}\times S_{\mathrm{S}})]/D_{\text{EC}}$$ (3)

where D_S is stomatal density, S_S is stomatal size and D_EC is epidermal cell density (total epidermal cells per unit area). The stomatal index (SI) was calculated according to Salisbury (1927) as:

$$\text{SI}=[D_{\mathrm{S}}/(D_{\mathrm{S}}+D_{\text{EC}})]\times 100$$ (4)

Leaf lignin content and LMA

From each plant, lignin content and LMA (Table 2) were measured for 5–7 leaves including the two leaves used to determine leaf hydraulic conductance, leaf size and anatomy. The midrib (or rachis in the case of T. ciliata) was removed from all leaves before they were scanned, freeze-dried and weighed. The dry leaves were then ground with a sample mill (Cyclotec 1093; FOSS, Hillerød, Denmark) and stored in air-tight plastic sample jars. Leaves were analysed for acid detergent lignin using the filter bag technique in an ANKOM Model 200 fibre analyser and the method for determining acid detergent lignin in beakers developed by ANKOM (ANKOM Technology, New York, USA). For analytical procedures see https://ankom.com/sites/default/files/document-files/Method_5_ADF_Method_A200_RevE_11_04_14.pdf and https://ankom.com/sites/default/files/document-files/Method_8_Lignin_in_beakers_3_13_13.pdf. Treatment with acid detergent solution removed the protein and other acid-soluble material that would interfere with lignin determination, leaving behind a residue that consisted of cellulose, lignin, cutin and acid-insoluble ash (mainly silica) (Goering and Van Soest, 1970). Treatment with 72 % sulphuric acid dissolved the cellulose, leaving behind the acid detergent lignin residue containing lignin, cutin and acid-insoluble ash (Goering and Van Soest, 1970). Acid detergent lignin as a percentage of sample dry weight was calculated as:

$$(({\mathrm{W}}_3–{ \mathrm{W}}_1)\times 100)/{\mathrm{W}}_2$$ (5)

where W₃ is the final filter bag weight after extraction, W₁ is the empty filter bag weight and W₂ is the sample weight before extraction. Lignin per unit dry weight was calculated as the lignin dry weight present in each sample in mg divided by the total sample dry weight in g, while lignin per unit area was calculated as the lignin dry weight present in each sample in mg divided by the sample leaf area in mm². LMA was calculated for each plant from the dry weight and area (without midrib) of the same leaves used for lignin quantification.

Statistical analysis

The plasticity of leaf size, LMA, anatomical traits (minor vein volume per unit area, minor vein diameter and epidermal cell size), leaf hydraulic conductance, midday leaf water potential, lignin per unit area and lignin per unit dry weight was assessed using two-way analysis of variance (ANOVA) on the influence of local irradiance and species on each of the traits listed above in R (R Core Team, 2014). Log and square root transformations were applied when needed to normalize the data. Where interaction effects were significant, the mean values for each trait in plants grown under sun and shade were compared with unpaired t-tests corrected for multiple comparison using the Dunn–Sidak method (Sokal and Rohlf, 1995). The effect of plant habit on lignin per unit area across light treatments and plant families was also assessed using three-way ANOVA. Toona ciliata was not included in analyses to assess the plasticity of leaf size, epidermal cell size or leaf hydraulic conductance because these data are included in Carins Murphy et al. (2012).

Analysis of covariance (ANCOVA) performed in R were used to test if single linear regressions could describe the relationships between the following pairs of traits irrespective of plant habit or local irradiance: vein density and 1/√epidermal cell size, stomatal density and 1/epidermal cell size, vein density and √stomatal density, lignin per unit area and minor vein volume per unit area, and leaf hydraulic conductance and vein density. Log transformations were applied when needed to normalize the data. Toona ciliata was not included in analysis of the relationship between vein density and leaf hydraulic conductance because this relationship has appeared previously in Carins Murphy et al. (2012). Where single regressions were present, the r² was calculated using R.

‘Passive dilution’ models

We compared modelled relationships that assume vein and stomatal density change due to a common dilution by epidermal cells with observed relationships across all species using ANCOVA in R. We modelled the relationship between stomatal density and epidermal cell size based on the assumption that the epidermis was made up of only epidermal and guard cells (no significant proportions of glandular cells or trichome bases were present in any of the species sampled), and that the ratio of stomata to epidermal cells (reflected in the stomatal index) remained constant. Thus, epidermal cell size was modelled as a function of stomatal density using a modified version of eqn (3) that incorporates the geometric relationship between stomatal size and density and the dependence of epidermal cell density on stomatal index:

$$S_{\mathrm{E}\mathrm{C}}=\frac{1-\left(D_{\mathrm{S}}\times \left(a\times D_{\mathrm{S}}^b\right)\right)}{\left(D_{\mathrm{S}}/\text{SI}\right)-D_{\mathrm{S}}}$$ (6)

Stomatal size is known to be negatively correlated with stomatal density (Franks and Beerling, 2009) so we fitted an empirical function to the data based upon the pooled data from all species to account for this association (a = 0·0085 and b = –0·5588) (Fig. 1). The r² for the relationship between stomatal density and size across all species was determined using SigmaPlot (Systat Software, San Jose, CA, USA). Epidermal cell density was calculated as:

$$D_{\text{EC}}=(D_{\mathrm{S}}/\text{SI}) – D_{\mathrm{S}}$$ (7)

according to the stomatal index. Three different values of stomatal index (the mean, minimum and maximum across all species) were used to illustrate the sensitivity to this parameter. Similarly we modelled the relationship between vein density and epidermal cell size using the simplified assumption that vein length is associated with a fixed proportion of the perimeter of an epidermal cell. Thus, a geometric model of vein density as a function of epidermal cell size was determined for a fixed stomatal index (all species mean) incorporating the measured relationship between stomatal density and stomatal size across all species as described above. Assuming vein density (D_V) was a function of epidermal cell size (i.e. there is a positive relationship between vein density and 1/√epidermal cell size), we fitted the function D_V = a × S_EC^–0·5 where a is proportional to the epidermal cell perimeter associated with vein length. This returned a value of 0·1865. This value was then used to predict the impact of epidermal cell size on vein density (using the equation D_V = 0·1865 × S_EC^–0·5). Finally, the expected relationship between vein density and √stomatal density was modelled by combining the relationships above.

Fig. 1.

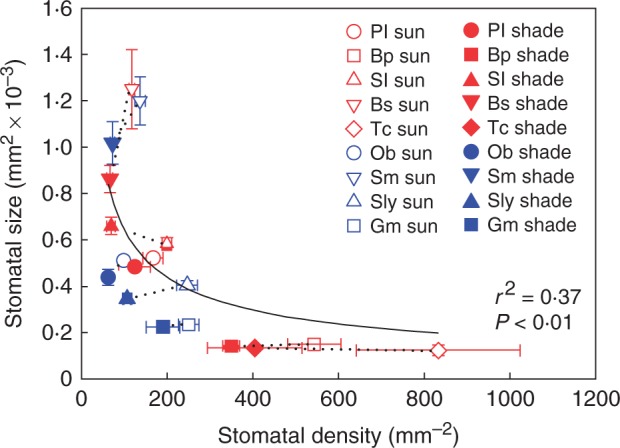
Mean stomatal size and stomatal density ± s.d. across the five woody species Bauhinia purpurea (Bp), Bedfordia salicina (Bs), Prostanthera lasianthos (Pl), Solanum laciniatum (Sl) and Toona ciliata (Tc), and the four herbaceous species Glycine max (Gm), Ocimum basilicum (Ob), Senecio minimus (Sm) and Solanum lycopersicum (Sly) grown in sun and shade (sun and shade species pairs joined by a black dotted line). Across all species, S_S = 0·0085 × D_S^–0·559 (r² = 0·37, F_1,16 = 9·26, P < 0·01).

RESULTS

Relationship between leaf size and epidermal cell size

There was no overall relationship between leaf and epidermal cell size among species (Fig. 2). In addition, the total number of cells per leaf was not predictive of light-induced changes to leaf size. Local irradiance had a general effect on epidermal cell size, with shade leaves having larger epidermal cells than sun leaves (Table 3; Supplementary Data Table S1). There was some variation in the size of the effect between species, as indicated by significant local irradiance by species interaction effects that were much smaller than the main effects (Table 3; Table S1). In contrast, the effect of local irradiance on leaf size varied substantially among species (Table 3; Table S1). Leaf size was not significantly affected by local irradiance in three woody species and two herbs (Table 3). However, the shade leaves of Solanum laciniatum (woody) and S. lycopersicum (herb) were significantly larger than the sun leaves, and the shade leaves of G. max (herb) were significantly smaller than the sun leaves (Table 3).

Fig. 2.

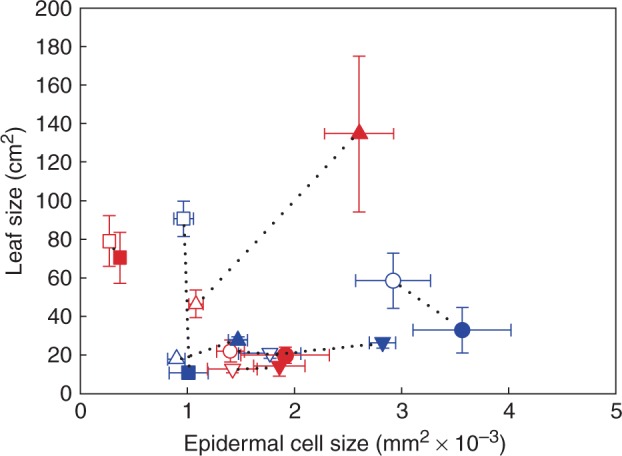
Mean leaf size and epidermal cell size ± s.d. of the four woody species and the four herbaceous species grown in sun and shade (symbols as in Fig. 1) (sun and shade species pairs joined by a black dotted line).

Table 3.

Epidermal cell size (S_EC), leaf size (S_L), leaf hydraulic conductance (K_L) and midday leaf water potential (Ψ_L) of leaves from sun and shade plants of woody (W) and herbaceous (H) species

Species	Habit	SEC (mm2 × 10–3)		P-value	SL (cm2)		P-value	KL (mmol m–2 s–1 MPa–1)		P-value	ΨL (MPa)		P-value
		Sun	Shade		Sun	Shade		Sun	Shade		Sun	Shade
Bauhinia purpurea	W	0·27 ± 0·02	0·37 ± 0·01	<0·01	79·1 ± 5·86	70·57 ± 6·63	0·97	17·24 ± 0·45	12·11 ± 1·13	<0·05	–0·73 ± 0·07	–0·44 ± 0·03	0·08
Bedfordia salicina	W	1·42 ± 0·13	1·86 ± 0·14	0·5	12·76 ± 0·95	14·33 ± 2·98	1	11·12 ± 1·03	5·19 ± 0·34	0·14	–1·16 ± 0·2	–0·64 ± 0·07	0·74
Prostanthera lasianthos	W	1·4 ± 0·06	1·91 ± 0·18	0·22	22·09 ± 2·49	19·89 ± 1·86	1	11·49 ± 0·68	9·05 ± 0·49	0·15	–0·72 ± 0·06	–0·37 ± 0·04	<0·05
Solanum laciniatum	W	1·08 ± 0·03	2·60 ± 0·14	<0·001	46·5 ± 3·2	134·7 ± 18·07	<0·05	15·13 ± 1·08	11·98 ± 1·04	0·43	–0·44 ± 0·01	–0·18 ± 0·01	<0·001
Glycine max	H	0·96 ± 0·05	1·01 ± 0·09	1	90·64 ± 4·55	10·8 ± 0·61	<0·001	30·25 ± 1·52	14·68 ± 1·93	<0·01	–0·25 ± 0·01	–0·31 ± 0·02	0·14
Ocimum basilicum	H	2·92 ± 0·16	3·56 ± 0·2	0·26	58·48 ± 6·41	32·88 ± 5·24	0·11	10·51 ± 0·97	13·77 ± 0·76	0·21	–0·28 ± 0·01	–0·19 ± 0·01	<0·01
Senecio minimus	H	1·77 ± 0·13	2·82 ± 0·05	<0·001	20·90 ± 1·09	26·32 ± 1·22	0·08	10·8 ± 0·88	7·85 ± 0·7	0·22	–0·5 ± 0·04	–0·52 ± 0·05	1
Solanum lycopersicum	H	0·9 ± 0·04	1·47 ± 0·04	<0·001	17·87 ± 0·38	27·6 ± 0·88	<0·001	11·97 ± 0·5	7·5 ± 0·34	<0·001	–0·39 ± 0·02	–0·23 ± 0·02	<0·01

Values are means ± s.e.

Means of the two light treatment groups were compared using unpaired t-tests. P-values < 0·05 are shown in bold.

Relationships between vein density, stomatal density, epidermal cell size and stomatal index

Separate highly significant linear regressions for sun and shade plants described the relationships between stomatal density and 1/epidermal cell size (sun plants, r² = 0·95, F_1,7 = 126·4, P < 0·001; shade plants, r² = 0·92, F_1,7 = 82·83, P < 0·001) and between vein density and 1/√epidermal cell size (sun plants, r² = 0·88, F_1,7 = 49·27, P < 0·001; shade plants, r² = 0·85, F_1,7 = 39·78, P < 0·001) irrespective of plant habit (Supplementary Data Table S2). This meant that shade leaves had fewer veins and stomata per epidermal cell than sun leaves. Additionally, light-induced changes to vein and stomatal density were independent from the total number of cells per leaf. A single highly significant linear regression described the relationship between vein density and √stomatal density (r² = 0·92, F_1,16 = 186·3, P < 0·001) irrespective of plant habit or local irradiance (Table S2).

The observed relationship between stomatal density and epidermal cell size when sun and shade plants were pooled together was not significantly different from the modelled relationship using the mean stomatal index across all species, and most variation in the data was accounted for when the observed range in stomatal index was plotted (mean stomatal index + 31·67 % and – 34·25 %) (Fig. 3; Supplementary Data Table S3). Likewise, the observed relationship between vein density and epidermal cell size when sun and shade plants were pooled together was not significantly different from the modelled relationship using the mean stomatal index (Fig. 4; Table S3), and the observed relationship between vein density and stomatal density was not significantly different from the modelled relationship expected if both parameters were co-dependent upon epidermal cell size (Fig. 5; Table S3). Although the shade leaves of most species had a lower stomatal index than sun leaves, there was no overall relationship between stomatal density and stomatal index among species (Fig. 6).

Fig. 3.

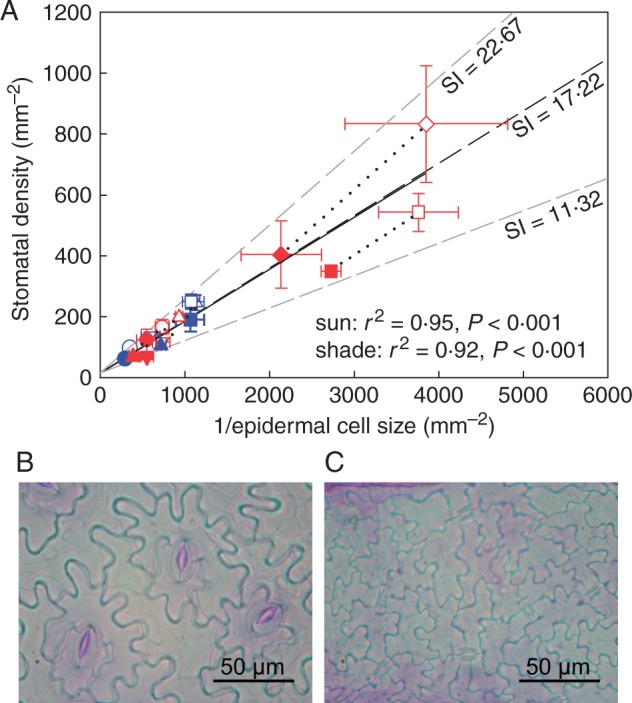
(A) Observed relationship between stomatal density and epidermal cell size (black solid line) compared with the modelled relationship where stomatal density is determined uniquely by changes in epidermal cell size (black dashed line, see the Materials and Methods for details). Stomatal density in all species is determined largely by epidermal cell expansion rather than changes in stomatal index (SI). The effect of epidermal cell size on stomatal density is shown at three different values of stomatal index; the mean stomatal index across all species (black dashed line) and the minimum and maximum stomatal indices (grey dashed lines). Symbols (as in Fig. 1) show the mean observed values ± s.d. of the five woody species (including Toona ciliata) and the four herbaceous species grown in sun and shade (sun and shade species pairs joined by a black dotted line). The observed relationship is not significantly different from the modelled relationship using the mean stomatal index for all species and treatments. Linear regressions describe the relationship between stomatal density and epidermal cell size under sun and shade conditions (log-transformed data); D_S under sun conditions = 0·853 × 1/S_EC – 0·23 (r² = 0·95, F_1,7 = 126·4, P < 0·001), D_S under shade conditions = 0·879 × 1/S_EC – 0·41 (r² = 0·92, F_1,7 = 82·83, P < 0·001). Also shown are representative cuticle preparations from leaves of (B) Ocimum basilicum and (C) T. ciliata. Note the higher density of stomata and epidermal cells in T. ciliata.

Fig. 4.

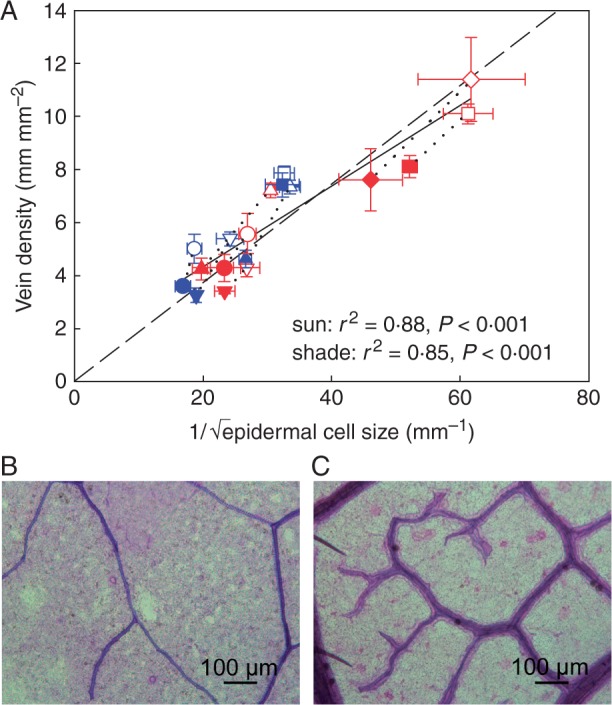
(A) Observed relationship between vein density and epidermal cell size (black solid line) compared with the modelled relationship (black dashed line, see the Materials and Methods for details). Vein density in all species follows a dependency on epidermal cell expansion similar to stomata, but vein density per epidermal cell size is significantly greater under sun conditions. The modelled effect of epidermal cell size on vein density is shown for the mean stomatal index across all species. Symbols show the mean observed values ± s.d. of the five woody species (including Toona ciliata) and the four herbaceous species grown in sun and shade (symbols as in Fig. 1) (sun and shade species pairs joined by a black dotted line). The observed relationship is not significantly different from the modelled relationship. Linear regressions describe the relationship between vein density and epidermal cell size under sun and shade conditions; D_V under sun conditions = 0·143 × 1/√S_EC + 2·102 (r² = 0·88, F_1,7 = 49·27, P < 0·001), D_V under shade conditions = 0·145 × 1/√S_EC + 0·984 (r² = 0·85, F_1,7 = 39·78, P < 0·001). Also shown are representative paradermal sections from leaves of (B) Ocimum basilicum and (C) T. ciliata. Note the higher density of veins in T. ciliata.

Fig. 5.

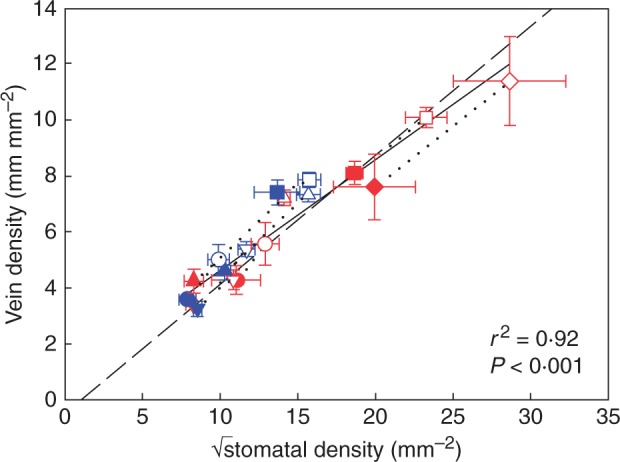
Observed relationship between vein density and stomatal density (black solid line) compared with the modelled relationship (black dashed line, see the Materials and Methods for details). Symbols show the mean observed values ± s.d. of the five woody species (including Toona ciliata) and the four herbaceous species grown in sun and shade (symbols as in Fig. 1) (sun and shade species pairs joined by a black dotted line). A single regression through the pooled data is shown as a black solid line; D_V = 0·395 × √D_S + 0·683 (r² = 0·92, F_1,16 = 186·3, P < 0·001). This linear regression is not significantly different from the modelled relationship.

Fig. 6.

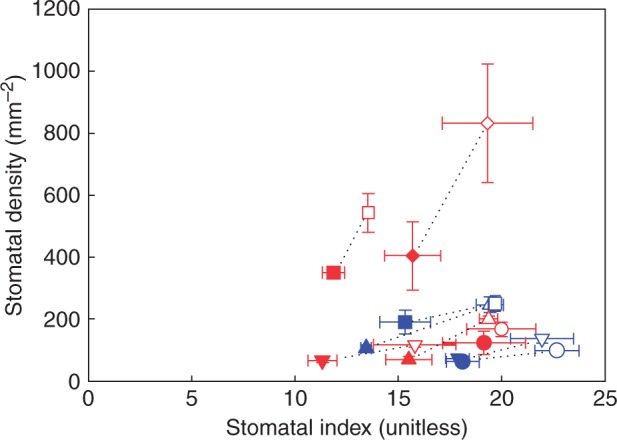
Mean stomatal density and stomatal index ± s.d. of the four woody species and the four herbaceous species grown in the sun and shade (symbols as in Fig. 1) (sun and shade species pairs joined by a black dotted line).

Leaf hydraulic conductance and vein density

A single significant linear regression (r² = 0·39, F_1,14 = 8·77, P < 0·05) described the relationship between leaf hydraulic conductance and vein density among species irrespective of plant habit or local irradiance (Fig. 7; Table S2). Local irradiance had a general effect on leaf hydraulic conductance in woody species, with shade leaves having lower leaf hydraulic conductance than sun leaves (Table 3; Table S1). There was some variation in the size of the effect, however, which was reflected by a significant local irradiance by species interaction effect that was much smaller than the main effects (Table 3; Table S1). The effect of local irradiance on leaf hydraulic conductance varied among the herbs (Table 3; Table S1). The shade leaves of two herbs (G. max and S. lycopersicum) had significantly lower leaf hydraulic conductance than sun leaves, but in the others light-induced changes to leaf hydraulic conductance were not significant (Table 3).

Fig. 7.

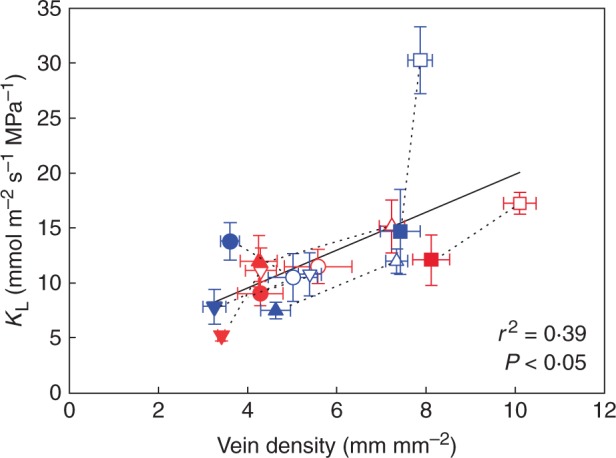
Mean leaf hydraulic conductance and vein density ± s.d. of the four woody species and the four herbaceous species grown in the sun and shade (symbols as in Fig. 1) (sun and shade species pairs joined by a black dotted line). The linear regression of the relationship between leaf hydraulic conductance and vein density across all species is represented by a black solid line; K_L = 1·724 × D_V + 2·656 (r² = 0·39, F_1,14 = 8·77, P < 0·05).

Midday leaf water potential

Shade leaves of woody species had higher midday leaf water potential than sun leaves (Table 3; Table S1). In contrast, the effect of local irradiance on midday leaf water potential varied significantly among the herbs (Table 3; Table S1). Among the herbs, the shade leaves of O. basilicum and S. lycopersicum had significantly higher midday leaf water potential than sun leaves, whereas in the remaining herbs, local irradiance did not significantly affect midday leaf water potential (Table 3).

Relationship between leaf lignin content and minor vein volume

A significant linear regression (r² = 0·42, F_1,16 = 11·46, P < 0·01) described the dependence of lignin per unit area upon minor vein volume per unit area among species when the data were pooled across light treatments and plant habits (Fig. 8A; Table S2). Data were pooled because all other effects and interactions were either insignificant or minor (Table S2). Furthermore, shade leaves had less lignin and minor vein volume per unit area than sun leaves (Table 4; Table S1). There was some variation between species in the size of the effect of local irradiance on lignin per unit area in woody species and on minor vein volume per unit area in the herbs, as indicated by significant local irradiance by species interaction effects that were much smaller than the main effects (Table 4; Table S1). Minor veins were also thinner in shade leaves than in sun leaves (Table 4; Table S1). As above, variation in the size of this effect between species was indicated by significant local irradiance by species interactions that were smaller than the main effects (Table 4; Table S1).

Fig. 8.

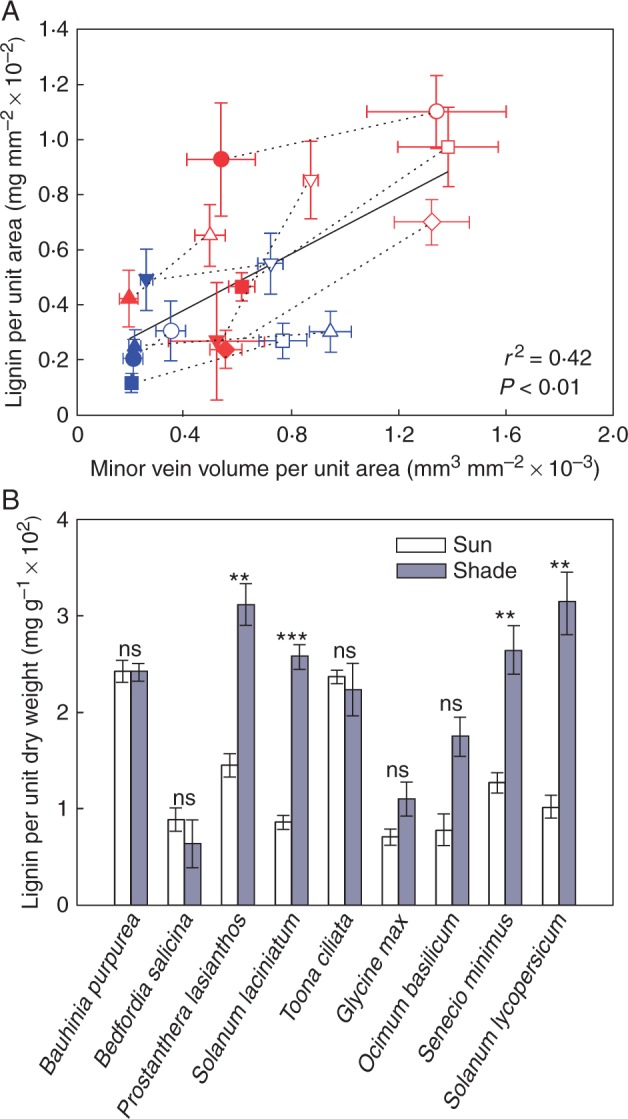
(A) Mean lignin per unit area and minor vein volume per unit area ± s.d. of the five woody species (including Toona ciliata) and the four herbaceous species grown in sun and shade (symbols as in Fig. 1) (sun and shade species pairs joined by a black dotted line). The linear regression of the relationship between lignin per unit area and minor vein volume per unit area across all species is represented by a black solid line. For the log-transformed data lignin per unit area = 438·17 × minor vein volume per unit area – 2·65 (r² = 0·42, F_1,16 = 11·46, P < 0·01). (B) Mean lignin per unit dry weight (± s.e.) of the five woody species and the four herbaceous species grown in the sun (white columns) and shade (grey columns). Results of unpaired t-tests are indicated above columns (***P < 0·001; **P < 0·01; *P < 0·05; ns, P > 0·05).

Table 4.

Lignin per unit area, minor vein volume per unit area, minor vein diameter and leaf mass per unit area (LMA) of leaves from sun and shade plants of woody (W) and herbaceous (H) species

Species	Habit	Lignin per unit area (mg mm–2 × 10–2)		P-value	Minor vein volume per unit area (mm3 mm–2 × 10–3)		P-value	Minor vein diameter (mm × 10–2)		P-value	LMA (mg mm–2 × 10–2)		P-value
		Sun	Shade		Sun	Shade		Sun	Shade		Sun	Shade
Bauhinia purpurea	W	0·97 ± 0·06	0·47 ± 0·03	<0·01	1·38 ± 0·08	0·61 ± 0·02	<0·001	1·31 ± 0·04	0·98 ± 0·02	<0·01	4·01 ± 0·18	2·02 ± 0·08	<0·001
Bedfordia salicina	W	0·85 ± 0·08	0·27 ± 0·12	0·14	0·87 ± 0·02	0·52 ± 0·1	0·23	1·64 ± 0·02	1·37 ± 0·14	0·5	10·93 ± 1·33	3·99 ± 0·4	0·07
Prostanthera lasianthos	W	1·1 ± 0·06	0·93 ± 0·09	0·76	1·34 ± 0·12	0·54 ± 0·06	<0·01	1·74 ± 0·05	1·23 ± 0·02	<0·001	7·77 ± 0·66	2·95 ± 0·11	<0·001
Solanum laciniatum	W	0·65 ± 0·05	0·42 ± 0·05	0·08	0·5 ± 0·03	0·19 ± 0·02	<0·001	0·93 ± 0·02	0·75 ± 0·01	<0·001	7·62 ± 0·16	1·64 ± 0·12	<0·001
Toona ciliata	W	0·70 ± 0·04	0·24 ± 0·03	<0·01	1·32 ± 0·07	0·55 ± 0·03	<0·001	1·28 ± 0·02	0·94 ± 0·02	<0·001	2·97 ± 0·15	1·06 ± 0·03	<0·001
Glycine max	H	0·27 ± 0·03	0·12 ± 0·02	<0·05	0·77 ± 0·04	0·2 ± 0·01	<0·001	1·1 ± 0·02	0·59 ± 0·01	<0·001	3·84 ± 0·07	1·08 ± 0·03	<0·001
Ocimum basilicum	H	0·31 ± 0·05	0·21 ± 0·03	0·68	0·35 ± 0·02	0·21 ± 0·02	<0·05	0·94 ± 0·04	0·85 ± 0·03	0·78	4·04 ± 0·34	1·16 ± 0·05	<0·001
Senecio minimus	H	0·55 ± 0·05	0·49 ± 0·05	1	0·72 ± 0·02	0·26 ± 0·01	<0·001	1·32 ± 0·03	1 ± 0·03	<0·001	4·34 ± 0·26	1·87 ± 0·09	<0·001
Solanum lycopersicum	H	0·30 ± 0·03	0·25 ± 0·03	0·93	0·95 ± 0·03	0·22 ± 0·01	<0·001	1·27 ± 0·02	0·77 ± 0·01	<0·001	2·98 ± 0·08	0·8 ± 0·01	<0·001

Values are means ± s.e.

Means of the two light treatment groups were compared using unpaired t-tests. P-values < 0·05 are shown in bold.

Lignin as a proportion of leaf dry weight

Woody species had more lignin per unit area than herbaceous species under both sun and shade conditions (Table 4; Supplementary Data Table S4). However, the shade leaves of all species had the same amount of lignin per unit dry weight as sun leaves or in some cases significantly more (Fig. 8B; Table S1). Specifically, the shade leaves of Prostanthera lasianthos and S. laciniatum had more lignin per unit dry weight than sun leaves, while in the remaining woody species there were no significant differences between sun and shade leaves (Fig. 8B). There was also some variation in the size of the effect between species in the herbs, as indicated by a significant local irradiance by species interaction effect that was smaller than the main effects (Fig. 8B; Table S1). At the same time, LMA was lower in shade leaves than in sun leaves (Table 4; Table S1). Again there was some variation in the size of the effects between species, as indicated by significant interaction effects that were much smaller than the main effects (Table 4; Table S1). Furthermore, on average, lignin comprised 13·1 and 21·7 % of leaf dry weight in sun and shade leaves, respectively.

DISCUSSION

Vein and stomatal density co-vary with epidermal cell size

The response of leaf size to local irradiance varied between species, whereas epidermal cell size either increased or remained static in response to shade in both herbs and woody species. Furthermore, modelling that assumed vein and stomatal densities respond passively to light- and phylogenetic-induced changes to epidermal cell size, accurately described observed relationships between vein density and 1/√epidermal cell size, stomatal density and 1/epidermal cell size, and between vein density and √stomatal density across all eight species from this study and T. ciliata from a previous study. Thus, we show here that co-ordinated variation in vein and stomatal density in a disparate group of woody and herbaceous eudicot angiosperms was predominately regulated by the size of epidermal cells, which was responsive to light environment in a plastic sense but also varied strongly among species. This remarkable finding suggests that eudicot angiosperms can achieve a balance between tissues regulating water loss and water transport in the leaf by fixing the ratio of the number of xylem cells to guard cells, while allowing epidermal cells (or associated cells) to respond to local irradiance or the intrinsic cell size limits of each species. Stomatal index, meanwhile, had a minor impact on variation in stomatal density. Thus, it appears that differential epidermal cell expansion in response to sun and shade can co-ordinate the density of veins and stomata in herbs and woody species, while leaf size and the number of cells per leaf can vary independently [as has been observed in T. ciliata plants grown under high and low vapour pressure difference (VPD)] (Carins Murphy et al., 2014). These findings compliment recently published work that accurately predicts stomatal density in a range of species using modelled relationships incorporating epidermal cell size, stomatal size and stomatal index (Sack and Buckley, 2016).

Although this kind of interaction between different cell types in the epidermal layer may seem an obvious outcome of a shared locality in the leaf, it is more surprising that the vascular system is also regulated in this way as veins are embedded in the mesophyll tissue and thus spatially isolated from the epidermis. This may result from mesophyll cells mirroring changes to epidermal cell size (Brodribb et al., 2013). While the present study utilized young plants, it is reasonable to expect that these relationships are also present in mature trees as vein density has been linked to leaf expansion (but not cell size) within the canopy of mature Q. rubra trees (Zwieniecki et al., 2004). Thus, the ‘passive dilution’ mechanism may also maintain the proportional relationship that has been observed between vein and stomatal density within individual trees (Brodribb and Jordan, 2011).

Despite the strong general influence of epidermal cell size, there was some indication that vein and stomatal density show a small amount of independence from epidermal cell size under different light conditions. Some of the model parameters we used were a fixed proportion of epidermal cell perimeter to minor vein length and a fixed stomatal index, but we found that these ratios were slightly higher in sun leaves. This represents further evidence of leaf acclimation to the growth conditions as plants grown under high light may have experienced greater leaf temperatures and evaporative demand (leaf temperature was not measured in this study), thus requiring enhanced water transport relative to stomatal pore size.

Co-ordination of vein and stomatal density balances the supply and demand for water

The general relationship found between vein density and leaf hydraulic conductance among all species, along with the fact that stomatal conductance is driven by stomatal density (and aperture), suggests that the co-ordinated acclimation of veins and stomata observed here balanced water supply with demand. Thus, we propose that the ‘passive dilution’ mechanism may co-ordinate plasticity in hydraulic supply and demand in the majority of eudicot angiosperms.

Although all species conformed to vein–stomatal co-ordination, we found that changes to leaf hydraulic conductance were independent of vein density in two herbs (G. max and O. basilicum). This suggests that pathways for water flow outside the veins may contribute to leaf hydraulic conductance in these species (which were both agricultural cultivars). In this respect, it has been suggested that in some species, dynamic changes to leaf hydraulic conductance in response to local irradiance are related to the activity of aquaporins (Nardini et al., 2005; Tyree et al., 2005; Cochard et al., 2007; Voicu et al., 2008; Ben Baaziz et al., 2012), and that in G. max, specifically, aquaporins impact leaf hydraulic conductance under some environmental conditions (Locke and Ort, 2014; Jyostna Devi et al., 2015).

Epidermal cell expansion enables plasticity in vein density and stomatal density

Irreversible expansion of plant cells during development results from water absorption and cell wall relaxation (Cosgrove, 1986). Cell division, on the other hand, is limited by photosynthetic input (Pantin et al., 2012). In this study, epidermal cells in shade leaves were larger than or the same size as those in sun leaves, implying that cell expansion was enhanced or continued for longer in the shade. This may have been due to an increased capacity for cell wall relaxation and/or generation of turgor pressure via the accumulation of solutes (Cosgrove, 1986). Additionally, more water may have been available for cell expansion in shade leaves due to relatively higher midday leaf water potential. A water potential gradient is maintained between growing cells and water sources in the leaf by adjusting the osmotic potential of the growing cells (Pantin et al., 2012). Lower midday leaf water potential may have reduced the water potential gradient towards growing cells in sun leaves, leading to reduced cell expansion (Pantin et al., 2012).

For example, midday leaf water potential and epidermal cell size were unaffected by local irradiance in G. max, and there was a small but significant response of stomatal density to sun and shade but no change in vein density. Thus, it appears that the lack of differential epidermal cell expansion under sun and shade in this species (possibly due to stable leaf water potential) limits the plasticity of vein density and stomatal density. Similarly, the limited response of vein and stomatal density to variation in VPD in T. ciliata may have also been due to the lack of variation in epidermal cell size between high and low VPD treatments (Carins Murphy et al., 2014). Thus, without large changes to epidermal cell size, adjustment of vein and stomatal density may be restricted.

Herbs co-ordinate vein density and stomatal density despite investing less biomass in veins

Lower costs involved with producing and maintaining herbaceous leaves may reduce the selective pressure to match hydraulic capacity with transpirational demand. This is because the severity of any disadvantages associated with having a mismatch between water supply and demand may be reduced if leaves are less energetically expensive to produce and can be cheaply replaced following irreversible xylem embolism (caused by insufficient water supply). Supporting the first part of this proposition, we found that leaves of the herbs included in this study had less lignin per unit area than the leaves of woody species. As lignin is a relatively expensive compound to produce (Lambers and Poorter, 1992), this is consistent with previous studies that found leaves of herbaceous species have lower construction costs than woody species (Poorter and Villar, 1997; Baruch and Goldstein, 1999; Navas et al., 2003). A general association between lignin per unit area and minor vein volume per unit area was observed here, suggesting that lignin in the minor veins constituted a substantial proportion of total leaf lignin. Deviation from this relationship may have been due to variation in the volume of lower order veins between sun and shade leaves and/or differences in vein anatomy (for example the number of bundle sheath fibres or the thickness of the xylem wall). Here we only consider vein volume as calculated from minor vein diameter and density, not xylem wall structure. It should be noted that there was a general decrease in minor vein diameter in the shade, meaning xylem wall thickness may have also decreased in the shade. This relationship between leaf lignin and minor vein volume indicates the potential application of lignin content as a measure of the construction cost of the vein network. As the glucose requirement during the synthesis of compounds such as lignin can be quantified (Lambers and Poorter, 1992), this might provide a reasonable estimate for the construction cost of the vein network. On this basis, leaves with low minor vein volume (such as herbaceous leaves) are inherently less expensive to produce. Despite this, the development of veins and stomata was still co-ordinated in all herbs examined here.

In both woody species and herbs, lignin content per unit dry weight of shade leaves was greater than or equal to that of sun leaves, while LMA was lower in shade leaves. This indicates that in all species the leaf vasculature makes up a larger proportion of the total leaf weight in shade leaves than in sun leaves. Our finding that lignin comprised 13·1 % of sun leaf dry weight is consistent with previously published data that suggests that lignin comprises 10·5 % of sun leaf dry weight in lowland tropical forest pioneer species and 12·5 % in persistent species (Coley, 1983). More recently published data also indicated that the minor veins account for <11 % of LMA on average when calculated using the volume of the leaf lamina occupied by the minor veins (Sack et al., 2013). However, we found that on average 21·7 % of shade leaf dry weight was lignin. Hence, if lignin content is representative of leaf minor vein volume then the minor veins represent a substantial investment in the shade. This may explain why optimizing relative investment in the vascular and stomatal systems seems to be a universal rule even in herbaceous species where new leaves are comparatively less costly to produce.

Conclusions

Differential epidermal cell expansion under sun and shade conditions and among species appears to be a universal mechanism in the woody species and herbs included in this study by which changes to vein and stomatal density are co-ordinated during leaf acclimation. The stomatal index, on the other hand, seems to play a minor role in determining variation in stomatal density. Thus, we suggest that the ‘dilution’ of veins and stomata by epidermal cell expansion may co-ordinate plasticity in hydraulic supply and demand in eudicot angiosperms. The fact that these relationships are conserved even in agricultural varieties gives some weight to the view that this ‘passive dilution’ mechanism may be a common feature of most angiosperms. Furthermore, it appears that the lower lignin content per unit area of herbaceous leaves does not have a systematic influence on whether co-ordination of vein and stomatal density is present or not. We suggest that the substantial proportion of leaf tissue dedicated to veins in both herbs and woody plants provides strong selective pressure to ensure investment in the vascular and stomatal systems is appropriate for photosynthetic capacity under contrasting light conditions and among species.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Table S1: results of two-way ANOVA tests for the effect of local irradiance on leaf traits in woody and herbaceous species. Table S2: ANCOVA tests to determine whether relationships between stomatal density and 1/epidermal cell size, vein density and 1/√epidermal cell size, vein density and √stomatal density, leaf hydraulic conductance and vein density, and lignin per unit area and minor vein volume per unit area are described by single linear regressions. Table S3: results of ANCOVA tests to determine whether observed relationships are explained by modelled relationships. Table S4: results of three-way ANOVA test for the effect of habit on lignin per unit area in plants grown under sun and shade.