Quantitative Validation of Anti-PTBP1 Antibody for Diagnostic Neuropathology Use: Image Analysis Approach

Abstract

Problem

Diagnostic neuropathology traditionally relies on subjective interpretation of visual data obtained from a brightfield microscope. This results in high variability, inability to multiplex, and unsatisfactory reproducibility even among experts. These diagnostic problems may affect patient outcomes and confound clinical decision-making. Furthermore, standard histological processing of pathological specimens results in auto-fluorescence and other artifacts, which have nearly blocked the implementation of fluorescent microscopy in diagnostic pathology. Thus, generation of objective and quantitative methodologies would augment the toolbox available to neuropathologists, which would ultimately enhance clinical decision making.

Objective

To develop image analysis methods to quantitatively validate anti-PTBP1 antibody for use in diagnostic neuropathology.

Method

We propose a computerized image analysis method to validate anti-PTBP1 antibody. Images were obtained from standard neuropathological specimens stained with anti-PTBP1 antibody. First, the noise characteristics of the images were modeled and images are de-noised according to the noise model. Next, images are filtered with sigma-adaptive Gaussian filtering for local normalization, and cell nuclei are detected and segmented with a k-means based deterministic approach.

Result

Experiments on 29 data sets from three cases of brain tumor (recurrent glioma, primary resections of glioblastoma harboring the EGFRVIII mutation, pilocytic astrocytoma) and reactive gliosis show statistically significant differences between the number of positively stained nuclei in images stained with and without anti-PTBP1 antibody (p values, t-test, are 40×10⁻⁴, 33×10⁻⁴, 6×10⁻⁴ and 46×10⁻³, respectively).

Conclusion

The experimental of analysis of specimens from three different brain tumor groups and one reactive gliosis group indicate the feasibility of using anti-PTBP1 antibody in diagnostic neuropathology and computerized image analysis provides a systematic and quantitative approach to explore feasibility.

1. INTRODUCTION

Diagnostic problems encountered by neuropathologists when evaluating the histopathology of a complex case could be solved by improving their diagnostic toolbox. Two branch points in neuropathological workflows require the generation of new image analysis tools and techniques. First, the ability to identify multiple biomarkers on the same cell would help pathologists identify distinct subtypes of cancers without exhausting tissue. A second problem exists in the objective interpretation of biomarker expression levels. Standard biomarker evaluation involves utilization of enzyme-based histochemical reactions, the most common of which is DAB precipitation by HRP-linked secondary antibody systems, which is optimally designed for binary designations of “positive” or “negative” or at best semi quantitative, subjective designations of “1+”, “2+”, “3+”. Both problems could be resolved by implementing modern fluorescence microscopy techniques, which permit multiplexing and are superior quantitative modalities relative to immunohistochemistry. Unfortunately, the implementation of fluorescence in routine diagnostic pathology is fraught with caveats. For example, erythrocytes fluoresce in the 500–600 nm spectrums, which are commonly used excitation spectra for epifluorescence. Furthermore, prolonged formalin fixation (a common practice in formalin fixed, paraffin embedded (FFPE) tissue sections) results in autofluorescence. Thus, fluorescent microscopy of routine neurosurgical biopsies would result in visually complex images. Our objective was to develop an automated image analysis technique that would overcome these challenges. We developed this technique by validating Poly-pyrimidine Tract-Binding Protein 1 (PTBP1) antibody in neuropathology specimens. We took advantage of the low autofluorescent background present in 300–500 nm spectrum of FFPE tissues, a naturally occurring idiosyncrasy of FFPE autofluorescence. Thus, staining with DAPI, which is characterized by a peak excitation/emission spectrum of 358 nm/461 nm, can be used as a tool to identify signals. While several histopathological image analysis methods exist in the literature [11–14], to the best of our knowledge, there is no work that uses multiplexed guided images with PTBP1 antibody with DAPI.

The main steps for the automated validation of anti-PTBP1 antibody are: 1) de-noising according to the type of noise in images, 2) local normalization with Sigma-Adaptive Gaussian (SAG) filtering, and 3) cell nuclei detection and segmentation with a k-means based deterministic approach. The contribution of this work is validating anti-PTBP1 antibody to use on routine neurosurgical biopsies by developing the computerized system that allows automated analysis of images, which removes fluorescent background from specimens stained with DAPI and anti-PTBP1 antibody. Quantitative evaluations are performed by using 29 data sets from reactive gliosis and three cases of brain tumors: 1) recurrent glioma, 2) primary resections of glioblastoma harboring the Epidermal Growth Factor Receptor (EGFRVIII) mutation, and 3) Pilocytic Astrocytoma (PA).

The remaining part of this paper is organized as follows: Description of data sets is given in Section II. Validation of anti-PTBP1 antibody is explained in Section III. Experimental results are shown in Section IV while conclusion and discussion is given in Section V.

2. DATA SETS

In this work, immunofluorescence images are used obtained from confocal photomicroscopy. The data sets are provided from 29 specimens (16 samples from patients with PA WHO Grade I, 4 samples of reactive gliosis from a patient with prior diagnosis of glioblastoma, 4 samples from recurrent high grade glioma in a patient with prior diagnosis of glioblastoma and 5 samples from a patient with EGFRVIII mutation positive glioblastoma) by using a laser scanning confocal fluorescence microscope (Zeiss LSM 700). All images were captured with a 20x objective since nuclei stained with/without anti-PTBP1 antibody or DAPI in these images can be seen clearly by pathologists. The pixel size is 0.312×0.312 micron2 (3.1991 pixels per micron) in the 8-bit uncompressed images of size of 2048×2048 pixels.

3. ANTIBODY VALIDATION BY IMAGE ANALYSIS

Due to the inherent variability amongst antibodies, quality control experiments are always required in diagnostic pathology [1–5]. Different studies suggest different proteins, which are likely suitable to use as glioma antibodies (such as ELTD1, F11R, LINGO1, SLIT3 etc.), with different validation approaches in the literature [6–11]. However, a method to quantitatively and objectively validate PTBP1 for gliomas (in human/animal) in formalin-fixed, paraffin embedded tissue evaluated by immunofluorescence confocal microscopy does not exist. Such automated testing is required to ultimately implement multiplexed image acquisition in solid-tissue biopsies. Therefore, we developed a methodology to validate PTBP1, a multifunctional RNA-binding protein, antibody using automated image analysis.

Automated validation of antibodies by image analysis is a very challenging task because of:

1. Tissue based problems: Cells may have irregular shapes/structures or may be clustered. Individual cells may not be distinguished easily.

2. Staining based problems: Cells may not stain well, which may cause incorrect number/shape/size of detected objects.

3. Antibody based problems: Quantity, quality and concentration of the antibody may be different in different data sets or even in different images of the same data set. These variations may cause unexpected/undesired results due to differences in images.

4. Microscope based problems: Quality of the camera and microscope being may be low. Therefore, images may be with low quality with unclear edges or noisy.

5. Target based problems: The variability of the target protein due to secondary modifications, localization, epitome availability etc.

Our approach is designed to overcome these problems by 1) noise modeling and reduction (Section 3.1), 2) intensity normalization (Section 3.2), 3) detection of nuclei using the images that are stained with DAPI (to get boundary and location information) and the images that are stained with anti-PTBP1 antibody (to get intensity values) (Section 3.3), and 4) segmentation of nuclei based on a deterministic approach (Section 3.4).

3.1. Noise Modeling and Reduction

There are different noise reduction methods, ranging from wavelet [12–15], iterative [16] and diffusion [17–21] methods to non-local mean [22–24] and graphical model frameworks [25–27] used for different types of noise e.g. uniform (Figure 1.a), Gaussian (Figure 1.b), impulsive (i.e., salt & pepper) (Figure 1.c) or speckle (Figure 1.d). To determine the most appropriate algorithm for noise reduction (i.e., to avoid poor de-noising), the type of noise in the image should be identified. Therefore, we chose three regions (at least 100×100 pixels), which have homogenous (or close to homogenous) intensity values, from images and analyzed their histograms to identify noise type.

Figure 1.

Noise types: Uniform noise (a); Gaussian noise (b); Impulsive noise (c); Speckle noise (d)

Figure 2 shows an example image stained with anti-PTBP1 antibody (Figure 2.a), three regions (with variance σ₁ = 0.5, σ₂ = 2.5 and σ₃ = 1), which are surrounded with yellow, red and cyan rectangular, on the grayscale form of the image (Figure 2.b) and the histogram of the grayscale image (Figure 2.c). We have modeled the noise in the images as speckle noise [28] based on the shape of the histograms (Figure 2.d,e,f) of those three regions. Therefore, we implemented a speckle filtering algorithm to reduce the noise in our images.

Figure 2.

Image stained with anti-PTBP1 antibody (a); Three homogenous regions are shown with yellow, red and cyan rectangular on the grayscale form of the image (b); Histogram of the grayscale image (c); Histogram of the regions with yellow (d), red (e) and cyan (f) rectangular. (For better visualization the brightness and contrast has been increased by 40% in figures (a) and (b))

In our work, we reduce the noise by a Non-local Median based Speckle Filtering (NMSF), which is inspired by the Non-local Means Filtering (NMF) of Coupe et al. [29]. However, unlike the non-local means filtering, we used median function (non-linear filter) since the data in our images are non-linear and mean function may not always be the most efficient in this case.

The NMSF method (1) is applied when we consider a grayscale image u = (u(x_i))_xi∈Ω², which is defined on a domain Ω² ⊂ R² and u(x_i) ∈ R₊ is the noisy at pixel x_i ∈ Ω² (please see [29] for details);

$$NL(u)(B_{ik})=\sum _{B_j\in {\mathrm{\Delta }}_{i_k}}w(B_{i_k},B_j)u(B_j)$$ (1)

where, B_i refers to the square block that is centered at x_i with size |B_i| = (2α + 1)², α ∈ N; v (B_i) is the unobserved vector of true values of block B_i; u(B_i) is the vector gathering the gray level values of block B_i; NL(u)(B_i) is restored block of pixel x_i; w(B_i, B_j) is the weight value used for restoring u(B_i) given u(B_j) and based on the similarity of blocks u(B_i) given u(B_j). The weight values are calculated by,

$$w\left(B_{ik},B_j\right)=\frac{1}{z_{ik}}exp-\frac{{\Vert u(B_{ik})-u(B_j)\Vert }_2^2}{h^2}$$ (2)

where u(B_i) = (u⁽¹⁾(B_i),........u^(p) (B_i))^T is an image patch gathering the intensities of the block B_i; z_ik is a constant value for normalization by ensuring that Σ_Bj∈Δik w(B_ik,B_j) = 1 and also

$${\Vert u(B_{ik})-u(B_j)\Vert }_2^2=\sum _{p=1}^p{(u^{(p)}(B_i)-u^{(p)}(B_i))}^2$$ (3)

In the NMSF method, for each block B_ik centered at pixel x_ik, a non-local means restoration is performed from blocks B_j. The restored value of the block B_ik is the weighted average of all the blocks B_j in the search volume. For a pixel x_i included in several blocks, several estimates are obtained and merged. The restored value of pixel x_i is the mean of the different estimations stored in vector A_i. The algorithm can be summarized as:

1. Divide the image into blocks with overlapping supports (The block B_ik contains P = 2α + 1 elements. Each block is centered on pixel x_i, which constitutes a subset of Ω² and pixels are equally distributed).

2. Calculate NL(u)(B_ik) to perform a non-local means restoration of these blocks.

3. Restore the pixel intensities. For a pixel x_i included in several blocks B_ik, different estimates from several NL(u)(B_ik) is computed and stored in a vector A_i. The restored intensity of pixel x_i is the mean of the restored values NL(u)(B_ik).

The noise reduction method is illustrated in Figure 3 with a Region of Interest (ROI) area, which is shown with the yellow rectangle in Figure 3.a. (The ROI part is magnified in Figure 3.b to increase visibility of individual nuclei). The ROI part after noise reduction (Figure 3.c), residual image (i.e. difference between the original and de-noised ROI area) (Figure 3.d) and the whole image after noise reduction (Figure 3.e) are shown as grayscale. To present better visualization, pseudo-color representation with the Hue-Saturation-Value (HSV) color model is given in Figure 3.f,g,h for the images shown in Figure 3.b,c,d respectively.

Figure 3.

Example grayscale image that shows ROI part as yellow rectangle on the image stained with DAPI but without anti-PTBP1 antibody from PA cases (a); ROI part magnified (b); ROI part after noise reduction (c); Residual image (d); The whole image after noise reduction (e); The ROI part, its de-noised form and the residual image are shown in HSV color space in (f),(g) and (h) respectively (To increase visualization in this figure (a–e), brightness and contrast has been increased (40%))

The effect of the noise reduction is demonstrated on a nucleus in Figure 4. The nucleus (Figure 4.a) in the original image has speckle and blurry edges, which are smoother (Figure 4.b) after de-noising. Difference between the original and de-noised image is shown in Figure 4.c.

Figure 4.

A nucleus in the original image (a); Shape and pattern of the nucleus after de-noising (b); Residual image data removed by the filtering (c)

The effect of noise reduction can be observed by comparing variance of 1) original image, 2) image de-noised with NMF, and 3) image de-noised with NMSF since there is no image obtained without noise in our work.

Figure 5 shows average variances, which are calculated from images in each data set, for three cases of brain tumor and reactive gliosis. It should be noted here that mean values of original images and de-noised images are the same although their variances change. Therefore, quantitative values in Figure 5 indicate that noise reduction with the NMSF method is more successful compared to the NMF method on our images.

Figure 5.

Effect of noise reduction methods is shown quantitatively for reactive gliosis (a), recurrent glioma (b), EGFRVIII (c), and PA (d)

3.2. Local Intensity Normalization with SAG Filtering

Another problem to tackle is the non-uniform staining of the images. Therefore, we applied a local intensity normalization method. The goal of the normalization process is to make the variance and mean of the grayscale images uniform. In our implementation, the spatial local normalization is performed by applying SAG filtering instead of a standard Gaussian filtering applied globally with a fixed sigma value.

We propose SAG filtering to solve two main problems of the traditional Gaussian smoothing: 1) It is not clear how to choose a fixed sigma that is fit to smooth each pixel with Gaussian filter. 2) Filtering with the fixed sigma (even if it is chosen carefully for an image) cannot smooth different images in different data sets (even different images in the same data set) well enough for the next step (Section 3.3).

Figure 6 illustrates a grayscale image (Figure 6.a) and normalized images obtained by standard Gaussian filtering applied globally with different sigma values (5 and 15) (Figure 6.b,c) to show variations.

Figure 6.

Grayscale image (a); Normalized image by Gaussian filtering with sigma 5 (b), and 15 (c) (to better visualize, the brightness has been increased by 40%)

The local SAG filtering based normalization is applied with the following equation:

$$I_N(x,y)=\frac{I_g(x,y)-\mu (x,y)}{\sigma (x,y)}$$ (4)

where the term I_N (x, y) and I_g (x, y) refers to the normalized and grayscale images, respectively. In (4), μ(x, y) and σ(x, y) correspond to the mean and variance that are estimated by filtering the image I_g (x, y) with a Gaussian filter whose sigma is selected adaptively for each image.

The adaptive sigma value of the Gaussian filter is calculated using the distance map obtained with Euclidean distance transform. To get the distance map, we use the binary image obtained from the grayscale image I_g (x, y) by applying the adaptive thresholding method described in [30].

The Euclidean distance transform is defined as a transformation, which assigns a number that is the distance between that pixel and the nearest zero pixel in the binary image (note that zero pixels correspond to background, non-zero pixels to nuclei in the binary image). Let maxD be the maximum value in the distance map, the adaptive sigma value of the Gaussian filter is obtained by:

$${\sigma }_{\mathit{Gauss}}=min(T,\text{maxD})$$ (5)

where T is set to 100 experimentally. In (5), we used maxD since pixels with the maximum distance value should be smoothed as much as possible. However, inter-cell boundaries should not be blurred while simultaneously smoothing intra-cell pixels. Therefore, the threshold value T is used in (5) to handle over-smoothing problem.

Under-smoothing problem may occur when maxD is low; therefore, the sigma value is defined adaptively as follows:

$${\sigma }_{\mathit{Gauss}}=\{\begin{array}{ll}\mathit{max}(T,\mathit{maxD}),\hfill & \hfill if\mathit{maxD}<t\hfill \\ \mathit{min}(T,\mathit{maxD}),\hfill & \hfill \mathit{otherwise}\hfill \end{array}$$ (6)

where t is set to 50 experimentally. The pseudo-code of the proposed local SAG filtering based normalization method is given in Table 1.

Table 1.

Pseudo-code of the local SAG filtering based image normalization method

Get grayscale image Ig and σGauss Calculate the mean value μGauss with cumulative distribution function by assigning zero to the mean and σGauss Apply Gaussian filtering with the grayscale image, μGauss and σGauss to obtain the first filtered image (If 1), whose values are used as μ(x, y) in equation (5) Take difference of the grayscale image and filtered image (If 1) to generate a new image, which we called as IDifference that correspond to the nominator in equation (4) (i.e., IDifference Ig − If 1) Obtain a temporary image, Itemp, by calculating squares of intensity values in the image IDifference (i.e., ITemp IDifference^2) Apply Gaussian filtering with the image ITemp, μGauss and σGauss to obtain the second filtered image (If 2). Calculate square root of all intensity values in the image If 2 to generate a new image, IDenominator, which correspond to the denominator in equation (5). Obtain the normalized image by dividing intensity values in the image IDifference to the intensity values in the image IDenominator.

Figure 7 shows the image obtained with the proposed normalization approach from the image given in Figure 6.a.

Figure 7.

Normalized image

3.3. Nuclei Detection and Segmentation

In this stage, nuclei are detected and segmented on grayscale DAPI image by a k-means based deterministic method. The proposed method mimics the pathologist workflow. Positively stained nuclei in the images stained with anti-PTBP1 antibody (primary or secondary) appear brighter than other objects (Figure 8.a). Therefore, visual detection of these nuclei is performed according to their brightness. If a bright region in these images corresponds to a nucleus in the image stained with “DAPI and anti-PTBP1 antibody” or “DAPI but without anti-PTBP1 antibody” then the nucleus having the bright region is considered as a nucleus positively stained with anti-PTBP1 antibody by pathologists. Similarly, in our work, automated detection and segmentation of these nuclei stained positively is achieved by using i) intensity values from images stained with/without anti-PTBP1 antibody, and ii) location and shape of the nuclei from the images stained with “DAPI and anti-PTBP1 antibody” or “DAPI but without anti-PTBP1 antibody”.

Figure 8.

Example image stained with anti-PTBP1 antibody (primary) from PA (a); Image stained with DAPI from PA (b); Grayscale forms of the image stained with anti-PTBP1 antibody (c) and DAPI (d); Generated DAPI_PTBP1 image (e); Nuclei positively stained with anti-PTBP1 antibody (f) (To better visualize images in (a–c), brightness and contrast has been increased by 10%)

In the proposed method, the first step is to convert anti-PTBP1 (Figure 8.a) and DAPI stained tissue images (Figure 8.b) into grayscale (Figure 8.c, d) (these images are originally gray-scale but then artificially colored for better visualization). After noise reduction, a new image, called DAPI_PTBP1 (Figure 8.e), is generated by combining the shape information from the DAPI-stained image and texture information from the anti-PTBP1-stained image. In the final step, k-means based clustering is applied with k=6 [31–34]. The first cluster corresponds to background (black) and remaining five clusters categorize gray level values into five groups (dark gray, gray, bright, brighter and the brightest gray level value). The sixth cluster contains the nuclei that are positively stained with anti-PTBP1 antibody with the brightest gray level values (Figure 8.f).

3.4. Numerical Analyses of Segmented Nuclei

In order to measure the effect of the anti-PTBP1 antibody, the ratio between total numbers of nuclei segmented from the images stained with anti-PTBP1 antibody and images stained with “DAPI and anti-PTBP1 antibody” is compared to the ratio from the images stained without anti-PTBP1 antibody and images stained with “DAPI but without anti-PTBP1 antibody”. The following ratio is calculated:

$$R_{\mathit{With}Pr\mathit{iAnti}}=\frac{N_{\mathit{withPTBP}1}}{N_{\mathit{withDAPIandPTBP}1}}$$ (7)

where N_withPTBP1 refers to number of nuclei stained (positively) with anti-PTBP1 antibody, N_{withDAPIandPTBP1} refers to number of nuclei stained (positively) with “DAPI and anti-PTBP1 antibody”. Similarly, the following ratio is calculated by using images stained with “DAPI but without anti-PTBP1 antibody” and images stained with anti-PTBP1 antibody:

$$R_{\mathit{No}Pr\mathit{iAnti}}=\frac{N_{\mathit{no}Pr\mathit{iPTBP}1}}{N_{\mathit{withDAPIno}Pr\mathit{iPTBP}1}}$$ (8)

where N_noPriPTBP1 refers to number of nuclei stained (positively) without anti-PTBP1 antibody, N_{withDAPInoPriPTBP1} refers to number of nuclei stained (positively) with “DAPI but without anti-PTBP1 antibody”.

We can deduce that the antibody is effective, if the ratio calculated with (7) is greater than the ratio calculated with (8), which can be written as:

$$\frac{N_{\mathit{withPTBP}1}}{N_{\mathit{withDAPIandPTBP}1}}>\frac{N_{\mathit{no}Pr\mathit{iPTBP}1}}{N_{\mathit{withDAPIno}Pr\mathit{iPTBP}1}}$$ (8)

Figure 9 shows the flow chart of applied method for validation of anti-PTBP1 antibody.

Figure 9.

Flow chart of the applied method for validation of anti-PTBP1 antibody

4. EXPERIMENTAL RESULTS

Quantitative evaluations are based on the total number of nuclei that match bright regions in images with and without anti-PTBP1 antibody. Example numerical values are given in Table 2, which is obtained from the data set of 7 images from 1 patient diagnosed with reactive gliosis.

Table 2.

Total number of nuclei matching bright regions in images stained with and without anti-PTBP1 antibody on 7 images from 1 patient diagnosed with reactive gliosis.

Image Number	Total Number of Nuclei That Match with Bright Regions in Images
	Image without anti-PTBP1 antibody	Image with anti-PTBP1 antibody
1	21	123
2	15	180
3	25	288
4	25	309
5	16	302
6	5	28
7	12	106
Mean:	17	190.9
Standard deviation:	7.2	111.2

Experimental results show that the total number of nuclei in images stained with anti-PTBP1 antibody is always more than those in the images stained without anti-PTBP1 antibody (p = 1×10⁻³ (t-test)).

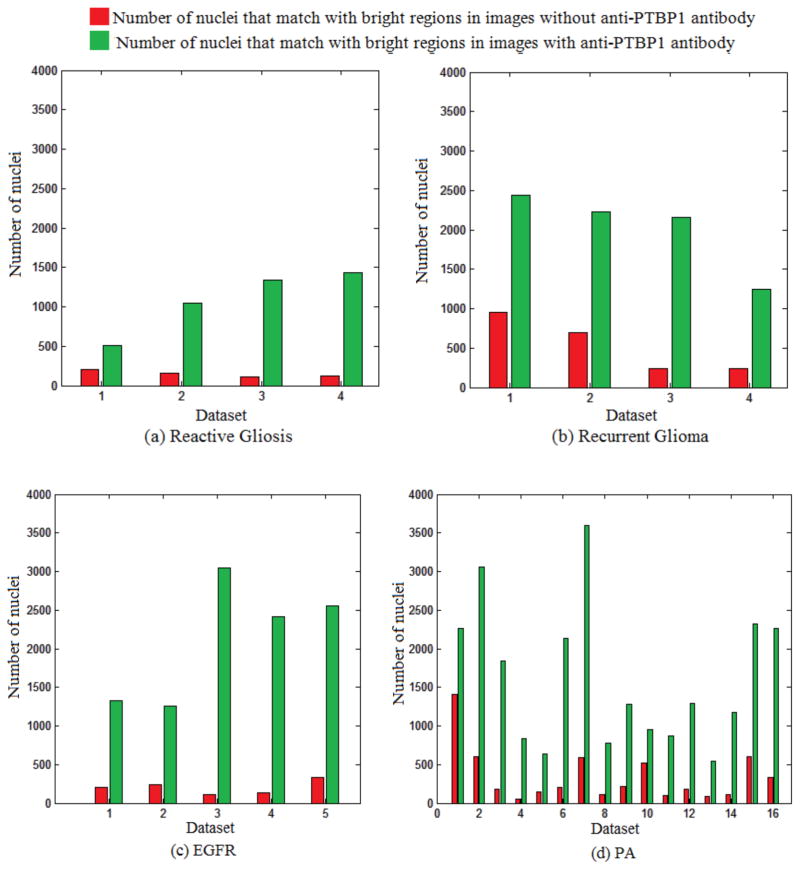
Figure 10 shows the total number of nuclei that match with bright regions in images stained with and without anti-PTBP1 antibody in data sets from recurrent glioma (Figure 10.a), reactive gliosis (Figure 10.b), EGFRVIII (Figure 10.c) and PA (Figure 10.d) data sets. The number of nuclei in images stained with anti-PTBP1 antibody is always higher than those in images stained without anti-PTBP1 antibody (Figure 10).

Figure 10.

Number of nuclei that match with bright regions in images with and without anti-PTBP1 antibody from reactive gliosis (a), recurrent glioma (b), EGFRVIII (c) and PA (d) data sets

The difference between numbers of nuclei is meaningful for those three cases of brain tumor and reactive gliosis. Table 3 shows p values (t-test), average (μ) and standard deviation (σ) of number of nuclei obtained from images stained with and without anti-PTBP1 antibody.

Table 3.

Result of t-test (p values), average (μ) and standard deviation (σ) of number of nuclei obtained from images stained with and without anti-PTBP1 antibody

Case	p value	Images stained with anti-PTBP1 antibody		Images stained without anti-PTBP1 antibody
		μ	σ	μ	σ
Reactive Gliosis	40×10−4	1082.5	412.1	147.2	41.1
Recurrent Glioma	33×10−4	2019.2	527.4	531.2	351.8
EGFRVIII	6×10−4	2124	791.7	203.6	92.2
PA	46×10−3	1615.3	911.2	153.4	71.6

Quantitative values in Table 4 are obtained without noise reduction. Values of μ and σ given in Table 3 are lower than those μ and σ values in Table 4 due to the effect of the NMSF method.

Table 4.

P values (t-test), average (μ) and standard deviation (σ) of number of nuclei obtained from images without noise reduction

Case	p value	Images stained with anti-PTBP1 antibody		Images stained without anti-PTBP1 antibody
		μ	σ	μ	σ
Reactive Gliosis	1×10−2	3321.5	1123.9	1188.7	476.1
Recurrent Glioma	1×10−3	3721.0	666.3	898.2	675.3
EGFRVIII	2×10−4	4113.2	1269.6	452.4	310.9
PA	3×10−4	2793.8	1191.7	981.7	552.9

Also, it is observed from numerical values of R _WithPriAnti and R _NoPriAnti that the anti-PTBP1 antibody works well (i.e., R_WithPriAnti > R_NoPriAnti, which can be seen in Figure 11).

Figure 11.

R _WithPriAnti and R _NoPriAnti values for each data set

5. CONCLUSION AND DISCUSSION

In this work, an automated image analysis method is proposed for validation of anti-PTBP1 antibody. The advantage of the proposed method is that it provides accurate, objective, repeatable and quantitative results. The method was tested on 29 data sets diagnosed with one of four cases: PA, WHO grade I, Second biopsy of a patient with a prior neurosurgical resection diagnosed as glioblastoma with the new resection showing reactive gliosis, Second biopsy of a patient with a prior neurosurgical resection diagnosed as glioblastoma with the new resection showing recurrent high grade glioma; and first surgery of a patient showing glioblastoma, WHO grade IV harboring EGFRVIII mutation.

The noise reduction method in this work is chosen according to the type of the noise in images. In our data sets, images show speckle type of noise (Figures 2.c, f). Therefore, the noise reduction approach is based on speckle filtering, which gives accurate results (Figures 3,4) because the numbers of nuclei detected with the proposed approach were confirmed by a neuropathologist who has more than 10 years of experience in traditional pathology. Figure 5 and Table 3 show the effect of noise reduction with the proposed NMSF technique.

Intensity normalization is provided by a local normalization approach. The proposed SAG filtering based normalization method assigns sigma value for each image automatically instead of using a constant sigma for the Gaussian filtering.

It is observed from numerical values in Table 2 and graphs in Figure 10 that images stained without anti-PTBP1 antibody always show less number of positively stained nuclei compared to images stained with anti-PTBP1 antibody. Comparisons of quantitative values show meaningful difference between those numbers of nuclei (Table 2). Ratios calculated using images stained with and without anti-PTBP1 and DAPI indicate the efficiency of the antibody (Figure 10). These data demonstrate and automated image analysis approach to antibody validation for PTBP1 that can easily be applied to other biomarkers showing nuclear localization.

The proposed approach will be tested on more data sets chosen from different cases in neuropathology as an extension of this work.