Abstract
Food-borne disease outbreaks caused by Listeria monocytogenes continue to impose heavy burdens on public health in North America and globally. To explore the threat L. monocytogenes presents to the elderly, pregnant woman and immuno-compromised individuals, many studies have focused on in-host infection mechanisms and risk evaluation in terms of dose-response outcomes. However, the connection of these two foci has received little attention, leaving risk prediction with an insufficient mechanistic basis. Consequently, there is a critical need to quantifiably link in-host infection pathways with the dose-response paradigm. To better understand these relationships, we propose a new mathematical model to describe the gastro-intestinal pathway of L. monocytogenes within the host. The model dynamics are shown to be sensitive to inoculation doses and exhibit bi-stability phenomena. Applying the model to guinea pigs, we show how it provides useful tools to identify key parameters and to inform critical values of these parameters that are pivotal in risk evaluation. Our preliminary analysis shows that the effect of gastro-environmental stress, the role of commensal microbiota and immune cells are critical for successful infection of L. monocytogenes and for dictating the shape of the dose-response curves.
Keywords: L. monocytogenes, Dose-response, Mechanistic model, Bi-stable, Guinea pig
1. Introduction
Listeriosis is a potential food-borne disease caused by L. monocytogenes. Unlike other common food-borne infections, listeriosis is associated with a high case-fatality rate of approximately 20–30% (Allerberger & Wagner, 2010). Posing a severe hazard to certain populations including pregnant women, older adults and individuals with weakened immune systems, L. monocytogenes is a critical public health problem (Cossart, 2011, Cossart and Toledo-Arana, 2008). The infection is also associated with high economic burden. The annual cost of listeriosis illness and death in Canada is estimated to be between 11.1 million and 12.6 million dollars. (Farber, Ross, & Harwig, 1996). Thus understanding the key infection processes of this pathogen supported by scientific knowledge is important in evaluation of infection risk (Cossart, 2011). Though much progress has been achieved in understanding the infection mechanisms of L. monocytogenes, their impact on risk assessment has received much less attention (Cossart, 2011, D'Orazio, 2014, Lecuit, 2001).
Numerous animal data show that infection potential of L. monocytogenes is dose dependent (Lecuit, 2001, Melton-Witt et al., 2012). An inoculation with 1 × 1011 CFU of L. monocytogenes confirms 100% mouse death, but inoculation with 1 × 1010 CFU results in 100% survival (Lecuit, 2001). Stelten et al. demonstrate that both number of guinea pigs and proportion of organs are increasingly infected with the higher doses of inoculation (Van Stelten et al., 2011). None, 50% and 100% guinea pigs were infected with inoculation doses of 1 × 106, 1 × 107, and 1 × 1010 CFUs of L. monocytogenes, respectively. MacDonald and Carter conducted an experiment with germ-free B6D2F1 mice. The mice inoculated with 2.5 × 108 CFU or more had consistent infection. However, no L. monocytogenes were recovered from the mice inoculated with 5.0 × 106 CFU (MacDonald & B Carter, 1980). Similar experiments with monkey (Smith et al., 2008), mouse (Golnazarian et al., 1989, Roulo et al., 2014, Smith et al., 2003), and Zebrafish (Shan et al., 2015) demonstrate that casualty, systemic infection or pregnancy disorder are highly associated with inoculation doses. Thus, understanding the with-in host dynamics of L. monocytogenes is critical for better understanding its pathogenesis and dose-response outcomes.
Scientific studies comprehensively demonstrate the intracellular transmission mechanisms of L. monocytogenes and how they cross the intestinal wall of a host (Cossart, 2011, Cossart and Toledo-Arana, 2008, Lecuit, 2001). More than 50 surface proteins are identified that are involved in invading host cells and cell-to-cell movement (Cossart & Toledo-Arana, 2008). In cell-to-cell contact, L. monocytogenes expresses surface proteins internalin, intA and intB, that interact with host's receptors E-cadherin and Met, respectively (Lara-Tejero and Pamer, 2004, Pizarro-cerda and Ku, 2012). Pore-forming gene listeriolysin O (LLO) helps bacteria escape from the vacuole of a cell and surface protein ActA promotes intra and inter-cellular movement. Several other proteins, Clathrin, Lecitinase, Septin and Tuba, facilitate the invasion process and help bacteria to avoid immune surveillance (Cossart, 2011). After crossing the intestinal barrier, L. monocytogenes can reach the liver, spleen, brain and placenta through lymph and blood vessels (Cossart, 2011, Cossart and Toledo-Arana, 2008, Lecuit, 2001, Melton-Witt et al., 2012). While, identification of the cellular transmission mechanism has enhanced our fundamental knowledge of pathogenesis, the dose-response relationship of L. monocytogenes still remains ambiguous.
During the past decades, dose-response relationships have been developed through statistical models supported by animal and surveillance data (Farber et al., 1996, Haas, 2015, Pouillot et al., 2015). These statistical models provide the probability of infection of certain susceptible populations given exposure levels - ignoring the mechanistic details of how L. monocytogenes grows and survives in the host after ingestion. To bridge the gap between exposure and infection, a mechanistic description is crucial (Cossart and Toledo-Arana, 2008, Haas, 2015). This approach could identify the true causes of responses and provide critical information useful for minimizing the risk. This paper is intended to provide a framework for host-pathogen interactions at the early stages of exposure-mouth to small intestine pathway-to elucidate the dose-response paradigm of L. monocytogenes infection.
In order to model the population dynamics of L. monocytogenes in the gut, a natural choice is the classical logistic model given by
| (1.1) |
where N is the number of bacteria population; r and K are the intrinsic growth rate of bacteria and the carrying capacity of the environment, respectively. However, model (1.1) cannot exhibit the bistable phenomenon that is observed in L. monocytogenes growth studies (Lecuit, 2001, Melton-Witt et al., 2012). To capture such dynamics in the small intestine, two inhibitory factors, carrying capacity and immune pressure, need to be included simultaneously in the model equation. Incorporating the host's immune response, the model can be written as
| (1.2) |
where I is the number of immune cells; β and α are constants. The second term of (1.2) describes the interaction between L. monocytogenes and the host's immune cells in the small intestine and follows a prey-predator interaction with Michaelis-Menten form (Creighton, 1999). Notice that this combination of logistic growth and the Michaelis-Menten killing form can exhibit bi-stability. For further details regarding these dynamics see Section 3.
This paper is organized as follows: Section 2 describes the key survival factors of L. monocytogenes in a host and provides the foundation of model formulation. A mathematical model describing the population dynamics of L. monocytogenes is developed in Section 3. This section also provides the model analysis, threshold and bi-stability phenomenon. Section 4 describes the applications of the model to guinea pigs. In this section, we estimate model parameters, perform sensitivity analysis, discuss the implication of the sensitivities of the model parameters to the dose-response relationships and validate the model outcomes with experimental results. Finally, in Section 5, we discuss the implication of the model results and outline how the model can be augmented to capture more realistic aspects of the L. monocytogenes infection. We also discuss the limitations of the model and the possible avenues to overcome these limitations.
2. Host defense and survival factors of L. monocytogenes
L. monocytogenes is a food-borne pathogen. It causes infection through contaminated food. To survive in a host and to cause infection, L. monocytogenes has to face and overcome multiple challenges posed by the host. Here we describe the potential hosts' defenses against L. monocytogenes.
2.1. Stomach fluid and low pH
After ingestion, L. monocytogenes travels along with food particles through the esophagus and reaches the stomach within a few seconds (note that we ignore the effect of saliva in the mouth on the bacterial population). Once in the stomach, enzymes and acid are secreted to sanitize and break food into digestible molecules. Among these secretions, stomach acid (HCl) is significant for a number of reasons. It initiates protein digestion by activating pepsinogen that secrets from the gastric gland. It also enhances the absorption of minerals, calcium and iron (Howden & Hunt, 1987). In addition, stomach acid plays a crucial role in clearing food pathogens from the stomach before they move down to the small intestine. Numerous in vitro and in vivo experimental results indicate that low pH levels are detrimental for bacterial survival (Giannella et al., 1972, Zhu et al., 2006).
Growth of L. monocytogenes is also affected in an acidic environment. Saucedo et al. found that L. monocytogenes can grow in Sapote mamey pulp at higher pH levels, but not at a pH of 4.0 or less (Saucedo-Reyes, Carrillo-Salazar, Reyes-Santamaría, & Saucedo-Veloz, 2012). Several studies observed that L. monocytogenes cannot grow at a pH less than 4.0 in different media (e.g. cheese, salami, beef), but may grow at higher pH values (Augustin et al., 2005). Scientific experiments with rats (Pron et al., 1998), mice (MacDonald & B Carter, 1980) and guinea pigs (Lecuit, 2001) showed that a significant portion of inoculated L. monocytogenes are killed following the first hours of ingestion (Melton-Witt et al., 2012). Melton-Witt et al. inoculated guinea pigs with 108 CFU of L. monocytogenes, but found only 142 CFU in the small intestine 4 h after inoculation (Melton-Witt et al., 2012). These data indicate that stomach fluid is a major deterrent for the survival and growth of L. monocytogenes. If the bacteria can manage to survive the stomach fluid and reach the small intestine, where the pH level is relatively neutral (6.4–7.4) (Merchant, McConnellLiuRamaswamyKulkarni, Basit, & Murdan, 2011), they may be able to replicate and grow.
2.2. Commensal bacteria
L. monocytogenes travels to the small intestine upon survival through stomach fluid. The small intestine is a favorable environment for bacterial growth as compared to the stomach. However, the bacteria still needs to overcome several obstacles to colonize. The small intestine is a niche for more than 500 species of commensal microbiota (Artis, 2008, Stecher and Hardt, 2011). The commensal bacteria are beneficial for the host, but fight against incoming pathogens through different mechanisms. By consuming unused nutrients, commensal microbiota compete with other pathogens for resources and inhibit their growth. By releasing microbial metabolites, acetate, and antimicrobial effector molecules called bacteriocins, resident microbiota can effectively inhibit colonization of pathogenic bacteria (Arpaia, 2014, Stecher and Hardt, 2011). Microbiota also induce innate and adaptive immunity by releasing microbial patterns, lipopolysaccharides (LPS) and peptidoglycan, which can be sensed by host epithelial cells. Upon sensing pathogens, goblet cells release gel-forming mucins and epithelial cells release defensins (Stecher and Hardt, 2011). These proteins help kill bacteria and defend the host from any chemical and physical injuries due to pathogenesis (Kim and Ho, 2010, Stecher and Hardt, 2011).
2.3. Host immune cells
The innate immune system is the first line of defense against pathogen colonization and is primarily responsible for clearing pathogens from the host. Dendritic cells (DCs) and Macrophages are two important components of the innate immune system and are effective, in particular, against L. monocytogenes. DCs sample luminal contents by stretching their long dendrites through tight junctions of epithelial cells. Macrophages destroy pathogens by uptaking and degrading them, releasing inflammatory mediators, and inducing adaptive immune response (Higginbotham et al., 1992, Smith et al., 2011, Stecher and Hardt, 2011). These immune cells have the ability to recognize microbial patterns through pattern recognition receptors (PRR) and toll like receptors (TLR) (Tanoue & Umesaki, 2010). The innate immune system in essence regulates the whole immune response against the invading pathogens and prevents them from spreading beyond the intestine and causing systemic infection. When an infection persists, the adaptive immune system becomes activated. CD8+ T cells proliferates rapidly and clear the infection (Pamer, 2004). Plasma cells mediated by DCs release IgA in the lamina propria (Artis, 2008, Stecher and Hardt, 2011). IgA can reach the small intestine and attach to bacteria to inactivate them (Stecher and Hardt, 2011). Both T cells and B cells retain memories which can promptly clear a possible secondary infection (Artis, 2008, Pamer, 2004).
In addition to microbial resistance and immune pressure, the host's liver secrets a significant amount of bile into the intestinal tract which exerts stress on pathogens (Barbosa et al., 2012, Begley et al., 2005). Bile can affect phospholipids and proteins of cell membrane and structure, and cause dissociation of the cell membrane (Gahan & Hill, 2014). It also induces DNA damage in bacterial cells (Begley et al., 2005). However, the bile resistance of L. monocytogenes in the small intestine has also been reported (Begley et al., 2002, Olier et al., 2004).
3. Population dynamics of L. monocytogenes: a mathematical model
In this section, we describe the population dynamics of L. monocytogenes at the very early stage of infection. L. monocytogenes can invade a host through contaminated food and travel, initially, from the mouth to the intestine along with food. Due to different environments along the gut we consider the population dynamics of L. monocytogenes in the stomach and small intestine separately. We assume that (1) while saliva in the mouth initiates the digestive process, we ignore its effect on the ingested bacteria population; (2) Bacteria do not grow in the stomach due to the presence of high acidity, but are killed, decaying exponentially; (3) Bacteria that survive in the stomach travel along with food particles and reach the small intestine. The gastric emptying time, denoted by tGI, for a human is 6–8 h and for a guinea pig is 2 h (Melton-Witt et al., 2012). Thus, if an ingested organism survives, it must reach the small intestine within this period; (4) The growth of the bacteria is limited by commensals and the intestinal environment. That is, bacteria cannot grow beyond the carrying capacity of the small intestine; (5) In the small intestine, L. monocytogenes can reproduce and may be killed by immune cells and other molecules (e.g. bile) as described in Section 2. We further assume that, initially, the population of immune cells and other molecules that kill L. monocytogenes collectively remain constant.
Following assumptions (1)–(5) above, the dynamics of L. monocytogenes in the gut can be described by the following ordinary differential equation model:
| (3.1) |
where LG (CFU) denotes the population of L. monocytogenes in the stomach at time 0 ≤ t ≤ tGI (in hours) and δ > 0 (h−1) represents the kill rate of the bacteria due to high acidity in the gastric environment. If the bacteria survive passing through the stomach, we assume that the population reaches the small intestine (on average) at time tGI. Thus for t > tGI, LI (CFU) represents the population of L. monocytogenes in the small intestine and we assume the population dynamics there follow a logistic growth function with an intrinsic growth rate r and carrying capacity K. Due to host defense, L. monocytogenes is killed at the rate of βI with a saturated killing mechanism (Malka et al., 2010, Skalski and Gilliam, 2001). Motivated by a prey-predator interaction of Michaelis-Menten type we assume that the availability of defense from immune cells for bacteria killing will be reduced as the number of bacteria increases (Creighton, 1999, Hsu et al., 2001). Banfi et al. demonstrate through an in vitro experiment with E. coli bacteria that when the bacteria-macrophages ratio increased from 10 to 50 the phagocytosis increased from 5 to 74 per 100 macrophages (Banfi, Cinco, & Zabucchi, 1986). However, when that ratio increased to 200 the phagocytosis increased only to 98. In a similar experiment with Campylobacter jejuni bacteria, Banfi et al. showed that bacterial phagocytosis did not change significantly with the increased ratio of bacteria-macrophages (Banfi et al., 1986). In light of these studies, we assume that the killing ability of an immune cell per unit time is limited and the total killing of bacteria by the available immune cells has an upper bound determined by the saturation factor α. Finally, C denotes the constant population of intestinal molecules/immune cells involved in killing the bacteria.
Note that L. monocytogenes can cross the intestinal wall through cell-to-cell transmission and can be passed out along with food or feces (intestinal contents) (Lecuit, 2001, Melton-Witt et al., 2012). Due to a lack of data and a desire to root the model with clear mechanistic processes we do not explicitly consider the population dynamics involved with L. monocytogenes being passed out of the intestine. However, the dissemination of bacteria is regulated by the carrying capacity K. Moreover, to focus on the initial growth of L. monocytogenes and to elucidate initial mechanisms that govern dose-dependent infections, we assume that the crossing of the intestinal wall has little effect on the colonization of L. monocytogenes in the small intestine. Thus, we intentionally ignore detailed descriptions of bacterial crossing and passage out in the modeling steps. Bacterial crossing of the intestinal barrier may be critical, particularly for systemic infections. These factors will be explored in future works.
Since C is constant, we combine βI and C into a single parameter β and consider the following model for further discussion:
| (3.2) |
3.1. Model analysis
After the initial decay in the stomach, during the period from time zero to tGI, the L. monocytogenes population enters the small intestine, where the density can approach either zero or a positive steady state described by the second equation of the model (3.2). The model (3.2) is well-posed in the sense that it has a non-negative, bounded, unique solution subject to an initial value. In other words, given an initially ingested dose of L. monocytogenes, model (3.2) can unambiguously describe the population dynamics of the bacteria in the gut.
The model (3.2) has three steady states, L0 = 0, L* and L+, where
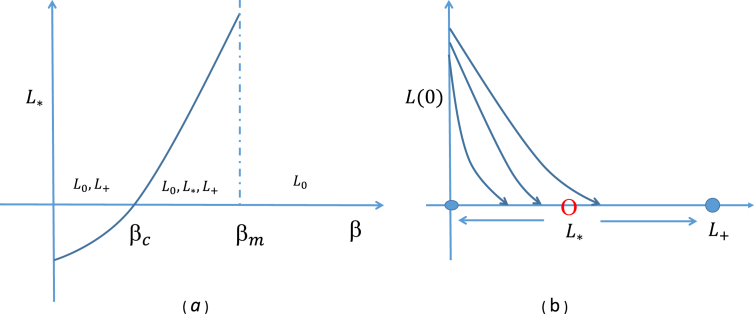
The steady state analysis of the model shows a bi-stable phenomenon (Regoes, Ebert, & Bonhoeffer, 2002). L0 and L+ are stable steady states while L* is unstable. That is, as time progresses, the model solution will approach either L0 or L+ depending on the initial values of L. monocytogenes entering the small intestine (Fig. 1). If the residue of the bacterial population at time tGI remains above L* then it grows and reaches L+, otherwise it approaches L0 and becomes extinct. This indicates that the final density of the bacterial population will be determined by the unstable steady state L*. In this sense, L* acts as a threshold for intestinal colonization, characterized by model parameters. A schematic view of this phenomenon is shown in Fig. 1. It shows that if L* is small in value, then a low density of bacteria entering the small intestine can invade and colonize. If L* is large in value, then a low density of L. monocytogenes entering the small intestine cannot survive. This shows that L* is an important threshold for the invasion of L. monocytogenes in the small intestine.
Fig. 1.
(a) Effect of β on the existence of the threshold, L*; (b) the density of L. monocytogenes approaches one of the two stable steady states (bi-stable phenomenon).
The threshold L* depends on several parameters, most of which typically remain constant across hosts. However, the parameter β, which characterizes a host's innate defensive potential, may vary across a population of hosts and therefore, L* may also vary. That is, the threshold value which determines the probability of infection at a certain dose of L. monocytogenes can be different for each individual. The parameter β has a critical value βc under which L* is negative. As β increases beyond the critical value, L* increases until it reaches a maximum at β = βm. If β increases further then L* does not exist. The existence of L* in terms of β is shown in Fig. 1. When β is less than βc, bacteria always grow and reach L+ and if β is larger than βm then they will die out. That is, an individual with a strong immune system (larger β) can prevent bacterial growth in the small intestine, but one with a weak immune system may not be able to prevent colonization of L. monocytogenes in the gut for a given dose.
4. Application of the model to guinea pigs
Since we have a relatively complete set of guinea pig data for the model processes described in Section 3, we tailor model (3.2) to address the population dynamics of L. monocytogenes ingested by guinea pigs (Lecuit, 2001). Multiple experiments provide us the opportunity for parameter estimation and comparison of results. Using the estimated parameters, we evaluate the probability of infection for different doses. We also perform sensitivity analysis of the estimated parameters to identify the critical parameters that can affect the shape of the dose-response curve.
4.1. Parameter estimation
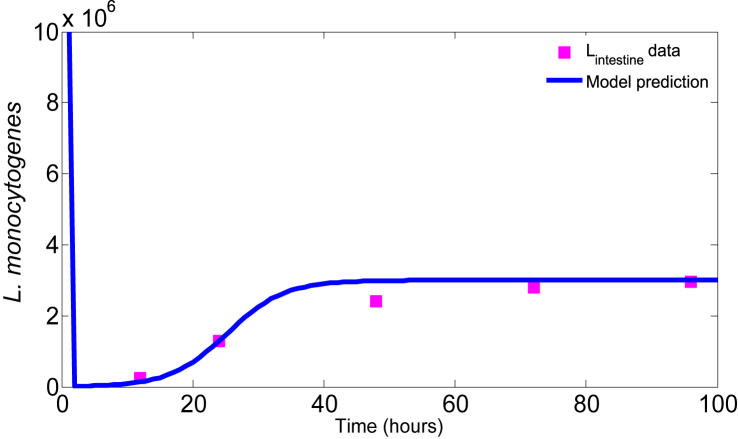
The model (3.2) has five parameters. To estimate the baseline value of the model parameters, we rely on existing literature and animal data. Melton-Witt et al. recovered 142 CFU of L. monocytogenes 4 h following infection with 1 × 108 CFU (Melton-Witt et al., 2012). Since the gastric emptying time of a guinea pig is 2 h, all the ingested L. monocytogenes that survive the stomach environment must reach the small intestine within this period. In line with (Melton-Witt et al., 2012), we assume that bacterial growth within 2 and 4 h is negligible (Melton-Witt et al., 2012). This allows us to estimate δ = 6.73 h−1, the killing rate of bacteria in the stomach. We assume that δ is completely determined by the acidity in the stomach. Zhu et al. showed through an in vitro experiment that the decay rate of E. coli bacteria in different media varied between 6.15 and 9.15 at pH 3.0 (Zhu et al., 2006). Since the growth/decay rate of E. coli and L. monocytogenes are similar at the same pH level (Saucedo-Reyes et al., 2012, Zhu et al., 2006), we consider the range of δ to be [6.15,9.15] (with mean 7.65 and sd 2.21). Lecuit et al. inoculated guinea pigs with 1 × 1010 CFU of L. monocytogenes and recovered a maximum bacterial load of 3 × 106 CFU in the small intestine during the course of infection (Lecuit, 2001). Therefore, we assume that the carrying capacity of L. monocytogenes in the small intestine is approximately K = 3 × 106 CFU. Banfi et al. conducted an in vitro experiment to observe the killing ability of two strains of bacteria, C. jejuni and C. coli, by guinea pig macrophages (Banfi et al., 1986). From their experimental results we estimate the killing rate of bacteria to be in the range [0.03,1.55] with mean 0.5767 and sd 0.64. Since this killing rate of two strains of bacteria is due to guinea pig macrophages, we explore the results with sensitivity analysis. Finally, using these estimated parameters, we further estimate α and r from guinea pig data in (Lecuit, 2001) by a data fitting procedure. Here we use the MATLAB function ode23s to solve the model (3.2) and then use an optimizer fmincon to minimize the error function:
where LI(ti) is the model prediction at time ti and is the datum at each time ti; and N is the total number of data points. The parameters, α and r, corresponding to the minimum error, are given in Table 1 and the model solutions corresponding to the estimated parameters together with the experimental data are shown in Fig. 2. It shows that the model solution fits the data quite well. Note that the estimated growth rate, r, is consistent with the growth rate of L. monocytogenes found in (Augustin et al., 2005, Bakardjiev et al., 2006).
Table 1.
The baseline values of the model parameters.
| Parameter | Description | Baseline value | Range | References |
|---|---|---|---|---|
| r | growth rate of L. monocytogenes | 0.23 h−1 | [0.1,0.55] | data fit |
| K | carrying capacity | 3 × 106 CFU | [106,108] | (Lecuit, 2001) |
| δ | killing rate of L. monocytogenes in the stomach | 6.73 h−1 | [6.15,9.15] | (Melton-Witt et al., 2012) |
| β | killing rate of L. monocytogenes in the small intestine | 0.58 h−1 | [0.03,1.55] | (Banfi et al., 1986) |
| α | saturating factor | 0.18 CFU−1 | [0.01,1.3] | data fit |
Fig. 2.
Data fit. The squares are the numbers of L. monocytogenes in the small intestine of guinea pig (Lecuit, 2001) and the solid curve is the model prediction.
4.2. Host defense
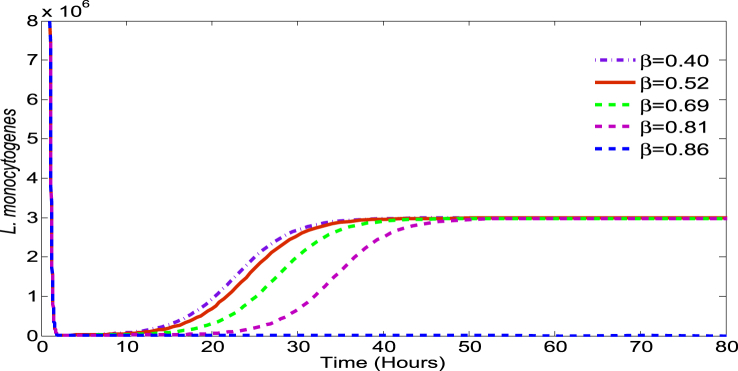
L. monocytogenes encounters major defenses from the host at the stomach and the small intestine in terms of high acidity and immune cells, respectively. The model parameter δ characterizes the killing of bacteria due to the stomach acid. Note that most of the bacteria are killed within hours of ingestion (Fig. 3), emphasizing that δ is a key parameter. To observe the relative effect of δ on the output, we consider the estimated value of 6.73 (h−1) as a base value and allow a variation within the range [6.15,9.15] derived from (Zhu et al., 2006).
Fig. 3.
Effect of β on bacteria survival: Initial dose = 1 × 1010 CFU, α = 0.18, r = 0.23, K = 3 × 106, δ = 6.73.
Host defense in the small intestine is characterized by the model parameter β which may vary depending on the individual host. That is, each individual may have a different defense potential against L. monocytogenes. Fig. 3 illustrates the effect of β (while other parameters remain constant) on LI, the L. monocytogenes population in the small intestine. If β is large (e.g. for β≈0.86), then even with a high dose of L. monocytogenes at ingestion, the bacteria cannot cause infection. However, for lower values of β, even with a low dose at ingestion, L. monocytogenes may be able to colonize the intestine to cause infection.
4.3. Sensitivity analysis and model validation
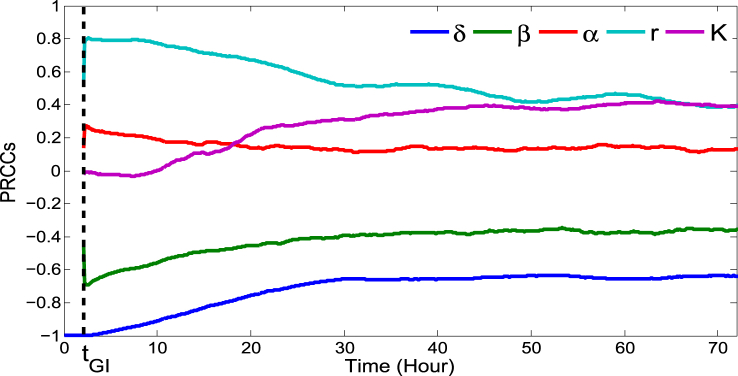
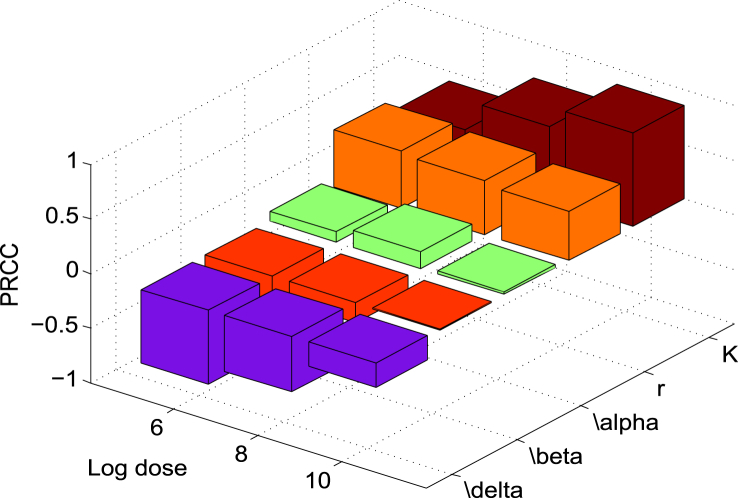
The baseline values of the model parameters are estimated from literature, experimental results and data fitting. These estimates, however, may not be precise given uncertainties in experimental data. In order to observe the sensitivity of the estimated parameters on the model outcomes, we determined the partial rank correlation coefficient (PRCC) with Latin hypercube sampling (LHS) (Marino, Hogue, Ray, & Kirschner, 2008). Dividing the interval range corresponding to each of the parameters into 1000 sub-intervals uniformly, we generate 1000 simulations to form the k × 1000 (k = 5, number of parameters) sampling matrix. Rank-transformations of this matrix are used to calculate PRCCs which lie between −1 and 1. Notice that the PRCC effectively measures the monotonicity between parameter and corresponding output. A positive PRCC indicates that the corresponding parameter with increased value will increase the growth of L. monocytogenes and the probability of infection, whereas the parameter with negative PRCC has the opposite effect on the output. The parameter with highest PRCC in absolute value is the most sensitive. The sensitivity of the parameters is shown in Fig. 4, Fig. 5. It shows that the sensitivities are time and dose dependent. Note that the sensitivity of the parameters does not change approximately after 48 h, when the L. monocytogenes population is stabilized at the steady state (Fig. 4). In the following, we discuss the sensitivity of each of the parameters in detail.
Fig. 4.
Temporal sensitivity of the model prediction LI relative to each parameter with fixed initial dose of 1 × 106 CFU. Time tGI is indicated by the vertical dotted line. Initially, the two model parameters, δ and r, are the most sensitive whereas K becomes more sensitive at the end of simulation. This sensitivity result is reasonable as δ and r play important roles in the survival and growth of L. monocytogenes at the beginning of infection while K dominates the population when it becomes large.
Fig. 5.
-
1)According to Fig. 4, δ is the most sensitive parameter at the beginning of the infection and it remains among the top sensitive parameters during the infection. It is even more sensitive at a lower initial dose (e.g. 106 CFU) (see Fig. 5). Recall that δ is the killing rate of bacteria in the stomach caused by the stomach acid. Being large, δ can reduce the initial dose of ingested bacteria below the threshold before they move down to the small intestine. Thus, large δ can effectively block the bacterial dissemination into the small intestine and across the body. Small δ, on the other hand, may allow sufficient amount of bacteria passing to the small intestine where the bacteria may colonize if not killed by the immune cells and commensals. Since δ acts on the bacteria during the first few hours of infection, the sensitivity declines quickly there after.
-
2)The growth rate r plays an important role in the survival of the L. monocytogenes. Its magnitude clearly influences the population size initially, but the sensitivity of r decreases over the time as the population approaches the steady state and stabilizes (see Fig. 4). Furthermore, if r is sufficiently large then the L. monocytogenes population can survive for a longer period of time. On the other hand, with a small growth rate, L. monocytogenes may not survive against host defenses.
-
3)The survival of L. monocytogenes is sensitive to the carrying capacity K in connection with the maximum level of the population and increases with the progression of time (Fig. 4). Since the carrying capacity has little effect on the initial growth or the survival of L. monocytogenes at the early stage of infection, it is not influential at the beginning of the infection. However, if the bacteria survives for a long time and continues to grow then K dominates the population, playing a more significant role. Fig. 5 also indicates that K is more sensitive at a higher inoculation dose. This is reasonable since the population more quickly reaches the carrying capacity with a higher initial dose.
-
4)The killing rate, β, of L. monocytogenes in the intestine is sensitive, with negative PRCC, similar to δ and r in magnitude. The population that survives in the stomach and reaches the small intestine is killed by the host's immune cells at the rate of β. Thus β, relative to our modeling context, corresponds to the final defense posed by the host. A weak defense (immune) system, with a small β, could allow the bacteria to grow. But, a strong immune system can clear the bacteria from the small intestine before they colonize. In terms of Fig. 5, we see that for lower doses β plays a more significant role as the immune system has a higher chance of suppressing the bacterial population.
-
5)The saturating constant, α, is the least sensitive among the model parameters. In the absence of α (i.e. α = 0) the bacteria may die out due to the host defense, but a positive value of α could help the bacteria survive. Note that in Fig. 5, the PRCC value of α seems to have maximum for initial doses near 108 CFU. While this result is not completely clear, due to the relative low sensitivity of α we defer an in depth analysis.
To summarize, the sensitivity results shown in Fig. 4, Fig. 5 are intuitive and have clear explanations in terms of the mechanisms associated to each parameter. These results give credence to model (3.2) as a useful tool for predicting Listeriosis dynamics in the gut of guinea pigs. In the next section we illustrate how our model can be linked to dose-response information, providing another test of validation.
4.4. Dose-responses
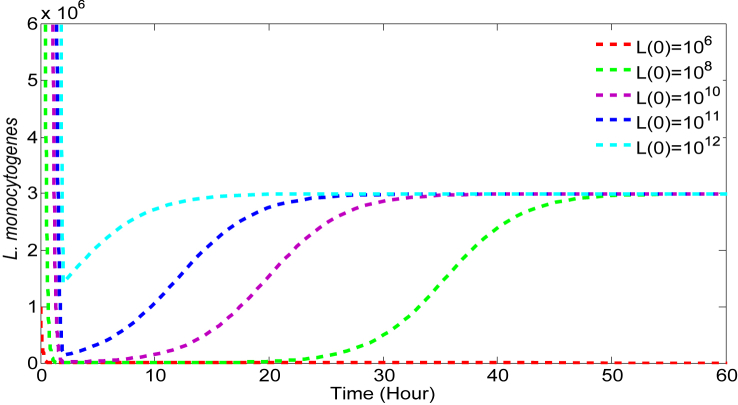
The main application of our model (3.2) is that it can produce dose-response curves that have a clear quantifiable connection to mechanisms of pathogen colonization and growth (parameters r, K, and α in Table 1) in the small intestine as well as host response to such ingested pathogens (parameters δ and β in Table 1). The key rests on the reasonable assumption that these model parameters are both host- and pathogen-dependent. That is, each host/ingested pathogen combination corresponds to set of particular parameter values (for the five parameters in model (3.2)). For instance, for the baseline set of values (as in Table 1), we can predict the dose dependent infection and bacterial growth. Referring to Fig. 6, the model predicts that with a relatively low dose at ingestion, L. monocytogenes dies out in the stomach before reaching the small intestine and causing infection. When the ingested dose is larger, a significant portion of the inoculum can reach the small intestine where they can grow against host defense and colonize. Thus, Fig. 6 indicates that a large ingested dose not only leads to colonization, but it helps L. monocytogenes to colonize and spread an infection faster.
Fig. 6.
Effect of initial doses on the survival of L. monocytogenes. The values of the parameters are β = 0.58, α = 0.18, r = 0.23, K = 3 × 106, δ = 6.73.
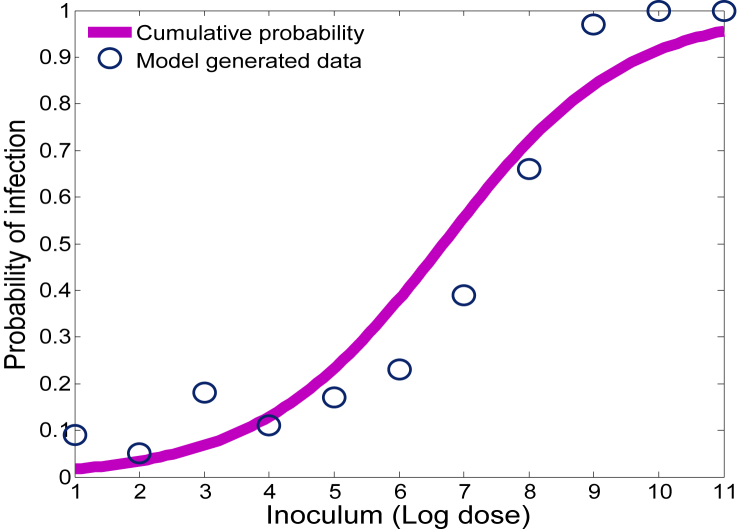
While this result is intuitive, the power of our approach utilizes the fact that the parameter values vary according to some distribution over the respective ranges as described in Section 4.1. We assume the distribution corresponding to each parameter is uniform and we simulate the model (3.2) 100 times for a given initial dose. If the simulation ends with a positive L. monocytogenes population (at the end of 96 h), we count it as a positive response, otherwise it is counted as zero/no response. In this sense, our model provides information much like a feeding trial experiment, connecting ingested dose levels with the probability of infection in the small intestine 96 h post inoculation. Referring to Fig. 7, the circles above each dose level indicate the probability (out of 100 guinea pigs) that L. monocytogenes is able to colonize in the gut, and thus lead to infection.
Fig. 7.
Probability of infection with respect to various inoculum levels of L. monocytogenes.
Typically, descriptive models such as the exponential, beta-poisson, and log-logistic are fit to such data to produce a dose-response curve (Haas et al., 1999, Van Stelten et al., 2011). For illustrative purposes, see the solid curve in Fig. 7, we input the model (3.2) generated dose-response data into a log-logistic model LLM (Farber et al., 1996, Haas et al., 2000, Pouillot et al., 2015, Smith et al., 2008, Van Stelten et al., 2011), given by
| (4.1) |
where x = log(d) (the log dose of L. monocytogenes) and b0 and b1 are constants to be estimated by maximizing the nonlinear likelihood function (Van Stelten et al., 2011). The model generated data together with the dose-response curve are shown in Fig. 7.
An important advantage of our modeling approach is that we can effectively examine how sensitive the infection probability is to each of the five parameters in model (3.2). Each of these parameters plays a clear mechanistic role in deciding the outcomes of the model and may affect the dose-response curve. In order to illustrate this parameter dependence, we again generate log-logistic dose-response curves, but vary a single parameter with respect to dose, to see the effect of the respective parameter on the shape of the curve.
4.4.1. Effect of r and K on the dose-response curves
The growth rate, r, and the carrying capacity, K, of L. monocytogenes can vary in different media (Augustin et al., 2005, Zhu et al., 2006) and hosts (Lecuit, 2001, Smith et al., 2008), but whether they can vary within a population is unknown. However, when these parameters are varied in their respective ranges the probability of infection is not affected significantly (see Fig. 8).
Fig. 8.
Dose-response curves with uniform distributions of r (a), and K (b). The solid curves are generated from the log-logistic model and the circles are the model generated data. The other parameters are set to the base values given in Table 1.
4.4.2. Effect of δ on the dose-response curve
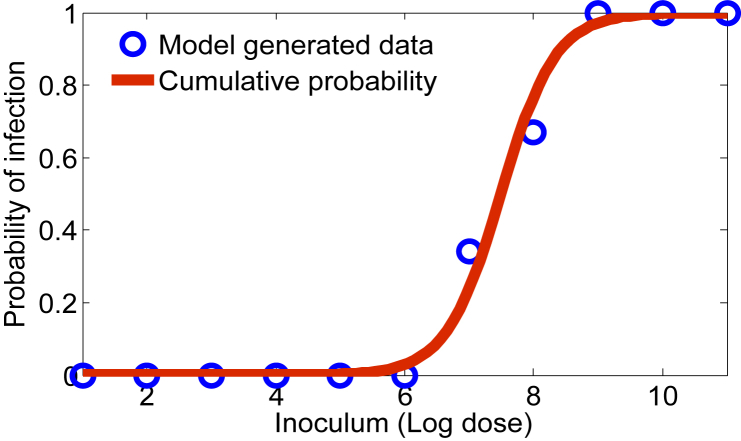
The primary killing of L. monocytogenes takes place in the stomach due to the acidic environment and is characterized by δ. When δ varies uniformly over the range [6.15,9.15], the resulting dose-response curve is illustrated in Fig. 9. It shows that δ plays a relatively stronger role in shaping the dose-response curve as compared with r and K. However, this effect is limited at lower inoculum levels by the potentially high values δ can take on in its range and indicates that further work should be done to identify more precisely relationship between pH and the kill rate of L. monocytogenes in the stomach.
Fig. 9.
Effect of δ on the dose-response curve. The solid curve represents the probability of infection when δ is distributed uniformly and the circles are the model generated data. The other parameters are set to the baseline values given in Table 1.
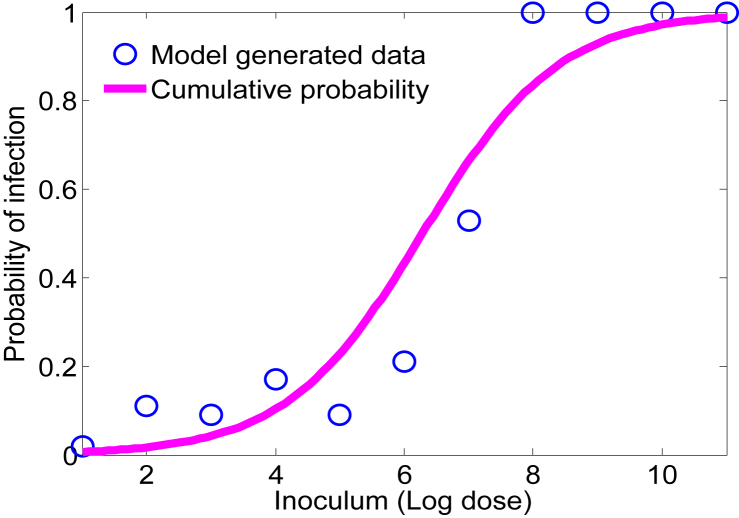
4.4.3. Effect of β on the dose-response relationship
As discussed earlier, the defense potential including immune response against L. monocytogenes is individual dependent. The parameter β which essentially characterizes the immune “strength” of hosts is assumed to have some distribution across the host population. Fig. 1, Fig. 3 show that the probability of infection reduces as β increases. If β is distributed uniformly, the median of the dose-response curve shifts to the left as compared with the dose-response curve with respect to δ (compare Fig. 9, Fig. 10). It also shows that β most strongly affects the dose-response curve among the model parameters.
Fig. 10.
The dose-response curve with a uniform distribution of β. The solid curve is generated from the log-logistic model and the circles are the model generated data. The other parameters are set to the baseline values given in Table 1.
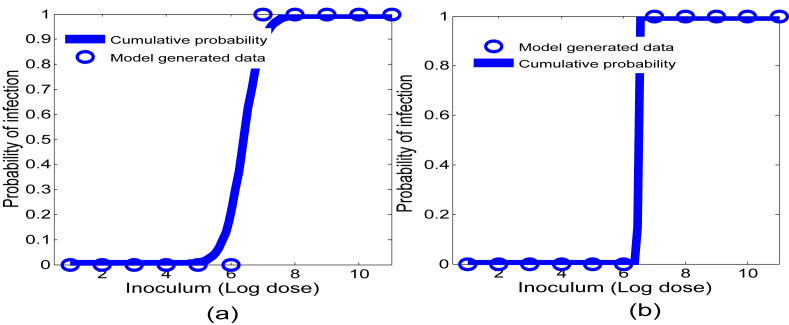
4.4.4. Comparison of model prediction to an experimental outcome
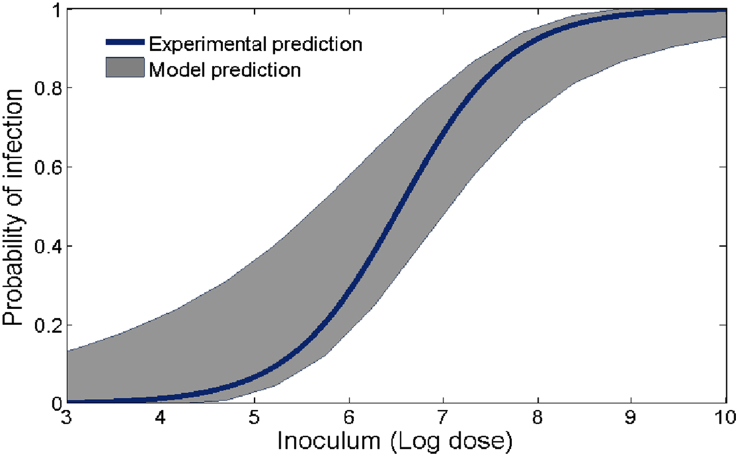
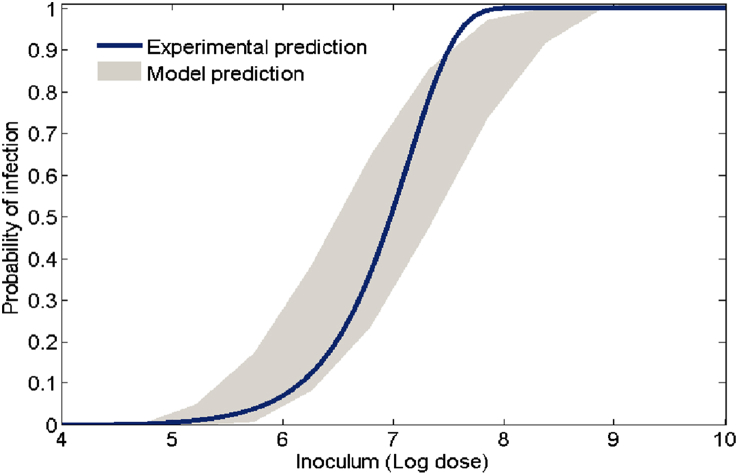
Since β affects the dose-response curve most significantly, we further explore model outcomes with respect to β and compare with an experimental result. Fixing the other four model parameters to their baseline values, we run the model 200 times (again we assume β is uniformly distributed) and generate the dose-response outcomes. Next we choose either a log-logistic or exponential model and fit each model run and then plot the minimum and maximum of these fits together with the corresponding (log-log or exponential) dose-response curve from the experimental result (Van Stelten et al., 2011) in Fig. 11, Fig. 12. Note that dose-response curve in Fig. 11 is a log-logistic fit of probability data from guinea pig livers that tested positive during L. monocytogenes feeding trials. Because of typical L. monocytogenes transmission pathways, the liver data was most representative of (as opposed to the spleen or ileum) L. monocytogenes presence in the upper regions of the small intestine and therefore useful for comparison (Lecuit, 2001). Fig. 12 also uses this data, except now an exponential model is used to produce the dose-response curve. Both Figures indicate that the model (3.2) prediction matches well with experimental outcomes. Note, however, that the experimental curve in Fig. 12, for doses between log107.5 and log108, is higher than the model (3.2) prediction, falling outside the predicted range. While this result may depend on many factors, it shows that model (3.2), together with valid parameter ranges, can be used as a gauge to determine the appropriateness of particular probability models.
Fig. 11.
Model generated dose-response region together with an experimental result. The shaded region is the model predicted outcomes given by the distribution of β and the solid curve results from fitting a log-logistic model to the guinea pig data (Van Stelten et al., 2011). The other parameters of the model are set to the base values given in Table 1.
Fig. 12.
Model generated dose-response region together with an experimental result. The shaded region is the model predicted outcomes given by the distribution of β and the solid curve results from fitting an exponential model (Haas et al., 1999) to the guinea pig data (Van Stelten et al., 2011). The other parameters of the model are set to the base values given in Table 1.
5. Discussion
We have developed a novel mathematical model (3.2) to quantify the within host dynamics of L. monocytogenes from ingestion to potential intestinal colonization. Unlike descriptive dose-response models, this model describes the transmission pathway of L. monocytogenes with respect to the mechanisms of digestion and initial immune response in the small intestine and predicts the infection potential of the bacteria relative to initial dose. A key feature in our model, that allows the link between ingested dose and infection probability, concerns a threshold phenomenon for L. monocytogenes survival in the small intestine. In the following section, we discuss this effect and illustrate how it emerges through combining experimentally supported mechanisms.
5.1. Bacterial growth at low density: Allee effect
Bacteria populations replicate through a cell division process. In theory, one bacterium can generate millions of bacteria. However, experimental results indicate that a minimum density is required for bacteria to grow (Darch et al., 2012, Huang et al., 2016, Smith et al., 2014). If the initial density is not sufficiently large then bacteria cannot reproduces and instead become extinct. This density dependent survival phenomenon is known as the Allee effect. The term was coined from the name Warder Clyde Allee, who first observed that cooperation is a critical factor for reproduction of an organism, especially at low density (Bowen and Allee, 1932, Regoes et al., 2002).
One example of such cooperation concerns the phenomenon of quorum sensing (QS). Essentially, bacteria communicate with each other by releasing chemical signal molecules (Waters & Bassler, 2005). Using the QS mechanism, bacteria monitor their neighborhood and alter their behavior in response to the environment. A recent study demonstrates that at high density, the bacterial population can express chloramphenicol acetyltransferase (CAT) that detoxifies chloramphenicol and helps ensure survival in the presence of chloramphenicol (Huang et al., 2016). However, at a low density the population is unable to survive due to lack of CAT.
In terms of our modeling context, this threshold phenomenon emerges as a result of combining a logistic form, for L. monocytogenes growth in the small intestine, and a Michaelis-Menten form that quantifies the interaction of the bacteria, innate immune cells and other molecules in the small intestine that can kill the pathogen. As discussed in Sections 3, 2.2, the presence of commensals and other factors in the intestinal environment (such as flow rate of fluid through the small intestine) limits the maximum L. monocytogenes population that can colonize, determining a carrying capacity K. Combined with the intrinsic growth rate r, the first term in the equation for LI in model (3.2) is given by rLI(1−LI/K). In addition, the second term in the equation for LI is the inactivation term due to immune cells and other molecules, and is of the form βLI/1+αLI. This limiting form is justified by the experimental studies discussed in Section 3. The point here is that the mathematical combination of these mechanisms provides a setting whereby a population threshold determines the survival or extinction of L. monocytogenes in the gut.
5.2. Dose-response implications
The model (3.2) dynamics of L. monocytogenes in the small intestine is completely determined by the model parameters. Unlike the parameters in probabilistic models that are fit to dose-response data, our model (3.2) parameters quantify the manner by which L. monocytogenes interacts with the gastro-intestinal environment and the initial immune response of the host. Therefore, an advantage of this modeling approach is that one can predict or control infections by altering parameters that can be explained via experiments.
In terms of guinea pigs, refer to Section 4.4, we find that δ (the killing rate of bacteria due to stomach acid) and β (the killing rate of bacteria due to immune response), as opposed to the other three parameters in model (3.2), play important roles in determining the shape of the dose-response relationship. These results are significant for at least two reasons. First, model (3.2) provides a quantifiable link between these parameters and the dose-response prediction. Second, by identifying the most influential parameters, model (3.2) provides a guide to streamline further experiments to elucidate both the appropriate range and distribution of these parameters.
For instance, assuming that β varies uniformly on its range and using a log-logistic model to fit the dose-response curve, Fig. 10 shows the effect of β on the infection probability given an initial dose. As mentioned in Section 4.4, β is the most influential parameter on the dose-response curve. While the range for β has support in the literature (Banfi et al., 1986), further experimental work is needed to confirm both its range limits and distribution. In particular, if the mass of β’s distribution is more concentrated on the upper part of its range, it would be less influential as compared with a distribution with the opposite skew. This type of detailed study is recommended also for δ (killing rate of bacteria due to stomach acid), and less critically for r (growth rate of L. monocytogenes in small intestine) and K (carrying capacity small intestine) in the context of guinea pigs.
Authentication of such parameter information is important for extending model (3.2) to be suitable for human application. For one, sensitivity analysis, as in Section 4, may be able to show that certain parameters play a minor role (like α) in determining infection probabilities and therefore can be informed by “animal data”. On the other hand, we anticipate that δ and β will be critical parameters. For example, experimental outcomes could confirm how δ is affected by H2 blockers. Coupling this information with our model predicted dose-response, we can provide a mechanistic prediction of Listeriosis risk for sub-populations who take such medicine to treat acid-reflux and other complications. Additionally, understanding how β varies across the population is worth further investigation. In-vitro experiments may be suggested to measure β with regards to susceptible sub-groups, e.g. pregnant women and the elderly.
5.3. Future work
The model (3.2) can also be augmented to investigate long-term and systemic infections. Bacterial crossing through the intestinal wall and dissemination to liver, spleen, brain and placenta are important aspects of systemic infections. The immune response, particularly how T-cell dynamics evolve with L. monocytogenes is critical to understand the disease dynamics. Delay of immune response is also significant for infection and could be linked to the susceptibility of immuno-compromised sub-groups. In addition, the effect of delay in the logistic form of model (3.2) may be of interest. Inclusion of such a delay would be useful if oscillations in the bacterial population in the small intestine are observed (Arino et al., 2006). Correlation between clinical symptoms and peak pathogen levels from model outputs could also be relevant for clinical uses. Furthermore, attachment and spatial movement of the bacteria in the intestinal wall, taking into account the food matrix and nutrient dynamics, may be an important aspect of initial growth and can be explained through spatial models. More broadly, our model can be used to explain the dose-response relationships of other food-borne pathogens. Investigation with such expanded models would uncover further insights towards pathogen-host dynamics and contribute significantly to public health.
Acknowledgments
Daniel Munther acknowledges support from Cleveland State University startup funding (STARTUP42). Ashrafur Rahman's postdoctoral fellowship is supported by a research contract from the Public Heath Agency of Canada and by the NSERC CREATE project Advanced Disaster, Emergency and Rapid Response Simulations. Jianhong Wu's research has been funded by the Natural Sciences and Engineering Research Council of Canada and by the Canada Research Chairs program. The authors would like to thank the anonymous reviewers for their valuable comments and suggestions for the improvements of this article.
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
References
- Allerberger F., Wagner M. Listeriosis: A resurgent foodborne infection. Clinical Microbiology and Infection. 2010;16(1):16–23. doi: 10.1111/j.1469-0691.2009.03109.x. [DOI] [PubMed] [Google Scholar]
- Arino J., Wang L., Wolkowicz G.S.K. An alternative formulation for a delayed logistic equation. Journal of Theoretical Biology. 2006;241(1):109–119. doi: 10.1016/j.jtbi.2005.11.007. [DOI] [PubMed] [Google Scholar]
- Arpaia N. Acetate dampens inflammatory cytokines in iec keeping peace with the microbiome : Acetate dampens inflammatory cytokine production in intestinal epithelial cells. Immunology and Cell Biology. 2014;92(7):561–562. doi: 10.1038/icb.2014.40. [DOI] [PubMed] [Google Scholar]
- Artis D. Epithelial-cell recognition of commensal bacteria and maintenance of immune homeostasis in the gut. Nature Reviews Immunology. 2008;8(6):411–420. doi: 10.1038/nri2316. [DOI] [PubMed] [Google Scholar]
- Augustin J.C., Zuliani V., Cornu M., Guillier L. Growth rate and growth probability of Listeria monocytogenes in dairy, meat and seafood products in suboptimal conditions. Journal of Applied Microbiology. 2005;99(5):1019–1042. doi: 10.1111/j.1365-2672.2005.02710.x. [DOI] [PubMed] [Google Scholar]
- Bakardjiev A.I., Theriot J.A., Portnoy D.A. Listeria monocytogenes traffics from maternal organs to the placenta and back. PLoS Pathogens. 2006;2(6):623–631. doi: 10.1371/journal.ppat.0020066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banfi E., Cinco M., Zabucchi G. Phagocytosis of Campylobacter jejuni and C. coli by peritoneal macrophages. Journal of General Microbiology. 1986;132(Pt 8):2409–2412. doi: 10.1099/00221287-132-8-2409. [DOI] [PubMed] [Google Scholar]
- Barbosa J., Borges S., Magalhães R., Ferreira V., Santos I., Silva J. Behaviour of Listeria monocytogenes isolates through gastro-intestinal tract passage simulation, before and after two sub-lethal stresses. Food Microbiology. 2012;30(1):24–28. doi: 10.1016/j.fm.2011.10.001. [DOI] [PubMed] [Google Scholar]
- Begley M., Gahan C.G.M., Hill C. Bile stress response in Listeria monocytogenes LO28: Adaptation, cross-protection, and identification of genetic loci involved in bile resistance. Applied and Environmental Microbiology. 2002;68(12):6005–6012. doi: 10.1128/AEM.68.12.6005-6012.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Begley M., Gahan C.G.M., Hill C. The interaction between bacteria and bile. FEMS Microbiology Reviews. 2005;29:625–651. doi: 10.1016/j.femsre.2004.09.003. [DOI] [PubMed] [Google Scholar]
- Bowen E., Allee W.C. Studies in animal aggregations: Mass protection against colloidal silver among goldfishes. Journal of Experimental Zoology. 1932;61(2):185–207. [Google Scholar]
- Cossart P. Illuminating the landscape of host-pathogen interactions with the bacterium Listeria monocytogenes. Proceedings of the National Academy of Sciences of the United States of America. 2011;108(49):19484–19491. doi: 10.1073/pnas.1112371108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cossart P., Toledo-Arana A. Listeria monocytogenes, a unique model in infection biology: An overview. Microbes and Infection. 2008;10(9):1041–1050. doi: 10.1016/j.micinf.2008.07.043. [DOI] [PubMed] [Google Scholar]
- Creighton T.E. John Wiley; New York: 1999. Encyclopedia of molecular biology. [Google Scholar]
- Darch S.E., West S.A., Winzer K., Diggle S.P. Density-dependent fitness benefits in quorum-sensing bacterial populations. Proceedings of the National Academy of Sciences of the United States of America. 2012;109(21):8259–8263. doi: 10.1073/pnas.1118131109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D'Orazio S.E.F. Animal models for oral transmission of Listeria monocytogenes. Frontiers in cellular and infection microbiology. 2014;4(February):15. doi: 10.3389/fcimb.2014.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farber J.M., Ross W.H., Harwig J. Health risk assessment of Listeria monocytogenes in Canada. International Journal of Food Microbiology. 1996;30(1–2):145–156. doi: 10.1016/0168-1605(96)01107-5. [DOI] [PubMed] [Google Scholar]
- Gahan C.G., Hill C. Listeria monocytogenes: Survival and adaptation in the gastrointestinal tract. Frontiers in Cellular and Infection Microbiology. 2014;4(February):9. doi: 10.3389/fcimb.2014.00009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giannella R.A., Broitman S.A., Zamcheck N. Gastric acid barrier to ingested microorganisms in man: Studies in vivo and in vitro. Gut. 1972;13:251–256. doi: 10.1136/gut.13.4.251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golnazarian C.A., Donnelly C.W., Pintauro S.J., Howard D.B. Comparison of infectious dose of Listeria monocytogenes F5817 as determined for normal versus compromised C57B1/6J mice. Journal of food protection. 1989;52(10):696–701. doi: 10.4315/0362-028X-52.10.696. [DOI] [PubMed] [Google Scholar]
- Haas C.N. Microbial dose response Modeling: Past, present, and future. Environmental Science & Technology. 2015;49(3):1245–1259. doi: 10.1021/es504422q. [DOI] [PubMed] [Google Scholar]
- Haas C.N., T Madabusi A., Rose J.B., Gerba C.P. Development and validation of dose-response relationship for Listeria monocytogenes. Quantitative Microbiology. 1999;1(1):89–102. [Google Scholar]
- Haas C.N., Thayyar-Madabusi A., Rose J.B., Gerba C.P. Development of a dose-response relationship for Escherichia coli O157:H7. International journal of food microbiology. 2000;56(2–3):153–159. doi: 10.1016/s0168-1605(99)00197-x. [DOI] [PubMed] [Google Scholar]
- Higginbotham J.N., Lin T.L., Pruett S.B. Effect of macrophage activation on killing of Listeria monocytogenes. Roles of reactive oxygen or nitrogen intermediates, rate of phagocytosis, and retention of bacteria in endosomes. Clinical and experimental immunology. 1992;88(3):492–498. doi: 10.1111/j.1365-2249.1992.tb06477.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howden C.W., Hunt R.H. Relationship between gastric secretion and infection. Gut. 1987;28(1):96–107. doi: 10.1136/gut.28.1.96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu Y., Hwang S.-B., Kuang T.-W. Global analysis of the Michaelis–Menten-type ratio-dependent predator-prey system. Journal of Mathematical Biology. 2001;681(42):498–506. doi: 10.1007/s002850100079. [DOI] [PubMed] [Google Scholar]
- Huang S., Lee A.J., Tsoi R., Wu F., Zhang Y., Leong K.W. Coupling spatial segregation with synthetic circuits to control bacterial survival. Molecular Systems Biology. 2016;12(2):1–13. doi: 10.15252/msb.20156567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.S., Ho S.B. Intestinal goblet cells and mucins in health and disease : Recent insights and progress. Current Gastroenterology Reports. 2010;12(5):319–330. doi: 10.1007/s11894-010-0131-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lara-Tejero M., Pamer E.G. T cell responses to Listeria monocytogenes. Current Opinion in Microbiology. 2004;7(1):45–50. doi: 10.1016/j.mib.2003.12.002. [DOI] [PubMed] [Google Scholar]
- Lecuit M. A Transgenic Model for Listeriosis: Role of Internalin in Crossing the Intestinal Barrier. Science. 2001;292(5522):1722–1725. doi: 10.1126/science.1059852. [DOI] [PubMed] [Google Scholar]
- MacDonald T.T., B Carter P. Cell-mediated-immunity to intestinal infection. Infection and Immunity. 1980;28(2):516–523. doi: 10.1128/iai.28.2.516-523.1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malka R., Shochat E., Rom-Kedar V. Bistability and bacterial infections. PLoS One. 2010;5(5) doi: 10.1371/journal.pone.0010010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marino S., Hogue I.B., Ray C.J., Kirschner D.E. A methodology for performing global ucertainty and sensitivity analysis in systems biology. Journal of Theoretical Biology. 2008;254(1):178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melton-Witt J.A., Rafelski S.M., Portnoy D.A., Bakardjiev A.I. Oral infection with signature-tagged Listeria monocytogenes reveals organ-specific growth and dissemination routes in Guinea pigs. Infection and Immunity. 2012;80(2):720–732. doi: 10.1128/IAI.05958-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merchant H.A., McConnell E.L., Liu F., Ramaswamy C., Kulkarni R.P., Basit A.W. Assessment of gastrointestinal pH, fluid and lymphoid tissue in the Guinea pig, rabbit and pig, and implications for their use in drug development. European Journal of Pharmaceutical Sciences. 2011;42(1–2):3–10. doi: 10.1016/j.ejps.2010.09.019. [DOI] [PubMed] [Google Scholar]
- Olier M., Rousseaux S., Piveteau P., Lemaître J.P., Rousset A., Guzzo J. Screening of glutamate decarboxylase activity and bile salt resistance of human asymptomatic carriage, clinical, food, and environmental isolates of Listeria monocytogenes. International Journal of Food Microbiology. 2004;93(1):87–99. doi: 10.1016/j.ijfoodmicro.2003.10.010. [DOI] [PubMed] [Google Scholar]
- Pamer E.G. Immune responses to Listeria monocytogenes. Nature Reviews Immunology. 2004;4(10):812–823. doi: 10.1038/nri1461. [DOI] [PubMed] [Google Scholar]
- Pizarro-cerda J., Ku A. Entry of Listeria monocytogenes in mammalian. Cold Spring Harbor Perspectives in Medicine. 2012:1–18. doi: 10.1101/cshperspect.a010009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouillot R., Hoelzer K., Chen Y., Dennis S.B. Listeria monocytogenes dose response revisited-incorporating adjustments for variability in strain virulence and host susceptibility. Risk Analysis. 2015;35(1):90–108. doi: 10.1111/risa.12235. [DOI] [PubMed] [Google Scholar]
- Pron B., Boumaila C., Jaubert F., Sarnacki S., Monnet J.P., Berche P. Comprehensive study of the intestinal stage of listeriosis in a rat ligated ileal loop system. Infection and Immunity. 1998;66(2):747–755. doi: 10.1128/iai.66.2.747-755.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regoes R.R., Ebert D., Bonhoeffer S. Dose-dependent infection rates of parasites produce the Allee effect in epidemiology. The Royal Society. 2002;269(1488):271–279. doi: 10.1098/rspb.2001.1816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roulo R.M., Fishburn J.D., Amosu M., Etchison A.R., Smith M.A. Dose response of Listeria monocytogenes invasion, fetal morbidity, and fetal mortality after oral challenge in pregnant and nonpregnant mongolian gerbils. Infection and Immunity. 2014;82(11):4834–4841. doi: 10.1128/IAI.01514-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saucedo-Reyes D., Carrillo-Salazar J.A., Reyes-Santamaría M.I., Saucedo-Veloz C. Effect of pH and storage conditions on Listeria monocytogenes growth inoculated into sapote mamey (Pouteria sapota (Jacq) H.E. Moore & Stearn) pulp. Food Control. 2012;28(1):110–117. doi: 10.1177/1082013217735472. [DOI] [PubMed] [Google Scholar]
- Shan Y., Fang C., Cheng C., Wang Y., Peng J., Fang W. Immersion infection of germ-free zebrafish with Listeria monocytogenes induces transient expression of innate immune response genes. Frontiers in Microbiology. 2015;6(APR):1–11. doi: 10.3389/fmicb.2015.00373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skalski G.T., Gilliam J.F. Functional responses with predator interference : Viable alternatives to the holling type II model functional responses with predator interference : Viable alternatives to the holling type II model. Ecology. 2001;82(11):3083–3092. [Google Scholar]
- Smith P.D., Smythies L.E., Shen R., Greenwell-Wild T., Gliozzi M., Wahl S.M. Intestinal macrophages and response to microbial encroachment. Mucosal immunology. 2011;4(1):31–42. doi: 10.1038/mi.2010.66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith M.A., Takeuchi K., Anderson G., Ware G.O., McClure H.M., Raybourne R.B. Dose-response model for Listeria monocytogenes-induced stillbirths in nonhuman primates. Infection and Immunity. 2008;76(2):726–731. doi: 10.1128/IAI.01366-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith M.A., Takeuchi K., Brackett R.E., McClure H.M., Raybourne R.B., Williams K.M. Nonhuman primate model for Listeria monocytogenes-induced stillbirths. Infection and Immunity. 2003;71(3):1574–1579. doi: 10.1128/IAI.71.3.1574-1579.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith R., Tan C., Srimani J.K., Pai A., Riccione K.A., Song H. Programmed Allee effect in bacteria causes a tradeoff between population spread and survival. Proceedings of the National Academy of Sciences of the United States of America. 2014;111(5):1969–1974. doi: 10.1073/pnas.1315954111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stecher B., Hardt W.D. Mechanisms controlling pathogen colonization of the gut. Current Opinion in Microbiology. 2011;14(1):82–91. doi: 10.1016/j.mib.2010.10.003. [DOI] [PubMed] [Google Scholar]
- Tanoue T., Umesaki Y. Immune responses to gut microbiota- commensals and pathogens. Gut Microbes. 2010;1(August):1–10. doi: 10.4161/gmic.1.4.12613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Stelten A., Simpson J.M., Chen Y., Scott V.N., Whiting R.C., Ross W.H. Significant shift in median Guinea pig infectious dose shown by an outbreak-associated Listeria monocytogenes epidemic clone strain and a strain carrying a premature stop codon mutation in inlA. Applied and Environmental Microbiology. 2011;77(7):2479–2487. doi: 10.1128/AEM.02626-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waters C.M., Bassler B.L. Quorum sensing : Communication in bacteria. Annual Reviews in Cell Development Biology. 2005;21(1):319–346. doi: 10.1146/annurev.cellbio.21.012704.131001. [DOI] [PubMed] [Google Scholar]
- Zhu H., Hart C.A., Sales D., Roberts N.B. Bacterial killing in gastric juice - Effect of pH and pepsin on Escherichia coli and Helicobacter pylori. Journal of Medical Microbiology. 2006;55(9):1265–1270. doi: 10.1099/jmm.0.46611-0. [DOI] [PubMed] [Google Scholar]