Abstract
Many pragmatic clustering methods have been developed to group data vectors or objects into clusters so that the objects in one cluster are very similar and objects in different clusters are distinct based on some similarity measure. The availability of time course data has motivated researchers to develop methods, such as mixture and mixed-effects modelling approaches, that incorporate the temporal information contained in the shape of the trajectory of the data. However, there is still a need for the development of time-course clustering methods that can adequately deal with inhomogeneous clusters (some clusters are quite large and others are quite small). Here we propose two such methods, hierarchical clustering (IHC) and iterative pairwise-correlation clustering (IPC). We evaluate and compare the proposed methods to the Markov Cluster Algorithm (MCL) and the generalised mixed-effects model (GMM) using simulation studies and an application to a time course gene expression data set from a study containing human subjects who were challenged by a live influenza virus. We identify four types of temporal gene response modules to influenza infection in humans, i.e., single-gene modules (SGM), small-size modules (SSM), medium-size modules (MSM) and large-size modules (LSM). The LSM contain genes that perform various fundamental biological functions that are consistent across subjects. The SSM and SGM contain genes that perform either different or similar biological functions that have complex temporal responses to the virus and are unique to each subject. We show that the temporal response of the genes in the LSM have either simple patterns with a single peak or trough a consequence of the transient stimuli sustained or state-transitioning patterns pertaining to developmental cues and that these modules can differentiate the severity of disease outcomes. Additionally, the size of gene response modules follows a power-law distribution with a consistent exponent across all subjects, which reveals the presence of universality in the underlying biological principles that generated these modules.
Keywords: Clustering, Inhomogeneous clusters, Power law
1. Introduction
Understanding a host temporal response to a disease is imperative to the development of predictive and preventive medicine. Many diseases have critical transition points that are linked to the severity of disease outcomes (Li et al., 2015, Rietkerk et al., 2004, Yu et al., 2014). Identifying these points and deciphering which genes are biomarkers for predicting these transitions is a challenging biological problem. Time course gene expression data provides a description of the dynamic features of the gene-level response to a disease and/or external stimulation. Genes with similar temporal response patterns can be grouped together to form temporal gene response modules.
Many clustering methods have been developed to identify temporal gene response modules for time course data. However, most of these methods do not incorporate the fact that there are many co-expressed or redundant genes that follow similar temporal patterns, but at the same time, there are genes with very few or even no co-expressed or redundant genes, and thus exhibit unique temporal response patterns. Consequently, the temporal gene response modules or clusters can be inhomogeneous, i.e., some clusters are very large and contain many genes while others are small or even only contain a single gene. For example the majority of the standard methods for clustering vectors, including high-dimensional vectors, such as centre-based clustering methods e.g., k-means (Hartigan & Wong, 1979), hierarchical clustering (Eisen, Spellman, Brown, & Botstein, 1998), graph-based or grid-based algorithms, model-based approaches and self-organizing maps (SOM) (Kohonen, 1995), see (Gan, Ma, & Wu, 2007) for a detailed review, are not flexible enough to deal with inhomogeneous clusters.
Density-based spatial clustering of applications with noise (DBSCAN) (Ester, Kriegel, Sander, & Xu, 1996) and model-based hierarchical clustering (Fraley and Raftery, 2002) have been proposed to identify clusters of different sizes, shapes and densities, although these methods cannot simultaneously identify both very large and very small (even single-element) clusters. As a result, mixture modelling approaches and iterative clustering algorithms have been introduced to identify the rare events or small cell populations from flow cytometry data (Chan and Vasconcelos, 2008, Cron et al., 2013, Naim et al., 2014). However, the computational implementation of these methods is expensive and the algorithms may not easily identify a consistent cluster assignment for large gene expression data sets with complex temporal structures.
Autoregressive time series models (Ramoni et al., 2002a, Ramoni et al., 2002b), hidden Markov models (Schliep, Schönhuth, & Steinhoff, 2003) and generalised mixed-effects models (GMM) (Bar-Joseph, 2004, Lu et al., 2011, Ma et al., 2006) have been proposed to cluster time course gene expression data. Typically, these procedures utilise a Bayesian clustering framework equipped with either a Markov chain Monte Carlo or an EM algorithm, which tend to be computationally intensive with a very slow convergence. Additionally, these algorithms require robust initial estimates of the model parameters which are often difficult to attain.
Graph theory approaches, namely, the Markov Cluster Algorithm (MCL) (van Dongen, 2000a, van Dongen, 2000b), the MCODE algorithm (Bader & Hogue, 2003), restricted neighbourhood search clustering (RNSC) (Douglas King, 2004) and super paramagnetic clustering (SPC) (King, Przulj, & Jurisica, 2004), which exploit the local structure in networks, have experienced an increase in popularity in the literature. This is mainly due to the simplicity of the algorithms, the automatic selection of the number of clusters and their capacity to identify inhomogeneous clusters. (Brohee and van Helden, 2006) show that in general the MCL outperforms the MCODE algorithm, RNSC and SPC. Furthermore, the MCL has been shown to be an apt method for identifying novel aspects of biological functions for gene expression data (Freeman et al., 2007).
In this article, we propose to use correlation-based iterative clustering methods to effectively identify inhomogeneous clusters from time course gene expression data. We expect that our methods will provide a more reliable approach for the identification of temporal gene response modules in comparison to the graph theory and mixture model approaches. This will be demonstrated by applying the proposed clustering methods to a publicly available time course gene expression (microarray) data set from human subjects who were challenged by the influenza virus (GEO ID: GSE30550) (Woods et al., 2013). In this study, a cohort of 17 healthy human volunteers received intranasal inoculation of influenza H3N2/Wisconsin virus. Nine of the 17 subjects developed mild to severe symptoms. Following from Linel et al. (Linel, Wu, Deng, & Wu, 2014), we identified the top ranking genes (TRG's) that have the largest dynamic response to the influenza virus for each of the subjects. In this analysis, we will focus on the nine symptomatic subjects since we are interested in identifying early signals of clinical outcomes.
The proposed clustering approaches identified inhomogeneous clusters with different sizes, shapes and densities, namely large, medium, small and single-gene clusters. These four types of temporal gene response modules assume different roles in modulating the dynamic response to the disease. For each subject we identified temporal gene response modules that can be used to predict the severity of the influenza infection. We also discover a power-law distribution for the size of the temporal gene response modules, which indicates that the response of the underlying biological system is driven by a few universal characteristics, this phenomenon is referred to as universality in complex systems (Barzel & Barabási, 2013). These novel findings may help us to understand the redundant design at the genetic level of a biological system.
The remainder of the paper is organized as follows. Section 1 reviews the MCL and GMM algorithms and describes the proposed correlation-based iterative hierarchical clustering (IHC) and iterative pairwise-correlation clustering (IPC) methods in detail. In Section 3, we provide a comparative analysis of clustering results from the real data and computer simulation studies for the proposed methods, the MCL and GMM algorithms. We also present the biological findings related to the temporal gene response modules in humans with influenza infection identified by the proposed methods. Finally, we conclude and discuss the important biological implications of these new findings.
2. Methods
2.1. Experimental data
The time course gene expression data GSE30550 (Woods et al., 2013) contains 17 subjects challenged with influenza H3N2/Wisconsin virus. During the challenge study, subjects had peripheral blood taken immediately prior to inoculation (pre-challenge) and at set intervals (8 h intervals) following challenge. From each of these whole blood samples, RNA was extracted (see Section S.1 of the supplementary material for details). This data set consists of a total of 22,277 gene expression time course profiles at 16 time points (0, 5, 12, 21.5, 29, 36, 45.5, 53, 60, 69.5, 77, 84, 93.5, 101, 108 h post infection). Symptoms were recorded twice daily using standardized symptom scoring (Carrat et al., 2008). Subjects ranked there symptoms (stuffy nose, scratchy throat, headache, cough, etc) in a scale of 0–4, “no symptoms”, “just noticeable”, “bothersome but can still do activities” and “bothersome and cannot do daily activities”.
2.2. Existing approaches for time-course clustering
The Markov Cluster Algorithm (MCL) and the Generalised Mixture Model (GMM) are popular methods for clustering time course gene expression data. MCL requires a Markov probability (transition) matrix that specifies the probability of gene i and gene j being contained in the same cluster. At each step in the random walk, the MCL algorithm directs the values of the transition matrix toward either 0 or 1 by expanding (raise the transition matrix to a set power creating more non-zero nodes) and inflating (take the element-wise product to strengthen strong nodes and weaken weak ones) the transition matrix. The MCL algorithm has many advantages: good convergence properties for high-dimensional data with very complex structures; computational efficiency and the ability to identify clusters of different sizes, shapes and densities (Pavlopoulos et al., 2011, Vlasblom and Wodak, 2009).
The GMM estimates a mixture model for the data, producing probabilistic clustering that quantifies the uncertainty of observations belonging to the multivariate normal density components of the mixture. The likelihood for data consisting of n observations is
where is multivariate normal density function. For a fixed number of components G, the model parameters τk (the probability that an observation comes from the kth multivariate normal density), μk (the mean of the kth multivariate normal density), and Σk (the covariance of the kth multivariate normal density) can be estimated using the EM algorithm. The optimal number of components G is typically chosen as the number of components that produces the minimum of a standard model selection criteria (i.e., AIC, BIC and cross-validation). The GMM approach has the advantage that its results are easy to interpret.
2.3. Iterative hierarchical clustering
Eisen et al (Eisen et al., 1998) clustered time course gene expression data using the conventional hierarchical clustering method with the Pearson correlation as the similarity metric. Here we propose to use an iterative hierarchical clustering (IHC) algorithm in order to identify inhomogeneous clusters, capture both the large and very small clusters, and provide an automated selection of the optimal number of clusters. The IHC algorithm is only reliant on a single parameter α, which controls the trade-off for the between- and within-cluster correlations. The IHC algorithm is outlined below:
-
1.
Initialization: Cluster the gene expression curves using hierarchical clustering. Let the distance metric be the Spearman rank correlation with a threshold of α and the linkage method be the average of the genes in the clusters.
-
2.
Merge: Treat each of the cluster centres (exemplars) as ‘new genes’, use the same rule as in Step 1 to merge the exemplars into new clusters. The cluster centres provide the average time-course pattern of the cluster members.
-
3.
Prune: Let ci be the centre of cluster i. If the correlation between the cluster centre and gene j, which will be denoted by ρi,j, is less than α, then remove genej from the cluster i. Let M be the number of genes removed from the existing N clusters. Assign all M genes into single-element clusters. Hence, there is now (N + M) clusters in total.
-
4.
Repeat Steps 2–3 until the index of clusters converges (see Section S.2 for details).
-
5.
Repeat Step 2 until the between-cluster correlations are less than α.
Ideally we would like the within-cluster correlation to be above α and the between-cluster correlation to be below α. However, enforcing these two competing criteria will result in convergence issues. In this algorithm, Steps 2–3 ensure that the within-cluster correlation will be above α, these steps are repeated until we obtain convergence. Once convergence has been achieved, we sacrifice the strict criteria on the within-cluster correlation at Step 5 to obtain a separation between the clusters that have an upper bound of α. This results in clusters that have an average within-cluster correlation close to α as opposed to having within-cluster correlations strictly above α.
2.4. Iterative pairwise-correlation clustering
Iterative Pairwise-correlation Clustering (IPC) is a simple procedure that has the same properties as the IHC method. However, the IPC method differs from the IHC method in two ways, the IPC method uses pairwise correlations to group the genes into clusters and has an additional reassignment step. This approach produces smoother optimisation surfaces that bring about more stability in the convergence of the algorithm. The IPC algorithm requires one parameter α, which controls the trade-off for the between- and within-cluster correlations. The IPC algorithm is outlined as follows:
-
1.Initialization:
-
(a)Calculate the pairwise non-parametric Spearman rank correlations of all the gene expressions to obtain the correlation matrix. Let n denote the row with the maximum pairwise non-parametric Spearman rank correlation.
-
(b)If all of the nth row correlations rn,j < α, put genen as a single-element cluster.
-
(c)If rn,j is the largest correlation in row n and , then put genej and genen into a cluster.
-
(d)If rn,k is the second largest in row n and all pairwise correlations among (genen, genej, genek)≥α, then put genek into the same cluster as (genen, genej).
-
(e)Continue until no gene can be assigned to this cluster using the rules outlined in b–d.
-
(f)Remove the corresponding rows and columns of the genes that have entered a cluster to obtain a new reduced correlation matrix.
-
(g)Repeat Steps b–f on the new correlation matrix until all genes are clustered.
-
(a)
-
2.
Merge: Treat each of the cluster centres (exemplars) as ‘new genes’, use the same rule (all pairwise correlations ≥α) as in Step 1 to merge the exemplars into new clusters. The cluster centres (exemplars) provide the average time-course pattern of the cluster members.
-
3.
Prune: Let ci be the centre of cluster i. If the correlation between the cluster centre and the gene j, denoted by ρi,j, is less than α, remove genej from the cluster i.
-
4.Reassign: Let ρi,j be the correlation between the pruned gene j and the cluster centre i. If ρi,j is the maximum correlation among all genes and centres. Then
-
(a)If all where N is the number of clusters, then set genej as a new single-element cluster.
-
(b)If any reassign genej to the cluster with the largest correlation with gene j.
-
(a)
-
5.
Repeat Steps 2–4 until the index of clusters converges (see Section S.3 for details).
-
6.
Repeat Step 2 until the between-cluster correlations are less than α.
3. Evaluations and comparisons of the clustering methods
3.1. Evaluations and comparisons based on experimental data
The collected time course gene expression data contain a total of 22,277 genes for each subject. Linel et al (Linel et al., 2014) ranked the genes for each subject by the extent to which the time course patterns differed from their means and performed a permutation test to identify the number of genes that had a statistically significant response. In their results different subjects had considerably different numbers of significant genes (between 2622 and 5954). Here we selected the genes that ranked in the top 3000 genes (TRG's) for each subject separately to ensure a fair comparison across subjects.
We use the correlation threshold α = 0.7 for the MCL, IHC and IPC methods and set the expansion parameter r1 and the inflation operator r2 to two for the MCL algorithm as suggested in (van Dongen, 2000a, van Dongen, 2000b). For the GMM, the optimal number of components G is chosen as the number of components that produces the minimum AIC criteria. Here we assess the performance of the clustering methods using the within-cluster correlation (WCC), which measures the average similarity of the time course gene response patterns that are contained in each cluster, the between-cluster correlation (BCC) measuring the average similarity of the time course gene response patterns between different clusters and the Davies-Bouldin criterion (DB) that measures the ratio of within-cluster and between-cluster correlations (see Section S.3 for details). The smaller the DB is, the better the clustering method performs. Table 1 provides the number of clusters and the evaluation criteria (WCC, BCC, and DB) for each of the four clustering methods for each of the nine symptomatic subjects respectively. Table 1 shows that the IHC and IPC methods produce a similar number of clusters for each of the nine subjects. In contrast, the GMM and MCL methods consistently produced fewer clusters than either the IHC and IPC methods. The IHC and IPC methods outperformed the MCL and GMM methods on all three criteria (WCC, BCC and DB) for all nine subjects. The IHC and IPC methods produce clusters that contain genes with larger similarity in temporal response patterns, with an average WCC of approximately 0.7, which is the pre-specified correlation threshold, while the MCL and GMM methods produce a much lower WCC, with values ranging from 0.62 to 0.66 and 0.45 to 0.53 respectively across all nine subjects. The minimum WCC for the IHC and IPC methods is consistently larger than that of the GMM and MCL methods for all nine subjects. The average BCC for all the four methods is similar and approximately zero. However, the maximum BCC for the GMM and MCL methods is larger than that of the IHC and IPC methods for each of the nine subjects. The convergence of the IHC and IPC clustering algorithms is very fast on average, the IHC method converged in 12 iterations and the IPC method converged in 10 iterations (see Figure S.1). The average computational cost is 108.73 s, 21 s, 17 s and 29 s for the GMM, MCL, the IHC, and the IPC methods respectively. The algorithms were all running in Matlab (2014) on a 3.46 GHz PC.
Table 1.
Comparison of the GMM, MCL, IHC and IPC methods for each of the 9 symptomatic subjects. The Davies-Bouldin criterion (DB) determines the performance of the clustering methods. The smaller the DB is, the better the clustering method performs. The homogeneity of the clusters is examined by computing the average, standard deviation and minimum of the within-cluster correlation (WCC). The separation of the clusters is examined by computing the average, standard deviation and maximum of the between-cluster correlation (BCC).
| Subject | No of clusters | WCC mean (std) [min] | BCC mean (std) [max] | DB |
|---|---|---|---|---|
| IHC | ||||
| 1 | 115 | 0.702 (0.069) [0.554] | −0.004 (0.321) [0.700] | 0.733 |
| 5 | 96 | 0.717 (0.075) [0.489] | −0.003 (0.323) [0.696] | 0.761 |
| 6 | 74 | 0.724 (0.054) [0.596] | −0.004 (0.340) [0.700] | 0.695 |
| 7 | 68 | 0.707 (0.058) [0.631] | −0.002 (0.347) [0.700] | 0.718 |
| 8 | 64 | 0.716 (0.057) [0.614] | −0.008 (0.352) [0.697] | 0.755 |
| 10 | 95 | 0.711 (0.077) [0.562] | −0.005 (0.323) [0.696] | 0.726 |
| 12 | 78 | 0.715 (0.057) [0.567] | −0.000 (0.340) [0.700] | 0.746 |
| 13 | 105 | 0.718 (0.079) [0.565] | −0.005 (0.331) [0.698] | 0.776 |
| 15 | 133 | 0.702 (0.083) [0.548] | −0.005 (0.313) [0.700] | 0.766 |
| IPC | ||||
| 1 | 125 | 0.697 (0.067) [0.555] | −0.003 (0.327) [0.700] | 0.766 |
| 5 | 96 | 0.713 (0.074) [0.546] | −0.001 (0.324) [0.700] | 0.752 |
| 6 | 75 | 0.722 (0.063) [0.609] | −0.005 (0.344) [0.696] | 0.695 |
| 7 | 65 | 0.701 (0.064) [0.541] | 0.006 (0.355) [0.700] | 0.796 |
| 8 | 61 | 0.697 (0.058) [0.559] | 0.016 (0.339) [0.692] | 0.761 |
| 10 | 84 | 0.692 (0.073) [0.558] | −0.003 (0.328) [0.696] | 0.712 |
| 12 | 85 | 0.714 (0.059) [0.603] | 0.006 (0.334) [0.700] | 0.717 |
| 13 | 98 | 0.692 (0.076) [0.500] | −0.002 (0.330) [0.698] | 0.808 |
| 15 | 135 | 0.672 (0.065) [0.493] | −0.000 (0.312) [0.700] | 0.779 |
| MCL | ||||
| 1 | 48 | 0.637 (0.106) [0.432] | 0.005 (0.332) [0.821] | 1.063 |
| 5 | 51 | 0.662 (0.095) [0.404] | 0.004 (0.319) [0.764] | 1.004 |
| 6 | 23 | 0.657 (0.075) [0.485] | −0.020 (0.330) [0.789] | 0.760 |
| 7 | 24 | 0.654 (0.068) [0.492] | −0.022 (0.332) [0.757] | 0.747 |
| 8 | 30 | 0.622 (0.097) [0.453] | −0.003 (0.358) [0.833] | 1.198 |
| 10 | 46 | 0.629 (0.098) [0.400] | 0.014 (0.334) [0.875] | 1.199 |
| 12 | 39 | 0.662 (0.092) [0.418] | 0.025 (0.344) [0.821] | 0.996 |
| 13 | 47 | 0.629 (0.099) [0.400] | −0.005 (0.331) [0.802] | 1.223 |
| 15 | 87 | 0.657 (0.087) [0.413] | −0.002 (0.338) [0.879] | 1.296 |
| GMM | ||||
| 1 | 16 | 0.492 (0.186) [0.168] | −0.034 (0.467) [0.885] | 2.771 |
| 5 | 15 | 0.492 (0.194) [0.178] | −0.053(0.489) [0.946] | 3.481 |
| 6 | 12 | 0.538 (0.141) [0.188] | −0.059 (0.388) [0.707] | 1.370 |
| 7 | 8 | 0.533 (0.150) [0.216] | −0.116 (0.574) [0.864] | 2.420 |
| 8 | 12 | 0.527 (0.205) [0.161] | −0.053 (0.490) [0.833] | 1.748 |
| 10 | 16 | 0.522 (0.180) [0.177] | −0.03 (0.430) [0.896] | 1.545 |
| 12 | 12 | 0.502 (0.169) [0.168] | −0.039 (0.493) [0.842] | 2.392 |
| 13 | 14 | 0.465 (0.158) [0.155] | −0.018 (0.406) [0.829] | 1.653 |
| 15 | 14 | 0.456 (0.145) [0.138] | −0.044 (0.395) [0.760] | 1.643 |
The adjusted rand index (ARI) (Hubert & Arabie, 1985) provides the overall similarity measure between two clustering assignments taking into account that the agreement between partitions could arise by chance alone. Thus, the ARI provides a measure of the similarity of two clustering methods. This index has expected value of zero for independent clusterings and maximum value 1 for identical clusterings. Table S.1 shows the adjusted rand index (ARI) (Hubert & Arabie, 1985) for each pair of clustering approaches (GMM, MCL, IHC and IPC). Overall, the four clustering methods produced relatively different clusters with an average ARI of 0.6101. As expected, the IPC and IHC have the most similar gene allocation with an ARI of 0.7042.
3.2. Evaluations and comparisons based on simulation studies
We also designed simulation experiments to evaluate and compare the performance of the proposed clustering methods with existing approaches. The simulated time course data for the jth gene in the ith cluster is generated as follows:
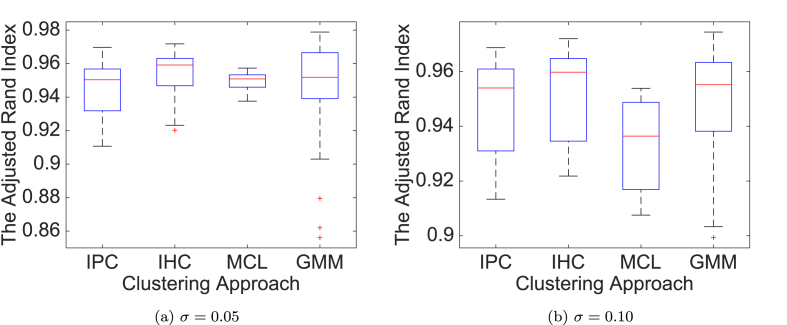
for j=1,…,K, where K is the number of genes in the ith cluster, βi is a random number drawn from a log normal distribution with mean 0 and variance 0.25 (this allows the simulated genes to have different mean expression levels), ci is the average expression level over time of the genes in the ith cluster produced by the MCL method for subject 1, εi,j(t) is a normally distributed random noise with a mean 0 and a variance of 1, and σ quantifies the magnitude of the measurement error. The simulated clusters are combined to form the test data set. The simulated data were generated for two measurement error levels σ = 0.05 and σ = 0.1. Figure S.2 shows a portion of the simulated data with σ = 0.1. Each simulation was performed 1000 times. Fig. 1 provides the box plots of the ARI between the estimated and true clustering assignments. In both cases, the IHC method produces a better agreement with the true cluster assignments on average compared to other methods. The IPC and GMM produce a similar agreement with the true cluster assignments and surprisingly MCL has the least agreement with the true cluster assignment.
Fig. 1.
Boxplots showing the accuracy of each method. Boxplots of the percentage of genes that are clustered into the correct functional modules for all three clustering procedures and σ=0.1,0.2,0.3.
4. Biological findings and discussions
In summary, the clustering analysis of both the real and simulated time course expression data has demonstrated that the proposed IHC and IPC methods outperformed the MCL and GMM methods. The IHC has been shown to perform better in the simulation study and it has the lowest computational cost, thus hereafter we will focus on presenting the biological results from the IHC method and may only briefly discuss the results from other methods.
4.1. Four types of temporal gene response modules to influenza infection
The IHC method with a correlation threshold of α=0.7 grouped the 3000 TRGs for each of the nine subjects into 64–133 temporal gene response modules (see Table 1). These modules can be classified into single-gene modules (SGM) with only one gene in each cluster, small-size modules (SSM) that contain between 2 and 10 genes in each cluster, medium-size modules (MSM) that consist of 11–99 genes in each of the clusters and large-size modules (LSM) which contain over 100 genes in each cluster. Table 2 shows that 31%–44% of temporal gene response modules are SGM, 32%–49% are SSM, 10%–19% are MSM and only 5%–14% are LSM. In contrast, the number of genes in each of these four types of modules displays the opposite trend, 1%–2% of the genes are categorised into SGM, 3%–7% are in SSM, 7%–20% are in MSM, and 72%–88% are in LSM. This indicates that many genes have a consistent reaction to influenza infection and thus exhibit similar time course patterns, while a few genes have atypical reactions to influenza infection and hence display dissimilar time course patterns. The results from the IPC method also confirmed this trend, but the MCL method identified fewer SGM and more SSM and the GMM method produced a large amount of LSM and MSM and no SSM or SGM (see Tables S.2, S.3 and S.4).
Table 2.
The distribution of the clusters and genes across the four categories (LSM, MSM, SSM and SGM) The number of clusters and number of genes (in parentheses) in each category of modules (LSM, MSM, SSM and SGM) for the IHC method for each of the 9 subjects.
| Subject | LSM % clusters (% genes) | MSM % clusters (%genes) | SSM %clusters (%genes) | SGM %clusters (%genes) |
|---|---|---|---|---|
| 1 | 6% (79%) | 13% (14%) | 37% (5%) | 44% (2%) |
| 5 | 6% (78%) | 10% (15%) | 49% (6%) | 34% (1%) |
| 6 | 14% (88%) | 12% (8%) | 34% (3%) | 41% (1%) |
| 7 | 9% (87%) | 15% (9%) | 32% (3%) | 44% (1%) |
| 8 | 8% (89%) | 14% (7%) | 47% (4%) | 31% (1%) |
| 10 | 5% (82%) | 13% (12%) | 44% (5%) | 38% (1%) |
| 12 | 8% (86%) | 12% (9%) | 44% (4%) | 38% (1%) |
| 13 | 5% (72%) | 19% (20%) | 44% (7%) | 32% (1%) |
| 15 | 5% (74%) | 15% (18%) | 38% (6%) | 42% (2%) |
4.1.1. The time course patterns of the LSM, MSM, SSM and SGMs
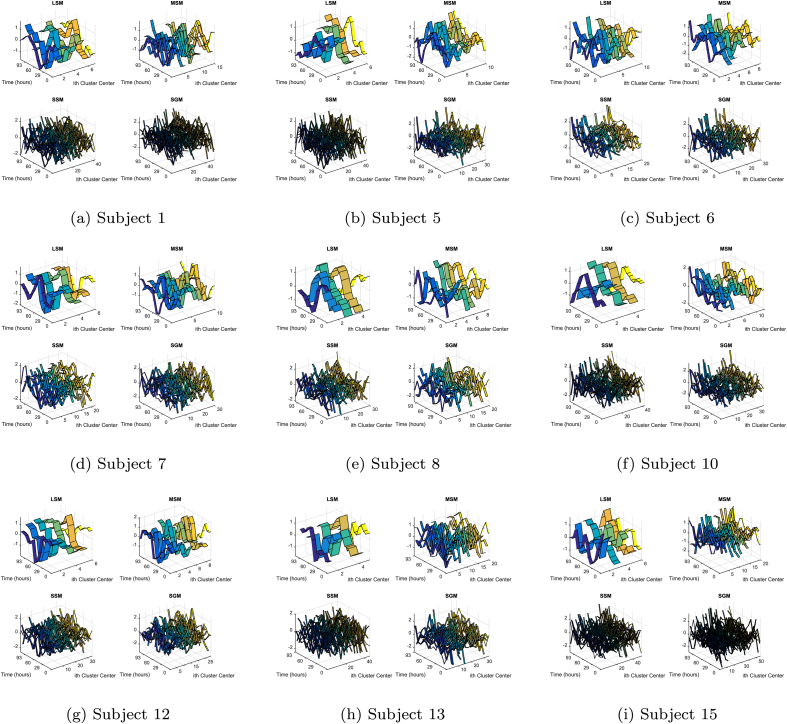
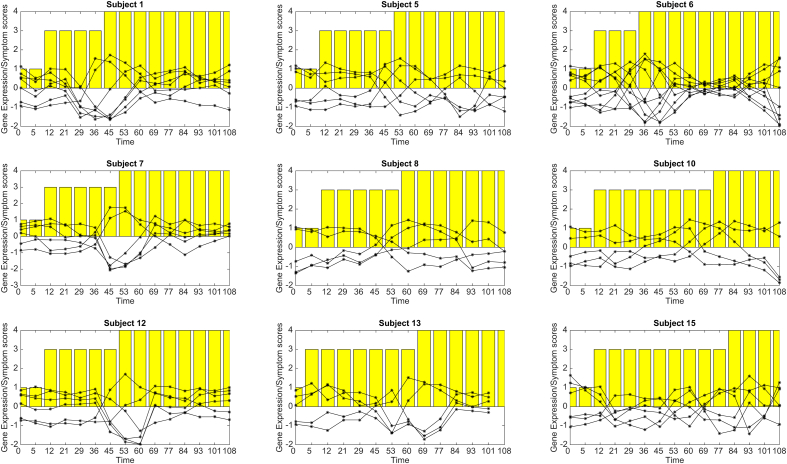
Fig. 2 illustrates the time course patterns of the centres of each cluster grouped by module size. The genes contained in the SGM and SSM have temporal patterns that vary considerably within subject and across subjects many of these responses are oscillatory and thus we suspect play integral roles in homeostasis. The genes contained in the MSM and LSM either have simple patterns with a single peak or trough a consequence of the transient stimuli or state-transitioning patterns pertaining to developmental cues. The timing of these features are similar within subject but vary across subjects. Fig. 3 shows the average time course patterns of the genes contained in the LSM and the reported symptom scores for each subject. It is clear that the timing of the peak/trough or transition of the response pattern provides either an early signal or coincides with an elevation in the symptom score. Thus these modules can be used to serve as a diagnosis biomarker for influenza symptoms.
Fig. 2.
The time course patterns of the clustering centres grouped by module size. Single-gene modules (SGM) with only one gene in each cluster, small-size modules (SSM) that contain between 2 and 10 genes in each cluster, medium-size modules (MSM) that consist of 11–99 genes in each of the clusters and large-size modules (LSM) which contain over 100 genes in each cluster.
Fig. 3.
The average time course patterns of the LSM gene clusters and the reported symptom scores for each subject.
4.1.2. Gene ontology (GO) enrichment analysis for the genes in the LSM, MSM, SSM and SGMs
The DAVID (the database for annotation, visualization and integrated discovery) functional annotation tool (Huang et al., 2009, Wei Huang et al., 2009) was used for functional enrichment analyses. Table 3 provides the enriched GO biological process terms that are related to the genes in each of the LSM clusters for each of the 9 subjects. From Table 3, we can see some common biological processes for the LSM clusters across many subjects, including metabolic process, translation/translational elongation and defence/immune/inflammatory response. The observed metabolic dynamics are most likely due to the onset of apoptosis of infected cells. Many authors (Fisher and Ginsberg, 1956, Klemperer, 1961, Ritter et al., 2010) have suggested that infection dynamics are reflected in host cell metabolism. This has also been observed in other viral infection studies such as rubella virus (Vaheri & Cristofalo, 1967), cytomegalovirus (Munger, Bajad, Coller, Shenk, & Rabinowitz, 2006), mumps virus (Green, Henle, & Deinhardt, 1958), newcastle-disease virus (Green et al., 1958), polio virus (Levy & Baron, 1956) and reovirus (Burgener, Coombs, & Butler, 2006). Influenza virus does not possess the required components to initiate mRNA translation, and it is obligated to utilize host cell factors to compete for and manipulate the translation apparatus to its own benefit. Thus the presence of translation in the enriched GO biological process terms and the enriched ribosome pathway (see Figure S. 3 for details) are consistent with our expectations (Huang et al., 2011) also reported the enriched translational terms through the ribosomal protein synthesis. The innate immune response is also enriched for the LSM genes. The enriched GO terms for the MSM, SSM and SGM are included in Tables S 5, S 6 and S 7 in Appendix. We can see that the MSM clusters contain genes related to regulation of protein kinase activity, cell proliferation, and response to hypoxia. The SSM clusters contain genes related to regulation of mitosis, oxidation reduction, negative regulation of cell differentiation, and macromolecular complex subunit organization. The SGM clusters are related to T cell activation, chemical homeostasis, response to organic nitrogen, and actin cytoskeleton organization.
Table 3.
The enriched GO biological process terms that are related to the genes in each of the LSM clusters for each of the 9 subjects.
| Subject | The most enriched gene ontology (GO) BP terms |
|---|---|
| 1 | (i) negative regulation of cell growth, (ii) translation, (iii) adaptive immune response, (iv) negative regulation of epithelial cell proliferation, (v) translational elongation, (vi) inflammatory response, (vii) sphingolipid metabolic process |
| 5 | (i) positive regulation of cell motion, (ii) negative regulation of cell growth, (iii) regulation of transcription, (iv) cellular macromolecule catabolic process, (v) DNA replication, (vi) protein modification by small protein conjugation |
| 6 | (i) protein amino acid phosphorylation, (ii) cholesterol metabolic process (iii) response to virus (iv) innate immune response (v) negative regulation of transcription, (vi) innate immune response (vii) DNA metabolic process, (viii) positive regulation of immune response, (ix) translational elongation (x) mRNA metabolic process |
| 7 | (i) phosphate metabolic process, (ii) hexose metabolic process, (iii) carboxylic acid catabolic process (iv) defense response (v) monosaccharide metabolic process (vi) translation |
| 8 | (i) chromatin modification (ii) positive regulation of I-kappaB kinase/NF-kappaB cascade (iii) cellular amide metabolic process (iv) proteolysis (v) positive regulation of macromolecule biosynthetic process |
| 10 | (i) response to wounding (ii) chromatin modification (iii) cofactor metabolic process (iv) positive regulation of I-kappaB kinase/NF-kappaB cascade (v) icosanoid metabolic process |
| 12 | (i) translational elongation (ii) nucleobase, nucleoside, nucleotide and nucleic acid biosynthetic process (iii) cellular carbohydrate catabolic process (iv) small GTPase mediated signal transduction (v) inflammatory response (vi) proteolysis |
| 13 | (i) membrane organization (ii) translational elongation (iii) regulation of protein amino acid phosphorylation (iv) inflammatory response (v) histone acetylation |
| 15 | (i) regulation of transcription (ii) cellular protein complex assembly (iii) nicotinamide metabolic process (iv) Wnt receptor signaling pathway (v) innate immune response (vi) steroid metabolic process |
4.1.3. Similarity of the LSM, MSM, SSM and SGMs
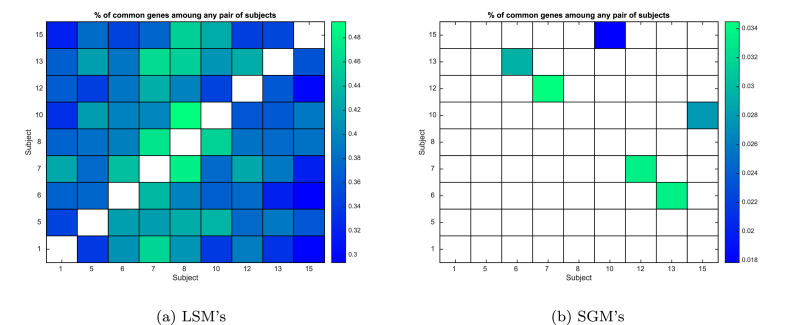
We examine the similarity of the genes contained in the LSM and SGM across different subjects, Fig. 4 shows that any pair of subjects share between 28% and 47% of the LSM genes whereas only 1%–3% of the SGM genes are shared between any pair of subjects. This may suggest that the LSMs contain more common genes that are typically utilised by most subjects to combat influenza infection, while the SGMs contain the genes that reflect more subject-specific response to influenza infection.
Fig. 4.
The percentage of the TRG's in the LSM's or SGM's that are common for each subject pair across all the 9 symptomatic subjects. The i,j block represents the % of genes in the LSM that are common for the ith and jth subject.
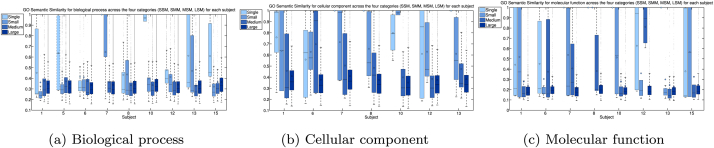
We also explored the semantic similarity (Resnik, 1999) of the genes in each of the four types of response modules (see the implementation details in Section S.7). Semantic similarity is a value between 0 and 1 that measures the similarity of the GO terms based on their closest common ancestor term. Fig. 5 shows the pairwise semantic similarity of the gene products in terms of their associated biological processes (BP), cellular components (CC) and molecular functions (MF) for each of the four module categories (LSM, MSM, SSM and SGM) and for all nine subjects respectively. Interestingly, we find that the genes in large modules (LSM) tend to have a consistently lower similarity in all three domains (i.e., BP, MF and CC) for all nine subjects. In contrast, the genes in single-gene modules and small modules (SGM and SSM) tend to exhibit a large variation in their semantic similarity both within and between subjects (i.e., some genes in SGM and SSM perform similar functions while others perform different functions and these functions vary from subject to subject).
Fig. 5.
The semantic similarity of the gene biological process/cellular component/molecular function as defined by the GO terms for the four-type of temporal gene response module categories (LSM, MSM, SSM and SGM).
4.2. Power-law for the size of temporal gene response modules
Power-law behaviour provides a concise mathematical description of an important biological feature: the sheer dominance of a few members over the overall population. Power-laws have been established for many areas of genomic biology, for example, the occurrence of protein families or folds (Qian, Luscombe, & Gerstein, 2001) and the number of intra- and intermolecular interactions of proteins (Rzhetsky and Gomez, 2001). We investigated if the small number of LSM and large number of SSM and SGM that our clustering methods have identified are a consequence of a power law. Table 4 provides the estimates of the exponent parameter β of the power distribution and the p-values for the hypothesis test if the power-law is a plausible model for the size of the modules generated by the MCL, IHC and IPC methods for each of the nine subjects (see Section S.8 for details). From Table 4, it clearly shows that the power-law is plausible for the size of the clusters for all nine subjects for the IHC and IPC methods but not for the MCL and GMM. In addition, our sensitivity analysis, which examined the sensitivity to different correlation thresholds for the three clustering methods (see Section S.9 for details), reveals that the power-law is preserved for the clustering results from the IHC and IPC methods across different thresholds but it is not preserved for the clustering results from the MCL or GMM method.
Table 4.
The estimates of the scaling exponentβfor the power-law model of the size of the clusters The p-value of the corresponding Kolmogorov-Smirnov goodness-of-fit statistic to test the hypothesis that the power-law model is feasible for the size of the clusters generated by all three clustering procedures with α = 0.70. If the p-value is greater than 0.1, we can infer that it is viable that the size of the clusters follows a power-law distribution.
| Subject | MCL |
IHC |
IPC |
GMM |
|---|---|---|---|---|
| (p-value) | (p-value) | (p-value) | (p-value) | |
| 1 | 1.64 (0.273) | 1.61 (0.980) | 1.58 (0.985) | 1.73 (0.591) |
| 5 | 1.76 (0.603) | 1.66 (0.199) | 1.59 (0.797) | 2.12 (0.882) |
| 6 | 1.50 (0.003) | 1.50 (0.513) | 1.50 (0.564) | 3.20 (0.977) |
| 7 | 1.50 (0.216) | 1.53 (0.827) | 1.50 (0.748) | 1.90 (0.774) |
| 8 | 1.64 (0.713) | 1.59 (0.625) | 1.51 (0.807) | 1.76 (0.938) |
| 10 | 1.65 (0.041) | 1.58 (0.485) | 1.56 (0.653) | 1.79 (0.981) |
| 12 | 1.61 (0.642) | 1.54 (0.219) | 1.56 (0.579) | 2.06 (0.727) |
| 13 | 1.78 (0.423) | 1.65 (0.724) | 1.53 (0.322) | 1.86 (0.781) |
| 15 | 1.79 (0.609) | 1.60 (0.859) | 1.61 (0.330) | 1.85 (0.256) |
5. Conclusions
The immune response to viral infection is a dynamic process, which is regulated by an intricate network of many genes and their products. Understanding the dynamics of this network will infer the mechanisms involved in regulating influenza infection and hence aid the development of antiviral treatments and preventive vaccines. There has been an abundance of literature regarding the dynamic network construction, e.g., (Shannon et al., 2003, Hecker et al., 2009, Lu et al., 2011), and (Wu, Liu, Qiu, & Wu, 2013). The curse of dimensionality is a common difficulty associated with the construction of the large dynamic networks. Lu et al (Lu et al., 2011) and Wu et al (Wu et al., 2013) intended to resolve this issue by utilizing temporal gene response co-expression modules as the nodes of the dynamic gene regulatory networks. Under this premise, it is crucial that these functional modules are sufficiently different from one another in order to avoid collinearity and that the genes within these functional modules have a very similar time course pattern that are adequately captured by the centre of the cluster.
Our aim is to develop a time course gene expression clustering procedure to identify these temporal gene response modules, ensuring that there is an adequate separation between different temporal gene response modules and a sufficient homogeneity within any given temporal gene response module. We also expected that the gene response modules have varied sizes and densities. Thus, some modules may be large (i.e., contain many genes), small (i.e., contain a few genes) or even only contain a single gene.
We proposed two clustering methods, the Iterative Hierarchical Clustering (IHC) and the Iterative Pairwise-correlation Clustering (IPC). These approaches both produce clusters with an increased separation between clusters and an increased homogeneity within clusters in comparison to the Markov Cluster Algorithm (MCL) and generalised mixed-effects modeling (GMM) approach. Our simulation studies also suggest that the IHC and IPC methods perform better than the MCL and GMM methods.
The proposed clustering methods produce many clusters, which contain single genes or only a few genes, some clusters that contain many genes, and very few clusters that contain a lot of genes. Moreover, the large-sized modules contain genes that perform various fundamental biological functions, which are common across subjects and exhibit either simple patterns with a single peak/trough, a consequence of the transient stimuli or state-transition patterns pertaining to developmental cues in response to the influenza virus. While the single-gene and small-sized modules contain genes that perform either different or similar biological functions and are unique to each subject. Many of these genes exhibit temporal responses that are oscillatory suggesting these genes play integral roles in homeostasis. Additionally, the size of the temporal gene response modules for influenza in humans is consistent with power-law distributions. Interestingly, the estimates of the critical exponent of the power-law distribution for the temporal gene response modules are very consistent (about 1.6) across all nine subjects, which demonstrates the “universality ” for the underlying biological processes that generated these modules. Similar observations have been made for various self-organized critical systems (Sornette, 2004).
The proposed correlation-based iterative clustering methods could effectively identify inhomogeneous temporal gene response modules. These modules reveal novel biological findings that provide classification, prediction and new insight into the organisation and the dynamics of the genetic level response to influenza infection in humans. One limitation of the proposed clustering methods is that the number of clusters is determined by a subjectively-selected correlation threshold, quantifying the tightness of gene response curves in a cluster. A different threshold will produce different clustering results, thus the results should be interpreted and used with caution. Since both the IHC and IPC methods often yield similar results and the IHC is computationally faster, we recommend to use the IHC method in practice.
Acknowledgements
This work was supported by NIAID/NIH grants HHSN272201000055C (CBIM), HHSN27220201200005C (RPRC), HHSN266200700008C (NYICE), P30AI078498 (CFAR), and R01 AI087135. The authors would like to thank Patrice Linel and Nan Deng for their helpful discussions and suggestions.
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Supplementary data related to this article can be found at http://dx.doi.org/10.1016/j.idm.2016.07.001.
Appendix A. Supplementary data
The following is the supplementary data related to this article:
The data set supporting the results of this article is available in the GEO repository, https://urldefense.proofpoint.com/v2/url?u=http-3A__www.ncbi.nlm.nih.gov_geo_query_acc.cgi-3Facc-3DGSE30550&d=BQIGAg&c=6vgNTiRn9_pqCD9hKx9JgXN1VapJQ8JVoF8oWH1AgfQ&r=ZuEc0L79L13cAwjFTsJymLqHpuCByTfVPYkhsFw8F-Q&m=bJYa0-bqOzGczJGjhbmNDB0g-ZVhk9z02h9j5vmAsyA&s=EbM7UhXIhEw-1AtoXL8x3omdyIzmx2TiF4_y-D0XUOQ&e=. The Matlab code for the IHC and IPC methods are provided in the supplementary material.
References
- Bader G.D., Hogue C.W.V. An automated method for finding molecular complexes in large protein interaction networks. BMC bioinformatics. 2003;4(1):2. doi: 10.1186/1471-2105-4-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-Joseph Z. Analyzing time series gene expression data. Bioinformatics. 2004;20(16):2493–2503. doi: 10.1093/bioinformatics/bth283. [DOI] [PubMed] [Google Scholar]
- Barzel B., Barabási A.-L. Universality in network dynamics. Nature physics. 2013;9(10):673–681. doi: 10.1038/nphys2741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brohee S., van Helden J. Evaluation of clustering algorithms for protein-protein interaction networks. BMC bioinformatics. 2006;7(1):488. doi: 10.1186/1471-2105-7-488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgener A., Coombs K., Butler M. Intracellular atp and total adenylate concentrations are critical predictors of reovirus productivity from vero cells. Biotechnology and bioengineering. 2006;94(4):667–679. doi: 10.1002/bit.20873. [DOI] [PubMed] [Google Scholar]
- Carrat F., Vergu E., Ferguson N.M., Lemaitre M., Cauchemez S., Leach S. Time lines of infection and disease in human influenza: A review of volunteer challenge studies. American journal of epidemiology. 2008;167(7):775–785. doi: 10.1093/aje/kwm375. [DOI] [PubMed] [Google Scholar]
- Chan A.B., Vasconcelos N. Modeling, clustering, and segmenting video with mixtures of dynamic textures. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2008;30(5):909–926. doi: 10.1109/TPAMI.2007.70738. [DOI] [PubMed] [Google Scholar]
- Cron A., Gouttefangeas C., Frelinger J., Lin L., Singh S.K., Britten C.M. Hierarchical modeling for rare event detection and cell subset alignment across flow cytometry samples. PLoS computational biology. 2013;9(7):e1003130. doi: 10.1371/journal.pcbi.1003130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Dongen S. University of Utrecht; May 2000. Graph clustering by flow simulation. (PhD thesis) [Google Scholar]
- Douglas King A. Citeseer; 2004. Graph clustering with restricted neighbourhood search. (PhD thesis) [Google Scholar]
- Eisen M.B., Spellman P.T., Brown P.O., Botstein D. Cluster analysis and display of genome-wide expression patterns. Proceedings of the National Academy of Sciences. 1998;95(25):14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ester M., Kriegel H.-P., Sander J., Xu X. vol. 96. 1996. A density-based algorithm for discovering clusters in large spatial databases with noise; pp. 226–231. (Kdd). [Google Scholar]
- Fisher T.N., Ginsberg H.S. The reaction of influenza viruses with Guinea pig polymorphonuclear leucocytes. ii. the reduction of white blood cell glycolysis by influenza viruses and receptor-destroying enzyme (rde) Virology. 1956;2(5):637–655. doi: 10.1016/0042-6822(56)90044-7. [DOI] [PubMed] [Google Scholar]
- Fraley C., Raftery A.E. Model-based clustering, discriminant analysis, and density estimation. Journal of the American Statistical Association. 2002;97(458):611–631. [Google Scholar]
- Freeman T.C., Goldovsky L., Brosch M., Van Dongen S., Mazière P., Grocock R.J. Construction, visualisation, and clustering of transcription networks from microarray expression data. PLoS computational biology. 2007;3(10):e206. doi: 10.1371/journal.pcbi.0030206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gan G., Ma C., Wu J. vol. 20. Siam; 2007. (Data clustering: Theory, algorithms, and applications). [Google Scholar]
- Green M., Henle G., Deinhardt F. Respiration and glycolysis of human cells grown in tissue culture. Virology. 1958;5(2):206–219. doi: 10.1016/0042-6822(58)90019-9. [DOI] [PubMed] [Google Scholar]
- Hartigan J.A., Wong M.A. Algorithm as 136: A k-means clustering algorithm. Applied statistics. 1979:100–108. [Google Scholar]
- Hecker M., Lambeck S., Toepfer S., Van Someren E., Guthke R. Gene regulatory network inference: Data integration in dynamic models?a review. Biosystems. 2009;96(1):86–103. doi: 10.1016/j.biosystems.2008.12.004. [DOI] [PubMed] [Google Scholar]
- Huang Da W., Sherman B.T., Lempicki R.A. Systematic and integrative analysis of large gene lists using david bioinformatics resources. Nature protocols. 2009;4(1):44–57. doi: 10.1038/nprot.2008.211. [DOI] [PubMed] [Google Scholar]
- Huang Y., Zaas A.K., Rao A., Dobigeon N., Woolf P.J., Veldman T. Temporal dynamics of host molecular responses differentiate symptomatic and asymptomatic influenza a infection. PLoS Genetics. 2011;7(8):e1002234. doi: 10.1371/journal.pgen.1002234. http://dx.doi.org/10.1371%2Fjournal.pgen.1002234 08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubert L., Arabie P. Comparing partitions. Journal of classification. 1985;2(1):193–218. [Google Scholar]
- King A.D., Przulj N., Jurisica I. Protein complex prediction via cost-based clustering. Bioinformatics. 2004;20(17):3013–3020. doi: 10.1093/bioinformatics/bth351. [DOI] [PubMed] [Google Scholar]
- Klemperer H. Glucose breakdown in chick embryo cells infected with influenza virus. Virology. 1961;13(1):68–77. doi: 10.1016/0042-6822(61)90033-2. [DOI] [PubMed] [Google Scholar]
- Kohonen T. Vol. 30. 1995. Self-Organizing Maps. Springer series in information sciences. (Self-organizing maps). [Google Scholar]
- Levy H.B., Baron S. 1956. Some metabolic effects of poliomyelitis virus on tissue culture. [DOI] [PubMed] [Google Scholar]
- Li Y., Jin S., Lei L., Pan Z., Zou X. Deciphering deterioration mechanisms of complex diseases based on the construction of dynamic networks and systems analysis. Scientific reports. 2015;5 doi: 10.1038/srep09283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linel P., Wu S., Deng N., Wu H. Dynamic transcriptional signatures and network responses for clinical symptoms in influenza-infected human subjects using systems biology approaches. Journal of pharmacokinetics and pharmacodynamics. 2014;41(5):509–521. doi: 10.1007/s10928-014-9365-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu T., Liang H., Li H., Wu H. High-dimensional odes coupled with mixed-effects modeling techniques for dynamic gene regulatory network identification. Journal of the American Statistical Association. 2011;106(496) doi: 10.1198/jasa.2011.ap10194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma P., Castillo-Davis C.I., Zhong W., Liu J.S. A data-driven clustering method for time course gene expression data. Nucleic Acids Research. 2006;34(4):1261–1269. doi: 10.1093/nar/gkl013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The MathWorks Inc.; Natick, Massachusetts: 2014. MATLAB: Version 8.3 (R2014b) [Google Scholar]
- Munger J., Bajad S.U., Coller H.A., Shenk T., Rabinowitz J.D. Dynamics of the cellular metabolome during human cytomegalovirus infection. PLoS Pathogens. 2006;2(12):e132. doi: 10.1371/journal.ppat.0020132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naim I., Datta S., Rebhahn J., Cavenaugh J.S., Mosmann T.R., Sharma G. Swift - Scalable clustering for automated identification of rare cell populations in large, high-dimensional flow cytometry datasets, part 1: Algorithm design. Cytometry Part A. 2014;85(5):408–421. doi: 10.1002/cyto.a.22446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlopoulos G.A., Secrier M., Moschopoulos C.N., Soldatos T.G., Kossida S., Aerts J. Using graph theory to analyze biological networks. BioData mining. 2011;4(1):10. doi: 10.1186/1756-0381-4-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian J., Luscombe N.M., Gerstein M. Protein family and fold occurrence in genomes: Power-law behaviour and evolutionary model. Journal of molecular biology. 2001;313(4):673–681. doi: 10.1006/jmbi.2001.5079. [DOI] [PubMed] [Google Scholar]
- Ramoni M., Sebastiani P., Cohen P. Bayesian clustering by dynamics. Machine learning. 2002;47(1):91–121. [Google Scholar]
- Ramoni M.F., Sebastiani P., Kohane I.S. Cluster analysis of gene expression dynamics. Proceedings of the National Academy of Sciences. 2002;99(14):9121–9126. doi: 10.1073/pnas.132656399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Resnik P. Semantic similarity in a taxonomy: An information-based measure and its application to problems of ambiguity in natural language. Journal Of Artificial Intelligence Research (JAIR) 1999;11:95–130. [Google Scholar]
- Rietkerk M., Dekker S.C., de Ruiter P.C., van de Koppel J. Self-organized patchiness and catastrophic shifts in ecosystems. Science. 2004;305(5692):1926–1929. doi: 10.1126/science.1101867. [DOI] [PubMed] [Google Scholar]
- Ritter J.B., Wahl A.S., Freund S., Genzel Y., Reichl U. Metabolic effects of influenza virus infection in cultured animal cells: Intra-and extracellular metabolite profiling. BMC systems biology. 2010;4(1):1. doi: 10.1186/1752-0509-4-61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rzhetsky A., Gomez S.M. Birth of scale-free molecular networks and the number of distinct dna and protein domains per genome. Bioinformatics. 2001;17(10):988–996. doi: 10.1093/bioinformatics/17.10.988. [DOI] [PubMed] [Google Scholar]
- Schliep A., Schönhuth A., Steinhoff C. Using hidden markov models to analyze gene expression time course data. Bioinformatics. 2003;19(suppl 1):i255–i263. doi: 10.1093/bioinformatics/btg1036. [DOI] [PubMed] [Google Scholar]
- Shannon P., Markiel A., Ozier O., Baliga N.S., Wang J.T., Ramage D. Cytoscape: A software environment for integrated models of biomolecular interaction networks. Genome research. 2003;13(11):2498–2504. doi: 10.1101/gr.1239303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sornette D. Springer Science & Business Media; 2004. Critical phenomena in natural sciences: Chaos, fractals, selforganization and disorder: Concepts and tools. [Google Scholar]
- Vaheri A., Cristofalo V.J. Metabolism of rubella virus-infected bhk21 cells enhanced glycolysis and late cellular inhibition. Archiv für die gesamte Virusforschung. 1967;21(3–4):425–436. doi: 10.1007/BF01241741. [DOI] [PubMed] [Google Scholar]
- van Dongen S.M. 2000. Graph clustering by flow simulation. [Google Scholar]
- Vlasblom J., Wodak S.J. Markov clustering versus affinity propagation for the partitioning of protein interaction graphs. BMC bioinformatics. 2009;10(1):99. doi: 10.1186/1471-2105-10-99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei Huang D., Sherman B.T., Lempicki R.A. Bioinformatics enrichment tools: Paths toward the comprehensive functional analysis of large gene lists. Nucleic acids research. 2009;37(1):1–13. doi: 10.1093/nar/gkn923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods C.W., McClain M.T., Chen M., Zaas A.K., Nicholson B.P., Varkey J. A host transcriptional signature for presymptomatic detection of infection in humans exposed to influenza h1n1 or h3n2. PLoS ONE. 2013;8(1):e52198. doi: 10.1371/journal.pone.0052198. http://dx.doi.org/10.1371%2Fjournal.pone.0052198 01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu S., Liu Z.-P., Qiu X., Wu H. Topics in applied statistics. Springer; 2013. High-dimensional ordinary differential equation models for reconstructing genome-wide dynamic regulatory networks; pp. 173–190. [Google Scholar]
- Yu X., Li G., Chen L. Prediction and early diagnosis of complex diseases by edge-network. Bioinformatics. 2014;30(6):852–859. doi: 10.1093/bioinformatics/btt620. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.