A comparative analysis of three different methods for the estimation of the basic reproduction number of dengue

Abstract

The basic reproduction number, R₀, is defined as the expected number of secondary cases of a disease produced by a single infection in a completely susceptible population, and can be estimated in several ways. For example, from the stability analysis of a compartmental model; through the use of the matrix of next generation, or from the final size of an epidemic, etc. In this paper we applied the method for estimating R₀ of dengue fever from the initial growth phase of an outbreak, without assuming exponential growth of cases, a common assumption in many studies. We used three different methods of calculating R₀ to compare the techniques' details and to evaluate how these techniques estimate the value of R₀ of dengue using data from the city of Ribeirão Preto (SE of Brazil) in two outbreaks. The results of the three methods are numerically different but, when we compare them using a system of differential equations developed for modeling only the first generation time, we can observe that the methods differ little in the initial growth phase. We conclude that the methods predict that dengue will spread in the city studied and the analysis of the data shows that the estimated values of R₀ have an equal pattern overtime.

1. Introduction

One of the main variables of interest with respect to infectious diseases epidemiology is the competency of the infection to establish itself in the host population (its potential of transmission). This potential of transmission is normally represented by the Basic Reproduction Number, R₀, which is very important in studies about epidemics, specially to evaluate the efficiency of control strategies (Heesterbeek, 1992, Massad et al., 1994). In addition, R₀ can be used to estimate the herd immunity threshold, that is, the proportion, p, of the population that should be immunized to control a disease. When p is greater than 1−1/R₀, the infection cannot establish itself in the host population, and it will die out over time (Nishiura, 2010, Roberts and Heesterbeek, 2003).

The basic reproduction number, R₀, is defined as the expected number of secondary infections produced by a single infective person in a completely susceptible population during his/her infectious period (Diekmann et al., 1990, Heesterbeek, 1992, Massad et al., 1994, van den Driessche and Watmough, 2002). In diseases transmitted by insect vectors, R₀ can be defined as expected number of people that will be infected by one person initially infected by a vector (Lopez et al., 2002, Massad et al., 2010).

It is important to note that it is possible to have a transitory outbreak even if R₀ < 1. In this case it is observed that the number of infected people start increasing but after a short period of time this number decreases until the disease dies out (Heesterbeek, 1992).

There are several ways to estimate R₀, for example, from the stability analysis of a compartmental model, through the matrix of next generation, from final size of an epidemic, from the initial growth rate, etc (Smith, 2008). In this work we study the method to estimate R₀ from the initial growth phase of the outbreak in diseases caused by vectors, without assuming an exponential growth of the number of cases.

One of the first studies to address R₀ of dengue using epidemic data was carried out by Koopman et al. (1991). In this paper the basic reproduction number was calculated using the final size of an epidemic in Mexico (Nishiura, 2006).

Massad et al. (2001) calculated the value of R₀ considering just the initial growth phase of dengue, proposing a modification of the method proposed by Marques, Forattini, and Massad (1994). Massad et al. (2001) obtained $R_0=\left(1+\frac{r}{\gamma }\right)\left(1+\frac{r}{{\mu }_V}\right)$, where r is the exponential growth rate of the epidemic curve, μ_V is the mortality rate of the vectors and γ is the dengue recovery rate of humans. In this work, Massad et al. (2001) calculated the value of R₀ of dengue and yellow fever. Some years later, Favier et al. (2006) improved this method by including an intrinsic incubation period of dengue. Favier et al. (2006) formula is $R_0=\left(1+\frac{r}{\gamma }\right)\left(1+\frac{r}{{\mu }_V}\right)e^{r({\tau }_e+{\tau }_i)}$, where τ_e and τ_i are the extrinsic and the intrinsic periods of dengue, respectively. As mention in Massad et al. (2001), all these methods performed well, but it is implicit in all of them the exponential growth of cases.

In this paper we studied the methods proposed by Ross (1911) and Macdonald, 1952, Nishiura, 2010, and White & Pagano (2008). The Ross (1911) model is specific for diseases caused by vectors and was originally formulated for malaria; the methods proposed by Nishiura (2010) and White & Pagano (2008), are likelihood-based methods, and are not specific for diseases caused by vectors. None of these methods assume an exponential growth of the number of cases.

Dengue is a vector-born disease caused by dengue fever virus, with four serotypes, namely, DENV-1, DENV-2, DENV-3 and DENV-4, which belong to genus Flavivirus family Flaviviridae (Gubler, 1998). Dengue is an urban disease and its viruses are kept in a lifecycle that involves humans and mosquitoes Aedes (Chowell and Clark, 1995). Dengue is transmitted to humans through bite of an infected female of Aedes aegypti (Coura, 2005, Gubler, 1998, Guzman and Istúriz, 2010).

The clinical picture of dengue ranges from asymptomatic infection or mild febrile illness and even lethal disease (Teixeira and Barreto, 2009). However, the general symptoms are: high fever, tiredness, muscle pain, lack of appetite, etc (Guzman & Istúriz, 2010). It is believed that people infected by one serotype acquire long-live immunity only to this serotype, and temporary cross-immunity to the other three serotypes (Simmons, Farrar, Chau, & Wills, 2012). Our objective is to compare different techniques and to evaluate how these techniques estimate the value the R₀, applying them to diseases caused by vectors without assuming exponential growth of cases. In this particular case we used data of dengue provided by the Brazilian Ministry of Health.

2. Methods

In this section we present description of the methods studied by Ross (1911) and Macdonald, 1952, Nishiura, 2010 and White & Pagano (2008) to estimate the basic reproduction number of dengue, without assuming an exponential growth for the initial phase of the outbreak.

2.1. Description of the Ross-Macdonald's method

The first method presented in this section is the Ross-Macdonald's model. The basic reproduction number, R₀, was presented for the first time in a paper wrote by George Macdonald in 1952. In it Macdonald proposed a threshold for Malaria spread and persistence based in a previous work made by Sir Ronald Ross (1911). The concept proposed by Ross and Macdonald (Macdonald, 1952) was used by many researches like Anderson and May (1992) or Aron and May (1982). Some improper notational mistakes in the original formulation related with the R₀ dimension were years later fixed (Massad & Coutinho, 2012). Hereafter we show the model studied by Massad et al. (2010), where these authors used the R₀ expression given by the Ross-Macdonald model (Macdonald, 1952) without assuming an exponential form for the initial growth phase of the outbreak, and they showed that even when R₀<1, an auto-limited outbreak can happen.

The following equations describe the dynamics of the disease, where the involved populations are divided into humans host population N_H(t) and vector population N_V(t). The human host population, in turn, is divided into susceptible S_H, infected, I_H(t) and recovered hosts, R_H(t). The total vector population, N_V(t) is divided into susceptible, S_V(t), latent, L_V(t), and infected vectors, I_V(t).

$$\frac{d{S}_H\left(t\right)}{dt}=-ab{I}_V\left(t\right)\frac{S_H\left(t\right)}{N_H\left(t\right)}+{\mu }_H\left(N_H\left(t\right)-S_H\left(t\right)\right)$$

$$\frac{d{I}_H\left(t\right)}{dt}=ab{I}_V\left(t\right)\frac{S_H\left(t\right)}{N_H\left(t\right)}-\left({\mu }_H+\gamma \right)I_H\left(t\right)$$

$$\frac{d{R}_H\left(t\right)}{dt}=\gamma I_H\left(t\right)-{\mu }_H{R}_H\left(t\right)$$

$$\frac{d{S}_V\left(t\right)}{dt}=-ac{S}_V\left(t\right)\frac{I_H\left(t\right)}{N_H\left(t\right)}+{\mu }_V\left(N_V\left(t\right)-S_V\left(t\right)\right)$$

$$\frac{d{L}_V\left(t\right)}{dt}=ac{S}_V\left(t\right)\frac{I_H\left(t\right)}{N_H\left(t\right)}-{\mu }_V{L}_V\left(t\right)-ac{S}_V\left(t-\tau \right)\frac{I_H\left(t-\tau \right)}{N_H\left(t-\tau \right)}{e}^{-{\mu }_V\tau }$$

$$\frac{d{I}_V\left(t\right)}{dt}=ac{S}_V\left(t-\tau \right)\frac{I_H\left(t-\tau \right)}{N_H\left(t-\tau \right)}{e}^{-{\mu }_V\tau }-{\mu }_V{I}_V\left(t\right)\text{.}$$ (1)

The total hosts and vectors populations, N_H=S_H+I_H+R_H and N_V=S_V+L_V+I_V, are kept constant, (births replace deaths).

The biological meaning of the parameters used in model (1) are given in Table 1.

Table 1.

Biological meaning of parameters.

Parameters	Biological meaning
a	Biting rate by A. aegypti
γ	Recovery rate for dengue
τ	Dengue extrinsic incubation period
μH	Natural mortality rate of humans
c	Probability that a vector to get infected
b	Probability that a host to get infected
μV	Mortality rate of A. aegypti

Macdonald (1952) demonstrated the existence of a threshold, the basic reproduction number, given by,

$$R_0=\frac{m{a}^{2}bc{e}^{-{\mu }_v\tau }}{(\gamma +{\mu }_H){\mu }_V}\text{.}$$ (2)

For estimating the value of R₀, we need information about some parameters, such as the death rate of humans, the recovery rate of dengue, the death rate of vectors, etc. However, some parameters are difficult to estimate like the mosquitoes' biting rate a, the probability that a human get infected when bitten by an infectious mosquito, b, the probability that a vector get infected when she bites an infectious human, c and the ratio between vectors and humans, $m=\frac{N_V\left(t\right)}{N_H\left(t\right)}$. In order to determine the values of these parameters, we fit the curve of the Ross-Macdonald's model (1) to real incidence data.

This fit is done in two steps. In the first step the number of new cases of dengue reported per week is fitted to a function (Massad, 1987):

$$g\left(t\right)=a_1\text{sech}{(a_2+a_3)}^2\frac{1}{1+e^{a_4(t-a_5)}},$$ (3)

where the fitting parameters a_i for i=1,…,5 are estimated using the Berkeley Madonna^® software.

For the second step we need consider the fact that the number of new dengue cases per week is equal to the product of the force of infection, λ(t), where $\lambda \left(t\right)=\frac{ab{I}_V}{N_H}$, by the number of susceptible individuals in each instant of time, S_H(t), such that $g\left(t\right)=\lambda \left(t\right)S_H\left(t\right)$.

Thus, it is possible to calculate the prevalence of dengue in each instant of time, I_H(t), using the Ross-Macdonald's Model,

$$\frac{d{I}_H\left(t\right)}{dt}=\lambda \left(t\right)S_H\left(t\right)-\left({\mu }_H+\gamma \right)I_H\left(t\right),$$ (4)

so

$$I_H\left(t\right)={\text{e}}^{-\left({\mu }_H+\gamma \right)\text{t}}\left[\underset{0}{\overset{s}{\int }}\lambda \left(s^{\text{'}}\right)S_H\left(s^{\text{'}}\right){\text{e}}^{\left({\mu }_H+\gamma \right){\text{s}}^{\text{'}}}{\text{ds}}^{\text{'}}+{\text{I}}_{\text{H}}\left(0\right)\right]$$ (5)

Thus the second step is to fit the Ross-Macdonald model (1) to Equation (5).

2.2. The Nishiura's method

The second method presented in this work was proposed by Nishiura (2010). In this paper Nishiura proposes a method to estimate the value of R₀ from the initial growth phase without assuming exponential function for the growth of infection. In addition, Nishiura (2010) presents a correction of the actual reproduction number R_a which is defined as the product of the average duration of infectiousness and the ratio of incidence to prevalence (White, Ward and Garner, 2006). After showing that R_a=R₀, Nishiura develops a likelihood-based method for the estimation of R₀.

Nishiura showed in his work that the process of infection acquisition is a binomial process, given by:

$$L\left(R_0\right)=\prod _{t=1}^T\left(\begin{array}{c}{j}_t\\ {\sum }_{s=0}^{\infty }{g}_s{j}_{t-s}\end{array}\right){\left(\frac{1}{R_0}\right)}^{\sum _{s=0}^{\infty }{g}_s{j}_{t-s}}{\left(1-\frac{1}{R_0}\right)}^{j_t-\sum _{s=0}^{\infty }{g}_s{j}_{t-s}},$$ (6)

where T is the most recent time point of observation in the early epidemic growth stage of the disease, and the maximum likelihood of R₀ is obtained by minimizing the negative logarithm of (6), and the term $\sum _{s=0}^{\infty }{g}_s{j}_{t-s}$ it is substitute by $\sum _{s=1}^{\text{min}(s_{max},t)}{g}_s{j}_{t-s}$.

The generation time was calculated using a Gamma Distribution as:

$$g_s=\frac{{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}\underset{j-1}{\overset{j}{\int }}{x}^{\alpha -1}{e}^{-\beta x}dx,$$ (7)

as given by White & Pagano (2008, see also Wallinga and Lipsitch, 2007).

Note that this method is valid only when R₀ is known to be greater than one.

2.3. The White and Pagano's method

The third method analyzed in this paper is the study proposed by White & Pagano (2008), where they proposed two ways to estimate R₀, 1) when the generation time is known; 2) and when the generation time is unknown. In the case 2 they estimate R₀ and generation time at the same time using the Gamma Distribution (7).

They developed a method that is related with branching process, and their work involves likelihood as Nishiura (2010).

For the case where the generation time is unknown, we have:

$$L\left(R_0,p\right)=\prod _{t=1}^T\frac{e^{-{\mu }_t}{\mu }_t^{N_t}}{N_t!},$$ (8)

where ${\mu }_t=R_0\sum _{j=1}^{\text{min}(k,t)}{N}_{t-j}{p}_j$, N_t is the incidence data and p_j is the generation time. Through this equation it is possible to use maximum likelihood techniques to estimate R₀ and p_j, with j=1,…,k. In this point these authors emphasize the importance of the value of k, (s_max in Nishiura's Method), because its value is directly linked to the correct estimation of R₀. They considered that if k is not large enough, it does not represent a complete probability distribution given by the generation time.

For the case where the generation time is known, we have:

$$\widehat{R_0}=\frac{{\sum }_{t=1}^T{N}_t}{{\sum }_{t=1}^T{\sum }_{j=1}^{\text{min}(k,t)}{p}_j{N}_{t-j}}\text{.}$$ (9)

2.4. The method of comparison

From the system of Equation (30) below is possible to observe that the patterns showed by R₀ considered only for the first two weeks, which corresponds to the infection generation time. (See the detailed calculations in the Appendix).

$$\frac{d{I}_H\left(t\right)}{dt}=R_0(\gamma +{\mu }_H){\mu }_V{e}^{{\mu }_v\tau }{e}^{-{\mu }_{V}t}K-\left({\mu }_H+\gamma \right)I_H\left(t\right),$$

$$\frac{dK}{dt}=I_H(\text{t}-\tau )e^{{\mu }_V(t-\tau )}$$ (30)

2.5. Additional calculations

Some additional calculations are needed to apply the method of Nishiura [3]. In his method, Nishiura (2010) estimates only the value of R₀ using Equation (6). In this work we do two kinds of calculation using this expression: to estimate R₀ and the generation time together; and to estimate the value of R₀ only.

We found some problems with expression (6), when j_t>100 because in this case it is necessary to calculate the factorial of 150, for instance, which tends to infinity. To surmount this difficulty, we used a Binomial distribution together with a Normal distribution. We have that for j_t large and 1/R₀ not too close to 0 or 1, the Binomial distribution approaches to a Normal distribution, and the larger the value of j_t the better the approximation between the distributions [31]. Thus the code of this function was divided in two parts: for j_t<100, the likelihood is calculated by minimizing the negative logarithm of (19), and for $j_t\mathrm{⩾}100$, the likelihood is calculated by minimizing the negative logarithm of the Normal distribution with mean $j_t\frac{1}{R_0}$ and variance $j_t\frac{1}{R_0}\left(1-\frac{1}{R_0}\right)$.

Nishiura (2010) applied his calculations for the linear phase of the data. Due to oscillations observed in our data set of dengue, we had to smooth the data. We calculated the moving average of cases in the following way: for the period 2009–2010, we calculated arithmetic average of 7 consecutive terms as follows: let Y_i be the week and S_i its arithmetic average, so $S_i^{2009-2010}=\frac{{\sum }_{i=i}^{i=i-6}{Y}_i}{7}$; for the period 2010-2011we calculated arithmetic average of 4 terms, as follows: $S_i^{2010-2011}=\frac{{\sum }_{i=i}^{i=i-3}{Y}_i}{4}$ [32]. For each data set this calculation was performed from Y_i to the first week.

In order to solve the problems with factorials for the estimation of R₀, using the expression (6) with fixed generation time, we made the following modification.

The first step is to substitute the term $\sum _{s=0}^{\infty }{g}_s{j}_{t-s}$ by μ_t just to simplify the notation,

$$L\left(R_0\right)=\prod _{t=1}^T\left(\begin{array}{c}{j}_t\\ {\mu }_t\end{array}\right){\left(\frac{1}{R_0}\right)}^{{\mu }_t}{\left(1-\frac{1}{R_0}\right)}^{j_t-{\mu }_t}\text{.}$$ (31)

Applying the logarithm,

$$\log \left(L\left(R_0\right)\right)=\sum _{t=1}^T\log \left(\begin{array}{c}{j}_t\\ {\mu }_t\end{array}\right)+\sum _{t=1}^T{\mu }_t\log \left(\frac{1}{R_0}\right)+\sum _{t=1}^T(j_t-{\mu }_t)\log \left(1-\frac{1}{R_0}\right)\text{.}$$ (32)

The term $\sum _{t=1}^T\log \left(\begin{array}{c}{j}_t\\ {\mu }_t\end{array}\right)$ does not involve R₀ and thus can be considered constant. Let's call it k,

$$\log \left(L\left(R_0\right)\right)=k+\sum _{t=1}^T{\mu }_t\log \left(\frac{1}{R_0}\right)+\sum _{t=1}^T(j_t-{\mu }_t)\log \left(1-\frac{1}{R_0}\right)\text{.}$$ (33)

If the calculation of j_t and μ_t does not depend on R₀, the term k is independent of R₀ and is constant. If it is not necessary calculate k because maximizing L(R₀) is equivalent to maximize L(R₀)−k, then:

$$\log \left(L\left(R_0\right)\right)-k=\sum _{t=1}^T{\mu }_t\log \left(\frac{1}{R_0}\right)+\sum _{t=1}^T(j_t-{\mu }_t)\log \left(1-\frac{1}{R_0}\right)\text{.}$$ (34)

So, by fixing the generation time in this way it is possible to estimate the value of R₀ using Equation (34).

3. Results

In this section we present the results for the estimation of R₀ of dengue from the city of Ribeirão Preto in the Southeastern State of Sao Paulo, Brazil in the period of 2009–2010 and 2010–2011. In both periods the city presented important outbreaks. The number of notified cases were multiplied by 4 since it is now known that the asymptomatic; symptomatic ratio is of the order 4:1 (Ximenes et al., 2016) and fitted to Equation (3). From this we calculated the point of inflexion of the epidemic curve, in order to determine the end of the initial growth phase of the outbreaks. For the period 2009–2010, the point of inflexion corresponds to the 21st week of data, with a₁ = 4,316,690, a₂ = −0.268801, a₃ = 4.97401, a₄ = −0.606375 and a₅ = 34.4913. For the period of 2010–2011, it corresponds to the 24th week of data, with a₁ = 15943.8, a₂ = −0.168003, a₃ = 4.83185,a₄ = 0.0543326 and a₅ = −8.7884.

For the methods proposed by Nishiura (2010) and White & Pagano (2008) knowledge about the generation time is necessary. The generation interval for dengue ranges from 14 to 19 days (Aldstadt, 2007, Aldstadt et al., 2012, Bennett et al., 2003) and we took the mean generation interval of dengue infection as 2.4 weeks, which comprises the intrinsic (within human) and the extrinsic (within mosquito) incubation periods. We assumed a variance within the range between 0.28 and 0.43, which correspond to the interval of 2–3 days.

3.1. The Ross-Macdonald's method

The Ross-Macdonald's (Macdonald, 1952, Ross, 1911) method was implemented using the fixed parameters used in the simulation as shown in Table 2:

Table 2.

Parameters used in the simulation.

Parameter	Value of the parameters (from Massad et al., 2010)
γ	0.98 weeks−1
τ	1 week
μH	2.38 × 10−4 weeks−1
μV	0.175 weeks−1

The fitted parameters are: a ranging between 1 and 3 (Favier et al., 2006, Massad et al., 2010), b,c and m ranging between 0 and 1. Although there are very few and sparse information about these parameters in the literature, we tried do not choose wrong (non-physical) values. The values of b and c are easier to estimate because these parameters corresponds to probabilities, whereas for the biting rate it is accepted that mosquitoes in general feed two each three times during the gonotrophic cycle (Gubler and Kuno, 1997). As for the mosquito densities with respect to humans, there are some works that state that the number of A. aegypti per person is normally low (Scott and Morrison, 2010). For instance, in a study carried out in the city of São Sebastião (a coastal city in the State of São Paulo/Brazil) it was observed that the female density of A. aegypti per person ranged between 0.02 and 0.64 (Rodrigues et al., 2015).

The initial condition are given by, $I_H=1,R_H=0,S_V=m\text{*}{N}_H,L_V=0$ and. I_V=0.

In order to define the approximated size of susceptible population summed up the number of infected individuals in the 10 years before to the period studied and subtracted this from the total population. Hence, for the period 2009–2010, the estimated size of the susceptible population ranged between 550000-589168, and for the 2010–2011 period, the figure ranged between 550000-582546.

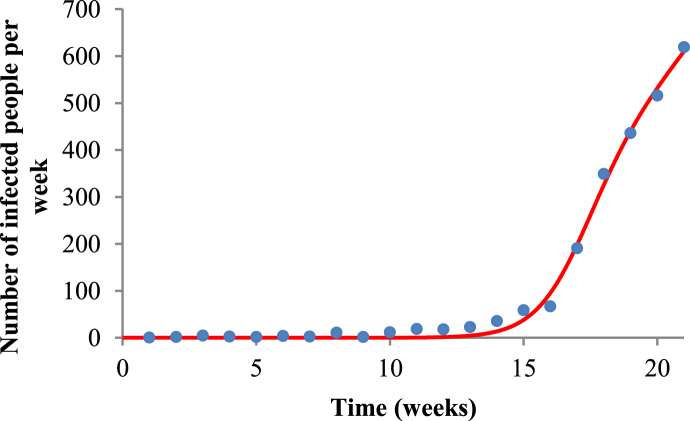
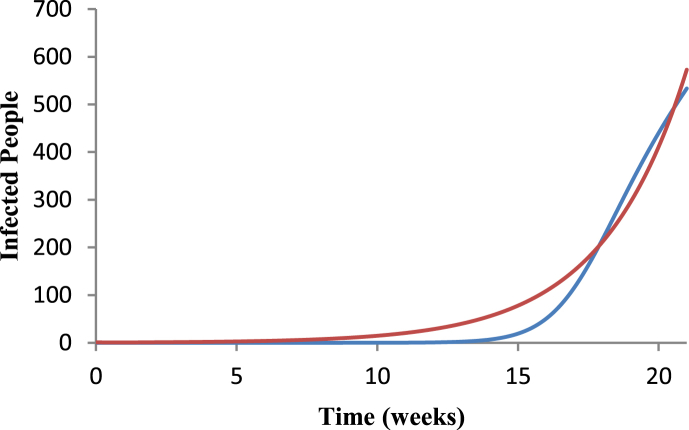
Fig. 1 shows the fit of Equation (3) to the raw data of dengue in Ribeirão Preto for the 2009–2010 period, and Fig. 2 shows the fit of system (1), (2), (3), (4), (5), where R₀=5.44, a=1.82257, b=0.692187, c=0.601626, m=0.80429 and S_H=589162.

Fig. 1.

Fit of Equation (3) to the raw data of dengue in Ribeirão Preto for the 2009–2010 period. Blue dots represent the real data, and red line the fit given by Equation (3) for the period of 2009–2010.

Fig. 2.

Fit of the second equation of system (1) to Equation (5), where R₀=5.44, a=1.82257, b=0.692187, c=0.601626, m=0.80429 and S_H=589162. Blue line represent the number of infected individuals according to Equation (5), and red line the fit using system (1) for the period 2009–2010.

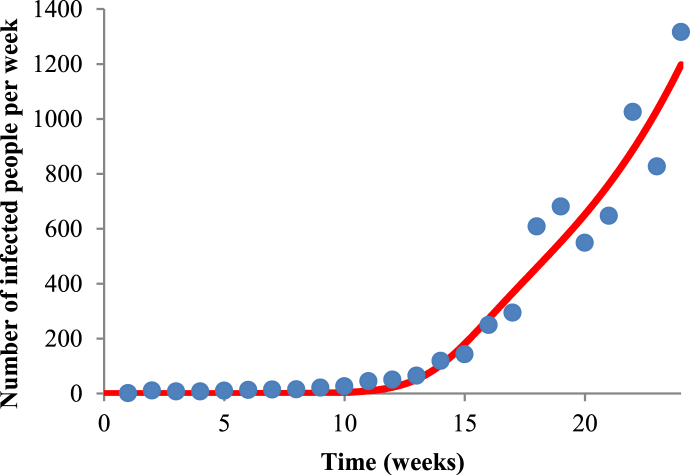
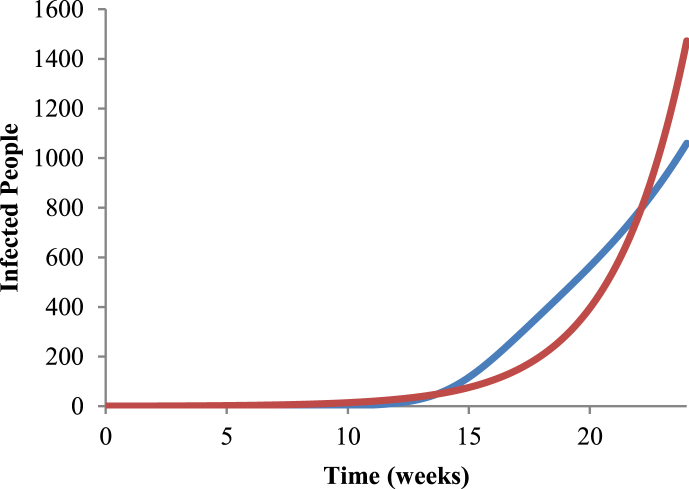
Fig. 3 shows the fit of Equation (3) to raw data of dengue in Ribeirão Preto for the 2010–2011 period, and Fig. 4 shows the fit of system (1) to Equation (5),R₀=5.41, a=2.36399, b=0.314763, c=0.823785, m=0.762838 and S_H=550000.

Fig. 3.

Fit of Equation (3) to raw data of dengue in Ribeirão Preto for the 2010–2011 period, and Fig. 4 shows the fit of the second equation of system (1) to Equation (4),R₀=5.41, a=2.36399, b=0.314763, c=0.823785, m=0.762838 and S_H=550000. Blue points represent the real data, and red line the fit given by Equation (3) for the period of 2010–2011.

Fig. 4.

Fit of the second equation of system (1) to Equation (5),R₀=5.41, a=2.36399, b=0.314763, c=0.823785, m=0.762838 and S_H=550000. Blue line represents the infected people given by Equation (5), and red line the fit using of system (1) for the period 2010–2011.

3.2. The Nishiura's method

In his work Nishiura (2010) estimates R₀ by minimizing the negative logarithm of (6). In this work, we carried out two calculations: in the first calculation we estimated R₀ and the generation time using the Binomial distribution together with Normal distribution, assuming s_max=8 and R₀ ranging between 1.2 and 10; the second calculation was made using Equation (34), applying the generation time gave by the Binomial distribution together with Normal distribution. R₀ ranging between 1 and 10.

For the 2009–2010 period we obtained R₀=3.10 and variance of 0.43, for the Binomial distribution together with Normal distribution, and R₀=3.11 for Equation (34).

For the 2010–2011 period we obtained R₀=1.84 and variance of 0.43, for the Binomial distribution together with Normal distribution, and R₀=1.83 for Equation (34).

3.3. The White and Pagano's method

White & Pagano (2008) proposed two techniques to estimate the value of R₀, one used when the generation time is known and the other when the generation time is unknown. Here we present the estimation using these two methods. When the generation time is unknown we minimized the negative logarithm of (8), whereas when the generation time is known we used the information given by Equation (9) to estimate R₀. In both cases we made k=8 and R₀ ranging between 1 and 10.

For the 2009–2010 period, we obtained R₀=2.67 and variance of 0.43 for Equation (8), and R₀=2.67 for Equation (9). For the 2010–2011 period, we obtained R₀=1.78 and variance of 0.43 for Equation (8), and R₀=1.78 for Equation (9).

3.4. Comparing the methods

In order to analyze the differences among the techniques we used the system of equation (46). We considered only the initial growing phase of the dengue outbreak, which corresponds to the first generation time fixed in 2 weeks.

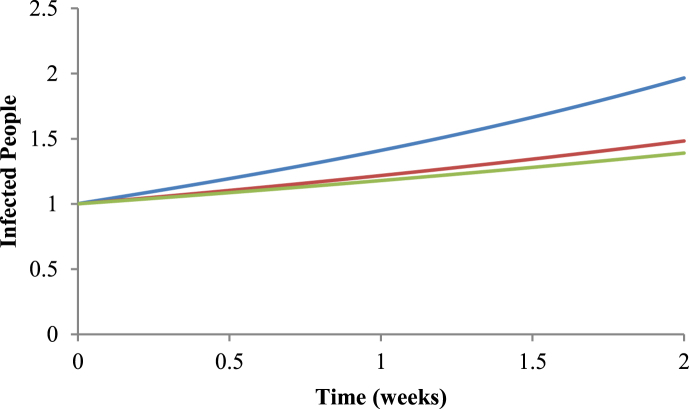
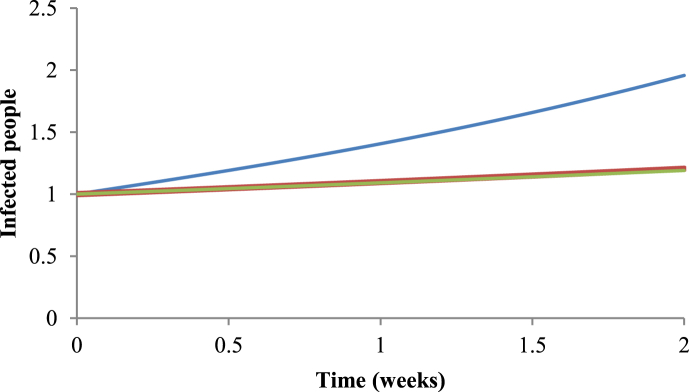
With the method of Nishiura (2010) we calculated the value of R₀ using Equation (34). With the method of White & Pagano (2008), in turn, we calculated the value of R₀ from Equation (9). Finally, with the Ross-Macdonald method, the value of R₀ was calculated using Equation (2). It can be noted from Fig. 5, Fig. 6 that the values are very similar in the initial growing phase for the Nishiura (2010) and White & Pagano (2008) methods, but the results obtained with these methods differ from the one with the Ross-Macdonald model.

Fig. 5.

Comparison between the three methods. The blue line represents the number of infected people using R₀=5.44 given by the Ross-Macdonald model (Macdonald, 1952); the red line represents the number of infected people using R₀=3.11 given by the Nishiura method (2010); and in the green line represents the number of infected people using R₀=2.67 given by the White & Pagano method (2008), for the period of 2009–2010.

Fig. 6.

Comparison between the three methods. The blue line represents the number of infected people using R₀=5.41 given by the Ross-Macdonald model (Macdonald, 1952); the red line represents the number of infected people using R₀=1.84 given by the Nishiura method (2010); and in the green line represents the number of infected people using R₀=1.78 given by the White & Pagano method (2008), for the period of 2010–2011.

Table 3, Table 4 show the comparison of the results of the estimation of R₀ for the periods of 2009–2010 and 2010–2011, respectively, for each method studied. The calculations were carried out considering the first 17th week, then 18th and so on.

Table 3.

Values of R₀ to the period 2009–2010.

Number of weeks	Equation (8)	Equation (34)	Binomial+Normal	Equation (9)	Equation (2)
17	2.96	2.58	2.58	2.97	4.70
18	3.79	2.99	2.97	3.80	5.05
19	3.90	3.32	3.31	3.90	5.35
20	3.25	3.34	3.33	3.25	5.46
21	2.67	3.11	3.10	2.67	5.44
22	2.54	2.91	2.90	2.54	5.40
23	2.42	2.75	2.74	2.42	5.38
24	2.29	2.59	2.58	2.29	5.32
25	2.10	2.41	2.40	2.10	5.25
26	1.96	2.24	2.23	1.96	5.17
27	1.82	2.09	2.09	1.82	5.06
28	1.68	1.96	1.96	1.68	4.94
29	1.58	1.84	1.84	1.58	4.81
30	1.52	1.73	1.75	1.52	4.69

Table 4.

Values of R₀ to the period 2010–2011.

Number of weeks	Equation (8)	Equation (34)	Binomial+Normal	Equation (9)	Equation (2)
14	2.25	2.18	2.18	2.26	5.97
15	2.35	2.26	2.26	2.35	5.98
16	2.54	2.39	2.38	2.55	5.99
17	2.53	2.47	2.47	2.53	5.99
18	2.81	2.63	2.63	2.81	6.03
19	2.79	2.72	2.72	2.79	6.09
20	2.37	2.60	2.60	2.37	6.04
21	1.97	2.35	2.34	1.97	5.84
22	1.88	2.13	2.12	1.88	5.84
23	1.78	1.94	1.94	1.78	5.49
24	1.78	1.83	1.84	1.78	5.41
25	1.75	1.79	1.80	1.75	5.23
26	1.66	1.73	1.74	1.66	5.09
27	1.66	1.70	1.71	1.66	4.99

Note that, it may seem at first inspection of Table 3, Table 4 that the values of R₀ varied with time. The results in these tables, however, should be interpreted as the values of R₀ when the generation time (in weeks) vary.

4. Discussion

In this work we present a comparative analysis of three different techniques to estimate the value of R₀ from the initial growing phase of dengue outbreaks, where it is not assumed an exponential growth for the number of cases. One of these techniques is specific for diseases caused by vectors, and the others techniques are general methods applicable for other kind of infection transmission.

As we used different methods, it should be expected that we obtained different results, especially if we consider only their numerical values. We can see in Fig. 5, Fig. 6, that the methods differ little in the initial dynamics of dengue, but all methods perform the “task” of calculating R₀, that is to say, they allowed to conclude whether the disease will invade or not the susceptible population. In this sense, all methods agree that, for the two periods studied, it should be expected an outbreak of dengue in Ribeirão Preto, which was indeed observed in that town.

Although the values we found for R₀ with the three methods are numerically different, they all have the same pattern of variations with the period considered. For instance, all methods begin with the value of R₀ that increases in the first sets of weeks; after some weeks R₀ reaches its maximum value; finally after this maximum value, R₀ decreases until the last week of the data set studied, irrespective of the method used.

Specifically we can observe that, for the 2009–2010 period: using the method proposed by Nishiura (2010), the largest value of R₀ happens with 20 weeks; for the White & Pagano method (2008) the largest value of R₀ happens with 19 weeks; and for Ross-Macdonald model the largest value of R₀ happens with 20 weeks. For the period 2010–2011 we found: using the method proposed by Nishiura (2010), the largest value of R₀ happens with 19 weeks; for the White & Pagano method (2008) the largest value of R₀ happens with 18 weeks; and for Ross-Macdonald model the largest value of R₀ happens with 19 weeks.

The calculation week by week is interesting when the disease is still going on. In this cases, all methods show that it will happen an outbreak, and this is an important fact because it may serve to alert the affected population about disease prevention. There is still no effective vaccine against dengue, but the current candidates are is a well advanced phase of development and/or clinical testing (Toledo, 2015). Regarding the protection provided by the vaccine, the higher the coverage the better, since there are no important adverse effects reported for the candidates so far, so the estimations of the herd immunity could be done from the calculated value of R₀ given by Equation (2).

It should be noted that the Nishiura (2010) and White & Pagano (2008) methods were developed to deal with directly transmitted infections. Nishiura (2010) used HIV/AIDS data and White & Pagano (2008) used Ebola, Avian Influenza and Swine Flu. Nishiura presents no reason why he used this kind of data, and White & Pagano (2008) argued that, for the correct calculation of R₀ and the generation time together, the data should be from a directly transmitted infection because the population has to be closed. In this study we assumed that, in spite of dengue being a vector-transmitted infection, Ribeirão Preto can considered a closed population. Physical boundaries were considered for the generation time, always keeping in mind that the generation time of diseases transmitted by vectors include the intrinsic and the extrinsic incubation periods of the disease, in other words, it includes humans and vectors (Aldstadt et al., 2012).

The calculations presented in this work using the methods of Nishiura (2010) and White & Pagano (2008) are consistent with each other. For the generation time we used field data from Puerto Rico and Thailand (Aldstadt, 2007, Aldstadt et al., 2012). The literature about the generation time for dengue is scarce. However, the generation time is, by its very definition, the sum of the extrinsic and the intrinsic incubation periods of dengue, which corresponds to the values used in the simulations.

The work published by Li et al. (2011) argues about the failure of R₀, in this paper they studied a simple model to malaria where they obtained several equations to estimate R₀. More specifically, they use the next generation operator, the constant term of the characteristic polynomial, an exponential formula, the Jacobian matrix and the formula of the constant term of the characteristic polynomial where authors add and subtract 9. This methods are equal only at threshold (R₀=1), in the others cases they have different results both R₀>1 and R₀<1, all methods show that for R₀>1 the disease will spread, and for R₀>1 cannot spread in the population.

Li et al. (2011) discuss several cases in which the value calculated for R₀ is wrong, at least in the sense of the amount of secondary cases generated by a single index case. However, they conclude that, besides all mistakes that can be implicit in the several ways to calculate R₀, this is the unique tool that exists with this purpose.

Finally, it should be mentioned that the poor vector control methods the health authorities of the site studied had proved very ineffective in reducing the number of dengue cases in the last years. If this was not the case then our results could be quantitatively distinct from those presented in the paper. We are sure, however, that this did not interfered with our results.

5. Conclusion

Comparing techniques so different is a difficult task because it is impossible to state which technique is better than others because there is not gold-standard for R₀. However, it is possible point out the following observations:

• •The values calculated differ little in the initial growing phase of a dengue outbreak, which refers to the first generation time;
• •In addition, although the results obtained with each method are numerically different all of them have the same pattern through the weekly calculations;
• •The values calculated with the Ross-Macdonald method (Macdonald, 1952) are systematically higher than with the other two methods.

Conflicts of interest

None.

Appendix.

In order to compare the results obtained by the methods presented above, it was developed a system of differential equations based on the Ross-Macdonald's Model. This system, however, is only valid for the very beginning of the outbreak. Therefore, this analysis is a crude approximation of reality. The equation for the infected people from the Ross-Macdonald's Model is given by,

$$\frac{d{I}_H\left(t\right)}{dt}=ab{I}_V\left(t\right)\frac{S_H\left(t\right)}{N_H\left(t\right)}-\left({\mu }_H+\gamma \right)I_H\left(t\right)\text{.}$$ (10)

First, we assume that S_H(0) = N_H(0), because in the beginning of the epidemic S_H(t)≈N_H(t). For t∼0. Then,

$$\frac{d{I}_H\left(t\right)}{dt}=ab{I}_V\left(t\right)-\left({\mu }_H+\gamma \right)I_H\left(t\right)\text{.}$$ (11)

Rewriting this equation we have,

$$\frac{d}{dt}\left[I_H\left(t\right)e^{\left({\mu }_H+\gamma \right)t}\right]=ab{I}_V\left(t\right)e^{\left({\mu }_H+\gamma \right)t}\text{.}$$ (12)

The next step is to integrate both sides of Equation (12)

$$\underset{0}{\overset{t}{\int }}\frac{d}{dt}\left[I_H\left(t\right)e^{\left({\mu }_H+\gamma \right)t}\right]=\underset{0}{\overset{t}{\int }}ab{I}_V\left(t\right)e^{\left({\mu }_H+\gamma \right)t}dt,$$ (13)

where we have,

$$I_H\left(t\right)e^{\left({\mu }_H+\gamma \right)t}-I_H\left(0\right)=\underset{0}{\overset{t}{\int }}ab{I}_V\left(s\right)e^{\left({\mu }_H+\gamma \right)s}ds\text{.}$$ (14)

and

$$I_H\left(t\right)=I_H\left(0\right)e^{-\left({\mu }_H+\gamma \right)t}+ab{e}^{-\left({\mu }_H+\gamma \right)t}\underset{0}{\overset{t}{\int }}{I}_V\left(s\right)e^{\left({\mu }_H+\gamma \right)s}ds\text{.}$$ (15)

To solve Equation (15), however, requires an expression to $I_V\left(s\right)$.

The equation for infected vectors from Ross-Macdonald's Model is given by,

$$\frac{d{I}_V\left(t\right)}{dt}=ac{S}_V\left(t-\tau \right)\frac{I_H\left(t-\tau \right)}{N_H\left(t-\tau \right)}{e}^{-{\mu }_V\tau }-{\mu }_V{I}_V\left(t\right)\text{.}$$ (16)

Let's suppose that S_V = N_V, that is, we consider that in the beginning of the outbreak that S_V≈N_V. Then, by the same token:

$$\frac{d{I}_V\left(t\right)}{dt}=acm{I}_H\left(t-\tau \right)e^{-{\mu }_V\tau }-{\mu }_V{I}_V\left(t\right),$$ (17)

where.$m=\frac{N_V}{N_H}\text{.}$

Rewriting this equation we have,

$$\frac{d}{dt}\left[I_V\left(t\right)e^{{\mu }_{V}t}\right]=acm{I}_H\left(t-\tau \right)e^{-{\mu }_V\tau }{e}^{{\mu }_{V}t}\text{.}$$ (18)

The next step is to integrate both sides of Equation (18),

$$\underset{0}{\overset{t}{\int }}\frac{d}{dt}\left[I_V\left(t\right)e^{{\mu }_{V}t}\right]=\underset{0}{\overset{t}{\int }}acm{I}_H\left(u-\tau \right)e^{{\mu }_V(u-\tau )}\text{.}$$ (19)

$$I_V\left(t\right)e^{{\mu }_{V}t}-I_V\left(0\right)=acm\underset{0}{\overset{t}{\int }}{I}_H\left(u-\tau \right)e^{{\mu }_V(u-\tau )}du\text{.}$$ (20)

It is assumed that $I_V\left(0\right)=0,$ because this system starts with one infected human:

$$I_V\left(s\right)=acm{e}^{-{\mu }_{V}s}\underset{0}{\overset{s}{\int }}{I}_H\left(u-\tau \right)e^{{\mu }_V(u-\tau )}du\text{.}$$ (21)

Replacing (21) in (15) we have:

$$I_H\left(t\right)=I_H\left(0\right)e^{-\left({\mu }_H+\gamma \right)t}+ab{e}^{-\left({\mu }_H+\gamma \right)t}\underset{0}{\overset{t}{\int }}{e}^{\left({\mu }_H+\gamma \right)s}acm{e}^{-{\mu }_{V}s}\underset{0}{\overset{s}{\int }}{I}_H\left(u-\tau \right)e^{{\mu }_V(u-\tau )}duds,$$ (22)

or,

$$I_H\left(t\right)=I_H\left(0\right)e^{-\left({\mu }_H+\gamma \right)t}+a^{2}bcm{e}^{-\left({\mu }_H+\gamma \right)t}\underset{0}{\overset{t}{\int }}{e}^{\left({\mu }_H+\gamma \right)s}{e}^{-{\mu }_{V}s}\underset{0}{\overset{s}{\int }}{I}_H\left(u-\tau \right)e^{{\mu }_V(u-\tau )}duds\text{.}$$ (23)

Taking the first derivative of Equation (23) with respect to time we have:

$$\frac{d}{dt}\left[I_H\left(t\right)e^{\left({\mu }_H+\gamma \right)t}\right]=m{a}^{2}bc{e}^{\left({\mu }_H+\gamma \right)t}{e}^{-{\mu }_{V}t}K\left(t\right),$$ (24)

where $K\left(t\right)=\underset{0}{\overset{s}{\int }}{I}_H\left(u-\tau \right)e^{{\mu }_V(u-\tau )}du$.

Then,

$$\frac{d}{dt}\left[I_H\left(t\right)e^{\left({\mu }_H+\gamma \right)t}\right]=\frac{d{I}_H\left(t\right)}{dt}{e}^{\left({\mu }_H+\gamma \right)t}+\left({\mu }_H+\gamma \right)I_H\left(t\right)e^{\left({\mu }_H+\gamma \right)t},$$ (25)

or,

$$\frac{d{I}_H\left(t\right)}{dt}{e}^{\left({\mu }_H+\gamma \right)t}=m{a}^{2}bc{e}^{\left({\mu }_H+\gamma \right)t}{e}^{-{\mu }_{V}t}K\left(t\right)-\left({\mu }_H+\gamma \right)I_H\left(t\right)e^{\left({\mu }_H+\gamma \right)t}\text{.}$$ (26)

Thus,

$$\frac{d{I}_H\left(t\right)}{dt}=m{a}^{2}bc{e}^{-{\mu }_{V}t}K\left(t\right)-\left({\mu }_H+\gamma \right)I_H\left(t\right),$$

$$\frac{dK\left(t\right)}{dt}=I_H(t-\tau )e^{{\mu }_V(t-\tau )}\text{.}$$ (27)

It is known, for this model, that the value of R₀ is given by:

$$R_0=\frac{m{a}^{2}bc{e}^{-{\mu }_v\tau }}{(\gamma +{\mu }_H){\mu }_V}\text{.}$$ (28)

Therefore,

$$m{a}^{2}bc=R_0\left(\gamma +{\mu }_H\right){\mu }_V{e}^{{\mu }_v\tau }\text{.}$$ (29)

So,

$$\frac{d{I}_H\left(t\right)}{dt}=R_0(\gamma +{\mu }_H){\mu }_V{e}^{{\mu }_v\tau }{e}^{-{\mu }_{V}t}K-\left({\mu }_H+\gamma \right)I_H\left(t\right),$$

$$\frac{dK}{dt}=I_H(\text{t}-\tau )e^{{\mu }_V(t-\tau )}$$ (30)