A mathematical modeling study of the HIV epidemics at two rural townships in the Liangshan Prefecture of the Sichuan Province of China

Abstract

Background

As a response to a severe HIV epidemic in the Liangshan Prefecture, one of the worst in China, population based HIV interventions, including two population-wide HIV screening, have been carried out since 2005 at two townships in a remote mountainous region of Liangshan. The objective of our mathematical modeling study is to assess the temporal dynamics of the HIV epidemic in the two townships based on the data collected in the study area during the period 2005–2010.

Methods

A mathematical model was set up to describe the population dynamics of HIV transmission in study area. The model was calibrated by fitting it to the HIV testing and treatment data from 2005 to 2008. Validation of the model was done by comparing its predicted value of HIV prevalence in 2010 to the prevalence data obtained in the 2010 population wide HIV testing. The validated model was used to produce estimation of HIV incidence, prevalence and death.

Results

Our model estimations show that population-based HIV interventions have significantly slowed down the rise of the HIV epidemic in the two townships. Over the five-year period from 2005 to 2010, the year-over-year rate of increase in HIV incidence, prevalence, and death has declined by 91.5%, 28.7%, and 52.3%, respectively.

Conclusion

Mathematical models, when integrated with epidemiological and surveillance data, can be an effective tool for predicting the temporal dynamics of HIV and assessing the impacts of HIV interventions.

1. Background

Major challenges to the effective control of the HIV epidemics in China include the heterogeneity of populations, economic conditions, social structures and local HIV transmission dynamics across its vast and diverse geographic regions. At the national level, it was estimated that about 740,000 people are living with HIV (PLHIV) in 2009, and an additional 105,000 people are surviving AIDS (CD4 count < 200/mm³) (Ministry of Health, China, 2011). While all of the country’s 31 provinces and autonomous regions have reported HIV cases, the top six high-prevalence provinces (Yunnan, Guangxi, Henan, Sichuan, Xinjiang, and Guangdong) in 2009 have accounted for 77.1% of the cumulative HIV reports in the country, and for over 60% of the national number of people living with HIV (PLHIV) (Ministry of Health, China, 2011). In certain remote rural townships, the HIV prevalence among adults can be 200 times higher than the national average (Li, 2013).

Liangshan Yi Autonomous Prefecture in the Sichuan Province is among the regions with the highest HIV prevalence rate, accounting for 56.4% of cumulative reported cases of HIV/AIDS in the province at the end of 2010. The severe HIV epidemic in Liangshan was attributed to the prefecture’s location along one of the major drug trafficking routes to northwest and central China from the “Golden Triangle”, one of the world’s largest illicit heroin production and distribution centers, and to the large number of injected drug users from the remote areas in the northeastern part of the prefecture. A large migrant population of farmers, who goes to other regions and provinces to seek work and travel between home and their work places, accounts for 15% of the prefecture’s 4.73 million population in 2011. National HIV surveillance data have shown that migrant workers from Liangshan have contributed to the spread of HIV to 30 other provinces. To effectively control the HIV epidemics in Liangshan, the local government has partnered with the Chinese Center for Disease Control and Prevention and the Sichuan Center for Disease Control and Prevention to start in 2005 comprehensive HIV intervention and control programs in two remote rural townships, Jiudu and Muer, with a combined population of about 10,000. The interventions included expanded methadone clinics to help people aviod injection drugs, and expanded HIV testing and ART treatment coverage. Experiences and lessons learned from these localized programs will help improve the HIV control programs in larger high-prevalence regions.

To fully understand the severity of the HIV epidemic and establish a baseline of the HIV prevalence in the Lianshan Prefecture, two population-wide HIV screening programs were carried out in 2008 and 2010 in the Jiudu and Muer townships. The 2008 screening program tested close to 50% of the population in both townships for HIV. Test data showed an HIV prevalence rate of 18.32% among adults aged between 15 and 49 (Li, 2013). In 2010, with the support from the National 11-5 Major Research Project on the Prevention and Control of HIV, Viral Hepatitis and Other Major Infectious Diseases, a population-wide physical examination was conducted in Jiudu and Muer. Baseline individual health records, including HIV status, were established for over 99% of the population in the two townships. Concurrent with the increase of HIV screening, enrollment into ART treatment programs was also greatly expanded. In 2005, there was only one HIV patient receiving ART treatment in Jiudu and Muer, and the number has risen to 166 by the end of 2010.

The extensive HIV data collected in the Jiudu and Muer townships, which were categorized and analyzed in the doctoral dissertation of Dr. Ping Li (2013), provided a unique dataset for a mathematical modeling study of temporal dynamics of the HIV epidemic. The prevalence data in year 2010 based on HIV testing of 99% of the population provided a “gold standard” for model validation.

Our mathematical model for the HIV transmission dynamics was first calibrated using the surveillance and treatment data for the period 2005–2008 collected in the two townships (Li, 2013). We validated our model by comparing its predicted value of HIV prevalence in 2010 to the prevalence data of 2010. The validated model produced estimations on the number of new HIV infections, people living with HIV (PLHIV), and HIV/AIDS related death for 2005–2010. These model estimations and their temporal trend provided the local health authorities with a better understanding of the true burden of the HIV epidemics among the studied populations, and were used to assess the impacts of HIV intervention programs.

2. Methods

2.1. Model

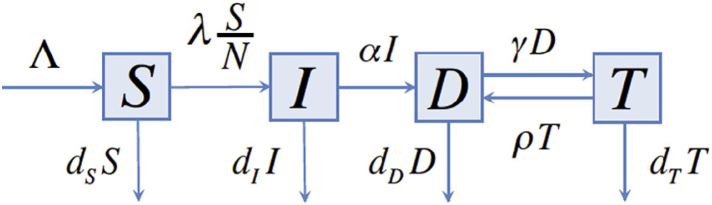
We constructed a deterministic transmission model that describes the process of susceptible people (in compartment S) becoming infected with HIV (in compartment I) through horizontal transmission, and being diagnosed (in compartment D) through HIV testing, and then being enrolled into ART treatment programs (in compartment T). By this categorization, people in compartment I are HIV positive but undiagnosed or unaware of their HIV status. People who were in a treatment program but experienced treatment failures or were lost to follow-up belong to compartment D. The model is depicted in the transfer diagram in Figure 1.

Fig. 1.

Transfer diagram of the HIV transmission model.

In the model, S(t) denotes the number of susceptible people at time t, I(t) denotes the number of undiagnosed HIV positive people at time t, D(t) denotes the number of people who are diagnosed of HIV but are not in a treatment program, and T(t) denotes the number of people who are diagnosed of HIV and are enrolled in a treatment program. The parameter Λ denotes the annual influx into the total population, and annual death rates ${\mathrm{d}}_{\mathrm{S}}$, ${\mathrm{d}}_{\mathrm{I}}$, ${\mathrm{d}}_{\mathrm{D}}$ and ${\mathrm{d}}_{\mathrm{T}}$ are specific to the compartments S, I, D and T, respectively. Terms $\gamma \mathrm{D}\left(\mathrm{t}\right)$ and $\rho \mathrm{T}\left(\mathrm{t}\right)$ denote numbers of annual treatment enrollment and loss to treatment follow-up, respectively. The term $\alpha \mathrm{I}$ denotes the number of annual new reports of HIV and AIDS combined. The force of infection $\lambda$ is expressed as $\lambda ={\beta }_{\mathrm{I}}\mathrm{I}\left(\mathrm{t}\right)+{\beta }_{\mathrm{D}}\mathrm{D}\left(\mathrm{t}\right)+{\beta }_{\mathrm{T}}\mathrm{T}\left(\mathrm{t}\right)$, where ${\beta }_{\mathrm{I}}$, ${\beta }_{\mathrm{D}}$ and ${\beta }_{\mathrm{T}}$ denote transmission coefficients for the compartments I, D and T, respectively.

The HIV and control programs at the Jiudu and Muer townships have drastically scaled up the HIV testing and treatment since 2005, which were reflected from the sharp increase in annual numbers of HIV/AIDS reports and new treatments. The population-wide screening programs in 2008 and 2010 had tested 50% and 99% of the population, respectively. To realistically account for the scale-ups in HIV testing and treatment, we modeled annual new HIV/AIDS reports by $\alpha \left(\mathrm{t}\right)\mathrm{I}\left(\mathrm{t}\right)$ and new treatments by $\gamma \left(\mathrm{t}\right)\mathrm{D}\left(\mathrm{t}\right)$ during 2005–2010. Here, time-dependent rates $\alpha \left(\mathrm{t}\right)$ and $\gamma \left(\mathrm{t}\right)$ are assumed to be piecewise linear functions.

2.2. Data source

Aggregated HIV/AIDS surveillance data from 2005 to 2010 was obtained from the Surveillance Database of the China Center for Disease Control and Prevention. Aggregated data on ART treatment for the same period were obtained from the Treatment Database of the China Center for Disease Control and Prevention. Population data for the two townships were obtained from the demographic database for the Liangshan prefecture. The following data from 2005–2008 were used for our model fitting:

• (1)Annual combined number of new reports of HIV and AIDS;
• (2)Annual number of deaths due to HIV and AIDS among diagnosed;
• (3)Annual number of treatment enrollment;
• (4)Annual number of deaths due to HIV and AIDS among people under ART treatment;
• (5)Annual number of the total population.

2.3. Parameter estimation

The demographic parameters Λ and ${\mathrm{d}}_{\mathrm{S}}$ were estimated by fitting the equation of the total population of the two townships. The death rates ${\mathrm{d}}_{\mathrm{D}}$, ${\mathrm{d}}_{\mathrm{T}}$, the treatment enrollment rate $\gamma \left(\mathrm{t}\right)$, and the rate of loss to treatment follow up $\rho$ were determined directly by regression from the surveillance and treatment data.

Other parameters including ${\beta }_{\mathrm{I}}$, ${\beta }_{\mathrm{D}}$, ${\beta }_{\mathrm{T}}$, ${\mathrm{d}}_{\mathrm{I}}$, and the size of undiagnosed population ${\mathrm{I}}_0$ at the end of 2005 cannot be determined directly from the epidemiological and surveillance data. Their values were estimated through fitting the model to the surveillance data. Due to the limited number of time points in the available data, not all of these parameters can be uniquely determined by model fitting: a continuum of values for these parameters can produce almost the same model output, a phenomenon often referred to as non-identifiability (Raue et al., 2009). A customary approach to resolve non-identifiability is to fix the value of some parameters so that the remaining ones can be uniquely fitted. In our model, we assumed ${\mathrm{d}}_{\mathrm{I}}=0.063$ based on analysis of survival data in the literature for treatment-naive HIV patients (Collaborative group on AIDS incubation and HIV survival, including the CASCADE EU concerted action, 2000, Todd et al, 2007). We assumed that the ratio between transmission coefficients satisfy $\mathrm{a}={\beta }_{\mathrm{D}}/{\beta }_{\mathrm{I}}\le 1$ and $\mathrm{b}={\beta }_{\mathrm{T}}/{\beta }_{\mathrm{I}}\le 1$. These assumptions reflect the reduction in transmission both for people in compartment D due to behavioral changes when they are aware of their HIV status (Fox et al, 2009, Marks et al, 2005), and for people in compartment T due to the reduced viral load level when they are under ART treatment (Bunnell et al, 2006, Castilla et al, 2005, Donnell, 2010, Donnell et al, 2010, Granich et al, 2010, Quinn et al, 2000). Conservatively, we fixed the ratio $\mathrm{a}={\beta }_{\mathrm{D}}/{\beta }_{\mathrm{I}}$ at 0.75 and the ratio $\mathrm{b}={\beta }_{\mathrm{T}}/{\beta }_{\mathrm{I}}$ at 0.1. Nonlinear least squares method (Glover, Jenkins, & Doney, 2008) was applied to obtain the point estimation of the remaining parameters: the transmission coefficient ${\beta }_{\mathrm{I}}$, the initial size ${\mathrm{I}}_0$ of compartment I at the end of 2005, and the piece-wise linear diagnosis rate $\alpha \left(\mathrm{t}\right)$.

We conservatively assumed that the confidence interval for ${\beta }_{\mathrm{D}}/{\beta }_{\mathrm{I}}$ was [0.5, 1] (Fox et al, 2009, Marks et al, 2005) and the confidence interval for ${\beta }_{\mathrm{T}}/{\beta }_{\mathrm{I}}$ was [0, 0.5] (Bunnell et al, 2006, Castilla et al, 2005, Donnell, 2010, Donnell et al, 2010, Granich et al, 2010, Quinn et al, 2000). The 95% confidence intervals for parameters ${\beta }_{\mathrm{I}}$, ${\beta }_{\mathrm{D}}$, ${\beta }_{\mathrm{T}}$, ${\mathrm{d}}_{\mathrm{I}}$, ${\mathrm{d}}_{\mathrm{D}}$, ${\mathrm{d}}_{\mathrm{T}}$ and ${\mathrm{I}}_0$ were obtained by using the Bayesian based MCMC method (Ghasemi et al, 2011, Gilks et al, 1995). Estimated parameter values, together with their confidence intervals, are shown in Table 1.

Table 1.

Values and confidence intervals for model parameters.

Parameter	Description	Best-fit value	95% CI	Source
${\beta }_{\mathrm{I}}$	Transmission rate for compartment $\mathrm{I}$	0.214	[0.184, 0.237]	Fitting
$\mathrm{a}={\beta }_{\mathrm{D}}/{\beta }_{\mathrm{I}}$	Ratio of transmission rates for$\mathrm{D}$ and $\mathrm{I}$	0.75	[0.5, 1]	(Fox et al, 2009, Marks et al, 2005)
$\mathrm{b}={\beta }_{\mathrm{T}}/{\beta }_{\mathrm{I}}$	Ratio of transmission rates for T and $\mathrm{I}$	0.1	[0.05, 0.15]	(Bunnell et al, 2006, Castilla et al, 2005, Donnell, 2010, Donnell et al, 2010, Granich et al, 2010, Quinn et al, 2000)
${\mathrm{d}}_{\mathrm{S}}$	Death rate for compartment $\mathrm{S}$	0.007	[0.00503, 0.0089]	Fitting
${\mathrm{d}}_{\mathrm{I}}$	Death rate for compartment $\mathrm{I}$	0.063	[0.045, 0.083]	(Collaborative group on AIDS incubation and HIV survival, including the CASCADE EU concerted action, 2000, Todd et al, 2007)
${\mathrm{d}}_{\mathrm{D}}$	Death rate for compartment $\mathrm{D}$	0.0427	[0.032, 0.055]	Data
${\mathrm{d}}_{\mathrm{T}}$	Death rate for compartment $\mathrm{T}$	0.0652	[0.051, 0.077]	Data
$\rho$	Treatment drop-out rate	0.0169	[0.0108, 0.025]	Data
${\mathrm{I}}_0$	Undiagnosed HIV positive population in 2005	813	[651, 934]	Fitting
$\Lambda$	Influx of susceptibles by birth and emigration	276	[199, 354]	Fitting
$\alpha \left(\mathrm{t}\right)$	Time-dependent diagnosis rate	$0.04345,\mathrm{t}\le 2004$ $0.0602\mathrm{t}-120.585,2004<\mathrm{t}\le 2007$ $0.55,2007<\mathrm{t}\le 2008$ $0.0602\mathrm{t}-120.585,2008<\mathrm{t}\le 2009$ $1,2009<\mathrm{t}\le 2010$ $0.0602\mathrm{t}-120.585,\mathrm{t}>2010$		Fitting
$\gamma \left(\mathrm{t}\right)$	Time-dependent treatment enrollment rate	$0,\mathrm{t}\le 2004$ $0.006228,2004<\mathrm{t}\le 2005$ $0\text{.}\text{01886t}-37\text{.}807,\mathrm{t}>2005$		Data
R2	Goodness of Fitting	0.97

2.4. Nonlinear least-squares fitting

The nonlinear least-squares fitting method was used to select the set of parameter values for which model outcomes best fit the data. The precision of fitting is measured using the ${\mathrm{R}}^2$ ratio defined by

$${\mathrm{R}}^2=1-\frac{{\displaystyle {\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{j}}-{\widehat{\mathrm{y}}}_{\mathrm{j}}\right)}^2}}{{\displaystyle {\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{j}}-\overline{\mathrm{y}}\right)}^2}}$$

Here ${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{j}}-{\widehat{\mathrm{y}}}_{\mathrm{j}}\right)}^2}$ and ${\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{j}}-\overline{\mathrm{y}}\right)}^2}$ are the least-squares residues between data ${\mathrm{y}}_{\mathrm{j}}$, the best fit ${\widehat{\mathrm{y}}}_{\mathrm{j}}$, and the data mean $\overline{\mathrm{y}}$ (Glover et al., 2008).

2.5. Bayesian inference

Bayesian inference is used to obtain the posterior distribution of parameter θ based on the real data $\mathrm{y}$. The posterior distribution can be expressed as:

$$\mathrm{p}\left(\theta |\mathrm{y}\right)=\frac{\mathrm{p}\left(\mathrm{y}|\theta \right)\mathrm{p}\left(\theta \right)}{{\displaystyle \int \mathrm{p}\left(\mathrm{y}|\theta \right)\mathrm{p}\left(\theta \right)\mathrm{d}\theta }}$$

Here $\mathrm{p}\left(\theta \right)$ is the prior distribution representing our knowledge about parameter θ before Bayesian estimation is made, $\mathrm{p}\left(\mathrm{y}|\theta \right)$ is the likelihood function representing how likely it is to observe the data $\mathrm{y}$ given the value of θ.

Results from the nonlinear least-squares fitting were used to inform the choice of prior distribution. Metropolis–Hastings algorithm in Matlab for the Markov chain Monte Carlo (MCMC) simulations was used to generate samples for the posterior distributions, and to compute the 95% confidence intervals of the fitted parameters.

2.6. Model validation

Validation of our model was carried out using three independent approaches.

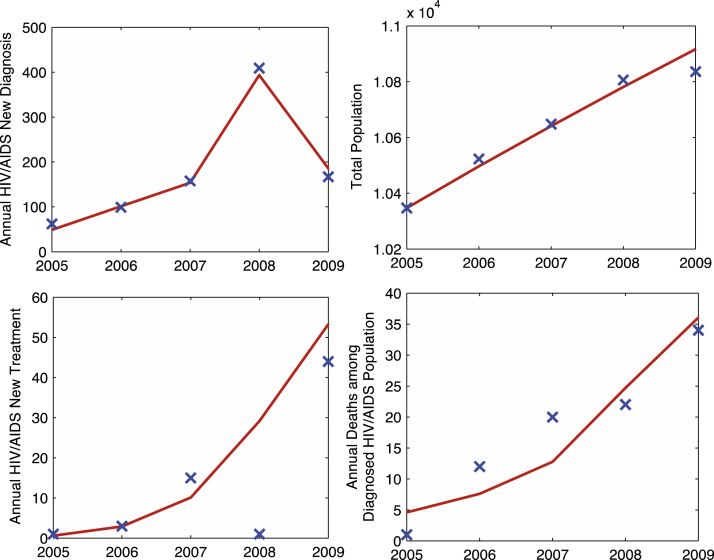
First, the goodness of fit ratio ${\mathrm{R}}^2=0.97$ indicates an excellent fit between our model output and the data (Figure 2). Second, leave-one-out cross-validation method was applied to further verify the consistency of the model fit.

Fig. 2.

Fitting to model outcome to data. Lines graphs are model outcomes, and crosses are data points.

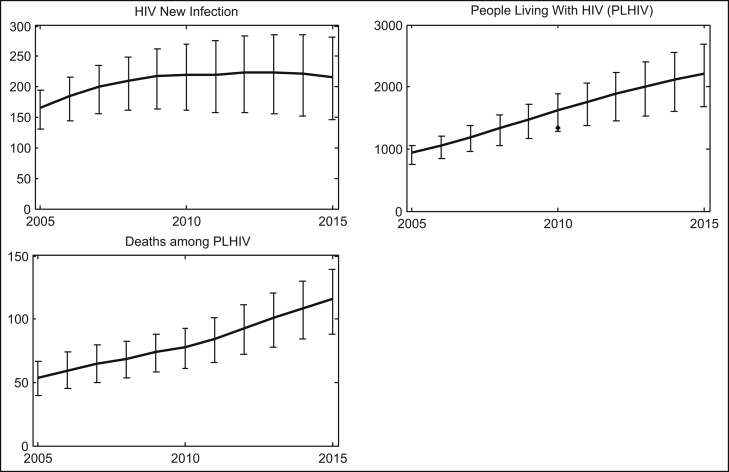
The population-wide physical examination at the two townships in 2010 provided the HIV prevalence data for over 99% of the population. The availability of such good prevalence data is rare and provides a “gold standard” for model validation. The prevalence data in 2010 were not used in our model fitting and reserved for model validation. As shown in Figure 3, this prevalence data point is within the 95% prediction interval of our model for the total number of people living with HIV (PLHIV) in 2010.

Fig. 3.

Model estimation from 2005 to 2015. Lines are baseline model estimations and vertical bars indicate 95% confidence intervals.

2.7. Sensitivity analysis and uncertainty analysis

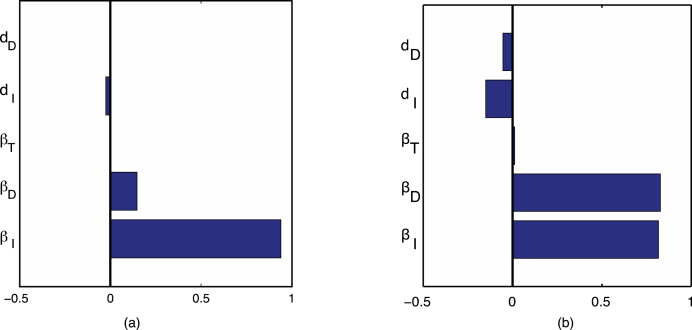
We carried out local sensitivity analysis of our model predictions for new HIV infections of year 2010, using one-at-a-time method at the best-fit parameter values (Daniel, 1973). Our analysis showed that the top three most sensitive parameters were transmission coefficients ${\beta }_{\mathrm{I}}$, ${\beta }_{\mathrm{D}}$, and death rate ${\mathrm{d}}_{\mathrm{I}}$ for the undiagnosed population; see Figure 4.

Fig. 4.

Results of sensitivity analysis showing the 5 most sensitive parameter for (a) HIV new infections in 2006 and (b) HIV new infections in 2010 with respect to model parameters.

For uncertain analysis, we computed our base model prediction using the best-fit parameter values from nonlinear least-squares fitting. To produce prediction intervals with high and low estimates, we allowed all parameters to vary within their confidence intervals, and applied Latin Hypercube sampling (LHS) (Blower & Dowlatabadi, 1994) to produce 20,000 samples of parameter values. Our prediction intervals contained 95% of the 20,000 model outputs using sampled parameter values.

3. Results

3.1. Estimation of HIV epidemic in Jiudu and Muer townships from 2005 to 2010

Three key assessment indicators for the HIV/AIDS dynamics: annual number of new HIV infections, annual number of HIV/AIDS related deaths, and the total number of people living with HIV (both diagnosed and undiagnosed), were estimated from 2005 to 2010 using the validated model.

The estimated annual number of new HIV infections rose from 166 in 2005 to 219 in 2010. In the meantime, the year-over-year rate of increase declined from 10.84% in 2006 to 0.92% in 2010, indicating that the momentum of rise of the HIV epidemics in the two townships has slowed down significantly during the 5-year period.

The estimated total number of people living with HIV and AIDS, including both diagnosed and undiagnosed people, increased from 931 in 2005 to 1615 in 2010. The year-over-year rate of increase declined from in 13.43% 2006 to 9.57% in 2010. The estimated HIV prevalence rate among the whole population at the end of 2010 was 14.57%.

The estimated total number of deaths among people living with HIV and AIDS increased from 53 in 2005 to 78 in 2010. The year-over-year rate of increase declined from 11.32% in 2006 to 5.4% in 2010.

3.2. Prediction of HIV epidemics in Jiudu and Muer townships from 2011 to 2015

Our model was used to further predict the three key indicators for the period 2011–2015, under the assumption that the treatment enrollment rate would continue to increase linearly following its pre-2010 trend, and that the diagnosis rate would maintain the same trend during the period from 2005 to 2007 before the population-wide screening.

Our model predicted that continuous scale-up of HIV testing and ART treatment will reverse the temporal trend of the HIV epidemics in the Jiudu and Muer townships; the predicted annual number of new HIV infections would decline starting from 2013 (Figure 3). The predicted number of new HIV infections in 2015 is 212, lower than its 2010 level. The predicted value for PLHIV in 2015 is 2208, with a HIV prevalence rate at 18.98%. The model prediction for the number of combined HIV and AIDS deaths in 2015 is 116. These predicted values would be updated using more recent HIV data between 2011 and 2015.

3.3. Evaluating the impact of two screening interventions in 2008 and 2010

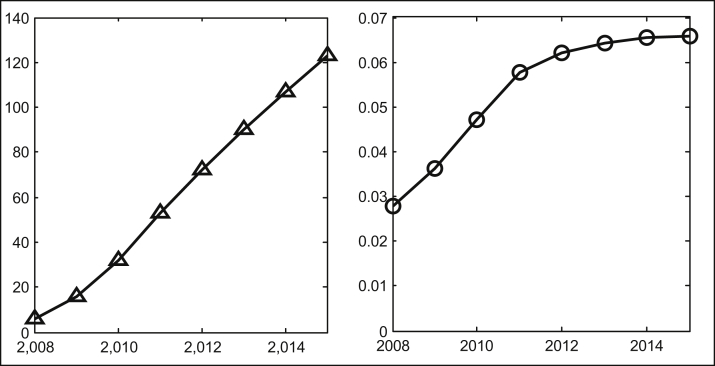
We used our model to estimate that the two population-wide screening programs in 2008 and 2010 alone have saved 134 life years, and averted 123 new HIV infections from the beginning of 2008 to the end of 2015. The number of averted new HIV infections account for 6.6% of the new HIV infections that would have occurred without the two screening interventions. Figure 5 shows the cumulative number and percentage of HIV new infections averted from 2008 to 2015.

Fig. 5.

Accumulative HIV new infection averted number (triangle) and percentage (circle) due to screening interventions.

4. Discussions

Mathematical models are becoming a useful tool for estimating HIV/AIDS incidence and prevalence and for predicting their temporal trends. Mathematical models can be constructed to describe HIV epidemic in a population, incorporating dynamic processes of HIV transmission, testing, treatment, as well as deaths. Mathematical models can be calibrated to a specific population by fitting them to epidemiological and surveillance data of the population. Model validation is of paramount importance for model predictions to be reliable. Validated mathematical models can be used to assess retrospectively the impacts of past intervention programs, predict temporal trends of HIV incidence and prevalence in the future, to project the effects of potential interventions, and to provide evidence to inform policies on HIV control and prevention.

In our study, we constructed and calibrated a mathematical model for the HIV epidemic among the populations in the two remote and rural townships, Jiudu and Muer, in the Liangshan Prefecture of the Sichuan Province during 2005–2010. The model was validated by a good agreement of its predicted value of the 2010 HIV prevalence with the true prevalence data based on a HIV screening of 99% of the population in 2010. Our model estimations have shown that, while the HIV epidemic in Jiudu and Muer were rising during the period of 2005–2010, the intervention programs have significantly slowed down the rising momentum. Our model further predicted that continuing the scale-up of HIV intervention programs, especially HIV testing and ART treatment as prevention of HIV transmission, would revert the temporal trend of the HIV epidemic in the two townships, and the annual new HIV infections would decline starting as early as 2013. These predictions will be updated when more recent data become available.

For the period from 2008 to 2015, our model projected that the two population-wide screening programs in 2008 and 2010 have averted 123 HIV new infections and saved 134 life-years from the prevented HIV deaths. Considering that the majority of people who live with HIV and AIDS in the two townships were male farmers of age from 25 to 49, and most of them were the only laborer and bread maker for their families, the social and economic impact of the screening programs are significant on the local population.

There are several limitations in our study due to the limited number of data points. The heterogeneity among the people living with HIV and AIDS was not considered in our model. The transmission coefficients ${\beta }_{\mathrm{I}}$, ${\beta }_{\mathrm{D}}$, and ${\beta }_{\mathrm{T}}$ in our model were averaged among people in different high-risk groups. Incorporating risk groups will make our model more realistic, while calibration of a more complex model will require a larger number of time points in the data than what was available to us. In our parameter estimation, the death rate ${\mathrm{d}}_{\mathrm{T}}$ for the population under treatment was larger than the death rate ${\mathrm{d}}_{\mathrm{D}}$ of people who were diagnosed of the HIV but not in treatment programs. This was likely because most patients receiving treatment in 2005 were in the late stage of HIV infection and suffered a higher fatality rate. As HIV testing and treatment being continuously scaled up, we expect that a larger proportion of the people receiving treatment will be in the early stage of infection, and the fatality rate will drop. It will be more reasonable to assume that the death rate ${\mathrm{d}}_{\mathrm{T}}$ is time-dependent and decreases in time. This would be possible when more recent data become available in a future study to yield a longer time series.

Our study demonstrated that mathematical models could be an effective research tool for HIV epidemiology. When integrated with epidemiological and surveillance data, models can produce estimations that are not readily available from standard epidemiological studies, including but not limited to the number of new HIV infections, the size of the hidden (undiagnosed) HIV positive populations, and death among the hidden HIV positive populations. These estimations can provide health authorities with reliable assessments for the true burden of the HIV epidemic and evidence for planning of HIV control and interventions.

Competing interests

The authors declare that they have no competing interests.

Authors’ contributions

YS, WY, and ML were responsible for study design and planning. CD, PL, HD, YG, SZ, MW, YR, GQ, WY, and YS contributed to data collection and analysis. ZS conducted model simulations. ZS, PL, YR, YS, and ML contributed to interpretation. ZS, PL, YR, YS, and ML contributed to writing the manuscript. All authors read and approved the final version of the manuscript.