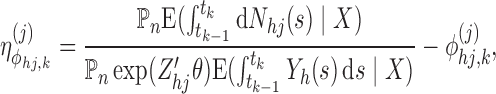Abstract
Semiparametric methods are well established for the analysis of a progressive Markov illness-death process observed up to a noninformative right censoring time. However, often the intermediate and terminal events are censored in different ways, leading to a dual censoring scheme. In such settings, unbiased estimation of the cumulative transition intensity functions cannot be achieved without some degree of smoothing. To overcome this problem, we develop a sieve maximum likelihood approach for inference on the hazard ratio. A simulation study shows that the sieve estimator offers improved finite-sample performance over common imputation-based alternatives and is robust to some forms of dependent censoring. The proposed method is illustrated using data from cancer trials.
Keywords: Cox model, Interval censoring, Method of sieves, Profile likelihood, Progression-free survival
1. Introduction
Vital status for individuals in a clinical trial is often readily available. Detection of non-fatal events requires closer surveillance, which can prove difficult and costly to maintain over time. As a result survival times are subject to right censoring, but the occurrence of intermediate events may be right-censored earlier or interval-censored between assessments. In general, we refer to this scenario as dual censoring. Various forms of dual censoring arise in trials involving tumor progression. Guidelines call for the analysis of so-called time to progression (TTP), coinciding with detection of progression, or progression-free survival (PFS), given by the earliest of TTP and death (FDA, 2007). TTP is typically right-censored at death or the preceding (negative) assessment, which induces dependent censoring. PFS is thus deemed preferable to TTP (FDA, 2007, p. 8), but this outcome is subject to systematic imputation.
Multistate models have been suggested as a more natural framework for assessing treatment effects on progression and death. A chain of events model (Figure 1, left), for example, is useful for settings in which progression always precedes death (Frydman, 1995b). Semicompeting risks (Figure 1, middle) have been proposed for the case where death may precede progression (Hu and Tsodikov, 2014). Xu and others (2010) observe that semicompeting risks essentially amount to the progressive illness-death model (Fix and Neyman, 1951; Figure 1, right), which is fully specified by the state-transition intensity functions.
Fig. 1.
Multistate alternatives to TTP and PFS: chain of events (left), semicompeting risks (middle), and progressive illness-death (right) models.
Among the three state-transition structures, methods to deal with specific instances of dual censoring are most developed for the illness-death model. Frydman (1995a) considers the nonparametric maximum likelihood estimator (NPMLE) from interval-censored progression times with known progression status. This is generalized by Frydman and Szarek (2009) to account for unknown status, which often arises when the last assessment is negative and long precedes right-censoring or death. Bebchuk and Betensky (2001) combine local likelihood and multiple imputation to estimate transition intensities under progression times right-censored before death. Joly and others (2002) propose spline-based penalized likelihood for the (Cox, 1972) proportional hazards model for an interval-censored variant of this observation scheme. Jackson (2011) considers a piecewise exponential analog by way of time-dependent covariates.
These works recognize that progression and death are observed in different ways, but the broader problem of dual censoring has not yet been considered. Methods for time-to-event endpoints that leave any dependence on time unspecified are generally preferred in practice. However, non- and semi-parametric maximum likelihood estimators require the locations of support for the distribution of each transition time, and these are ambiguous whenever the progression status is unknown. To address these issues, we develop a sieve estimator for a multistate extension of the Cox model and compare its numerical performance with routine analysis of imputation-based PFS under a variety of censoring scenarios.
2. Dual censoring of the progressive illness-death process
Let  be a one-jump counting process representing the transition from state
be a one-jump counting process representing the transition from state 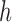 to state
to state 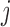 (
( ) in the progressive illness-death model and
) in the progressive illness-death model and  be the corresponding transition time. So
be the corresponding transition time. So  is the time to progression,
is the time to progression, 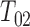 is the time to progression-free death, and
is the time to progression-free death, and 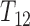 is the time of death following progression. Over the observation period
is the time of death following progression. Over the observation period  ,
, 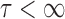 , suppose that the survival time
, suppose that the survival time  is observed up to a right censoring time
is observed up to a right censoring time 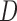 ,
, 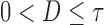 , but progression status
, but progression status 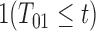 is not necessarily known for all
is not necessarily known for all  ,
, 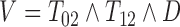 . For example, progression may be right-censored at some random time preceding
. For example, progression may be right-censored at some random time preceding 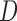 . Alternatively, progression status could assessed periodically, leading to interval censoring.
. Alternatively, progression status could assessed periodically, leading to interval censoring.
Whatever the form of this inspection process, we presume that it yields a potential censoring interval 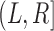 for the progression time
for the progression time 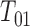 . We say “potential” because we may not know with certainty that
. We say “potential” because we may not know with certainty that 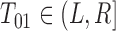 . Put
. Put  to denote whether or not the survival time is observed. Let
to denote whether or not the survival time is observed. Let 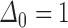 whenever progression status is known to be negative at
whenever progression status is known to be negative at 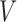 and
and  otherwise. Similarly, let
otherwise. Similarly, let  indicate that progression status is known to be positive at
indicate that progression status is known to be positive at 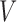 . So
. So  denotes that, based on the available data, we are certain
denotes that, based on the available data, we are certain 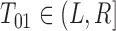 for some
for some 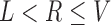 . Otherwise either
. Otherwise either 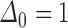 , indicating that
, indicating that 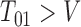 , or progression status is unknown at
, or progression status is unknown at  . If the status is unknown, then
. If the status is unknown, then  and we cannot rule out the possibility that either
and we cannot rule out the possibility that either 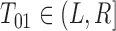 or
or  .
.
2.1. Example: Bone lesions and their complications
Dual right-censored data are encountered in cancer trials evaluating the effect of bisphosphonates on bone metastases and their complications, known as skeletal-related events (SREs). The time of an SRE is often self-evident, but can otherwise be measured accurately through frequent clinic visits, so SREs are typically considered subject only to right censoring. Growth of new or existing bone lesions is assessed by radiographic surveys, which are carried out less frequently. This results in interval-censored lesion progression times. Standard practice is to evaluate SREs and lesions as separate endpoints, as SREs provide the most direct measure of clinical benefit. Time-to-event analysis of either outcome is complicated by the fact that the mortality rate is non-negligible. Use of PFS can circumvent this issue. However, since the treatment is intended to manage symptoms rather than prolong survival, the measured effect on PFS will likely underestimate any symptom benefit. The illness-death model offers an alternative that isolates the effect of interest.
A dual-censored observation from this multistate process with first SRE as the intermediate event is illustrated in the top panel of Figure 2, where we know that no SREs occurred within an initial loss to follow-up time and that the subject survived at least up to final right-censoring time  . We cannot rule out the possibility that progression may have occurred between these two times, so
. We cannot rule out the possibility that progression may have occurred between these two times, so  . The censoring interval
. The censoring interval 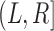 here is indeed “potential” from the observed data because in reality, the subject did not experience any SREs. The PFS endpoint has no standard definition in this setting. Practitioners might simply discard all data collected after the initial loss to follow-up time so that PFS is right-censored early. Alternatively, the negative progression status at this earlier right censoring time could be carried forward to
here is indeed “potential” from the observed data because in reality, the subject did not experience any SREs. The PFS endpoint has no standard definition in this setting. Practitioners might simply discard all data collected after the initial loss to follow-up time so that PFS is right-censored early. Alternatively, the negative progression status at this earlier right censoring time could be carried forward to  , giving PFS with a form of last observation carried forward (LOCF) imputation.
, giving PFS with a form of last observation carried forward (LOCF) imputation.
Fig. 2.
Top: A dual right-censored observation in which progression, coinciding here with first SRE, status is unknown at the last observation time 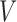 . Bottom: A dual-censored observation in which lesion progression status is observed to be positive, but the progression time is known only up to the interval
. Bottom: A dual-censored observation in which lesion progression status is observed to be positive, but the progression time is known only up to the interval 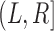 .
.
The bottom panel of Figure 2 considers lesion progression rather than SRE. Here a new lesion developed some time between the first and second radiographic surveys, which gives a censoring interval 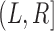 that captures the progression time with certainty:
that captures the progression time with certainty:  and
and 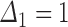 . Loss to follow-up occurs after the second survey but before death, giving
. Loss to follow-up occurs after the second survey but before death, giving  and
and 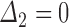 . Guidelines suggest imputing PFS to the time at which progression is first detected, carrying forward the last known progression status to death, and sensitivity analysis to examine variations on this imputation scheme (FDA, 2007, Appendix 2).
. Guidelines suggest imputing PFS to the time at which progression is first detected, carrying forward the last known progression status to death, and sensitivity analysis to examine variations on this imputation scheme (FDA, 2007, Appendix 2).
Let 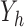 be the at-risk process for any transition out of state
be the at-risk process for any transition out of state 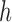 , so that
, so that 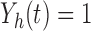 if state
if state  is occupied at time
is occupied at time 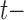 and
and 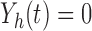 otherwise. Define the
otherwise. Define the  transition probability
transition probability  , with
, with 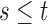 and
and 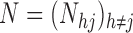 . Suppose that the observation scheme renders the complete data
. Suppose that the observation scheme renders the complete data  coarsened at random in the sense of Heitjan and Rubin (1991). Then the likelihood of a dual-censored observation
coarsened at random in the sense of Heitjan and Rubin (1991). Then the likelihood of a dual-censored observation 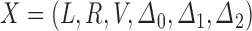 is
is
 |
(2.1) |
where 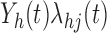 is the transition intensity process or instantaneous transition probability at time
is the transition intensity process or instantaneous transition probability at time  . Whatever model we choose for the transition intensity function
. Whatever model we choose for the transition intensity function 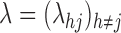 , the likelihood a priori maximizes to infinity;
, the likelihood a priori maximizes to infinity; 
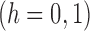 can be made arbitrarily large at any time we observe
can be made arbitrarily large at any time we observe 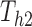 exactly. The usual way out is to replace
exactly. The usual way out is to replace 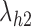 by the jump discontinuity
by the jump discontinuity 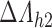 in the cumulative transition intensity function
in the cumulative transition intensity function 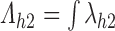 . However, consider an individual with unknown progression status
. However, consider an individual with unknown progression status 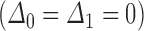 and known survival time
and known survival time 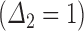 . Surely, we need
. Surely, we need 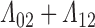 to increase at
to increase at  , but the observed data are insufficient to jointly estimate
, but the observed data are insufficient to jointly estimate  and
and  . Nonparametric maximum likelihood will assign mass to at least one of the two potential transition times, but the manner in which support is allocated is subject to bias. Since the so-called risk set for
. Nonparametric maximum likelihood will assign mass to at least one of the two potential transition times, but the manner in which support is allocated is subject to bias. Since the so-called risk set for 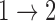 transitions is empty at
transitions is empty at  , the likelihood can be increased appreciably by allocating more mass to potential or observed support for the distribution of
, the likelihood can be increased appreciably by allocating more mass to potential or observed support for the distribution of 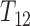 early in the observation period. So the initial increments in the NPMLE for
early in the observation period. So the initial increments in the NPMLE for 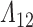 will tend to be large in finite samples. All of these difficulties can be mitigated by maximizing the likelihood with respect to a sieve—a finite-dimensional approximation to
will tend to be large in finite samples. All of these difficulties can be mitigated by maximizing the likelihood with respect to a sieve—a finite-dimensional approximation to 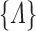 whose size increases with
whose size increases with 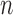 . Such an approach is generally known as the method of sieves (Grenander, 1981).
. Such an approach is generally known as the method of sieves (Grenander, 1981).
3. Method of sieves for dual-censored data
Here a sieve is defined for a given random sample  ,
, 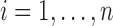 , of dual-censored observations. Each element of a sieve corresponds to a piecewise parametric cumulative intensity function
, of dual-censored observations. Each element of a sieve corresponds to a piecewise parametric cumulative intensity function 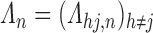 defined on a data-driven partition of the observation period
defined on a data-driven partition of the observation period 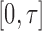 . Let
. Let  and
and  respectively denote the set of left- and right-endpoints from the collection of known censoring intervals
respectively denote the set of left- and right-endpoints from the collection of known censoring intervals 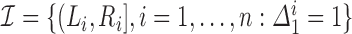 . Define
. Define 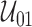 as the set of right-endpoints from the maximal intersections (Wong and Yu, 1999) for
as the set of right-endpoints from the maximal intersections (Wong and Yu, 1999) for  ; that is, the set of
; that is, the set of  from
from  such that
such that 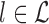 ,
,  , and
, and 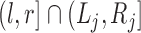 is either
is either  or
or  for every
for every 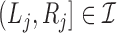 . In addition, let
. In addition, let  , for
, for 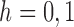 , denote the set of exactly observed terminal event times
, denote the set of exactly observed terminal event times  with known progression status and non-empty
with known progression status and non-empty  risk set at
risk set at 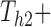 .
.
From Frydman (1995a, Theorem 1), the NPMLE for  based on the subsample with known progression status (
based on the subsample with known progression status (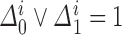 ) can be uniquely defined as the discrete maximizer concentrating its support on
) can be uniquely defined as the discrete maximizer concentrating its support on 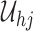 ,
, 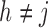 . This implies that
. This implies that 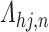 should, at minimum, have support on
should, at minimum, have support on 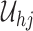 . To ensure that
. To ensure that 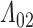 and
and 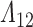 are jointly estimable, the sieve partition must not isolate any
are jointly estimable, the sieve partition must not isolate any  with
with 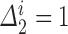 and unknown progression status
and unknown progression status 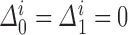 . We can achieve this by defining
. We can achieve this by defining 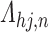 on a partition
on a partition 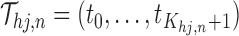 , such that
, such that  for
for 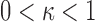 ,
, 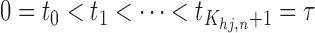 ,
, 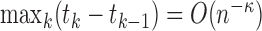 , and every subinterval
, and every subinterval 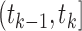 contains at least one point from
contains at least one point from 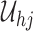 . Here
. Here  is a tuning parameter that determines the rate at which the sieve or partition size
is a tuning parameter that determines the rate at which the sieve or partition size  increases with
increases with 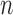 .
.
For consistency, we need  as
as 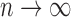 . This can be met if the true parameter
. This can be met if the true parameter 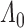 is sufficiently smooth and increasing on
is sufficiently smooth and increasing on  and the distribution of the inspection times has positive support on
and the distribution of the inspection times has positive support on 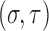 for some small
for some small 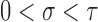 . We express these and other assumptions throughout this paper more precisely in Appendix A of the supplementary material available at Biostatistics online, but essentially this means
. We express these and other assumptions throughout this paper more precisely in Appendix A of the supplementary material available at Biostatistics online, but essentially this means 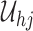 must be dense in
must be dense in  as
as 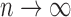 . Such a requirement is stronger than the ones imposed by Joly and others (2002) and Frydman and Szarek (2009), which allow for unobservable terminal event times with negative progression status:
. Such a requirement is stronger than the ones imposed by Joly and others (2002) and Frydman and Szarek (2009), which allow for unobservable terminal event times with negative progression status: 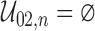 . A consequence of this is that the support for the distribution of
. A consequence of this is that the support for the distribution of 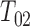 is not apparent from the available data, so imposing at least a weakly parametric model for
is not apparent from the available data, so imposing at least a weakly parametric model for 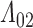 is needed to achieve consistency.
is needed to achieve consistency.
Apart from the location of support points, estimation from dual-censored data poses two additional challenges: (i) inference under convergence rates possibly slower than the parametric rate, as encountered with various forms of interval censoring, and (ii) consideration of  that depends arbitrarily on aspects of the event history, such as the duration in state 1. We avoid these complications by considering a sieve estimator for the Cox model with fixed covariates. This permits inference on the familiar hazard ratio via Murphy and van der Vaart's (2000) profile likelihood theory and, barring the standard Markov assumption, puts little restriction on any dependence with time. A variety of extensions or alternatives could be considered, but we adopt this model as a starting point.
that depends arbitrarily on aspects of the event history, such as the duration in state 1. We avoid these complications by considering a sieve estimator for the Cox model with fixed covariates. This permits inference on the familiar hazard ratio via Murphy and van der Vaart's (2000) profile likelihood theory and, barring the standard Markov assumption, puts little restriction on any dependence with time. A variety of extensions or alternatives could be considered, but we adopt this model as a starting point.
4. Sieve estimation of the Cox model
Sieve estimators have been previously proposed for interval-censored survival data. Huang and Rossini (1997) examine the proportional odds model. Zhang and others (2010) devise a spline-based sieve for the Cox model. Our setting is complicated by multiple event types and censoring schemes, but these works provide a useful basis for extension. Herein assume that each 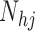 has cumulative intensity function
has cumulative intensity function
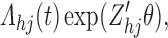 |
(4.1) |
where 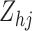 is an
is an  transition-type-specific
transition-type-specific 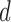 -vector based on the fixed covariate
-vector based on the fixed covariate  ,
, 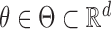 is a regression parameter, and
is a regression parameter, and  is now a nondecreasing cumulative baseline
is now a nondecreasing cumulative baseline  transition intensity function. Note that the parameter
transition intensity function. Note that the parameter 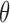 is common to each transition type, but
is common to each transition type, but 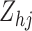 can be suitably constructed from
can be suitably constructed from 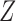 to give type-specific covariate effects (Andersen and Borgan, 1985, pp. 478–480). For example, if we wish to estimate the effect of the scalar covariate
to give type-specific covariate effects (Andersen and Borgan, 1985, pp. 478–480). For example, if we wish to estimate the effect of the scalar covariate 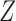 on each transition type separately, we may put
on each transition type separately, we may put 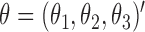 ,
,  ,
, 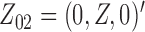 , and
, and 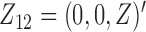 . The effect of
. The effect of 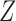 on the risk of the
on the risk of the  ,
,  , and
, and  transitions then corresponds to
transitions then corresponds to 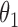 ,
, 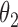 , and
, and  , respectively.
, respectively.
Under (4.1) the cumulative  transition intensity process
transition intensity process 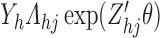 depends on only the current state occupied and thus satisfies the Markov property
depends on only the current state occupied and thus satisfies the Markov property 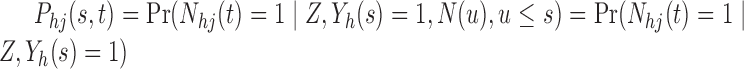 . So
. So 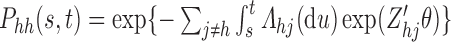 and
and  , for any
, for any  (e.g. (Andersen and Borgan, 1985, Theorem II.6.7)). Let
(e.g. (Andersen and Borgan, 1985, Theorem II.6.7)). Let 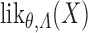 denote the likelihood of an observation
denote the likelihood of an observation 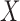 given by (2.1), evaluated under these transition probabilities. Then the sieve maximum likelihood estimator (SMLE),
given by (2.1), evaluated under these transition probabilities. Then the sieve maximum likelihood estimator (SMLE), 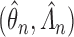 , corresponds to the maximizer of the log-likelihood function
, corresponds to the maximizer of the log-likelihood function 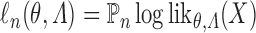 over
over  . The sieve
. The sieve 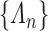 is defined by its piecewise parametric family and partition
is defined by its piecewise parametric family and partition 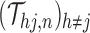 . For a sufficiently large partition size, one would not anticipate
. For a sufficiently large partition size, one would not anticipate  to be particularly sensitive to the parametric form on the subintervals. This general notion is demonstrated in the survival case by Huang and Rossini (1997). We defer a discussion on selection of the partition to the end of Section 4.2. The remainder of this section describes the estimation scheme, with illustrations for the piecewise exponential sieve. Numerical results for this sieve are examined in Sections 5 and 6.
to be particularly sensitive to the parametric form on the subintervals. This general notion is demonstrated in the survival case by Huang and Rossini (1997). We defer a discussion on selection of the partition to the end of Section 4.2. The remainder of this section describes the estimation scheme, with illustrations for the piecewise exponential sieve. Numerical results for this sieve are examined in Sections 5 and 6.
4.1. Parameter estimation
Suppose that the cumulative baseline intensity functions from a given sieve 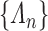 are specified by the (finite-dimensional) parameter
are specified by the (finite-dimensional) parameter 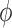 . The piecewise exponential sieve, for example, is characterized by the piecewise constant values taken by the cumulative intensity function. These range through positive values in
. The piecewise exponential sieve, for example, is characterized by the piecewise constant values taken by the cumulative intensity function. These range through positive values in 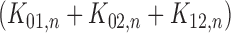 -space. In general, let
-space. In general, let  denote the parameters specifying
denote the parameters specifying 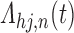 for
for 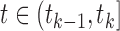 and
and 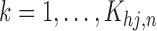 . Then the SMLE satisfies the score equations
. Then the SMLE satisfies the score equations  . These can be solved using the following self-consistency algorithm, which is akin to the routine outlined by Frydman (1995b) under the null model with
. These can be solved using the following self-consistency algorithm, which is akin to the routine outlined by Frydman (1995b) under the null model with 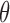 fixed at zero and no dual censoring.
fixed at zero and no dual censoring.
Step 4.1 —
For
and
, define
as a partition of
in which each subinterval contains
points from
. Set
,
, and
to some “neutral” value that ensures
is increasing. For example, with the piecewise exponential sieve
.
Step 4.2 —
Find a candidate increment
. For
, apply the Newton-Raphson method:
. Obtain
via the self-consistency equations (Turnbull, 1976) that result from re-arranging the score equation
to give a recursive expression for
. For the piecewise exponential sieve, this is loosely:
where the conditional expectations are evaluated under
and
. These are equal to one if
provides
exactly. A precise expression for this ratio is provided in Appendix D of the supplementary material available at Biostatistics online.
Step 4.3 —
Increment
and
by
and
, respectively, with
the smallest nonnegative integer ensuring no decrease in the log-likelihood. This gives
. If, for some small positive value
,
then stop. Otherwise, set
to
and return to Step 4.2.
For each 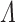 the log-likelihood is concave in
the log-likelihood is concave in  , which implies that the Newton-Rapshon method yields a profile maximizer for
, which implies that the Newton-Rapshon method yields a profile maximizer for  . Similar properties are not readily available for
. Similar properties are not readily available for 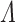 . So the score equations may neither uniquely characterize the SMLE nor identify global maxima. Multiple (local) maxima may be detected with different starting values and examination of the profile log-likelihood. Our experience thus far has uncovered rare instances where the increment-halving procedure in Step 4.3 reduces the first and only candidate increment to its starting value. In this narrow form of local maxima, the algorithm could be initialized with starting values based on imputed data.
. So the score equations may neither uniquely characterize the SMLE nor identify global maxima. Multiple (local) maxima may be detected with different starting values and examination of the profile log-likelihood. Our experience thus far has uncovered rare instances where the increment-halving procedure in Step 4.3 reduces the first and only candidate increment to its starting value. In this narrow form of local maxima, the algorithm could be initialized with starting values based on imputed data.
4.2. Variance estimation
In Appendices B and C of supplementary material available at Biostatistics online, we show that if the 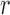 th (
th (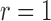 or 2) derivative of
or 2) derivative of 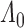 is continuous, positive, and bounded on
is continuous, positive, and bounded on  and some regularity conditions hold, then the SMLE
and some regularity conditions hold, then the SMLE 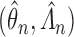 converges to the truth
converges to the truth 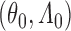 at the rate
at the rate 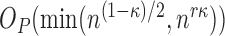 with
with 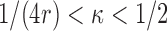 . However,
. However, 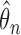 achieves the semiparametric efficiency bound. Both the limiting distribution of
achieves the semiparametric efficiency bound. Both the limiting distribution of  and interval estimation for
and interval estimation for 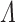 remain as open problems.
remain as open problems.
Holding 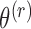 fixed in the self-consistency algorithm described in Section 4.1 evaluates the profile log-likelihood needed to estimate standard error for
fixed in the self-consistency algorithm described in Section 4.1 evaluates the profile log-likelihood needed to estimate standard error for  under Murphy and van der Vaart (2000, Corollary 3), which gives an approximation to the curvature in the profile log-likelihood at
under Murphy and van der Vaart (2000, Corollary 3), which gives an approximation to the curvature in the profile log-likelihood at 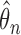 akin to numerical differentiation. This entails successively perturbing the entries in
akin to numerical differentiation. This entails successively perturbing the entries in 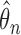 by a chosen value
by a chosen value  . The data-driven procedure outlined in Boruvka and Cook (2015, Section 6) reduces the choice to specifying typical
. The data-driven procedure outlined in Boruvka and Cook (2015, Section 6) reduces the choice to specifying typical 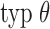 and extreme
and extreme  (absolute) values for any given entry in
(absolute) values for any given entry in 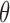 .
.
Estimation thus entails setting a number of parameters—namely the sieve constants 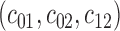 , sieve rate
, sieve rate  , typical and large values for
, typical and large values for 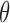 , and the threshold
, and the threshold  . The
. The 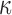 achieving the fastest rate of convergence is
achieving the fastest rate of convergence is 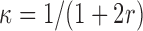 , although better finite sample properties may be obtained with a larger sieve. In practice, we set
, although better finite sample properties may be obtained with a larger sieve. In practice, we set 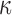 to the (presumed) asymptotically optimal value for discrete inspection processes and closer to
to the (presumed) asymptotically optimal value for discrete inspection processes and closer to 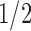 under dual right censoring. We have not formally investigated performance for different values of
under dual right censoring. We have not formally investigated performance for different values of 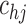 , but this could be set to some positive value invariant to
, but this could be set to some positive value invariant to 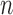 that represents the presumed degree of non-linearity in
that represents the presumed degree of non-linearity in 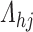 relative to the other cumulative transition intensity functions. Empirical motivation for these choices is provided in Section 5, but further study is warranted. Our experience suggests that estimates are not particularly sensitive to the choice of the remaining parameters provided that
relative to the other cumulative transition intensity functions. Empirical motivation for these choices is provided in Section 5, but further study is warranted. Our experience suggests that estimates are not particularly sensitive to the choice of the remaining parameters provided that  is moderately valued,
is moderately valued, 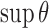 is relatively large, and
is relatively large, and  is sufficiently small. In the simulation studies described below, we set
is sufficiently small. In the simulation studies described below, we set 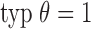 ,
, 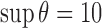 , and
, and 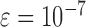 to ensure convergence within a reasonable number of iterations over the censoring schemes and sample sizes considered.
to ensure convergence within a reasonable number of iterations over the censoring schemes and sample sizes considered.
5. Simulation study
Numerical properties of the piecewise exponential SMLE were investigated for right- and interval-censored variants of dual censoring. In both cases, we considered the same model with cumulative  ,
, 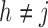 , transition intensity
, transition intensity 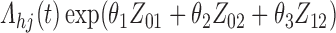 , where
, where 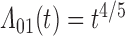 ,
, 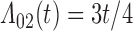 ,
, 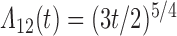 ,
,  uniform on
uniform on 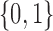 ,
,  the product of
the product of  and the
and the  transition type indicator,
transition type indicator,  and
and  . Here
. Here  influences only the exit time from initial state 0 and its effect is the same for each transition type. However, neither of these properties were assumed in estimating
influences only the exit time from initial state 0 and its effect is the same for each transition type. However, neither of these properties were assumed in estimating 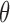 . Throughout
. Throughout  was right censored by the fixed time
was right censored by the fixed time  representing study closure. Under these fixed parameters, roughly 56% of subjects in the sample progressed (
representing study closure. Under these fixed parameters, roughly 56% of subjects in the sample progressed ( ), 12% were event-free at
), 12% were event-free at 
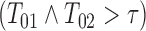 , and 16% survived to study closure (
, and 16% survived to study closure ( ).
).
The censoring scheme acting on the progression status is described in Sections 5.1 and 5.2 below, where we summarize findings from 10 000 Monte Carlo replicates of the sample sizes 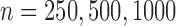 under four general scenarios: (1) independent dual censoring, (2) independent dual censoring with increased censoring of progression, (3) conditionally independent dual censoring given
under four general scenarios: (1) independent dual censoring, (2) independent dual censoring with increased censoring of progression, (3) conditionally independent dual censoring given 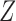 , and (4) dependent dual censoring. The sieve parameters were held fixed at
, and (4) dependent dual censoring. The sieve parameters were held fixed at  ,
, 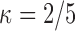 for dual right-censored data, and
for dual right-censored data, and  for interval-censored progression. The first scenario was revisited with alternative values for
for interval-censored progression. The first scenario was revisited with alternative values for 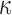 .
.
In each scenario, we also considered estimates of the Cox model obtained by some combination of early right censoring, mid- or right-endpoint imputation the progression time, or carrying the last negative progression status forward to the final right censoring time or death (LOCF). Details on these alternatives and referenced displays can be found in Appendices E and F of supplementary material available at Biostatistics online.
5.1. Dual right censoring
To obtain dual right-censored data, an early censoring time  was generated by
was generated by 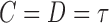 with probability
with probability 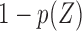 ,
, 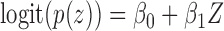 . Otherwise
. Otherwise  followed some distribution with
followed some distribution with 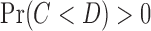 . This gave a dual right censoring scheme in which
. This gave a dual right censoring scheme in which 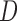 coincides with administrative censoring and
coincides with administrative censoring and 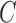 is a dropout time taking place earlier in the observation period. The four scenarios were, respectively, specified as: (1)
is a dropout time taking place earlier in the observation period. The four scenarios were, respectively, specified as: (1) 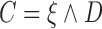 , where
, where 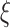 is exponential-distributed with mean
is exponential-distributed with mean  ,
, 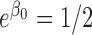 and
and  ; (2)
; (2) 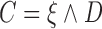 ,
,  ,
,  and
and  ; (3)
; (3)  ,
, 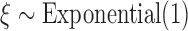 ,
, 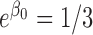 and
and  ; and (4)
; and (4)  , where
, where  follows
follows  truncated to
truncated to 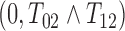 ,
, 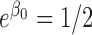 and
and 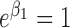 . The rates of exact observation, singly right-censored and doubly right-censored data were roughly 70, 15, and 15%, respectively, under Scenarios 1 and 3. Under Scenario 2, the censoring rates were
. The rates of exact observation, singly right-censored and doubly right-censored data were roughly 70, 15, and 15%, respectively, under Scenarios 1 and 3. Under Scenario 2, the censoring rates were 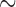 15 and 40%. In Scenario 4, these were 25 and 20%.
15 and 40%. In Scenario 4, these were 25 and 20%.
The SPMLE based on “singly” right-censored data was also considered for three alternative outcomes given, respectively, by the observed transition times right-censored by 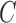 , PFS right-censored at
, PFS right-censored at 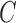 , and PFS with LOCF imputation under exactly observed survival times with unknown progression status. These two variants of PFS are depicted in Figure 2.
, and PFS with LOCF imputation under exactly observed survival times with unknown progression status. These two variants of PFS are depicted in Figure 2.
Table E.1 of supplementary material available at Biostatistics online summarizes performance in estimating 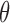 . Results for the SMLE support the asymptotic properties stated in Appendices B and C of supplementary material available at Biostatistics online with average bias generally diminishing in larger samples, average standard error estimates nearing the Monte Carlo sample standard deviations, and empirical coverage probabilities of the 95% confidence intervals at or near the nominal level. The SPMLE from right-censored data at
. Results for the SMLE support the asymptotic properties stated in Appendices B and C of supplementary material available at Biostatistics online with average bias generally diminishing in larger samples, average standard error estimates nearing the Monte Carlo sample standard deviations, and empirical coverage probabilities of the 95% confidence intervals at or near the nominal level. The SPMLE from right-censored data at 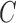 shows higher variability and lower bias under independent censoring (Scenarios 1–3). Under dependent censoring (Scenario 4), the SPMLE has larger finite-sample bias. The SPMLE for PFS right-censored at
shows higher variability and lower bias under independent censoring (Scenarios 1–3). Under dependent censoring (Scenario 4), the SPMLE has larger finite-sample bias. The SPMLE for PFS right-censored at  also performed relatively well under independent censoring; however, its regression coefficient is defined on the basis of the restrictive assumption that
also performed relatively well under independent censoring; however, its regression coefficient is defined on the basis of the restrictive assumption that  . The PFS variant incorporating LOCF imputation is clearly biased under independent censoring, particularly when the rate of dual censoring is higher. LOCF imputation fared better in Scenario 4. This is not surprising since
. The PFS variant incorporating LOCF imputation is clearly biased under independent censoring, particularly when the rate of dual censoring is higher. LOCF imputation fared better in Scenario 4. This is not surprising since 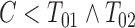 often closely preceded
often closely preceded 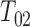 in this dependent censoring scheme.
in this dependent censoring scheme.
Figure E.1 of supplementary material available at Biostatistics online depicts the pointwise average and percentiles of the SMLE 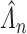 under Scenarios 1–4 with
under Scenarios 1–4 with  . Estimates appear unbiased, with the exception of overestimates for
. Estimates appear unbiased, with the exception of overestimates for 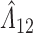 early in the observation period. Results under
early in the observation period. Results under  and 500 (not shown here or the supplement) indicate that bias and variability decreases with increasing sample size, but are otherwise similar. The SPMLE obtained by right censoring observations at
and 500 (not shown here or the supplement) indicate that bias and variability decreases with increasing sample size, but are otherwise similar. The SPMLE obtained by right censoring observations at 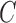 demonstrate little to no bias under independent censoring. This is however not the case under the dependent censoring scheme of Scenario 4. Estimates for
demonstrate little to no bias under independent censoring. This is however not the case under the dependent censoring scheme of Scenario 4. Estimates for 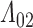 are clearly biased (Figure E.2 of supplementary material available at Biostatistics online), with the pointwise
are clearly biased (Figure E.2 of supplementary material available at Biostatistics online), with the pointwise 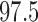 th percentiles consistently smaller than the truth.
th percentiles consistently smaller than the truth.
From Table E.2 of supplementary material available at Biostatistics online, it is apparent that the largest sieve size (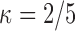 ) achieves the smallest finite-sample bias with little to no increase in variability compared with the sieves under
) achieves the smallest finite-sample bias with little to no increase in variability compared with the sieves under 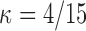 and
and  . A larger sieve, sample size or degree of dual censoring increased computational demands for estimation, but the routine we implemented typically converged within a few seconds in all settings considered (Table E.3 of supplementary material available at Biostatistics online).
. A larger sieve, sample size or degree of dual censoring increased computational demands for estimation, but the routine we implemented typically converged within a few seconds in all settings considered (Table E.3 of supplementary material available at Biostatistics online).
5.2. Interval-censored progression times
To generate interval-censored progression times, status was inspected on the basis of  “scheduled” visits, evenly spaced on
“scheduled” visits, evenly spaced on  . “Actual” visit times followed
. “Actual” visit times followed  independent normal distributions centered at the scheduled times with common standard deviation
independent normal distributions centered at the scheduled times with common standard deviation 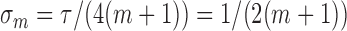 and truncated at zero,
and truncated at zero,  , and the midpoints between consecutive scheduled times. So the inspection times were continuously distributed on
, and the midpoints between consecutive scheduled times. So the inspection times were continuously distributed on 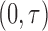 with greater density around the scheduled targets. This setup is similar to the one in Zeng and others (2015); however, here the spread of the inspection times better cover
with greater density around the scheduled targets. This setup is similar to the one in Zeng and others (2015); however, here the spread of the inspection times better cover 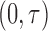 so that we can reasonably expect the SMLE to be consistent over the observation period.
so that we can reasonably expect the SMLE to be consistent over the observation period.
Under the independent censoring schemes of Scenarios 1–3, every inspection after the first was missed with probability 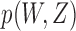 , where
, where 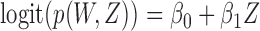 . Dependent censoring in Scenario 4 was obtained by discarding inspections taking place after
. Dependent censoring in Scenario 4 was obtained by discarding inspections taking place after  . In all scenarios, the last observation time
. In all scenarios, the last observation time 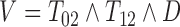 offered one further inspection of progression status with a fixed probability of
offered one further inspection of progression status with a fixed probability of 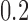 . Parameters in each scenario were set to: (1)
. Parameters in each scenario were set to: (1)  ,
, 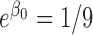 and
and 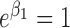 ; (2)
; (2) 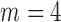 ,
,  and
and 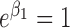 ; (3)
; (3)  ,
,  and
and 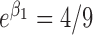 ; and (4)
; and (4) 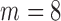 and
and 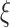 follows
follows 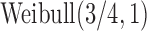 truncated to
truncated to 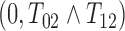 . With
. With  and
and 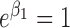 , the probability of a missing inspection was
, the probability of a missing inspection was  , irrespective of
, irrespective of  . Under
. Under 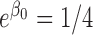 and
and 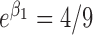 , the probability remained the same for subjects with
, the probability remained the same for subjects with  . With
. With 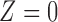 , inspections were two times more likely to be missed. Under Scenario 4,
, inspections were two times more likely to be missed. Under Scenario 4,  can be interpreted as a dropout time closely preceding death. In Scenarios 1 and 3, progression status was known by
can be interpreted as a dropout time closely preceding death. In Scenarios 1 and 3, progression status was known by  in just over half of the sample. For Scenarios 2 and 4 this rate was 44 and 40%, respectively. In all four scenarios, the rate was 20% among progression-free subjects, so status was known more often among subjects who progressed.
in just over half of the sample. For Scenarios 2 and 4 this rate was 44 and 40%, respectively. In all four scenarios, the rate was 20% among progression-free subjects, so status was known more often among subjects who progressed.
We also fit the SPMLE to two forms of singly right-censored data. The first arises by midpoint-imputing progression times if progression status is known to be positive, as depicted in the lower panel of Figure 2; otherwise, the negative progression status is carried forward to 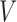 . The second is the guideline-based definition for PFS, given by the earliest of progression detection, death, and right-censoring at
. The second is the guideline-based definition for PFS, given by the earliest of progression detection, death, and right-censoring at  .
.
From Table F.1 of supplementary material available at Biostatistics online numerical results for the SMLE 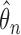 support the asymptotic properties in Appendices B and C with bias generally decreasing with increasing sample size, average standard error estimates reasonably approximating the Monte Carlo sample standard deviations, and empirical coverage probabilities of the 95% confidence intervals close to the nominal level. The SPMLE based on midpoint- and LOCF-imputed data and PFS had, on average, larger finite-sample bias. Bias in both of these estimators generally did not diminish with increasing sample size.
support the asymptotic properties in Appendices B and C with bias generally decreasing with increasing sample size, average standard error estimates reasonably approximating the Monte Carlo sample standard deviations, and empirical coverage probabilities of the 95% confidence intervals close to the nominal level. The SPMLE based on midpoint- and LOCF-imputed data and PFS had, on average, larger finite-sample bias. Bias in both of these estimators generally did not diminish with increasing sample size.
Pointwise average and percentiles of the SMLE  are depicted in Figure F.1 of supplementary material available at Biostatistics online. The SMLE overestimates increments in
are depicted in Figure F.1 of supplementary material available at Biostatistics online. The SMLE overestimates increments in 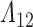 early in the observation period. This pattern persists across scenarios and sample sizes, but the bias decreases with larger
early in the observation period. This pattern persists across scenarios and sample sizes, but the bias decreases with larger  . The imputation-based SPMLE for
. The imputation-based SPMLE for 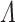 is clearly biased (Figure F.2 of supplementary material available at Biostatistics online), with the degree of bias largest under survival-dependent interval censoring (Scenario 4). Imputation-based estimates for survivor and hazard functions typically exhibit a step pattern according to the density of the inspection times, as noted by Panageas and others (2007). For
is clearly biased (Figure F.2 of supplementary material available at Biostatistics online), with the degree of bias largest under survival-dependent interval censoring (Scenario 4). Imputation-based estimates for survivor and hazard functions typically exhibit a step pattern according to the density of the inspection times, as noted by Panageas and others (2007). For 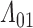 , this artifact of the observation scheme is a persistent departure from the true shape of the cumulative intensity function.
, this artifact of the observation scheme is a persistent departure from the true shape of the cumulative intensity function.
On average, a smaller sieve with  achieved increased bias and similar variability compared with
achieved increased bias and similar variability compared with 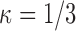 (Table F.2 of supplementary material available at Biostatistics online). A larger sieve (
(Table F.2 of supplementary material available at Biostatistics online). A larger sieve ( ) gave similar variability, but did not always yield an improvement in average bias. Parameter estimation under interval censoring is more computationally demanding than under dual right-censored data, with average processing times about 100 times slower than those seen in Section 5.1 (Table F.3 of supplementary material available at Biostatistics online).
) gave similar variability, but did not always yield an improvement in average bias. Parameter estimation under interval censoring is more computationally demanding than under dual right-censored data, with average processing times about 100 times slower than those seen in Section 5.1 (Table F.3 of supplementary material available at Biostatistics online).
6. Applications
We return to the examples of Section 2.1, which demonstrate two variants of dual censoring—one arising from loss to follow-up for SREs and the other from periodic assessment for lesion progression. Data were obtained from similarly designed trials where SREs were recorded at clinic visits every 3 weeks and lesion progression was diagnosed on the basis of radiographic surveys every 3–6 months. Actual assessment times roughly followed this schedule, but with enough variation to justify use of the sieve. Since the assessment times were largely determined by a prespecified schedule, one might guess that coarsening at random assumption is plausible. However, loss to follow-up for both SREs and lesion progression occurred due to treatment discontinuation and death, although discontinuation rates were similar in the treatment groups. The simulation study offers some reassurance that the SMLE performs relatively well under survival dependent loss to follow-up. Another consideration is the plausibility of the Markov proportional hazards assumption, though one could argue that this model offers an adequate tool for detecting a difference in the risk of progression between treatment groups. Further investigation of the SMLE's requirements as they relate to the study design and features of the data is warranted, but out of scope for a simple demonstration of the proposed estimator.
6.1. Dual right censoring: Skeletal-related events
Rosen and others (2001) reported that two bisphosphonates, zolendronic acid and pamidronate disodium, showed equivalent efficacy and safety in preventing SREs among patients with breast cancer and multiple myeloma. This conclusion was partly drawn from the evaluation of time to the first SRE within 9 months of randomization in an international trial of 1600 patients. Here we evaluate time to first SRE and death via an illness-death model among the trial's North American breast cancer cohort. Within this subsample of 777 patients, the available trial data provide SREs up to 30 months following randomization. The majority of patients died during this period, so observation of SREs typically ceased earlier.
Under this three-state, outcome  was observed exactly in just over one-third of the sample. Incomplete transition times and known progression status was observed for 28% of the patients. Almost 15% had unknown progression status but exact survival time, leaving the remaining 23% of the sample dual censored. Table 1 and Figure 3 give the SMLE under
was observed exactly in just over one-third of the sample. Incomplete transition times and known progression status was observed for 28% of the patients. Almost 15% had unknown progression status but exact survival time, leaving the remaining 23% of the sample dual censored. Table 1 and Figure 3 give the SMLE under 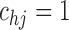 (
(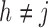 ) and
) and 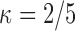 . Estimates obtained from both smaller and larger sieves provide similar results, with changes in
. Estimates obtained from both smaller and larger sieves provide similar results, with changes in 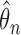
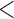 0.009. Also depicted is the SPMLE obtained by discarding any observations after the initial right censoring time. The same conclusion can be drawn from both approaches; under the assumed Markov illness-death process, any influence of zoledronic acid on the risk of bone interventions and death is not significantly different from that of pamidronate. The two methods diverge in estimating
0.009. Also depicted is the SPMLE obtained by discarding any observations after the initial right censoring time. The same conclusion can be drawn from both approaches; under the assumed Markov illness-death process, any influence of zoledronic acid on the risk of bone interventions and death is not significantly different from that of pamidronate. The two methods diverge in estimating 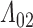 (Figure 3). Since patients near death would presumably be unable to attend clinic visits, early right censoring likely yields underestimates. This may explain why the SPMLE for
(Figure 3). Since patients near death would presumably be unable to attend clinic visits, early right censoring likely yields underestimates. This may explain why the SPMLE for 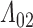 is substantially smaller.
is substantially smaller.
Table 1.
Regression coefficients for zolendronic acid versus pamidronate specific to first SRE, 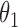 , death without SRE,
, death without SRE, 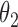 , and death following SRE,
, and death following SRE, 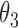
| Early-censored |
LOCF | |||||||
|---|---|---|---|---|---|---|---|---|
| SMLE |
SPMLE |
PFS | PFS | |||||
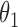 |
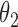 |
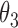 |
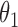 |
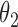 |
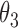 |
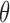 |
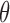 |
|
| Estimate | 0.02 | 0.16 |
 0.01 0.01 |
0.02 | 0.16 |
 0.01 0.01 |
0.03 | 0.06 |
| SE | 0.11 | 0.19 | 0.15 | 0.11 | 0.28 | 0.14 | 0.10 | 0.09 |
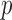 -value -value |
0.89 | 0.40 | 0.94 | 0.86 | 0.58 | 0.97 | 0.78 | 0.51 |
| HR 95% LCL | 0.82 | 0.80 | 0.74 | 0.82 | 0.67 | 0.75 | 0.85 | 0.89 |
| UCL | 1.26 | 1.72 | 1.32 | 1.26 | 2.04 | 1.32 | 1.24 | 1.27 |
Fig. 3.
The SMLE (solid) and early-censored SPMLE (dotted) for the cumulative baseline transition intensity functions between study entry (state 0), first SRE (state 1), and death (state 2).
6.2. Interval-censored progression times: Lesion progression
Hortobagyi and others (1996) showed that pamidronate reduced SREs in a placebo-controlled trial of 380 breast cancer patients with bone metastases. Lesion progression was considered as a secondary outcome. This was assessed using radiographic surveys scheduled at 3- to 6-month intervals over the course of follow-up, rendering the time to lesion progression interval-censored. Surveys were carried out up to 30 months after randomization, but over half of the patients died during this observation period. To account for interval censoring and the occurrence of death, we analyze lesion progression and survival as an illness-death process. Both the progression status and survival time was observed in 28% of the sample. An additional 13% had known progression status but right-censored survival time. In the remaining subjects, right-censoring (11%) or survival (48%) took place long after the last (negative) radiographic survey, resulting in unknown progression status. We defined “long after” as more than 6 weeks, which enabled us to carry forward recent lesion status to the last observation time. Similar results were obtained by carrying forward fewer weeks. This narrow form of LOCF imputation is problematic, but can be avoided when it is possible to randomly assess progression at death.
Table 2 suggests that pamidronate had no influence on mortality, but there is evidence that the bisphosphonate reduces the risk of lesion progression. Based on the SMLE with 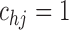 and
and  , an individual treated with pamidronate had 0.68 (95% CI 0.47–0.97) times the rate of progression versus a patient who received placebo. Results obtained under different sieve sizes were similar. The SPMLE from midpoint- and LOCF-imputed data did not detect any significant treatment effect. The difference between the SMLE and SPMLE for the cumulative transition intensities is large (Figure 4) and likely indicative of bias due to imputation, considering the simulation results in Figure F.2 of supplementary material available at Biostatistics online.
, an individual treated with pamidronate had 0.68 (95% CI 0.47–0.97) times the rate of progression versus a patient who received placebo. Results obtained under different sieve sizes were similar. The SPMLE from midpoint- and LOCF-imputed data did not detect any significant treatment effect. The difference between the SMLE and SPMLE for the cumulative transition intensities is large (Figure 4) and likely indicative of bias due to imputation, considering the simulation results in Figure F.2 of supplementary material available at Biostatistics online.
Table 2.
Regression coefficients for pamidronate versus control specific to lesion progression, 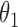 , death without lesion progression,
, death without lesion progression, 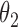 , and death following lesion progression,
, and death following lesion progression, 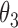
| Imputation-based |
|||||||
|---|---|---|---|---|---|---|---|
| SMLE |
SPMLE |
PFS | |||||
 |
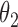 |
 |
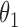 |
 |
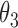 |

|
|
| Estimate |
 0.39 0.39 |
 0.04 0.04 |
 0.05 0.05 |
 0.23 0.23 |
 0.11 0.11 |
 0.03 0.03 |
-0.17 |
| SE | 0.18 | 0.21 | 0.20 | 0.17 | 0.14 | 0.21 | 0.11 |
 -value -value |
0.03 | 0.85 | 0.82 | 0.20 | 0.42 | 0.88 | 0.12 |
| HR 95% LCL | 0.47 | 0.64 | 0.65 | 0.57 | 0.68 | 0.65 | 0.68 |
| UCL | 0.97 | 1.45 | 1.41 | 1.12 | 1.18 | 1.45 | 1.04 |
Fig. 4.
The SMLE (solid) and imputation-based SPMLE (dotted) for the cumulative baseline transition intensity functions between study entry (state 0), lesion progression (state 1), and death (state 2).
7. Discussion
This paper examined dual censoring and its challenges for semiparametric maximum likelihood estimation. Methods for special cases of dual-censored data have been previously developed, but the issue of support finding and the resulting imperative for smoothing has not been granted much attention. Our proposed estimator addresses the problem in a general manner, using a model familiar to practitioners. The result gives a multistate alternative to PFS that enables separate assessment of treatment effect on progression and survival without progression. A primary assumption of the maximum likelihood approach is that the observation scheme renders the underlying transition times coarsened at random. The simulation study shows that this requirement implies that the estimator is robust to survival-dependent censoring of progression provided that the censoring rate for survival is relatively low.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
This work was supported by a Discovery Grant from the Natural Sciences and Engineering Research Council of Canada (RGPIN 155849) and the Canadian Institutes of Health Research (FRN 13887). Richard Cook is a Canada Research Chair in Statistical Methods for Health Research.
Supplementary Material
Acknowledgments
The authors thank Novartis Pharmaceuticals for permission to use data from the bone metastases trials and Jerry Lawless for comments on an earlier version of this manuscript. Conflict of Interest: None declared.
References
- Andersen P. K., Borgan Ø. (1985). Counting process models for life history data: A review. Scandinavian Journal of Statistics 122, 97–158. [Google Scholar]
- Bebchuk J. D., Betensky R. A. (2001). Local likelihood analysis of survival data with censored intermediate events. Journal of the American Statistical Association 96, 449–457. [Google Scholar]
- Boruvka A., Cook R. J. (2015). A Cox-Aalen model for interval-censored data. Scandinavian Journal of Statistics 422, 414–426. [Google Scholar]
- Cox D. R. (1972). Regression models and life-tables. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 342, 187–220. [Google Scholar]
- FDA (2007). Clinical trial endpoints for the approval of cancer drugs and biologics: Guidance for industry. Rockville, MD: Food and Drug Administration.
- Fix E., Neyman J. (1951). A simple stochastic model of recovery, relapse, death and loss of patients. Human Biology 233, 205–241. [PubMed] [Google Scholar]
- Frydman H. (1995a). Nonparametric estimation of a Markov ‘illness-death’ process from interval-censored observations, with application to diabetes survival data. Biometrika 824, 773–789. [Google Scholar]
- Frydman H. (1995b). Semiparametric estimation in a three-state duration-dependent Markov model from interval-censored observations with application to aids data. Biometrics 512, 502–511. [PubMed] [Google Scholar]
- Frydman H., Szarek M. (2009). Nonparametric estimation in a Markov ‘illness-death’ process from interval censored observations with missing intermediate transition status. Biometrics 651, 143–151. [DOI] [PubMed] [Google Scholar]
- Grenander U. (1981) Abstract Inference. New York: Wiley. [Google Scholar]
- Heitjan D. F., Rubin D. B. (1991). Ignorability and coarse data. Annals of Statistics 194, 2244–2253. [Google Scholar]
- Hortobagyi G. N., Theriault R. L., Porter L., Blayney D., Lipton A., Sinoff C., Wheeler H., Simeone J. F., Seaman J., Knight R. D.. and others (1996). Efficacy of pamidronate in reducing skeletal complications in patients with breast cancer and lytic bone metastases. New England Journal of Medicine 33524, 1785–1792. [DOI] [PubMed] [Google Scholar]
- Hu C., Tsodikov A. (2014). Joint modeling approach for semicompeting risks data with missing nonterminal event status. Lifetime Data Analysis 204, 563–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J., Rossini A. J. (1997). Sieve estimation for the proportional-odds failure-time regression model with interval censoring. Journal of the American Statistical Association 92439, 960–967. [Google Scholar]
- Jackson C. (2011). Multi-state models for panel data: The msm package for R. Journal of Statistical Software 388, 1–28. [Google Scholar]
- Joly P., Commenges D., Helmer C., Letenneur L. (2002). A penalized likelihood approach for an illness-death model with interval-censored data: Application to age-specific incidence of dementia. Biostatistics 33, 433–443. [DOI] [PubMed] [Google Scholar]
- Murphy S. A., van der Vaart A. W. (2000). On profile likelihood. Journal of the American Statistical Association 95450, 449–465. [Google Scholar]
- Panageas K. S., Ben-Porat L., Dickler M. N., Chapman P. B., Schrag D. (2007). When you look matters: The effect of assessment schedule on progression-free survival. Journal of the National Cancer Institute 996, 428–432. [DOI] [PubMed] [Google Scholar]
- Rosen L. S., Gordon D., Kaminski M., Howell A., Belch A., Mackey J., Apffelstaedt J., Hussein M., Coleman R. E., Reitsma D. J.. and others (2001). Zoledronic acid versus pamidronate in the treatment of skeletal metastases in patients with breast cancer or osteolytic lesions of multiple myeloma: A phase 3, double-blind, comparative trial. Cancer Journal 75, 377–387. [PubMed] [Google Scholar]
- Turnbull B. W. (1976). The empirical distribution function with arbitrarily grouped, censored and truncated data. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 383, 290–295. [Google Scholar]
- Wong G. Y. C., Yu Q. (1999). Generalized MLE of a joint distribution function with multivariate interval-censored data. Journal of Multivariate Analysis 692, 155–166. [Google Scholar]
- Xu J., Kalbfleisch J. D., Tai B. (2010). Statistical analysis of illness-death processes and semicompeting risks data. Biometrics 663, 716–725. [DOI] [PubMed] [Google Scholar]
- Zeng L., Cook R. J., Wen L., Boruvka A. (2015). Bias in progression-free survival analysis due to intermittent assessment of progression. Statistics in Medicine 3424, 3181–3193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Hua L., Huang J. (2010). A spline-based semiparametric maximum likelihood estimation method for the Cox model with interval-censored data. Scandinavian Journal of Statistics 372, 338–354. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.