Propensity Score: an Alternative Method of Analyzing Treatment Effects

Abstract

Background

In intervention trials, only randomization guarantees equal distributions of all known and unknown patient characteristics between an intervention group and a control group and enables causal statements on treatment effects. However, randomized controlled trials have been criticized for insufficient external validity; non-randomized trials are an alternative here, but come with the danger of intervention and control groups differing with respect to known and/or unknown patient characteristics. Non-randomized trials are generally analyzed with multiple regression models, but the so-called propensity score method is now being increasingly used.

Methods

The authors present, explain, and illustrate the propensity score method, using a study on coronary artery bypass surgery as an illustrative example. This article is based on publications retrieved by a selective literature search and on the authors’ scientific experience.

Results

The propensity score (PS) is defined as the probability that a patient will receive the treatment under investigation. In a first step, the PS is estimated from the available data, e.g. in a logistic regression model. In a second step, the actual treatment effect is estimated with the aid of the PS. Four methods are available for this task: PS matching, inverse probability of treatment weighting (IPTW), stratification by PS, and regression adjustment for the PS.

Conclusion

The propensity score method is a good alternative method for the analysis of non-randomized intervention trials, with epistemological advantages over conventional regression modelling. Nonetheless, the propensity score method can only adjust for known confounding factors that have actually been measured. Equal distributions of unknown confounding factors can be achieved only in randomized controlled trials.

There is consensus in medical research that the primary method for evaluating treatments is the randomized controlled trial. Randomization is the only method that guarantees equal distributions of known and unknown patient characteristics between an intervention group and a control group and enables causal statements on treatment effects. However, randomized controlled trials are in some cases “unnecessary, inappropriate, impossible, or inadequate” (1) and also continue to be criticized for a lack of external validity: patients in randomized controlled trials are usually younger and healthier than the average patient (2, 3).

Non-randomized studies can be an alternative for evaluating treatments. However, they suffer from a lack of internal validity: treatment allocation is not randomized and the intervention and control groups may be systematically different in terms of known and (even worse) unknown patient characteristics. Any differences between groups that arise during a study are therefore not necessarily due to differences in treatment: they may have been caused by the systematic differences between the groups.

A range of statistical procedures have been developed to take account of these differences during analysis. The standard procedures for this are multiple regression models. However, propensity scores are also being used more and more frequently (4). This article introduces propensity scores and describes and explains them in detail, first in general terms and then using an example from coronary bypass surgery. Next, the differences between propensity scores and conventional regression models are stated. The article concludes with a number of essential observations on obtaining knowledge in medical research.

Propensity score

The propensity score (PS) is the probability of a patient receiving the treatment being tested. In a 1:1 randomized trial, this is exactly 0.5. In a non-randomized study, this probability for each individual patient is unknown and depends on patient characteristics. The PS must therefore first be estimated from the available data. A logistic regression model in which the allocated treatment is the dependent variable and the patient characteristics before treatment are used as the independent variable can be used for this. Using the estimated parameters of this PS model, the propensity score can then be calculated for each individual patient. When selecting independent variables for the PS model, care must be taken to use characteristics that predict subsequent treatment success (rather than treatment allocation), as these limit the variance of the treatment effect without giving rise to any additional bias (5). Naturally, the PS model cannot take into account factors that are unknown or were not measured.

The second step is to use the propensity score to estimate the treatment effect of interest. There are four methods for using the propensity score (6):

• PS matching

• Inverse probability of treatment weighting (IPTW) estimation

• Stratification

• Regression adjustment for the PS.

PS matching: In PS matching, each treated patient is allocated one untreated patient (in 1:1 matching), or more than one untreated patient (in 1:n matching), with the same PS or with a PS that differs only slightly, within previously defined limits. The treatment effect is then estimated in the matched population, while accounting for the matching process in the statistical analysis (7).

IPTW estimation: In IPTW estimation, each patient is allocated the reciprocal of the treatment probability associated with his/her actual treatment as a statistical weight: a treated patient receives the weight 1/PS, and an untreated patient the weight 1/(1-PS). There are mathematical reasons for this definition of weights, but it can also be interpreted intuitively (8): A treated patient with a low PS (for the treatment) receives a high weighting because he/she is similar to an untreated patient in terms of his/her characteristics (expressed as his/her low PS), so a valid comparison can be made between the two. For the evaluation of the treatment effect, patients enter the statistical analysis according to their weight.

Stratification: PS stratification is a coarsened form of PS matching. Here, the total dataset is divided into several subsets of equal size (e.g. quintiles) on the basis of the estimated PS. In each subset, treatment effect is estimated using conventional methods, and the treatment effects obtained in this way are then summarized by meta-analytic methods.

Regression adjustment for the PS: In regression adjustment for the PS, a conventional regression model is estimated using the outcome of interest as the dependent variable and treatment effect and PS as independent variables. The effect of the treatment on the outcome is thus adjusted for the PS, and thereby for all patient characteristics included in the PS.

Each of these methods has specific strengths and weaknesses, but PS matching is generally described as the preferred procedure (9, 10). The main advantage of PS matching is the ability to display the recorded characteristics of treated and untreated patients explicitly, similarly to a Table 1 in a randomized controlled trial. This enables assessment of whether the distribution of these characteristics is similar in treated and untreated patients. In addition, the distribution of patient characteristics before PS matching should be shown, in order to make clear the extent to which PS matching has compensated for differences that were originally present.

Inevitably, PS matching excludes patients for whom no matching partner can be found, while all other PS methods use the entire dataset for analysis. This can result in lower case numbers and so less statistical power for PS matching, but it does have the advantage that looking at excluded patients makes clear which patients were overrepresented or underrepresented in the treatment group. As a result, no statements can subsequently be made on these subgroups either.

Finally, the question when considering PS matching versus other PS methods always involves a trade-off between a biased or imprecise estimate of treatment effect (8). PS matching should be used when the groups need to be as similar as possible (thus minimizing bias). However, because case numbers will then be smaller, a greater variance of the estimated treatment effect must be accepted. Table 1 gives an overview of the strengths and weaknesses of the various methods. The Figure provides a schematic representation of the four PS methods versus those for a randomized controlled trial and a conventional regression analysis.

Table 1. Properties of the four different propensity score (PS) methods and of conventional regression analysis in evaluating non-randomized treatment effects.

	Method
	PS method				Conventional regression analysis
	PS matching	IPTW estimation	Stratification	Regression adjustment for the PS
Allows for easy assessment of comparability of treated and untreated patients	+	(+)	(+)	−	−
Allows assessment of balance of characteristics in the data	+	+	(+)	−	−
Uses complete dataset (smaller variance of the treatment effect. greater danger of bias)	−	+	+	+	+
Similar to an RCT (generates comparable groups. ignores outcomes)	+	(+)	(+)	−	−
Robust against outliers (patients with extreme propensity scores)	+	−	+	+	+
Fewer statistical assumptions in the model	+	+	(+)	−	−

RCT. randomized controlled trial; IPTW. inverse probability of treatment weighting; PS. propensity score_

“+” stands for “yes”; “-” stands for “no”; “(+)” stands for “partially given”

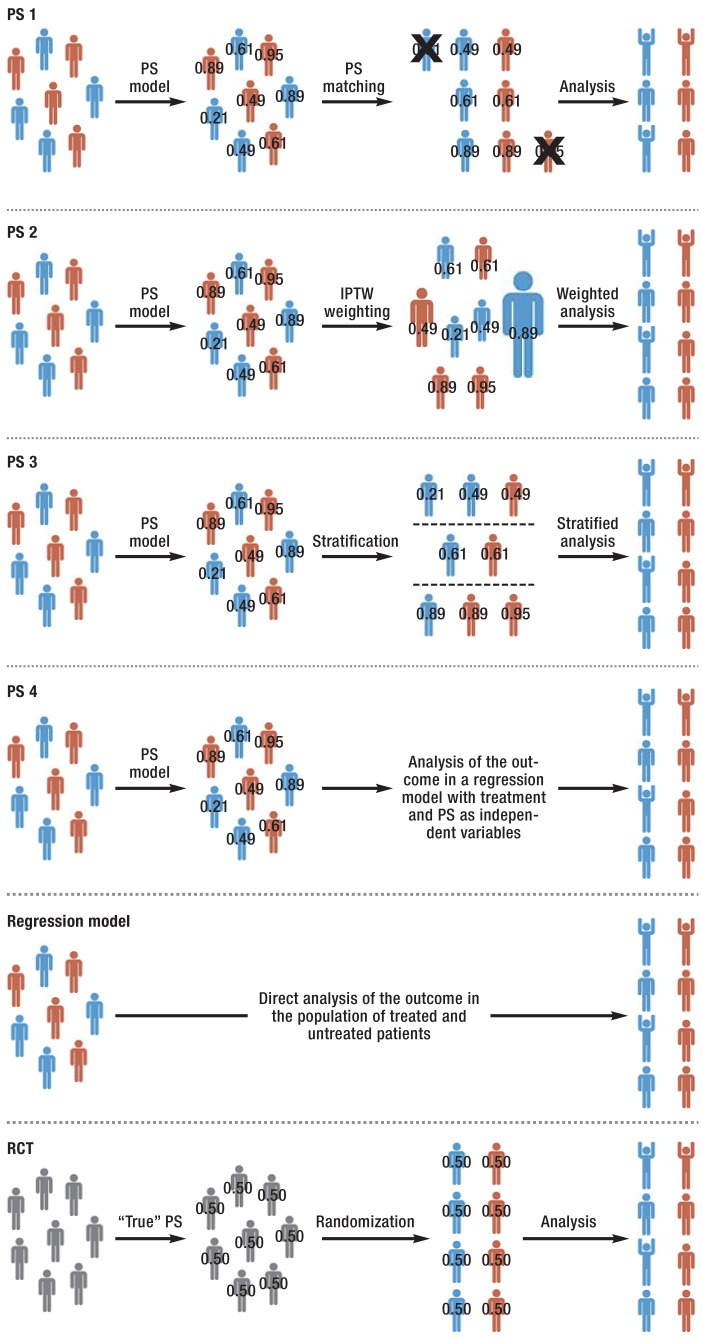
Figure.

PS analysis versus conventional regression analysis and randomized controlled trial

The abbreviations “PS 1” to “PS 4” stand for the four methods of propensity score (PS) analysis:

PS 1 = PS matching

PS 2 = Inverse probability of treatment weighting (IPTW) estimation

PS 3 = Stratification

PS 4 = Regression adjustment for the PS

At the beginning of every PS analysis there is a group of patients who either have been treated with the intervention of interest (red) or with a control intervention (blue). The available patient characteristics are used to estimate a PS model, and each patient’s propensity score is calculated (shown as numerical values on the pictograms in the Figure). Depending on the PS method used, patients are then either matched (PS 1: patients for whom no matching partner has been found are usually excluded; these are labeled with an X), weighted according to their PS (PS 2: patients with a higher IPTW are larger in the Figure), stratified (PS 3: here in tertiles), or included in a regression model with the PS as an independent variable (PS 4). Clinical outcomes are analyzed with respect to the chosen PS method. (For simplicity, the Figure shows cured patients in a cheering pose.)

In contrast, in a conventional regression model a single statistical model is calculated. The clinical outcome is the dependent variable of the model, while treatment and other patient characteristics are independent variables.

The bottom section of the Figure illustrates the similarity between a randomized controlled trial (RCT) and a PS analysis: initially, patients in an RCT have not yet been treated (gray). Their PS (i.e. the probability of undergoing the intervention) is known: it is 0.5. On randomization, each patient is allocated to receive a treatment, so, as with PS, one group of treated patients and one group of control patients is formed. Finally, clinical outcomes are analyzed

The quality of a PS model should only be judged on the basis of how well patient characteristics are balanced between the two treatment groups. Neither goodness-of-fit tests such as the Hosmer–Lemeshow test (11) nor discrimination measures such as the c-statistic (12) are suitable for this. Both these procedures are inappropriate for revealing unknown confounding factors (13). Worse still, a high c-statistic is neither necessary nor sufficient for good adjustment for confounding factors. This can be illustrated by the example of a randomized controlled trial, the design of which by definition achieves a very good balance between confounding factors, but which will have a very small c-statistic (approx. 0.5) (14). Many measures have been proposed specifically to measure balance between patient characteristics (6, 15).

Further methodological development of the propensity score method continues. Unfortunately, it is impossible to examine other important aspects (e.g. dealing with missing values, minimum requirements for sample sizes, software, influence of various matching algorithms) in more detail here.

An example

In the following we report on a published PS analysis on coronary bypass surgery (16) which was performed by the first and last author of this article together. It was based on a dataset from a total of 1282 patients who underwent isolated heart surgery at the Herz- und Diabeteszentrum NRW, Bad Oeynhausen between July 2009 and November 2010. Of these patients, 69.2% (n= 887) underwent conventional coronary artery bypass grafting (cCABG) with extracorporeal circulation (ECC) in cardioplegic cardiac arrest, while 30.8% (n = 395) underwent clampless off-pump coronary artery bypass (clampless OPCAB) without ECC and without clamping of the aorta. The patients’ surgeons had decided which surgery each one would undergo. A logistic regression model was used to estimate each patient’s PS. All patient characteristics used as independent variables in this model were determined a priori and are shown in Table 2. An optimal matching algorithm with a caliper width of 0.2 standard deviations of the linear predictor was used to perform a 1:1 matching (17).

Table 2. Preoperative patient characteristics before and after PS matching^* (modified according to [16]).

	All patients (n = 1282)			PS-matched patients (n = 788)
	Clampless _OPCAB (n = 395)	cCABG _(n = 887)	z-difference	Clampless _OPCAB (n = 394)	cCABG _(n = 394)	z-difference
Age (years)	69.3 ± 9.1	67.5 ± 9.4	3.24	69.3 ± 9.1	69.0 ± 8.9	0.46
Male (%)	78.2	77.9	0.13	78.2	77.9	0.09
BMI (kg/m²)	27.8 ± 4.2	28.3 ± 4.5	−1.83	27.8 ± 4.2	28.0 ± 4.2	−0.60
Left main artery disease (%)	25.3	25.5	−0.06	25.1	24.9	0.08
LVEF (%)	56.7 ± 12.3	55.4 ± 14.1	1.64	56.6 ± 12.2	56.9 ± 13.3	−0.28
Preoperative myocardial infarction (%)	27.1	35.7	−3.14	27.2	26.7	0.16
Hypertension (%)	82.3	84.1	−0.80	82.2	82.2	0
Diabetes mellitus (%)	22.8	31.7	−3.39	22.8	19.8	1.05
COPD (%)	5.8	7.1	−0.88	5.8	6.1	−0.15
Renal insufficiency (%)	0.8	1.2	−0.86	0.8	0.3	1.16
Stroke (%)	1.0	2.4	−2.03	1.0	1.8	−0.95
PAOD (%)	11.9	11.4	0.26	11.7	14.7	−1.27
Previous cardiac surgeries (n)	0.05 ± 0.26	0.08 ± 0.39	−1.56	0.05 ± 0.26	0.06 ± 0.27	−0.80
Urgency (%) Elective Urgent Emergency Last resort	91.9 2.5 5.3 0.3	81.0 9.8 8.7 0.6	−4.82	91.9 2.5 5.3 0.3	92.4 2.3 4.8 0.5	0.25
Preoperative IABP (%)	1.0	1.5	−0.71	1.0	1.0	0

^*Mean ± standard deviation is given for continuous patient characteristics. Relative frequency as a percentage is given for categorical patient characteristics.

BMI. body mass index; cCABG. conventional CABG; CABG. coronary artery bypass grafting; COPD. chronic obstructive pulmonary disease; IABP. intra-aortic balloon pump; clampless OPCAB. clampless off-pump coronary artery bypass grafting; LVEF. left-ventricular ejection fraction; PAOD. peripheral arterial occlusive disease; PS. propensity score

The question of whether there was sufficient balance of preoperative patient characteristics between the two treatment groups following PS matching was also examined. Either standardized differences (9) or z-differences (18) can be used to this end. In a randomized controlled trial, z-differences follow a standard normal distribution (N[0,1]); in a perfectly matched study, they follow normal distribution, still with expected value 0 but with variance ½ (N[0,½]) (19). This means that PS matching usually achieves better balance for known variables than randomization. The well-known 2s rule (20) can be used to assess the size of z-differences: if data are normally distributed (N[m,s²), about 95% of all observed values will lie in the region between m-2s and m+2s. If z-differences have the distribution N(0,½), absolute z-differences of √2 = 1.4142… or higher would therefore be considered as outliers. Such outlying z-differences should thus account for no more than 5% of patient characteristics if PS matching worked well. In the unmatched population we do, indeed, find a number of patient characteristics with substantially larger z-differences, but we no longer find any of those in the PS-matched population.

To evaluate the treatment effect, three clinical outcomes were considered in the PS-matched sample (Table 3):

Table 3. Results for the three clinical outcomes in the PS-matched patient group (n = 788) (modified according to [16]).

Binary outcome
	Clampless OPCAB (n = 394)	cCABG (n = 394)	Odds ratio [95% CI]	p-value
Postoperative death or stroke [n (%)]	6 (1.5)	22 (5.6)	0.27 [0.11; 0.67]	0.005
Continuous outcome
	Clampless OPCAB (n = 394)	cCABG (n = 394)	MD [95% CI]	p-value
Operative time in minutes [mean (SD)]	175 (38)	180 (47)	5 [−1; 11]	0.12
Time-to-event outcome
	Clampless OPCAB (n = 394)	cCABG (n = 394)	Hazard ratio [95% CI]	p-value
Time to death or stroke in follow-up (probability of neither event at one year in %)	94.7	89.8	0.60 [0.35; 1.03]	0.06

cCABG. conventional coronary artery bypass grafting; CI. confidence interval; clampless OPCAB. clampless off-pump coronary artery bypass grafting; MD. mean difference; _PS. propensity score; SD. standard deviation

• One binary outcome (death or stroke in hospital, yes/no)

• One continuous outcome (operative time in minutes)

• One time-to-event outcome (time to death or stroke during follow-up).

A standardized follow-up procedure has been established at the Herz- und Diabeteszentrum NRW, in which all patients who have undergone surgery are sent a questionnaire every year. Serious events reported in the questionnaires are validated at the treating institutions (e.g. local hospital, primary care practice). As described above, statistical analysis must account for the PS matching, for example by conditioning on the matching stratum (7). As can be seen in Table 3, clampless OPCAB is superior to cCABG in terms of all three outcomes. Qualitatively very similar outcomes are obtained using the other three PS methods and the parallel conventional regression model.

PS analyses versus conventional regression models

PS methods have a range of advantages over conventional regression models, the latter still being the standard method for adjusting for patient characteristics in non-randomized studies. One advantage of PS methods is that the procedure for PS analysis is similar to that used for randomized controlled trials (Figure). In particular, a PS model is estimated without using information on the outcomes of interest: only the patient characteristics present at the beginning of the study are included (21). PS model calculation is therefore part of study design, not of analysis.

Another similarity between randomized controlled trials and PS matching is that they are both two-step procedures: in the first step, efforts are made to ensure that the two treatment groups are similar in terms of patient characteristics (using randomization in RCTs and matching in PS studies). Next, in the second step, the actual treatment effect of interest is estimated in the balanced sample. In contrast, a conventional regression model is a one-step procedure: the effect of treatment on the outcome is estimated simultaneously with the other independent variables (22).

One problem with conventional regression models is that they always estimate treatment effects, even if there are such extreme differences between the treated and untreated groups that such an estimate is not sensible. Regression models can be used to make statements concerning what would have happened if treated patients had not been treated. However, this is done using information from untreated individuals who are sometimes very different than the treated patients. Information concerning untreated individuals is, by extrapolation, only estimated, rather than actually observed (8). In other words, if, for example, the oldest treated patient is a 30-year-old male, a conventional regression model will also use information on an untreated 80-year-old woman to evaluate the intervention (23).

Finally, propensity scores are particularly superior to conventional regression models for modelling rare events (24). This is because if the treatments to be compared are used frequently, but the outcome event of interest is rare, there will not usually be enough information available in a conventional regression model to estimate the association between outcome and patient characteristics (including treatment) well. In contrast, the PS model can be estimated well, because there is sufficient information available to measure the association between the allocated treatment (the dependent variable in the PS model) and patient characteristics (the independent variables in the PS model) (25).

Conclusion

Propensity scores cannot replace randomization but are a good alternative for analyzing non-randomized treatment studies and have epistemiological advantages over conventional regression modelling. PS matching, in particular, has a number of advantages. The most important of these is the ability to compare risk factors in the two treatment groups explicitly.

One thing, however, must always be remembered: like conventional regression models, propensity scores can only adjust for patient characteristics that are known and have actually been measured. Only randomized controlled trials can achieve equal distributions of unknown confounding factors too.

The randomized controlled trial remains the study design of choice for evaluating treatments. However, it is important to ensure that this principle does not ossify into dogma in clinical research. For instance, there is increasing evidence that in most cases randomized controlled trials and non-randomized studies yield similar findings (26, 27). Examples in which the findings of randomized controlled trials and non-randomized studies explicitly contradict each other (e.g. the Women’s Health Initiative [WHI] trial of hormone replacement therapy in postmenopausal women [28]) are important for historical, pragmatic, or pedagogical reasons (29) but remain exceptions, and the contradictions can often be explained through closer analysis (30). In addition, the danger caused by unknown patient characteristics in PS analysis is not always as great as feared. These unknown patient characteristics only truly pose a danger when they are not associated with known patient characteristics. If known and unknown patient characteristics are associated with each other, adjusting for known characteristics also adjusts for unknown ones (31).

Like Borah et al. (32), we expect increasing demand from patients, clinicians, and the health-care system for evidence from non-randomized studies in the next few years. There are simply too many questions in health care for all of them to be answered in randomized controlled trials. In addition, society will not want or be able to provide either the means or the time necessary for this.

Key Messages.

• Propensity scores are increasingly being used to analyze non-randomized studies.

• The randomized controlled trial remains the study design of choice for testing treatment efficacy. However, it is important to ensure that this knowledge does not ossify into dogma in clinical research.

• Propensity scores cannot replace randomization but are a good alternative for analyzing non-randomized trials.

• Like conventional regression models, propensity scores can only adjust for patient characteristics that are known and have actually been measured. Only randomized controlled trials can achieve equal distribution of unknown confounding variables too.

• Demand from patients, clinicians, and the health-care system for evidence from non-randomized studies will continue to increase in the next few years.