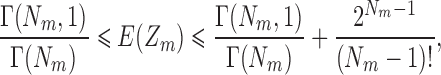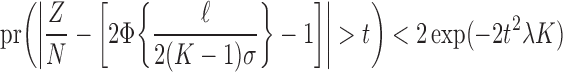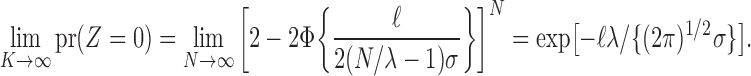SUMMARY
There has been substantial recent interest in record linkage, where one attempts to group the records pertaining to the same entities from one or more large databases that lack unique identifiers. This can be viewed as a type of microclustering, with few observations per cluster and a very large number of clusters. We show that the problem is fundamentally hard from a theoretical perspective and, even in idealized cases, accurate entity resolution is effectively impossible unless the number of entities is small relative to the number of records and/or the separation between records from different entities is extremely large. These results suggest conservatism in interpretation of the results of record linkage, support collection of additional data to more accurately disambiguate the entities, and motivate a focus on coarser inference. For example, results from a simulation study suggest that sometimes one may obtain accurate results for population size estimation even when fine-scale entity resolution is inaccurate.
Keywords: Closed population estimation, Clustering, Entity resolution, Microclustering, Record linkage, Small clusters
1. Introduction
Record linkage refers to the problem of assigning records to unique entities based on observed characteristics. One example, which is the motivating problem for this work, arises in human rights research (Lum et al., 2013; Sadinle & Fienberg, 2013; Sadinle, 2014), where there is interest in recording deaths or other human rights violations attributable to a conflict, such as the ongoing conflict in Syria. In this setting, the data are incomplete records of violations, which usually consist of a name, a date of death, and a place of death. In the turbulent atmosphere accompanying a conflict, often multiple organizations record information on deaths with little communication or standardization of recording practices. Because these data are usually gathered from oral recollections of survivors, measurement errors are common. The result is multiple databases consisting of noisy observations on features of the deceased that in some cases would not uniquely identify the individual even in the absence of noise. There are two distinct inferential goals when applying record linkage in this setting: identification of specific victims and estimation of the total number of casualties in the conflict. These two objectives are shared by other common application areas. For example, in fraud detection, entity resolution itself is the objective, whereas in social science applications, coarser inferences such as correlations between linked variables or estimated regression coefficients (Lahiri & Larsen, 2005) are of primary interest; see D’Orazio et al. (2006) for specific examples.
A variety of methods for record linkage have been proposed (Winkler, 2006; Christen, 2012), though much of the literature has focused on the theoretical framework of Fellegi & Sunter (1969). In this set-up, every pair of records from two databases is compared using a discrepancy function of record features and classified as either a match, a nonmatch, or possibly a match. The goal is to design a decision rule that minimizes the number of possible matches for fixed match and nonmatch error rates. The necessity of performing pairwise comparisons leads to a combinatorial explosion, and a related literature has focused on the construction of blocking rules to limit the number of comparisons performed (Jaro, 1989, 1995; Al-Lawati et al., 2005; Bilenko et al., 2006; Michelson & Knoblock, 2006).
An alternative and more recent approach is to perform entity resolution through clustering, where the goal is to recover the entities from one or more noisy observations on each entity (Steorts et al., 2014, 2015; Steorts, 2015; Zanella et al., 2016). In this framework, entities and clusters are equivalent. Model-based or likelihood-based methods of this sort can be equated with mixture modelling, where the number of mixture components is large and the number of observations per component is very small. Historically, the focus in mixture modelling has been on regularization that penalizes large numbers of clusters, in order to obtain a more parsimonious representation of the data-generating process. Recognizing that this type of regularization is inappropriate for most record linkage problems, Miller et al. (2015) defined the concept of microclustering, where the cluster sizes grow at a sublinear rate with the number of observations. They proposed a Bayes nonparametric approach to clustering in this setting that takes advantage of a novel random partition process that has the microclustering property. This is applied to multinomial mixtures in Zanella et al. (2016).
While microclustering is appropriate for most record linkage problems, there is a lack of literature on performance guarantees and other theoretical properties of entity resolution procedures. Because microclustering methods favour sublinear growth in cluster sizes, the number of parameters of these models can grow at the same rate as the number of observations, so basic asymptotic properties such as central limit theorems, strong laws and consistency will not hold. For example, in the human rights applications that motivated Miller et al. (2015), the number of unique records per entity is thought to be very small, generally less than 10, while the number of unique entities is thought to be in the thousands or hundreds of thousands. As such, it is critical to consider the finite-sample performance of microclustering in cases where the number of records per cluster is a tiny fraction of the sample size, and to obtain theoretical upper bounds on how accurate cluster-based entity resolution can possibly be when the microclustering condition holds.
Working with simple mixture models where some of the parameters are known, we characterize the exact distributions of quantities related to entity resolution. Achievable performance is shown to be a function of entity separation and the noise level. Using these results, we provide minimal conditions for accuracy in entity resolution to be bounded away from zero asymptotically as the number of records grows. We also provide an information-theoretic bound on the best possible performance in the case where some of the entities cannot be uniquely identified from noiseless observations of the available features. These results are supported by several simulation studies. Our problem is related to the extensive literature on mixture identifiability (Teicher, 1961, 1963; Yakowitz & Spragins, 1968; Holzmann et al., 2006) and estimation of the number of components (Day, 1969; Richardson & Green, 1997; Lo et al., 2001; Tibshirani et al., 2001), as well as the voluminous literature on clustering (see Hastie et al., 2009, Ch. 3 and works cited therein), with the important distinction that we focus on microclusters, mixtures with many components and few observations per component, and we are interested primarily in entity resolution, not in estimation of the parameters of the mixture.
Our results initially present a very dim view of entity resolution by microclustering; indeed, it appears that the full problem is unsolvable without further information except under very strong conditions. However, in many cases interest is focused on certain summary statistics of the linked records, which may be relatively insensitive to errors in entity resolution. Motivated by the human rights application mentioned above, we consider the case where the ultimate goal of entity resolution is to recover the total number of entities in the population. This corresponds to the total number of casualties in the conflict, the coarser inferential goal mentioned previously. A variety of methods exist for this problem, which is referred to as closed population estimation, and generally use as data a relatively small contingency table that characterizes the number of unique records appearing in every possible combination of the databases (Wolter, 1986; Zaslavsky & Wolfgang, 1993; Griffin, 2014). In a simulation study, we show that relatively accurate estimation of the total population size is possible even when entity resolution is inaccurate. The success of population estimation in this admittedly limited simulation study suggests further investigation of whether low-dimensional summaries are in general recoverable from linked databases even when the error rate in entity resolution is high.
2. Main results
2.1. Preliminaries
We work primarily with Gaussian mixtures of the form
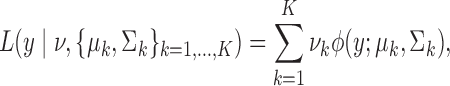 |
(1) |
where  is an element of the
is an element of the 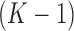 -dimensional probability simplex,
-dimensional probability simplex, 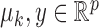 ,
, 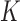 is a positive integer,
is a positive integer,  is a
is a  positive-definite matrix, and
positive-definite matrix, and 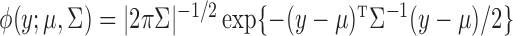 is the Gaussian density function. In (1),
is the Gaussian density function. In (1), 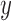 are observed entity-specific features that we will use to perform record linkage. In our motivating application, typical features are name, time/date of death, and place of death. It is natural to treat time and place as continuous variables, and it is common to embed name into an abstract continuous space by way of a metric on text, such as Jaccard similarity or Levenshtein distance. As such, (1) provides a reasonable default mixture in our setting.
are observed entity-specific features that we will use to perform record linkage. In our motivating application, typical features are name, time/date of death, and place of death. It is natural to treat time and place as continuous variables, and it is common to embed name into an abstract continuous space by way of a metric on text, such as Jaccard similarity or Levenshtein distance. As such, (1) provides a reasonable default mixture in our setting.
The mixture (1) differs from the mixture considered in Zanella et al. (2016), which is similar to that in Dunson & Xing (2009), a nonparametric Bayesian model for multivariate categorical data. Our rationale for using Gaussian mixtures comes from the results of Johndrow et al. (2017) and Fienberg et al. (2009), which make clear that the maximum number of unique mixture components in the model of Dunson & Xing (2009) is strictly less than 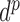 , where
, where 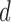 is the number of distinct levels of the categorical variables. Thus, it is impossible to resolve more than
is the number of distinct levels of the categorical variables. Thus, it is impossible to resolve more than  entities on the basis of
entities on the basis of 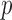 categorical measurements, motivating our focus on the case of continuous features, which does not suffer from this fundamental limitation.
categorical measurements, motivating our focus on the case of continuous features, which does not suffer from this fundamental limitation.
In providing an upper bound on performance in entity resolution, we focus on a case that favours good performance; in particular, we consider the task of correctly determining which mixture component generated each 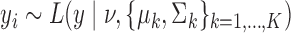 (
( ), assuming that (1) is known. We focus on the estimator
), assuming that (1) is known. We focus on the estimator
 |
(2) |
We will assign 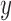 to the mixture component that maximizes the likelihood; this is the Bayes rule classifier with equal prior weight on each component. This estimator allows many-to-one matches. In what follows, we will study a series of cases where the set of unknown parameters in the model is gradually expanded, which provides a set of theoretically tractable finite-sample bounds on the best-case performance of clustering-based approaches to entity resolution. Although we focus on Gaussian mixtures for simplicity, many of the results apply equally to mixtures of any kernels that are functions of a metric on
to the mixture component that maximizes the likelihood; this is the Bayes rule classifier with equal prior weight on each component. This estimator allows many-to-one matches. In what follows, we will study a series of cases where the set of unknown parameters in the model is gradually expanded, which provides a set of theoretically tractable finite-sample bounds on the best-case performance of clustering-based approaches to entity resolution. Although we focus on Gaussian mixtures for simplicity, many of the results apply equally to mixtures of any kernels that are functions of a metric on 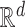 , and we point out extensions where appropriate.
, and we point out extensions where appropriate.
2.2. An information-theoretic bound
We first consider multiple true entities with identical values of the entity-specific parameters  . Suppose that we observe two complete enumerations of a population, each containing a nearly mutually exclusive set of covariates about each individual. We assume that these two lists contain only one field in common. For example, suppose one list contains each individual’s name and date of birth and the other contains each individual’s name, location of death, and date of death. The goal is to match each individual on the first list to the correct individual on the second list to produce a complete dataset consisting of name, date of birth, date of death, and location of death for each individual in the population.
. Suppose that we observe two complete enumerations of a population, each containing a nearly mutually exclusive set of covariates about each individual. We assume that these two lists contain only one field in common. For example, suppose one list contains each individual’s name and date of birth and the other contains each individual’s name, location of death, and date of death. The goal is to match each individual on the first list to the correct individual on the second list to produce a complete dataset consisting of name, date of birth, date of death, and location of death for each individual in the population.
In locations with low entropy in the name distribution, as is the case in Syria, this list is likely to be composed of many individuals sharing exactly the same first and last name. In this section, we illustrate the limitations in performance of record linkage when multiple entities have identical values of  and the data are observed without noise. In the context of (1), this corresponds to the limit as the maximum eigenvalue of
and the data are observed without noise. In the context of (1), this corresponds to the limit as the maximum eigenvalue of 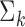 approaches zero, resulting in a mixture of delta measures. For simplicity, we focus on the case where the features are names, with an obvious parallel to the case where features are vectors in
approaches zero, resulting in a mixture of delta measures. For simplicity, we focus on the case where the features are names, with an obvious parallel to the case where features are vectors in 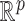 and multiple entities have identical true values of the feature vector.
and multiple entities have identical true values of the feature vector.
Suppose that we observe a list of names  for
for 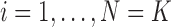 , where
, where 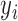 takes
takes 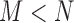 unique values. Let
unique values. Let 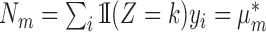 for
for 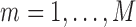 , where
, where  is the set of unique values of
is the set of unique values of 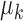 ;
; 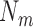 is the number of times the name
is the number of times the name  appears in the database. Let
appears in the database. Let 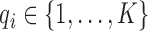 denote an unobserved identifier of the component that generated
denote an unobserved identifier of the component that generated 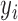 . For example, the full data could look like Table 1 and we only observe the name column.
. For example, the full data could look like Table 1 and we only observe the name column.
Table 1.
Example of data for name problem
Name (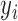 ) ) |
Identifier (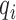 ) ) |
|---|---|
| John Smith | 1 |
| John Smith | 2 |
| Jane Wang | 8 |
| Jane Wang | 9 |
| Anna Rodriguez | 11 |
| Anna Rodriguez | 14 |
The goal is to assign the correct identifier to each record or, equivalently, to determine from which component each record was generated. This is related to the problem of relinking two paired variables when the ordering of the variables has been independently permuted, as outlined in DeGroot & Goel (1980) and references therein. We consider the case where it is known that there is exactly one record corresponding to each person, and use a random allocation procedure. When multiple true entities have identical values of 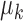 , the estimator in (2) does not give a unique solution, since
, the estimator in (2) does not give a unique solution, since  if
if 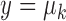 and
and 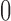 otherwise, so the likelihood has identical values for all
otherwise, so the likelihood has identical values for all 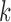 such that
such that  .
.
Let 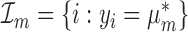 be the set of all records with name
be the set of all records with name 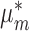 , and let
, and let  be the set of all components with mean
be the set of all components with mean  ; this is the set of values
; this is the set of values 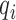 can potentially take for each
can potentially take for each  . The procedure used is to randomly assign records
. The procedure used is to randomly assign records 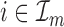 to a permutation of the elements of
to a permutation of the elements of  such that each record is assigned to exactly one of the mixture components that could have generated it. After making this assignment, the true value of
such that each record is assigned to exactly one of the mixture components that could have generated it. After making this assignment, the true value of  is revealed and the number of correct assignments enumerated. Clearly, there are
is revealed and the number of correct assignments enumerated. Clearly, there are 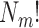 ways to assign each individual with the same name to an element of
ways to assign each individual with the same name to an element of  , where
, where 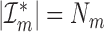 , and only one of these assignments will be exactly right. Let
, and only one of these assignments will be exactly right. Let 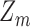 be the number of correct assignments with name
be the number of correct assignments with name 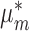 , and let
, and let 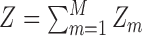 . Then the probability of assigning every record
. Then the probability of assigning every record 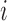 to its true
to its true 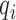 is
is  . On the log scale this turns out to be very intuitive since, by Stirling’s approximation,
. On the log scale this turns out to be very intuitive since, by Stirling’s approximation,
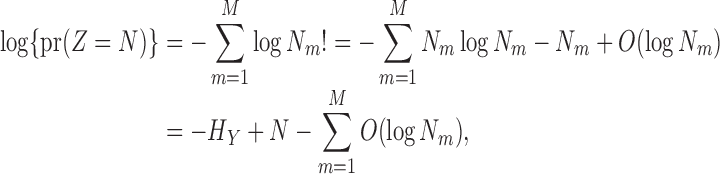 |
where 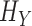 is the entropy of the name distribution. Moreover, the distribution of
is the entropy of the name distribution. Moreover, the distribution of 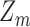 can be described by the probability mass function
can be described by the probability mass function
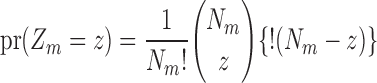 |
(3) |
where, for an integer 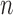 ,
,  is the number of derangements of the integers
is the number of derangements of the integers 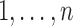 , i.e., the number of ways to rearrange the sequence
, i.e., the number of ways to rearrange the sequence  such that none of the elements of the sequence are in their original locations. We have the relation
such that none of the elements of the sequence are in their original locations. We have the relation
 |
(4) |
for 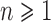 , where
, where  is the floor function; also,
is the floor function; also, 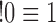 .
.
We now consider the expectation of 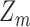 . It is straightforward to compute upper and lower bounds; proofs are deferred to the Appendix.
. It is straightforward to compute upper and lower bounds; proofs are deferred to the Appendix.
Remark 1.
The expectation of
satisfies
where
is the incomplete gamma function.
The difference between the upper and lower bounds is less than 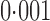 when
when  , so for large
, so for large 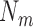 the lower bound is very accurate. Figure 1 shows the upper and lower bounds as well as the exact value of
the lower bound is very accurate. Figure 1 shows the upper and lower bounds as well as the exact value of 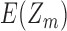 , which can quickly be computed exactly for
, which can quickly be computed exactly for 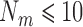 and is identically 1 in all cases. From this it is clear that taking
and is identically 1 in all cases. From this it is clear that taking 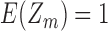 for all
for all  is at least a very accurate approximation, and is probably the exact value of the expectation. Assuming it is exact, we have
is at least a very accurate approximation, and is probably the exact value of the expectation. Assuming it is exact, we have 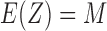 , and the expected proportion of correct assignments is
, and the expected proportion of correct assignments is 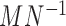 .
.
Fig. 1.

Upper and lower bounds on  (lines) and the exact value of
(lines) and the exact value of 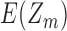 (points) for
(points) for 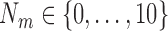 .
.
We give a concentration inequality for the proportion of correct assignments, 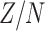 . We have
. We have 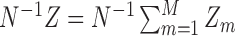 . As the
. As the 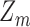 are independent and
are independent and  , by Hoeffding’s inequality we have
, by Hoeffding’s inequality we have
 |
We obtained data from the U.S. Census Bureau on the frequency of all surnames and given names in the U.S. population. Assuming independent selection of first and last names in the overall population, we estimate 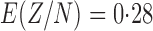 for entity resolution of the U.S. population on the basis of only first name and last name. Dependence between first and last names will tend to decrease this expectation. We have
for entity resolution of the U.S. population on the basis of only first name and last name. Dependence between first and last names will tend to decrease this expectation. We have  , so
, so
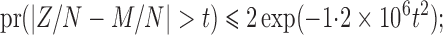 |
for example, the probability that  is less than
is less than 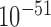 . Hence, in the United States names example, the distribution is highly concentrated around its expectation and there is an extremely low probability of getting even one third or more of the assignments correct.
. Hence, in the United States names example, the distribution is highly concentrated around its expectation and there is an extremely low probability of getting even one third or more of the assignments correct.
For additional context, we also computed 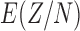 for two states. For the least populated state, Wyoming, we estimate
for two states. For the least populated state, Wyoming, we estimate 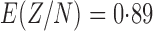 , while for the most populated state, California, we estimate
, while for the most populated state, California, we estimate  . We also compute
. We also compute 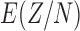 for the entire United States, assuming that in addition to first and last names we also observe the last four digits of each person’s social security number. We assume that these digits are assigned uniformly at random from integers between 0000 and 9999 independently of first and last name. Adding this extra information to first name and last name for the U.S. population gives
for the entire United States, assuming that in addition to first and last names we also observe the last four digits of each person’s social security number. We assume that these digits are assigned uniformly at random from integers between 0000 and 9999 independently of first and last name. Adding this extra information to first name and last name for the U.S. population gives 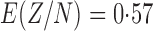 . Thus, in each case a substantial proportion of errors is likely. These examples illustrate the fact that in many entity resolution problems, the best possible performance is substantially less than perfect accuracy due to redundancy in the true values of the entity features. This provides an upper bound on the performance achievable when features are observed with noise.
. Thus, in each case a substantial proportion of errors is likely. These examples illustrate the fact that in many entity resolution problems, the best possible performance is substantially less than perfect accuracy due to redundancy in the true values of the entity features. This provides an upper bound on the performance achievable when features are observed with noise.
2.3. Analysis of noisy observations when mixture parameters are known
Having established the limitations resulting from redundancy of the true entity features, we now analyse the effect of noise in the setting where all true entity features are distinct. We begin with a highly simplified case. Suppose we observe a data sequence 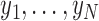 and that each observation originates from the mixture in (1) with
and that each observation originates from the mixture in (1) with 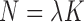 for
for 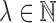 ,
, 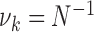 ,
, 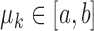 , and
, and 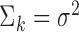 for all
for all  . Although the results are general, we have in mind situations in which
. Although the results are general, we have in mind situations in which  is some small positive integer and most entities have on the order of
is some small positive integer and most entities have on the order of 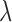 records in the data, the typical situation in our motivating human rights applications.
records in the data, the typical situation in our motivating human rights applications.
Assume that the parameters 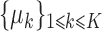 ,
, 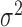 and
and 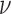 are known. On observing
are known. On observing 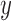 , we use estimator (2) of the mixture component it originated from. Let
, we use estimator (2) of the mixture component it originated from. Let  be the true value of
be the true value of  . Then, letting
. Then, letting 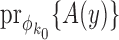 denote the probability of event
denote the probability of event 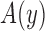 if
if  is drawn from component
is drawn from component  of (1),
of (1),
 |
where 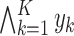 denotes the minimum of the collection
denotes the minimum of the collection 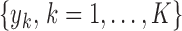 . We make the simplifying assumption that the
. We make the simplifying assumption that the 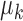 are equally spaced, so that
are equally spaced, so that 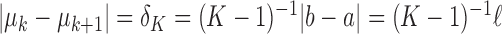 for all
for all 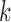 . Then, letting
. Then, letting 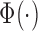 denote the standard normal distribution function,
denote the standard normal distribution function,
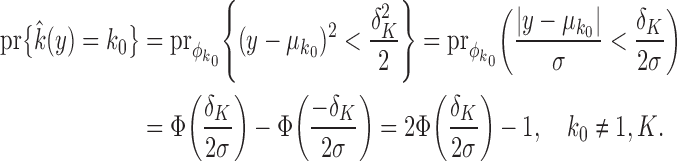 |
(5) |
For 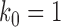 or
or 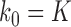 , the expression is
, the expression is 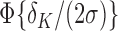 . When
. When 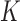 is large, the effect of using (5) for all
is large, the effect of using (5) for all 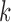 is negligible, so to simplify exposition we will do so. A condition like that in (5) would hold for any mixtures where the component densities are a function of a metric on
is negligible, so to simplify exposition we will do so. A condition like that in (5) would hold for any mixtures where the component densities are a function of a metric on  , with
, with  replaced by a different distribution function. This includes many of the kernel functions commonly used in machine learning, as well as other common densities such as the
replaced by a different distribution function. This includes many of the kernel functions commonly used in machine learning, as well as other common densities such as the 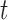 density.
density.
With  being the number of correct classifications, we have the following result for the Gaussian mixture.
being the number of correct classifications, we have the following result for the Gaussian mixture.
Remark 2
(Infeasibility result for microclustering). Suppose
are equally spaced and restricted to a compact set, so that
. Then
and
Therefore, in large populations, the proportion of correct assignments,  , is highly concentrated around its expectation given by (5), which will be very near zero when
, is highly concentrated around its expectation given by (5), which will be very near zero when 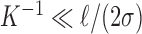 . Evidently,
. Evidently,  almost surely and the probability of zero correct assignments is bounded away from zero unless
almost surely and the probability of zero correct assignments is bounded away from zero unless  , which requires
, which requires 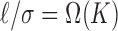 , where
, where 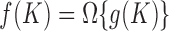 means that there exist constants
means that there exist constants 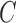 and
and 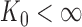 such that
such that  for all
for all 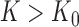 . In other words, either the width of the set containing the means must grow at a rate of at least
. In other words, either the width of the set containing the means must grow at a rate of at least 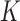 , or the observation noise must go to zero at least as fast as
, or the observation noise must go to zero at least as fast as 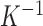 . We refer to the condition
. We refer to the condition 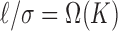 as infinite separation, as it effectively requires that the entities be infinitely far apart relative to the noise level in the limit. Practically, this means that for entity resolution via microclustering, measurements on entity-specific features must get more precise as the number of entities increases. Given that this regime applies when all the parameters of the mixture are known, Remark 2 suggests that the full problem of entity resolution by clustering is practically impossible in most cases. Estimates of these parameters would have standard error of the order
as infinite separation, as it effectively requires that the entities be infinitely far apart relative to the noise level in the limit. Practically, this means that for entity resolution via microclustering, measurements on entity-specific features must get more precise as the number of entities increases. Given that this regime applies when all the parameters of the mixture are known, Remark 2 suggests that the full problem of entity resolution by clustering is practically impossible in most cases. Estimates of these parameters would have standard error of the order 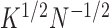 . Therefore, when
. Therefore, when 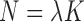 , which is the case in most record linkage applications, standard errors are constant in the number of observations, and uncertainty in parameters remains even asymptotically, so the result in Remark 2 understates the futility of the problem.
, which is the case in most record linkage applications, standard errors are constant in the number of observations, and uncertainty in parameters remains even asymptotically, so the result in Remark 2 understates the futility of the problem.
2.4. The effect of dimension
We now consider the case where the dimension  grows with
grows with  , and show that when the parameters of the mixture are known, infinite separation can be achieved when the means reside on a compact set and observation noise does not decay to zero as
, and show that when the parameters of the mixture are known, infinite separation can be achieved when the means reside on a compact set and observation noise does not decay to zero as 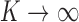 . Consider the mixture in (1) with
. Consider the mixture in (1) with 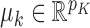 and
and 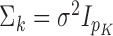 for all
for all 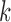 . Assume that the means are restricted to the Euclidean unit ball
. Assume that the means are restricted to the Euclidean unit ball  in
in 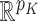 and they are arranged so that
and they are arranged so that 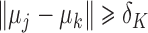 for every
for every 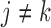 , where
, where  is the Euclidean norm. The maximum number of means that can fit inside
is the Euclidean norm. The maximum number of means that can fit inside 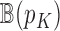 while satisfying this separation condition is the
while satisfying this separation condition is the 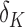 -packing number
-packing number 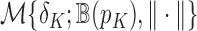 , which is related to the
, which is related to the  -covering number
-covering number 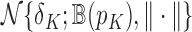 by the inequality
by the inequality
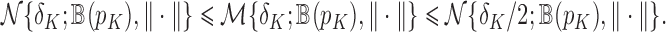 |
(6) |
The covering number of the unit ball satisfies
 |
(7) |
If we have 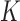 points inside
points inside 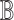 that are
that are 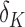 -separated, then at most
-separated, then at most 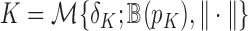 , so combining (6) and (7) gives
, so combining (6) and (7) gives
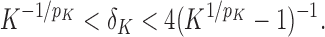 |
(8) |
The maximum likelihood estimator (2) satisfies
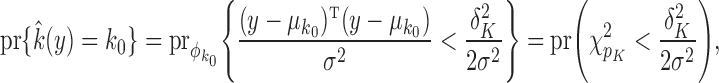 |
where 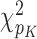 is chi-squared with
is chi-squared with  degrees of freedom. Appealing to the central limit theorem,
degrees of freedom. Appealing to the central limit theorem,
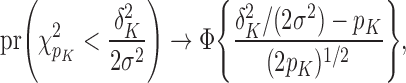 |
so 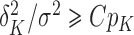 for all large
for all large 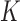 with
with 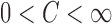 is a necessary and sufficient condition for
is a necessary and sufficient condition for 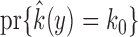 to converge to a nonzero constant as
to converge to a nonzero constant as 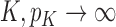 . Combining this with (8), we obtain that
. Combining this with (8), we obtain that  implies
implies 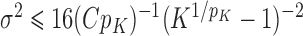 . Thus, it is even possible to have
. Thus, it is even possible to have  bounded away from zero if
bounded away from zero if 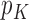 grows fast enough with
grows fast enough with 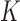 . For example, if
. For example, if 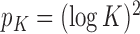 , then
, then  . Of course, having
. Of course, having 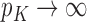 in the case where the mixture parameters are unknown means that for each mixture component we must estimate a growing number of parameters, and
in the case where the mixture parameters are unknown means that for each mixture component we must estimate a growing number of parameters, and 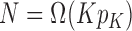 is a necessary condition for consistency. Therefore
is a necessary condition for consistency. Therefore  will not be sufficient, and we must have the number of records per entity growing faster than
will not be sufficient, and we must have the number of records per entity growing faster than 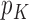 , which cannot occur in the microclustering setting. The practical ramification is that, if we ignore the need to estimate the parameters of each component, one way to combat the failure of entity resolution as the number of entities increases is to attempt to increase the number of variables collected per record on each entity.
, which cannot occur in the microclustering setting. The practical ramification is that, if we ignore the need to estimate the parameters of each component, one way to combat the failure of entity resolution as the number of entities increases is to attempt to increase the number of variables collected per record on each entity.
2.5. The case where means are unknown: Bayesian mixtures
We now consider the case where the mixture component means are unknown. Suppose that 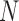 observations are generated from the mixture given in (1) with
observations are generated from the mixture given in (1) with 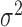 and
and 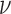 known. Consider a Bayesian analysis with independent priors
known. Consider a Bayesian analysis with independent priors 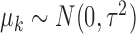 . The calculations leading to the following results can be found in the Appendix and Supplementary Material.
. The calculations leading to the following results can be found in the Appendix and Supplementary Material.
Let 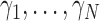 for
for 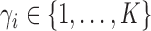 be a configuration of the
be a configuration of the 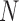 observations into
observations into 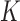 classes, and let
classes, and let  . Let
. Let  be the set of all possible configurations, with
be the set of all possible configurations, with 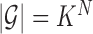 . The marginal likelihood of the configuration, integrating out the means, is
. The marginal likelihood of the configuration, integrating out the means, is
 |
(9) |
where 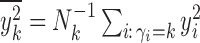 and
and 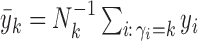 ; so the posterior probability of the configuration is
; so the posterior probability of the configuration is
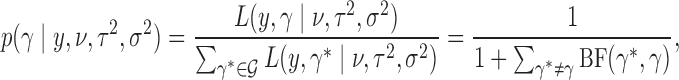 |
where the Bayes factor is 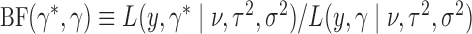 . Consider the case where
. Consider the case where  consists of all singleton clusters while
consists of all singleton clusters while 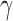 consists of
consists of  singleton clusters, one empty cluster, and a single cluster with two observations. There are
singleton clusters, one empty cluster, and a single cluster with two observations. There are 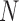 such elements of
such elements of 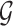 . The Bayes factor is
. The Bayes factor is
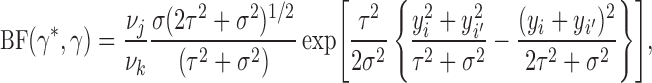 |
where 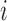 and
and 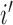 are the indices of the two observations that are allocated to the same cluster in
are the indices of the two observations that are allocated to the same cluster in 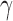 and different clusters in
and different clusters in 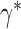 ,
, 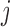 is the cluster that contains
is the cluster that contains 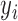 in configuration
in configuration 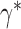 and is empty in configuration
and is empty in configuration 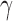 , and
, and  is the index of the cluster that contains observation
is the index of the cluster that contains observation 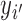 in configuration
in configuration 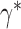 and contains both
and contains both 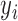 and
and 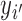 in configuration
in configuration 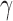 . Suppose that the truth is configuration
. Suppose that the truth is configuration 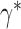 , with
, with 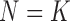 distinct entities. Integrating the Bayes factor over the data distribution, we obtain
distinct entities. Integrating the Bayes factor over the data distribution, we obtain
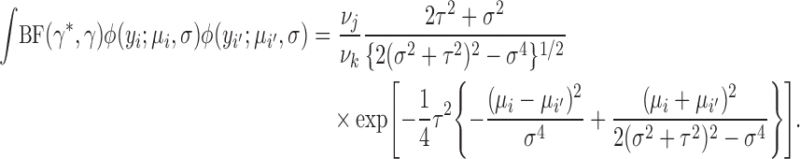 |
(10) |
From this it is clear that when  , as
, as  , the expectation of the Bayes factor converges to a constant, and a necessary condition for
, the expectation of the Bayes factor converges to a constant, and a necessary condition for 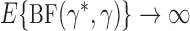 is
is  . Therefore, when the
. Therefore, when the 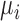 are confined to a compact set, Bayes factors for infinitely many incorrect configurations will converge to constants in expectation as
are confined to a compact set, Bayes factors for infinitely many incorrect configurations will converge to constants in expectation as 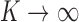 , since
, since 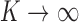 implies
implies 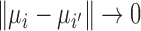 for infinitely many pairs
for infinitely many pairs 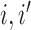 . It follows that the posterior will not even be consistent for entity resolution, and will fail to concentrate on any finite set of configurations asymptotically.
. It follows that the posterior will not even be consistent for entity resolution, and will fail to concentrate on any finite set of configurations asymptotically.
3. Empirical analysis of entity resolution by microclustering
We show through simulation studies that the infeasibility results are borne out empirically. We first consider the case where there are 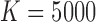 entities and we observe data
entities and we observe data 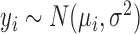 for
for 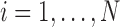 with
with  . The common variance parameter
. The common variance parameter 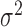 is
is 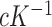 , and
, and  is varied between
is varied between 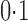 and
and 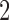 across the simulations. In every case
across the simulations. In every case 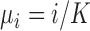 , so the means are equally spaced on the unit interval. Entity resolution is performed using the estimator in (2).
, so the means are equally spaced on the unit interval. Entity resolution is performed using the estimator in (2).
The results are shown in Fig. 2(a). As expected, the proportion correctly assigned decreases with 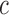 . Entity resolution is nearly perfect for
. Entity resolution is nearly perfect for 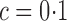 , but begins to decline noticeably around
, but begins to decline noticeably around 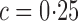 , which is intuitive since at that value, half the distance between the true means, the threshold at which misassignment occurs using the maximum likelihood estimate is twice the standard deviation. For
, which is intuitive since at that value, half the distance between the true means, the threshold at which misassignment occurs using the maximum likelihood estimate is twice the standard deviation. For  , approximately half of the observations are correctly assigned. When
, approximately half of the observations are correctly assigned. When 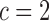 , the proportion correctly assigned is about
, the proportion correctly assigned is about 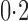 .
.
Fig. 2.
Performance of Bayes mixtures in entity resolution: (a) proportion of entities correctly assigned using maximum likelihood assignment when parameters are known; (b) boxplot of Markov chain Monte Carlo samples of 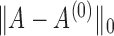 for Bayes mixtures with unknown means versus
for Bayes mixtures with unknown means versus  .
.
We perform a second simulation in which we conduct entity resolution without knowledge of the true means. We simulated 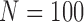 observations from
observations from
 |
with 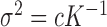 , where
, where  varied between
varied between 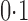 and
and  across the simulations. We then performed posterior computation by collapsed Gibbs sampling for the Bayesian mixture model with known component weights and component variances described in § 2.5. We used identical priors
across the simulations. We then performed posterior computation by collapsed Gibbs sampling for the Bayesian mixture model with known component weights and component variances described in § 2.5. We used identical priors 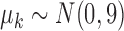 on the means for each component. For each Markov chain Monte Carlo sample, we computed an adjacency matrix
on the means for each component. For each Markov chain Monte Carlo sample, we computed an adjacency matrix 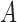 for the 100 observations, where
for the 100 observations, where  if observations
if observations  and
and 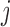 are assigned to the same component and
are assigned to the same component and  otherwise. We then computed the
otherwise. We then computed the 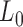 distance between the sampled
distance between the sampled 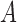 and the true adjacency matrix
and the true adjacency matrix 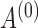 , defined as
, defined as 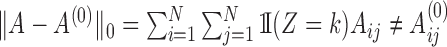 , for each Markov chain Monte Carlo sample. Perfect entity resolution corresponds to
, for each Markov chain Monte Carlo sample. Perfect entity resolution corresponds to  , while the value of
, while the value of 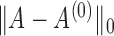 can conceivably be as large as
can conceivably be as large as 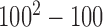 , which occurs when
, which occurs when 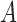 is a matrix of ones and
is a matrix of ones and 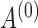 is the identity. Figure 2(b) shows boxplots of the approximate posterior distribution of
is the identity. Figure 2(b) shows boxplots of the approximate posterior distribution of 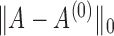 as a function of
as a function of 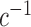 . As expected, performance in entity resolution degrades as
. As expected, performance in entity resolution degrades as 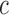 increases, with the error rate increasing sharply near the value
increases, with the error rate increasing sharply near the value 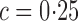 .
.
4. Population size estimation when entity resolution is poor
4.1. Overview of population size estimation
Estimation of the number of unique entities when some entities may not appear in any database is referred to as population size estimation and is the ultimate objective of entity resolution in our motivating human rights setting. In this section we give a positive empirical result for this inference problem. We construct a simulation in which it is possible to accurately estimate the number of unique entities from a clustering assignment even when the proportion of records correctly assigned to clusters is small.
We first describe the population size estimation problem and its relationship to entity resolution. Our observed data consist of noisy observations 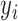 of entity characteristics and an integer
of entity characteristics and an integer 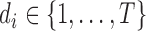 such that
such that  indicates that record
indicates that record 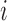 appeared in database
appeared in database 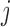 , and we aim to estimate
, and we aim to estimate 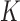 , the number of unique entities. The typical approach uses a two-stage procedure. First, we perform entity resolution on the observed data. The linked records are summarized as a
, the number of unique entities. The typical approach uses a two-stage procedure. First, we perform entity resolution on the observed data. The linked records are summarized as a 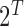 contingency table that records the estimated number of individuals appearing in every possible combination of the
contingency table that records the estimated number of individuals appearing in every possible combination of the 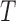 databases. Specifically, for every
databases. Specifically, for every  , let
, let 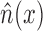 be the estimated count of the number of entities that appeared in databases
be the estimated count of the number of entities that appeared in databases 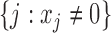 . For example, the entry
. For example, the entry  in the case of three databases gives the estimated count of the number of entities that appear in the second and third databases but not the first. Performing entity resolution gives us
in the case of three databases gives the estimated count of the number of entities that appear in the second and third databases but not the first. Performing entity resolution gives us  for every
for every 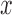 except
except 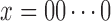 . In the following, we use
. In the following, we use 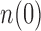 as shorthand for
as shorthand for 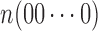 . One then uses a second-stage population estimation procedure to estimate
. One then uses a second-stage population estimation procedure to estimate 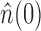 , resulting in
, resulting in 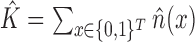 .
.
4.2. Simulation set-up
To simulate observations  , we use the following procedure. We first generate a collection of
, we use the following procedure. We first generate a collection of 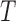 database-specific observation probabilities
database-specific observation probabilities 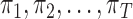 from
from 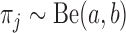 . These are population-level probabilities that any given entity will appear in database
. These are population-level probabilities that any given entity will appear in database 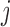 . We then use Algorithm 1 to generate data.
. We then use Algorithm 1 to generate data.
Fig. A1.

Generation of synthetic databases.
This results in 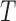 synthetic databases which do not contain entries for any of the entities for which the sampled value of
synthetic databases which do not contain entries for any of the entities for which the sampled value of 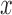 in Algorithm 1 was the zero vector. These are the unobserved entities that are estimated in the second stage of the procedure, and their true count is
in Algorithm 1 was the zero vector. These are the unobserved entities that are estimated in the second stage of the procedure, and their true count is  . In general, we choose
. In general, we choose 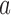 and
and 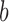 in the beta distribution to make
in the beta distribution to make 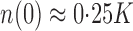 . This is consistent with real population estimation problems encountered in the human rights field and makes the problem relatively challenging compared to, say, the choice
. This is consistent with real population estimation problems encountered in the human rights field and makes the problem relatively challenging compared to, say, the choice 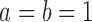 , which results in much smaller proportions of unobserved entities.
, which results in much smaller proportions of unobserved entities.
4.3. Inference procedure
We perform inference using the following two-stage procedure. For the observed records 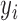
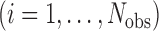 , we first calculate an estimate
, we first calculate an estimate 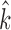 of the cluster assignments using (2). Let
of the cluster assignments using (2). Let 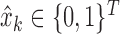 denote a binary vector with a 1 in element
denote a binary vector with a 1 in element 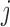 if entity
if entity 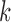 is estimated to appear in database
is estimated to appear in database 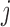 and with zero entries otherwise, for
and with zero entries otherwise, for  . For any
. For any  , define
, define  , giving an estimate of the list intersection counts
, giving an estimate of the list intersection counts  for all
for all 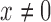 . Then, in the second stage, we estimate the number of unobserved entities
. Then, in the second stage, we estimate the number of unobserved entities 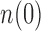 using a standard estimator implemented in the R (R Development Core Team, 2018) package Rcapture. We then define
using a standard estimator implemented in the R (R Development Core Team, 2018) package Rcapture. We then define  , the sum of the estimated number of entities appearing in every possible combination of the databases, including those that appear in no databases. We perform this inference process for 250 replicate, independent simulations for several values of
, the sum of the estimated number of entities appearing in every possible combination of the databases, including those that appear in no databases. We perform this inference process for 250 replicate, independent simulations for several values of 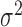 .
.
To assess performance, we consider four metrics: (i) the mean proportion of records assigned to their correct entity/cluster; (ii) mean coverage of 95% confidence intervals for 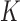 , which is an output of Rcapture; (iii) accuracy of point estimates for the total number of entities
, which is an output of Rcapture; (iii) accuracy of point estimates for the total number of entities 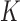 , as measured by
, as measured by
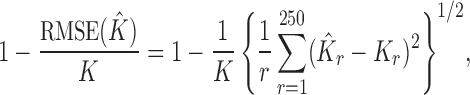 |
where  indexes simulation replicate; and (iv) accuracy in estimation of
indexes simulation replicate; and (iv) accuracy in estimation of  , as measured by
, as measured by 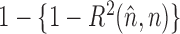 , where
, where 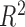 is the squared correlation of
is the squared correlation of 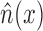 with
with  taken over the entries in
taken over the entries in  with
with 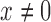 and the 250 replicate simulations.
and the 250 replicate simulations.
The results are presented in Fig. 3 for a series of simulations with 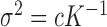 for values of
for values of 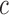 between
between 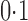 and
and 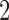 and
and 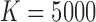 in each case. As expected, as
in each case. As expected, as  increases, accuracy in entity resolution decreases markedly. On the other hand, coverage of 95% confidence intervals for
increases, accuracy in entity resolution decreases markedly. On the other hand, coverage of 95% confidence intervals for 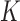 and the root mean squared error for estimation of
and the root mean squared error for estimation of 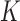 by
by 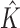 are insensitive to the value of
are insensitive to the value of  . Thus, at least in this example, population estimation on the basis of linked records is not sensitive to the accuracy of entity resolution. This is particularly interesting, since estimation of
. Thus, at least in this example, population estimation on the basis of linked records is not sensitive to the accuracy of entity resolution. This is particularly interesting, since estimation of 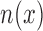 by
by  for
for 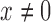 is sensitive to the value of
is sensitive to the value of  , as shown in Fig. 3(d). In other words, poor entity resolution results in poorer estimates of the individual cells
, as shown in Fig. 3(d). In other words, poor entity resolution results in poorer estimates of the individual cells 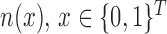 , of the contingency table, but their sum
, of the contingency table, but their sum 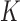 is still estimated accurately.
is still estimated accurately.
Fig. 3.
Plots of simulation results as a function of  for population estimation after entity resolution as described in the text: (a) mean proportion of records correctly assigned; (b) mean coverage of 95% confidence intervals for
for population estimation after entity resolution as described in the text: (a) mean proportion of records correctly assigned; (b) mean coverage of 95% confidence intervals for  ; (c)
; (c) 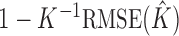 ; (d)
; (d) 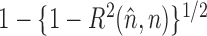 .
.
5. Discussion
This work exposes a fundamental problem with entity resolution via clustering, even in idealized cases, such as when the true data-generating model is known. Empirically, it appears that some functionals of the linked records may be reliably estimated even if entity resolution performance is poor. Understanding which classes of functionals we can estimate and under what conditions is an important area for future research. Another interesting direction is to consider ways of checking whether extensive errors in entity resolution are likely to have occurred after performing model-based clustering by comparing component-specific variance with the separation between the cluster centres.
Supplementary Material
Acknowledgement
This work was inspired by research conducted at the Human Rights Data Analysis Group. The authors gratefully acknowledge funding support for this work from the Human Rights Data Analysis Group and the U.S. National Institutes of Health.
Supplementary material
Supplementary material available at Biometrika online includes a Mathematica notebook with computation of the expression in (10).
Appendix
Proof of Remark 1
 |
where 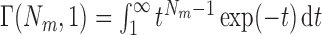 is the incomplete gamma function. The corresponding upper bound is
is the incomplete gamma function. The corresponding upper bound is
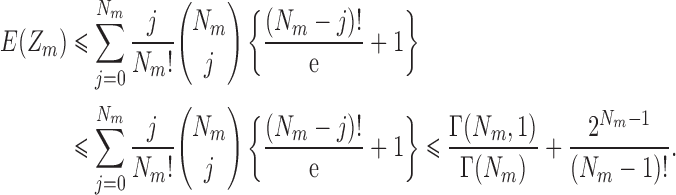 |
Proof of Remark 2
If 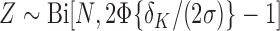 then
then  . Clearly, if the
. Clearly, if the  are equally spaced and restricted to be on a compact set of width
are equally spaced and restricted to be on a compact set of width  , then
, then  for
for 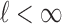 . Since
. Since
 |
we obtain the second assertion. The first statement is obtained by an application of Hoeffding’s inequality.
Gaussian mixture marginal likelihoods
We do the calculation that gives rise to (9). Since each 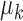 is assigned an independent prior, we have
is assigned an independent prior, we have
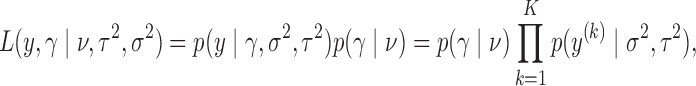 |
where 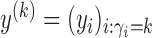 are the observations in class
are the observations in class  . The terms
. The terms 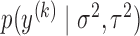 are marginal likelihoods of the data class
are marginal likelihoods of the data class 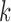 in the conjugate Gaussian model with unknown mean, with
in the conjugate Gaussian model with unknown mean, with
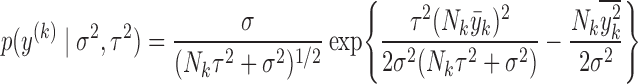 |
and  , where
, where 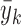 and
and 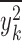 are defined in the main text.
are defined in the main text.
Bayes factors
The Bayes factor for comparing all singleton clusters 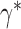 to
to  singleton clusters, one empty cluster, and one cluster with two observations
singleton clusters, one empty cluster, and one cluster with two observations  is
is
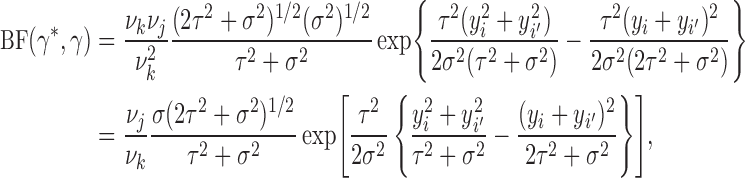 |
where the notation  and
and  is defined in the main text.
is defined in the main text.
Expectation of the Bayes factor
This expression can be obtained by repeatedly completing the square. The calculation is simple but tedious and was performed in Mathematica. A Mathematica notebook is provided in the Supplementary Material.
References
- Al-Lawati, A., Lee, D. & McDaniel, P. (2005). Blocking-aware private record linkage. In Proceedings of the 2nd International Workshop on Information Quality in Information Systems. Association for Computing Machinery, pp. 59–68. [Google Scholar]
- Bilenko, M., Kamath, B. & Mooney, R. J. (2006). Adaptive blocking: Learning to scale up record linkage. In Sixth International Conference on Data Mining (ICDM’06). IEEE, pp. 87–96. [Google Scholar]
- Christen, P. (2012). Data Matching: Concepts and Techniques for Record Linkage, Entity Resolution, and Duplicate Detection. Berlin: Springer. [Google Scholar]
- Day, N. E. (1969). Estimating the components of a mixture of normal distributions. Biometrika 56, 463–74. [Google Scholar]
- DeGroot, M. H. & Goel, P. K. (1980). Estimation of the correlation coefficient from a broken random sample. Ann. Statist. 8, 264–78. [Google Scholar]
- D’Orazio, M., Di Zio, M. & Scanu, M. (2006). Statistical Matching: Theory and Practice. Chichester: Wiley. [Google Scholar]
- Dunson, D. B. & Xing, C. (2009). Nonparametric Bayes modeling of multivariate categorical data. J. Am. Statist. Assoc. 104, 1042–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fellegi, I. P. & Sunter, A. B. (1969). A theory for record linkage. J. Am. Statist. Assoc. 64, 1183–210. [Google Scholar]
- Fienberg, S. E., Rinaldo, A. & Zhou, Y. (2009). Maximum likelihood estimation in latent class models for contingency table data. In Algebraic and Geometric Methods in Statistics, Gibilisco, P. Riccomagno, E. Rogantin M. P. & Wynn, H. P. eds., ch. 2.Cambridge: Cambridge University Press, pp. 27–63. [Google Scholar]
- Griffin, R. A. (2014). Potential uses of administrative records for triple system modeling for estimation of census coverage error in 2020. J. Offic. Statist. 30, 177–89. [Google Scholar]
- Hastie, T. J., Tibshirani, R. J. & Friedman, J. H. (2009). Unsupervised learning. In The Elements of Statistical Learning. New York: Springer, pp. 485–585. [Google Scholar]
- Holzmann, H., Munk, A. & Gneiting, T. (2006). Identifiability of finite mixtures of elliptical distributions. Scand. J. Statist. 33, 753–63. [Google Scholar]
- Jaro, M. A. (1989). Advances in record-linkage methodology as applied to matching the 1985 census of Tampa, Florida. J. Am. Statist. Assoc. 84, 414–20. [Google Scholar]
- Jaro, M. A. (1995). Probabilistic linkage of large public health data files. Statist. Med. 14, 491–8. [DOI] [PubMed] [Google Scholar]
- Johndrow, J. E., Bhattacharya, A. & Dunson, D. B. (2017). Tensor decompositions and sparse log-linear models. Ann. Statist. 45, 1–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lahiri, P. & Larsen, M. D. (2005). Regression analysis with linked data. J. Am. Statist. Assoc. 100, 222–30. [Google Scholar]
- Lo, Y., Mendell, N. R. & Rubin, D. B. (2001). Testing the number of components in a normal mixture. Biometrika 88, 767–78. [Google Scholar]
- Lum, K., Price, M. E. & Banks, D. (2013). Applications of multiple systems estimation in human rights research. Am. Statistician 67, 191–200. [Google Scholar]
- Michelson, M. & Knoblock, C. A. (2006). Learning blocking schemes for record linkage. In Proceedings of the National Conference on Artificial Intelligence, vol. 21.Association for the Advancement of Artificial Intelligence, pp. 440–5. [Google Scholar]
- Miller, J., Betancourt, B., Zaidi, A., Wallach, H. & Steorts, R. C. (2015). Microclustering: When the cluster sizes grow sublinearly with the size of the data set. arXiv: 1512.00792. [Google Scholar]
- R Development Core Team (2018). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria: ISBN 3-900051-07-0.http://www.R-project.org. [Google Scholar]
- Richardson, S. & Green, P. J. (1997). On Bayesian analysis of mixtures with an unknown number of components (with Discussion). J. R. Statist. Soc. B 59, 731–92. [Google Scholar]
- Sadinle, M. (2014). Detecting duplicates in a homicide registry using a Bayesian partitioning approach. Ann. Appl. Statist. 8, 2404–34. [Google Scholar]
- Sadinle, M. & Fienberg, S. E. (2013). A generalized Fellegi–Sunter framework for multiple record linkage with application to homicide record systems. J. Am. Statist. Assoc. 108, 385–97. [Google Scholar]
- Steorts, R., Hall, R. & Fienberg, S. E. (2014). SMERED: A Bayesian approach to graphical record linkage and de-duplication. In Artificial Intelligence and Statistics. pp. 922–30. [Google Scholar]
- Steorts, R. C. (2015). Entity resolution with empirically motivated priors. Bayesian Anal. 10, 849–75. [Google Scholar]
- Steorts, R. C., Hall, R. & Fienberg, S. E. (2015). A Bayesian approach to graphical record linkage and de-duplication. J. Am. Statist. Assoc. 111, 1660–72. [Google Scholar]
- Teicher, H. (1961). Identifiability of mixtures. Ann. Math. Statist. 32, 244–8. [Google Scholar]
- Teicher, H. (1963). Identifiability of finite mixtures. Ann. Math. Statist. 34, 1265–9. [Google Scholar]
- Tibshirani, R. J., Walther, G. & Hastie, T. J. (2001). Estimating the number of clusters in a data set via the gap statistic. J. R. Statist. Soc. B 63, 411–23. [Google Scholar]
- Winkler, W. E. (2006). Overview of record linkage and current research directions. Research Report Series (Statistics #2006-2). Washington, DC: U.S. Bureau of the Census. [Google Scholar]
- Wolter, K. M. (1986). Some coverage error models for census data. J. Am. Statist. Assoc. 81, 337–46. [PubMed] [Google Scholar]
- Yakowitz, S. J. & Spragins, J. D. (1968). On the identifiability of finite mixtures. Ann. Math. Statist. 39, 209–14. [Google Scholar]
- Zanella, G., Betancourt, B., Wallach, H., Miller, J., Zaidi, A. & Steorts, R. C. (2016). Flexible models for microclustering with application to entity resolution. arXiv: 1610.09780. [Google Scholar]
- Zaslavsky, A. M. & Wolfgang, G. S. (1993). Triple-system modeling of census, post-enumeration survey, and administrative-list data. J. Bus. Econ. Statist. 11, 279–88. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.