Evaluating motion processing algorithms for use with functional near-infrared spectroscopy data from young children

Abstract.

Motion artifacts are often a significant component of the measured signal in functional near-infrared spectroscopy (fNIRS) experiments. A variety of methods have been proposed to address this issue, including principal components analysis (PCA), correlation-based signal improvement (CBSI), wavelet filtering, and spline interpolation. The efficacy of these techniques has been compared using simulated data; however, our understanding of how these techniques fare when dealing with task-based cognitive data is limited. Brigadoi et al. compared motion correction techniques in a sample of adult data measured during a simple cognitive task. Wavelet filtering showed the most promise as an optimal technique for motion correction. Given that fNIRS is often used with infants and young children, it is critical to evaluate the effectiveness of motion correction techniques directly with data from these age groups. This study addresses that problem by evaluating motion correction algorithms implemented in HomER2. The efficacy of each technique was compared quantitatively using objective metrics related to the physiological properties of the hemodynamic response. Results showed that targeted PCA (tPCA), spline, and CBSI retained a higher number of trials. These techniques also performed well in direct head-to-head comparisons with the other approaches using quantitative metrics. The CBSI method corrected many of the artifacts present in our data; however, this approach produced sometimes unstable HRFs. The targeted PCA and spline methods proved to be the most robust, performing well across all comparison metrics. When compared head to head, tPCA consistently outperformed spline. We conclude, therefore, that tPCA is an effective technique for correcting motion artifacts in fNIRS data from young children.

Functional near-infrared spectroscopy (fNIRS) measures the absorption and scattering of photons as near-infrared light passes through brain tissue, allowing measurement of changes in localized hemodynamic responses in the cortex. It specifically monitors changes in intensity as near-infrared light is passed through tissue from a source to a detector. fNIRS has been widely used to investigate the neural processes that underlie multiple cognitive abilities across development and is becoming a tool of choice when studying challenging populations including infants, young children, and clinical patients who cannot be easily studied with functional magnetic resonance imaging (fMRI).^1–11 Despite recent advances in methodological and analytical tools for use with fNIRS data, questions remain regarding the optimal method for removing motion artifacts from the measured signal.

Motion artifacts are often a significant component of the measured fNIRS signal. This is due to the fact that movement can cause transient displacements of the source/detector optodes on the scalp that are reflected in the time series. The speed and strength of movement as well as the tolerance of the probes to this motion play a role in how these artifacts are reflected in the signal. Motion artifacts are highly variable and often complex. They can be generally classified as spikes, baseline shifts, and low-frequency variations.¹² They take many forms that can appear as isolated, high amplitude events (spikes), or pervasive low-frequency events that are temporally correlated with the measured hemodynamic response and therefore hard to detect and correct for. To estimate the true response, however, it is crucial that motion artifacts are detected and removed.

A variety of methods have been proposed to address this issue. Some include the addition of complementary measurements such as short-separation channels^13,14 or an accelerometer.^15–17 These methods provide a direct measure of the artifacts making it possible to regress these artifacts from the measured signal of interest. Alternative approaches include detecting optode fluctuations prior to data collection to prevent unstable and weak connections that would result in motion artifacts.¹⁸ Other approaches take into consideration spatial and/or temporal features of the measured signal and serve as post-processing techniques. Among these approaches are principal component analysis (PCA),¹⁹ Kalman filtering,²⁰ correlation-based signal improvement (CBSI),²¹ wavelet filtering,²² spline interpolation,²³ autoregressive algorithms,²⁴ and more recently, a kurtosis-based wavelet algorithm,²⁵ empirical mode decomposition (EMD),²⁶ and an optical model on the influence of optode fluctuation on the fNIRS signal.²⁷

Several papers have explored the efficacy of different motion correction techniques for fNIRS data.^{12,17,25–32} The majority of these reports have investigated this problem by adding a simulated hemodynamic response to resting-state data. Recently, Chiarelli et al.²⁵ introduced a kurtosis-based wavelet algorithm that proved to be more efficient in removing motion artifacts when compared with other techniques in a resting-state dataset. Additionally, Gu and colleagues²⁶ introduced the EMD approach, which is adaptive and data-driven. This approach performed well when compared with spline, Wavelet, and kurtosis-based wavelet in a resting-state dataset by increasing the signal-to-noise ratio and decreasing the mean squared error.

Only two studies have used real, task-based data.^12,30 Comparison of the techniques has shown that the most effective methods for motion correction are wavelet filtering,^12,28 spline interpolation,²⁸ and targeted PCA (tPCA).³² Critically, the complexity of motion artifacts makes it likely that the efficacy of motion correction techniques is data-dependent.¹² Consistent with this, several recent studies have found that wavelet filtering is a promising technique for motion correction; however, the specific type of wavelet filtering that is optimal differs across cohorts and data types. Brigadoi et al.¹² quantitatively compared six motion correction techniques in a sample of adult data measured during a simple cognitive task. They concluded that wavelet filtering showed the most promise as an optimal technique for motion correction. Hu et al.³⁰ reported that a combination of wavelet and a moving average yielded the best results in a study of 9- to 12-year-old children.

In the present study, we compared the performance of multiple motion correction techniques as implemented in the HomER2 analysis package³³ using fNIRS data from a cognitive task with young children. The study was unique in two ways. First, our understanding of how motion correction techniques fare when dealing with task-based cognitive data is limited. In the present study, we examined fNIRS data from a study of visual working memory (VWM) where children had to explicitly compare multiple items from a sample and test array. Second, no previous studies have compared motion correction techniques with fNIRS data from young children. Young children are much more likely to move during data collection, resulting in far noisier data than data from adult participants with motion artifacts distributed throughout the time series. They also routinely engage in jerky movements that can result in more motion epochs and yield artifacts that are faster and of greater amplitude relative to adults. Furthermore, because fNIRS is often used with infants and young children, it is critical to evaluate the effectiveness of motion correction techniques directly with data from these age groups. Thus, we investigated whether the conclusions reached by Brigadoi et al.¹² extend to data from young children. To address this question, we compared spline interpolation, PCA, tPCA, Wavelet filtering, and CBSI on data acquired during a working memory paradigm with 3- and 4-year-old children.

Note that some adult populations, such as adults with epilepsy, might also produce many motion artifacts. Thus, the issues explored here may be relevant to some adult populations as well. In this context, we note that Selb and colleagues³¹ reported that the best approach to minimize the effects of motion artifacts on oscillation fNIRS data from healthy subjects and stroke patients is to correct motion artifacts using a spline interpolation, apply bandpass filtering, and then discard the epochs that were originally identified as containing motion artifacts. We did not evaluate this approach here because data collection with infants, children, and clinical populations often results in quite limited data; consequently, discarding segments of data is not an optimal approach to denoise the optical signal.

1. Methods

1.1. Participants

Eleven 3.5-year-old ($M=3.5\mathrm{y}$, $\mathrm{SD}=0.06$) and 14 4.5-year-old ($M=4.51\mathrm{y}$, $\mathrm{SD}=0.08$) participated in the study, after parents provided informed consent. Children were recruited from a participant registry maintained by the Department of Psychology at a Midwestern University in the United States. Parents were sent a letter inviting them to participate and then received a follow-up phone call. All children had normal or corrected-to-normal vision. The study was approved by the University’s Institutional Review Board.

1.2. Materials and Procedure

Each participant was seated in front of a 46-in. LCD television that was connected to a PC running E-Prime (Psychology Software Tools, Pittsburgh, Pennsylvania). The paradigm consisted of a change detection task³⁴ (Fig. 1). In this task, participants are presented with a sample array of one to three colored squares, after which there is a 1-s delay, and then a test array appears in which either all the objects match the memory array, or the feature (i.e., color) of one object is changed to a new value. The test display remained on the screen until children provided a verbal response (i.e., “same” or “different”) that the experimenter entered using a keyboard. After each trial, there was a random intertrial interval. These intervals consisted of a blank 1 s (50% of trials), 2 s (25% of trials), or 4 s (25% of trials) delay followed by the appearance of a fixation dot. The next trial began once the experimenter pushed a button indicating that the participant was attending to the fixation dot. On average, the total duration of the interval between trials was 12.3 s (SD = 8.23 s; range varied from 2.23 to 53.32 s).

Fig. 1.

Change detection task. Sequence of events during a trial. Each trial began with an auditory prompt saying, “Let’s look for color changes!” along with a fixation circle on the left or right side of the screen that preceded where the target stimuli appeared. The experimenter initiated the trial when the child was ready. The sample array then appeared on the screen for 2 s, followed by a blank interval of 1 s. The test array was then presented until the child verbally responded “same” or “different.” The experimenter entered the child’s response on a keyboard.

There were six conditions in the experimental design: children were asked to remember 1, 2, or 3 items (set sizes, SS, 1 to 3) and the trials either contained a change or did not (same, different). Participants came in for two sessions and completed 24 trials per condition.

1.3. Functional Near-Infrared Spectroscopy Data

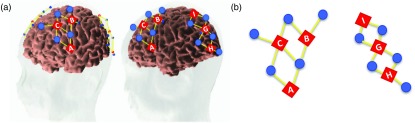
fNIRS data were collected at 50 Hz using a TechEn CW6 system with 690- and 830-nm wavelengths. Near-infrared light was delivered via 12 fiber optic cables (sources) to the participant’s scalp and detected by 20 fiber optic cables (detectors) spaced into four arrays embedded in a cap. Each array contained three sources and five detectors placed over the frontal, temporal, and parietal cortices bilaterally to tap target regions of interest (ROI). Figure 2 shows views of the probe geometry (see Wijeakumar et al.³⁵ for details). There were a total of 36 channels, which formed part of an optimized probe geometry using ROIs from the fMRI VWM literature.³⁰ ROIs included right superior intraparietal sulcus, bilateral intraparietal sulcus, bilateral anterior intraparietal sulcus, bilateral ventral occipital cortex, bilateral dorsolateral prefrontal cortex, left superior frontal gyrus, bilateral inferior frontal gyrus (IFG), frontal eye fields, bilateral middle frontal gyrus, bilateral occipital, and bilateral temporoparietal junction.

Fig. 2.

Probe geometry. Panel A shows two views of the probe geometry. Red diamonds depict sources and blue circles depict detectors, whereas yellow lines represent the channels. Figure was created using AtlasviewerGUI (HOMER2, Massachusetts General Hospital/Harvard Medical School, Massachusetts). Panel B shows a schematic of the left side view of the probe.

To account for variations in head size across participants, source–detector distances were scaled relative to the head circumference using the 10 to 20 system; thus, the source–detector distance ranged from 25 to 27 mm.³⁵

At the beginning of each session, each participants’ head circumference was measured and the appropriate fNIRS cap was selected. Prior to the experimental task, children were fitted with a custom EEG cap that contained grommets to secure the fiber optics to the scalp. Experimenters then cleared out hair that could obstruct the optical signal. Sources and detectors were then fitted into grommets onto the child’s head, and secured using an elastic band to limit optode fluctuation as a result of participant movement. The source and detector gains were adjusted to optimize signal quality prior to starting the experimental procedures. Optode positions were recorded in three-dimensions using a Polhemus Patriot system before the task.

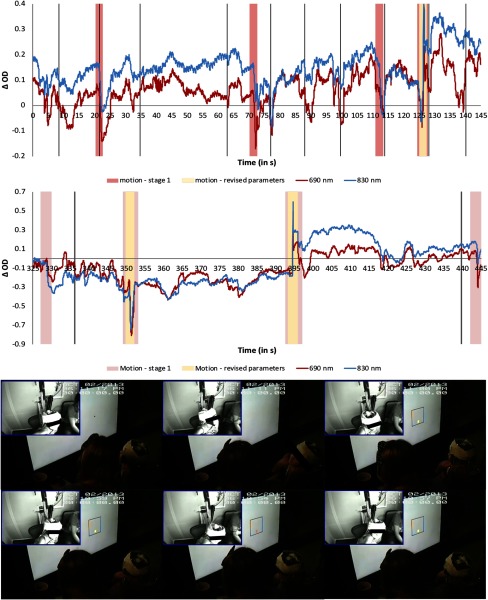
The data acquired during this experiment contained a variety of motion artifacts. Figure 3 shows an example of the artifacts present in one representative subject’s data. Artifacts were generated by the participants’ mouth and jaw movements when they gave verbal responses or talked spontaneously as well as by a variety of head and body movements. Figure 4 shows an excerpt of the session video that illustrates some of the movements participants routinely engaged on while completing the task. In particular, the images show how the participant moves his head while changing his line of focus from the display to the experimenter. Note that this period likely included talking with the experimenter. Similarly, the figure also shows how the participant moves back-and-forth while the trial is on. Not all participants had artifacts of the same type and magnitude, likely because they engaged in slightly different behaviors and had different physical characteristics. However, moving back and forth, changing focus from the display to the experimenter and talking were behaviors that are likely present across all participants. The shape and duration of the artifacts were also variable, although many were fast, high-amplitude artifacts. Such individual differences are unavoidable with young children and pose a great challenge when trying to detect and remove motion artifacts using the same method across participants.

Fig. 3.

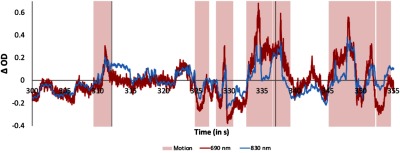
Motion artifacts. Example motion artifacts (highlighted in pink) present during a segment of the time series for one channel for one participant. The red line shows the 690-nm wavelength, whereas the 830-nm wavelength is shown in blue. Vertical lines depict the onset of a trial (i.e., timepoint 0). The figure shows the raw time series, before any motion correction is applied and before bandpass filtering.

Fig. 4.

Examples of motion artifacts (highlighted in pink for the parameters used in stage 1 and yellow for the revised parameters) present during a segment of the time series for one channel for one participant. The red line shows the 690-nm wavelength, whereas the 830-nm wavelength is shown in blue. Vertical lines depict the onset of a trial (i.e., time point 0). The bottom panel shows an excerpt of this participant’s behavior while completing the task.

1.4. Motion Correction Techniques

1.4.1. Spline interpolation

This method is a channel-by-channel approach based on Scholkmann et al.²³ As it is implemented on HomER2,³³ this algorithm acts on motion artifacts that have been previously detected; therefore, it is dependent upon having a good motion detection algorithm. Artifacts are modeled using cubic spline interpolation, which is then subtracted from the original time-series to correct for motion artifacts. The time-series is then reconstructed and normalized by shifting the corrected segments by a value given by the combination of the mean value of the segment and the mean value of the previous segment to ensure a continuous signal. For a more detailed description, see Scholkmann et al.²³ The interpolation depends on a parameter, which determines the degree of the spline function. In this study, the parameter was set to 0.99 to be consistent with previous studies.^12,23,28

1.4.2. Principal components analysis

This method applies an orthogonal transformation to decompose the original signal into uncorrelated components based on the amount of variance accounted for by each component. The first components account for the largest proportion of variance and are assumed to represent the motion artifacts as these epochs are characterized by large changes in amplitude and a high degree of variability. Therefore, removing the first components should correct for motion artifacts.¹⁹

The performance of this technique is highly dependent on both the number of measurements available and the number of components removed. Cooper et al.²⁸ suggested that PCA performs optimally when removing 97% of the total variance; thus, we used this value. Following the suggestion of Brigadoi et al.¹² that 97% was too high, we also performed the correction using 80%. Results for both parameters were very similar; thus, we only include the results for 97% in this report. We also employed a targeted principal component analysis (tPCA),³² which applies a similar PCA filter but only on segments previously identified as motion artifact. Thus, similar to the spline interpolation method described above, this technique relies on a motion detection algorithm. The corrected motion epochs are then reintroduced to the time series by shifting the corrected segments by a value given by the combination of the mean value of the segment and the mean value of the previous segment to ensure a continuous signal, identical to the procedure employed in the spline interpolation correction method. This procedure was repeated five times to identify and correct any residual artifacts.

1.4.3. Wavelet filtering

This method is a channel-by-channel approach that follows the one proposed by Molavi and Dumont.²² It relies on the differences in amplitude and duration between motion artifacts and the measured signal of interest.²² As a first step, the signal is expanded using a discrete wavelet transform after which motion artifacts appear as isolated large coefficients. The goal is to remove those coefficients that are not likely to be an outcome of the distribution of wavelet coefficients.

The measured signal is assumed to be a sum of the physiological signal of interest and an interference term. The distribution of wavelet coefficients is a mixture of Gaussians.^36,37 Within this method, the wavelet distribution is assumed to have a single Gaussian probability distribution. As the hemodynamic signal and motion artifacts differ in timing and amplitude, with the first being a slow and smooth signal, most wavelet coefficients of the signal of interest center around zero while motion artifacts behave like outliers. Therefore, for any given coefficient, if the coefficient exceeds iqr times the interquartile range, that coefficient is assumed to not belong in the original signal and must be a reflection of artifacts that should be removed. Iqr was set to 1.0 in this experiment. Outlier terms were removed by setting them to zero preceding the reconstruction of the artifact-free signal using the inverse discrete wavelet transform.

1.4.4. Correlation-based signal improvement

This method is a channel-by-channel approach developed by Cui et al.²¹ It reduces motion artifacts caused by head movements. The main assumption is that HbO and HbR should be strongly negatively correlated during functional activation and become more positively correlated during motion. Furthermore, the ratio between HbO and HbR is assumed to be the same with and without the presence of motion artifacts. Within this method, the measured signal is assumed to have three components: the true signal of interest, motion-induced noise, and other white noise.²¹ As the white noise component can be easily removed with filters, the purpose then is to compute the true HbO and HbR signal. To do so, two assumptions must be met: first, the correlation between HbO and HbR should be close to $-1$ and the correlation between the motion artifact and HbO should be close to 0. Solving the following equations should then produce the true signal of interest

$$x_0=(x-\alpha *y)/2,$$

$$y_0=-(1/\alpha )*x_0$$

with

$$\alpha =\mathrm{std}(x)/\mathrm{std}(y),$$

where $\mathrm{std}(x)$ is the standard deviation of $x$.

1.5. Data Processing

The NIRS data were processed using HomER2³³ based in MATLAB (Mathworks, Massachusetts). Raw optical signals were first converted to optical density. Channels with very low optical density [$<80\mathrm{dB}$; $\mathrm{dB}=20*\mathrm{LOG}10(y)$, where $y$ is the intensity level measured by the CW6 system] were discarded from the analysis. Incorrect trials were also discarded from further analysis. The mean number of trials included for each participant in each condition was 17.3 ($\mathrm{SD}=4.8$). The mean number of trials per participant and condition was quite high, giving us confidence in the ability to detect differences between the motion processing algorithms.

1.6. Selection of Motion Detection Parameters

fNIRS data from young children often has far more motion epochs than data collected from typical adults. Moreover, young children can only perform a handful of trials, making each trial crucially important. Therefore, it is important to employ a set of parameters and a correction technique that recovers as many trials as possible while still decontaminating the data. However, the process of selecting the “right” parameters for a given dataset is an ambiguous one. There are no well-defined metrics for setting parameters other than exploring the properties of each dataset or using values that other groups have used and exploring how those parameter values affect the data.

Before comparing the motion correction techniques, we explored two different set of motion detection parameters (Table 1). We used the parameters from Brigadoi et al.¹² as a starting point because this allows for a direct comparison with this previous study. Specifically, motion artifacts were identified in the optical density (OD) time series using the motion detection algorithm, hmrMotionArtifact. Signal changes with amplitude (AmpThresh) $>0.4\mathrm{au}$ and exceeding a threshold of 50 in change of standard deviation (StDevThresh) within 1 s were identified as motion artifacts (tMotion). Artifacts were masked for an additional 1 s before and after the motion epochs (tMask). Trials were rejected if an artifact appeared 10 s after the stimulus onset (enStimRejection: 0 to 10 s). Periods masked as motion artifacts on a given channel were identified on all channels. Note that a channel-specific approach, hmrMotionArtifactByChannel, was used for the spline interpolation technique. This algorithm works the same way but on a channel-by-channel basis.

Table 1.

Motion detection parameters.

	Original parameters	Relaxed parameters
tMotion	1	0.3
tMask	1	1
StDevThresh	50	100
AmpThresh	0.4	0.4

This parameter set did a good job identifying a variety of artifacts (Fig. 4). However, it resulted in a limited number of trials remaining after motion correction for some motion correction approaches. This might accurately reflect our data: it is possible that there was too much motion in our dataset and the excluded trials really should be excluded. Examination of the dataset suggested, instead, that the motion detection parameters were too conservative in some cases. For instance, in the lower panel of Fig. 4, the first motion artifact is relatively minor, whereas the second and third artifacts are large.

Thus, we took a second look through the data, identifying motion detection parameters that would still do a good job of identifying large motion artifacts in the data, but would let more minor motion artifacts pass through. Note that, although this allows some noise to pass through to the final analysis, this noise trades off with the increase in the number of trials we are averaging over per participant. We relaxed the motion detection parameters (see Table 1) such that signal changes with amplitude $>0.4\mathrm{au}$ and exceeding a threshold of 100 in change of standard deviation within 0.3 s were identified as motion artifacts. Artifacts were masked for an additional 1 s before and after the motion epochs. Thus, in this stage, we are in effect capturing fast, high-amplitude artifacts. The segments identified in yellow in Fig. 4 reflect motion detection using the second “relaxed” set of parameters. As is evident, the second set is most sensitive to fast changes in amplitude. Note, however, that both set of parameters do a good job detecting clear epochs of motion present in the data.

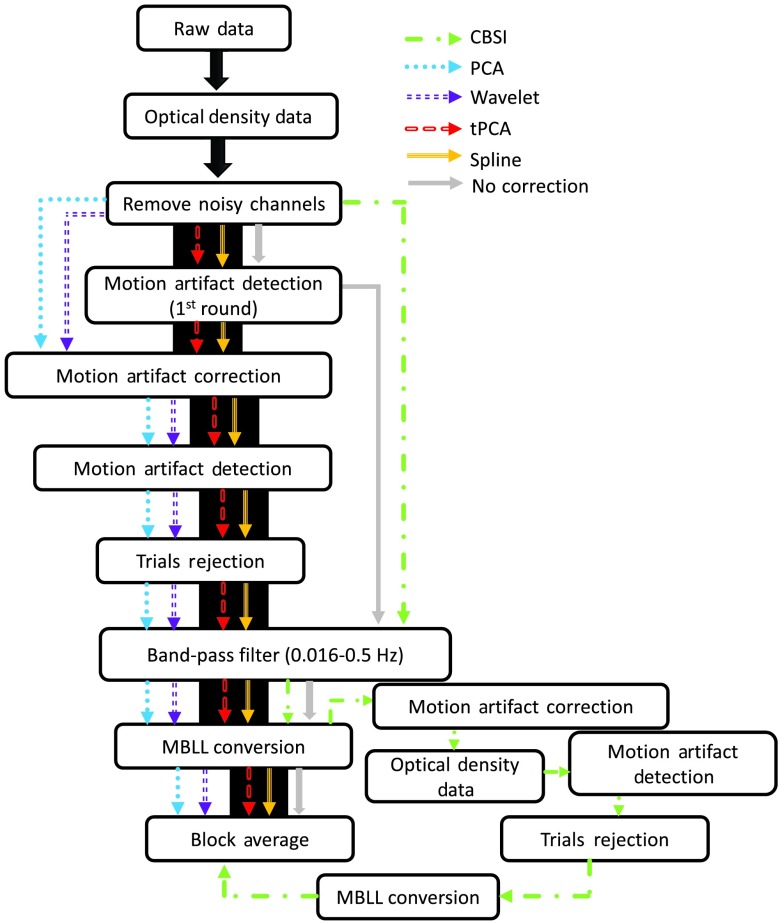
Five processing approaches (PCA, Wavelet, tPCA, spline, CBSI) were applied to the data after noisy channels were removed. Figure 5 shows the processing stream for all techniques. Four of these techniques (PCA, Wavelet, tPCA, and spline) applied the correction on the OD data. Two of these techniques—tPCA and spline—did correction based on a first round of motion artifact detection. Here, we used the more conservative parameters borrowed from Brigadoi et al.¹² to detect—and possibly correct—as much motion as possible. After each correction technique had been applied to the data, motion artifact was detected (assuming motion across all channels) using the “relaxed” parameters. Trials with motion artifact at this step were rejected. Data were then bandpass filtered (0.016 to 0.5 Hz) and the concentrations of oxygenated hemoglobin (HbO), deoxygenated hemoglobin (HbR), and total hemoglobin (HbT) were computed using the modified Beer–Lambert Law.^38,39 A differential path length (DPF) factor of 6.0 was used for both wavelengths.⁴⁰

Fig. 5.

Processing stream for all techniques. Processing steps for all techniques are represented by a colored arrow: green for CBSI, blue for PCA, purple for Wavelet, red for tPCA, orange for spline, and gray for no correction. Note that tPCA and spline require motion to be detected before applying the correction.

The fifth correction technique, CBSI, applies the motion correction on concentration changes (see Fig. 5). Therefore, the OD data were bandpass filtered and then converted to concentration changes. The correction method was then applied, motion artifact was detected using the “relaxed” parameters, and trials with motion artifact were rejected. As a final step, the data from the five motion correction techniques were block-averaged to recover the mean hemodynamic response by condition. This yielded six mean measured hemodynamic responses for HbO and HbR for each channel and participant. The performance of these techniques was compared with each other and to uncorrected data.

1.7. Quantitative Comparison of the Approaches

The first step in the quantitative analysis was to identify channels with task-relevant hemodynamic response. The goal was to reduce the number of comparisons and to evaluate the motion correction approaches only on those channels with task-relevant signals. Thus, we compared the concentration of HbO and HbR and included all channels showing a significant difference ($p<0.05$) between these signals within the task-relevant window (0 to 10 s; see Buss et al.²). Thirty-four channels passed this criterion. Next, a block average time series for HbO and HbR was created by averaging data from all six experimental conditions. The central dataset analyzed was from 34 channels and 25 participants contributing two values (HbO and HbR) for each of the metrics described below.

Following Brigadoi et al.,¹² we quantitatively compared the efficacy of each correction technique using five metrics. The metrics were defined to provide estimates of how physiologically plausible the recovered mean hemodynamic responses are. The first, the area-under-the-curve (${\mathrm{AUC}}_{0-2}$), encompasses the first two seconds after the onset of the first stimulus array and it is assumed to be composed of artifacts. Therefore, smaller values for this index indicate better performance. The second metric is the ${\mathrm{AUC}}_{2-6}$ that captures the rise and peak of the hemodynamic response specific to our task. Buss et al.² found task-related functional activity between 4 and 6 s after the onset of the first stimulus array in the working memory paradigm used here. Thus, higher values in this time window indicate better performance. Third, we computed the ratio between ${\mathrm{AUC}}_{2-6}$ and ${\mathrm{AUC}}_{0-2}$. Larger ratio values indicate better performance with low levels of initial noise (${\mathrm{AUC}}_{0-2}$) and a strong rise of task-related functional activity (${\mathrm{AUC}}_{2-6}$). Fourth, we computed the mean standard deviation of each trial-specific hemodynamic response included in the block average by condition and then averaged across conditions so we end up with one value for this metric for each channel (SubSD). This captures the variability present within subjects. This variability is assumed to be affected by motion artifacts, so higher variability indicates poorer motion correction performance. Finally, we computed the number of trials included after motion correction for each subject and condition. All motion correction techniques were compared with each other quantitatively using ANOVA.

2. Results

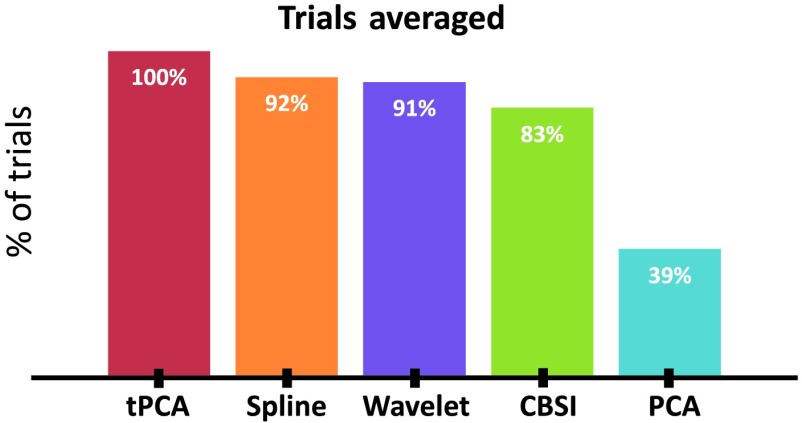
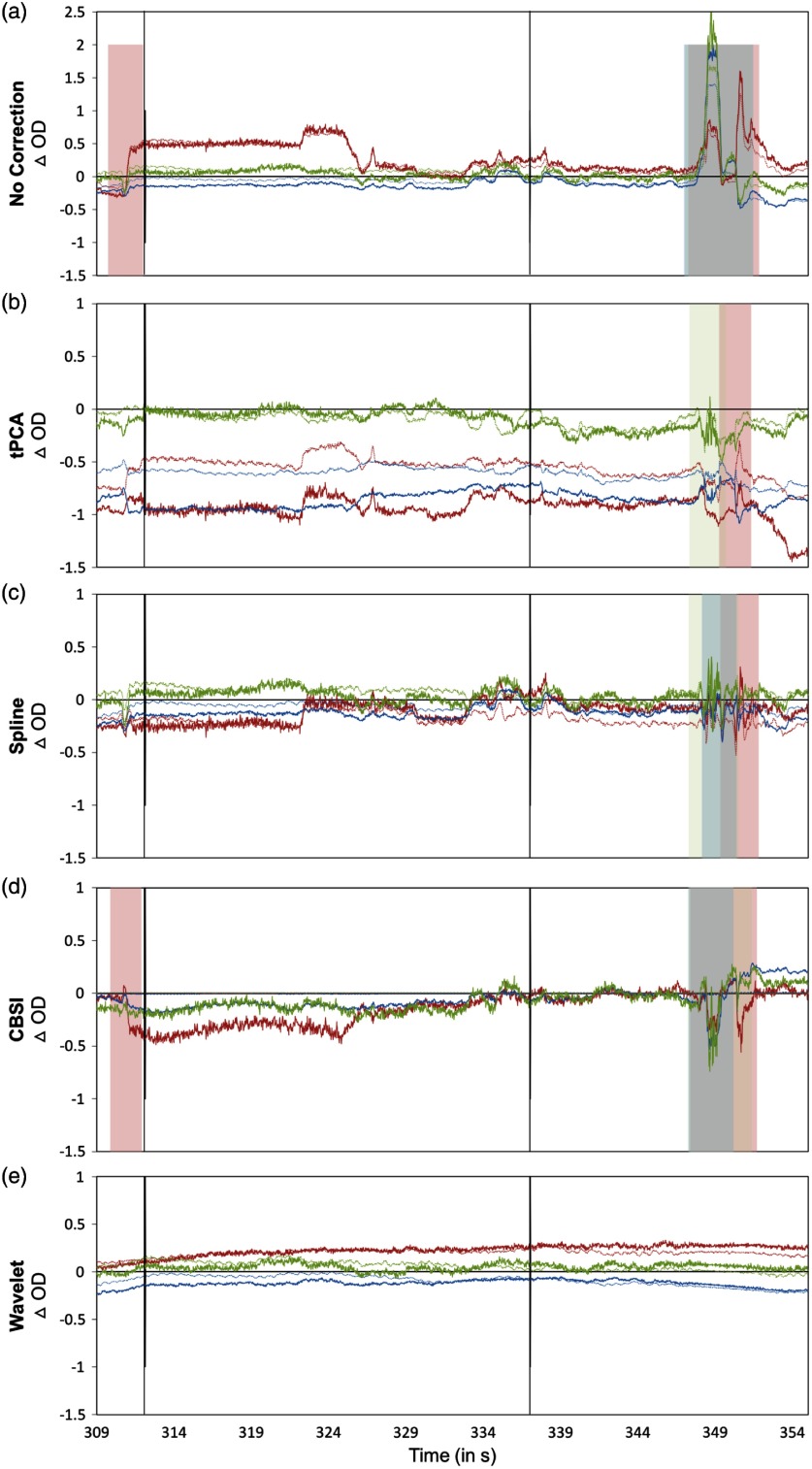
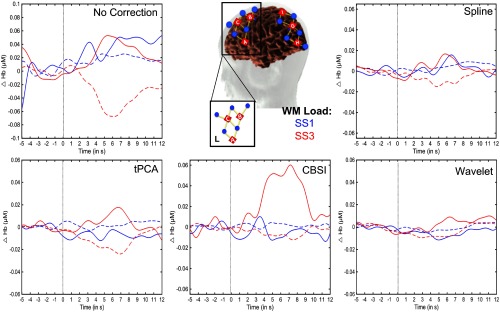
Figure 6 shows the percent of trials recovered after correction by each technique using these parameters. PCA did not recover a substantial number of trials after processing and thus was removed from this stage of the analysis. Figure 7 shows representative examples of a time series precorrection and postcorrection. The top panel shows the uncorrected OD data, whereas panels B, C, D, and E show the OD data after applying the tPCA, spline, CBSI, and Wavelet techniques, respectively. The figure shows data for three channels (for both wavelengths) with motion epochs color coded by channel. All correction techniques influenced the data by either reducing the amplitude of the artifacts or completely correcting them. The figure also shows that the epochs that remain flagged as artifacts, after correction, are clear motion epochs. Figure 8 shows a representative example of the recovered hemodynamic response. The figure shows concentration changes across working memory loads (SS1 and SS3) for both HbO and HbR for all motion correction techniques. Overall, all correction techniques effectively remove the motion-induced noise present in the SS1 hemodynamic response. Note that the no correction plot (top left) shows an increase in both HbO and HbR at SS1, which is inconsistent with functional hemodynamics and could be attributed to motion epochs. Indeed, the figure shows that after motion correction this pattern is no longer present. Note that SS3 evoked a canonical hemodynamic response, with increasing HbO and a decreasing HbR response. Note that CBSI, despite fabricating the hemodynamic response, reduced the HbR response. Similarly, the wavelet algorithm dampened the hemodynamic response.

Fig. 6.

Figure shows the percent of trials recovered using each motion processing technique.

Fig. 7.

Pre and postmotion correction. The figure depicts example channel before and after each motion processing technique is applied. The time series plotted is optical density data. The solid line shows the 690-nm wavelength, whereas the 830-nm wavelength is depicted by the dotted lines. The shaded areas reflect motion artifacts, color coded to reflect each channel. Vertical lines depict the onset of a trial (i.e., time point 0).

Fig. 8.

Hemodynamic responses examples. Figure shows an example of the recovered hemodynamic response as the working memory load increases for a channel in the left frontal cortex for each of the motion correction technique. Solid lines represent ${\mathrm{HbO}}_2$ and dotted lines represent HbR.

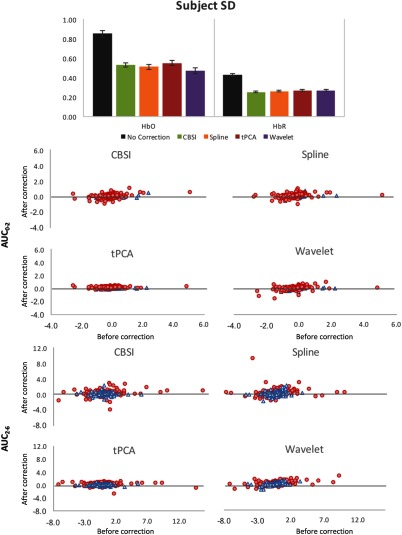
We conducted a mixed factor ANOVA with technique (CBSI, Wavelet, spline, tPCA) and Hb (HbO, HbR) as within-subject factors and age as a between-subject factor on a channel-by-channel basis for the different metrics. For each analysis that showed an effect of Technique (technique main effect, $\text{technique}\times \text{age}$ interaction, or $\text{technique}\times \mathrm{Hb}$ interaction), we conducted posthoc comparisons to determine which technique performed quantitatively better along that metric. The number of instances in which each technique performed better than its counterparts was tallied. Results are shown in Table 2. Overall, CBSI outperformed the other techniques, with 69 instances where this technique outperformed one of the other techniques. Two other techniques also performed well, namely spline and tPCA. Note that most of the significant technique effects were seen on the ${\mathrm{AUC}}_{0-2}$ and SubSD metrics, whereas the techniques performed similarly on ${\mathrm{AUC}}_{2-6}$ and Ratio. Particularly, CBSI outperformed all techniques in the ${\mathrm{AUC}}_{0-2}$ metric, whereas spline and tPCA outperformed the other techniques on the SubSD metric. This latter effect is important, showing that spline and tPCA are effectively reducing the subject-specific variability, which is likely influenced by motion artifacts.

Table 2.

Quantitative analysis summary. Table shows the number of times a technique outperformed its counterparts in channels where there was a significant effect of technique, technique by Hb or technique by age interaction on each metric.

	Metrics				Total
	AUC02	AUC26	Ratio	SubSD
CBSI	24	3	3	39	69
Wavelet	6	2	0	13	21
Spline	0	4	1	45	50
tPCA	10	1	0	42	53

Figure 9 shows the quantitative metrics across comparisons relative to the data with no motion correction. The top panel of Fig. 9 shows the mean subject SD for CBSI, spline, tPCA, and Wavelet relative to no correction. The techniques performed similarly along this metric and all reduced subject SD relative to no correction. The bottom panels of Fig. 9 show scatter plots of the ${\mathrm{AUC}}_{0-2}$ and ${\mathrm{AUC}}_{2-6}$ values that were computed from the recovered mean hemodynamic response for no motion correction ($x$-axis) and all other techniques ($y$-axis). Results were consistent for both HbO and HbR; thus, results are plotted together. Note that the spread of the data is narrower for the corrected data ($y$-axis), resulting in a cleaner signal for the corrected data.

Fig. 9.

Results for the comparison analysis. Top panel shows the mean standard deviation averaged across subjects. Error bars depict the standard error of the mean. The bottom panel shows the scatter plots for the ${\mathrm{AUC}}_{0-2}$ and ${\mathrm{AUC}}_{2-6}$ metrics for both HbO (shown in red circles) and HbR (shown in blue triangles), no motion correction on the $x$-axis versus CBSI, spline, tPCA, and Wavelet on the $y$-axis.

To ensure all techniques outperformed the data without motion correction, we conducted a mixed factor ANOVA with technique (no correction, correction) and Hb (HbO and HbR) as within-subject factors and age as a between-subject factor on a channel-by-channel basis for each technique separately for the different metrics. For each analysis that showed an effect of technique, we conducted posthoc comparisons to determine which technique performed quantitatively better along that metric. Results are shown in Table 3. Consistent with expectations, all the techniques showed a quantitative improvement in the NIRS signal relative to No Correction, although Wavelet showed the weakest performance on this front. As in the previous ANOVA, most significant effects resulted from comparisons of the ${\mathrm{AUC}}_{0-2}$ and the SubSD metrics. For the ${\mathrm{AUC}}_{0-2}$ metric, tPCA substantially outperformed no correction relative to its counterparts. Similarly, for the SubSD metric, tPCA and spline outperformed No Correction relative to the other techniques. Note that No Correction outperformed all techniques on the ${\mathrm{AUC}}_{2-6}$ metric. Recall that this metric captures the rise and peak of the hemodynamic response. This suggests that the motion correction techniques are reducing the amplitude of the hemodynamic response as a result of correcting artifacts. Importantly, however, the ratio metric, which is a normalized index of the amplitude relative to the signal at the start of the hemodynamic response window, reveals that tPCA outperformed No Correction in more instances than the other techniques.

Table 3.

Technique versus no correction. Table shows a summary of the number of times a technique outperformed the no correction method in channels, where there was a significant effect of technique, technique by age interaction or technique by Hb interaction on each metric. Numbers in parenthesis indicate the number of times the no correction method outperformed a technique.

Metrics	Techniques (no correction)
	CBSI	Wavelet	Spline	tPCA
AUC02	20 (0)	24 (0)	27 (5)	44 (0)
AUC26	5 (14)	7 (17)	3 (5)	7 (19)
Ratio	1 (2)	6 (7)	0 (2)	9 (6)
SubSD	57 (0)	39 (26)	87 (0)	90 (0)
Total	83 (16)	76 (50)	117 (12)	150 (25)

Considered together, our results show that CBSI does a good job along some metrics quantitatively, but we note that this technique sometimes yields inconsistent corrected hemodynamic responses. tPCA and spline, on the other hand, do a good job quantitatively across the board and yield robust measured hemodynamic responses. Thus, as a last analysis step, we explored how these two approaches fared against each other.

A mixed factor ANOVA with technique (spline, tPCA) and Hb (HbO and HbR) as within-subject factors and age as a between-subject factor was computed on a channel-by-channel basis for each of the metrics. The number of instances where each technique performed better than its counterpart in channels with a significant effect of technique was tallied. Overall, tPCA outperformed spline in 35 versus 13 cases across all metrics. Thus, tPCA appears to be the most effective motion correction method for our dataset.

Note that an additional set of analyses following the procedure from Buss et al.² was implemented to explore whether removing outliers would influence how these techniques perform. Outlier trials were removed that contained amplitudes that were more than 3.5 standard deviations above or below a participant’s mean in each condition for 18 consecutive time samples. A technique $X$ outlier removal ANOVA was computed for all the metrics. Given that some of these techniques rely on the variability present in the time series, we hypothesized that removing outlier observations from the data would improve how the techniques performed. This was not the case; removing outliers did not have a significant effect on the performance of the techniques for any of the quantitative metrics ($p>0.05$).

3. Discussion

Given the prevalence of motion artifacts, several recent papers have evaluated the efficacy of different motion correction techniques for fNIRS data. These comparisons have mostly relied on simulated data; less is known about how these techniques work on empirical data from cognitive tasks. Brigadoi et al.¹² showed that Wavelet outperformed the other motion techniques in a dataset from adult participants, whereas Hu et al.³⁰ showed that a combination of wavelet filtering and a moving average outperformed other techniques on a dataset from older children ($\text{mean age}=9.9\text{years}$). In the present study, we used a comparable approach to examine which techniques are most effective with data from young children. This is an important contribution given that data from young children often have more, and potentially different, motion artifacts. Moreover, discarding trials due to motion is less viable given that participants can only complete a handful of trials. Note that the present investigation may also provide useful information for researchers using fNIRS to study brain activity in aging adults or patient populations (i.e., epileptic or Alzheimer’s patients). Like young children, these participants may generate a higher quantity of motion artifacts and may also generate different kinds of motion artifacts. Selb at al.³¹ reported that the best way to limit the effect of motion artifacts in oscillation data from stroke patients is to discard the contaminated epochs. This approach, is not optimal given how frequent these artifacts can be present in these population. Thus, continuous development of correction techniques and investigating its effects with real-task based data remains an important topic of study.

In their report, Hu et al.³⁰ classified motion artifacts info four different types. Those types include fast spikes (within 1 s), peaks with a standard deviation of 100 from the mean with a duration of 1 to 5 s, gentle slopes between 5 and 30 s that deviated 300 from the mean, and a slow baseline shift longer than 30 s. In the present study, motion artifacts consisted primarily of type 1 from Hu et al., that is, fast spikes (0.3 to 1 s).

Our results suggest that CBSI was effective at correcting for motion artifacts for some metrics, although a qualitative look at how CBSI affected the resultant hemodynamic response across conditions raised concerns that this approach might be producing unstable hemodynamic responses. tPCA and spline performed more robustly, outperforming the other motion correction techniques both in the number of trials recovered and across multiple quantitative metrics of interest. Note that both of these techniques rely on a first pass of motion artifact detection and we used conservative detection parameters from Brigadoi et al.¹² for this initial pass through the data. This has the advantage of detecting multiple types of motion epochs and attempting to correct them. Then, we used relaxed motion detection parameters in the second pass to exclude primarily fast spikes and allow more data to pass through to the block average for each participant. This approach seemed quite effective. Although both approaches fared well, in a head-to-head comparison, tPCA performed quantitatively better. Thus, we conclude that tPCA is the most effective motion correction technique with our data.

Another advantage of tPCA is that it targets specific epochs, where the artifacts are present.³² Given that motion artifacts are often distributed throughout a data collection session, this means that fewer trials are likely to be lost due to motion. This is particularly important in cases where there is a high quantity of artifacts and a small number of trials. Consistent with this, the PCA algorithm—which does not target motion epochs, but rather requires that an artifact be presented in multiple channels to be identified as a principal component—eliminated too many trials to make it viable for our dataset.

The spline technique performed well in the quantitative analysis but interestingly, it did not fully correct as many artifacts as other techniques (see Fig. 7), even though it does reduce the amplitude of these epochs. This could explain why it performed similarly to the no correction method on the ratio metric. Previous studies have reported that spline can yield inconsistent results across studies.^{12,23,28,30,41} This technique works by generating a cubic spline function based on previously detected artifacts and then removing this function from the signal. The inconsistency might arise because artifacts can be highly variable; thus, using umbrella parameters (i.e., the same parameters across participants) could result in the interpolation function fitting some artifacts but not others.

One concern with the motion correction approaches is that they appear to be dampening the resultant amplitude of the hemodynamic response. For instance, after correction, the signal amplitude in Fig. 9 is narrow, particularly for Wavelet. Recall that in this article we calculated an average measured hemodynamic response across conditions to reduce the number of comparisons. This could be having a dampening effect in the measured response. However, this effect could also suggest that when many artifacts are present, there is a risk of over-correcting, that is, removing important variance from the hemodynamic response of interest. This is particularly plausible in data from young children where artifacts are distributed throughout the time series, including within the response of interest. In the present report, the amplitudes of the resultant hemodynamic response when plotted by condition were around $0.2\mu \mathrm{M}$. Hemodynamic response amplitudes from our previous study² were in the same range (0.2 to $0.5\mu \mathrm{M}$). Thus, it appears that overcorrection is not a major concern here. That said, it is important to tailor the motion correction parameters to the properties of each dataset to ensure that overcorrection does not occur.

Our results also provide insights into why some techniques perform better than others with data from young children. For instance, techniques that do not rely on any motion detection algorithm and assume that an artifact should be present on multiple channels, such as PCA, performed poorly because this assumption was not met in our data; consequently, these approaches eliminated too many trials. On the contrary, techniques relying on motion detection performed better because, after detection and then correction, more trials are kept, thus increasing the signal-to-noise ratio of the data. Furthermore, our data suggest that tPCA performed better than spline because spline removes the signal when an artifact is identified. If many motion artifacts are identified, as in our dataset, this method removes potentially useful signal. By contrast, tPCA removes only some of the variance, potentially retaining a portion of the signal of interest even if many artifacts are identified. These results highlight the importance of not only selecting the right parameters when processing fNIRS data but also sheds light on why some techniques outperform others with highly contaminated data.

Great strides have been made in finding reliable motion correction techniques for fNIRS data. Our study has contributed to this body of work by evaluating different techniques head to head with data from young children from a cognitive task, and considering multiple motion detection parameter settings. Of course, new motion processing approaches are always in development; thus, future work will be needed to continually re-evaluate new approaches such as a recent kurtosis-based wavelet filtering approach,²⁵ EMD,²⁶ and an optical model on the influence of optode fluctuation on the fNIRS signal²⁷ as well as the autoregressive algorithm developed by Barker et al.²⁴ We note that the autoregressive algorithm was not included in our analysis because this approach uses deconvolution techniques rather than the block average approach evaluated here.

Note that Umeyama’s approach to detect optode fluctuations prior to starting data collection provides a great advancement in our understanding of how some artifacts are generated,¹⁸ and could potentially help reduce the quantity of artifacts. We suspect, however, that this approach may have limited application with young children given that it adds an extra step to data collection, which might result in the participant not completing the task. Future work should investigate Yamada’s optical model²⁷ to correct for these placement faults in data from children.

Although our results provide evidence that tPCA is a promising choice for correcting motion artifacts in fNIRS data, it is necessary to consider some details about our design. In this experiment, we used a variable intertrial-interval (mean 12.3 s, min 2.3 s), mostly driven by the child being ready and paying attention to continue on to the next trial. This, of course, means that the hemodynamic response of interest, recovered by block average, is different for short ITI versus long ITI trials. However, this added between-trials variability is present for all techniques; thus, we do not think this concern undermines our conclusions. Furthermore, the DPF factor used in the study was the default parameter in HomER2, 6.0 for both wavelenghts, and was not corrected for age. Note that recent work by Li et al.,⁴² used the same parameter (6.0) in a comparable sample (3- to 5-year-olds). Previous work suggests that a DPF of 4.8 to 5.13, depending on the wavelength, should be used when estimating concentration changes in frontal–frontotemporal data from children.⁴³ However, anatomical differences across individuals may also play a role in regard to this calculation.⁴³ Although we acknowledge this parameter is important to accurately model concentration changes, we used a parameter previously used in the literature⁴² and kept it consistent across techniques thus we do not think this undermines out conclusions. Future work should explore if this has an effect in our ability to investigate the efficacy of motion correction techniques.

4. Conclusion

Correcting motion artifacts that contaminate the signal of interest is a critical step when processing fNIRS data. To estimate the true hemodynamic response, it is crucial that these artifacts are detected and removed. Our results showed that tPCA, spline, Wavelet, and CBSI outperformed PCA in terms of retaining a higher number of trials. CBSI, spline, and tPCA also performed well in direct head-to-head comparisons with the other approaches using a set of quantitative metrics. The CBSI method corrected many of the artifacts present in our data; however, this approach produced sometimes unstable corrected hemodynamic responses. The targeted PCA and spline methods, on the other hand, proved to be the most robust, performing well across all comparison metrics. When compared head-to-head, tPCA consistently outperformed spline. This is consistent with what Yücel et al.³² reported when comparing tPCA, spline, and Wavelet in a dataset where a synthetic hemodynamic response was introduced to a raw NIRS signal. Thus, we conclude that tPCA is a promising choice for correcting motion artifacts in fNIRS data from young children as well as datasets with a high number of motion artifacts.

Biographies

Lourdes M. Delgado Reyes received her MA degree from the University of Iowa in 2015. She is a PhD candidate in the School of Psychology at the University of East Anglia. Her research interest includes understanding the neurobehavioral precursors of executive function in early development using a combination of fNIRS, MRI, and eye-tracking methodologies.

Kevin Bohache received his MA degree from the University of Iowa in 2014. Currently, he is a high school science teacher at Teach for America in Cincinnati, Ohio.

Sobanawartiny Wijeakumar received her PhD in visual perception from Glasgow Caledonian University, Scotland, U.K., in 2012. She is a lecturer in the School of Psychology at the University of Stirling, Scotland, U.K. Her research interests include understanding the neurobehavioral correlates of visual working memory, inhibition and cognitive flexibility along the lifespan using a combination of fNIRS, fMRI, EEG, and eye-tracking methodologies.

John P. Spencer received his Sc.B. with honors from Brown University in 1991 and his PhD in experimental psychology from Indiana University in 1998. He is a professor of psychology at the University of East Anglia in Norwich, U.K. He is the recipient of the 2003 Early Research Contributions Award from the Society for Research in Child Development, and the 2006 Robert L. Fantz Memorial Award from the American Psychological Foundation.

Disclosures

The authors have no conflict of interest.