Development and Validation of RAPID: A Patient-Specific Monte Carlo Three-Dimensional Internal Dosimetry Platform

Abstract

This work describes the development and validation of a patient-specific Monte Carlo internal dosimetry platform called RAPID (Radiopharmaceutical Assessment Platform for Internal Dosimetry). RAPID utilizes serial PET/CT or SPECT/CT images to calculate voxelized three-dimensional (3D) internal dose distributions with the Monte Carlo code Geant4. RAPID's dosimetry calculations were benchmarked against previously published S-values and specific absorbed fractions (SAFs) calculated for monoenergetic photon and electron sources within the Zubal phantom and for S-values calculated for a variety of radionuclides within spherical tumor phantoms with sizes ranging from 1 to 1000 g. The majority of the S-values and SAFs calculated in the Zubal Phantom were within 5% of the previously published values with the exception of a few 10 keV photon SAFs that agreed within 10%, and one value within 16%. The S-values calculated in the spherical tumor phantoms agreed within 2% for ¹⁷⁷Lu, ¹³¹I, ¹²⁵I, ¹⁸F, and ⁶⁴Cu, within 3.5% for ²¹¹At and ²¹³Bi, within 6.5% for ¹⁵³Sm, ¹¹¹In, ⁸⁹Zr, and ²²³Ra, and within 9% for ⁹⁰Y, ⁶⁸Ga, and ¹²⁴I. In conclusion, RAPID is capable of calculating accurate internal dosimetry at the voxel-level for a wide variety of radionuclides and could be a useful tool for calculating patient-specific 3D dose distributions.

Introduction

Patient-specific internal dosimetry is important for establishing dose–response relationships during radiopharmaceutical clinical trials and for treatment planning during targeted radionuclide therapy. Currently, the only internal dosimetry software approved by the U.S. Food and Drug Administration (FDA), is OLINDA/EXM (Organ Level Internal Dose Assessment for EXponential Modeling).¹ OLINDA/EXM calculates absorbed doses using the RAdiation Dose Assessment Resource (RADAR) formalism, which is almost identical to the formalism developed by the Medical Internal Radiation Dose (MIRD) committee of the Society of Nuclear Medicine.² OLINDA/EXM uses tabulated activity-to-dose scaling factors, commonly referred to as dose factors or S-values, that are generated based on standard phantoms and are used to estimate organ-level absorbed doses.^3,4 Tumors are modeled separately as unit-density spheres in an infinite unit-density medium.

The major limitations of the organ S-value method implemented in OLINDA/EXM are that (1) phantoms are not an accurate representation of each patient's unique geometry, (2) the radioactivity uptake and dose deposition are assumed to be uniformly distributed within each organ, and (3) the tumor not being modeled as part of the phantom could lead to an underestimate of the normal tissue and tumor dose.⁵ Studies^5–11 comparing the differences in mean absorbed doses computed using OLINDA/EXM with doses computed using Monte Carlo simulations based on patient CT images have reported differences as high as 31% for tumors⁵ and 97% (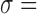 83%) for normal tissues.¹¹

Currently three main approaches exist that are capable of calculating internal dosimetry on the voxel-level: dose point kernel convolution, dose voxel kernel convolution that uses voxel-level S-values based on the MIRD formalism, and direct Monte Carlo radiation transport.

Dose point kernels describe the dose deposition from an isotropic point source as a function of the distance from the source and are obtained from Monte Carlo simulations tallying the energy deposition in concentric spherical shells around a point source in a homogeneous medium.¹² To account for tissue heterogeneities, the dose point kernels are commonly scaled linearly as a function of the radiological distance and a collapsed cone superposition algorithm can be used to speed up the convolution of the dose point kernel with the three-dimensional (3D) activity distribution.^13,14

The voxel-level S-value method was developed as an extension of the MIRD formalism from organ S-values to voxel S-values.² Several software packages have been developed that utilize voxel-level S-values for internal dosimetry including STRATOS,¹⁵ VoxelDose,¹⁶ MrVoxel,¹⁷ VoxelMed,¹⁸ RTDS,¹⁹ RMDP,²⁰ VRAK.²¹ Voxel-level S-values are calculated by integrating the dose point kernels over the source and target voxels. Voxel-level S-values must be tabulated for each radionuclide, voxel size, source-to-target distance, and absorbing medium. The voxelized dose distribution is calculated by convolving the activity distribution with the voxel S-values typically using a fast Fourier transform or fast Hartley transform²² rather than direct convolution to speed up the calculation. The increase in speed comes at the cost of using a spatially invariant kernel that does not take into account tissue heterogeneities. A simple density correction suggested by Dieudonné et al. was shown to reduce organ-level dose errors from 5.9% to 1.1% and voxel-level dose errors from 14% to 4% in the abdomen.²³ However, the application of this technique may not be well suited for more heterogeneous regions like the thorax, head, and neck, and skeletal site such as the bone marrow.

Direct Monte Carlo methods based on general purpose Monte Carlo codes such as Geant4,²⁴ MCNP,²⁵ or EGS²⁶ calculate voxelized distributions based on direct radiation transport and are capable of accounting for tissue inhomogeneity. Many groups have developed voxel-based Monte Carlo internal dosimetry programs including DOSIMG,²⁷ simDOSE,²⁸ SIMDOS,²⁹ MINERVA,³⁰ VIDA,⁷ OEdipe,³¹ RAYDose,³² JADA,³³ SCMS,³⁴ DPM,³⁵ and 3D-RD.⁸ These programs vary widely in their complexity, capabilities, and applications. Despite the large variety of promising software packages, a direct Monte Carlo dosimetry treatment planning system has not gained wide enough acceptance to be utilized in clinical practice.

This work describes the development and validation of a Monte Carlo internal dosimetry platform called RAPID (Radiopharmaceutical Assessment Platform for Internal Dosimetry) that was developed to facilitate more accurate and patient-specific internal dosimetry calculations. Each step of the RAPID's workflow is described including the image acquisition and preprocessing, Monte Carlo dose calculations, temporal image coregistration, pharmacokinetic fitting, radiobiological modeling, and output visualization and analysis. In this work, RAPID's dose calculations were computationally benchmarked by comparing S-values and specific absorbed fractions (SAFs) calculated in standard phantoms with previously published reference values. RAPID's normal tissue dosimetry was benchmarked against S-values and SAFs calculated by Yoriyaz et al.³⁶ and Chiavassa et al.³⁷ for monoenergetic photon and electron sources within the Zubal phantom.³⁸ Additionally, RAPID's tumor dosimetry was benchmarked against S-values calculated with OLINDA/EXM¹ for a variety of radionuclides within spherical tumor phantoms with sizes ranging from 1 to 1000 g.

Materials and Methods

Platform framework

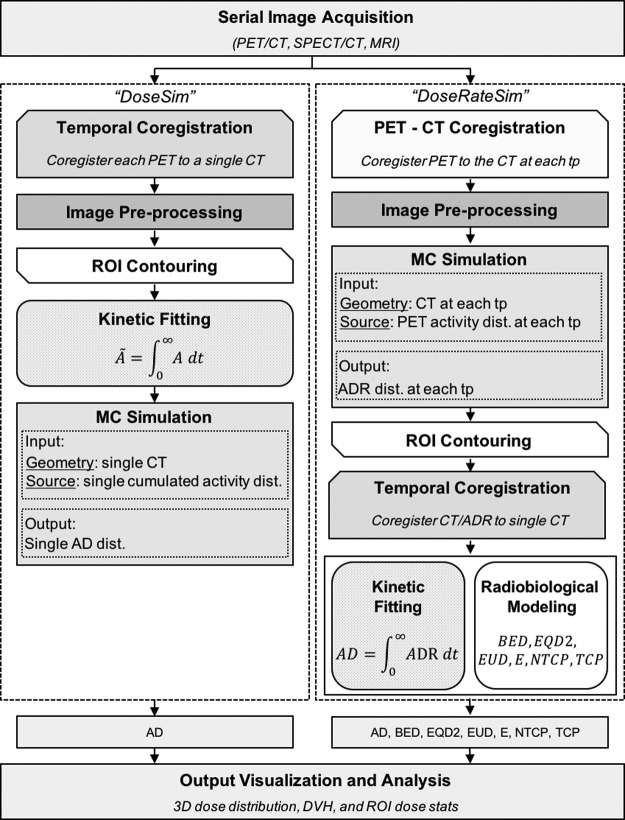
The framework of the dosimetry platform is presented in Figure 1. First, images are acquired at multiple time points to map the agent's pharmacokinetics. The absorbed dose is calculated using either the “DoseSim” or the “DoseRateSim” workflow.

FIG. 1.

The RAPID framework and workflow. Serial 3D images (PET/CT or SPECT/CT) are acquired to map the agent's pharmacokinetics and geometry. The AD can be calculated using either the “DoseSim” or “DoseRateSim” method. In the “DoseSim” method, the activity distribution is time-integrated on a voxel-by-voxel basis to obtain a single cumulated activity distribution in the pharmacokinetic fitting module. A single CT and cumulated activity distribution are used as the input for the MC simulation that then generates a single absorbed dose distribution as output. In the “DoseRateSim” method, the PET/SPECT and CT at each TP are used as input for the Monte Carlo simulation and an ADR distribution is simulated for each time point. The absorbed dose rate at each time point is coregistered to a single CT and resampled. The absorbed dose is calculated by time-integrating the absorbed dose rate in kinetic fitting module and radiobiological dose metrics are calculated in the radiobiological modeling module. The dosimetry output includes 3D dose distributions, DVHs, DVH stats, and region of interest dose stats. 3D, three-dimensional; AD, absorbed dose; ADR, absorbed dose rate; DVHs, dose volume histograms; MC, Monte Carlo; RAPID, Radiopharmaceutical Assessment Platform for Internal Dosimetry; TP, time point.

In the “DoseSim” method, the PET/SPECT at each time point are coregistered and resampled to a single CT. The activity is then time-integrated on a voxel-by-voxel basis to obtain a single cumulated activity distribution in the pharmacokinetic fitting module. A single CT and cumulated activity distribution are used as the input for the Monte Carlo simulation, which then generates a single absorbed dose distribution as output.

In the “DoseRateSim” method, first the PET/SPECT images are fused to the CT at each time point. Then, the PET/SPECT and CT at each time point are used as input for the Monte Carlo simulation and an absorbed dose rate distribution is simulated for each time point. The absorbed dose rate at each time point is coregistered to a single CT and resampled. The absorbed dose rate is then time-integrated in the kinetic fitting module to obtain the absorbed dose and radiobiological dose metrics are calculated in the radiobiological modeling module.

If radiobiological dose metrics are not needed, then the “DoseSim” method is advantageous because there is only one simulation that makes the method less computationally intensive. The “DoseRateSim” method must be used, however, if radiobiological dose metrics are needed because they are calculated based on absorbed dose rates.

The majority of RAPID is written in MATLAB (Mathworks, Natick, MA) with the exception of the image coregistration and region of interest (ROI) contouring, which is performed using the AMIRA software (AMIRA, Mercury Computer Systems, Berlin, Germany) and the Monte Carlo simulations that are run using Geant4.²⁴ The development and functionality of each element in the platform's workflow are detailed in the following sections.

Image acquisition and preprocessing

Patient-specific dosimetry is calculated based on serial quantitative preclinical or clinical SPECT/CT or PET/CT images acquired at multiple time points after injection of a radiopharmaceutical to map the patient's unique pharmacokinetics and anatomy. Following acquisition, the images are coregistered, resampled, rescaled, corrected for partial volume effects, and masked. First, the PET/SPECT images are coregistered to the CT at each time point, using a normalized mutual information affine transformation with 12 degrees of freedom (3 rotational, 3 translational, 3 scaling, and 3 shearing). This type of registration is commonly used for the fusion of multi-modality images.^39,40 The temporal image coregistration over all time points will be discussed in Temporal Image Coregistration section.

The PET/SPECT is either up-sampled to match the higher CT resolution or the CT is down-sampled to match the lower PET/SPECT resolution. Given that Monte Carlo dosimetry relies both on accurate quantification of the activity distribution by the PET/SPECT and the material composition/density by the CT, each resampling option has both advantages and disadvantages. Up-sampling the PET/SPECT is advantageous because ROIs can be more accurately delineated on the higher resolution CT and the simulation results in finer dose deposition grid since energy deposition is scored on the CT. However, higher resolutions increase the simulation run time and uncertainty in the activity quantification is introduced when up-sampling the PET/SPECT image. Down-sampling the CT is advantageous because the lower resolution reduces the simulation time. However, the loss of resolution in the CT reduces the accuracy of ROI segmentation and dose deposition scoring and introduces uncertainties in the CT number to material conversion. Resampling is performed using the Mitchell filter kernel, which offers a good compromise between ringing and blurring artifacts.⁴¹

If the pre-treatment PET/SPECT images were acquired using a different radionuclide than the therapeutic radionuclide, then the radioactivity of the imaging/tracer radionuclide is converted to the radioactivity of the therapeutic radionuclide by assuming the same injection activity and accounting for the difference in physical decay rates. If needed, partial volume corrections are applied to the PET/SPECT images to correct for the apparent loss of activity in small regions due to the limited image resolution.^42,43 A mask contour of the whole body is created based on the CT volume at each time point and is applied to the PET/SPECT to remove any background activity outside the patient. This reduces the Monte Carlo simulation time by eliminating extraneous sources.

ROI contouring

The tumors and normal tissues are contoured using anatomical and functional images. The ROIs are contoured manually or by using a thresholding method based on the CT hounsfield units (HU), PET/SPECT radioactivity concentration, standardized uptake values, or tumor-to-background ratios.

Monte Carlo simulations

The Monte Carlo dose calculations are performed using Geant4 version 9.6.²⁴ Geant4 is a versatile object-oriented simulation toolkit that allows for the modeling of complex geometries, radiation sources, and detectors. Geant4 has been benchmarked for a variety of different medical physics applications.^44–47

The CT and the PET/SPECT images are used in the Monte Carlo simulation to define the geometry and source distribution, respectively. The CT images define the material composition and mass density of the simulation geometry. The entire HU range is segmented into 27 materials based on the human tissue compositions defined by Schneider et al.⁴⁸ Each HU is assigned a unique mass density according to the CT scanner specific calibration. If the scanner CT-to-density information is unknown, then the conversion defined in Schneider et al. is used.

For the “DoseRateSim” method, the PET/SPECT images are used to define the radionuclide activity in each voxel and the absorbed dose rate distribution is simulated at each time point. For the “DoseSim” method, the time-integrated activity distribution is used to define the cumulated activity in each voxel and a single absorbed dose distribution is simulated. The decay is simulated using the G4RadioactiveDecay module⁴⁹ that allows the simulation of the decay of more than 2000 radioactive nuclei using the decay information from the ENSDF database.⁵⁰ The point of the radionuclide decay is sampled uniformly throughout each voxel.

The statistical relative error in the mean absorbed dose rate is calculated on the voxel and ROI-level. Sufficient particles are simulated such that the average ROI-level relative error is less than 1% and the average voxel-level relative error within the patient volume is less than 10%. Note that the relative error only refers to the statistical precision of the Monte Carlo dose calculation and does not take in to account other sources of uncertainty such as the activity quantification, material/density quantification, coregistration, resampling, kinetic fitting, or ROI contouring.

To speed up the simulation time, the simulation jobs can be parallelized into individual slices. The whole patient CT is used to define the patient geometry and calculate the dose deposition but each job only contains one slice of the PET/SPECT defined source distribution. For example, a whole patient simulation would run 1 job containing 80 slices while a simulation parallelized into slices would run 80 jobs each containing 1 slice of the PET/SPECT defined activity distribution. The simulation efficiency of the slice parallelization method was compared with the whole patient parallelization method by calculating the absorbed dose rate distribution at a single time point based on a SPECT/CT image. The image contained 80 slices with a matrix size of 512 × 512 voxels. All simulations were run on the UW Center for High Throughput Computing (CHTC) cluster.

Temporal image coregistration

In addition to the multi-modal image coregistration, the four-dimensional (4D) image series must also be coregistered temporally before integrating on the voxel-level. For the “DoseRateSim” method, the PET/SPECT and the CT images are temporally coregistered before the Monte Carlo simulation. For the “DoseSim” method, the absorbed dose rate distributions and the CT images are temporally coregistered after the simulation.

For cases with reproducible and rigid immobilization during imaging and clinical sites with small variations in the intra- and inter-image growth/movement, whole body affine CT-CT sequential coregistration may be adequate. This method is implemented by registering the CT at each time point is to a single reference CT using normalized mutual information based affine CT-CT coregistration. The CT transformations are then applied to the absorbed dose rate (or activity) distributions at each corresponding time point and the absorbed dose rate (or activity) images are resampled to match the voxel coordinate system of the absorbed dose rate (or activity) at the reference time point. The absorbed dose (or cumulated activity) is calculated on a voxel-basis over the entire image volume.

For most 4D image sets in TRT, a single global affine coregistration may not be able to accurately register each region throughout the entire body due to setup variations during imaging, respiratory/cardiac motion, bladder/rectal filling, tumor shrinkage/growth, or patient weight loss/gain. For these cases, locally affine coregistration may be an attractive alternative to more complicated deformable methods.^32,51,52 The locally affine piecewise ROI-ROI coregistration method used within RAPID was adapted from Pitiot et al.⁵³ who proposed a piecewise affine registration algorithm where sub-images are extracted and coregistered independently using a hybrid affine/nonlinear interpolation scheme. First, ROIs are generated from the PET/CT or SPECT/CT at each time point. Each ROI contour is then isolated and registered independently to the ROI at a single reference time point using a normalized mutual information based affine coregistration. The transformation used to register the ROIs is then replicated for the absorbed dose rate distribution at each time point. The absorbed dose rate distribution at each time point is then resampled so that the coregistered absorbed dose rate distributions will have the same voxel coordinate system and the absorbed dose rate can be integrated on a voxel-by-voxel basis. The absorbed dose is then calculated by integrating the absorbed dose rate only for the voxels within each of the ROIs.

One drawback of this method is that the ROI contours must be generated a priori at each time point. Another drawback is that full body dose distributions cannot be calculated because the absorbed dose rate is integrated only within the ROIs. However, dose statistics and dose volume histograms (DVHs) can be generated for any coregistered ROI.

Alternatively, deformable image registrations could be performed using an external software such as RayStation (RaySearch Laboratories, Stockholm, Sweden), MIM (Cleveland, OH), or Velocity (Varian Medical Systems, Palo Alto, CA), however, that is not currently a part of the validated RAPID workflow.

Kinetic fitting

The total absorbed dose (or cumulated activity) is calculated by integrating the absorbed dose rate (or activity) over all time on the voxel- or ROI-level. The shape of the pharmacokinetic curve depends on the targeted radionuclide therapy agent- and radionuclide-specific kinetics in addition to the number and frequency of time points chosen to image and track the kinetics. The curve consists of three main regions: preimaging- the time from injection to the first imaging time point (), imaging- the time between the first and final time points (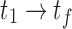), and postimaging- the time from the final time point to infinity (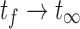). Since imaging data is not available for the first and third regions, the absorbed dose rate must be extrapolated from the imaging region.

The temporal absorbed dose rate curve is fitted with one of the following options: (1) bi-exponential fit, (2) mono-exponential fit, (3) piecewise linear fit, and (4) mono-exponential fit with linear uptake.

The first two methods use a single bi-exponential or mono-exponential curve to fit the absorbed dose rate and the absorbed dose is calculated by integrating the equation analytically.^{1,32,33,54–56} These methods should only be used if the curve fitting degrees of freedom (i.e., the difference between the number of measured image time points and the number of parameters in the fit) is greater than one.

The third method uses a piecewise linear fit within the imaging region that is integrated numerically (i.e., trapezoidal rule).^32,57 Within the postimaging region, the decay is extrapolated exponentially with the physical decay,⁵⁷ decay fitted from the last two time points,³² or a combination of both.⁵⁷ Within the preimaging region, the absorbed dose rate is extrapolated back linearly from t₁ to t₀ either by assuming no initial uptake at the injection time so that 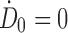^55,58 or assuming instantaneous uptake and fitting a line from the first two time points so that 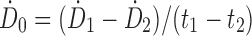, where 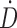is the dose rate and t is the time of the first and second time points.³² The linear extrapolation is advantageous because it can model uptake or decay. The impact of the preimaging fitting method decreases when the first image is acquired promptly after injection.

The fourth method fits the absorbed dose rate with a mono-exponential equation and the uptake is fit linearly using the first two time points.^32,55,59 The absorbed dose is calculated by integrating the linear uptake from t₀ to the intersection point of the line and the mono-exponential between the first and second time points and integrating the mono-exponential analytically from the intersection point to .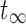

The fits are applied using either the “ForcedFit” or “AutoFit” option. The ForcedFit option applies one of the above fitting methods to all voxels or ROIs regardless of the number of image time points or the goodness of fit. Alternatively, the AutoFit option automatically fits the absorbed dose rate curve with a mono- or bi-exponential function if there are a sufficient number of image time points. AutoFit uses the exponential fit with the largest squared Pearson correlation coefficient (R²) value. If there are not enough time points for curve fitting or the analytical equation does not fit the curve well (i.e., the R² value is less than a desired threshold), then a piecewise linear fit is used for that voxel or ROI.

Radiobiological modeling

Radiobiological dose metrics are calculated from the absorbed dose rate including voxel-level metrics such as the biological effective dose (BED) and equivalent dose in 2 Gy fractions (EQD_2) and ROI-level metrics such as the equivalent uniform dose (EUD), equivalent biological effect 60 (E), normal tissue complication probability (NTCP), and tumor control probability (TCP). Default values for the necessary radiobiological parameters (e.g., 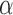, , 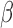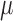) are provided for common tissues and tumor types.

Output visualization and analysis

The absorbed dose is normalized by the administration activity and doses are calculated in units of Gy/GBq of activity administered. The dosimetry output is displayed as 3D absorbed and biological dose distributions overlaid on anatomical images, DVHs, and tables of ROI dose stats (i.e., minimum, mean, maximum, and the standard deviation), and DVH stats such as the volume that receives at least a certain amount of dose (e.g., V_50Gy) or the dose received by a certain percentage of the volume (e.g., D_90%). The 3D dose images are output as binary files and the DVHs and tables are output as .txt files that can be imported into other visualization and plotting programs.

Computational benchmarking

RAPID's dose calculations were benchmarked against reference S-values and SAFs (as defined by the MIRD formalism²) calculated in standard phantoms.

Spherical tumor phantom

To benchmark the tumor dosimetry, S-values were calculated for 1, 10, 100, and 1000 g (∼1.2, 2.6, 5.8, and 12.4 cm diameter) unit-density spherical tumors with uniform activity distributions of 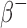(¹⁷⁷Lu, ¹³¹I, ¹⁵³Sm, and ⁹⁰Y), 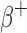(¹⁸F, ⁶⁴Cu, ⁸⁹Zr, ⁶⁸Ga, and ¹²⁴I), 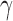(¹¹¹I), Auger (¹²⁵I), and 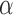(²²³Ra, ²¹¹At, and ²¹³Bi) -emitting radionuclides. The sphere geometries were created out of 1 mm³ voxels to also ensure consistent voxel transport and scoring between the benchmark and patient CT geometries. The spherical sources were embedded in a semi-infinite unit-density voxelized medium. The S-values calculated with RAPID were compared to the references values for spheres of the same mass calculated by the OLINDA/EXM software.¹

Monoenergetic photon SAFs and electron S-values in the Zubal phantom

To benchmark the normal tissue dosimetry, SAFs and S-values were calculated with RAPID and compared with reference values. SAFs for monoenergetic photons of 10 keV, 100 keV, and 1 MeV and S-values for monoenergetic electrons of 935 keV were calculated in the Zubal phantom.³⁸ The Zubal phantom is a voxel based representation of an adult male head and torso that consists of 33 segmented organs and structures. The SAFs and S-values calculated in this work were benchmarked against values previously published by Yoriyaz et al.³⁶ and Chiavassa et al.³⁷ who have developed similar Monte Carlo-based dosimetry software. The calculations done by Yoriyaz et al. used the MCNP-4B Monte Carlo code²⁵ with the SCMS software interface and the calculations done by Chiavassa et al. used the MCNPX Monte Carlo code²⁵ with the OEDIPE software interface. In both cases, the Zubal geometry was simplified to only include air, lung, soft tissue, and bone with densities of 0.0012, 0.296, 1.04, and 1.40 g/cm³, respectively. The tissue material compositions were not mentioned in the previous publications. For the calculations in this work, the material compositions were chosen based on the tissues published by Schneider et al.⁴⁸ that had the closest densities to the density values assumed above. The material compositions are shown in Table 1 for each tissue.

Table 1.

The Density and Material Composition of the Tissues Used in the Simplified Zubal Phantom

		Material composition weights (%)
Tissue	Density (g cm−3)	H	C	N	O	Na	Mg	P	S	Cl	Ar	K	Ca
Air	0.0012	—	—	75.5	23.2	—	—	—	—	—	1.3	—	—
Lung	0.296	10.3	10.5	3.1	74.9	0.2	—	0.2	0.3	0.3	—	0.2	—
Soft tissues	1.04	10.3	13.4	3.0	72.3	0.2	—	0.2	0.2	0.2	—	0.2	—
Bone	1.4	6.6	31.0	3.3	39.4	0.1	0.1	6.1	0.2	—	—	—	13.2

The “—” indicates that the element is not present in the material definition of the tissue.

Results

RAPID simulation performance

Parallelizing the Monte Carlo simulation into individual slices rather than simulating the whole patient at once increased the simulation efficiency and resulted in significantly shorter calculation times. The simulation parameters for each parallelization method are listed in Table 2. Each whole patient job contained approximately 3.5 million source voxels and the slice job with the most sources (which required the longest run time) contained approximately 48.5 thousand source voxels. To achieve an average ROI-level relative error within 1% and a voxel-level relative error within 10%, 100 particles per source voxel were simulated for both parallelization methods (10 jobs with 10 particles per source voxel). Both simulations used approximately 400 MB of memory and 1 central processing unit (CPU) per job. Parallelizing the simulation into slices took 25.8 min to run and simulated 313 particles/sec per job while parallelizing the whole patient took 71.9 h to run and simulated 136 particles/sec per job. Thus, the individual slice parallelization was approximately 167 times faster and 2.3 times more efficient. The slice simulations, however, required extra postprocessing time (around 20 min) to combine the dose from each job into a single absorbed dose rate distribution. Additionally, the slice simulations required additional disk space to store the compressed dose files output for each slice (approximately 2.5 MB each). However, once the dose was extracted and combined into a single absorbed dose rate distribution the individual files were deleted and that disk space was restored. Thus, the use of cluster- or cloud-based computing could allow for patient-specific internal dose calculations in a more clinically feasible time frame.

Table 2.

A Comparison of the Simulation Parameters When Jobs Are Parallelized Using the Whole Patient or Individual Slices to Define the Radionuclide Source Distribution

	Parallelization method
	Whole patient	Slice
Max source voxels/job	3,508,650	48,505
Number of slices/job	80	1
Number of jobs	10 (1 10)	800 (80 10)
Run time	71.9 h	25.8 min
Efficiency (particles/sec)	136	313
Memory (MB)/job	406	400
CPUs/job	1	1

CPUs, central processing units.

Computational benchmarking

Spherical tumor phantom

The percent differences between the RAPID and OLINDA/EXM S-values calculated in the spherical phantoms are shown in Table 3 for each radionuclide and sphere size. A positive difference indicates that the RAPID S-value was larger than the OLINDA/EXM S-value. The S-values calculated with RAPID agreed well with the OLINDA/EXM reference values. The agreement was within 2% for ¹⁷⁷Lu, ¹³¹I, ¹²⁵I, ¹⁸F, and ⁶⁴Cu, within 3.5% for ²¹¹At and ²¹³Bi, within 6.5% for ¹⁵³Sm, ¹¹¹In, ⁸⁹Zr, and ²²³Ra, and within 9% for ⁹⁰Y, ⁶⁸Ga, and ¹²⁴I.

Table 3.

The Percent Difference in the Spherical S-Values Calculated with RAPID and the OLINDA/EXM Reference Values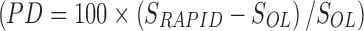

	Percent difference between RAPID and OLINDA/EXM (%)
Sphere mass (g)	177Lu	131I	153Sm	90Y	111In	125I	18F	64Cu	89Zr	68Ga	124I	223Ra	211At	213Bi
1	0.2	0.1	−2.6	−7.2	6.3	2.0	−0.5	−1.2	3.4	−7.4	−8.8	6.0	3.4	3.0
10	−2.1	−0.6	−4.7	−4.8	4.0	−0.6	−1.8	−2.0	3.8	−5.6	−6.5	5.4	1.0	0.9
100	−1.1	−0.3	−4.0	−1.4	4.6	0.2	−0.2	−0.2	5.1	−2.5	−3.4	6.3	1.8	1.9
1000	−1.4	−0.5	−5.3	−1.0	1.4	1.1	−0.4	−0.2	3.6	−1.6	−2.3	6.4	1.8	2.1

A positive value indicates that the RAPID S-value was larger than the reference value.

OLINDA/EXM, Organ Level Internal Dose Assessment for EXponential Modeling; RAPID, Radiopharmaceutical Assessment Platform for Internal Dosimetry.

Monoenergetic photon SAFs and electron S-values in Zubal phantom

The 10 keV, 100 keV, and 1 MeV photon SAF ratios calculated with SCMS, OEdipe, and RAPID are shown in Tables 4–6, respectively. The 935 keV electron S-value ratios are shown in Table 7. Overall, the Zubal Phantom SAFs and S-values calculated with RAPID agreed well with the reference values. All 935 keV electron S-values and 100 keV and 1 MeV photon SAFs differed by less than 5% from the reference values. Out of the 36 photon SAFs calculated for the 10 keV photons, 22 of them had an agreement within 5%, 12 agreed within 5–10%, and the SAF (Liver Pancreas) and SAF (Pancreas Liver) agreed within 16%.

Table 4.

Ratios of the 10 keV Photons Specific Absorbed Fraction Values Calculated with SCMS, OEdipe, and RAPID in the Zubal Phantom

		Source organ
Target organ	Method	Liver	Kidneys	Lungs	Pancreas	Spleen	Adrenals
Liver	RAPID vs. SCMSa	1.004	0.047	0.939	0.843	1.000	0.899
	RAPID vs. OEdipe	1.004	0.918	0.971	0.823	1.000	0.912
	SCMSa vs. OEdipe	1.000	19.398	1.035	0.977	1.000	1.014
Kidneys	RAPID vs. SCMSa	0.937	1.005	1.000	0.900	0.914	0.902
	RAPID vs. OEdipe	0.917	1.005	1.000	0.913	0.912	0.909
	SCMSa vs. OEdipe	0.979	1.000	1.000	1.015	0.998	1.008
Lungs	RAPID vs. SCMSa	0.915	1.000	1.004	1.000	0.910	0.910
	RAPID vs. OEdipe	0.894	1.000	1.002	1.000	0.904	0.904
	SCMSa vs. OEdipe	0.977	1.000	0.999	1.000	0.993	0.993
Pancreas	RAPID vs. SCMSa	0.846	0.883	1.000	1.012	1.000	0.930
	RAPID vs. OEdipe	0.846	0.929	1.000	1.012	1.000	0.873
	SCMSa vs. OEdipe	1.000	1.053	1.000	1.000	1.000	0.939
Spleen	RAPID vs. SCMSa	1.000	1.000	1.000	1.000	1.000	1.000
	RAPID vs. OEdipe	1.000	1.000	1.000	1.000	1.000	1.000
	SCMSa vs. OEdipe	1.000	1.000	1.000	1.000	1.000	1.000
Adrenals	RAPID vs. SCMSa	0.992	0.921	1.000	0.937	1.000	1.016
	RAPID vs. OEdipe	0.937	0.927	1.000	0.947	1.000	1.016
	SCMSa vs. OEdipe	0.944	1.006	1.000	1.011	1.000	1.000

SAF, specific absorbed fraction.

Table 5.

Ratios of the 100 keV Photons SAF Values Calculated with SCMS, OEdipe, and RAPID in the Zubal Phantom

		Source organ
Target organ	Method	Liver	Kidneys	Lungs	Pancreas	Spleen	Adrenals
Liver	RAPID vs. SCMSa	0.982	0.973	0.948	0.991	0.969	0.974
	RAPID vs. OEdipe	1.021	1.031	1.043	1.026	1.051	1.006
	SCMSa vs. OEdipe	1.039	1.059	1.101	1.036	1.085	1.033
Kidneys	RAPID vs. SCMSa	0.976	1.000	0.954	1.000	0.968	0.986
	RAPID vs. OEdipe	1.043	1.018	1.056	1.031	1.031	1.009
	SCMSa vs. OEdipe	1.069	1.019	1.107	1.031	1.064	1.023
Lungs	RAPID vs. SCMSa	0.942	0.939	0.981	0.951	0.937	0.937
	RAPID vs. OEdipe	1.029	1.028	1.009	1.014	1.021	1.021
	SCMSa vs. OEdipe	1.092	1.095	1.029	1.065	1.090	1.090
Pancreas	RAPID vs. SCMSa	1.002	1.014	0.991	1.002	0.968	1.000
	RAPID vs. OEdipe	1.013	1.026	1.009	1.008	1.026	1.020
	SCMSa vs. OEdipe	1.011	1.012	1.018	1.006	1.060	1.019
Spleen	RAPID vs. SCMSa	0.954	0.974	0.952	0.965	0.988	0.967
	RAPID vs. OEdipe	1.044	1.040	1.032	1.033	1.020	1.021
	SCMSa vs. OEdipe	1.095	1.068	1.084	1.070	1.032	1.056
Adrenals	RAPID vs. SCMSa	0.978	1.023	0.943	0.972	1.042	0.978
	RAPID vs. OEdipe	1.041	1.021	1.013	0.997	1.015	0.987
	SCMSa vs. OEdipe	1.064	0.997	1.074	1.025	0.975	1.009

Table 6.

Ratios of the 1 MeV Photons SAF Values Calculated with SCMS, OEdipe, and RAPID in the Zubal Phantom

		Source organ
Target organ	Method	Liver	Kidneys	Lungs	Pancreas	Spleen	Adrenals
Liver	RAPID vs. SCMSa	0.994	0.995	0.985	0.996	1.000	0.988
	RAPID vs. OEdipe	0.999	1.001	0.994	1.006	1.000	0.997
	SCMSa vs. OEdipe	1.005	1.006	1.009	1.010	1.000	1.009
Kidneys	RAPID vs. SCMSa	0.985	1.002	0.991	0.995	1.000	0.992
	RAPID vs. OEdipe	1.008	1.002	0.999	1.004	1.000	0.994
	SCMSa vs. OEdipe	1.023	1.000	1.007	1.009	1.000	1.002
Lungs	RAPID vs. SCMSa	0.986	0.988	1.009	0.995	1.000	0.977
	RAPID vs. OEdipe	1.014	0.997	1.002	1.007	1.000	0.982
	SCMSa vs. OEdipe	1.029	1.009	0.993	1.012	1.000	1.005
Pancreas	RAPID vs. SCMSa	0.991	1.021	1.011	1.005	1.000	0.986
	RAPID vs. OEdipe	0.963	1.005	0.957	1.007	1.000	0.993
	SCMSa vs. OEdipe	0.972	0.985	0.947	1.003	1.000	1.007
Spleen	RAPID vs. SCMSa	1.000	0.996	0.991	0.993	1.000	0.971
	RAPID vs. OEdipe	1.000	1.003	1.015	1.009	1.000	0.987
	SCMSa vs. OEdipe	1.000	1.007	1.024	1.017	1.000	1.016
Adrenals	RAPID vs. SCMSa	0.981	1.029	0.978	0.977	1.000	0.987
	RAPID vs. OEdipe	1.038	0.968	0.930	0.991	1.000	0.981
	SCMSa vs. OEdipe	1.058	0.941	0.952	1.015	1.000	0.994

Table 7.

Ratios of the 935 KeV Electron S-Values Calculated with SCMS, OEdipe, and RAPID in the Zubal Phantom

		Source organ
Target organ	Method	Liver	Kidneys	Lungs
Liver	RAPID vs. SCMSa	1.003	1.019	0.938
	RAPID vs. OEdipe	1.002	0.996	0.960
	SCMSa vs. OEdipe	0.999	0.978	1.023
Kidneys	RAPID vs. SCMSa	0.969	1.000	0.962
	RAPID vs. OEdipe	0.990	1.004	1.211
	SCMSa vs. OEdipe	1.022	1.004	1.258
Lungs	RAPID vs. SCMSa	0.978	—	1.006
	RAPID vs. OEdipe	0.972	—	1.006
	SCMSa vs. OEdipe	0.994	—	1.000

The “—” indicates that the S-values were zero.

Discussion

The S-values calculated with RAPID in the 1–1000 g uniform spherical phantoms for different radionuclides agreed well with the OLINDA/EXM reference values and RAPID's tumor dosimetry was successfully validated for a variety of radionuclides. The agreement was within 2% for¹⁷⁷Lu, ¹³¹I, ¹²⁵I, ¹⁸F, and ⁶⁴Cu, within 3.5% for²¹¹At and ²¹³Bi, within 6.5% for¹⁵³Sm, ¹¹¹In, ⁸⁹Zr, and ²²³Ra, and within 9% for ⁹⁰Y, ⁶⁸Ga, and ¹²⁴I (Table 3).

Several other groups have calculated S-values in spherical phantoms with Monte Carlo methods and compared to those given by OLINDA/EXM. Kost et al. compared S-values calculated with Geant4 (VIDA platform) to OLINDA/EXM for spheres ranging from 10 to 1000 g and found differences up to 1.4%, 5.0%, 3.8%, and 1.3% for ¹³¹I, ⁹⁰Y, ¹¹¹In, and ¹⁷⁷Lu, respectively.⁷ Another study comparing Geant4 (RAYDOSE platform) S-values to OLINDA/EXM for spheres ranging from a diameter of 1.7–3.7 cm (∼1–30 g) found differences up to 3.1%, 7.8%, and 7.0% for ¹³¹I, ¹⁵³Sm, and ¹⁷⁷Lu, respectively, where the largest differences were for the smallest sphere size. These are in excellent agreement with the results from RAPID, which also uses Geant4 for dose calculations. A slightly larger disagreement, of the same magnitude as RAYDOSE, was also seen for the smallest 1 g sphere (e.g., ⁹⁰Y, ¹¹¹I, ⁶⁸Ga, and ¹²⁴I). This is most likely due to the decreasing accuracy of the voxelized representation of the sphere for smaller sphere sizes. The difference between the voxelized sphere volumes and an exact sphere with the same radius were 3.04%, 0.37%, 0.07%, and 0.04% for the 1, 10, 100, and 1000 g sphere, respectively. However, the voxelized representation of the sphere (rather than an analytically defined geometry) was necessary to validate Monte Carlo dose calculations using the same voxel transport and scoring methods used for patient CT geometries.

The S-values calculated with RAPID for the β (both 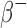and 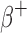) emitting radionuclides were almost all smaller than the OLINDA/EXM values. Kost et al.⁷ also found that S-values calculated with the Geant4-based VIDA application were smaller than OLINDA/EXM and explains that this is most likely due to the fact that OLINDA/EXM assumes βs (both 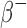and 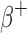) are emitted with the average energy while Geant4 samples the entire energy spectrum.⁴⁹ Because of this, the βs simulated with Geant4 that have larger energies than the average energy, will have a larger probability of escaping the sphere and not contributing to the dose. In general, the disagreement with the OLINDA/EXM S-values increased with increasing β energies. The agreement was within ∼2% for the lower energy emitters (i.e., ⁶⁴Cu, ¹⁸F, ¹⁷⁷Lu, ¹³¹I) and within 8.8% for the higher energy emitters (i.e., ¹²⁴I, ⁶⁸Ga, ⁹⁰Y). For the α emitting nuclides, the agreement was within 3.4% for ²¹¹At and ²¹³Bi and within 6.4% for ²²³Ra.

Overall, the Zubal Phantom SAFs and S-values calculated with RAPID agreed well with the reference values (Tables 5–7). Thirteen of the 36 SAFs for the 10 keV photon differed from the reference values by greater than 5% with the largest difference being 16% for the SAF (Liver 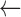Pancreas) and SAF (Pancreas 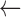Liver) values. At low energies there was also some discrepancy between the two reference SAF values. Differences between the two references were greater than 5% for 4 of the 10 keV photon SAFs and 19 of the 100 keV photon SAFs.

There are a couple factors that could account for these differences. First, the disagreements at low energies are mostly likely due to the uncertainties in cross sections and other physical parameters and how they are modeled by different Monte Carlo codes. Pacilio et al. compared the differences in voxel S-values when calculated with different Monte Carlo codes (Geant4, EGS, and MCNP) and found differences up to 10% for monoenergetic photon and electron sources.⁶¹ Second, the material composition used to define the materials in Zubal phantom for the reference calculations were not mentioned. Yoriyaz et al. investigated how different material compositions could affect photon and electron SAF calculations.⁶² SAFs varied by up to ∼6% for electrons and 15.8% for photons when using the tissue-equivalent composition defined by the MIRD Pamphlet No. 3^63,64 and with those from ICRU 44.⁶⁴ The percent difference decreased with increasing electron energy but generally increased with decreasing photon energies reaching a maximum difference at 40 keV. Therefore, the differences between the Geant4 and MCNP calculated SAFs/S-values could be attributed to differences in the Monte Carlo code simulation parameters.

This work focused on the description of the RAPID platform and its implementation process and a computational dosimetric validation. Further, ¹³¹I film-based experimental benchmarking measurements are planned, which will allow for a complete end-to-end validation of the platform. Additionally, because this work only focused on validation of the Monte Carlo dose calculations using phantoms with known geometries and activity distributions, the accuracy and dosimetric impact of each step in the workflow for patient-specific dose calculations such as the pharmacokinetic fitting method, the number of image acquisition time points, ROI contouring, material definition, voxel resolution and resampling, and temporal coregistration method and will need to be assessed next.

Conclusion

This work described the development of a patient-specific 3D Monte Carlo internal dosimetry platform called RAPID. RAPID was developed to utilize serial PET/CT or SPECT/CT images to calculate voxelized 3D internal dose distributions with the Monte Carlo code Geant4. The platform contains modules for pharmacokinetic fitting, temporal image coregistration, and radiobiological modeling. RAPID's dose calculations have been computationally validated for a variety of radionuclides and over a wide range of photon and electron energies for many different organs and tumor sizes. Additionally, the unique parallelization of the simulation jobs allows for fast simulation times and makes implementation feasible for clinical use. The ability to calculate accurate 3D internal dosimetry will hopefully lead to more informed decisions during the radiopharmaceutical drug development and approval process and should ultimately lead to improved outcomes in patients in the clinical setting.

Acknowledgments

We would like to thank the UW CHTC for the use of their cluster and their computational support. This study was partially funded by NIH Grant R01 CA 158800, NIH Grant 9U54TR000021, and NIH Grant R21 CA198392-01. No competing financial interests exist.

Disclosure Statement

There are no existing financial conflicts.