Abstract
Timing processes have been implicated as potential mechanisms that underlie self-controlled choice. To investigate the impact of an intervention that has been shown to increase self-controlled choice on timing processes, accuracy and precision of temporal discrimination were assessed in an 18-s peak procedure (18-s fixed interval trials; 54-s peak trials). During an intervention phase, mice in three treatment groups experienced differential reinforcement of low rate (DRL) schedules of reinforcement of 27 s, 18 s, or 9 s. A fourth group received continued exposure to the peak procedure. After the DRL intervention, timing was reassessed using the peak procedure. In contrast to previous reports, the DRL intervention resulted in less precise timing as indicated by increased peak spread and disrupted single-trial measures of temporal control. These effects were only detected just after the DRL intervention suggesting a transient effect of DRL exposure on timing. The increase in peak spread in the present experiment suggests delay exposure via DRL schedules may produce a “dose-dependent” effect on temporal discrimination, which may also increase self-controlled choice.
Keywords: DRL intervention, peak procedure, interval timing, mice
1. Impulsive choice and temporal discrimination
Recently, there has been growing interest in designing behavioral interventions to decrease impulsive choice (Morrison, Madden, Odum, Friedel, and Twohig, 2014; Smith, Marshall, and Kirkpatrick, 2015; Stein, Renda, Hinnenkamp, and Madden, 2015). The operational definition of impulsive choice – the selection of a small, immediate outcome at the expense of a larger, delayed outcome (Ainslie, 1975) – provides two useful targets in determining the focus of the intervention. These targets could be considered reward valuation (e.g., Marshall and Kirkpatrick, 2016) and interval timing (e.g., Smith et al., 2015). While both processes affect the extent to which impulsive choices occur (Mazur, 2001), several reports have indicated that the latter may be more integral in practice (Marshall, Smith, and Kirkpatrick, 2014; McClure, Podos, and Richardson, 2014). If an intervention that reduces impulsive choice does so by altering timing processes, it should have complementary effects on temporal discrimination. Given the importance of timing processes in accounting for impulsive choice, it is important to consider how interval timing might be altered after exposure to an intervention shown to reduce impulsive choice. Understanding how interval timing itself is altered by these interventions may provide insight as to the specific behavioral mechanisms involved.
A common method used to assess interval timing is the peak procedure (Catania, 1970; Roberts, 1981). In the peak procedure, the subject is exposed to reinforced fixed-interval (FI) trials and no-food, or peak, trials throughout the testing session. On FI trials, the first response after the FI has elapsed is reinforced. On peak trials, the trial duration is lengthened to two or three times the FI value, and responding is not reinforced. Response gradients are constructed by organizing response times (since trial onset) from many peak trials into discrete time bins. After sufficient training, these peak response gradients resemble a bell curve in which the probability of responding increases as a function of time, peaks around the FI criterion, and declines steadily thereafter. The degree to which the peak in responding aligns with the FI duration is taken as a measure of accuracy and the width of the function is taken as a measure of precision. These aspects of temporal discrimination can be quantified by fitting a Gaussian function to normalized peak response gradients defined as:
| (1) |
where t is the normalized elapsed time since trial onset, b is the normalized time since trial onset at which the normalized response rate peaks (peak time), c is the standard deviation of the function (peak spread), m is the slope of the linear function fitted to the rightward tail of the distribution, and y0 is the y-intercept of that linear function. A linear function is often added to account for a slight resurgence in responding near the end of the peak trial (Ludvig et al., 2007; Sanabria and Killeen, 2007; Subramaniam and Kyonka, 2017).
Several studies have reported successful reductions in impulsive choice following exposure to time-based schedules of reinforcement. Madden and colleagues (Renda and Madden, 2016; Stein et al., 2013, 2015) have shown that pre-exposing rats to delayed reinforcement reduces subsequent impulsive choice. However, interval timing was not assessed directly in those experiments. In other experiments with rats, differential reinforcement of low rate (DRL), FI, or variable interval (VI) schedules were shown to be effective interventions in reducing impulsive choice while also improving timing precision in a peak procedure (Smith et al., 2015). Because of the selective action of these interventions on timing precision without an appreciable effect on accuracy, it was hypothesized that improving timing precision is essential in reducing impulsive choice (Marshall et al., 2014; Smith et al., 2015). Although those experiments assessed interval timing, intervention schedule durations were matched to the delay of either the smaller or larger reinforcer, so potential differential effects of different schedule durations remain unknown.
The DRL intervention of Smith et al. (2015) is potentially interesting because of the suppression in response rate associated with that schedule. In DRL schedules, a reinforcer is delivered if a certain amount of time has elapsed between responses. Smith et al.’s DRL results could be considered paradoxical in that more self-controlled choice is consistent with decreased sensitivity to delay, whereas increased timing precision suggests that sensitivity to delay increased. However, without assessing a range of DRL requirements in conjunction with a single interval schedule, the relation between DRL exposure and interval timing remains unclear. For example, it may be that shorter DRL schedules selectively affect the left half of the peak distribution (e.g., Matell and Portugal, 2007) without an appreciable effect on response rate thereby increasing timing precision. It would also follow from this reasoning that longer DRL schedules may depress response rates sufficiently so as to reduce timing precision. This hypothesis would predict a “dose-dependent” decrease in timing precision as a function of DRL value.
Monterosso and Ainslie (1999) considered DRL schedules to be an experimental paradigm for studying impulsivity in which the proportion of inter-response times (IRTs) that exceed the DRL schedule value (IRT>t) is a measure of an animal’s ability to wait. By this reasoning, exposure to DRL schedules could be said to train subjects to wait. Larger DRL schedules are expected to have greater effects on timing because they train subjects to wait longer. However, if Monterosso and Ainslie’s conjecture about IRT>t is correct, contact with the DRL contingency would determine the efficacy of the intervention, not delay exposure alone. If that is the case, the magnitude of the DRL schedule’s effects on timing precision should be moderated by rate of reinforcement during DRL exposure.
The main objective of the current study was to determine the extent to which exposure to different DRL schedules has schedule-dependent effects on timing, that is, whether the size or duration of any effects is systematically related to the DRL schedule value. Mice received one of three DRL schedules after stable response patterns were established in a peak procedure. The interval requirement of the DRL schedule either matched (1x), was shorter than (0.5x), or was longer than (1.5x) the FI used in the preceding peak procedure. After sufficient training on the DRL schedule, the peak procedure was reinstated, and timing performance after the DRL intervention was compared to performance before the intervention.
2. Method
2.1. Subjects
Twenty-seven experimentally naïve male C57/BL 6J mice served as subjects, and were six weeks old upon arrival. Mice were housed three per cage in a temperature-controlled vivarium operating on a 12/12-hour light cycle. Sessions were conducted seven days per week between the hours of 0830 – 1800 during the subjects’ light cycle. Water was freely available in the home cage, and food was restricted to approximately 2 g of chow per mouse per day. Across all mice, weights ranged from 21 – 25 g. All protocols were approved by the Animal Care and Use Committee of West Virginia University.
2.2. Apparatus
Nine MED-Associates® operant-conditioning chambers for mice were used for data collection (17.8 cm L × 15.2 cm W × 18.4 cm H). The work panel of the chambers consisted of two nose-poke holes spaced 9 cm apart, both of which could be illuminated by a small yellow LED bulb. Head entries into the active nose-poke aperture were detected by breaks in an infrared photobeam. Sucrose water (15% wt/v; 20 μl/delivery) could be accessed from a dipper cup equidistant between both nose-poke holes. The floor of each chamber consisted of a stainless-steel grid of 19 horizontal bars. A houselight centered at the top of the back wall opposite the work panel illuminated the interior of the chamber during sessions. Chambers were enclosed in a sound-attenuating box with a wall-mounted fan that provided ventilation and white noise during sessions. All experimental events were controlled by a MED-Associates® interface and desktop computer in an adjacent room using MED-PC notation.
2.3. Procedure
2.3.1. Pre-training
Nose poking was established using an autoshaping procedure (Balci et al., 2010; Brown and Jenkins, 1968). In this procedure, sucrose water was made available according to a conjoint fixed-time (FT) 60 s, fixed-ratio (FR) 1 schedule of reinforcement. Each trial began with the illumination of the houselight and active nose-poke aperture. During reinforcer presentations, the nose-poke light was extinguished and the houselight flashed on and off in 0.5-s increments for a total of five seconds of reinforcer presentation. This reinforcer duration remained in effect for the entirety of the study. Each pre-training session terminated after 60 reinforcers had been delivered. Once responding was reliable, an FR 1 schedule was in place for at least five sessions.
2.3.2. FI training
FI training was in effect for 33 sessions. Throughout the first 16 sessions, successively incrementing FI schedules were arranged. The interval progression across sessions was 2 s, 4 s, 8 s, and 12 s. Each schedule was in effect for at least three sessions. For the remaining sessions, the FI duration was 18 s. To promote responding near the criterion time, a 3-s limited hold was in effect along with a variable 20-s intertrial interval (ITI). Upon trial onset, the houselight and active nose-poke aperture were illuminated, and the FI timer started. Once a response occurred following the criterion time, reinforcement was delivered as described in pre-training. Responses that occurred before the criterion time elapsed were recorded but had no other programmed consequence. If responding did not occur between the criterion time and the end of the limited hold, the trial was scored as an omission. Sessions terminated after 60 reinforcers were earned or 90 minutes elapsed, whichever occurred first.
2.3.3. Phase 1: Peak procedure
After 17 sessions of training on the FI 18-s schedule, peak trials were incorporated into sessions. During a peak trial, all stimuli in the chamber were identical to the stimuli associated with the FI schedule except that the trial duration was extended to 54 s, and responses were recorded but not reinforced. Once peak trials were implemented, each session consisted of 45 reinforced FI trials and 15 non-reinforced peak trials. In Phase 1, each session terminated after 45 reinforcers were delivered or 90 minutes elapsed, whichever occurred first. Phase 1 was in effect for a total of 25 sessions. The last 10 sessions were analyzed to determine pre-intervention measures of temporal discrimination.
After 25 sessions in Phase 1, mice were separated into four groups for the subsequent intervention phase. Groups were matched in terms of average peak spread. Peak spread was calculated by fitting a ramped Gaussian function (Eq. 1) to normalized peak-trial response gradients for each mouse. See data analysis for a more complete description of model fitting, group assignment, and statistical analyses.
2.3.4. Phase 2: DRL intervention
Three groups of mice were trained on different DRL schedules during the DRL intervention (n = 7). For mice in the DRL 9-s, 18-s, and 27-s groups, a response produced sucrose water if at least 9 s, 18 s, and 27 s, respectively, had elapsed since the last response. Mice in the PI 18-s group (n = 6) acted as a control group by remaining on the peak procedure for the duration of the study. Pizzo, Kirkpatrick, and Blundell (2009) suggested that training DRL responding using progressive increases in the DRL criterion can come with some potential training difficulties. For this reason, the three DRL groups began DRL training on their respective target criterion. During DRL sessions, responses with inter-response times (IRTs) that satisfied the required interval were reinforced. Responses with an IRT shorter than the required interval reset the DRL timer. The DRL timer did not begin elapsing until a single response occurred after each reinforcer. DRL training was in effect for a total of 38 sessions. The last five sessions were analyzed to determine terminal DRL response patterns as indicated by IRT distributions.
2.3.5. Phase 3: Peak procedure
The purpose of Phase 3 was to determine effects of the DRL intervention on temporal discrimination. Phase 3 was identical to Phase 1 in all respects using the same peak procedure. Sessions in Phase 3 terminated after 45 reinforcers were delivered or 90 minutes elapsed, whichever occurred first. This phase was in effect for 25 sessions. Whereas we included the last 10 sessions in Phase 1 for baseline analyses, we included all 25 sessions from Phase 3 to assess any proximal or distal effects of the DRL intervention.
2.4. Data Analysis
To characterize overall peak-trial responding during Phases 1 and 3, responses during peak trials were binned into 1-s time bins and summed across trials within blocks of five sessions each to provide adequate Gaussian fits. Eq. 1 was fitted to peak-trial response gradients using a nonlinear optimization algorithm in Microsoft Excel®. The primary measures derived from these fits were peak spread, peak time, and peak rate.
Because a Gaussian analysis can overlook some important single-trial response characteristics, a low-high-low analysis (Church, Meck, and Gibbon, 1994) was also conducted to characterize single-trial responding. On peak trials, response rate follows a low-high-low pattern where response rate is initially low, increases to a high rate prior to the criterion time of reinforcement, stabilizes for some duration, and decreases back to a low rate after the criterion time (Church, et al., 1994). The “start time” and “stop time” are the points of maximum acceleration and deceleration in response rate during a peak trial. For all single-trial analyses, the start time and stop time were defined using an index that identifies the temporal locations of the points of greatest acceleration and deceleration, respectively, by maximizing the difference between the high-rate and low-rate states (Church et al., 1994). The index that was maximized was defined as LS1(r − rLS1) + HS(rHS − r) + LS2(r − rLS2) where LS1, HS, and LS2, are the period of the trial before the start time, the period of high response rate after the start and before the stop time, and the remaining time from the stop time until the end of the peak trial, respectively. The variables rLS1, rHS, and rLS2 are the response rates within each respective time period during the trial, and r is the mean response rate for the entire peak trial. This index assumes the start of the high state can begin at any one response during a trial except the last response, and the end of the high state can begin at any subsequent response to the response that marks the start time.
To assign groups for the DRL intervention, estimates of peak spread and peak rate were obtained for each mouse by fitting Eq. 1 to on response gradients from the last 5 sessions of Phase 1. The mice were then ranked from highest to lowest in terms of peak spread. Mice were then assigned to each group using matched random assignment. Separate one-way analyses of variance (ANOVA) on estimates of Pre-DRL peak spread and peak rate with group as the factor were conducted to confirm that no significant difference in these measures existed between groups prior to the DRL intervention.
DRL data were analyzed by constructing IRT distributions for each DRL group. The IRT distributions were defined in 0.5-s bins ranging from 0 – .5 s to 49.5 – 50 s. Any IRTs above 50 s were counted as “50+”. In addition, DRL reinforcement rate, percent of IRTs at or above the DRL criterion, and mean IRT were calculated for each mouse.
To assess effects of the DRL intervention on temporal discrimination in Phase 3, a mixed-factorial ANOVA was conducted with group as the between-subjects factor and session as the within-subjects factor. Measures included in this analysis included peak spread, peak time, start time, stop time, midpoint ((start time - stop time)/2), and high-state duration (start time - stop time). The assumption of sphericity held for all repeated-measures factors, so no correction factors were applied. When significant differences were found, Tukey’s Honestly Significant Difference post-hoc tests were conducted. All statistical analyses assumed an alpha level of .05.
3. Results
The matched random assignment was successful in producing groups with equivalent Pre-DRL peak spread and peak time. Analyses of variance confirmed that there were no significant group differences in mean peak spread (F(3,23) = 0.133, p = 0.93, ηp2 = .02) or peak time (F(3,23) = 0.192, p = 0.9, ηp2 = .08).
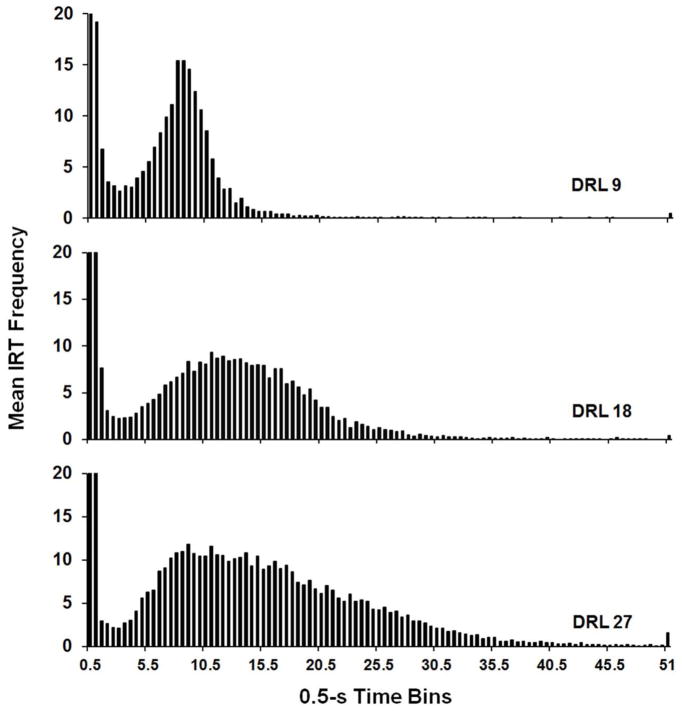
Figure 1 shows IRT distributions averaged across mice within each DRL group. During the DRL intervention, there was evidence of temporal control by the DRL schedule for mice in the DRL 9 and 18 groups. Control of DRL contingencies was less evident for mice in the DRL 27 group. When IRTs < 1 s were excluded, the modal IRTs were 8 s, 11 s, and 9 s, for mice in the DRL 9, DRL 18, and DRL 27 groups respectively. The DRL 27 group had the largest percentage of IRTs > the PI schedule value (M = 12.75%, SEM = 1.25) but the lowest percentage of reinforced IRTs (M = 4.28%, SEM = 0.81) as compared to the DRL 9 group (M = 11.63%, SEM = 1.28) and the DRL 18 group (M = 8.86%, SEM = 1.73). Nevertheless, 4.28% (SEM = 0.81%) of IRTs were longer than 27 s for mice in the DRL 27 group. Only 0.17% (SEM = 0.13%) and 1.3% (SEM = 0.42%) of IRTs were longer than 27 s for mice in the DRL 9 and DRL 18 groups. A one-way ANOVA on percentage of IRTs > 27 s showed a main effect of Group, F(2,18) = 15.61, p = .0001, ηp2 = .63, and post hoc tests confirmed that the percentage was significantly higher for the DRL 27 mice than mice in either of the other groups. Thus, while DRL requirements did not exert equivalent control over responding for all groups, the three different schedules had systematic effects on IRT distributions.
Fig. 1.
Inter-response time (IRT) histograms for each group during the last five sessions of the differential reinforcement of low rate (DRL) intervention. Each panel shows histograms for different DRL groups as indicated in the bottom right. Bars show group means.
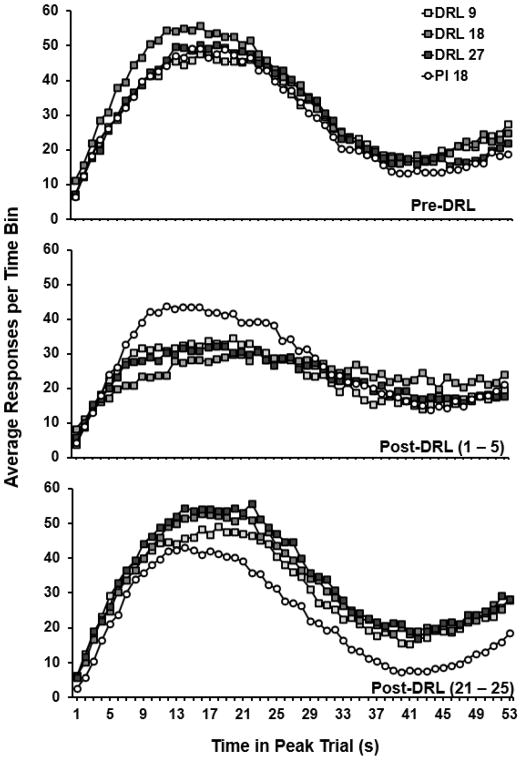
To illustrate effects of the DRL intervention on temporal discrimination, Figure 2 shows average peak-trial response distributions across phases for each group. During the last five Pre-DRL sessions (top panel), response distributions were similar for all groups showing a Gaussian-like shape with a peak in responding around the criterion time (18 s). During the first five Post-DRL sessions of (middle panel), the distributions for all of the DRL groups widened and showed a decline in peak maximum suggesting a disruption of temporal discrimination. At the end of the Post-DRL phase (bottom panel), response distributions for each group approximated their respective baselines with the exception of the PI 18 control, which showed a somewhat decreased peak maximum and a slight leftward shift. This analysis suggests that the effects of the DRL intervention were transient.
Fig. 2.
Average peak trial response distributions for each group across select time points. The bottom right of each panel denotes the selected time point with session number in parentheses. Data points represent averages of five sessions within groups.
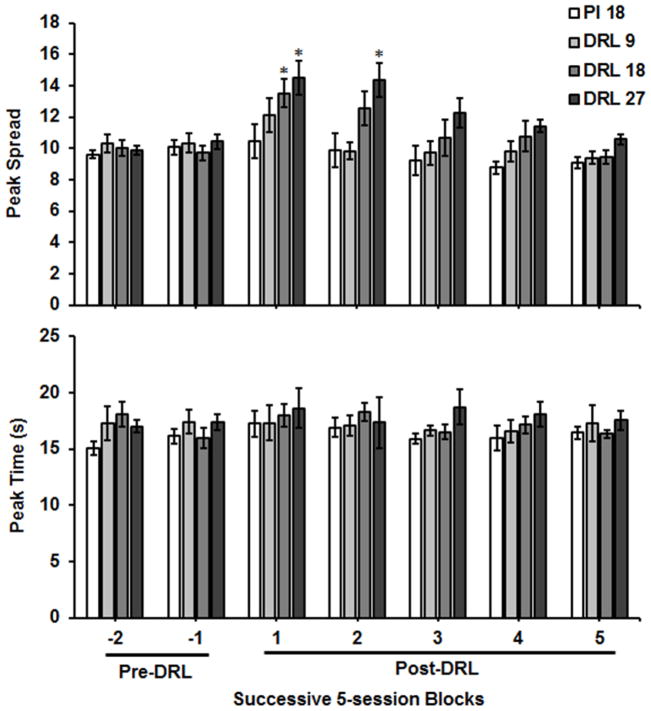
Figure 3 shows Gaussian parameter estimates for each group across five-session blocks before and after the DRL intervention. An ANOVA on peak spread found a main effect of Phase, F(6,138) = 10.29, p < .0001, ηp2 = .31, and a Phase × Group interaction, F(18,138) = 1.69, p = .048, ηp2 = .18. Tukey’s post hoc tests revealed that peak spread was elevated for both the DRL 18 (M= 13.51, SEM = 0.89) and DRL 27 (M = 14.51, SEM = 1.81) groups for the first five Post-DRL sessions relative to their respective baseline measures (DRL 18 – M = 9.7, SEM = 0.49; DRL 27 – M = 10.4, SEM = 0.56). Peak spread did not change for the DRL 9 group. Peak spread also remained elevated for the DRL 27 group (M = 14.36, SEM = 1.82) during the second five-session block after the DRL intervention. Peak spread subsequently returned to baseline levels for the remainder of Post-DRL sessions. Thus, the DRL intervention disrupted timing precision in an ordinal manner with respect to the DRL value, but this effect was transient. Peak spread did not change for the PI 18 control group. No significant differences were found with respect to peak time.
Fig. 3.
Gaussian parameter estimates of peak spread and peak time for each group. Estimates were derived for the two blocks of 5 sessions before the differential reinforcement of low rate (DRL) intervention and for each block of 5 sessions after DRL. Data represent means (+/− SEM). Asterisks (*) denote values that were significantly (p < .05) different than Pre-DRL (−1) baseline average.
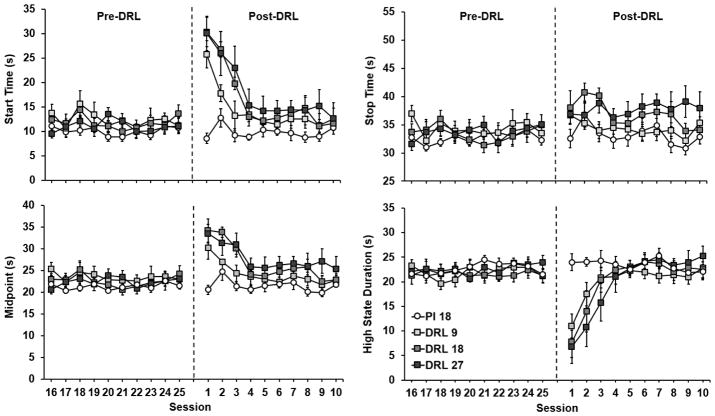
For a more nuanced understanding of how the DRL intervention might have affected temporal discrimination, Figure 4 shows all measures from the single-trials analysis for each group before and after the DRL intervention. Table 1 shows the mean start and stop time across sessions for each group. An ANOVA on start time found significant main effects of Group, F(3,23) = 3.52, p = .031, ηp2 = .28, and Phase, F(10,230) = 24.83, p < .0001, ηp2 = .52, as well as a Phase × Group interaction, F(30,230) = 3.48, p < .0001, ηp2 = .31. Tukey’s post hoc tests revealed this interaction was qualified by selective delays in start time for each DRL group but to differing degrees across groups. Relative to their respective Pre-DRL averages, Post-DRL start times were delayed for the DRL 9 group for the first session, the DRL 18 group for the first two sessions, and the DRL 27 group for the first three sessions. Start times subsequently returned to baseline levels for each group. Thus, similar to peak spread, start times increased in ordinal schedule-dependent manner, but returned to baseline levels in fewer sessions than peak spread. An ANOVA on stop time only found a significant main effect of Phase, F(10,230) = 2.73, p = .003, ηp2 = 0.11, suggesting somewhat later stop times after the DRL intervention in general. Analysis of midpoints showed significant main effects of Group, F(3,23) = 4.10, p = .018, ηp2 = .34, and Phase, F(10,230) = 14.23, p < .0001, ηp2 = .38, as well as a Phase × Group interaction, F(30,230) = 2.04, p = .0019, ηp2 = .21. Post hoc analyses showed that this interaction was qualified by both the DRL 18 and DRL 27 groups showing later midpoints during the first three Post-DRL sessions relative to their respective baseline averages. No change in midpoint was detected in the DRL 9 and PI 18 groups. Analysis of high state duration showed a significant main effect of Phase, F(10,230) = 19.85, p < .0001, ηp2 = .46, as well as a Phase × Group interaction, F(30,230) = 3.56, p < .0001, ηp2 = 0.32. Post hoc analyses showed that high state duration was reduced following the DRL intervention in the DRL 9 and DRL 18 groups for only the first Post-DRL session and in the DRL 27 group for the first two Post-DRL sessions. No change in high state duration was detected for the PI 18 group.
Fig. 4.
Single trial measures for the last 10 Pre-DRL sessions and the first 10 Post-DRL sessions for each group. Data points represent group means.
Table 1.
Mean (SEM) start and stop times for each group before and after the DRL intervention.
| Start Time (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| Group | Pre-DRL | Post-DRL Session | |||||||||
|
|
|
|
|||||||||
| Avg. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| DRL 9 | 11.8 | 25.7* | 17.7 | 13.14 | 13.4 | 11.9 | 11.4 | 12.5 | 12.5 | 11.2 | 12.5 |
| (1.4) | (2.7) | (1.7) | (3.03) | (2.2) | (1.8) | (1.3) | (1.9) | (1.9) | (2.4) | (2.2) | |
| DRL 18 | 11.4 | 30.3* | 26.7* | 19.8 | 12.9 | 12.2 | 12.8 | 13.6 | 14.8 | 11.1 | 11.7 |
| (1.3) | (3.2) | (3.1) | (2.1) | (1.3) | (2.1) | (2.5) | (0.6) | (1.9) | (1.8) | (1.6) | |
| DRL 27 | 10.8 | 30.1* | 25.9* | 22.9* | 15.3 | 14.2 | 14.1 | 14.4 | 14.3 | 15.2 | 12.7 |
| (1.0) | (3.5) | (4.5) | (4.4) | (3.3) | (2.9) | (2.2) | (1.9) | (3.0) | (3.3) | (3.2) | |
| PI 18 | 9.97 | 8.6 | 12.7 | 9.2 | 8.8 | 10.3 | 9.9 | 9.6 | 8.8 | 8.9 | 10.7 |
| (0.8) | (1.0) | (1.8) | (1.3) | (0.6) | (1.4) | (0.7) | (1.6) | (1.1) | (0.9) | (0.5) | |
| Stop Time (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| Group | Pre-DRL | Post-DRL Session | |||||||||
|
|
|
|
|||||||||
| Avg. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| DRL 9 | 34.2 | 36.7 | 35.3 | 34.1 | 34.5 | 34.2 | 33.4 | 33.8 | 33.9 | 32.1 | 35.3 |
| (1.6) | (1.7) | (1.1) | (1.5) | (1.2) | (1.2) | (1.3) | (1.5) | (1.4) | (1.7) | (1.0) | |
| DRL 18 | 32.9 | 38.1 | 40.7 | 40.2 | 35.4 | 35.2 | 36.8 | 37.3 | 36.8 | 33.8 | 34.1 |
| (1.2) | (2.3) | (1.6) | (1.3) | (0.9) | (1.4) | (1.7) | (1.4) | (2.2) | (1.3 | (0.9) | |
| DRL 27 | 34.0 | 36.8 | 36.7 | 38.7 | 36.3 | 36.9 | 38.3 | 38.9 | 37.7 | 39.1 | 37.9 |
| (1.3) | (1.6) | (2.1) | (1.7) | (1.5) | (2.2) | (2.2) | (1.6) | (3.7) | (2.8) | (2.8) | |
| PI 18 | 33.2 | 32.5 | 36.8 | 33.5 | 32.4 | 32.7 | 33.8 | 34.8 | 31.5 | 30.8 | 32.8 |
| (0.7) | (1.6) | (2.2) | (1.5) | (1.5) | (1.5) | (1.6) | (1.9) | (1.4) | (1.1) | (1.2) | |
Note.
indicates p < .05 as compared to the mean start or stop time from the Pre-DRL Phase.
Because a DRL schedule is likely to produce reductions in reinforcement rate, especially at large DRL values, it is possible that the observed effects on temporal discrimination could be driven by lower reinforcement rates (Killeen & Fetterman, 1988). To investigate this issue, we compared average reinforcers per minute during the last 5 sessions of the DRL intervention for each DRL group to average reinforcement rate for the PI 18 control group during the same sessions. A one-way ANOVA on reinforcement rates showed a significant effect of Group, F(3,23) = 32.62, p < .0001, ηp2 = 0.81. Follow-up analyses showed that the DRL 9 group (M = 1.14, SEM = 0.08) had higher reinforcement rates than the PI 18 group (M = 0.79, SEM = 0.11) and the DRL 18 (M = 0.57, SEM = 0.06) and DRL 27 (M = 0.32, SEM = 0.05) had lower reinforcement rates than the control group.
At the group level, mean peak spread was negatively correlated with DRL reinforcement rates. If the observed changes in Post-DRL timing precision were caused by changes in reinforcement rate rather than by alterations to response patterns during the DRL, the negative correlation between peak spread and rate of reinforcement would be as strong within groups as it was between groups. If rate of reinforcement did moderate effects of exposure to different DRL schedules, it would support the conjecture that IRT>t is the operative variable. To determine if this was the case, we compared DRL reinforcement rate to peak spread from the first 10 Post-DRL sessions for each mouse. Figure 5 shows peak spread as a function of reinforcement rate for individual subjects. Although the correlation for mice in the PI 18 control group (r = −0.43, p = .39) was similar to the overall correlation (r = −0.43, p = .02), this relation did not hold within DRL groups. Correlations for each DRL group were all weaker (DRL 9: r = −0.33, p = .47; DRL 18: r = −0.17, p = .72) and the correlation for mice in the DRL 27 group was positive (r = 0.27, p = .56). Thus, it does not appear that IRT>t is responsible for the observed effects on temporal discrimination.
Fig. 5.
Average peak spread during the first 10 Post-DRL sessions as a function of reinforcement rate during the last five DRL sessions. Dotted lines show the line of best fit for each group.
4. Discussion
The purpose of the present study was to characterize the relation between DRL schedule values and temporal discrimination as assessed in a peak procedure. This goal followed from a previous report that showed impulsive choice to be reduced and timing precision to be enhanced following exposure to a DRL schedule (Smith et al., 2015). Consistent with previous research, DRL exposure did not affect timing accuracy as measured by peak times. In contrast to previous findings, Post-DRL differences in peak spread indicated that the DRL intervention reduced timing precision. The reduction in timing precision was transient, with the largest reduction observed just after the DRL intervention. Peak spread returned to baseline levels within 15 sessions and did not improve thereafter. This reduction in timing precision was schedule-dependent. Specifically, the reduction in precision was both larger and longer-lasting for mice exposed to longer DRL requirements. Consistent with the Gaussian analysis, effects of DRL exposure on single-trial measures were also transient and schedule-dependent. Start times were most affected just after the DRL intervention, and the increase in start times was both larger and longer-lasting for mice exposed to longer DRL schedules. A somewhat similar trend was observed in midpoints. Interestingly, stop times were relatively unaffected by the DRL intervention resulting in short high state durations following at the DRL.
While general disruptions in temporal discrimination were observed following the DRL intervention, the mechanism by which these changes occurred remains unclear. Within Scalar Expectancy Theory (SET; Gibbon, 1977; Gibbon and Church, 1984), reductions in timing precision (increased peak spread in the current study) are thought to be related to threshold setting whereas changes in peak time are related to clock speed. SET assumes that temporal control of behavior is primarily accomplished through an internal clock mechanism consisting of a pacemaker-accumulator system (Gibbon and Church, 1984). A pacemaker generates pulses at a rate determined by the current experimental context. A switch then gates these pulses into an accumulator. At the time of reinforcement, the number of pulses in the accumulator is stored in reference memory as a measure of the average elapsed time from trial onset to reinforcement. On subsequent trials, the number of pulses in the accumulator are constantly compared with the number of reference memory. When the pulses generated during the current trial approximate the number in reference memory, responding begins. Because peak times were unaffected by the DRL intervention, it is unlikely that clock speed (pulse rate) was affected. Instead, it is possible that the DRL-dependent increases in peak spread could be due to a decreased threshold setting. Although, this interpretation would assume relatively equal effects on start and stop times. Specifically, if the response threshold were to be lowered after DRL exposure, one would expect earlier start times and later stop times. Likewise, if the threshold were to be raised, later start times would result in earlier stop times (Gallistel, King, and McDonald, 2004). Thus, the current results cannot be easily interpreted as selective changes in clock speed or threshold from the perspective of SET. Perhaps this difficulty lies in the tendency for SET to be relied upon when behavior has reached steady state (Gallistel and Gibbon, 2000; Staddon and Higa, 1999). The effects observed in the current study (both Gaussian and single-trial measures) were detected most reliably during the first five Post-DRL sessions when responding was in transition from a DRL schedule back to the peak procedure.
Another possible interpretation of the wider peak spreads in the current study is that reinforcement rate, rather than DRL exposure, was the operative variable responsible for perturbing temporal discrimination (Killeen and Fetterman, 1988). In support of this claim, there were consistent ordinal relations between DRL requirement, peak spread and rate of reinforcement across groups. Reinforcement rates during DRL exposure were lower and peak spreads were higher among mice exposed to longer DRL schedules. However, two arguments can be made against this interpretation. First, while reinforcement rate during the DRL intervention was negatively correlated with peak spread, this relation did not hold within groups. The absence of a consistent correlation between DRL reinforcement rate and Post-DRL peak spread confirmed that the dose-dependent reduction in precision was a function of DRL schedule value and not obtained reinforcement. Second, start times were delayed in each DRL group without a corresponding effect on stop time. Although different DRL schedules might be expected to affect start times selectively, it is unclear why different reinforcement rates might do so. This finding, coupled with an inconsistent correlation between reinforcement rate and peak spread, suggests that the inhibitory nature of the DRL schedule was responsible for the observed effects.
Monterosso and Ainslie (1999) suggested that amount of contact with the contingency, IRT>t, is a measure of self-control in DRL schedules. There was no evidence that reinforcement rate moderated DRL schedule-dependent effects on peak spread, which suggests that the decrement in timing precision was determined by exposure to the DRL schedule rather than contact with the contingency. While we did not assess impulsive choice, the overall dose-dependent decrease in sensitivity to time to sucrose we observed across DRL exposures is consistent with previous attempts to decrease impulsive choice using delay exposure (Madden, Francisco, Brewer, and Stein, 2011; Mazur and Logue, 1978; Renda and Madden, 2016; Stein et al., 2013, 2015). Whether the delay exposure is fixed (Stein et al., 2013, 2015) or gradual (Mazur and Logue, 1978), delay exposure has been shown to decrease subsequent impulsive choice. Furthermore, Madden et al (2011) showed that longer delays in general engender greater improvements in impulsive choice. One caveat in this interpretation is that the current study used a DRL schedule whereas previous studies have used interval or time-based (response non-contingent) schedules. Further research is needed to tease apart the parametric relation between interval exposure and impulsive choice. Perhaps an interval exposure regimen similar to the DRL intervention employed here will also result in a dose-dependent decrease in impulsive choice. However, the greater impact of DRL schedules on Post-DRL start times than stop times suggests that treatment effects observed after a DRL intervention may not be due to improvements to temporal discrimination, per se. Instead, they appear to be a function of the suppressive nature of the DRL contingency, though this suppressive effect was primarily mediated by a slower ramping of response rate during individual trials as opposed to a general impact on IRTs.
In the current study, temporal control deteriorated in an ordinal fashion with respect to the DRL requirement and did not appear to improve beyond baseline levels through continued exposure to the peak procedure. Thus, in particular experimental contexts, DRL schedules do not always result in improvement of timing precision. Although our study did not evaluate effects of DRL interventions on choice explicitly, reduced timing precision is consistent with a reduction in sensitivity to delay as a consequence of the DRL contingency driving changes in impulsive choice (Renda and Madden, 2016). It is still unclear as to how the reinforcement context (single operant vs. choice), stimulus context (external cue vs. response-initiated cues), and the targeted process (e.g., timing, motivation and attention) may interact to affect the outcomes of these interventions. Perhaps future studies may consider these unexplored interactions when designing novel interventions or replicating previous ones.
Highlights.
Interventions that reduce impulsive choice should improve timing precision
Mice were exposed to a peak procedure and a DRL intervention
DRL schedules temporarily reduced timing precision and increased start times
Effects on timing were larger, longer-lasting for longer DRL schedules
Exposure to DRL suppressed subsequent responding in the peak procedure
Acknowledgments
This research was conducted in partial fulfillment of the requirements of the Master of Science degree in Psychology from West Virginia University by the first author and mentored by the second author, and was partially funded by the Department of Psychology at WVU and the WVU ADVANCE Center. Preparation of this manuscript was partially supported by the National Institutes of Health grant R15AR066806. Special thanks to Shrinidhi Subramanium, Daniel Bell-Garrison, Katie Slone, and Paige Patterson for their technical assistance.
Footnotes
Conflicts of Interest: None
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ainslie G. Specious reward: A behavioral theory of impulsiveness and impulse control. Psych Bull. 1975;82:463–496. doi: 10.1037/h0076860. [DOI] [PubMed] [Google Scholar]
- Balci F, Ludvig EA, Abner R, Zhuang X, Poon P, Brunner D. Motivational effects on interval timing in dopamine transport (DAT) knockdown mice. Brain Res. 2010;1325:89–99. doi: 10.1016/j.brainres.2010.02.034. [DOI] [PubMed] [Google Scholar]
- Brown PL, Jenkins HM. Auto-shaping of the pigeon’s key-peck. J Exp Anal Behav. 1968;11:1–8. doi: 10.1901/jeab.1968.11-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catania AC. Reinforcement schedules and psychophysical judgements: A study of some temporal properties of behavior. In: Schoenfled WN, editor. The theory of reinforcement schedules. New York: Appleton-Century-Crofts; 1970. [Google Scholar]
- Church RM, Meck WH, Gibbon J. Application of scalar timing theory to individual trials. J Exp Psych: Anim Behav Processes. 1994;20:135–155. doi: 10.1037//0097-7403.20.2.135. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gibbon J. Time, rate, and conditioning. Psych Rev. 2000;107:289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, King A, McDonald R. Sources of variability and systematic error in mouse timing behavior. J Exp Psych: Anim Behav Processes. 2004;30:3–16. doi: 10.1037/0097-7403.30.1.3. doi:10.1037-0097.7403.30.1.3. [DOI] [PubMed] [Google Scholar]
- Gibbon J. Scalar expectancy theory and Weber’s law in animal timing. Psych Rev. 1977;84:279–325. [Google Scholar]
- Gibbon J, Church RM. Sources of variance in an information processing theory of timing. In: Roitblat HL, Bever TG, Terrace HS, editors. Animal Cognition. Elrbaum; Hillsdale, NJ: 1984. [Google Scholar]
- Killeen PR, Fetterman JG. A behavioral theory of timing. Psych Rev. 1988;95:411–422. doi: 10.1037/0033-295x.95.2.274. [DOI] [PubMed] [Google Scholar]
- Ludvig EA, Conover K, Shizgal P. The effect of reinforcer magnitude on timing in rats. J Exp Anal Behav. 2007;87:201–218. doi: 10.1901/jeab.2007.38-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madden GJ, Francisco MT, Brewer AT, Stein JS. Delay discounting and gambling. Behav Process. 2011;87:43–49. doi: 10.1016/j.beproc.2011.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall AT, Kirkpatrick K. Mechanisms of impulsive choice: III. The role of reward processes. Behav Processes. 2016;123:134–148. doi: 10.1016/j.beproc.2015.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall AT, Smith AP, Kirkpatrick K. Mechanisms of impulsive choice: I. Individual differences in interval timing and reward processing. J Exp Anal Behav. 2014;102(1):86–101. doi: 10.1002/jeab.88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matell MS, Portugal GS. Impulsive responding on the peak-interval procedure. Behav Processes. 2007;74:198–208. doi: 10.1016/j.beproc.2006.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazur JE. Hyperbolic value addition and general models of animal choice. Psych Rev. 2001;108:96–112. doi: 10.1037/0033-295X.108.1.96. [DOI] [PubMed] [Google Scholar]
- Mazur JE, Logue AW. Choice in a self-control paradigm: Effects of a fading procedure. J Exp Anal Behav. 1978;30:11–17. doi: 10.1901/jeab.1978.30-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClure J, Podos J, Richardson HN. Isolating the delay component of impulsive choice in adolescent rats. Front Integ Neuro. 2014;8:1–9. doi: 10.3389/fnint.2014.00003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monterosso J, Ainslie G. Beyond discounting: Possible experimental models of impulse control. Psychopharm. 1999;146:339–347. doi: 10.1007/pl00005480. [DOI] [PubMed] [Google Scholar]
- Morrison KL, Madden GJ, Odum AL, Friedel JE, Twohig MP. Altering impulsive decision making with an acceptance-based procedure. Behav Ther. 2014;45(5):630–639. doi: 10.1016/j.beth.2014.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pizzo MJ, Kirkpatrick K, Blundell PJ. The effect of changes in criterion value on differential reinforcement of low rate schedule performance. J Exp Anal Behav. 2009;92:181–198. doi: 10.1901/jeab.2009.92-181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Renda CR, Madden GJ. Impulsive choice and pre-exposure to delays: III. Four-month test-retest outcomes in male wistar rats. Behav Processes. 2016;126:108–112. doi: 10.1016/j.beproc.2016.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts S. Isolation of an internal clock. J Exp Psych: Anim Behav Processes. 1981;7:242–268. [PubMed] [Google Scholar]
- Smith AP, Marshall AT, Kirkpatrick K. Mechanisms of impulsive choice: II. Time-based interventions to improve self-control. Behav Processes. 2015;112:29–42. doi: 10.1016/j.beproc.2014.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein JS, Johnson PS, Renda CR, Smits RR, Liston KJ, Shahan TA, Madden GJ. Early and prolonged exposure to reward delay: Effects of impulsive choice and alcohol self-administration in male rats. Exp Clin Psychopharm. 2013;21:172–180. doi: 10.1037/a0031245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein JS, Renda CR, Hinnenkamp JE, Madden GJ. Impulsive choice, alcohol consumption, and pre-exposure to delayed rewards: II. Potential mechanisms. J Exp Anal Behav. 2015;103(1):33–49. doi: 10.1002/jeab.116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramaniam S, Kyonka EGE. Selective attention in pigeon temporal discrimination. Quart J Exp Psychol. 2017 doi: 10.1080/17470218.2017.1360921. Manuscript in press. [DOI] [PubMed] [Google Scholar]