A Method to Assess Randomness of Functional Connectivity Matrices

Abstract

Background

Functional magnetic resonance imaging (fMRI) allows for the measurement of functional connectivity of the brain. In this context, graph theory has revealed distinctive non-random connectivity patterns. However, the application of graph theory to fMRI often utilizes non-linear transformations (absolute value) to extract edge representations.

New method

In contrast, this work proposes a mathematical framework for the analysis of randomness directly from functional connectivity assessments. The framework applies random matrix theory to the analysis of functional connectivity matrices (FCMs). The developed randomness measure includes its probability density function and statistical testing method.

Results

The utilized data comes from a previous study including 603 healthy individuals. Results demonstrate the application of the proposed method, confirming that whole brain FCMs are not random matrices. On the other hand, several FCM submatrices did not significantly test out of randomness.

Comparison with existing methods

The proposed method does not replace graph theory measures; instead, it assesses a different aspect of functional connectivity. Features not included in graph theory are small numbers of nodes, testing submatrices of an FCM and handling negative as well as positive edge values.

Conclusion

The random test not only determines randomness, but also serves as an indicator of smaller non-random patterns within a non-random FCM. Outcomes suggest that a lower order model may be sufficient as a broad description of the data, but it also indicates a loss of information. The developed randomness measure assesses a different aspect of randomness from that of graph theory.

Introduction

Brain functional connectivity is an important emerging topic due to its potential for use in a clinical setting (Castellanos et al., 2013; Matthews and Hampshire, 2016). Deviations from normal connectivity patterns are investigated as possible biomarkers in several diseases including schizophrenia (Damaraju et al., 2014), traumatic brain injury (Vergara et al., 2017b), attention deficit disorder (Cao et al., 2009), and bipolar and major depressive disorders (He et al., 2016). Brain signals are initially collected using diverse techniques such as magneto-encephalography (MEG), functional magnetic resonance imaging (fMRI) or electro-encephalography (EEG) (Brookes et al., 2011; Srinivasan et al., 2007). After appropriate signal preprocessing, functional connectivity is then assessed through correlation, coherence, or measure of causality (Sporns, 2011). At this stage, one straightforward option is to analyze the connectivity between pairs of interesting brain areas or alternatively consider a network-based approach to extract global measures of connectivity (Kim et al., 2014). In this networking approach, functional connectivity can be seen as a collection of spatially distributed brain nodes linked through temporal dependency of neuronal activations (van den Heuvel and Hulshoff Pol, 2010). A long and current line of research has found non-random patterns in brain connectivity along with evidence linking deviations from this structure to known neuropathologies (Buckner et al., 2008; Nelson et al., 2017; van den Heuvel et al., 2016). Consequently, a complete characterization of non-random patterns in brain connectivity has become an important topic for the understanding of dysfunctions in pathological brains.

Because of its simplicity, one of the types of connectivity that is also widely used is temporal correlation, where time-courses measured from a specific part of the brain are correlated with time-courses of a different brain area. When more than two brain areas are involved in the analysis, a set of correlations can be expressed as a correlation matrix. Since this matrix is the expression of identified connectivities, we renamed this matrix the functional connectivity matrix (FCM). FCMs are used for the analysis of many types of data, including positron emission tomography (Friston et al., 1993) and magneto-encephalography (Stam, 2004); among other definitions, they are also known as functional connectivity or functional network connectivity (Allen et al., 2011) matrices in fMRI data. At first, an FCM may not appear to follow a specific pattern or structure if its elements are not appropriately organized. However, patterns within FCMs become evident after reordering brain areas in anatomical and functional groups. One of the most studied patterns in FCMs involves a set of areas that reduce their activity during attention demanding tasks. This set of brain areas is known as the default mode network (DMN) and includes the ventromedial prefrontal cortex, posterior cingulate cortex. and angular gyrus (Buckner et al., 2008; Greicius et al., 2009). A pattern formed due to the existence of a DMN is easy to recognize in appropriately ordered resting state FCMs. Other networks have been discovered to be part of the resting state layout, which includes sensorimotor, visual, attention, executive control and salience networks (Ptak, 2012; Smith et al., 2009; Sutherland et al., 2012).

Connectivity patterns in FCMs have also been extensively studied using the mathematical graph theory framework, revealing important characteristics of brain networks. One important conclusion is that the brain has evolved into a connected network consisting of sparse local clusters with few long-range connections among clusters, which is an organization known as “small-world” (Bassett and Bullmore, 2006). This type of organization allows for an optimal trade-off between complexity and wiring cost, thus achieving an economic flow of information through the brain. One of the first accounts for small-world organization using fMRI data that was reported (Salvador et al., 2005) demonstrated the existence of local connectivity clusters. Later studies provided evidence for the existence of modular and community like structure. Modularity measures are important because modular systems show small-world properties, but not all small-world systems exhibit modularity (Meunier et al., 2010). The modular structure of the brain has been established after analyzing the structural MRI data identifying six brain modules (auditory/language, executive, sensorimotor, visual and mnemonic) of strong overlap with known functional domains (Chen et al., 2008). Another important property of the brain is the existence of “rich-nodes”, which have a large number of connections that also tend to form interconnected subgraphs (Colizza et al., 2006). A “rich-club” of highly interconnected nodes have been identified in the human brain localized in key hub regions that includes precuneus, superior frontal, superior parietal, hippocampus, putamen and thalamus (van den Heuvel and Sporns, 2011). Overall, this wiring of the human brain has evolved to exhibit a non-random pattern of connected nodes for an optimal flow of information.

The advances obtained from graph theory are not free of pitfalls in analysis that need to be considered when interpreting results (Fornito et al., 2013). In the context of fMRI data, the definition of nodes remains a problem with only an approximated solution. The issue is to find an optimal parcellation of the brain into functional areas, each of which represents a node. We can solve this problem using the data driven technique known as group independent component analysis (gICA), which uses the concept of maximally independent nodes to achieve brain parcellation (Calhoun and Adali, 2012b). Another challenge is the definition of edges. The type of connectivity obtained after using gICA to analyze fMRI is based on the synchronic behavior between nodes primarily measured through correlation. Several concerns arise when translating correlation into edge information that can be either weighted or binary connectivity (connection vs. no-connection). In practice, the main concerns for FCMs has to do with handling the sign (positive vs. negative) of correlation measures and the binarization (if required) of edge weights through thresholding (Fornito et al., 2013).

This work assesses and characterizes randomness in FCMs. The main concept is to measure how close an FCM is to a random matrix whose elements are random and follows a normal distribution. Different from common approaches of edge weight estimation, our approach considers Fisher's Z–transformation (Fisher, 1915) when applied to correlation values in the FCM. Fisher's Z–transformation helps stabilize the variance of the correlation coefficient and produces approximately normal distributed values that span the range of the real numbers. These characteristics facilitate the application of several statistical methods to analyze the significance of correlation values. In the same line of thought, we can consider the transformed correlation as a normally distributed value that characterizes the edge connectivity strength between two brain nodes. The ensemble of transformed correlation connections results in the natural concept of a matrix possibly constituted by random values. In contrast, known methods of graph theory first apply a threshold to decide the existence or lack of edges in the case of binarization, or it can otherwise apply a non-linear (absolute value) transform to deal with negative correlation values and produce weights. The resulting graph is compared against a randomly connected graph defined in the space of binary or weight values for each edge (Rubinov and Sporns, 2010; Watts and Strogatz, 1998). In our case, the random value associated to each edge is neither a weight nor a binary value, but is assumed to follow a Gaussian distribution that has similar properties to the Fisher transformed correlation. The proposed randomness test utilizes the characteristics of the whole matrix ensemble as determined by matrix eigen-spectrums. Our hypothesis is that random matrices exhibit a specific eigen-spectrum that is distinct from the eigen-spectrum of a non-random FCM. The focus of our analysis is the temporal coherence of brain activity among areas of the brain and whether the coherence structure expressed through FCM eigen-spectrum is similar to that obtained by chance or exhibits a more deterministic nature. The current work utilizes resting state data from a former study to exemplify the applications of the randomness test developed.

Theoretical Development

The objective of our work is the development of a formal framework to distinguish random from non-random connectivity matrices, but also use raw assessments of connectivity and avoid connectivity to edge transformations. The proposed technique compares singular values (SVs) from a connectivity matrix that might be composed of non-random values against SVs from matrices composed of random elements. The development of this technique makes strong use of random matrix theory, which will be explained in the following sections.

Random Matrices

We define a random matrix as a matrix composed of independent identically distributed (i.i.d.) random elements following a Gaussian distribution with a specific mean and variance. These kind of random matrices have well defined eigen-value characteristics. An eigen-value λ for a given matrix X is a scalar that fulfills the equation Xν = Xν for a specific vector known as the eigen-vector ν. The eigen-decomposition X = V∧V⁻¹ consists of all eigen-values in the diagonal matrix ∧ and all the eigen-vectors contained in matrix V (Meyer, 2000). The pioneering work of Girko (Girko, 1985) demonstrated that the eigen-value distribution of a square random matrix tends to fill a disk in the complex plane as shown in Figure 1(a and c). This fact established an important starting point in distinguishing random and non-random matrices rooted in the concept that matrices with an eigen-spectrum deviating from the disk shape are not composed by random i.i.d. Gaussian components. Although important, Girko's original result has limitations and caveats among which the most important are an eigen-spectrum composed of complex numbers and a restriction of square matrices. Important work by Wigner (Trotter, 1984), Marčhenko and Pastur (Marchenko and Pastur, 1967) has expanded our understanding to include the behavior for singular values and rectangular random matrices.

Figure 1.

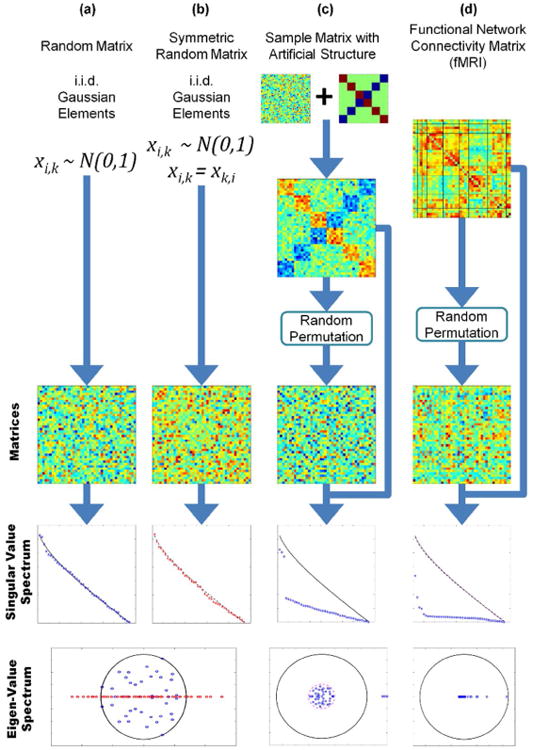
Different types of matrices and their eigen-spectrum. Random permutations have been applied to demonstrate that it is visually difficult to determine if the matrix is random or not. Column (a) corresponds to random matrices with Gaussian i.i.d. elements. The eigen-values tend to fill a circle in the complex plane following Girko's Circle Law. Column (b) shows the case of random symmetric matrices (in this particular case, the main diagonal has been set to zero) where the eigen-values are real due to the symmetry. However, both matrix cases exhibit a similar bulk distribution of the SVs that reveals the randomness of the matrices. The matrix in column (c) is a combination of a specific pattern plus a random matrix. Both eigen-value and SV spectrums reveal two distinct patterns. One pattern is similar to that found in random matrices with its eigenvalues following the Circle Law. The second pattern includes eigen-values and SVs with larger magnitude that separates them from the rest. Column (d) show a typical FCM obtained from fMRI data. All eigen-values are real, making it difficult to compare with the Circle Law. On the other hand, the SV spectrum is always real and can be compared with the SV spectrum of random matrices. The figure illustrates the notable difference between the SV spectrums of random and FCM matrices.

We will focus our attention on Wishart-Laguerre ensembles that can be obtained as follows: given a random matrix X, where X have i.i.d. Gaussian elements, the Wishart-Laguerre ensemble is the matrix X*X, where * may denote the real or complex transpose operation (Katzav and Castillo, 2010). Without lack of generality and for simplicity, we assume that a transpose operation may be necessary to let X*X be a full rank matrix. This applies to rectangular matrices X_M×N where X is of size M × N with N < M and the assumed multiplication is $X_{M\times N}^{\ast }{X}_{M\times N}$. Under these conditions, the resulting matrix X*X is full rank, square and its eigen-values are real, thus simplifying any further theoretical development. An important characteristic of the matrix X*X is the relationship of its eigen-values with the singular values of the matrix X. Considering the singular value decomposition (SVD) X = U∧V* where ∧ is a diagonal matrix containing the SVs of X, the matrix X*X can be decomposed as X*X = V∧²V* (notice that V⁻¹ = V*) indicating that the eigen-values of X*X are equal to the squared SVs of X. From this point we move our attention to the SVs rather than the eigen-values of X, leaving behind complex numbers and issues with matrix size.

The eigen-values of X*X are known to follow the joint Wishart distribution (Wishart, 1928), which does not describe the distribution of any particular eigen-value but rather their multivariate behavior. Given their relationship to a matrix condition number, efforts have been made to describe the distribution of the largest and minimum eigen-values (Edelman and Rao, 2005), but we lack a closed form probability distribution formula for all the eigen-values of X*X. The bulk behavior of SVs has been characterized thanks to the work of Marčenko and Pastur (Marchenko and Pastur, 1967) and some efforts have been made to estimate the expected SV magnitudes based on these results (Dette and Imhof, 2007; Vergara et al., 2008). However, individual SV variances have not been obtained from SV bulk behavior and there is no theoretical development, to the best knowledge of the authors, providing a closed form formula for the full set of individual SV variances and other central moments. Although a closed-form formula for the probability distribution of individuals SVs is yet unknown, required parameters can be estimated using Monte Carlo methods. In the present context, the necessary parameters are means and variances for each of the SVs of X.

Functional Connectivity Matrices

For the purpose of theoretical development, we will assume that all elements in a random matrix follow a Gaussian distribution. In the context of this work, the random elements will eventually represent random correlations. Through Fisher's Z–transformation (Fisher, 1915) the variance of random correlations is normalized such that transformed correlations can be modeled as Gaussian random variables. It is common practice to organize the set of connectivity values in matrix form (an FCM) grouping strongly connected elements together. Figure 1(d) displays a typical ordered whole brain FCM where, as customary, the Z–transformation has been applied to all correlations.

In general, an FCM can appear to be a random set of numbers. It is only after appropriate permutations that a visual pattern can be identified, which is unlikely to happen by chance. Figure 1(d) exemplifies this last statement using fMRI data. The pattern we see in the FCM at the top of Figure 1(d) show how fMRI data is expected to display after the rows and columns have been properly permuted. In the case of fMRI connectivity, these permutations are anchored on a corpus of knowledge that has been acquired through many years of extensive research and development (Allen et al., 2011; Buckner et al., 2008; Fox et al., 2005; van den Heuvel et al., 2016). This work proposes a formal technique to test whether observed patterns in an FCM are random or not.

Random Functional Connectivity Matrices

Most of the studies in random matrices assume i.i.d. Gaussian elements with zero mean (m=0) and unitary variance (s²=1). As illustrated in Figure 2(a), the eigen-values in this instance tend to fill a circle in the complex plane following the Circular Law (Girko, 1985). This case is good for theoretical development, but it is rarely found in practice. For example, the connectivity among brain areas belonging to the DMN (PCC, precuneus, AG, etc.) is different from zero during resting state (Buckner et al., 2008), indicating a strong synchronicity and coherent temporal activation. A removal of the mean value could be applied to compare a connectivity matrix with theoretical zero-mean random matrices. However, this procedure will change the characteristics of the original SV spectrum. Figure 2(b) illustrates the existence of an eigenvalue related to the non-zero mean value (|m|>0) of matrix elements. Removing the mean will leave that eigenvalue unrepresented, thus changing the original matrix spectrum. A different approach is to consider the SV spectrum of a random matrix as composed of two parts, one following a zero-mean random matrix spectrum and the other part being determined strongly by the mean. As exemplified in Figure 2, random matrices composed of elements with a nonzero mean have one singular value that is distinct from the rest. The mathematical background for the previous assertion can be found in the work of Silverstein (Silverstein, 1994), who proved the existence of the largest eigenvalue as real and positive after perturbing the zero mean random matrix with a nonzero rank one matrix. Further analysis of this theory, including conditions to assume a clear differentiation of the largest singular value, has since been presented (Vergara and Barbin, 2010). The bulk of eigen-values different from the largest one tend to fill a disk in the complex plane, just as in zero-mean random matrices. Arguably, the strong eigen-value represents the signal within the matrix and the rest represents random deviations from the main signal (Vergara and Barbin, 2010).

Figure 2.

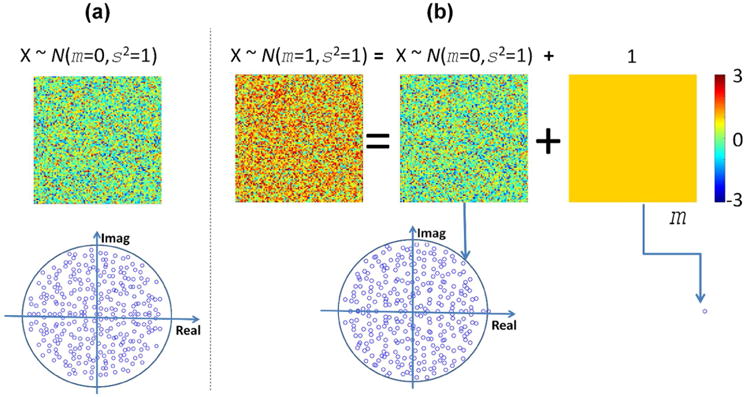
Eigen-value spectrums for zero and non-zero mean random matrices. In (a), the zero mean case follows the Circle Law as the spectrum fills a disk in the imaginary plane. In the non-zero mean case (b), all except for one eigen-value follows the Circle Law. This largest eigen-value is linked to the mean of matrix elements. The mean value can be argued to represent the amplitude of the whole matrix while the random part following the Circle Law represents only deviations from the mean.

Based on the presented analysis, the reasonable assumption illustrated in Figure 2 is that a random matrix can be summarized by the mean value of its elements and deviations from the mean are due to random changes. This idea is especially useful in analyzing and interpreting connectivity submatrices, where groups of brain regions may exhibit a highly coherent activation but small deviations from the mean coherence can be attributed to chance.

Distance from a Random Matrix

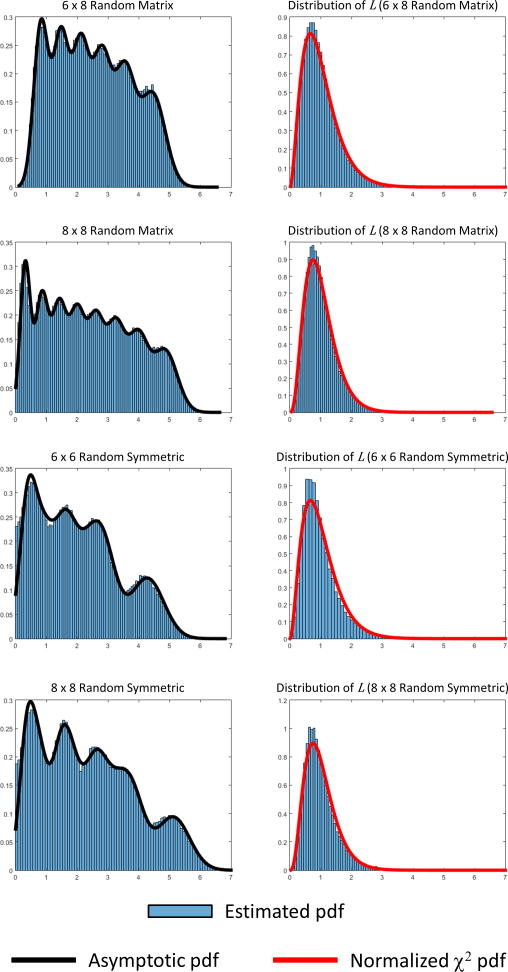
We propose an assessment of randomness by comparing the similarity between SV spectrums of an FCM of interest against that of homologous random matrices. Following the discussion of the last section, we propose to look at the difference (λ_i – μ_i) between the SVs (λ_i, i = {1 …N}) of the FCM of interest and corresponding mean SVs (μ_i, i = {1 …N}) obtained from random matrices. Both sets of values λ_i and μ_i are assumed to be sorted in descending order. The difference identifies a measure of farness from randomness. One important characteristic is that the eigenvalue spectrum of the wishart-laguerre ensemble used in this work asymptotically follows multivariate Gaussian distributions. This asymptotic behavior was mathematically proven by Dumitriu and Edelman (Dumitriu and Edelman, 2005). For a given i^th SV, mean μ_i and variance ${\sigma }_i^2$ parameterize the corresponding probability distribution. Figure 3 illustrates this result for Wishart-Laguerre ensembles where the composite distribution of SVs follows closely the composite distribution obtained from Gaussian distributions.

Figure 3.

SV histograms for several random matrices. At the left, the picture shows histograms for random and random symmetric matrices where elements follow a Gaussian distribution. In the case of random symmetric matrices, the main diagonal has been set to ones to make them similar to the FCM matrices found in fMRI data analysis. The histograms resemble a composite histogram made out of individual Gaussian distributions, but this behavior is only asymptotic (Dumitriu and Edelman, 2005). The composite Gaussian distribution has been included to compare with the estimated histogram. The estimated histogram is also influenced by cross correlated SVs. This characteristic is also different from the independency assumption used to build the composite Gaussian distribution. At the right, histograms and theoretical chi-square (χ2) distributions are plotted for the metric L. The SV mean values and covariance matrix have been estimated using 100000 realizations of corresponding random matrices.

At this point it makes sense to use a chi-square distribution from squared Z-scores $\sum {({\lambda }_i-{\mu }_i)}^2/{\sigma }_i^2$, where ${\sigma }_i^2$ is the variance associated to the mean SVs μ_i. One interpretation of this procedure is to determine a chi-square type “goodness of fit” (Lancaster and Seneta, 2005) between FCMs and random matrices. One problem with this initial approach is that SVs are not uncorrelated with each other and the simple sum of squares will not work. Instead, the matrix of covariance must be applied to correct for the correlation among SVs. For this purpose, we employ the Mahalanobis distance since it is known to correct for correlation within the data (De Maesschalck et al., 2000). Using matrix notation, the normalization can be included in the metric as (λ − μ)Σ⁻¹(λ − μ)* where Σ is the covariance matrix of the SVs. Assuming that all matrices considered are full rank N, we can normalize and define the metric

$$L=\frac{1}{N}(\mathit{\lambda }-\mathit{\mu }){\sum }^{-1}{(\mathit{\lambda }-\mathit{\mu })}^{\ast }.$$

After considering the covariance matrix Σ, the metric L follows a chi-square distribution corrected by N. The probability density function (pdf) of L can be obtained from the chi-square distribution (Mulholland and Jones, 1968), namely f_x,N, with N degrees of freedom by substituting x = NL to find the closed form as

$$f_{L,N}=\frac{{\left(\frac{N}{2}\right)}^{N/2}}{\mathbf{\Gamma }(N/2)}{L}^{(\frac{N}{2}-1)}{e}^{-NL/2}.$$

The proposed procedure requires estimating the N SVs of a given connectivity matrix to test against the SV spectrum of random matrices of rank N with random elements exhibiting sample mean m and standard deviation s. The first step is to determine the number of SVs N, m and s for the FCM of interest. The second step is to estimate the mean values μ_i for each of the N SVs from random matrices and the covariance matrix Σ. This step can be achieved by using Monte Carlo methods. Figure 3 shows pdfs of L for a few matrix sizes where means and covariance matrix were obtained algorithmically. Statistical testing for L can be accomplished by using the chi-square without normalizing by N or simply using the pdf of L. In any case, the pdf of L depends on N and significance thresholds may change for different values of N.

Randomness Examples

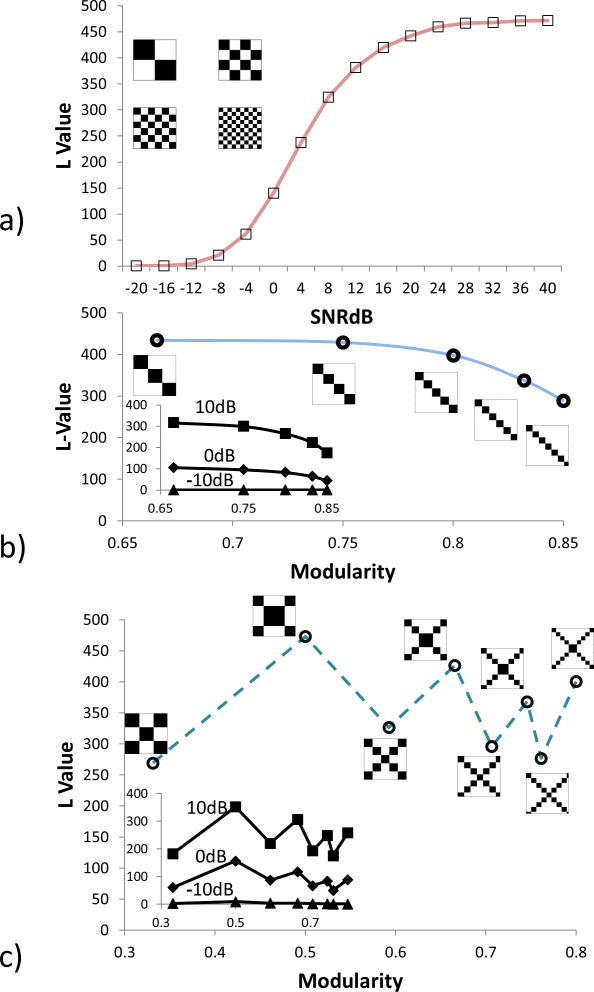
In this section, we present a set of matrix examples to understand the sensibility of the presented random matrix measure. Three set of binary matrices (containing only 0 or 1 on each entry) were selected with a size of 100 × 100 and displaying different connectivity patterns. The outcomes are displayed in Figure 4. The first set of matrices was designed to follow chessboard patterns of different sizes with the same modularity, randomness, sample mean (m = 0.5) and standard deviation (s = 0.25). The second set shows adjacency matrices with disconnected communities and the third set shows connected communities. The modularity (denoted as q) of adjacency matrices were calculated using the Newman's method (Newman, 2006) included in the Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/Home) (Rubinov and Sporns, 2010).

Figure 4.

Examples of connectivity matrices. In a), the noiseless adjacency matrices have a modularity q-value of 0.5 and an L-value of 470. Gaussian noise of different variances is added to the uncorrupted adjacency matrix simulating noise. SNRdB values are decibels of the ratio between the adjacency matrix and the Gaussian noise. In b), L-values for modular matrices forming unconnected communities are calculated for noiseless (main plot) and noise added. In c), the plot is similar to b), but considering connected communities.

In Figure 4(a), random Gaussian noise was added to the four noiseless adjacency matrices; then randomness value L was estimated for different leves of signal-to-noise ratios. The adjacency matrices had a value of L = 470. Signal variance was estimated from the noiseless matrices having all the same value (s² = 0.5). The power of Gaussian noise decreases the value of L indicating the presence of randomness. Note that all noiseless matrices in these examples were rank deficient (rank<=10) with more than 90 zero value SVs. However, matrices contaminated by noise were all full rank (rank=100). The normalization value N was set equal to the total number of SVs (N =100) in each case even if some SVs were zero. L values for noisy matrices approaches their noiseless version as the SNR increases thanks to this normalization. Figure 4(b) and Figure 4(c) illustrate randomness variations with different levels of modularity. In the case of unconnected communities of different sizes, randomness and modularity seems to follow a trend of decreasing L as modularity increases. As noise corrupts the ideal matrices, the trend starts vanishing. At -10dB, the noise has practically obscured the relationship between L and modularity. Although informational, unconnected communities are simple uninteresting patterns. Figure 4(c) displays a more practical case where communities are connected using two different patterns, but with different community sizes. The monotonic relationship observed in Figure 4(b) seems to break in Figure 4(c) because the connectivity patterns are different, despite being generated with the same in-house algorithm. However, the effect of adding noise is the same as before since noise grows stronger and the ability to discern a pattern between L and q decreases. Overall, Figure 4 shows that a monotonic relationship between L and q is not likely to be observed if the connectivity pattern changes from one observation to the other. In practical terms, if noiseless adjacency matrices could be determined from different brains, the exhibited patterns would need to be “the same” in the sense of the characteristics of Figure 4 (varying only in their size and number of communities). Even small dissimilarities, likely to occur when comparing the brains of different subjects, can break the relationship between L and q.

Randomness Assessment in Vectors

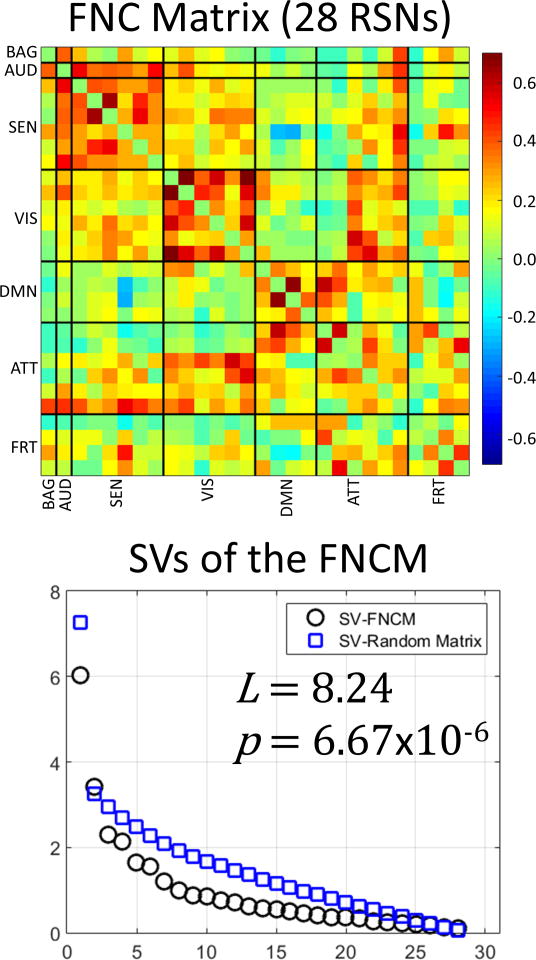
The overall theoretical development presented here focuses on matrices (i.e. arrays with a minimum of two SVs). For matrices larger than 2 × 2, the shape of a matrix SV spectrum can be characterized and compared to the SV spectrum of random matrices. However, there will be situations where the assessed array is a vector and the proposed method fails to be adequate. This situation occurs in practice when the connectivity is estimated between a region of interest and multiple other regions. The matrix in Figure 5 provides some examples of functional connectivity vectors. There is only one row and one column representing the basal ganglia (BAG) thus forming column and row vectors. In contrast, the DMN is represented by more than one row and one column forming a submatrix when the DMN connectivity is assessed against itself.

Figure 5.

Results for whole mean FCM. The connectivity pattern coincides with previously observed connectivity. The SVs of this mean matrix, averaged across all subjects, were compared with random matrices using the metric L that achieved a magnitude of 8.24. The resulting small p-value corroborates the assumption that FCM matrices do not display a connectivity pattern that can be easily found by chance; thus it qualifies as a non-random matrix.

The SV spectrum of a vector has always the same shape because is composed of only one singular value that is a function of the second moment (m² + s²). In other words, all random vectors with the same mean and variance have the same SV (i.e. not quite the random SVs found in the random matrix theory). The method proposed for random matrices requires the estimation of m² and s², thus losing the degrees of freedom necessary to test for the single SV of a vector. For these reasons, the randomness test described in previous subsections applies only to matrices and is not suitable for vectors.

In fact, there are efficient random tests developed for vectors (Cammarota, 2011; Wald and Wolfowitz, 1940). One of the most widely used tests for vector randomness is the runs test (Bradley, 1960; Wald and Wolfowitz, 1940) which checks randomness for data sequences [x₁ x₂ x₃ …]. Just as random matrix theory fails when dealing with vectors because of the low dimensionality, so too will the runs test fail to be adequate if the vector dimensionality falls below two. This happens because a single scalar [x₁] does not characterize a sequence. When needed, vector randomness will be assessed utilizing the Matlab implementation of the runs test (the runs test() command) given that random matrix theory does not apply.

Materials and Methods

Subjects

The study data comes from 603 subjects, 305 of which were females. The age of participants ranged from 12 to 71 years with mean and standard deviations of 23.4 ± 9.2. Participants were not taking psychoactive medications, did not have a history of neurological or psychiatric disorders, and did not report high levels of substance use (smoking an average of less than 11 cigarettes per day; drinking less than 2.5 more drinks per day). This data was used in a previous publication where it was carefully curated to minimize motion effects (Allen et al., 2011) and utilized to describe a baseline for the multivariate analysis of fMRI data; more information regarding this population can be found there. The variables of interest for our work here are age and gender, which are well represented in this dataset.

Imaging and Preprocessing

All images were collected on a 3-Tesla Siemens Trio scanner with a 12-channel radio frequency coil. High resolution T1-weighted structural images were acquired with a five-echo MPRAGE sequence with TE = 1.64, 3.5, 5.36, 7.22, 9.08 ms, TR = 2.53 s, TI = 1.2 s, flip angle = 7°, number of excitations = 1, slice thickness = 1 mm, field of view = 256 mm, and resolution = 256 × 256. T2*-weighted functional images were acquired using a gradient-echo EPI sequence with TE = 29 ms, TR = 2 s, flip angle = 75°, slice thickness = 3.5 mm, slice gap = 1.05 mm, field of view 240 mm, matrix size = 64 × 64, voxel size = 3.75 mm × 3.75 mm × 4.55 mm. Resting-state scans were a minimum of 5 min, 4 s in duration (152 volumes). Any additional volumes were discarded to match data quantity across participants. Subjects were instructed to keep their eyes open during the scan and stare passively at a foveally presented fixation cross.

Data were pre-processed using statistical parametric mapping (http://www.fil.ion.ucl.ac.uk/spm) (Friston, 2003). The preprocessing steps included slice-timing correction (resliced to 3 mm × 3 mm × 3 mm voxels) realignment, co-registration, spatial normalization and transformation to the Montreal Neurological Institute (MNI) standard space. We followed recent recommendations (Vergara et al., 2017a) for pipeline preprocessing. Time courses were orthogonalized with respect to i) linear, quadratic and cubic trends; ii) the six realignment parameters; iii) realignment parameters derivatives; and iv) spike regressors. The DVARS method (Power et al., 2012) was used to find spike regressors where the RMS exceeded 3 standard deviations. The fMRI data were smoothed using a full-width-half-maximum Gaussian kernel size of 6 mm.

As previously described (Allen et al., 2011), data were analyzed with Infomax based gICA (Calhoun and Adali, 2012a) resulting in 75 gICA components. Time courses were then filtered using a band-pass filter from 0.01 to 0.15 Hz. The 28 RSNs described (Allen et al., 2011) were identified in the current analysis and clustered in the same seven domains: BAG (basal ganglia), AUD (auditory), SEN (sensorimotor), VIS (visual), DMN (default mode), ATT (attentional) and FRT (frontal). The correlation matrix of the 28 RSNs, grouped according to the seven defined domains, constitute the FCM utilized in this study.

Randomness Test of the FCM

For all of the following calculations, we utilized 100,000 realizations of the Wishart-Laguerre ensemble to estimate the mean values and the covariance matrix of the SVs. The number 100,000 was selected to ensure an accurate estimation. The mean m and standard deviation s of matrix elements were matched to the sample mean and sample standard deviation of the FCM of interest. The first test seeks to identify the level of randomness of the mean FCM averaged over all subjects. The p-value of L was measured to determine statistical significance. The second test seeks to find any relationship between randomness and subjects' age and sex. One FCM was calculated for each subject, each resulting in a corresponding L value. The 603 L values were used as dependent variables for a regression model with age and sex as independent variables. Finally, the correlation between modularity q, as defined in (Newman, 2006), and L was performed to assess the relationship between these two measures.

Based on the seven RSN groups previously defined, it is possible to subdivide the FCM into 28 submatrices. Randomness was tested on each of the 28 submatrices along with similar age and sex regression models to the one performed for the whole FCM. Those submatrices with significant L value (i.e. significantly not random) were partitioned in even smaller submatrices. The secondary submatrices were also tested. The partitioning stopped when either all submatrices were random or it was not possible to find another partition to make them random. This algorithm was applied manually to find patterns in the matrix based on their randomness.

Results

Figure 5 shows the result for the mean FCM. The value of L is very large and equal to 8.24 with a p-value of 6.67×10⁻⁶, confirming the non-random pattern visually observed for this matrix. We applied two regression models differing on the inclusion or exclusion of a quadratic term for age. The first regression test for L applied to the whole matrix shows no significant effects with sex (β =-0.224, p-value=0.20, var. explained = 0.3 %) or age (β = -0.004, p-value = 0.64, var. explained = 0.04 %). The second regression included a quadratic term with no significant effect for sex (β_sex = -0.202, p-value = 0.26, var. explained = 0.2 %), but a significant age effect with linear (β_age = 0.102, p-value = 0.020, var. explained = 18.6 %) and quadratic (β_age² = -0.002, p-value = 0.01, var. explained = 21.3 %) terms. Supplementary Figure 1 displays the scatter plot of L versus age.

Before measuring the correlation between L and q, the FCM of each of the 603 subjects were binarized by applying an absolute value function and thresholding with a value between 0.001 and 0.999. A first attempt was made by keeping the same threshold for all subjects, but no significance was observed. Instead, the threshold chosen was different for each FCM to keep the same number of nonzero edges on the FCM of each subject. Figure 6(a) displays the relationship between the correlation L vs. q and the number of non-zero edges. For the current data, L and q has a maximum correlation of 0.536 when the number of non-zero edges is 220. Figure 6(b) shows a scatter plot for the maximum correlation.

Figure 6.

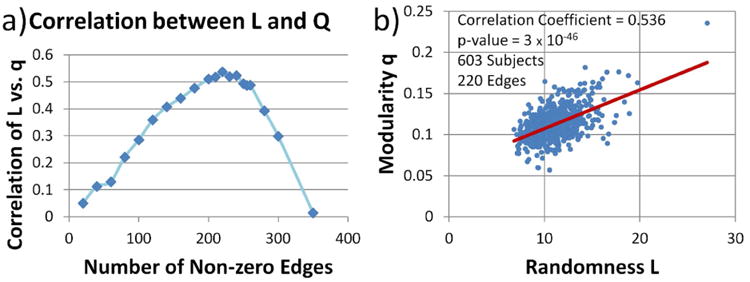
Correlation between L and q. This correlation exists when the number of non-zero edges is kept constant. In the figure, the FCM for each subject was binarized using different value thresholds to achieve the same non-zero edges. a) shows the dependence between selected number of non-zero edges and the correlation between L and q. b) shows the scatter plot for the maximum correlation detected.

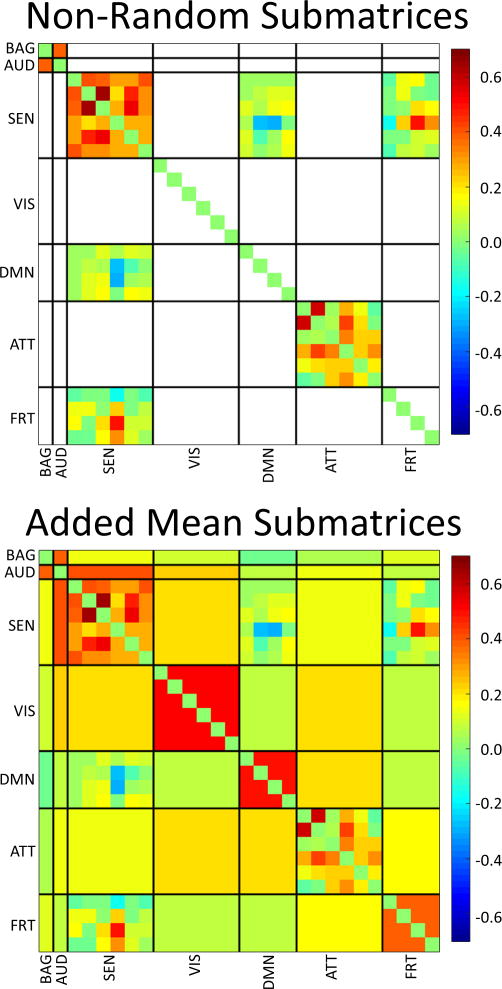
The test for submatrices reveals a high incidence of randomness. Out of the 24 possible submatrices, excluding scalar (1×1) arrays, only four were significantly non-random (p-values < 0.05) after false discovery rate (FDR) correction (see Table I). Notice that submatrices corresponding to pairs BAG-BAG, BAG-AUD, AUD-AUD and AUD-BAG were scalar and randomness could not be tested. Following the concept displayed in Supplementary, we used mean values to represent the connectivity within those submatrices with L values that did not achieve significance. Figure 7 shows this mean value representation, but leaves unchanged submatrices with significant non-randomness. This representation displays the general pattern expected for the whole FCM without noisy random variations. Only one significant age result survived FDR correction (p<0.05) on the ATT-ATT submatrix (β_age² = 0.0005, p-value=0.00714, var. explained = 24.8 %). Supplementary Figure 2 provides the scatter plot for the L value of the ATT-ATT submatrix.

Table I. Submatrices with significant non-randomness (L value). Results survived false discovery rate (p<0.05) correction.

Domain 1	Domain 2	L value	p value (uncorrected)
SEN	SEN	3.215	0.004
SEN	DMN	3.929	0.003
SEN	FRT	3.509	0.007
ATT	ATT	2.864	0.009

Figure 7.

Randomness test results on all submatrices. White-out submatrices had a non-significant L value. Since some submatrices were indeed just vectors, we utilized the Matlab command runstest() to test randomness for vectors. It was out of scope to test randomness for single values and thus we avoided performing such tests. Following the idea presented in Figure 2, we filled in the non-significant submatrices with their mean value and present a picture of the non-random content of each submatrix.

Because there are still some submatrices with significant non-randomness in Figure 7, we proceeded to analyze a bit further the content of the FCM. We specifically looked for permutations and partitions that allowed for all submatrices to be considered as random. The non-random matrices in Figure 7 may still contain patterns that could be separated. After manually looking for smaller submatrices, the two domains SEN and ATT were broken into smaller subdomains SEN1-SEN2 and ATT1-ATT2 correspondingly. With this rearrangement, almost all submatrices were considered random except for ATT2-ATT2. Figure 8 displays the new matrix partition. It was not possible to find a partition and permutation for ATT2-ATT2 that rendered all matrices random. However, the increment of random submatrices revealed a finer structure in the FCM than the original set of domains selected.

Figure 8.

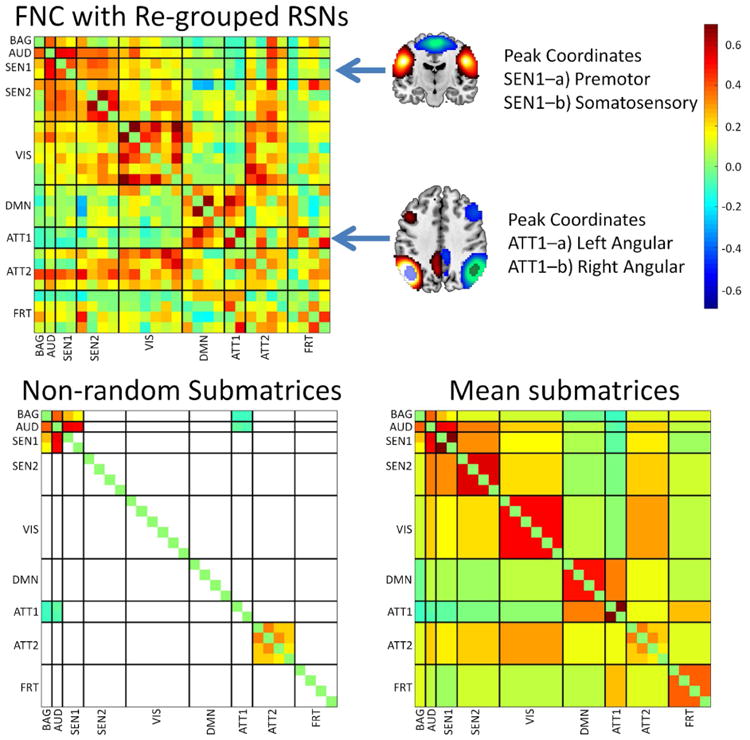
Results after permuting and regrouping the RSNs. Two attention RSNs with peaks in the angular gyrus and two sensorimotor RSNs with peaks in somatosensory and motor areas were segregated in their own groups. This step provided a larger number of random submatrices than the results presented in Figure 7. The larger number of random submatrices might indicate that groups have more similar elements than groups exhibiting smaller quantities of random submatrices.

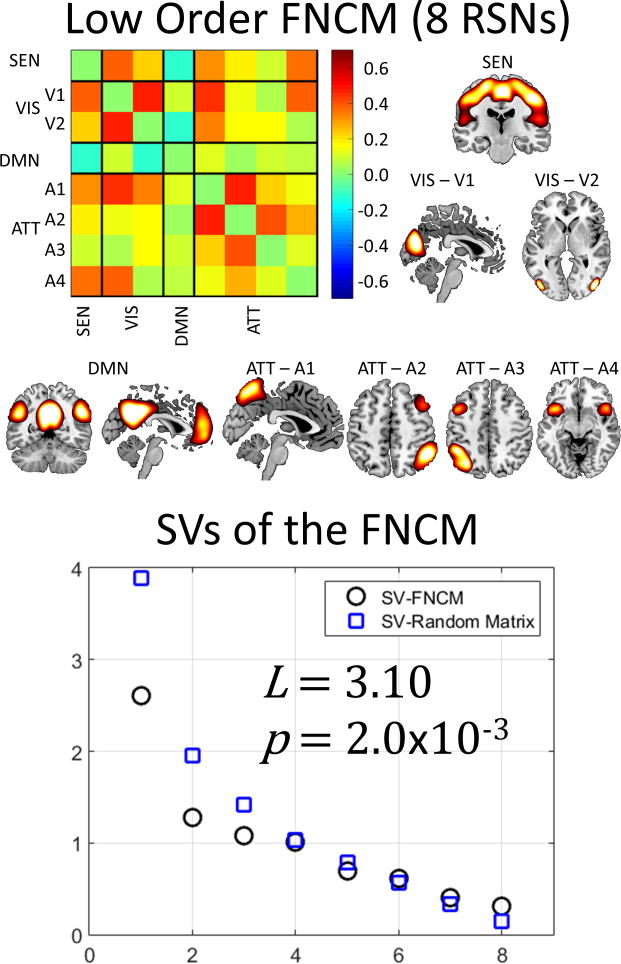
The collapsing of almost all submatrices into their mean values, based on their randomness level L, suggests that a lower order gICA (less number of components) may be sufficient to describe the data. A final analysis using just 15 gICA components was performed for comparison. Figure 9 displays these results. Basal ganglia RSNs were discarded because of CSF noise contamination. The spatial content of the components were matched as closely as possible to the domains originally selected for this dataset (Allen et al., 2011). The low order gICA exhibit a similar parietal region in the DMN to that catalogued as ATT1 in the high order model, thus providing data-driven evidence that left and right angular giri do not belong to the ATT group. As in the high order case, the low order matrix tested significant for non-randomness with L=3.10 and a p-value of 2.0×10^-3. The low order regression did not show significant results for age or sex in any linear or quadratic relationship.

Figure 9.

Results from a lower order gICA for comparison. The original gICA from Figure 5 exhibited a large number of random submatrices, suggesting that a lower order model could describe the data. The FCM of this figure is closer to a random matrix than the FCM of the higher order, not only because of the L value, but also because of the larger p-value.

Discussion

The proposed randomness test serves to determine how far from random chance a given FCM is and provides evidence for the existence of non-random patterns that are difficult to see with the naked eye. The FCM pattern in this manuscript has been previously presented (Allen et al., 2011) and is the typical pattern found in resting state fMRI data. Evidence from functional (Greicius et al., 2003; van den Heuvel et al., 2016) and structural (Greicius et al., 2009; Honey et al., 2009) studies provide evidence that observed functional connectivity is not a random observation. Based on this evidence, it was determined that the test outcome result was positive for non-randomness. This result verifies that the proposed method does provide a measure of non-randomness that can also measure farness from chance.

There are some key points with respect to the definition of connectivity utilized in our method. The considered functional connectivity has been extensively used for statistical testing of functional abnormalities related to several neuropathologies. Fisher transformed correlations were used to classify subjects into schizophrenia and healthy controls (Arbabshirani et al., 2013), detect differences between bipolar and depression disorder patients (He et al., 2016) and to differentiate mild traumatic brain injury patients from controls (Vergara et al., 2017b) to mention a few applications. The definition and usage of connectivity used to develop the proposed random matrix test is the same as in the studies mentioned, but is different from those used in graph analysis of brain networks (Fornito et al., 2013; Rubinov and Sporns, 2010). Our results found a moderate relationship between the randomness measure defined here and modularity. This relationship depends on the conversion applied from raw data (correlations in the FCM example) to node-edge representation. We argue that our randomness metric is a more direct measure that avoids the transformations to node-edge representation, but addresses different aspects of the data when compared to modularity. The argument does not demerit graph analysis; it only states the existence of differences despite existing similarities that can be concluded from the resulting moderate correlation. In the same line, the eigen-spectrum method used here resembles the application of the Laplacian matrix in the context of graph measures (Banerjee and Jost, 2008; Jalan and Bandyopadhyay, 2008). However, these two theories are designed for different aspects of connectivity. Specifically, the Laplacian approach allows for the comparison of graph structures, even if the graphs are of different sizes (Banerjee, 2012). On the other hand, our metric seeks to detect randomness in a different sense where, if the test is not significant, then all elements in the matrix might be realizations of the same normal distribution. The only structure in this case is that all values in the matrix probably have the same mean value corrupted by random noise. Significance in our test indicates the existence of a different structure than equal mean among matrix elements, but it does not specify the structure. Another characteristic of the randomness metric defined here is the ability of testing off-diagonal submatrices, a feature not contemplated in graph theory. Attempting to analyze off-diagonal submatrices will leave out necessary information about the graph structure, but this is not the case for the proposed randomness test since the existing structure is not confined to that of a graph. To this ability of handling off-diagonal submatrices we can add a lesser restriction with size allowing randomness testing if more than one edge is included. The presented randomness metric can detect randomness of matrix sizes as low as 2 × 2 in the case of off-diagonal submatrices and 3×3 in the case of those in the diagonal. The problem with 2 × 2 connectivity matrices (also 2 × 2 in-diagonal submatrices) is that only one edge is represented. On the other hand, the case of 2 × 2 off-diagonal submatrices include information for four edges. However, the lesser restrictiveness with size does come with the characteristic sensitivity of the chi-square to degrees of freedom that in our case are directly represented by the FCM size.

Submatrix randomness tests provide evidence to suggest that connectivity within and between resting state domains can be summarized by a single value as conceptually illustrated in Figure 2 and empirically demonstrated in Figure 7. This mean value representation can be interpreted as all brain areas of certain domain A exhibit the same connectivity level with all brain areas of another domain B plus some random variations of lesser magnitude and smaller power as compared to their mean value. This last statement assumes a domain connectivity matrix that, except for the mean value of its matrix elements, could not be ruled occurring out of chance. This interpretation leads to the conclusion that the matrix mean is the solely embedded pattern within the matrix and suggests that if all submatrices in an FCM are random then the RSN grouping form very cohesive domains.

The distance from chance presented in this work provides a new dimension of functional connectivity to be tested against covariates of interest. The findings in the current data showed no sex or age effects in the FCM for the regression model with no quadratic terms. The absence of ageing effects seem to coincide with the lack of brain modularity difference between young and old populations previously observed (Meunier et al., 2009). However, a different topological study considering brain topological organization did find whole brain effects, but the observations were not of a linear fashion (Wu et al., 2012). The regression model included a quadratic age term that resulted in a significant age effect that is more in agreement with Wu's data (Wu et al., 2012), where the brain's global efficiency is larger for mature than either young or old populations. Similarly, the negative direction of β_age² indicates less randomness towards maturity and more randomness for the younger and older sides of the ageing spectrum. On the other hand, a quadratic relationship with L was found for the domain submatrix ATT-ATT, but with an opposite direction of effect compared to the whole brain results. This case demonstrates that randomness trends in whole FCMs are different from those in its constituent submatrices.

An important fact is observed in the subdomain ATT1, which is composed of RSNs with peak activations in left and right angular gyri. Although the angular gyrus is a parietal region that may be grouped among the attention brain areas, it has been also identified as part of the default mode network (Greicius et al., 2009). After separating both angular giri in Figure 8, we can visually observe a similar connectivity to the DMN with the exception of the connectivity for the FRT RSNs. In this case, randomness assessment helped in finding an extra level of modularity within the ATT domain. The angular giri placement in the DMN is further supported by the results obtained in the lower order gICA displayed in Figure 9. The case of the modularity in the SEN domain, also illustrated in Figure 8, is less obvious because the two RSNs in the subdomain SEN1 embrace sensorimotor anatomical areas. Visual inspection of Figure 8 allows us to see small differences of connectivity between SEN1 and SEN2 in relation to themselves and to the VIS domain.

Finding the mean FCM in this analysis as composed by many random submatrices would raise the concern that a lower model order could describe the data and remove the observed randomness. Randomness in this view could be seen as unnecessary noise. However, this is not consistent with the results. In our data, lowering the model order increased the FCM randomness. This can be seen after comparing Figure 5 and Figure 9. The increased randomness indicates that some structure is missing. This loss of structure is expected since the low order model provides fewer degrees of freedom. As part of this loss of randomness, the relationship with age found in the higher order model is also lost. We must conclude that compared to low order, high order gICA contains structure and information important for data analysis.

An important limitation of the current method is rooted on the asymptotic characteristic of its Gaussianity assumptions. Although pdf and histogram comparisons in Figure 3 fit very closely, we have to consider small discrepancies between the two. These discrepancies asymptotically disappear as the matrix elements changes from real, complex, quaternion, etc. as previously described (Dumitriu and Edelman, 2005). Since the complex numbers can be seen as an extension of the real numbers, quaternions (first described by William Rowan Hamilton (Rosenfeld, 1988)) are a similar extension of complex numbers. Dimitriu and Edelman (Dumitriu and Edelman, 2005) described several systems of these numerical extensions as applies to random matrix theory. However, our case of real FCM matrices is in fact the lowest point in this asymptote and prone to errors. Moving beyond correlation, other studies of coherence have estimated complex valued FCMs (Yaesoubi et al., 2015). Future applications of the randomness metric to other types of FCMs (including complex or possibly quaternion) will decrease the inexactitude of the chi-square pdf describing the distribution of metric L. Another caveat in our theory is the comparison between random matrices with statistically independent elements and correlation matrices with interdependent elements. Pitfalls of the use of correlation in connectivity matrix have been previously studied in graph theory (Zalesky et al., 2012). Although the comparison between dependent and independent matrix elements might be unfair, the results demonstrate that some matrices with dependent elements exhibit a similar spectrum to that of a random matrix with independent elements (see Figure 1). A theoretical development for the similarity of random matrices with dependent and independent elements, including the case of symmetric matrices, has been presented by Adamczak (Adamczak, 2011). Results obtained must be interpreted with this limitation in mind.

In conclusion, the randomness test developed here allows us to identify purely random matrices from non-random. This can be used as a first test for new observations with a pattern that is not known or readily found by manual and visual methods. Further, as illustrated, the randomness test can be an important resource in identifying subpatterns within a matrix. In the context of functional connectivity, this translates into an extra resource that improves our ability to assess RSN grouping in different functional domains and a more data-driven FCM structure. In this work, the advantage of RSN grouping assessment was demonstrated by the fracture of the ATT and SEN in smaller subdomains due to their lack of randomness. This is important because correct matching between RSNs and domains is crucial when interpreting functional connectivity results. Furthermore, randomness of whole brain FCMs may be a time dependent measure (Hutchison et al., 2013; Sakoğlu et al., 2010). Future work on dynamic FCM can examine these momentary FCM configurations to characterize possible changes over time in randomness and modularity. Such dynamic analysis of randomness could provide further evidence to support temporal connectivity dysfunctions seen in schizophrenia and other brain diseases (Calhoun et al., 2014; Damaraju et al., 2014; Liu et al., 2016; Mayer et al., 2014). Finally, as FCM randomness varies with age, this may also be an important variable to consider in future research.

Highlights.

• This work proposes a measure of randomness for functional connectivity matrices.

• The method is based on Random Matrix Theory comparing against matrices with Gaussian elements.

• This assessment based on Random Matrix Theory measures a different aspect of randomness than similar methods using Graph Theory.

• The randomness measure is more resilient to matrix size problems and can be applied to whole matrices as well as its submatrices.