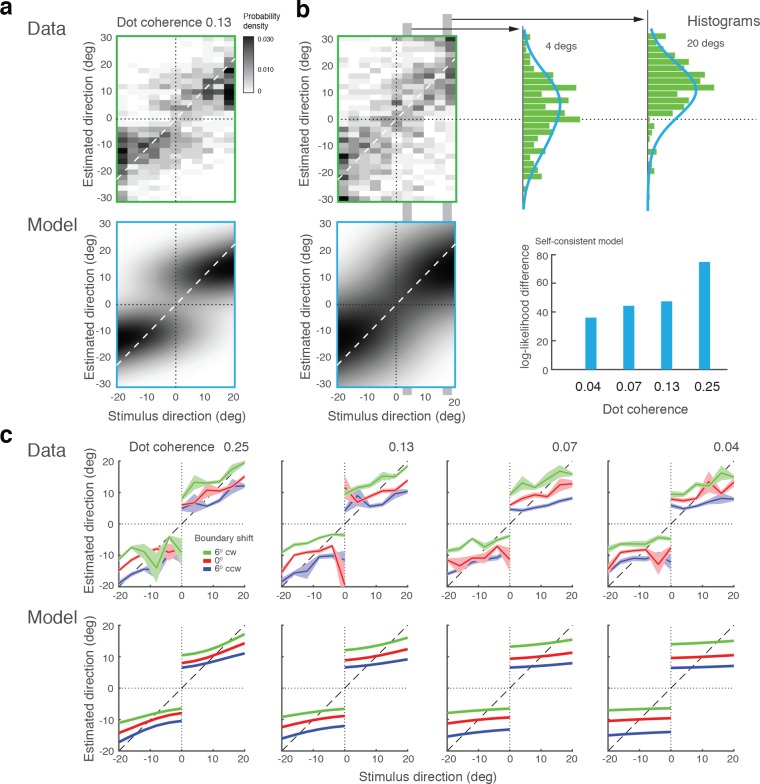
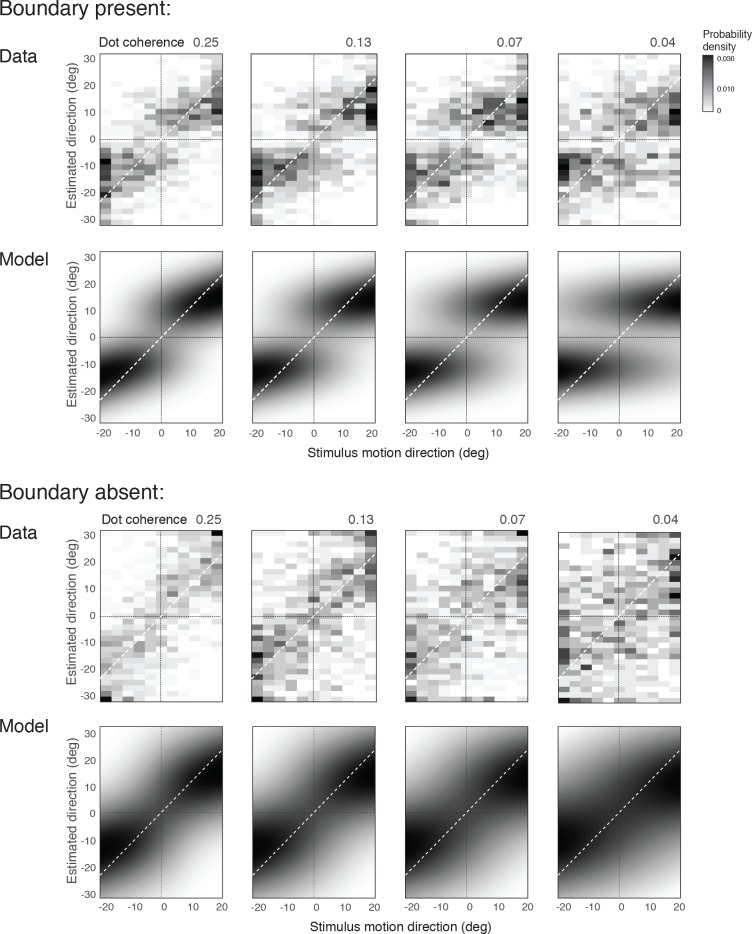
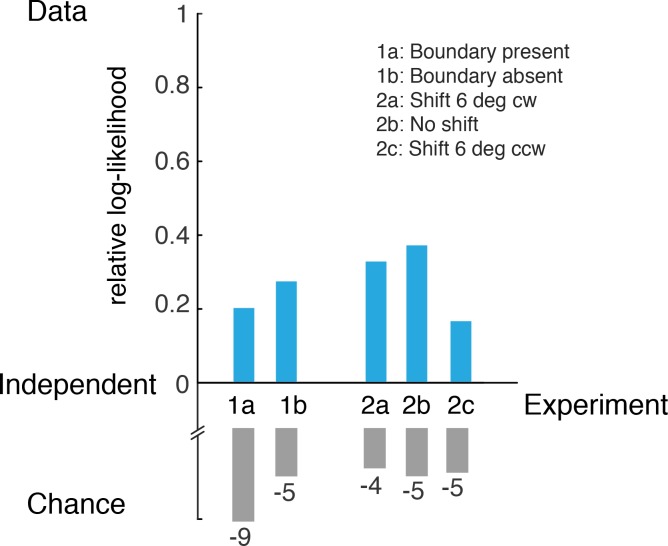
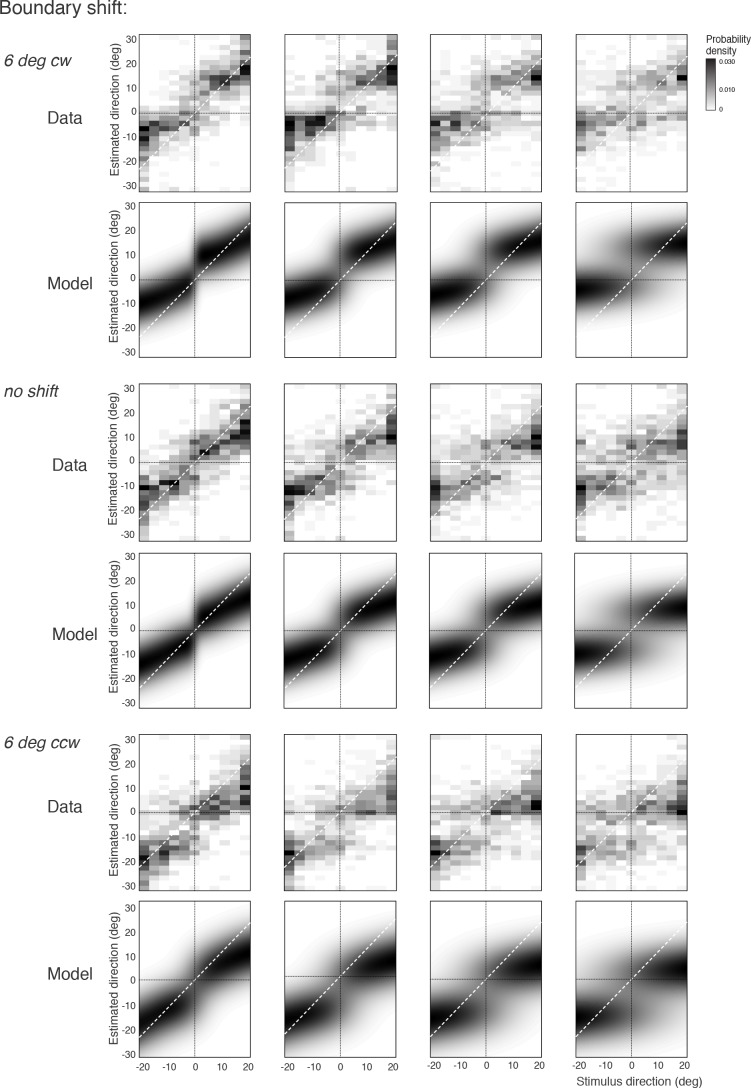
Figure 10. Model fits for experimental data by Zamboni et al., (2016).
(a) Experiment 1a: Exact replication of the original experiment (Jazayeri and Movshon, 2007). Exemplarily shown is the estimation data (combined subject) at one stimulus coherence level (0.13) together with our model fit. (b) Experiment 1b was identical except that the boundary was not shown during the estimation task. Estimate distributions are no longer bimodal yet the self-consistent observer, relying on a noisy memory of the boundary orientation, consistently better fit the data than the independent observer model (log-likelihood difference). (c) Experiment 2 introduced a shift in the boundary orientation right before the estimation task, which subjects were not aware of (six degrees). Subjects’ estimates were shifted accordingly (combined subject). The self-consistent model can account for the shift if we assume that the conditional prior is applied to the shifted boundary orientation. See Figure 10—figure supplements 1–3 for distributions, fits, and goodness-of-fits for all conditions.