Abstract
Rounis et al. (2010) reported that stimulation of prefrontal cortex impairs visual metacognition. Bor et al. (2017) recently attempted to replicate this result. However, they adopted an experimental design that reduced their chance of obtaining positive findings. Despite that, their results appeared initially consistent with the effect reported by Rounis et al., but the authors subsequently claimed it was necessary to discard ~30% of their subjects, after which they reported a null result. Using computer simulations, we found that, contrary to their supposed purpose, excluding subjects by Bor et al.’s criteria does not reduce false positive rates. Including both their positive and negative result in a Bayesian framework, we show the correct interpretation is that stimulation of PFC likely impaired visual metacognition, exactly contradicting Bor et al.’s claims. That lesion and inactivation studies demonstrate similar positive effects further suggests that Bor et al.’s reported negative finding isn’t evidence against the role of prefrontal cortex in metacognition.
Keywords: consciousness, visual awareness, metacognition, prefrontal cortex, transcranial magnetic stimulation
Introduction
Visual metacognition refers to how well one can give subjective judgments to discriminate between correct and incorrect perceptual decisions (Fleming & Lau, 2014). As visual metacognition appears to be closely linked to conscious awareness (Ko & Lau, 2012, Maniscalco & Lau, 2016), it is of interest that the prefrontal cortex has been heavily implicated in mediating both of these faculties (Baird Smallwood, Gorgolewski, & Margulies, 2013; Del Cul, Dehaene, Reyes, Bravo, & Slachevsky, 2009; Fleming, Ryu, Golfinos, & Blackmon, 2014; Lau & Passingham, 2006; Lumer, Friston, & Rees, 2008; McCurdy et al., 2013; Rounis, Maniscalco, Rothwell, Passingham, & Lau, 2010; Turatto, Sandrini, & Miniussi, 2004). Specifically, one prefrontal area with an empirical link to these abilities is the dorsolateral prefrontal cortex (DLPFC; Lau and Passingham, 2006; Rounis et al., 2010, Turatto et al., 2004).
It has been reported that continuous theta-burst transcranial magnetic stimulation (TMS) to DLPFC can impair visual metacognition (Rounis et al., 2010). Recently, Bor, Schwartzman, Barrett, & Seth (2017) attempted to replicate this finding but reported a null result, which they took to suggest that DLPFC might not be “critical for generating conscious contents” (Bor et al., 2017, p. 16).
However, although the researchers motivated their experiments as direct replications (e.g., Bor et al., 2017, p. 3), they made several changes to the original study design, some of which are known to undermine the chance of finding meaningful results from the outset. In particular, in their main experiment (their Experiment 1) the researchers used a between-subjects design instead of the within-subjects design used by Rounis et al. (2010), which might have limited their statistical power (Greenwald, 1976). Although they attempted to address this potential issue in a second study (their Experiment 2), we will show below that this study design was unsatisfactory for other reasons.
Importantly, despite these modifications, Bor et al. (2017) in fact found a positive result akin to Rounis et al.’s (2010), with both studies reporting comparable changes in metacognition for subjects who received TMS to DLPFC. However, the researchers proceeded to set stringent exclusion criteria, which they claimed should lower false positive rates (i.e., rate of incorrectly detecting an effect). This caused the removal of a relatively large number of subjects (27 out of 90), and ultimately a null result was found, leading Bor et al. to conclude that the initial significant finding must have been spurious. But their criteria for subject exclusion may have resulted in other important unintended consequences for statistical hypothesis testing and interpretation; therefore, here we formally evaluate the consequences of adopting such criteria in a simulation, and what the interpretation of their results should have been in a Bayesian framework.
Methods
Our goal was to assess whether excluding subjects as in Bor et al. (2017) was needed to curb false positive rates as they claim, and also whether doing so led to increased false negative rates and thus lower statistical power (i.e., probability of successfully detecting a true effect). Therefore, we simulated two populations of subjects, one that exhibited the TMS-induced metacognitive impairments, as in Rounis et al. (2010), and one that did not, and included them in two sets of 1,000 “experiments” that mirrored Bor et al.’s Experiment 1 (between-subjects design). We then compared statistical power and false positive rates both before and after implementing the exclusion criteria used by Bor et al.
Building two populations of “subjects”
Each simulated “subject” was characterized by four parameters to produce behavioral outputs with and without TMS. For the first three parameters – objective performance capacity (d’s), response bias (Type 1 criterion; cs,1), and subjective response biases (Type 2 criteria; cs,2) – the values were taken from Rounis et al. (2010) to mimic the distributions seen there. These values were then fixed for each simulated subject across task conditions (pre- and post-TMS).
To simulate the effect of degraded metacognitive sensitivity by TMS, we defined a fourth parameter corresponding to Type 2 (i.e. metacognitive) noise (σs,TMS), such that in the TMS condition Type 2 criteria (cs,2) become unstable and the trial-by trial correspondence between confidence and accuracy is lowered (Maniscalco & Lau, 2012; Maniscalco & Lau, 2016; Peters et al., 2017). Thus, for each simulated subject for these TMS conditions, over trials we added TMS noise (σs,TMS) to the subject’s internal response, after their discrimination judgment but before their confidence judgment (see task description in Figure 1), such that across all simulated subjects the average reduction in metacognitive sensitivity mimicked that found in Rounis et al. (2010; see Supplementary Materials for more details).
Figure 1. Signal detection theoretic framework for the simulated spatial 2AFC task.
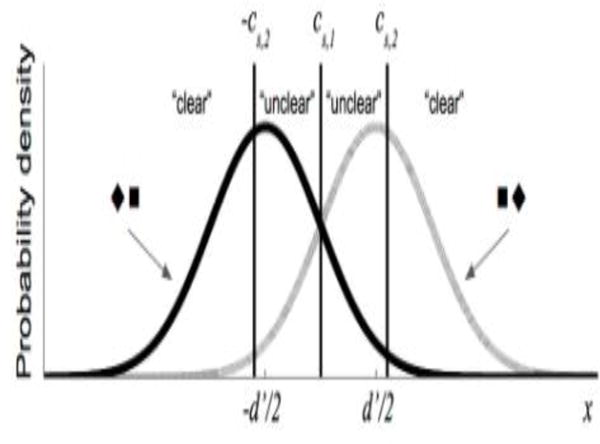
For a given subject s, each stimulus presentation (either ◼◆or ◆◼) caused an internal response value (x), with X◼◆ ~ N(d’/2, 1) and X◆◼ ~ N(-d’/2, 1), and the subject then indicated which of the two shape configurations appeared. If x exceeds the subjects Type 1 criterion (cs,1), then the subject responded “◼◆;” otherwise the subject responded “◆◼.” Objective performance capacity (d’) is the normalized distance between the two distributions. The subject then indicated how clearly/confidently they saw the stimulus, based on a comparison between x and the Type 2 criterion (-cs,2 and cs,2). If x < cs,1 or x > cs,2 the subject responded “clear”; otherwise the subject responded “unclear.” If TMS is present and assumed to degrade metacognitive sensitivity, noise (σs,TMS) is added for the Type 2 responses, such that the relevant computations are whether x < cs,1 + εtrial or x > cs,2 + εtrial, with εtrial ~ N(0,σs,TMS) and resampled on each trial (see Supplementary Materials for more details).
Simulating the behavioral task
Our simulated task followed the spatial two-alternative forced-choice (2AFC) task design used by Rounis et al. (2010) and Bor et al. (2017) (see Figure 1).
Assessing Metacognitive Performance
For all simulated subjects, we calculated meta d’, a bias-free measure of metacognitive sensitivity (Maniscalco & Lau, 2012), using a standard toolbox (Maniscalco, 2014) whereby estimation was conducted by minimizing the sum of squared errors (SSE), as in Rounis et al. (2010) and Bor et al. (2017). As with both of these studies, our measure of interest was meta d’ - d,’ which indicates a participant’s metacognitive sensitivity for a given level of basic task performance (Fleming and Lau, 2014).
Simulating populations of subjects
Before running our simulated “experiments,” we first built two populations of subjects: one designed to show the impairing effect of TMS on metacognitive performance (“effect-present population”), based on the results found in Rounis et al. (2010), and the other showing no such effect (“effect-absent population”, such that the above mentioned parameter σs,TMS was set to 0). The two populations each contained 10,000 subjects (5,000 completing the Pre-Real-TMS and Post-Real-TMS conditions and 5,000 completing the Pre-Sham-TMS and Post-Sham-TMS conditions). As described above, between-subjects variability in the simulation parameters was based on the empirical between-subject variability reported by Rounis et al. (2010).
To verify that the effect on metacognitive sensitivity reported by Rounis et al. (2010) was successfully recreated in our simulated effect-present population and not in the effect-absent population, we compared the means for each condition and also ran a mixed-design ANOVA on metacognitive sensitivity (meta d’ - d) for each population, with between-subjects factor TMS type (Real TMS, Sham TMS) and within-subject factor time (Pre-TMS, Post-TMS). We confirmed the impairing effect of TMS on metacognitive sensitivity in the effect-present population with a significant TMS type × time interaction; F(1,9998) = 307.86, p < .001, and the means for each condition were as follows: for group 1, Pre-Real-TMS d’=1.698 and meta d’=1.557, Post-Real-TMS d’= 1.713 and meta d’ = 1.172; for group 2, Pre-Sham-TMS d’= 1.678 and meta d’ = 1.540, Post-Sham-TMS d’= 1.698 and meta d’ = 1.577. Conversely, we confirmed no impairing effect of TMS on metacognitive sensitivity for the effect-absent population; F(1,9998) = 1.79, p = 0.18, and condition means were as follows: for group 1, Pre-Real-TMS d’=1.680 and meta d’=1.576, Post-Real-TMS d’= 1.694 and meta d’ = 1.580; for group 2, Pre-Sham-TMS d’= 1.685 and meta d’ = 1.534, Post-Sham-TMS d’= 1.702 and meta d’ = 1.565.
Simulating Bor et al.’s (2017) Experiment 1
As in Bor et al.’s (2017) between-subjects experiment, the simulated subjects were randomly assigned to either the Real or Sham TMS group. As in their study, each condition contained 300 trials of the spatial 2AFC task.
We simulated 1,000 ‘experiments’, each containing samples of 35 subjects drawn with replacement from both the corresponding effect-present and effect-absent populations. Subjects in each sample were randomly assigned to one of two groups: 17 subjects were exposed to the two real TMS conditions and 18 subjects were exposed to the two sham TMS conditions, as in Bor et al.’s (2017).
For each simulated experiment, we first performed statistical tests with all subjects. Each ‘experiment’ was analyzed with a mixed-design ANOVA on metacognitive sensitivity (meta d’ -d’) with between-subjects factor TMS type (Real TMS, Sham TMS) and within-subject factor time (Pre-TMS, Post-TMS); a ‘positive’ effect of TMS on metacognitive sensitivity was found if the interaction between TMS type and time was found to be significant (p<.05).
We then performed the same tests after excluding subjects using Bor et al’s criteria (Type 1 and/or Type 2 hit rates or false alarm rates < 0.05 or > 0.95, or with Type 1 percent correct values less than or equal to 65%). Similarly to Bor et al. (2017), we excluded about 30% of subjects on average for all 1,000 simulations for both our effect-present simulations (mean = 30.20%, S.D. = 7.77%) and effect-absent simulations (mean = 30.86%, S.D. = 7.96%).
We assessed the consequences of excluding subjects on statistical power by examining the percentage of simulated experiments done on the effect-present population for which the TMS × time interaction correctly reached significance (p < .05) when subjects were not excluded (as done by Rounis et al., 2010) versus excluded (as done by Bor et al., 2017).
(We also simulated other experiments, and the details are in Supplementary Materials.)
Results
The results of simulations based on Bor et al.’s (2017) Experiment 1 showed that false positive rates were nearly identical for non-exclusion and exclusion (0.046 and 0.048, respectively; Figure 2a, Table 1). This suggests that excluding subjects has no effect on false positive rates, contrary to what Bor et al. (2017) claimed.
Figure 2. Excluding subjects yields little impact on statistical power or false positive rates.
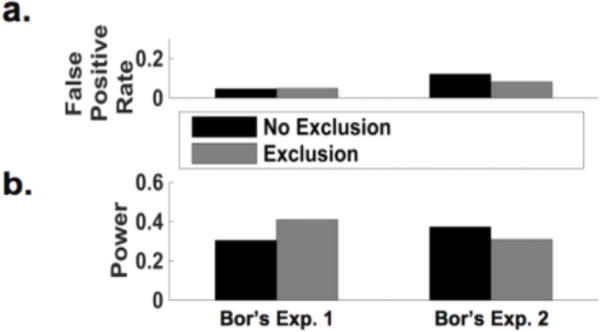
As in the actual empirical studies, the effect of TMS was assessed by the statistical significance of the interaction between TMS (DLPFC or control) and time (before TMS and after TMS). (a) Excluding versus not excluding subjects yielded no meaningful change in false positive rate for the between-subjects design (Bor’s Exp. 1). Exclusion led to a small decrease in false positive rate for the double-repeat design (Bor’s Exp. 2), but this design inflated false positive rate in comparison to the between-subjects design (Bor Exp. 1) – although the inflation disappeared when we used permutation tests to address violations of normality assumptions (see main text). (b) Excluding subjects yielded an increase in statistical power compared with not excluding subjects for the between-subjects design (Bor’s Exp. 1), and the magnitude of this increase was even greater when using nonparametric permutation tests to evaluate statistical significance (see main text). Conversely, exclusion resulted in a decrease in power in comparison with no exclusion for the atypical double-repeat within-subjects design (Bor’s Exp. 2). Importantly, the double-repeat design (Bor’s Exp. 2) led to considerably lower rather than the intended higher statistical power when excluding subjects.
Interestingly, excluding subjects led to an increase in power (powerno exclusion = 0.304 vs. powerexclusion = 0.409; Figure 2b, Table 1), contrary to what might be expected from a reduced sample size. However, we note that despite this modest increase, power is still fairly low; given an effect is present, one is more likely to miss it than to not miss it.
Bor et al.’s (2017) stated reason to exclude subjects was that such ‘unstable’ subjects’ data led to violations of the assumption of normality, which we note might impact false positive rates in the parametric statistical tests used. Therefore, we re-ran the above analysis but with two important changes: (1) we additionally tested each simulated sample for normality using the Shapiro-Wilk test (Shapiro & Wilk, 1965); (2) for each simulated experimental sample that violated normality assumptions, we ran a permutation test in lieu of comparing the F-statistic to the standard parametric F distribution in order to obtain an empirical p-value. In these permutation tests, we permuted the sample 1,000 times by randomly shuffling the Real and Sham condition labels independently for each simulated subject, and ran the aforementioned mixed-design ANOVA at each permutation. This yielded a null distribution of F-values against which the F-value of the original data could be compared to evaluate statistical significance. If the F statistic for the interaction term for the non-permuted sample was greater than or equal to 95% of the of F statistics for the interaction term for the 1,000 permuted samples, then the TMS × time interaction for that sample was taken to be significant.
The non-parametric tests revealed similar results to those from our analyses that only incorporated parametric tests. False positive rates were identical for non-exclusion and exclusion (0.053 and 0.053, respectively). Excluding subjects led to an increase in power (powerno exclusion = 0.315 vs. powerexclusion = 0.420). For the between-subjects design and all others introduced below, we also calculated power and false positive rates for normal versus non-normal samples, for both exclusion and non-exclusion separately, as well as how many simulated experiments failed tests of normality both before and after subject exclusion. These results are detailed in Supplementary Materials.
What should be the correct interpretation given the results?
We used Bayesian analysis to calculate the probability that TMS actually caused metacognitive sensitivity deficits in the population of human subjects tested by Bor et al. (2017), given the pattern of results they observed. We used Bayes’ rule,
| (1) |
where the posterior probability p(e|d) refers to the probability of a true effect e on metacognitive sensitivity due to TMS given the observed data d, as a function of the likelihood of observing the present data given the effect is true, p(d|e), and the prior probability of the effect being true, p(e). We assign the observed data d as being a significant interaction before excluding subjects that then disappeared when subjects were excluded, as reported by Bor et al. (2017). So as to not bias the calculation in either direction, we assign equal prior probability (0.5) to the effect being present or not at the population level.
In 8.9% of simulated experiments, an effect was correctly detected when no subjects were excluded, but subsequently excluding subjects led to a false negative (i.e., p(d|e)). In 2.9% of simulated experiments a false positive was initially found when not excluding subjects, but subsequently excluding subjects resulted in correctly finding no effect (i.e., p(d|~e)). Putting these values into Bayes’ rule (Equation 1), we find that the probability of TMS actually causing metacognitive deficits at the population level given that an effect was observed but then disappeared to be high, p(e|d) = .7542. This is because the probability that an effect was observed (without exclusion) but then disappeared with exclusion is 3.07 times higher when the effect was actually present in the population than when it was absent.
In other words, had one not been initially persuaded by Rounis et al (2010)’s findings, and assumed that there was only half a chance of the effect’s being true (0.5), upon seeing Bor et al’s (2017) pattern of results one should update this belief – if one were rational – to recognize that the effect is 75.42% likely to be true. This is exactly the opposite of what Bor et al. concluded. Moreover, we should be even surer of this conclusion if we take Rounis et al.’s findings at face value. For example, setting the prior at .95 would yield a 98.31% posterior probability of the effect being true.
We observed similar findings when using the results from analyses that incorporated permutation tests to deal with violations of normality. Plugging in p(d|e) = 0.088 and p(d|~e) = 0.037, with p(e) = p(~e) = 0.5, we found that p(e|d) = .704.
Simulating Other Experiments
Bor et al. (2017) acknowledged that their Experiment 1 may have lacked power due to using a between-subjects instead of a within-subjects design (despite our findings above); therefore, they ran a second experiment using an unusual “double-repeat within-subjects” design. This design involved up to four days of real and sham TMS manipulations (two days of each) in which subjects only advanced to subsequent days if their performance met certain benchmarks. After Bor et al. excluded 10 of their 27 subjects on Day 1 of their design due to their exclusion criteria, they found that none of the remaining 17 subjects showed the expected effects (based on Rounis et al.’s, 2010, results) of real TMS or vertex control for all four days of the experiment. To assess the impact of this atypical design on statistical power (ideally an increase, as stated by Bor et al. (2017)), we ran a second simulation akin to what we did above (described in detail in Supplementary Materials).
Contrary to what Bor et al. (2017) intended, following their subject exclusion procedure we actually observed a decrease in power from 0.409 in the between-subjects design to 0.308 in their double-repeat design (Figure 2b), and a striking loss of power to 0.189 when we used permutation tests to assess statistical significance in cases of violations of normality even after excluding subjects. Also, there was a small increase in the false positive rate from 0.048 (in the between-subjects design) to 0.081 (in the double-repeat design), although this increase went away when we used permutation tests to address concerns of non-normality (false positive rate for exclusion was 0.026). Moreover, for this atypical double-repeat design we found that not excluding subjects yielded slightly higher power (0.372) compared with excluding subjects (0.308; Figure 2b), and this advantage for non-exclusion was much greater when including permutation tests (0.348 for no exclusion and 0.189 for exclusion). Also, false positive rates were slightly higher for non-exclusion (0.121) than for exclusion (0.081; Figure 2a), and the same was true when incorporating permutation tests (0.085 for non-exclusion and 0.026 for exclusion).
In fact, had Bor et al. (2017) simply used the same sample size in this second experiment (n=27) to actually replicate Rounis et al.’s (2010) simple within-subject experiment, the authors would have achieved their intended purpose. We ran an additional simulation and showed that implementing this design with n=27 would have increased power to 0.567 (0.604 with permutation tests). We found similar false positive rates for exclusion and non-exclusion (0.053 and 0.053, respectively, or 0.070 and 0.069 with permutation tests), although as in Bor et al.’s Experiment 1 power was higher for exclusion (0.567, or 0.604 with permutation tests) in comparison with non-exclusion (0.388, or 0.425 with permutation tests).
For completeness we ran a final simulation to assess whether exclusion could have been useful in Rounis et al.’s (2010) original study with original sample size of n=20. We found similar false positive rates for exclusion and non-exclusion (0.048 and 0.042, respectively, or 0.067 and 0.064 with permutation tests), and that power was higher for exclusion than non-exclusion (0.432 and 0.311, respectively, or 0.453 and 0.363 with permutation tests).
(See Table 1 in Supplementary Materials for a complete listing of results for all experimental designs. We also note that the simulations presented here are not intended to represent the entire gamut of possible simulations; we leave other simulation variants, such as those based on different summary statistics or different datasets, to future studies.)
Discussion
We found that Bor et al. (2017) did not achieve their presumed goal of causing meaningful reductions in statistical false positives by the use of their subject exclusion criteria. Such exclusion is not necessary because false positive rates were low to begin with, reflecting the general robustness of this kind of statistical analysis. Although in some instances excluding subjects improved power, presumably by removing noisy outliers, the resulting power is still low and this improvement does not always happen (e.g. the double repeat-design). Most importantly, upon seeing the pattern of results in Bor et al.’s Experiment 1 (positive result turned negative after exclusion), we showed with Bayesian analysis that the correct interpretation should be to conclude that the effect is very likely to be present, contrary to their claims.
While Bor et al. (2017) acknowledge that their Experiment 1 may lack power, because it uses a between-subject design, their attempt to alleviate this with their Experiment 2 (an atypical ‘double-repeat’ design) did not work well. In particular, after using their exclusion criterion, power actually decreased in that experiment. False positive rate also increased slightly, although this increase disappeared when we used nonparametric permutation tests to address violations of normality assumptions.
The supposed goal of Bor et al.’s (2017) series of experiments, according to the authors themselves, was to “attempt to replicate Rounis and colleagues’ key finding that theta-burst TMS to DLPFC reduced metacognitive sensitivity” (p. 14). We think such effort is important and should be applauded, and in fact Rounis et al. shared their source code with Bor et al. in support of their endeavor. However, despite this stated goal, Bor et al. changed several potentially critical elements of the original study, in addition to the above-described changes in experimental design (from within-subjects to between-subjects or to the atypical double-repeat design). For example, they used confidence ratings instead of the visibility ratings used by Rounis et al. It’s possible that the effect of TMS to prefrontal cortex may work better with visibility rather than confidence judgments, as it is known that different subjective measures can lead to systematically different results (Sandberg, Timmermans, Overgaard, & Cleeremans, 2010; King & Dehaene, 2014). Specifically in the context of metacontrast masking, Maniscalco & Lau (2016) recently replicated a dissociation between stimulus discrimination performance and visual metacognitive awareness (Lau & Passingham, 2006) when using visibility ratings, but not when utilizing confidence ratings (personal communication). Additionally, Rausch & Zehetleitner (2016) found that subjects performing an orientation discrimination task used more liberal criteria when giving confidence judgments compared to visibility judgments, and furthermore that visibility, but not confidence, was positively related to stimulus contrast on trials with incorrect discrimination performance. We also note that confidence and visibility (awareness) judgments are generally not believed to be equivalent, despite many similarities (Rosenthal, in press). Another notable change is that Bor et al. didn’t instruct subjects to use their two metacognitive ratings evenly – unlike Rounis et al., who did give this instruction.
If Bor et al. (2017) were concerned about the robustness of meta d’ estimations, they could have used more than two levels of metacognitive ratings, which is commonly done in the literature (Overgaard, 2015). Using only two metacognitive rating levels (as both studies did) will only provide one point on the Type 2 receiver operating characteristic (ROC) curve, which may limit the efficiency of meta d’ estimations (Maniscalco & Lau, 2012). Using more than two rating levels helps because even if one (or even two) point on the Type 2 ROC curve is extreme, it is unlikely that the other point(s) will also be so extreme. This point should be easily appreciated by Bor et al., as one of the authors’ own analysis (Barrett, Dienes, & Seth, 2013) showed that they would have had to use many more trials (i.e., thousands) to accurately estimate of meta d’ if there were only two rating levels.
These considerations would probably have made the impression of needing to exclude subjects unnecessary – which we now show is the case regardless. Moreover, research indicates that exclusion of influential outliers is an extreme approach (e.g., Miller, 1991), which should only rarely be performed; a number of more helpful corrective actions can be taken that will typically make excluding outliers unnecessary (Bollen & Jackman, 1985). Thus, although it might seem correct to exclude subjects from the outset on the basis that including the “unstable” data violated the assumption of normality in Bor et al.’s (2017) between-subjects experiment, ultimately assumptions in statistical inferences are never meant to be perfectly realistic and precise. What matters is whether the corresponding inference may be correct or not based on the data. Our analysis shows that subject exclusion serves no benefit in improving the validity of such inferences when it comes to false positive rates, contrary to what Bor et al. might have supposed. Further supporting this point, we used the Shapiro-Wilk (Shapiro & Wilk, 1965) test on distributions of metacognitive sensitivity (meta d’ - d’) for the 1000 effect-absent simulations and found that significant violations of normality were more prevalent without subject exclusion (98.5% of simulations) than with exclusion (75.7% of simulations). Thus, although subject exclusion tends to produce distributions that are more Gaussian (consistent with Bor et al.’s findings), not all distributions that result are in fact Gaussian, and the improvement in normality due to exclusion was not accompanied by a reduction in false positive rates. These simulation findings are inconsistent with Bor et al.’s conclusion that the significant effect found in their data prior to subject exclusion was a false positive driven by non-normality of the data.
In discussion with Bor and colleagues, we were asked to try excluding data on the original Rounis et al. (2010) data set. However, given the above results, especially the Bayesian analysis and the lack of meaningful differences in false positive rates for exclusion versus non-exclusion for any of the simulated experimental designs, including Rounis et al.’s design, it seems that such an exercise would be unjustifiable and most likely lead to misleading conclusions. Bor et al’s. (2017) primary justification for subject exclusion is based on their work showing that sufficiently large or small hit and false alarm rates tend to induce large changes in meta d’ estimates (Barrett et al., 2013). However, we emphasize that in classical hypothesis testing there are two main types of error: Type I and Type II. Within this standard framework, any statistical decision or justification of a choice of procedure is meaningful only with respect to its impact on these two kinds of error. Importantly, testing and confirming a specific hypothesis is in fact strictly the purpose here, as we are evaluating Bor et al.’s report of a ‘replication.’ As such, our analysis strongly suggests that their insistence on subject exclusion is not reasonable within this context, and the results are such that it would not be logically consistent for us to comply with the exclusion they recommend. Nonetheless, to satisfy Bor and colleagues’ request, we performed analyses on Rounis et al.’s original dataset after applying Bor et al.’s exclusion criteria, although we have added the results to Supplementary Materials instead of the main text given our aforementioned disagreements with such analyses. We furthermore executed additional analyses on Rounis et al.’s dataset to check for violations of normality, and in the case of such a violation we re-ran analyses with nonparametric methods. We found that Bor et al.’s exclusion criteria led to exclusion of 65% of the original participants, which unsurprisingly resulted in a null effect (after exclusion via Bor et al.’s criteria, remaining n = 7). Given the present result in the main manuscript, these results are not strictly meaningful for the current purpose, but others should be able to see them if they so wish.
One may also note that after excluding subjects, Bor et al.’s (2017) Experiment 1 did include 63 subjects in total. However, that experiment used a between-subjects design, unlike Rounis et al. (2010). Also, it is important to consider that only two of their experimental groups are related to the attempted replication of Rounis et al.’s original study: the DLPFC and control group. Other groups included in this study do not map onto the within-subjects design used by Rounis et al., and therefore cannot be included in the ultimate count of subject numbers. Thus, the relevant conditions in Bor et al.’s Experiment 1 included 17 and 12 subjects for the DLPFC group before and after exclusion, respectively, and 18 and 12 for the control group before and after exclusion. Although Bor et al.’s Experiment 2 included 27 subjects before exclusion, the atypical nature of this study makes it difficult to compare to the standard within-subjects design used by Rounis et al., which included 20 subjects. Moreover, after exclusion, Bor et al. were left with fewer than 20 subjects (17, to be exact). Thus, our conclusion is that to the extent that Bor et al.’s attempt should be considered a ‘replication’, they are clearly underpowered (see Figure 2b). That the original study (Rounis et al., 2010) was also underpowered is unfortunate, but such is the norm for most cognitive neuroscience studies (Szucs & Loannidis, 2017). That said, if a study’s explicit goal is to replicate, it would be especially problematic not to have sufficient power. This is because with insufficient power, a null finding is essentially uninterpretable (Cohen, 2008), precluding the ability to make meaningful claims regarding why the attempted replication may have failed.
Another noteworthy change that Bor et al. (2017) made to Rounis et al.’s (2010) design is that they used an active control site instead of sham TMS. We feel that in principle, an active control is laudable; however, in practice, we’re not sure it’s truly a control. An active control of this nature may itself induce changes in behavior, rather than being neutral with respect to its effect on behavior. Regardless, the introduction of an active control represents a significant and important departure from the Rounis protocol; another reason why the results may not look the same. Interestingly, Bor et al. note that the positive result they found in their between-subjects Experiment 1 appeared to be driven to a larger extent by an increase in metacognitive sensitivity in the control group than a decrease in metacognitive sensitivity in the DLPFC group. This observation is consistent with the possibility that the active control actually drove a behavioral change which resulted in the observed effects.
We recognize that TMS is limited in sensitivity compared to more invasive methods. In fact, power in the concerned studies is in general quite low according to our simulations (Fig. 2b). Also, neuronavigation techniques (e.g., Brainsight TMS Navigation) are probably needed to ensure targeting precision of stimulation – a technique that neither Rounis et al (2010) nor Bor et al. (2017) used. Of relevance, Rahnev, Nee, Riddle, Larson, & D’Esposito (2016) recently reported that theta-burst TMS to DLPFC actually increased metacognitive performance, which the authors suggest may have been due to the fact that a very anterior portion of DLPFC was stimulated for most study participants. This may suggest that different parts of DLPFC perform different functions.
Taken together, these considerations suggest that replicating the findings of Rounis et al. (2010) is possibly non-trivial; even if the results are indeed true, attempts at replication with insufficient power means that an apparent null result is easy to obtain. We therefore find it striking that Bor et al.’s (2017) results appear to demonstrate a successful replication prior to subject exclusion, despite their interpreting otherwise, and despite the changes they made to the design of the experiment including using a between-subject design with limited power: When they re-ran their analysis “including those participants we had previously excluded” (p. 12), they reported a significant difference in meta d’ - d’ scores between their DLPFC and vertex control group (“t(31) = 1.85, p(1-tailed) = 0.037”) and a moderate effect size (“Cohen’s d = 0.623”) (p. 12), consistent with the main findings by Rounis et al. (2010). In correspondence, we found unfortunately that Bor et al. remain unconvinced by our arguments outlined above, but we hope these discussions will bring up interesting issues for other readers.
Ultimately, whether theta-burst TMS to DLPFC can robustly impair visual metacognition concerns the specific method and details. More important is the general question regarding the role of the prefrontal cortex in metacognition and conscious perception (Odegaard, Knight, & Lau, in press; Lau & Rosenthal, 2011). Bor et al. (2017) claim that lesions to the prefrontal-parietal network (PPN) tend to show “at best subtle impairments in conscious detection” (Del Cul et al., 2009; Simons, Peers, Mazuz, Berryhill, & Olson, 2010). However both of these cited studies actually found positive results, and it is unclear by what standard Bor et al. (2017) judge them to be “subtle.” Contradictorily, in a 2012 review, Bor & Seth (2012) themselves cite Del Cul et al. (2009) and Simon et al. (2010), among other positive results, claiming that these findings “strongly implicate all key individual components of the PPN in conscious processing” (Bor & Seth, 2012, p. 3).
Importantly, in another study adopting similar psychophysical measures and task procedures as Bor et al. (2017), Fleming et al. (2014) found a ~50% decrease in metacognitive efficiency for patients with prefrontal lesions. Presumably, a 50% decrease should not be considered a small, subtle effect. Furthermore, Cortese, Amano, Koizumi, Kawato, & Lau (2016) showed that manipulation of PFC activity via biofeedback of decoded fMRI information can alter metacognitive confidence ratings. Also, chemical inactivation of the PFC has recently been shown to induce deficits in metamemory in monkeys (Miyamoto et al., 2017). At the same time, we do note that the effect size found in Rounis et al. (2010) was small. Importantly, however, small effects are the norm in psychology and cognitive neuroscience, and power is typically low in such experiments (Szucs & Loannidis, 2017). Taken alongside the wealth of findings supporting a role for prefrontal cortex in metacognition (as above), and the results of our simulations, this suggests that the effect found in Rounis et al. (2010), albeit a small one, may very well reflect a true effect.
While we think the current attention to the issue of replicability within psychology and cognitive neuroscience is a most useful and important development, we worry that this may occasionally generate undue excitement in some studies with non-replication results. We hope that the above discussion makes clear that the reported non-replication by Bor et al. (2017), even if true (which we have shown is unlikely), does not meaningfully speak to the role of PFC in visual metacognition and conscious perception in general.
Bor et al failed to replicate Rounis et al’s results when excluding certain subjects.
Simulations show subject exclusion does not reduce false positive rates as intended.
Bayesian analysis shows Bor et al’s approach hides consistency with Rounis et al.
Acknowledgments
We thank Dr. Hakwan Lau for his invaluable insight and guidance with experimental design, data analysis, and manuscript preparation. Because of his disagreement with several editorial decisions arising from the review process, he has declined to be a co-author on this final version.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosure of Interest
The authors report no conflict of interest.
References
- Baird B, Smallwood J, Gorgolewski KJ, Margulies DS. Medial and Lateral Networks in Anterior Prefrontal Cortex Support Metacognitive Ability for Memory and Perception. J Neurosci. 2013;33(42):16657–65. doi: 10.1523/JNEUROSCI.0786-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett A, Dienes Z, Seth AK. Measures of metacognition on signal-detection theoretic models. Psychol Methods. 2013;18(4):535–52. doi: 10.1037/a0033268. [DOI] [PubMed] [Google Scholar]
- Bollen KA, Jackman RW. Regression diagnostics: An expository treatment of outliers and influential cases. Sociol Methods Res. 1985;13(4):510–42. [Google Scholar]
- Bor D, Seth AK. Consciousness and the Prefrontal Parietal Network: Insights from Attention, Working Memory, and Chunking. Front Psychol. 2012;3:63. doi: 10.3389/fpsyg.2012.00063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bor D, Schwartzman DJ, Barrett AB, Seth AK. Theta-burst transcranial magnetic stimulation to the prefrontal or parietal cortex does not impair metacognitive visual awareness. PLoS One. 2017;12(2):e0171793. doi: 10.1371/journal.pone.0171793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen BH. Explaining psychological statistics. John Wiley & Sons; 2008. [Google Scholar]
- Colquhoun D. Lectures on biostatistics: an introduction to statistics with applications in biology and medicine. David Colquhoun; 1971. [Google Scholar]
- Cortese A, Amano K, Koizumi A, Kawato M, Lau H. Multivoxel neurofeedback selectively modulates confidence without changing perceptual performance. Nat Commun. 2016;7:13669. doi: 10.1038/ncomms13669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Cul A, Dehaene S, Reyes P, Bravo E, Slachevsky A. Causal role of prefrontal cortex in the threshold for access to consciousness. Brain. 2009;132(Pt 9):2531–40. doi: 10.1093/brain/awp111. [DOI] [PubMed] [Google Scholar]
- Greenwald AG. Within-subjects designs: to use or not to use? Psychol Bull. 1976;83(2):314–20. [Google Scholar]
- Fleming SM, Lau H. How to measure metacognition. Front Hum Neurosci. 2014;8:443. doi: 10.3389/fnhum.2014.00443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming SM, Ryu J, Golfinos JG, Blackmon KE. Domain-specific impairment in metacognitive accuracy following anterior prefrontal lesions. Brain. 2014;137(Pt 10):2811–22. doi: 10.1093/brain/awu221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King JR, Dehaene S. A model of subjective report and objective discrimination as categorical decisions in a vast representational space. Philos Trans R Soc Lond B Biol Sci. 2014;369(1641):20130204. doi: 10.1098/rstb.2013.0204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ko Y, Lau H. A detection theoretic explanation of blindsight suggests a link between conscious perception and metacognition. Philos Trans R Soc Lond B Biol Sci. 2012;367(1594):1401–11. doi: 10.1098/rstb.2011.0380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau HC, Passingham RE. Relative blindsight in normal observers and the neural correlate of visual consciousness. Proc Natl Acad Sci, USA. 2006;103(49):18763–8. doi: 10.1073/pnas.0607716103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau H, Rosenthal D. Empirical support for higher-order theories of conscious awareness. Trends Cogn Sci. 2011;15(8):365–373. doi: 10.1016/j.tics.2011.05.009. [DOI] [PubMed] [Google Scholar]
- Lumer ED, Friston KJ, Rees G. Neural correlates of perceptual rivalry in the human brain. Science. 1998;280(5371):1930–4. doi: 10.1126/science.280.5371.1930. [DOI] [PubMed] [Google Scholar]
- Macmillan NA, Creelman CD. Detection theory: a user’s guide. Mahwah, NJ: Lawrence Erlbaum; 2004. [Google Scholar]
- Maniscalco B, Lau H. A signal detection theoretic approach for estimating metacognitive sensitivity from confidence ratings. Conscious Cogn. 2012;21(1):422–30. doi: 10.1016/j.concog.2011.09.021. [DOI] [PubMed] [Google Scholar]
- Maniscalco B. Type 2 signal detection theory analysis using meta-d. 2014 Oct; Retrieved from http://www.columbia.edu/~bsm2105/type2sdt/
- Maniscalco B, Lau H. The signal processing architecture underlying subjective reports of sensory awareness. Neurosci Conscious. 2016;2016(1):niw002. doi: 10.1093/nc/niw002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCurdy LY, Maniscalco B, Metcalfe J, Liu KY, de Lange FP, Lau H. Anatomical Coupling between Distinct Metacognitive Systems for Memory and Visual Perception. J Neurosci. 2013;33(5):1897–906. doi: 10.1523/JNEUROSCI.1890-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller J. Reaction time analysis with outlier exclusion: bias varies with sample size. Quart J Exp Psy. 43A(4):907–912. doi: 10.1080/14640749108400962. [DOI] [PubMed] [Google Scholar]
- Miyamoto K, Takahiro O, Setsuie R, Takeda M, Tamura K, Adachi Y, Miyashita Y. Causal neural network of metamemory for retrospection in primates. Science. 2017;355(6321):188–193. doi: 10.1126/science.aal0162. [DOI] [PubMed] [Google Scholar]
- Odegaard B, Knight R, Lau H. Should A Few Null Findings Falsify Prefrontal Theories of Consciousness? J Neurosci. doi: 10.1523/JNEUROSCI.3217-16.2017. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Overgaard M. Behavioral Methods in Consciousness Research. Oxford, United Kingdom: Oxford University Press; 2015. Print. [Google Scholar]
- Peters MAK, Thesen T, Ko YD, Maniscalco B, Carlson C, Davidson M, Doyle W, Kuzniecky R, Devinsky O, Halgren E, Lau H. Perceptual confidence neglects decision-incongruent evidence in the brain. Nat Hum Behav. 2017;1:0139. doi: 10.1038/s41562-017-0139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahnev D, Nee DE, Riddle J, Larson AS, D’Esposito M. Causal evidence for frontal cortex organization for perceptual decision making. Proc Natl Acad Sci U S A. 2016;113(2):6059–6064. doi: 10.1073/pnas.1522551113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rausch M, Zehetleitner M. Visibility is not equivalent to confidence in a low contrast orientation discrimination task. Front Psychol. 2016;7:591. doi: 10.3389/fpsyg.2016.00591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenthal D. Consciousness and confidence. Neuropsychologia in press. [Google Scholar]
- Rounis E, Maniscalco B, Rothwell JC, Passingham RE, Lau H. Theta-burst transcranial magnetic stimulation to the prefrontal cortex impairs metacognitive visual awareness. Cogn Neurosci. 2010;1(3):165–75. doi: 10.1080/17588921003632529. [DOI] [PubMed] [Google Scholar]
- Sandberg K, Timmermans, Overgaard M, Cleermans A. Measuring consciousness: Is one measure better than the other? Conscious Cogn. 2010;19(4):1069–78. doi: 10.1016/j.concog.2009.12.013. [DOI] [PubMed] [Google Scholar]
- Shapiro SS, Wilk MB. An analysis of variance test for normality (complete samples) Biometrika. 1965;52(3/4):591–611. [Google Scholar]
- Simons JS, Peers PV, Mazuz YS, Berryhill ME, Olson IR. Dissociation between memory accuracy and memory confidence following bilateral parietal lesions. Cereb Cortex. 2010;20(2):479–85. doi: 10.1093/cercor/bhp116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turatto M, Sandrini M, Miniussi C. The role of the right dorsolateral prefrontal cortex in visual change awareness. Neuroreport. 2004;15(16):2549–52. doi: 10.1097/00001756-200411150-00024. [DOI] [PubMed] [Google Scholar]


