Exploring Relationships in Gene Expressions: A Partial Least Squares Approach

Abstract

Microarray technology has revolutionized the way gene functions are monitored. Analysis of microarray data is a fast growing research area that interfaces various disciplines such as biology, biochemistry, computer science, and statistics. While various clustering and classification techniques have been successfully employed to group genes based on the similarity of their expression patterns, much is yet to be learned about the interrelationship of the expression levels among various genes. We approach this problem with a statistical technique called partial least squares that is capable of modeling a large number of variables each with relatively few observations. This property of the partial least squares methodology appears to be attractive for application to microarray data sets where the simultaneous expression levels of many genes are collected each at a few time points (or individuals). We use it to analyze publicly available microarray data on sporulation of budding yeast (Saccharomyces cerevisiae). We investigate a number of representative genes, one from each temporal group (based on the time of first induction) of positively expressed genes and show that in each case most of the variability was explained by only two partial regression terms based on all remaining genes. Moreover, the predicted expression levels of the representative genes from partial least squares fit very well on the average with the true expression levels over time. Finally, we compare the biological functions of the genes with largest coefficients with those of the predicted genes. In many cases, the genes are involved in similar or related biological functions including negative relationships. We show that this method can identify established gene relationships; we argue that it can be an exploratory tool for identifying potential gene relationships requiring further biological investigation.

WITH the advent of microarray technology, simultaneous expression levels of thousands of genes can be monitored. Several researchers have proposed new and existing clustering algorithms in conjunction with microarray data sets to classify genes in various groups [(5,6,9,10); see (1) for a minireview]. All these techniques are based, in one way or the other, on the similarity of the temporal expression patterns of various genes. Whereas these analyses often help the scientist in identifying genes with similar biological functions, they do not address the question of how the genes interact among each other as a whole and in particular among distinct temporal groups. Numerous current research are under way in understanding the global relationship between the gene expression levels, and theoretical models from various disciplines are being attempted to model such relationships.

In this article we explore the possibility of using a statistical approach to this end. We investigate the question of how well the expression levels of a given gene can be predicted from the expression levels of the other genes using a simple model. As a subsequent investigation, one may be interested in identifying genes that have the “most” influence in determining the expression level of this given gene in this fashion. We found that while many such genes are in the same temporal class as the predicted gene, there are some belonging to a different temporal group whose expression levels may be in negative correlation to that of the predicted gene. For example, out of 10 predictor genes with largest coefficients corresponding to the metabolic gene ACS1, three are involved in carbon or other metabolism whereas five are ribosomal protein (the function of the other two are unknown). We show that this method may identify important gene relationships that warrant further biological investigation. For example, we hypothesize that the gene SP016 plays a role early in the meiotic program but must be repressed by XBPI at later stages to promote efficient sporulation.

The method we choose for our analysis is that of partial least squares. In the next section we give a brief description of the method and the data set used. The results are then presented. We end the article with a discussion section.

MATERIALS AND METHODS

Partial least squares is a statistical technique that is capable of modeling a large number of explanatory variables when only a few observations on each are present. An ordinary least squares regression would be impossible because the number of possible parameters will be lot more than what the available data can estimate. Because this is typically the case of a microarray data set where expression levels of thousands of genes are measured each at only a handful of time points (or for a handful of samples), we felt this will be a proper occasion for the use of partial least squares.

Note that the use of other regression techniques presents difficulties because the number of variables is large. For example, an attempt to fit a standard least squares regression would lead to a saturated model. Due to potential collinearity, stepwise regression would potentially select one or two genes in each case that are highly correlated to the predicted gene, not leading to a “rich” model involving all the genes. If forward selection is carried out by force, soon it will lead to a saturated model only with a handful of genes. A competing technique that can be used is principal component regression, which has a similar approach as partial least squares. However, unlike partial least squares, the principal component directions are not chosen to make the linear combinations correlated to the predicted gene and therefore the final fit may not be as good.

Suppose we have observations on a large number, say M, genes each at a set of time points T ₁, . . ., T _k. Let us denote the log-expression ratio of gene i at time j by x _ij and let the multivariate vector x _i = (x _i1, . . ., x _ik) be all the observations on gene i. Our goal is to explore the relationship of any given x _i with the rest of the x.

The method of partial least squares fits a relationship as follows. First, center and scale each data vector x _i so that each is normalized and has zero average. Let us suppose we want to predict x ₁ from x ₂, . . ., x _M. Partial least squares fits a regression model, using the principle of least squares, of the form

$$x_1={\displaystyle \sum _{l=1}^p{\text{β}}_{1l}{t}_1^{(l)}}$$

where p will typically be a small integer (much smaller that M). The advantage of such a model is that it only involves p unknown parameters, which can be estimated with observations on relatively fewer time points than the number of genes. The variables t ^(l) ₁ are formed recursively from the x _i, i > 1, in a special way as follows: having obtained t ⁽¹⁾ ₁, . . . , t ^(l−1) ₁, find the linear combination $t_1^{(l)}={\displaystyle \sum _{i=2}^M{c}_{1i}^{(l)}}{x}_i$, for constants c ^(l) _1i norming to unity, such that it is orthogonal to the previous t ⁽ⁱ⁾ ₁, i < l, and has the largest covariance with x ₁. It turns out that c ^(l) ₁ have simple expressions such as

$$\begin{array}{c}{c}_1^{(1)}\propto d_1,\\ c_1^{(2)}\propto d_1-(d_1^T{D}_1{d}_1/d_1^T{D}_1^2{d}_1)D_1{d}_1\end{array}$$

etc., where d ₁ = (x ^T ₂ x ₁, . . ., x ^T _M x ₁)^T, and D ₁ = (x ₂, . . ., x _M)^T(x ₂, . . ., x _M). For a more detailed account on partial least squares the reader may consult Brown (2) and Stone and Brooks (8).

We use the Microarray data on the transcriptional program of Sporulation in Budding Yeast (Saccharomyces cerevisiae) collected by Chu et al. (4). The data set is publicly available at http://cmgm.stanford.edu/pbrown/sporulation. They used DNA microarray s containing 97% of the known and predicted genes involved, 6118 in total. The mRNA levels were measured at seven time points during sporulation. The data values x equal log R, where R = ratio of each gene’s mRNA level to its mRNA level in vegetative cells just before transfer to sporulation medium. As stated before, we scale and center each vector x _i before applying the partial least squares.

Out of 6118 genes, 1143 genes showed “significant” changes in mRNA levels during sporulation (i.e., root mean square of log₂R > 1.13). This is the same threshold used in Chu et al. (4). The rest of the genes were dropped from further analysis.

Chu et al. (4) used a small training set of hand-picked genes to classify about 500 genes that were expressed during sporulation into seven temporal classes. We investigate here how well partial least squares models the expression levels of each of these representative genes based on the levels of all other genes (including those that were repressed during sporulation). These handpicked genes are shown in Table 1. (KNR4 was dropped from the list because it was not significantly expressed. Also the gene PDS1 appears to have been incorrectly listed as Early-Mid.)

TABLE 1.

HANDPICKED GENES (ORF) IN VARIOUS TEMPORAL GROUPS

Metabolic	YAL054C, YGL062W, YJL089W, YML042W, YOR100C, YPL111W
Early I	YDR285W, YDR374C, YER179w, YIL072W, YJL106W
Early II	YDR148C, YGL032C, YGL210W, YPR112C, YHR153C, YOL123W, YPR192W, YDR113C
Early-Mid	YDR118W, YLR045c, YNL013C, YDL103C, YBL078C, YOR033C
Middle	YBR148W, YDR218C, YDR522C, YLR227C, YLL004w, YLL005C, YLL012W
Mid-Late	YBL084C, YDR402C, YDR403W
Late	YHR139C, YKL050C, YMR322C, YOR391C

RESULTS

For each of the 39 genes in Table 1, we model its expression level using those of the remaining 1142 genes. The partial least squares model described in Materials and Methods up to l = 4 regression terms. Figure 1 describes the fit for a gene from each temporal class. The models with l = 4 fits extremely well, explaining at least 90% variability in each case. In fact, a R ² statistic near 80% or more is achieved in each case just with two terms. For the subsequent analysis we choose to use l = 2.

Figure 1.

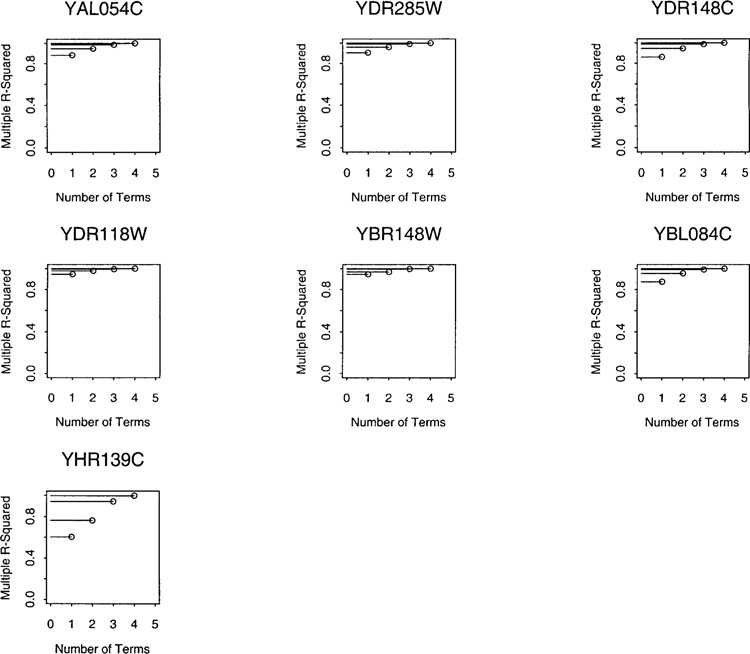
Examples of proportion of variability in gene expression levels explained by a partial least squares model.

Figure 2 shows the average (over the handpicked genes in a temporal group) observed expression data along with that predicted by the partial least squares. Clearly, once again the prediction appears to be very good and the prediction errors average out.

Figure 2.

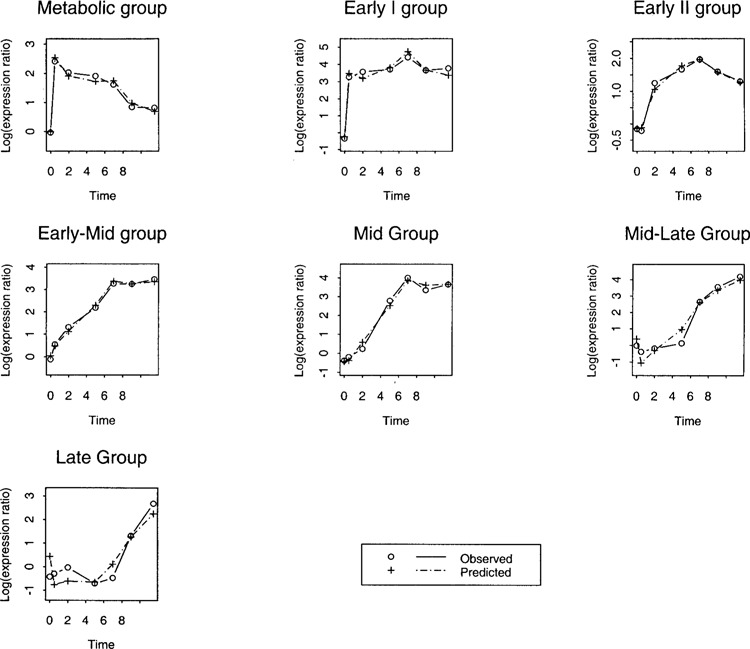
Average observed and predicted (using partial least squares with two terms) log expression ratio in various temporal groups.

Finally, we looked at the magnitude of the coefficients of the genes in the fitted models. Because the variables were all scaled, it is not unreasonable to interpret genes with larger absolute coefficients to have a larger “influence” in controlling the expression level of the predicted gene. For the sake of compactness we only list the top 10 predictor genes for a representative gene from each temporal group. These genes are listed in Table 2 in a reverse (i.e., decreasing) order given by the size of their model coefficients. A careful examination of this collection reveals some interesting facts.

TABLE 2.

GENES WITH (10) LARGEST COEFFICIENTS IN THE PARTIAL LEAST SQUARES MODELS FOR SOME OF THE HANDPICKED GENES

Group	Gene	Predictor Genes With Largest Coefficients
Metabolic	YAL054C	YOR369C, YPR002W, YPR044C, YPR006C, YOR095C, YDR064W, YLR061W, YLR388W, YCL064c, YOL120C
Early I	YDR285W	YKL128C, YER150w, YGL045W, YJR078W, YBR072W, YCR005c, YNR010W, YKR097W, YLR120c, YLR350W
Early II	YHR153C	YIL101C, YOR347C, YKL187C, YMR076C, YBL015W, YJL074C, YCL042W, YLR150w, YLR411W, YGL188C
Early-Mid	YDR118W	YDR403W, YDR402C, YGR043C, YMR114C, YLL029W, YLR012C, YBR168W, YIL045W, YLR265C, YEL057c
Middle	YDR522C	YOR247W, YPR078C, YOR338W, YJR107W, YHR124W, YPR077C, YHR128W, YAL018C, YOL126C, YGL138C
Mid-Late	YDR402C	YEL057c, YGR043C, YDR403W, YGR088W, YLR012C, YDL024c, YHL028W, YCR034w, YDR096W, YOR114W
Late	YHR139C	YOR391C, YLR107W, YGR052W, YMR322C, YGR088W, YOR369C, YCL064c, YMR250W, YLR048w, YOR234C

Metabolic Group

For the metabolic or rapid, transient induction group there are six handpicked genes. This group of genes was induced shortly after transferring to the sporulation medium. Most of the genes in this group are of known metabolic functions. The predicted gene we study in the metabolic group is ACSI (ORF YAL054C). The gene is involved in carbohydrate metabolism, playing one of the major role of TCA cycle in catabolic pathway.

We found that all the top predictor genes (with the possible exception of a couple whose biological functions are not understood at present) are either involved in (carbohydrate or other) metabolism or ribo-somal proteins used for protein synthesis. The first category of genes includes ICL2 (ORF YPR006C), PDH1 (ORF YPR002), and RK11 (ORF YOR095C), and the second category of genes includes RSP12 (ORF YOR369C), RPL22A (ORF YLR061W), RPS 29A (ORF YLR388W), RPL18A (ORF YOL120C), RPL9A (ORF YGL147), and RPS24B (ORF YILO 69C). Interestingly, the later group of genes is all repressed during sporulation and thus this relationship would not have been picked by an analysis (e.g., clustering) based only on the positively expressed genes.

Finally, comparing the top 30 collection (not reported) of the genes in Table 1, we have identified two genes—BUD28 (ORF YLR062C) and N1993 (ORF YNL119W)—that are present in the top 30 collection of all genes in the metabolic group and are in negative correlation with a typical metabolic gene. These two genes are highly correlated. The first one, BUD28 (ORF YLR062C), is involved in cell polarity. The second one, N1913 (ORF YNL119W), is possibly a ribosomal protein (3).

Early I

In the early I induction group there are five hand-picked genes. Their expression pattern is detectable after 0.5 h of the transfer to the sporulation medium. Most of the handpicked genes in early I group are structural genes and meiosis-specific protein associated with lateral elements of the synaptonemal complex, involved in homologous chromosome synapsis and chiasmata formation or recombination.

We study the top 10 predictor genes for the gene ZIP1 (ORF YDR285W), which is responsible for functions in meiotic recombination. Most of the predictor genes are in a negative associative relationship with the expression level of ZIP1. Their temporal pattern shows high level of expression at time zero, which decays over time. These include SP11 (ORF YER150W), a structural protein involved in cell wall maintenance, HSP26 (ORF YBR072W), a heat shock protein involved in protein folding and cell stress, CSE2 (ORF YNR010W), involved in miosis, etc. The gene CIT2 (ORF YCR005C) is in positive association with ZIP1, and it converts acetyl-CoA and oxaloacetate into citrate plus Co A generating energy.

Early II

Most of the genes in this early II induction group are involved in meiotic chromosome pairing and recombination (4). Here we study the handpicked gene SP016 (ORF YHR153C) in detail, which is an early miotic protein required for efficient spore formation.

The predictor genes have various degrees of association with SP016 and are involved in a variety of biological functions. The top predictor gene, XBP1 (ORF YIL101C), is involved in meiosis and cell stress but is in negative correlation with SP016. It is known to be a transcriptional repressor of S. cerevisiae. It is known that that XBP1 target genes are normally repressed late in meiosis (7). For example, Mai and Breeden (7) hypothesize that the gene CLN1 plays a role early in the meiotic program but must be repressed by XBP1 at later stages to promote efficient sporulation. We hypothesis that a similar role is played by XBP1 on SP016.

Other predictor genes include PDS5 (ORF YMR076C), which is involved in meiosis, recombination, and chromatin/chromosome structure, and SMC3 (ORF YJL074), which is a coiled-coil protein of the SMC family involved in chromosome condensation, segregation, and recombination; both of these genes are in positive associations with SP016. The rest of the top 10 predictors were involved in basic metabolisms.

Early-Mid

In the early-middle group the handpicked genes are responsible for various functions such as mitosis, cell cycle control, protein degeneration, meiosis, vesicular transport, and carbohydrate metabolism. We looked at the top 10 predictor genes for APC4 (ORF YDR118W) and found that all of them have similar temporal profile. The majority of these genes are of unknown function at the present time.

Middle

In the middle induction group there are seven handpicked genes. Most of the genes with known functions in this group are involved in meiosis (meiotic division) or in spore morphogenesis (4). We investigate the handpicked gene SPS2 (ORF YDR 522C) involved in meiosis. Partial least squares method finds NDT80 (ORF YHR124W), which is a meiosis-specific protein as one of the top 10 predictors. As mentioned in (4), NDT80 plays a very important role in the regulation of middle genes.

The gene ORF YJR107W appears in the top 30 list of most of the handpicked genes in this group. However, its biological function is unknown.

Mid-Late

We consider the gene DIT2 (ORF YDR402C), which is the second enzyme in the pathway for biosynthesis of dityrosine in the outer layer of the spore wall and is involved in cell wall maintenance.

Many of the predictor genes have related functions. For example, WSC4 (ORF YHL028W), which is present in the top 30 list of all mid-late handpicked genes in Table 1, is a protein required for secretory protein translocation, and for maintenance of cell wall integrity. All the predictor genes are strongly positively associated with DIT2. The gene GIS1 (ORF YDR096W) has a similar profile as DIT2 because its abundance increases following glucose depletion.

Late

SPS100 (ORF YHR139C) is a sporulation-specific protein involved in spore wall maturation. Most of the top 10 predictors are in positive association with the gene except for YLR107W, whose predicted biological function is RNA processing. The top predictor is YOR391C, whose function is unknown at the moment. Interestingly, it can be checked that (not shown) SPS100, in turn, appears very high in the list of top predictors for YOR391C; thus, it can be conjectured to have a similar role as SPS100.

DISCUSSION

We show that the method of partial least squares provides a very simple regression type model for the expression levels of a gene based on other genes. On the sporulation data, the method worked quite well, resulting in very good fit.

It is perhaps interesting to note that the simple model of partial least squares, in most cases, is a nontrivial one. That is to say, it does not distribute most of the weights to a few genes with the same temporal pattern. As expected, many of the genes with the largest coefficients have similar biological function as the predicted gene. What is more interesting is that many of the genes with the largest coefficients in the resulting model have a different temporal profile than the candidate gene that is being modeled. Often these genes, in turn, have a common or related biological function that is different from that of the predicted gene.

To verify that partial least squares indeed has some power of classification, we compared the “top 30” collection of several genes (details not shown). We found that out of these compared genes, genes belonging to different temporal groups had very few to none of the predictor genes in common, in most cases. In fact, it was in this way that we first noted that the gene PDS1 (ORF YDR113C) was perhaps incorrectly listed in Chu et al. (4) as an Early-Mid gene; it is correctly listed in the data set as an Early II gene. Similarly, the regulatory gene Ndt80 (ORFYHR124W) only appears in the top 30 collection of the middle group of genes.

In general, insight about a gene’s role in the biological process may be gained by studying the biological functions of the top predictor genes. In the case of the yeast data, the findings are often consistent with current knowledge of the biological roles of the top predictor genes. Unfortunately, the exact biological role of some of these genes was not known at the moment. We feel this method may identify important gene relationships warranting further biological investigation.