Inference for the difference in the area under the ROC curve derived from nested binary regression models

Summary

The area under the curve (AUC) statistic is a common measure of model performance in a binary regression model. Nested models are used to ascertain whether the AUC statistic increases when new factors enter the model. The regression coefficient estimates used in the AUC statistics are computed using the maximum rank correlation methodology. Typically, inference for the difference in AUC statistics from nested models is derived under asymptotic normality. In this work, it is demonstrated that the asymptotic normality is true only when at least one of the new factors is associated with the binary outcome. When none of the new factors are associated with the binary outcome, the asymptotic distribution for the difference in AUC statistics is a linear combination of chi-square random variables. Further, when at least one new factor is associated with the outcome and the population difference is small, a variance stabilizing reparameterization improves the asymptotic normality of the AUC difference statistic. A confidence interval using this reparameterization is developed and simulations are generated to determine their coverage properties. The derived confidence interval provides information on the magnitude of the added value of new factors and enables investigators to weigh the size of the improvement against potential costs associated with the new factors. A pancreatic cancer data example is used to illustrate this approach.

1. INTRODUCTION

Receiver operating characteristic (ROC) curves and the areas under the ROC curves (AUCs) are popular tools for assessing how well biomarkers and clinical risk prediction models distinguish between patients with and without a health outcome of interest. Historically, in cases where a new biomarker panel was developed and interest lies in evaluating its ability to add information beyond that provided by established risk factors, a three-step approach was taken. First, analysts would fit a binary regression model containing both the established factors and the new biomarkers and test whether the association between the outcome and the new markers was statistically significant. If the test of association was significant, using for example a Wald or likelihood ratio test, then the linear predictor function from this model would be used to compute the area under the curve (AUC). Second, an additional statistical test would be carried out to compare the difference in the AUC for this model and the AUC from a model containing only the established risk factors. Third, if this direct test of AUC equality was significant, a confidence interval was constructed to determine the magnitude of this difference.

In recent years, this multi-step approach has come under criticism. Pepe and others (2013) demonstrate that the null hypothesis of no association between the new biomarkers and the outcome, when established risk factors are included in the model, is equivalent to the null hypothesis that the AUCs from the two models are equal. Thus, it is redundant to perform both the association test and the difference in AUC test. Further, Vickers and others (2011); Seshan and others (2013) and Pepe and others (2013) have illustrated through simulation that the null asymptotic normal distribution assumption for the difference in AUC test does not provide accurate operating characteristics. As a result of these findings, it is recommended that only the test of association be used to infer if the difference in AUCs has improved as a result of the inclusion of new markers.

However, tests of association are not sufficient for understanding the magnitude of the population AUC increase. The new markers may be costly or require an invasive procedure to obtain, and their introduction into a clinical risk prediction model may be justified only if the AUC improvement is meaningful. Conversely, new markers that are not costly and demonstrate no harm to the patient, may have a lower threshold of AUC increase for acceptance. A point estimate for the population difference in AUCs along with a confidence interval for this population difference often provides this important additional information. An interval where the lower confidence bound is close to zero may indicate that the additional factors provide little benefit for use in a clinical decision algorithm. To date, methodology to construct accurate confidence intervals for the difference in AUCs from nested models is incomplete. This work fills the gaps in the AUC methodology by developing a proper null asymptotic distribution for the difference in AUCs and an accurate confidence interval for the population difference when the new markers are associated with the binary outcome.

The outline of the paper is as follows. In Section 2, the nested binary regression models are defined and maximum rank correlation (MRC) methodology is used to estimate the AUC. In Section 3, the asymptotic distribution for the difference in AUCs from nested models is developed. The asymptotic distribution is differentially determined based on whether any of the new factors are associated with the clinical outcome. A confidence interval, derived from a reparameterized population difference in AUC, is proposed in Section 4 and its coverage properties are estimated in Section 5 through simulation. A pancreatic cancer data example is used to illustrate the methodology in Section 6 and a discussion follows in Section 7.

2. THE DIFFERENCE IN AUCS WITH NESTED MODELS

A binary regression model

$$\text{Pr}(Y=1|\mathbf{X})=G({\mathit{\beta }}^T\mathbf{X})$$

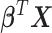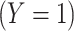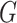is used to create risk scores that predict a binary classifier , with outcomes referred to as response and nonresponse . In this model, is a monotone link function. Common link functions for a binary outcome include the logit and the probit.

The model based performance in terms of classification is evaluated using the area under the receiver operating characteristic curve (AUC). The AUC is defined as

$$\text{Pr}({\mathit{\beta }}^T{\mathbf{X}}_1>{\mathit{\beta }}^T{\mathbf{X}}_2|Y_1=1,Y_2=0),$$

which represents the probability that a responder’s risk score is greater than a nonresponder’s risk score.

Often a new set of markers are under consideration to improve risk classification. This evaluation is based on the difference in AUCs from the nested models

$$\begin{array}{c}\text{Pr}(Y=1|\mathbf{X},\mathbf{Z})=G({\mathit{\beta }}_0^T\mathbf{X}+{\mathit{\gamma }}_0^T\mathbf{Z}),\hfill \\ \text{Pr}(Y=1|\mathbf{X})=G({{\mathit{\beta }}^0}^T\mathbf{X}),\hfill \end{array}$$

where the existing markers are denoted by the 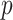-dimensional covariate vector , the new markers are represented by the 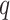-dimensional covariate vector 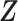, and 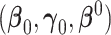represent the true parameter values from the respective models. The estimated AUC for the nested models are:

$$\begin{array}{ccc}& & {\tilde{A}}_n(\hat{\mathit{\beta }},\hat{\mathit{\gamma }})=(n_0{n}_1{)}^{-1}\sum _i\sum _{j}I[y_i>y_j]I[{\hat{\mathit{\beta }}}^T{\mathbf{x}}_{ij}+{\hat{\mathit{\gamma }}}^T{\mathbf{z}}_{ij}>0],\hfill \\ & & {\tilde{A}}_n({\hat{\mathit{\beta }}}^0,0)=(n_0{n}_1{)}^{-1}\sum _i\sum _{j}I[y_i>y_j]I[{\hat{\mathit{\beta }}}^{0^T}{\mathbf{x}}_{ij}>0],\hfill \end{array}$$

where the notation 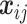is used to represent the pairwise difference , , 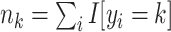and 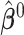denotes the 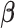parameter estimate when 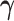is set to 0. The difference in the estimated AUCs, derived from the nested models, is written as

$$\tilde{\delta }={\tilde{A}}_n(\hat{\mathit{\beta }},\hat{\mathit{\gamma }})-{\tilde{A}}_n(\widehat{{\mathit{\beta }}^0},0).$$

Note that the statistic of interest is a function of estimated regression coefficients.

The regression parameter estimates from these nested models are computed using the MRC procedure (Han, 1987). The use of MRC estimates rather than the more commonly applied logistic or probit maximum likelihood estimates results in a simplification in the asymptotic distribution theory, which will be explained further in Section 3, comment 3. The MRC is a rank based estimation procedure that maximizes the AUC. For the full model, the MRC estimates 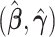are computed as

$$\begin{array}{c}{\mathit{\beta }}^T=(1,{\eta }_1,\dots ,{\eta }_{p-1}),{\mathit{\gamma }}^T=({\gamma }_1,\dots ,{\gamma }_q),\mathit{\theta }=({\mathit{\eta }}^T,{\mathit{\gamma }}^T{)}^T\\ \hfill A_n(\mathit{\theta })=(n_0{n}_1{)}^{-1}\sum _i\sum _{j}I[y_i>y_j]\mathrm{\Phi }\left(\frac{{\mathit{\eta }\mathit{t}\mathit{a}}^T{\mathbf{x}}_{ij}+{\mathit{\gamma }}^T{\mathbf{z}}_{ij}}{h_n}\right).\end{array}$$

These estimates are scale invariant (Han, 1987), which creates an identifiability problem for the parameters (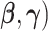. To resolve the identifiability, the first component of 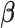is set to one, and hence 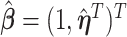, 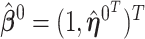and the corresponding parameters are denoted by 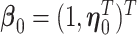, 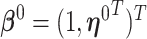. Sherman (1993) proves that 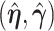and 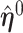are asymptotically normal and are consistent estimates of 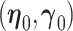and .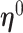

3. ASYMPTOTIC DISTRIBUTION THEORY

We denote the limiting values of the estimated AUC from the full model and reduced model as 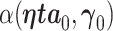and 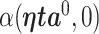, respectively. (Han, 1987) demonstrates that these limiting forms represent the maximum population AUCs when the markers are combined linearly. The difference in the limiting AUCs is denoted by

$$\delta =\alpha ({\mathit{\eta }\mathit{t}\mathit{a}}_0,{\mathit{\gamma }}_0)-\alpha ({\mathit{\eta }\mathit{t}\mathit{a}}^0,0),$$

and asymptotic distribution theory is derived for inference on this parameter.

A standard approach to derive the asymptotic distribution for a statistic with estimated parameters is via a Taylor series expansion around the true parameter vectors. This expansion, however, requires differentiation with respect to the unknown parameters 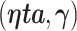, which is problematic due to the discontinuity induced by the indicator function in the AUC statistic. As a result, the expansions utilized in this paper use a smooth version of 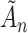based on the asymptotic approximation

$$I[{\mathit{\eta }\mathit{t}\mathit{a}}^T{\mathbf{x}}_{ij}+{\mathit{\gamma }}^T{\mathbf{z}}_{ij}>0]\approx \mathrm{\Phi }\left(\frac{{\mathit{\eta }\mathit{t}\mathit{a}}^T{\mathbf{x}}_{ij}+{\mathit{\gamma }}^T{\mathbf{z}}_{ij}}{h_n}\right),$$

where 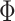is the standard normal distribution function and 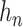is a bandwidth that goes to 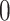as the sample size 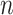gets large (Horowitz, 1992). The smoothed empirical AUCs are written as

$$\begin{array}{cc}& A_n(\hat{\beta },\hat{\gamma })={(n_0{n}_1)}^{-1}\sum _i\sum _{j}I[y_i>y_j]\mathrm{\Phi }\left(\frac{{\hat{\beta }}^T{\mathbf{x}}_{ij}+{\hat{\gamma }}^T{\mathbf{z}}_{ij}}{h_n}\right),\hfill \\ & A_n(\widehat{{\beta }^0},0)={(n_0{n}_1)}^{-1}\sum _i\sum _{j}I[y_i>y_j]\mathrm{\Phi }\left(\frac{{\widehat{{\beta }^0}}^T{\mathbf{x}}_{ij}}{h_n}\right).\hfill \end{array}$$

The asymptotic normality of the smoothed AUC parameter estimates and the uniform consistency of the smoothed AUCs are derived in Ma and Huang (2007). As a result, the smoothed versions of the AUC estimates are used to derive the asymptotic distribution of

$$\hat{\delta }=A_n(\hat{\mathit{\beta }},\hat{\mathit{\gamma }})-A_n(\widehat{{\mathit{\beta }}^0},0).$$

The asymptotic distribution is derived under two separate conditions: (i) no new factors are associated with the outcome 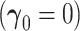and (ii) at least one new factor is associated with the outcome .

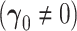3.1. New factors provide no added value -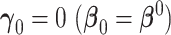

The new set of factors are not associated with the clinical outcome, and as a result, the limiting AUCs are equal (Pepe and others, 2013). The derived distribution of the difference in the AUC statistic under this condition is useful for deriving a direct test of equality. An approach commonly used to test for the equality of population AUCs from nested models is to apply an asymptotic normal reference distribution to the studentized difference in empirical AUCs (DeLong and others, 1988). However, root-n normality is not the correct null reference distribution for this difference. The theorem below provides the asymptotic distribution for the difference in nested AUCs when the new factors are not associated with response. The proof of this theorem is found in the Appendix.

Theorem 1

Assume the following standard conditions for MRC estimation (Han, 1987):

• (1) a compact subspace of .

• (2) The domain of is not contained in a linear subspace of .

• (3) The density of the first component of conditional on all other covariates is everywhere positive.

When the new factors are not associated with the response , as ,

$$\text{Pr}(2n[A_n(\hat{\mathit{\beta }},\hat{\mathit{\gamma }})-A_n(\widehat{{\mathit{\beta }}^0},0)]\le u)=\text{Pr}(\sum _{j=1}^q{\lambda }_j{\chi }_j^2\le u),$$

where are independent chi-square random variables each with one degree of freedom and are the eigenvalues of the product matrix . The matrix is the asymptotic variance of the MRC estimate and is the second derivative matrix of . The partitioned forms of and its inverse are represented as

$$D=\left[\begin{array}{cc}{D}_{\mathit{\eta }\mathit{\eta }}& D_{\mathit{\eta }\mathit{\gamma }}\\ D_{\mathit{\gamma }\mathit{\eta }}& D_{\mathit{\gamma }\mathit{\gamma }}\end{array}\right]D^{-1}=\left[\begin{array}{cc}{D}^{\mathit{\eta }\mathit{\eta }}& D^{\mathit{\eta }\mathit{\gamma }}\\ D^{\mathit{\gamma }\mathit{\eta }}& D^{\mathit{\gamma }\mathit{\gamma }}\end{array}\right].$$

Comment 1: Although the distribution of a weighted sum of independent chi-square random variables does not have a closed form, the distribution can be approximated by generating 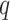independent squared standard normal random variables 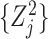, computing the linear combination 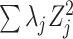, and repeating a large number of times.

Comment 2: The result in Theorem 1 is a generalization of the asymptotic distribution theory for the likelihood ratio statistic. If 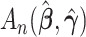and 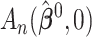were replaced by the loglikelihoods from the full and constrained parametric regression models, then 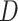is the negative information matrix and from standard likelihood theory 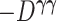approximates 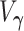. It follows that the 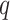eigenvalues of 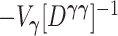are each equal to 1, and the result reduces to the standard result that the likelihood ratio test statistic is a chi-square with 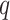degrees of freedom. In addition, Vuong (1989) and Fine (2002) present similar results to Theorem 1 for the likelihood ratio statistic from misspecified nested parametric and semiparametric models.

Comment 3: The first derivative of the AUC, when evaluated at the MRC parameter estimate, is equal to zero. Thus, as a result of using MRC estimates, the quadratic term is the lowest order nonzero term in the asymptotic expansion of the difference in AUCs. Hence, the intrinsic MRC estimates produce a straightforward asymptotic distribution for the difference in AUC statistics. In contrast, if the link function 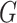were specified and the maximum likelihood estimates were used to estimate (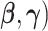, then the linear and quadratic terms in the Taylor series expansion are nonzero. As a result, maximum likelihood estimation significantly complicates the asymptotic distribution.

Comment 4: Seshan and others (2013) used maximum likelihood from a logistic model to estimate the regression coefficients for the AUC calculations. Their results indicated that a nontrivial percentage of the simulations produced a negative difference in the nested AUCs, which was difficult to interpret. The MRC coefficient estimates, derived through maximization of the AUCs from the constrained and unconstrained models, result in a non-negative difference in AUCs up to the limitations of the algorithmic maximization search.

3.2. New factors provide added value—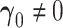

Theorem 2

When at least one of the new set of factors is associated with response after controlling for the established risk factors, the difference in nested AUCs is asymptotically represented as

$$\begin{array}{ccc}& & n^{1/2}[A_n(\hat{\mathit{\beta }},\hat{\mathit{\gamma }})-A_n({\hat{\mathit{\beta }}}^0,0)-\delta ]\hfill \\ & & \hspace{0.17em}=n^{1/2}[(n_0{n}_1{)}^{-1}\sum _i\sum _{j}I[y_i>y_j]\{\mathrm{\Phi }\left(\frac{{\mathit{\beta }}_0^T{\mathbf{x}}_{ij}+{\mathit{\gamma }}_0^T{\mathbf{z}}_{ij}}{h_n}\right)-\mathrm{\Phi }\left(\frac{{{\mathit{\beta }}^0}^T{\mathbf{x}}_{ij}}{h_n}\right)-\delta \}]+o_p(1).\hfill \end{array}$$

The asymptotic expression is the zero order term in the asymptotic expansion and is a two-sample U-statistic of degree 2 with no estimated parameters. It follows from asymptotic U-statistic theory that this expression is asymptotically normal with mean 0. The asymptotic variance estimate from this U-statistic is provided in the Appendix. We again note that if the maximum likelihood estimation for 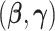were used rather than MRC estimation, the linear term in the asymptotic expansion would be nonzero and would need to be incorporated into the asymptotic variance calculation.

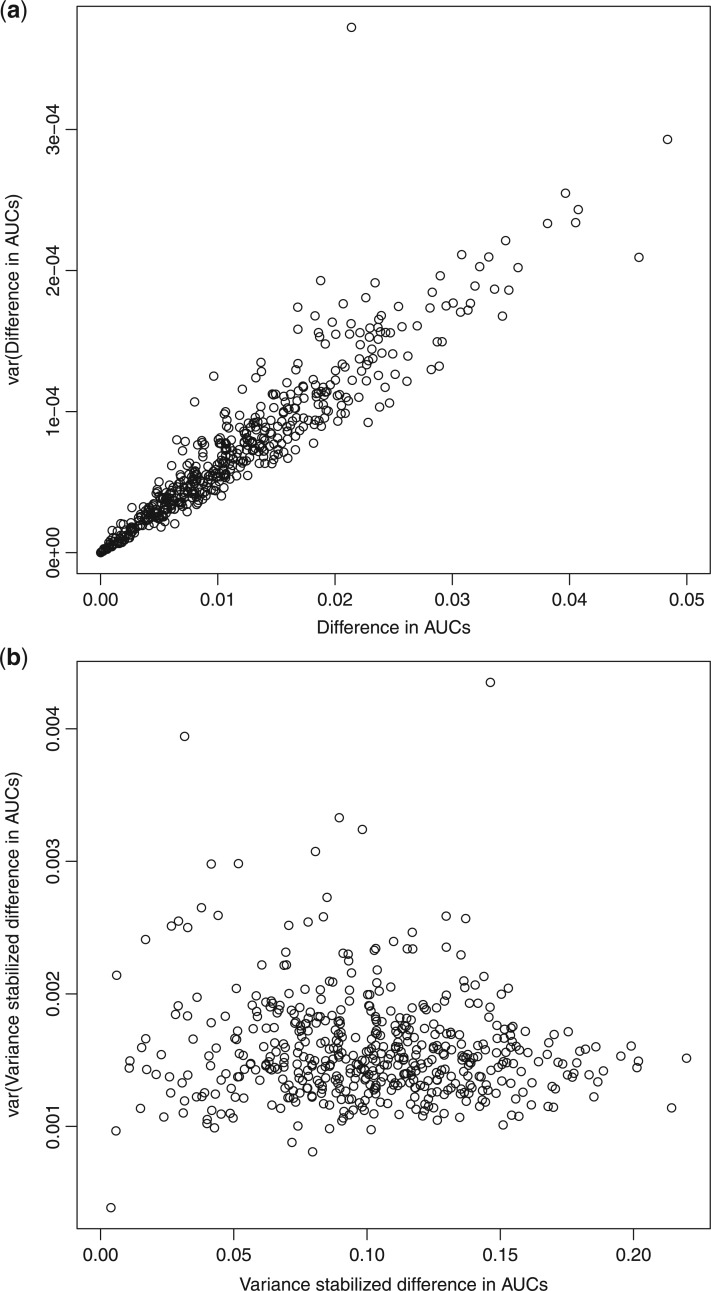
Although asymptotic normality is obtained when 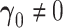, statistics derived from nested models (such as the likelihood ratio statistic) tend to be positively skewed with finite samples. For the difference in AUC statistic, Figure 1(a) depicts a plot of this difference 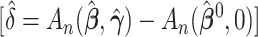and its estimated asymptotic variance 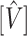. The points are the realizations of a simulation where the true difference 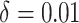, the true baseline AUC is 0.70, and the sample size within each replication is 500. The graph indicates a strong linear relationship between the estimated difference in AUCs and its asymptotic variance, indicating that the normal approximation is inaccurate. To remove this mean-variance linear relationship, a square root reparameterization 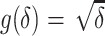is applied. The transformed estimate and its asymptotic variance are

$$\hat{\tau }=\sqrt{\hat{\delta }}\widehat{\text{var}}(\hat{\tau })=\frac{\hat{V}}{4\hat{\delta }}.$$

Fig. 1.

(a) Difference in AUCs. (b) Variance stabilized difference in AUCs.

Stemming from comment 4, estimating the regression parameters by maximizing the AUCs in the reduced and full models leads to a non-negative 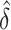and removes a barrier to applying the square root transformation. Figure 1(b) demonstrates the variance stabilization after the square root transformation was applied, suggesting improved accuracy for the normal approximation. Subsequently, we will explore the use of this transformation for the development of accurate confidence intervals.

Finally we note that the asymptotic distribution theory in this section, including the square root transformation, can be applied to develop an accurate test under the null 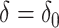, with 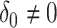. The Wald test for 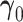is inappropriate for the nonzero null, since the mapping 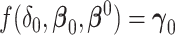for the inverse of the limiting difference in AUCs is unknown and not 1-1.

4. CONFIDENCE INTERVALS

An interval estimate for the magnitude of the improvement in the AUC due to the inclusion of new factors is important. A confidence interval enables the investigator to weigh this improvement relative to the potential costs in obtaining new markers. An asymptotic 95% confidence interval, derived directly from Theorem 2, for the population difference in AUCs is

$$\text{DIFF\hspace{0.5em}}=(\hat{\delta }-1.96\sqrt{\text{var}(\hat{\delta })},\hat{\delta }+1.96\sqrt{\text{var}(\hat{\delta })}).$$

A variance stabilizing square root transformation should provide a more accurate asymptotic confidence interval for the difference in the AUC parameters. The 95% confidence interval is obtained by using the reparameterization 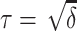, as described above, and selecting the set of values not in the critical region of the asymptotic normal test

$$\{\tau :\left|\frac{\hat{\tau }-\tau }{\sqrt{\text{var}(\hat{\tau })}}\right|<1.96\}.$$

A back transformation of the upper and lower 95% confidence limits for 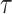leads to the confidence interval for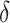

$$\text{DIFFvst\hspace{0.5em}}=({\{\hat{\tau }-1.96\sqrt{\text{var}(\hat{\tau })}\}}^2,{\{\hat{\tau }+1.96\sqrt{\text{var}(\hat{\tau })}\}}^2).$$

If 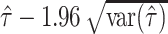is negative, then the lower confidence bound is set to zero.

5. SIMULATIONS

A simulation study was performed to assess the operating characteristics of the direct test of equality of AUCs from nested models and coverage properties of the confidence interval for the difference in AUCs parameter. A binormal logistic risk model was generated with covariate correlation parameters 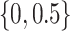and . To evaluate the robustness of the proposed method, a probit model with the same covariate structure was generated. Five hundred observations per replicate and 5000 replicates were run for each simulation. The range of population AUCs examined was (0.55–0.85).

For the test statistic, the normal density smooth 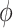was used to compute the second derivative matrix 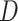. Guidance from kernel density estimation led to the bandwidth 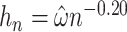, where 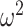is the variance of 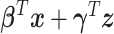(Simonoff, 1996). However, when the AUC was near the 0.5 boundary, there were cases when 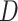was not negative definite. For those cases, 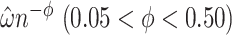were evaluated and the exponent closest to 0.20 (if one existed) which produced a negative definite 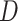was chosen. If a bandwidth could not be found that enabled 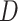to be negative definite, then that replication used 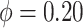. For confidence interval estimation, the normal distribution function 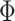was used to estimate the smooth AUCs and using the kernel smoothing literature for distribution functions, was chosen (Lloyd, 1998). The choice of bandwidth used for smoothing in both cases is flexible, since the only asymptotic constraint is that it goes to zero as the sample size gets large.

Tables 1 and 2 compare the size and power estimates for the AUCs test of equality to the Wald test of association for the new factors. The results in Table 1 demonstrate that the difference in AUCs test statistic, based on a linear combination of chi-square random variables as the asymptotic null reference distribution, is a valid test under the null. The results also confirm the validity of the Wald test under this scenario. The power results in Table 2 illustrate that the parametric Wald test is more efficient than the nonparametric difference in AUC test.

Table 1.

Size simulations 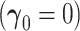. All entries multiplied by 100

			Logistic		Probit
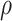
AUCf	AUCr		LCCS	WALD	LCCS	WALD
0.55	0.55	0	5.30	4.42	5.34	5.42
		0.5	5.34	4.50	5.40	5.34
0.60	0.60	0	4.38	6.02	3.92	5.84
		0.5	4.42	5.94	3.88	5.68
0.65	0.65	0	4.34	5.00	4.00	4.68
		0.5	4.34	5.06	4.00	4.60
0.70	0.70	0	4.70	5.22	4.44	4.78
		0.5	4.70	5.28	4.44	4.74
0.75	0.75	0	4.52	4.64	4.92	5.22
		0.5	4.52	4.62	4.94	5.22
0.80	0.80	0	4.68	4.94	4.56	4.32
		0.5	4.68	4.70	4.56	4.38
0.85	0.85	0	5.60	4.88	4.68	4.76
		0.5	5.62	4.94	4.68	4.76

AUCf = area under the curve for full model with covariates ;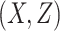

AUCr = area under the curve for reduced model with covariate ;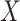

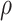= correlation between the covariates ;

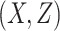LCCS, linear combination of chi-square random variables;

WALD = Wald statistic.

Table 2.

Power simulations 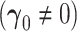. All entries multiplied by 100

			Logistic		Probit
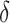
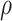
	AUCr		LCCS	WALD	LCCS	WALD
0.02	0.55	0	28.80	50.48	30.18	50.12
		0.5	28.00	51.60	29.80	50.24
0.02	0.60	0	63.70	74.68	63.06	74.14
		0.5	65.40	73.40	62.90	74.10
0.01	0.65	0	54.34	61.02	60.56	67.76
		0.5	54.20	60.20	60.38	67.50
0.01	0.70	0	68.46	73.18	75.88	80.82
		0.5	65.00	69.80	75.96	80.72
0.01	0.75	0	81.30	84.38	88.34	91.72
		0.5	80.60	83.40	88.32	91.94
0.005	0.80	0	62.86	65.60	81.68	85.14
		0.5	63.60	65.20	81.66	85.02
0.005	0.85	0	75.14	75.76	96.74	97.82
		0.5	75.60	77.80	96.70	97.70

AUCf = area under the curve for full model with covariates ;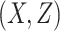

AUCr, area under the curve for reduced model with covariate ;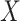

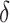= AUCf AUCr;

= correlation between the covariates ;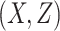

LCCS = linear combination of chi-square random variables; WALD, Wald statistic.

The coverage properties of the proposed confidence interval are summarized in Table 3. The simulations evaluated the standard asymptotic normal 95% confidence interval for 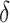(DIFF) and the variance stabilized square root transformed confidence interval for 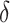(DIFFvst). The variance stabilized confidence interval produced accurate coverage across the simulations explored. In contrast, the untransformed confidence interval was inaccurate. However, at the largest 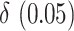, the difference in coverage between the two methods was small, indicating that as the true difference in AUCs increase, the asymptotic normality of 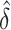improves.

Table 3.

Coverage estimates for 95% confidence intervals for 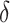. Average length of intervals in parentheses. All entries multiplied by 100.

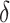
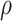
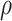
	AUCr		DIFF	DIFFvst		DIFF	DIFFvst
0.002	0.55	0	94.60 (3.4)	93.62 (6.4)	0.5	94.52 (3.4)	93.68 (6.5)
	0.60	0	91.92 (2.0)	95.70 (4.0)	0.5	92.00 (2.0)	95.72 (4.1)
	0.65	0	89.04 (1.5)	96.54 (3.1)	0.5	88.92 (1.5)	96.48 (3.0)
	0.70	0	87.66 (1.2)	96.28 (2.5)	0.5	87.48 (1.7)	96.18 (2.5)
	0.75	0	86.32 (1.0)	96.20 (2.0)	0.5	86.12 (1.0)	96.16 (2.0)
	0.80	0	86.26 (0.9)	95.88 (1.8)	0.5	86.00 (0.9)	95.76 (1.9)
	0.85	0	85.84 (0.8)	95.80 (1.5)	0.5	85.80 (0.8)	95.68 (1.5)
0.005	0.55	0	89.54 (3.9)	94.06 (6.5)	0.5	89.52 (3.9)	94.12 (6.6)
	0.60	0	86.56 (2.6)	95.34 (4.3)	0.5	86.44 (2.6)	95.46 (4.2)
	0.65	0	86.10 (2.1)	95.92 (3.2)	0.5	86.08 (2.1)	95.90 (3.2)
	0.70	0	85.96 (1.8)	95.54 (2.6)	0.5	85.92 (1.8)	95.42 (2.6)
	0.75	0	87.64 (1.6)	95.48 (2.1)	0.5	87.44 (1.6)	95.52 (2.1)
	0.80	0	89.40 (1.5)	95.10 (1.9)	0.5	89.40 (1.5)	95.22 (1.9)
	0.85	0	89.02 (1.3)	94.18 (1.6)	0.5	89.16 (1.3)	94.20 (1.5)
0.01	0.55	0	86.10 (4.7)	93.74 (7.1)	0.5	86.00 (4.7)	93.72 (7.1)
	0.60	0	86.18 (3.6)	94.52 (4.8)	0.5	86.16 (3.6)	94.46 (4.8)
	0.65	0	88.88 (3.0)	95.14 (3.9)	0.5	88.74 (3.0)	95.16 (3.9)
	0.70	0	88.90 (2.7)	93.90 (3.2)	0.5	89.08 (2.7)	93.88 (3.2)
	0.75	0	90.92 (2.4)	94.16 (2.7)	0.5	90.78 (2.4)	94.20 (2.7)
	0.80	0	92.06 (2.2)	94.40 (2.4)	0.5	91.98 (2.2)	94.38 (2.4)
	0.85	0	91.48 (2.0)	93.90 (2.1)	0.5	91.56 (2.0)	93.96 (2.1)
0.02	0.55	0	86.12 (6.2)	92.04 (8.0)	0.5	86.32 (6.2)	91.94 (8.0)
	0.60	0	88.96 (5.1)	92.86 (6.0)	0.5	88.86 (5.1)	92.96 (6.0)
	0.65	0	90.92 (4.5)	94.32 (4.9)	0.5	91.12 (4.5)	94.38 (4.9)
	0.70	0	91.66 (4.0)	93.70 (4.2)	0.5	91.70 (4.0)	93.78 (4.2)
	0.75	0	92.80 (3.6)	94.42 (3.7)	0.5	92.64 (3.6)	94.44 (3.7)
	0.80	0	93.44 (3.2)	94.38 (3.3)	0.5	93.54 (3.2)	94.42 (3.3)
	0.85	0	92.60 (2.8)	94.06 (2.8)	0.5	92.56 (2.8)	94.08 (2.8)
0.05	0.55	0	90.14 (9.2)	91.40 (9.6)	0.5	90.06 (9.2)	91.34 (9.7)
	0.60	0	92.00 (8.0)	93.20 (8.1)	0.5	92.00 (8.0)	93.32 (8.1)
	0.65	0	93.44 (7.0)	93.90 (7.0)	0.5	93.46 (7.0)	93.86 (7.0)
	0.70	0	93.34 (6.1)	93.82 (6.1)	0.5	93.36 (6.1)	93.86 (6.1)
	0.75	0	93.52 (5.4)	93.90 (5.4)	0.5	93.54 (5.4)	93.84 (5.4)
	0.80	0	94.02 (4.7)	94.02 (4.7)	0.5	94.06 (4.8)	94.04 (4.8)
	0.85	0	93.30 (4.2)	93.54 (4.2)	0.5	93.38 (4.2)	93.58 (4.2)

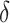= AUCf AUCr;

AUCr = area under the curve for reduced model with covariate ;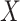

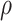= correlation between the covariates ;

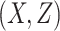DIFF = conventional confidence interval;

DIFFvst = confidence interval using variance stabilizing transformation.

Although the square root transformation produced accurate confidence interval coverage in the simulations, a data-based transformation may prove useful on individual datasets. One approach is to use the Box–Cox transformation

$$\begin{array}{ccc}h(\delta )=\hfill & \frac{{\delta }^{\lambda }-1}{\lambda }\hfill & \lambda \ne 0\hfill \\ & \ln (\delta )\hfill & \lambda =0\hfill \end{array}$$

and choose 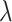to minimize the correlation between 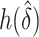and 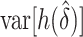(DiCiccio and others, 2006).

6. APPLICATION TO PANCREATIC CANCER

Intraductal papillary mucinous neoplasms (IPMN) are cystic lesions of the pancreas and present with difficult treatment decisions. Surgical removal is difficult and morbid. It is essential if the lesions are high-risk (defined as malignant or high-grade) but also a potential for harm to the patient for low-risk lesions (low-grade or benign). Unfortunately lesion risk (malignancy and grade) can only be evaluated pathologically, leaving the clinician to use alternative clinical markers of risk such as main duct involvement. It is widely accepted that lesions involving the main pancreatic duct are at higher risk of being malignant and current guidelines of the International Association of Pancreatology recommend resection of all main-duct lesions (Tanaka and others, 2012). Using the data which supported these guidelines one can infer that 40% of patients with main duct IPMN will undergo resection to remove low-risk lesions. Therefore the search for markers that improve our ability to select patients for resection continues. Lesion size and presence of a solid component on imaging are recently reported to be predictors of high-risk lesions (Correa-Gallego and others, 2013) although they are not yet incorporated into the international guidelines. In this analysis we evaluate whether a novel marker, recent weight loss, provides incremental improvement in risk classification, when used in conjunction with main duct involvement, lesion size and the presence of a solid component in imaging.

Two hundred and six patients at Memorial Sloan Kettering who were candidates for surgical removal of IPMNs were evaluated. The Wald statistic, derived from a logistic regression analysis, indicated that recent weight loss is positively associated with high vs. low risk lesions in the presence of a solid component on imaging, main duct involvement, and the logarithm of lesion size. The MRC AUC estimates from models without and with the weight loss factor were 0.794 and 0.813, respectively. Thus, although the Wald statistic indicates that weight loss is associated with resection, it is unclear whether its inclusion is sufficiently helpful in terms of risk classification.

We examined the importance of weight loss, first confirming the logistic analysis that weight loss is associated with high-risk lesions. The observed difference in model AUCs was 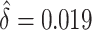and the test that the added factor increased the population AUC generated a p-value equal to 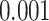. The 95% confidence interval for 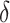, using the variance stabilizing square root transformation, was . Since the lower bound is close to zero, it is unclear whether adding recent weight loss to the existing clinical factors provides a meaningful benefit to the current surgical risk classification algorithm.

7. DISCUSSION

The complexity of human disease and response to treatment can only be captured by the use of multiple clinical features and biomarkers. While most clinical features that are in use for predictive purposes are well-established, new biomarkers (including genomic and proteomic ones) are rapidly being introduced into clinical research. These novel markers are useful to the extent that they improve our ability to prognosticate and predict response to therapy over and beyond what we can currently do using clinical features and established biomarkers. This requires the development of a statistical model that includes both established and novel markers, and using this model to assess the added predictive value of the novel components. This is typically done comparing the AUCs from the full model (containing all variables) and the reduced model (excluding the novel variables) resulting in nested models.

The current recommendation to establish an increase in the AUC for nested models is to perform a likelihood ratio or Wald test on the additional factors and if the test is significant compute a confidence interval for the difference in AUCs parameter. These parametric association test statistics are more sensitive than the nonparametric difference in AUC statistic. Specifically, high odds ratios and small p-values corresponding to new markers in a classification model can produce only modest increments in the observed difference in AUCs. Such seemingly incongruous results may lead to dissonance when explaining the results to a collaborator not sufficiently versed in statistical inference. In this article we develop the asymptotic theory necessary for the statistical comparison of two AUCs resulting from nested models and provide a method to construct accurate confidence intervals for the difference in AUCs filling another gap in the methodology.

In addition to providing a direct test of equality for the difference in AUCs, the development of the asymptotic distribution theory for the difference in AUCs 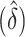when its limiting difference 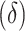is zero enables the analyst to assess how large can be due to sampling variability alone. An upper quantile of this null sampling distribution may be useful when designing future studies to test for the incremental value of new biomarkers. A further usage of this derivation occurs when the objective of the analysis is model selection and the metric used to select variables is AUC. Here the proposed methodology provides a coherent framework for model building and final model selection.

There are other metrics for model performance such as sensitivity and specificity, or more recently introduced metrics such as net benefit (Vickers and Elkin, 2006), net reclassification improvement and integrated discriminant improvement (Pencina and others, 2008), and proportion of cases followed and proportion needed to follow-up (Pfeiffer and Gail, 2013; Pfeiffer, 2013). It is noted that the methodological framework, including the smoothing approximation for indicator functions and the distribution theory for nested models, is sufficiently general to be applied to assess the added value of new markers using these metrics. The application of the proposed methodology to these statistics will be explored in future work. These alternative metrics notwithstanding, the AUC remains the most popular measure of medical test performance. It is ubiquitous in clinical, bioinformatic, and radiology journals, and many researchers are familiar with it. The proposed methodology, which provides proper inferential tools to assess the change in AUCs, will prove useful in multiple contexts.

APPENDIX

The following notation and regularity conditions are used in this Appendix.

Notation:

$$\begin{array}{c}{\mathit{\beta }}^T=(1,{\eta }_1,\dots ,{\eta }_{p-1}),{\mathit{\gamma }}^T=({\gamma }_1,\dots ,{\gamma }_q),\mathit{\theta }=({\mathit{\eta }}^T,{\mathit{\gamma }}^T{)}^T\hfill \\ A_n(\mathit{\theta })=(n_0{n}_1{)}^{-1}\sum _i\sum _{j}I[y_i>y_j]\mathrm{\Phi }\left(\frac{{\mathit{\eta }\mathit{t}\mathit{a}}^T{\mathbf{x}}_{ij}+{\mathit{\gamma }}^T{\mathbf{z}}_{ij}}{h_n}\right).\hfill \end{array}$$

The second derivative matrix of and its inverse are partitioned as

$$D(\mathit{\theta })=\left[\begin{array}{cc}{D}_{\mathit{\eta }\mathit{\eta }}& D_{\mathit{\eta }\mathit{\gamma }}\\ D_{\mathit{\gamma }\mathit{\eta }}& D_{\mathit{\gamma }\mathit{\gamma }}\end{array}\right],D^{-1}(\mathit{\theta })=\left[\begin{array}{cc}{D}^{\mathit{\eta }\mathit{\eta }}& D^{\mathit{\eta }\mathit{\gamma }}\\ D^{\mathit{\gamma }\mathit{\eta }}& D^{\mathit{\gamma }\mathit{\gamma }}\end{array}\right],\text{where\hspace{0.5em}}{D}_{\mathit{\eta }\mathit{\gamma }}=\frac{{\mathrm{\partial }}^2{A}_n(\mathit{\theta })}{\mathrm{\partial }\mathit{\eta }\mathrm{\partial }\mathit{\gamma }}.$$

MRC Regularity Conditions:

• (1) 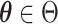a compact subspace of .

• (2) The domain of is not contained in a linear subspace of .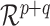

• (3) The density of the first component of 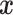conditional on all other covariates is everywhere positive.

Theorem 1

The asymptotic distribution for the difference in AUCs when are MRC estimates and .

To derive the expansion when 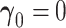(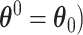, the difference in AUCs is divided into two components

$$[A_n(\hat{\mathit{\theta }})-A_n({\mathit{\theta }}_0)]-[A_n(\widehat{{\mathit{\theta }}^0})-A_n({\mathit{\theta }}^0)].$$

For the first component, a three term expansion of 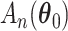around 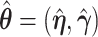is,

$$A_n(\hat{\mathit{\theta }})-\{A_n(\hat{\mathit{\theta }})+0+\frac{1}{2}({\mathit{\theta }}_0-\hat{\mathit{\theta }}{)}^{T}D(\hat{\mathit{\theta }})({\mathit{\theta }}_0-\hat{\mathit{\theta }})\},$$

where the first order term is zero since the MRC estimate 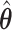is obtained through maximization of .

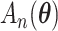A similar argument produces a three term expansion of 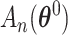around 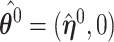for the second component,

$$A_n(\widehat{{\mathit{\theta }}^0})-\{A_n(\widehat{{\mathit{\theta }}^0})+0+\frac{1}{2}({\mathit{\eta }}^0-\widehat{{\mathit{\eta }}^0}{)}^T{D}_{\mathit{\eta }\mathit{\eta }}({\hat{\mathit{\theta }}}^0)({\mathit{\eta }}^0-\widehat{{\mathit{\eta }}^0})\}.$$

Therefore, the statistic 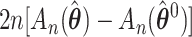is asymptotically approximated by

$$n({\mathit{\theta }}_0-\hat{\mathit{\theta }}{)}^T[-D(\hat{\mathit{\theta }})]({\mathit{\theta }}_0-\hat{\mathit{\theta }})-n({\mathit{\eta }}^0-\widehat{{\mathit{\eta }}^0}{)}^T[-D_{\mathit{\eta }\mathit{\eta }}({\hat{\mathit{\theta }}}^0)]({\mathit{\eta }}^0-\widehat{{\mathit{\eta }}^0})+o_p(1).$$

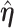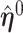Further simplification may be achieved by relating the unrestricted and the restricted MRC estimates and when 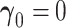(Cox and Hinkley, 1974, page 308),

$$({\mathit{\eta }}^0-{\hat{\mathit{\eta }}}^0)=({\mathit{\eta }}_0-\hat{\mathit{\eta }})+D_{\mathit{\eta }\mathit{\eta }}^{-1}({\hat{\mathit{\theta }}}^0)D_{\mathit{\eta }\mathit{\gamma }}({\hat{\mathit{\theta }}}^0)({\mathit{\gamma }}_0-\hat{\mathit{\gamma }})+o_p(n^{-1/2}).$$

Thus, the statistic is asymptotically approximated by

$$2n[A_n(\hat{\mathit{\theta }})-A_n(\widehat{{\mathit{\theta }}^0})]=n({\mathit{\gamma }}_0-\hat{\mathit{\gamma }}{)}^T[-D^{\mathit{\gamma }\mathit{\gamma }}(\hat{\mathit{\theta }}){]}^{-1}({\mathit{\gamma }}_0-\hat{\mathit{\gamma }})+o_p(1).$$

The quadratic form on the right-hand side asymptotically has a distribution which is a weighted sum of independent chi-square random variables, each with one degree of freedom. Therefore, as ,

$$\text{Pr}(2n[A_n(\hat{\mathit{\theta }})-A_n(\widehat{{\mathit{\theta }}^0})]\le u)=\text{Pr}(\sum _{j=1}^q{\lambda }_j{\chi }_j^2\le u),$$

where the weights 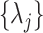are the eigenvalues of the product matrix 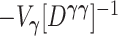, 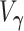is the asymptotic variance of the MRC estimate , and is the second derivative matrix of 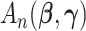(Baldessari, 1967).

Theorem 2

The asymptotic distribution of the difference in AUCs when .

Consider the first order asymptotic approximation

$$\begin{array}{ccc}{n}^{1/2}[A_n(\hat{\mathit{\theta }})-A_n({\hat{\mathit{\theta }}}^0)-\delta ]\hfill & \hspace{0.17em}=\hfill & n^{1/2}[A_n({\mathit{\theta }}_0)-A_n({\mathit{\theta }}^0)-\delta ]\hfill \\ & & \hspace{0.17em}+{\left[\frac{\mathrm{\partial }{A}_n(\mathit{\theta })}{\mathrm{\partial }\mathit{\theta }}{|}_{\mathit{\theta }=\hat{\mathit{\theta }}}\right]}^T{n}^{1/2}(\hat{\mathit{\theta }}-{\mathit{\theta }}_0)-{\left[\frac{\mathrm{\partial }{A}_n(\mathit{\eta },0)}{\mathrm{\partial }\mathit{\eta }}{|}_{\mathit{\eta }={\hat{\mathit{\eta }}}^0}\right]}^T{n}^{1/2}({\hat{\mathit{\eta }}}^0-{\mathit{\eta }}^0)+o_p(1).\hfill \end{array}$$

Because 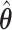and 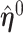maximize their respective smooth AUCs, it follows that

$$n^{1/2}[A_n(\hat{\mathit{\theta }})-A_n({\hat{\mathit{\theta }}}^0)-\delta ]=n^{1/2}[A_n({\mathit{\theta }}_0)-A_n({\mathit{\theta }}^0)-\delta ]+o_p(1).$$

Since,

$$\begin{array}{ccc}& & n^{1/2}[A_n({\mathit{\theta }}_0)-A_n({\mathit{\theta }}^0)-\delta ]\hfill \\ & & \hspace{0.17em}=n^{1/2}[(n_0{n}_1{)}^{-1}\sum _i\sum _{j}I[y_i>y_j]\{\mathrm{\Phi }\left(\frac{{\mathit{\beta }}_0^T{\mathbf{x}}_{ij}+{\mathit{\gamma }}_0^T{\mathbf{z}}_{ij}}{h_n}\right)-\mathrm{\Phi }\left(\frac{{{\mathit{\beta }}^0}^T{\mathbf{x}}_{ij}}{h_n}\right)-\delta \}]\hfill \end{array}$$

is a two-sample U-statistic of degree 2 with no estimated parameters, the asymptotic normality for the difference in AUCs follows from U-statistic theory. Its asymptotic variance is (Wei and Johnson, 1985)

$$V=\frac{n}{n_0}{\sigma }_1^2+\frac{n}{n_1}{\sigma }_2^2,$$

which may be estimated with the following components

$$\begin{array}{ccc}{\hat{\sigma }}_1^2\hfill & \hspace{0.17em}=\hfill & \hspace{0.17em}[n_0{n}_1(n_0-1){]}^{-1}\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1,k\ne j}^{n}I[y_i=1]I[y_j=0]I[y_k=0](e_{ij}-\hat{\delta })(e_{ik}-\hat{\delta }),\hfill \\ {\hat{\sigma }}_2^2\hfill & \hspace{0.17em}=\hfill & \hspace{0.17em}[n_0{n}_1(n_1-1){]}^{-1}\sum _{i=1}^n\sum _{j=1}^n\sum _{k=1,k\ne j}^{n}I[y_i=1]I[y_j=0]I[y_k=1](e_{ij}-\hat{\delta })(e_{kj}-\hat{\delta }),\hfill \\ & & \text{and\hspace{0.5em}}{e}_{ij}=\mathrm{\Phi }\left[\frac{{\hat{\mathit{\beta }}}^T{\mathbf{x}}_{ij}+{\hat{\mathit{\gamma }}}^T{\mathbf{z}}_{ij}}{h_n}\right]-\mathrm{\Phi }\left[\frac{{\widehat{{\mathit{\beta }}^0}}^T{\mathbf{x}}_{ij}}{h_n}\right].\hfill \end{array}$$

FUNDING

National Institutes of Health (grants P30 CA008748 to all and R01 CA136783 to C.S.M.)