Investigating Measurement Invariance in Computer-Based Personality Testing

Abstract

A popular method to assess measurement invariance of a particular item is based on likelihood ratio tests with all other items as anchor items. The results of this method are often only reported in terms of statistical significance, and researchers proposed different methods to empirically select anchor items. It is unclear, however, how many anchor items should be selected and which method will provide the “best” results using empirical data. In the present study, we examined the impact of using different numbers of anchor items on effect size indices when investigating measurement invariance on a personality questionnaire in two different assessment situations. Results suggested that the effect size indices were not influenced by using different numbers of anchor items. The values were comparable across different number of anchor items used and were small, which indicate that the effect of differential functioning at the item and test level is very small if not negligible. Practical implications are discussed and we discuss the use of anchor items and effect size indices in practice.

Many employment firms and government agencies use the same questionnaire for different purposes, for example, for both personnel selection and for employees’ training and development. Also, with the increasing use of online testing, the administration of the same questionnaire to different (ethnic) groups is becoming the rule more than the exception. In these situations, it is important to determine whether items and scales function similarly across different administrations or across different groups, that is, it is important to determine measurement invariance.

Both confirmatory factor analytic methods and item response theory (IRT; Embretson & Reise, 2000) methods have been proposed to investigate measurement invariance. In this study, we focus on IRT-based methods. One way to investigate whether the psychometric quality of a scale is comparable across different contexts is to apply IRT-based differential item functioning (DIF) and differential test functioning (DTF) techniques.

A popular method to detect differential functioning (DF) is IRTLRDIF (Thissen, 2001), which incorporates the popular likelihood ratio test (LRT) proposed by Thissen, Steinberg, and Wainer (1988, 1993) to determine statistical significant DF, to estimate the item parameters for both groups, and to link them to a common metric. The most common approach to the LRT is the constrained baseline approach in which all other items are used as anchor items (AOAA). An anchor item is an item which is invariant across groups. A large drawback of this approach is inflated Type I error rates (e.g., Kim & Cohen, 1995; Lautenschlager, Flaherty, & Park, 1994; Navas-Ara & Gómez-Benito, 2002; Woods, 2009), because items that are functioning differently across groups are also used as anchor items.

Meade and Wright (2012) provided an overview of different approaches to select anchor items and, based on simulated data, recommended to use the LRT based “maxA5” approach that uses five anchor items. Other researchers recommended using a different number of anchor items. For example, Stark, Chernyshenko, and Drasgow (2006) showed that using one nonsignificant DF item as anchor item is preferable to the AOAA approach. Wang and Yeh (2003) recommended using four nonsignificant DF items as anchor items, whereas Lopez Rivas, Stark, and Chernyshenko (2009) recommended three anchor items.

In most studies simulated data were used to assess the power and Type I error rates of the LRT, where anchor items were known by design. For real data, anchor items should be determined using the data at hand. Therefore, the first aim of the present study was to investigate whether the “maxA5” approach could be successfully applied using empirical data. As an alternative, we considered Woods’s (2009) rank-based strategy to select anchor items. The difference between the rank-based strategy and the “maxA5”approach will be discussed below. The second aim was to evaluate the effect of using anchor items when investigating DF in terms of effect size indices. Most DF studies only report statistical significant test results without reporting any effect size measures. Because DF results may be statistical significant without having much practical implications, several authors have recently argued that some kind of effect size should be reported when conducting DF research. Meade (2010) discussed different types of DF effect size measures and proposed a taxonomy for group mean comparisons and for the comparison of individual respondents across different groups. To our knowledge, there are no studies that investigate the effect of empirically selecting anchor items in terms of effect sizes. Some recent studies (e.g., Behrend, Sharek, Meade, & Wiebe, 2011; Chen, Hwang, & Lin, 2013; Farrington & Lonigan, 2013) applied Meade’s effect size indices on real data but did not take different number of anchor items into account.

Different DF Methods

Likelihood Ratio Approach

Many different IRT-based approaches have been proposed to investigate DF. In this study, we investigated DF using methods based on the popular LRT proposed by Thissen et al. (1988, 1993). The LRT compares the fit (i.e., the likelihood) of a compact model in which all item parameters are assumed to be equal across both groups with the fit of an augmented model in which all item parameters are assumed to be equal for two groups except for one item. A significance test of DIF can be conducted by the statistic:

$$X^2(df)=-2(\ln L_C-\ln L_A),$$

where df is the degrees of freedom (i.e., number of item parameters), lnL_C is the log-likelihood of the compact model, and lnL_A is the log-likelihood of the augmented model. An item exhibits significant DIF when X² exceeds a critical value of the χ² distribution at a prespecified level of Type I error. This means that the augmented model fits better than the compact model for the selected item, suggesting that it is better to use different parameters in both groups on that specific item.

To obtain the best results with the LR method, the anchor items should be nonsignificant DF items across groups (Cheung & Rensvold, 1999). Unfortunately, with real data it is almost always unknown, which items are invariant. Meade and Wright (2012) compared 11 different approaches to select anchor items and they recommended using the “maxA5” approach. However, this method relies heavily on significance testing. For large samples, small differences will be significant whereas these small differences most likely do not have practical relevance (i.e., the size of the effect is small). A method that relies less on statistical significance testing is Woods’s (2009) rank-based strategy. Both methods start with the AOAA approach, but the “maxA5” approach selects items based on their p values (i.e., [non]significance) and a parameters, whereas Woods’s rank-based strategy selects items based on the rank order of their X² values.

MaxA5 Approach

The “maxA5” approach is based on a procedure recommended by Lopez Rivas et al. (2009) to select anchor items from the nonsignificant DF items that have the largest estimated discrimination parameter (a parameter). The name “maxA5” refers to using five nonsignificant DF items with the largest a parameter. In their simulation study, they examined the effect of different characteristics of the anchor items (i.e., item discrimination, item difficulty, and number of anchor items) on the accuracy of DIF detection. The results showed that power improves when using one highly discriminating nonsignificant DF item as anchor. In other specific situations (e.g., small DIF indicated as a shift of .4 in the difficulty parameter, or small sample size of around 500), it is recommended to use a group of (at least three) anchor items among which at least one item is highly discriminating. A disadvantage of this approach is that it is unclear how many anchor items should be used. Therefore, Meade and Wright (2012) examined the effect of using one, three, and five highly discriminating non-DF items on DIF detection. They found that using five highly discriminating anchor items yielded the best results.

Meade and Wright (2012) suggested the following steps in their “maxA5” approach: (a) conduct a LRT with the AOAA approach, (b) select the five highest discriminating items from the nonsignificant DF items, and (c) use them as anchor items in the final DF analyses.

In this study, we will be using different numbers of anchor items (“maxA” approach).

Rank-Based Strategy

The so-called rank-based strategy was proposed by Woods (2009). The first step in this approach is to conduct an LRT with the AOAA approach. The next step is to rank order the items based on their X² value (in case all items have the same number of response categories, otherwise divide each X² value by the number of response categories for that item) and select the g items with the smallest X² (or X² ratio) value to be used as anchor items in the final DF analyses.

In general, Woods (2009) recommended using approximately 10% to 20% of the number of scale items as anchor items. For specific situations, it might be better to use a single anchor item (e.g., with 80% or more DF items) or always more than one anchor item (e.g., with small sample sizes).

Effect Size Indices

To judge whether significant DF differences have practical meaning, different effect size measures have been proposed. Stark, Chernyshenko, and Drasgow (2004) discussed two different methods: an effect size measure for the raw score and an effect size measure using the ratio of selection ratios. By means of these methods they investigated the impact of DIF and DTF on potential selection decisions when comparing the scores of applicants and nonapplicants on personality scales. Although their results showed that a lot of items exhibit DIF, the overall effect on selection decisions was small. Recently, Meade (2010) presented a taxonomy of different effect size measures for differential item and test functioning. In the present study we applied several of these indices, which will be discussed below.

Description of Effect Size Indices

Meade (2010) used four criteria on the basis of which different effect size indices were distinguished: (a) DF on the item and/or scale level, (b) DF cancels across items and/or latent trait values, (c) DF is reported in the original metric or normed to a standard deviation metric, and (d) DF on the basis of a sample distribution or on the basis of an assumed theoretical distribution. Cancellation across the latent trait is also known as nonunifom DF and cancellation across items as compensatory DF.

Here, we focused on polytomous item scores and we used the same notation as in Meade (2010). All indices use the expected score (ES) for respondent s (s = 1, . . . , N), with estimated latent trait value $\widehat{\text{θ}}$, for item i (i = 1, . . . , j). This ES equals the sum of the probabilities of a response to each of the k = 1, . . . , m response options times the value of that response option X_ik, that is,

$$E{S}_{s(\widehat{\theta })i}={\displaystyle \sum }_{k=1}^m{P}_{ik}(\widehat{\theta })X_{ik}.$$

The expected score is similar to an item-level true score and has a potential range from the lowest response option to the highest response option. Similarly, the expected test score (ETS) equals

$$ET{S}_s={\displaystyle \sum }_{i=1}^{j}E{S}_{si}.$$

Effect size indices can be used to investigate whether each item and the test function differently in a focal and a reference group. In general, the minority (e.g., Blacks, or the group with the lowest test score) is chosen as the focal group and the majority (e.g., Whites, or the group with the highest test score) as the reference group (e.g., Stark et al., 2004). First, item parameters are estimated in both groups separately and linked to a common metric via, for example, concurrent calibration as is done in the LRT approach. Once linked, each item has one set of item parameters associated with the focal group and one set of item parameters associated with the reference group. After estimating the latent trait values $\widehat{\text{θ}}$ for the focal group, the ESs can be computed for the focal group based on both the focal group item parameters and the reference group item parameters. These ESs are then compared.

A simple effect size index at the item level is the average difference in ESs across the persons in the focal group sample. This index is called the signed item difference in the sample (SIDS). The sum of these differences across the j items will result in a scale-level index: the signed test difference in the sample (STDS). Both indices use the sample distribution and display the differences in the original metric. This means that when, for example, for a five category item SIDS = −2.2, it is expected that persons in the focal group will score 2.2 points lower on that item than persons in the reference group with the same latent trait value. For the STDS this difference is related to the difference in summed scale score. The SIDS allows for cancellation of DF across θ and the STDS allows for cancellation across items and persons. At the item level, this implies that the SIDS might indicate that there is no DF present, whereas DF might be present at different trait levels but the sum of these differences equals zero (i.e., cancellation across θ). At the scale level, cancellation can also take place across items.

To prevent cancellation across items and/or θ, Meade (2010) proposed the unsigned item difference in the sample (UIDS) and the unsigned test difference in the sample (UTDS), in which the average absolute difference in ESs and ETSs across the persons in the focal group sample is taken. Like the SIDS and the STDS, the UIDS and the UTDS use the sample distribution and display the differences in the original metric. The difference is that the UIDS does not allow cancellation across θ and the UTDS does not allow cancellation across items and θ. UIDS can be interpreted as the hypothetical difference in ESs had the DF in that item been uniform across θ, which means always favoring one group. UTDS can be interpreted in the same way, but now at the test level.

The indices described above all report the differences in the original metric. A standardized difference at the item level can be computed by the expected score standardized difference (ESSD) and at the test level by the expected test score standardized difference (ETSSD). The differences are normed to a standard deviation metric and can, therefore, be interpreted using Cohen’s (1988) rules of thumb for small, medium, and large effect sizes¹ (Meade, 2010). These indices also use the sample distribution. Like SIDS and STDS, ESSD allows for cancellation across θ and ETSSD allows for cancellation across both items and θ.

Finally, we discuss the unsigned expected test score difference in the sample (UETSDS). This index at the scale level differs from the other scale-level indices, because it allows cancellation across items (because ETS is the sum of the item ESs), but not across θ (due to the absolute differences). Like the other indices, the sample distribution is used instead of an assumed theoretical distribution. The differences in ETSs are displayed in the metric of observed scores. UETSDS can be interpreted as the hypothetical amount of DF at the scale level had the DF been uniform in nature, which means always favoring one group.

Application of Effect Size Indices

Meade (2010) suggested that researchers should always report the STDS, UETSDS, and the ETSSD regardless of their research purposes. Comparing STDS and UETSDS provides information with regard to cancellation of DF across the trait score. When STDS and UETSDS are equal, cancellation of DF might occur across items, but it does not occur across the latent trait. The ETSSD is very useful since the differences in ETSs are normed to a standardized metric and this index can be used for tests containing items with different numbers of response categories. Furthermore, different indices are recommended for different situations. Some indices are more appropriate for group mean comparison (e.g., STDS and ESSD) and others for comparing individuals (e.g., UTDS and UETSDS). Therefore, in this study we examined the impact of using anchor items on effect size indices in two different situations. The first comparison was between incumbents and applicants (i.e., group mean comparison) and the second comparison between different ethnic groups in a selection context (i.e., comparing individuals). Besides examining the effect size indices, we visually inspected the ES and ETS plots.

In this study we only used indices based on the sample distribution. For the use of indices based on an assumed theoretical distribution, we refer to Appendix B in Meade (2010). Also, for a detailed description of the indices and how they can be calculated, we refer to Meade (2010).

Method

Instrument

Reflector Big Five Personality (RBFP)

The RBFP (Schakel, Smid, & Jaganjac, 2007) is a computer-based Big Five personality questionnaire applied to situations and behavior in the workplace. It consists of 144 items, distributed over five scales (Emotional Stability, Extraversion, Openness, Agreeableness, and Conscientiousness). Each scale consists of 30 items, with the exception of 24 items in the Openness scale. The items are scored on a 5-point Likert-type scale. The answer most indicative for the trait being measured is scored “4”, and the answer least indicative for the trait is scored “0”. The RBFP is a Dutch version of the Workplace Big Five Profile constructed by Howard and Howard (2001). This profile is based on the NEO-PI-R (Costa & McCrae, 1992) and adapted to workplace situations. For the Dutch version, both conceptual analyses and exploratory factor analyses showed the Big Five structure (Schakel et al., 2007).

Table 1 displays the mean and standard deviations for the total scores on the five scales for different groups². Since the largest differences were found between incumbents and applicants on the Conscientiousness scale (Cohen’s d = 0.54; applicants have higher scores), and for the same scale between Dutch natives and non-Western immigrants in the selection context (Cohen’s d = 0.35; non-Western immigrants have higher scores), the Conscientiousness scale was selected for this study.

Table 1.

Means and Standard Deviations of the Total Scores on the Big Five Scales For Different Groups.

	Incumbents		Applicants		Native applicants		Western applicants		Non-Western applicants
Scale	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
EMS	81.4	14.7	87.9	12.1	87.7	12.2	88.6	12.0	88.6	11.4
EXT	82.7	12.9	85.5	11.2	85.7	11.2	85.8	10.9	83.6	10.7
OPE	67.9	10.8	71.0	9.0	71.1	9.0	71.5	9.0	69.2	9.0
AGR	74.8	9.9	73.5	8.5	73.6	8.6	73.4	8.5	72.1	8.4
CON	86.2	14.1	93.4	12.1	92.8	11.9	94.9	12.5	96.9	12.1

Note. EMS = Emotional Stability; EXT = Extraversion; OPE = Openness; AGR = Agreeableness; CON = Conscientiousness.

Sample and Procedure

Data were collected between September 2009 and January 2011 in cooperation with a Dutch human resources assessment firm. We distinguished two groups: (a) applicants who apply for a job at an organization and (b) incumbents who already worked for an organization and completed the RBFP as part of their own personal career development. We used data from 4,050 applicants (M_age = 33.5, SD = 9.23); 62.1% men; 80.9% native, 9.5% Western immigrants, and 9.6% non-Western immigrants. Of the participants 34.6% had a university degree, 44.7% had higher education, and 20.7% had secondary education. Data from the incumbents consisted of 4,217 persons (M_age = 39.4, SD = 9.31); 55.0% men; 88.8% native, 7.0% Western immigrants, and 4.2% non-Western immigrants. Of the participants 27.6% had a university degree, 49.4% had higher education, and 23.0% had secondary education.

Analysis

Differential Item and Test Functioning

DF was investigated across two groups within different administration contexts: applicants within a selection context (reference group) and incumbents within a career development context (focal group), and we compared Dutch natives (reference group) and non-Western immigrants (focal group) in a selection context. So, we ran two different DF analyses. The first one is for the comparison between incumbents and applicants, because group mean comparison is of interest in this situation. The second analysis was conducted to compare different ethnic groups in a selection context, because in this situation comparing individuals across different groups is of interest.

We used the program IRTPRO 2.1 (Cai, Thissen, & du Toit, 2011) to determine statistically significant DF, to estimate the item parameters for both groups, and to link them to a common metric. An advantage of IRTPRO over IRTLRDIF (Thissen, 2001) or MULTILOG (Thissen, Chen, & Bock, 2003) is that IRTPRO reports item parameters for the anchor items (see also Meade & Wright, 2012). For the present study, we used the graded response model (Samejima, 1969, 1997), which is appropriate for Likert-type scales (e.g., Ankenmann, Witt, & Dunbar, 1999; Embretson & Reise, 2000) like our personality questionnaire. The estimated and linked parameters together with the focal group data were then used as input for VisualDF (Meade, 2010) to compute the effect size indices. VisualDF can be downloaded from http://www4.ncsu.edu/~awmeade.

The initial LRT with AOAA stopped due to estimation problems because for some items the lowest response category (i.e., “0”) was not used by at least one respondent in the different groups. We, therefore, collapsed the lowest two response categories (i.e., “0” and “1”). Furthermore, we removed item 13 because the non-Western immigrants only used the highest three response categories (instead of four), and IRTPRO requires that the number of response categories used per item should be the same when comparing groups. So, for the analyses we used 29 items with four categories (i.e., “0” through “3”).

Based on the recommended number of anchor items in Woods (2009) and Meade and Wright (2012), we used one, three (i.e., 10% of the scale items), five (based on the “maxA5” approach), six (i.e., 20% of the scale items), and seven anchor items (i.e., 25% of the scale items, comparable with 5 out of 20 scale items as anchors in Meade & Wright, 2012). The anchor items will be selected using Meade and Wright’s (2012)“maxA” approach and/or Woods’s (2009) rank-based strategy.

Effect Size Indices

For the comparison of the mean scores of the applicants and the incumbents cancellation of DF across items, θ is appropriate, because only group means are compared. Therefore, we used SIDS and ESSD at the item level and STDS and ETSSD at the scale level. For the comparison of Dutch natives and non-Western immigrants in a selection context cancellation across items is appropriate, but not across the latent trait. In selection settings, candidates are often selected (or not) based on a certain cutoff score. DF around that cutoff score is of interest and might have an adverse impact on the decision. Therefore, we used UIDS at the item level and UTDS and UETSDS at the scale level. Furthermore, we compared SIDS and STDS to UIDS and UTDS to assess the extent to which cancellation of DF across items and trait values occurs.

Results

Differential Functioning Analyses

Comparing Group Means

The higher mean total score of the applicants (reference group) compared with the incumbents (focal group) may be due to a shift in the latent trait distribution, but items may also show DF in the two groups. To investigate DF, we first show the results of the LRT statistics with the AOAA approach in Table 2 together with the item parameters for the reference group. As expected, due to the large sample sizes all items are statistically significant (i.e., p < .05), with the exception of Item 4 (p = .191). Therefore, the “maxA” approach cannot be applied to select anchor items and instead we used Woods’s (2009) rank-based strategy.

Table 2.

Results of the LRT with AOAA and the Item Parameters for the Reference Group of the Incumbents–Applicants Comparison.

		Reference group (applicants)
Item	X 2	a	b 1	b 2	b 3
1	67.7	1.74	−2.31	−1.34	0.34
2	54	1.03	−1.88	−0.82	1.57
3	16.4	1.20	−1.85	−0.81	1.58
4	6.1	0.76	−1.28	−0.12	2.65
5	27.6	1.63	−1.75	−0.81	1.16
6	30.3	1.49	−2.09	−1.27	0.71
7	26.2	1.32	−3.33	−2.45	−0.16
8	29.2	1.52	−3.18	−2.60	−0.67
9	42.1	1.52	−2.25	−1.39	−0.06
10	63.6	1.98	−2.69	−1.77	0.02
11	26.6	1.91	−2.09	−1.19	0.23
12	25.6	1.84	−2.89	−1.88	0.31
14	81.8	0.67	−4.78	−2.70	1.11
15	222.4	0.66	−3.97	−0.83	2.42
16	80.8	0.70	−5.46	−3.33	0.70
17	41.1	1.04	−4.85	−3.98	−0.82
18	35.7	1.36	−3.60	−2.31	−0.06
19	98	0.87	−3.26	−1.12	1.64
20	45.5	1.29	−2.33	−1.18	0.89
21	62.7	1.00	−1.34	−0.06	2.21
22	74.7	1.36	−2.01	−1.03	1.17
23	77.5	1.42	−2.15	−1.10	1.14
24	33.7	0.95	−3.68	−1.97	1.10
25	29.4	0.93	−4.74	−3.59	−0.56
26	41.1	1.78	−3.07	−2.18	−0.25
27	20.6	0.98	−3.86	−2.16	1.67
28	31.7	1.81	−3.03	−1.84	0.24
29	27.1	1.47	−3.62	−2.41	0.47
30	31.6	1.64	−2.45	−1.48	0.56

Note. LRT = likelihood ratio test; AOAA = all other items as anchors.

Based on the X² values from Table 2, the items were rank ordered and the items with the lowest X² values were selected as anchors. The following items were used as anchor items in the subsequent DF analyses with different numbers of anchor items (in the order that they are used): Items 4, 3, 27, 12, 7, 11, 29. The results (not tabulated) showed, independent of the number of anchor items used, both positive and negative SIDS values, which indicate that for some items the incumbents scored lower than the applicants (i.e., negative SIDS values) and for some items the incumbents scored higher (i.e., positive SIDS values). Positive and negative SIDS values also indicated that, at the test level, cancellation across items will occur. Regardless of the number of anchor items used, the SIDS values were low. The highest negative SIDS value was −0.198 (Item 22, when using one anchor item) and the highest positive SIDS value was 0.123 (Item 16, when using five anchor items). This means that for Item 22 (when using one anchor item) the incumbents scored 0.198 points lower than the applicants, and for Item 16 (when using five anchor items) the incumbents scored 0.123 points higher than the applicants with the same latent trait value. Note that SIDS values are reported in the item expected score metric and that the items have four response categories, scored 0 to 3, which suggests that the found differences were small. This is confirmed by the ESSD values. The results showed that all differences were small (i.e., |ESSD| < 0.30), with the exception of Items 14 and 16 when using different numbers of anchor items. These differences are of medium effect size (i.e., 0.30 < |ESSD| < 0.70).

When we compared the SIDS and ESSD values across analyses using different numbers of anchor items, the difference were small. The correlations between the SIDS values across conditions range from .946 through 1, and for the ESSD values the correlations range from .998 through 1, which indicates that the SIDS and ESSD values are very similar across conditions. Also, the root mean squared differences across conditions were small ranging from .002 through .085 for the SIDS values and ranging from .005 through .191 for the ESSD values. These results suggest that the item-level effect size indices were not much affected by using different numbers of anchor items.

Table 3 displays the test-level effect size indices when using different numbers of anchor items for the incumbents–applicants comparison. The STDS values were different when using different numbers of anchor items; they ranged from −1.782 when using one anchor item through 0.537 when using five anchor items. An STDS value of −1.782 indicates that the incumbents scored 1.782 points lower than the applicants on the Conscientiousness scale. However, since the STDS values are reported in the expected test score metric, these differences are small given the theoretical total score range of 0 to 87. This is also confirmed by the values of the standardized effect size, ETSSD, which suggests that the differences are small (i.e., |ETSSD| < 0.30). Furthermore, since STDS and UETSDS values were comparable regardless of the number of anchor items used, there was no cancellation across θ at the scale level, but there might be cancellation across items. Cancellation across items was confirmed by the differences between STDS and UTDS values.

Table 3.

Test-Level Effect Size Statistics for the Comparison Between Applicants (Reference Group) and Incumbents (Focal Group).

	AOAA	1 Anchor	3 Anchors	5 Anchors	6 Anchors	7 Anchors
STDS	−0.22	−1.78	0.15	0.54	0.23	−0.03
UTDS	1.69	2.27	1.64	1.65	1.54	1.44
UETSDS	0.25	1.78	0.18	0.56	0.26	0.06
ETSSD	−0.02	−0.15	0.01	0.04	0.02	−0.00

Note. AOAA = all other items as anchors; 1-7 anchor(s) = one through seven items with the lowest X² values are used as anchor items; STDS = signed test difference in the sample; UTDS = unsigned test difference in the sample; UETSDS = unsigned expected test score difference in sample; ETSSD = expected test score standardized difference.

The differences for the test-level indices across analyses using different numbers of anchor items are larger compared with the differences for the item-level indices. This is expected due to summing up over items at the test level. However, when considering the ETSSD values, the standardized differences were small. This suggests that also the test-level effect size indices were not much affected by using different numbers of anchor items.

Comparing Different Ethnic Groups

To investigate DF for the comparison between Dutch natives and non-Western immigrants, we first conducted the LRT with the AOAA approach. The results of that analysis and the item parameters for the reference group are displayed in Table 4. The results showed that 15 items were identified as nonsignificant DF items (i.e., p > .05), which could be used for the “maxA” approach. The smaller sample sizes compared with our first study most likely resulted in more nonsignificant DF items.

Table 4.

Results of the LRT with AOAA and the Item Parameters for the Reference Group of the Dutch Natives–Non-Western Immigrants Comparison.

	LRT (AOAA)			Reference group (Dutch natives)
Item	X 2	df	p	a	b 1	b 2	b 3
1	5.4	4	.250	1.69	−2.34	−1.30	0.44
2	12.2	4	.016	1.01	−1.87	−0.83	1.66
3	6.1	4	.192	1.16	−1.82	−0.77	1.72
4	11.3	4	.023	0.77	−1.26	−0.10	2.71
5	4.6	4	.331	1.58	−1.73	−0.75	1.26
6	8.7	4	.069	1.42	−2.08	−1.24	0.83
7	2.7	4	.605	1.30	−3.37	−2.42	−0.08
8	37.1	4	<.001	1.49	−3.33	−2.69	−0.63
9	12.5	4	.014	1.53	−2.18	−1.34	0.02
10	8.0	4	.093	1.90	−2.75	−1.75	0.08
11	4.0	4	.403	1.85	−2.10	−1.17	0.30
12	4.2	4	.386	1.81	−2.86	−1.85	0.35
14	4.8	4	.309	0.64	−5.00	−2.78	1.28
15	3.5	4	.482	0.62	−4.16	−0.83	2.65
16	44.3	4	<.001	0.68	−5.69	−3.55	0.71
17	22.9	4	<.001	1.04	−5.00	−4.15	−0.82
18	4.6	4	.334	1.28	−3.70	−2.37	0.01
19	14.3	4	.006	0.88	−3.17	−1.10	1.69
20	17.1	4	.002	1.26	−2.36	−1.13	1.02
21	41.3	4	<.001	0.96	−1.24	0.09	2.51
22	14.9	4	.005	1.27	−2.02	−0.98	1.34
23	5.4	4	.247	1.35	−2.14	−1.06	1.28
24	57.3	4	.000	0.99	−3.64	−1.97	1.11
25	7.8	4	.098	0.94	−4.78	−3.58	−0.51
26	17.4	4	.002	1.76	−3.18	−2.21	−0.22
27	7.8	4	.101	0.98	−3.82	−2.14	1.77
28	30.7	4	<.001	1.75	−3.10	−1.90	0.28
29	12.7	4	.013	1.46	−3.62	−2.39	0.50
30	0.8	4	.936	1.63	−2.44	−1.45	0.62

Note. LRT = likelihood ratio test; AOAA = all other items as anchors.

The nonsignificant DF items are ordered based on their discrimination parameter to select anchor items for the subsequent DF analyses with different numbers of anchor items. The following items were selected as anchor items (in the order that they are used): Items 10, 11, 12, 1, 30, 5, and 6. Because cancellation across θ is not appropriate in a selection context, UIDS was used at the item level and UTDS and UETSDS at the scale level. Also UIDS and SIDS, and UTDS and STDS were compared to assess whether there is cancellation across θ and/or items. Since total scores, and not item scores, are used to compare candidates in a selection context, cancellation across items is also appropriate. The results at the item level are not tabulated.

Comparison of the SIDS and UIDS indices suggested that there is cancellation of DF across θ for some items (i.e., differences between |SIDS| and UIDS values). However, the differences were small, which indicates that cancellation across θ did not have a large impact. Figure 1 shows the ES plots for two items of the Conscientiousness scale. Item 11, “Is neat and tidy”, had the largest difference between |SIDS| and UIDS when using one anchor item, which indicates that cancellation across θ was most present with this item. The plot of Item 11 (upper panel) shows that for latent trait values below the mean (i.e., θ < 0.00) Dutch natives scored higher than non-Western immigrants and that the opposite was true for trait values above the mean (i.e., θ > 0.00). Thus, there was cancellation of DF across θ for this item. However, the differences in expected scores were relatively small. Item 21, “Keeps working on a task without interruption until it is finished”, had the largest SIDS and UIDS values in the different analyses, but the values were the highest when using three anchor items (i.e., SIDS = UIDS = 0.330). These values indicated that non-Western immigrants always scored 0.330 points higher than Dutch natives with the same latent trait value on this item. This can be seen in the plot of Item 21 (lower panel) because the gray line (i.e., non-Western immigrants) is always above the black line (i.e., Dutch natives). However, note that SIDS and UIDS values are reported in the item expected score metric and that the items have four response categories, scored 0 to 3, which suggests that the found differences are small.

Figure 1.

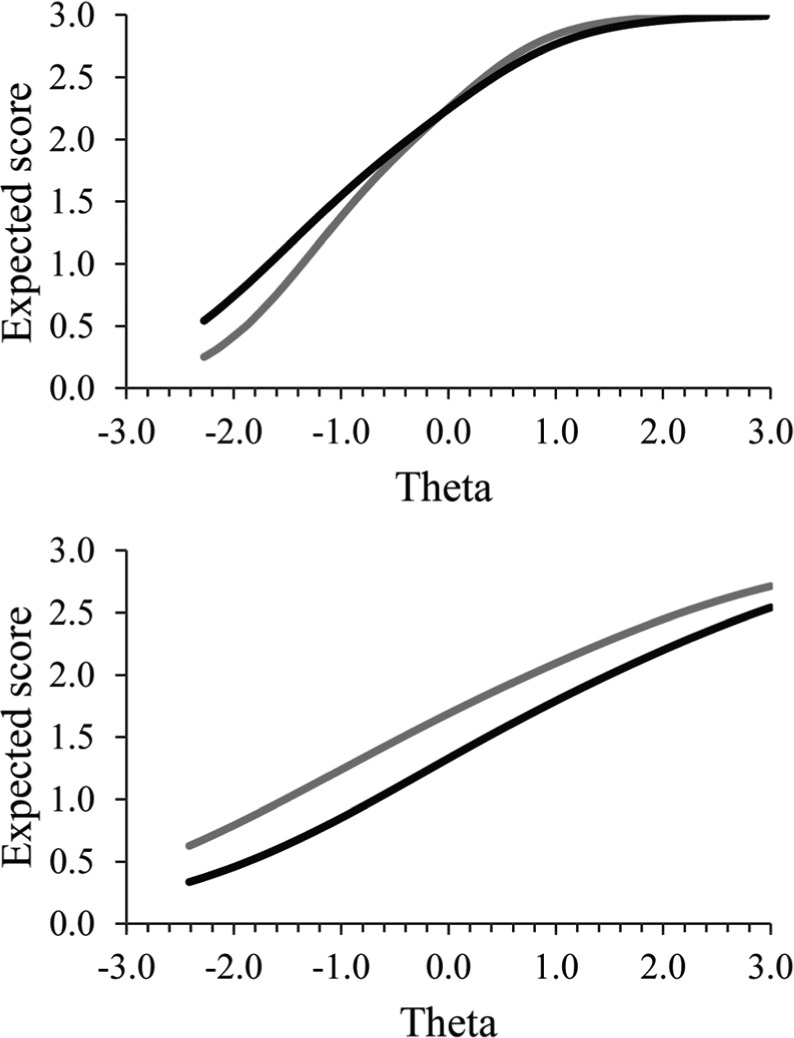
Expected score plots of Item 11, “Is neat and tidy” (upper panel; SIDS = −0.006, UIDS = 0.072; in this analysis one anchor item is used), and Item 21, “Keeps working on a task without interruption until it is finished” (lower panel; SIDS = 0.330, UIDS = 0.330; in this analysis three anchor item are used), of the Conscientiousness scale for the comparison of Dutch natives and non-Western immigrants.

Note. The gray line represents the expected scores for the non-Western immigrants (=focal group) and the black line represents the expected scores for the Dutch natives (=reference group).

Overall, the SIDS and UIDS values are comparable for all analyses. The correlations between the SIDS values across conditions were almost 1 and for the UIDS values the correlations ranged from .936 through 1, which indicates that the SIDS and UIDS values are very similar across conditions. Furthermore, the root mean squared differences across conditions ranged from .001 through .022 for the SIDS values and they ranged from .001 through .025 for the UIDS values, which indicate that the differences were very small across conditions. These results suggest that the item-level effect size indices were not much affected by using different numbers of anchor items.

Table 5 displays the test-level effect size indices when using different numbers of anchor items for the comparison between Dutch natives and non-Western immigrants. The STDS values were different when using different numbers of anchor items; they ranged from −0.682 when using seven anchor items through 0.193 when using three anchor items. An STDS value of −0.682 indicates that the non-Western immigrants scored 0.682 points lower than the Dutch natives on the Conscientiousness scale. However, since the STDS values were reported in the expected test score metric, these differences were small given the theoretical total score range of 0 to 87. This was also confirmed by the ETSSD values, which suggests that the differences are small (i.e., |ETSSD| < 0.30). Furthermore, STDS and UETSDS values were not comparable when using one, three, or five anchor items, which suggests cancellation across θ. Also, STDS and UTDS values were different, which indicates cancellation across items for those analyses. However, inspecting the ETS plots of those four analyses showed that both lines for the Dutch natives and the non-Western immigrants are almost identical, suggesting that cancellation across θ may be very small. The results of the analyses in which six and seven anchor items were used show that the STDS and UETSDS values were the same, indicating that there is no cancellation across θ at the scale level, but there might be cancellation across items. Cancellation across items was confirmed by the large differences between STDS and UTDS values for those two analyses.

Table 5.

Test-Level Effect Size Statistics for the Comparison Between Dutch Natives (Reference Group) and Non-Western Immigrants (Focal Group).

	AOAA	maxA1	maxA3	maxA5	maxA6	maxA7
STDS	−0.08	0.00	0.19	−0.09	−0.38	−0.68
UTDS	2.74	2.73	2.72	2.57	2.46	2.35
UETSDS	0.13	0.21	0.38	0.23	0.38	0.68
ETSSD	−0.01	0.00	0.02	−0.01	−0.03	−0.06

Note. AOAA = all other items as anchors; maxA1 through maxA7 = one through seven nonsignificant DF items with the highest discrimination parameter are used as anchor items; STDS = signed test difference in the sample; UTDS = unsigned test difference in the sample; UETSDS = unsigned expected test score difference in sample; ETSSD = expected test score standardized difference.

When comparing the results across analyses using different numbers of anchor items at the test level, the differences were larger compared with the differences for the item level indices. This is expected due to summing up over items at the test level. However, when considering the ETSSD values, the standardized differences were small. This suggests that also the test-level effect size indices were not much affected by using different numbers of anchor items.

Discussion

Meade (2010) concluded that “over the past two decades, significant progress has been made with methods of detecting statistically significant DF. However, a broader understanding and utilization of DF effect size is an essential next step in the progression of understanding invariance” (p. 740). In this study, we contributed to the understanding of invariance by investigating the impact on the effect size indices when using different numbers of anchor items and by investigating two different methods to select anchor items in real life assessment situations.

Most DF studies conducted the LRT with AOAA and only reported statistically (non)significant test results. In the past few years, researchers have showed that AOAA will inflate Type I error rates and that it is therefore recommended to use anchor items. Different methods have been proposed to empirically select anchor items. The power of these methods was investigated by conducting simulation studies, because with real data it is unknown which items are invariant across different groups. Furthermore, different studies showed different results with regard to which method should be used to select anchor items, also with regard to the number of anchor items that should be used. Besides using anchor items, researchers have argued that it is better to report the results of DF studies as effect size indices since they provide researchers with an idea about the effect and practical importance of statistically significant DIF. Therefore, the aim of this study was to examine the influence of using different numbers of anchor items on effect size indices when investigating DF in different assessment situations.

Since Meade and Wright (2012) recommended the “maxA5” approach after comparing 11 different methods to select anchor items, we investigated whether this approach could also be successfully applied in a real-life application with large sample sizes. Furthermore, Meade’s (2010) effect size indices were used, since there are different effect size indices for different situations. In this study, we examined the impact of using anchor items on effect size indices in two different real life assessment situations. First we compared incumbents and applicants (i.e., group mean comparison) and second we compared Dutch natives and non-Western immigrants in a selection context (i.e., comparing individuals).

The results of our study showed that using the “maxA” approach resulted in problematic results when using large samples. Woods’s (2009) rank-based was a good alternative. This approach is also simple and straightforward and can therefore be easily applied by researchers and practitioners.

Furthermore, the results suggested that the effect size indices were not influenced by using different numbers of anchor items, both when comparing incumbents and applicants and when comparing Dutch natives and non-Western immigrants. The values of the effect size indices at the item level were comparable for the different analyses in both situations. At the test level, the results were less stable, but the differences were small. Specifically, the ETSSD values were very small, regardless of the number of anchor items that were used, which indicates that the effect at the test level was very small if not negligible. This phenomenon was observed in both our empirical examples. These results were in agreement with the results obtained by Robie, Zickar, and Schmit (2001) and Stark et al. (2004). Robie et al. (2001) used the program DFITP4 (Raju, 1998) to investigate DIF and DTF for six scales from the Personal Preferences Inventory comparing applicants and incumbents. Their results showed that only a few items exhibit DIF and that there was no DF at the scale level. With regard to measurement equivalence across different ethnicity groups in a selection context, our results are in agreement with Meade (2010). He also showed in his cross-cultural example that DF might not be as large as studies so far indicated (e.g., Mitchelson, Wicher, LeBreton, & Craig, 2009; Sheppard, Han, Colarelli, Dai, & King, 2006).

Practical Implications

Based on our results we recommend using Woods’s (2009) rank-based strategy to select anchor items when investigating DF in large samples. The “maxA” approach proposed by Lopez Rivas et al. (2009) and recommended by Meade and Wright (2012) can be used when investigating DF in smaller samples.

It is difficult to recommend a fixed number of anchor items when using real data, since it is unknown beforehand which items are invariant. Based on earlier recommendations done by Lopez Rivas et al. (2009) and Woods (2009) and our results, we recommend to conduct DF analyses in which three and five anchor items are used (for scales with at least 20 items), and to compute and to compare the effect size indices both at the item and test levels. Because of the uncertainties inherent to real data, it is important to compare the results of these different analyses and to express the results in terms of effect size indices, instead of only reporting statistically significant results. This will provide researchers and practitioners an impression of the impact of using different numbers of anchor items and an impression of the practical importance of the differences in scores between groups.

UIDS and UTDS values are problematic to interpret and use when it is known that cancellation across θ occurs (i.e., |SIDS| ≠ UIDS, nonuniform DF). In that case, knowing the size of a hypothetical uniform difference does not add useful information. Furthermore, in that case SIDS is no longer useful, since the difference in ES between groups is no longer equal for everyone conditional on the latent trait. Closer to the θ value where cancellation across θ occurs, the difference between the reference group and the focal group conditional on the latent trait value will diminish. In cases where cancellation across θ occurs, we recommend to inspect the ES and ETS plots for more information.

Furthermore, while interpreting the effect size indices, we noticed that although few items may function differently for different groups, the effect at the test level is often small and negligible. When comparing groups and/or individuals across groups based on their test score, cancellation across items is appropriate. Thus, as long as the test score is of primary interest, DTF will only occur when many items in the scale exhibit uniform DIF (i.e., always favoring one group). This may, for example, occur when an item bank is used for the construction of short scales and accidently only items with uniform DIF were selected, resulting in measurement bias against one group. In this case, routinely checking effect size indices may help a researcher to get an idea about the practical importance of the differential item and test functioning.