Improving Measures via Examining the Behavior of Distractors in Multiple-Choice Tests

Abstract

The purpose of the present article was to illustrate, using an example from a national assessment, the value from analyzing the behavior of distractors in measures that engage the multiple-choice format. A secondary purpose of the present article was to illustrate four remedial actions that can potentially improve the measurement of the construct(s) under study. Participants were 2,248 individuals who took a national examination of chemistry. The behavior of the distractors was analyzed by modeling their behavior within the Rasch model. Potentially informative distractors were (a) further modeled using the partial credit model, (b) split onto separate items and retested for model fit and parsimony, (c) combined to form a “super” item or testlet, and (d) reexamined after deleting low-ability individuals who likely guessed on those informative, albeit erroneous, distractors. Results indicated that all but the item split strategies were associated with better model fit compared with the original model. The best fitted model, however, involved modeling and crediting informative distractors via the partial credit model or eliminating the responses of low-ability individuals who likely guessed on informative distractors. The implications, advantages, and disadvantages of modeling informative distractors for measurement purposes are discussed.

It is estimated that the development costs for one item on a high-stakes, statewide assessment average $1,800 to $2,000, and this development process takes at least two years (Florida Department of Education, 2009). (Koon, 2010, p. 1)

Beyond reliability and validity in measurement, which cannot be compromised, efficiency is the next most important challenge. As Koon (2010) reported above, the cost for one good item in high-stakes testing requires a vast amount of time and resources, all of which are associated with great cost. Koon and Kamata (2013) further commented on the fact that field testing of those items often results in them performing in unexpected ways, possible due to issues of bias and unfairness. The use of multiple-choice questions (MCQs) in high-stakes testing is the rule rather than the exception, and empirical evidence has linked this format to high reliability (Epstein, 2007) and also the criticism that they oftentimes assess recall rather than higher order thinking (Vahalia, Subramaniam, Marks, & De Souza, 1995). In the present study, the quality of items is traced to the qualities of the available distractors, which, in our view, play a crucial role in framing the correct response and providing proper levels of item difficulty. Using the “History of Chemistry” subscale from a national chemistry examination in Saudi Arabia, a thorough analysis of the distractors is presented along with a series of remedial means for improving the measure under study using the Rasch model (Rasch, 1961, 1980).

Distractors in Multiple-Choice Questions and Their Role in Measurement

Historically, the analysis of distractors’ behavior (i.e., the erroneous options in MCQs) has been used as a supplement to differential item functioning (DIF; Holland & Thayer, 1988; Schmitt & Dorans, 1990; Thissen, Steinberg, & Wainer, 1993) in order to potentially explain the source of DIF (Penfield, 2010; Thissen & Steinberg, 1986). Malau-Aduli and Zimitat (2012) distinguished between functional distractors in that they reflect plausible responses due to some identification with the correct response and nonfunctional distractors that are rarely chosen. The later have little contribution to measurement, and the former, however, may indirectly improve the quality of the item and result in enhanced accuracy (Haladyna & Downing, 1993). Several methods have been developed to evaluate the potentially differential behavior of distractors across groups (e.g., Banks, 2009; Green, Crone, & Folk, 1989; Penfield, 2008; Suh & Talley, 2015). The present study takes on a different approach, that is, it evaluates the consequences of misbehaving distractors on measurement, with the goal of improving measures rather than investigating group bias. In other words, the present study does not deal with achieving test fairness across populations but rather on remediating distractors that are the cause of model misfit with the ultimate goal of improving the measurement qualities of an instrument (through lowering measurement error and item misfit).

Why Is the Analysis of Distractors Important?

One can easily question the necessity to evaluate the behavior of the distractors for measurement purposes, particularly given the fact that they do not directly deal with the correct response (Levine & Drasgow, 1983). Provided that person abilities are based on the correct response only, choosing one distractor over another will not directly change the person’s score, unless of course the distractor contains relevant to the correct response information (Love, 1997). In other words, it is important to note that the correct response is considerably a function of the alternative options provided and how close they are in content to the correct response (Thissen, Steinberg, & Fitzpatrick, 1989). Furthermore, the goal of the distractor analysis is to seek any additional stochastic information that likely resides on the item, with the potential need to model them further (Bock, 1972). Figure 1 displays an item with at least one potentially informative distractor (dashed line). That distractor seems to be the preferred choice for individuals up to +0.2 logit in terms of ability and also seems to be selected by several individuals of higher ability (25%), up to +1.2 logits. One needs to qualitatively examine whether selecting this option is associated with some knowledge (distractor containing correct “partially” information) that need to be credited to individuals when evaluating their performance. This could be easily accomplished through evaluating the efficacy of a dichotomous versus a polytomous response structure (see section below on remedial actions) by use of the dichotomous Rasch model versus the partial credit model (PCM; Masters, 1982). This remedial action, among others, is described in the next section. It is important to note, however, that although the analysis is restricted to one distractor, it is very likely that a second distractor proves to also be informative. In those instances, the remedial actions implemented to one distractor should apply to all distractors that potentially contain useful information. Among distractors in Figure 1, for example, the distractor close to the x-axis has very low endorsability and, thus, as an option was likely too easy to be endorsed by individuals of any ability level (likely be a nonfunctional distractor). However, the distractor above the lowest one seems to be endorsed by about 20% of the sample, across all ability levels. Thus, this latter option may also prove to be useful for measurement purposes.

Figure 1.

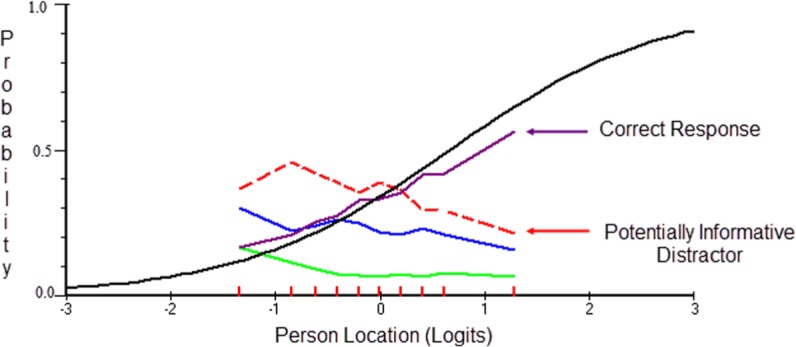
Behavior of distractors with potentially constructive (stochastic) information for measurement purposes.

Remedial Action for the Presence of Informative Distractors

For the purpose of examining the necessary actions to improve measurement based on informative distractors, the prerequisite Rasch model and the PCM need to be defined.

Rasch Model

In the family of item response theory models, the one-parameter logistic model posits that the probability of person n providing X responses (0 or 1) on item i is given by the following expression (Reise & Waller, 2009):

$$P(X_{\mathrm{ni}}=1|B_n,D_i)=\frac{e^{[-a(B_n-D_i)]}}{1+e^{[-a(B_n-D_i)]}}$$ (1)

with that probability being a function of person’s ability B_n and item’s difficulty level D_i. As noted there is only one D_i because there is only one level of difficulty per item for dichotomous items. The term e = 2.71828 is the Euler number, and a = 1.702 places the item on the normal ogive metric (Rasch model). The one-parameter model only manipulates the ability of a person and assumes that the relationship between person ability and item difficulty is consistent across items (Mantel & Haenszel, 1959). We now turn our discussion to the presentation of four remedial approaches to the problem of encountering informative distractors.

Modeling Informative Distractors Using the Partial Credit Model

One approach to dealing with distractors with information is to model that information using the PCM (Masters, 1982) compared with the dichotomous model. The difference between the two lies on the fact that the PCM model contains ordered performance levels (e.g., 0, 1, 2, 3, . . . , k) with the probability of success being defined as the ability of the person to reach the highest level k of performance. As Andrich and Styles (2011) pointed out, the item with informative distractors can be reparametrized by giving the correct response a value of 2 and the distractor with information a response of 1 (with all remaining distractors obtaining a score of 0). In that case, informative distractors contribute stochastic information to the latent variable being measured. The PCM estimated in the present study (Andrich, 2005) is as follows:

$$P(X_{\mathrm{ni}}=1|B_n,D_{\mathrm{ik}})=\frac{e^{[-a(B_n-D_{\mathrm{ik}})]}}{1+e^{[-a(B_n-D_{\mathrm{ik}})]}}$$ (2)

With the probability of correct responding 1 being a function of the ability B of person n achieving the highest level of difficulty D_k on item i. In the present conceptualization of the PCM model, a person cannot reach Level 2 without first having achieved Level 1, a phenomenon termed threshold or category disordering (Andrich, 1978; Masters, 1982). This multistep approach to estimating person abilities involves estimation of ability (theta) for each successive step, as shown below, for a partial credit item having options 0, 1, and 2. Specifically, for individuals obtaining a score of 1 instead of 0, the following must hold:

$$P(X_{\mathrm{ni}}=1|B_n,D_{i1})=\frac{e^{[-a(B_n-D{i}_1)]}}{1+e^{[-a(B_n-D_{i1})]}}$$ (3)

With D_i1 being the difficulty level from achieving a 1 instead of a 0, on item i; thus, it is the first step of the item’s difficulty. A person cannot achieve a score of 2 by being successful on this step or a score of 0 for that matter. For individuals to achieve a score of 2 instead of 1 or 0, the following must hold:

$$P(X_{\mathrm{ni}}=2|B_n,D_{i2})=\frac{e^{[-a(B_n-D{i}_2)]}}{1+e^{[-a(B_n-D_{i2})]}}$$ (4)

With D_i2 being the difficulty level from achieving a score of 2 instead of a score of 1 on item i. A score of 0 is not possible under this conceptualization. Under Masters’ (1982) formulation, the difficulty of the item refers to the intersection between successive category probability curves, while under Andrich’s (1978) conceptualization, it is the intersection between the lowest and the highest category probability curves. Thus, under Andrich’s conceptualization the difficulty of the item refers to the average of all thresholds. In the present article, we follow Andrich’s conceptualization regarding ordering of the thresholds in that in the latent continuum of person ability with d_i1 and d_i2 two successive thresholds, one cannot be successful on d_i2 without being successful on d_i1. Using a Guttman structure, Andrich further proposed that the three possible outcomes in the sample space can be {(0, 0), (1, 0), and (1, 1)}, that is, failure overall (a score of zero), partial success (a score of 1), and full success (a score of 2), but not (0, 1), which implies disordering (being successful on category k without being successful in category k− 1). For that purpose he proposed the following estimation for the conditional probabilities for failure P₀₀, partial credit P₀₁, and full credit P₁₁:

$$P_{00}=(0,0)=\frac{1}{1+e^{[-a(B_n-D_{i1})]}+e^{[-a(2B_n-D_{i1}-D_{i2})]}}$$ (5)

$$P_{10}=(1,0)=\frac{e^{[-a(B_n-D_{i1})]}}{1+e^{[-a(B_n-D_{i1})]}+e^{[-a(2B_n-D_{i1}-D_{i2})]}}$$ (6)

$$P_{11}=(1,1)=\frac{e^{[-a(2B_n-D_{i1}-D_{i2})]}}{1+e^{[-a(B_n-D_{i1})]}+e^{[-a(2B_n-D_{i1}-D_{i2})]}}$$ (7)

The above conditional probabilities are estimated to provide the scored responses of zero (0, 0), one (1, 0), and two (1, 1). An application of Andrich’s conceptualization of the PCM is described below.

Splitting Items With Informative Distractors Onto Separate Items

A second approach to dealing with informative distractors is to employ the resolved design (Andrich & Styles, 2011), through splitting the partial credit item onto two items, one with the correct option being identified by the distractor and one being identified by the original, correct response. In that case, it is expected that the item with the correct option being defined by the distractor will be easier and would require lower person ability levels, compared with the item that contained the originally correct option. A potential disadvantage of this approach would be the presentation of the same essentially item twice; instead, we recommend that the developers create a parallel item for that purpose so that the resemblance between the two items would not be apparent and would not confuse testees.

Creation of a “Super Item” or Testlet

A third approach would be to combine dichotomous items that have informative distractors onto one polytomous item with the correct and partial correct responses due to informative distractors represented as ordered thresholds¹ within a new single item (we term it super item). The formulae for creating one super item from two informative distractors have been described under the PCM (Equations 5, 6, and 7) with the second threshold describing the difficulty level of a second item (if the second item is more difficult compared with the first time). Thus, the idea of combining several items onto one polytomous item is identical to modeling a partial credit item with the number of responses being equal to the number of items combined. All these reparameterizations should be tested for efficiency using chi-square difference tests, in the case of nested models and Akaike information criterion (AIC)/Bayesian information criterion (BIC) indices in the case of nonnested models along with other evaluative criteria (e.g., unidimensionality vs. multidimensionality, misfitted items, presence of DIF, presence of DDF, etc.). In the present report, both chi-square tests and AIC/corrected AIC (AICc)/consistent AIC (CAIC) indices are shown, but the later are used for model comparison as the models tested were not nested.

Deleting Low-Ability Individuals Who Chose the Informative Distractor

A fourth approach to dealing with informative distractors is to evaluate whether the information provided by the distractors is only applicable to lower ability individuals with the choice of that distractor likely being a function of erroneous guessing,² particularly for low-ability individuals (Waller, 1989). Then, if one eliminates individuals who employed erroneous guessing through selecting specific distractors in the resolved design, the item should no longer contain any practically useful information, and it should be an easier than the previous item, as most of the high-ability individuals would answer it correctly and most of the low- or mid-ability individuals who would still select it due to guessing would have no response (as they would be eliminated using this approach). The model can then be tested for efficacy through removing individuals’ responses to that distractor using psychometric criteria. It is important to also note here that we do not recommend deleting individuals whenever there is either a model misfit or person misfit. Linacre (2010) developed a four-step procedure that should guide the elimination of person who misfit the Rasch model and advised caution toward using conventional criteria that may prove to be too strict when evaluating model fit. Curtis (2003, 2004) also advised caution and recommended evaluating other sources of misfit (e.g., DIF) before deleting persons. Keeves and Masters (1999) recommended down-weighing extreme value persons to improve estimates of model fit.

Although some of these procedures, particularly the diagnostic ones, are well known, the remedial ones have been less well communicated in the literature. For example, the differential behavior of the distractors has been the objective of a few only applied investigations (e.g., Batty, 2015) although several proper methodologies are available to conduct those analyses including the odds ratio approach (Penfield, 2010), the log-linear method (Green et al., 1989), the standardization approach (Dorans, Schmitt, & Bleistein, 1992), logistic regression (Abedi, Leon & Kao, 2008), and item response theory (Thissen, Steinberg, & Gerrard, 1986), to name a few. To our knowledge, however, the remedial actions referring to informative distractors described herein have not been fully described in the extant literature.

The purpose of the present article was to illustrate, using an example from a national assessment of chemistry, the value from analyzing the behavior of the distractors in tests that employ the MCQ format. A secondary purpose of the present article was to illustrate remedial actions that can potentially improve the measurement of the construct under study.

Empirical Study on the Assessment and Remediation of Informative Distractors on a Chemistry National Examination

Participants

Participants were 2,248 high school postgraduates who took on a science achievement test as part of their entrance to college/university. They represented one cohort of examinees only, as the yearly number of participants on the specific measure exceeds 100,000, the total who took the test during 2015. There were 1,771 females and 472 males (with five cases having missing data on gender). The mean age was 26.080 years with a standard deviation equal to 3.547 years (ranging between 21 and 43 years).

Measure and Procedures

The chemistry subscale of the “History and Nature of the Science of Chemistry” was implemented in the present study. The measure is for high school graduates who intend to apply to colleges or universities, and its content is covered in the last three grades of general secondary school. Question type varies from questions measuring comprehension, application, inference, and so on. The measure is delivered on a strict 30-minute time protocol. The mode of delivery is multiple-choice. No calculator, mobile phone, or other electronic device is allowed during the examination. Directions during testing were provided using a slide presentation, and it was emphasized that incorrect choices would not be penalized but selecting two options would immediately be linked to incorrect responding and the provision of a score of zero (National Center for Assessment in Higher Education, 2016).

Evaluation of Model Fit of Original Conceptualization of History of Chemistry Subscale

The Rasch model fit the data well as an adjusted chi-square statistic for sample size³ was nonsignificant, χ²(63) = 34.824, p = .998. Furthermore, local dependency was absent as no bivariate residual correlation exceeded an absolute value of r = .20. A principal components analysis of the residuals suggested no significant differences in level between two testlets formed by the negatively and positively loaded items, respectively, on the second principal component. Additionally, no item displayed significant DIF (uniform or nonuniform) across gender. Last, item misfit via the chi-square statistic never exceeded a modified Bonferroni significance level of .0001, suggesting proper item fit. All analyses were conducted using the RUMM2030 software (Andrich, Sheridan, & Luo, 2010), which employs the Pairwise Conditional Estimation procedure (Zwinderman, 1995).

Behavior of Distractors in the Original Conceptualization

Using as an example the History of Chemistry domain, one item⁴ stated the following:

• Historically speaking the science of chemistry commenced first with:

  1. The pioneering ideas of Democritus about the atom
  2. The pioneering ideas of Aristotle about the four elements of Empedocles including the atom
  3. The work of practical scientists in India
  4. None of the above

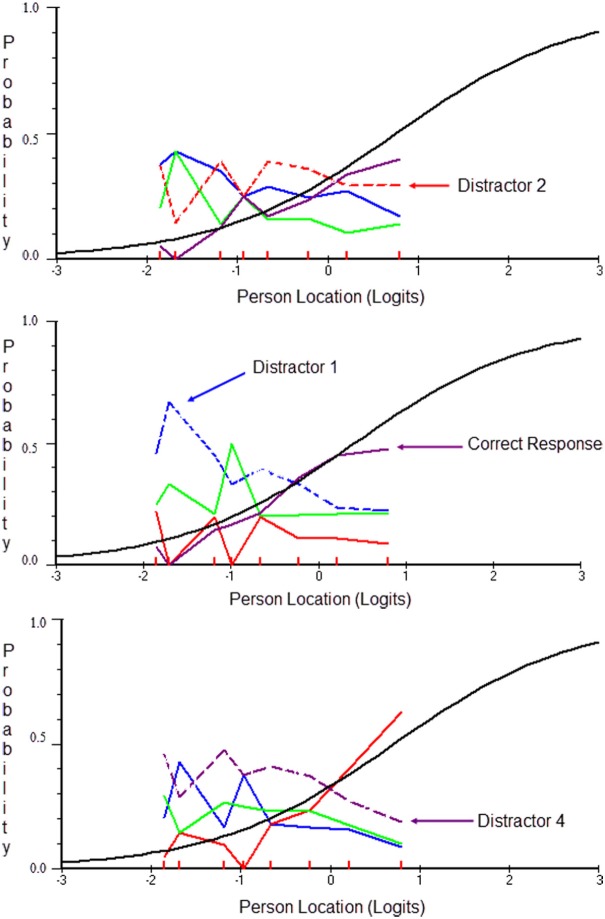
The correct option is (a) as Democritus in late 5th century set up the basic elements of a new theory where combinations of different substances form new objects. It was his ideas that gave birth to the atom. The (b) option contains correct information about the contribution of Aristotle but those ideas came later compared with Democritus (4th century). Furthermore, Aristotle built on the work of Democritus by making use of the atom. Thus, by choosing incorrect option (b) one may be tricked by the relevance of time between the two theorists or the common elements of the two theories (e.g., the atom). Consequently, although it was Democritus who came first, Aristotle’s response, if chosen, also contains knowledge about the history of chemistry that in the form of a distractor may behave as distractor 2 of Item 5 (upper graph of Figure 2). In this instance one may correctly question the fairness of a dichotomous scaling system that fails to provide credit for a partially correct response. If an extended scoring option due to informative distractors is deemed essential, rescoring the item and testing its overall contribution via a different model (e.g., PCM) to the measuring instrument is warranted (Andrich & Styles, 2011). Below there is an illustration of the four remedial actions described above and their contribution to the measuring instrument.

Figure 2.

Distractor options for Items 5, 2, and 9 from top to bottom with the selected distractor options hypothesized to contain information that is useful for measurement purposes.

Modeling Informative Distractors via the Partial Credit Model

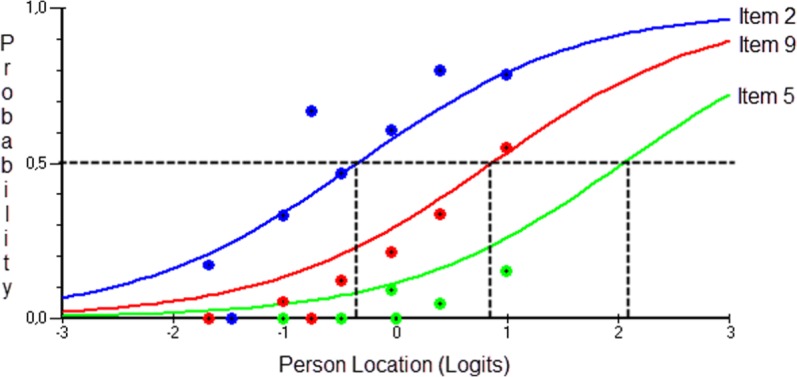
Figure 2 shows two more items (Items 2 and 9 in the middle and lower panels, respectively) for which distractors potentially contain valuable information. For Item 2 of Figure 2 (middle panel), the potentially informative distractor is Option 1 for which individuals of low (−2 logits) to average ability (0 logits) tend to favor, with only individuals with above average (>0 logits) ability levels selecting the correct response over that distractor. It is also plausible that the distractor below Distractor 1 also contains useful information but modeling more than one distractor via the PCM was beyond the scope of the present report. Last, for Item 9 (bottom graph of Figure 2), the distractor that may also contain valuable information is Option 4, whose behavior strongly resembles that of Item 5. Before proceeding with remedial actions with those items, however, it is important to test the hypothesis that these items have something in common, compared with all other items in the scale. When constructing test characteristic curves for the three identified items compared with all other items of the scale, results indicated that Items 2, 5, and 9 as a subset were significantly more difficult compared with the remaining items, treated as a second subset (see Figure 3). Specifically, the mean test difficulty for the combination involving the informative distractors was equal to 0.604 logits compared with −0.753 for the remaining items subtest. The difference between subtests was significant using a Student’s t test statistic, t(2,243) = 20.556, p < .001, and also indices of effect size (>0.8 logit; Wang & Chen, 2004). Despite the difference between the two subtests on their mean levels, there does not appear to be a third variable that is accountable for the three items with the informative distractors as their residual correlations were all below <.20 in the first principal component from the principal component analysis of the residuals, after fitting the Rasch model to the data. Thus, despite ability per se being the third variable, the residual analysis suggested that there was nothing related to the content of the items or the stem that could potentially explain their behavior (another systematic source of measurement error).

Figure 3.

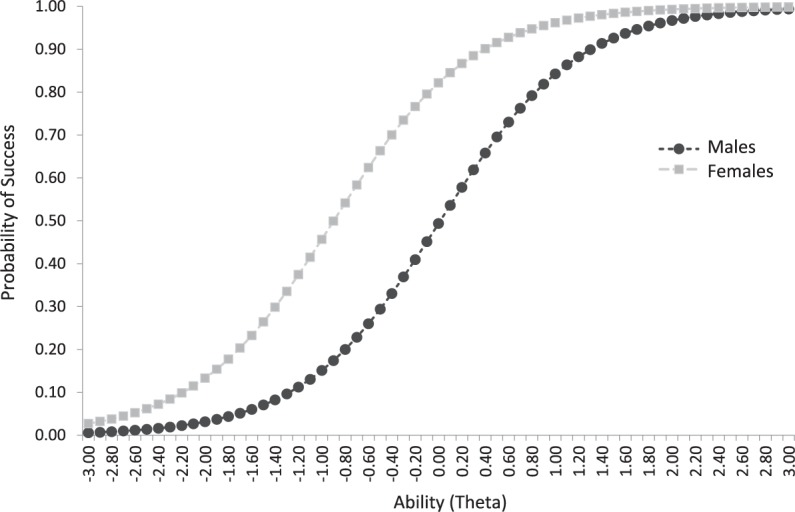
Test characteristic curves (TCCs) for subtest containing the three items with informative distractors (DDF items), compared with a subtest comprising all remaining items (Rest items).

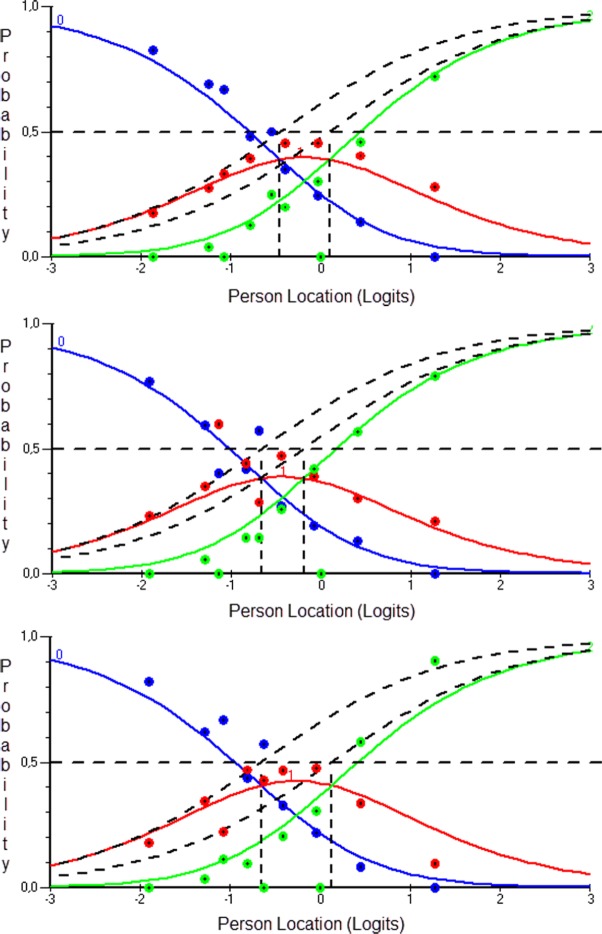
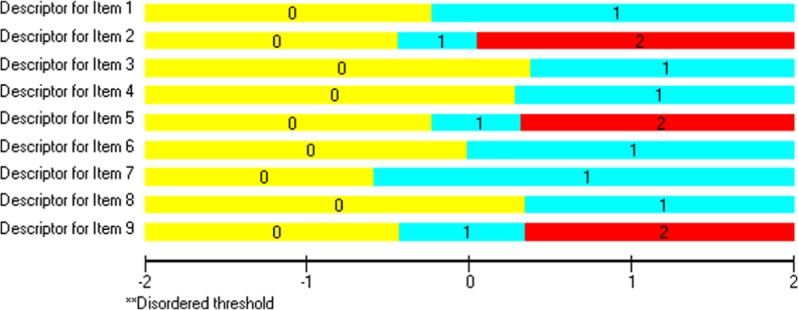
Figure 4 displays Items 5, 2, and 9, which were modeled under the PCM. It is apparent that modeling the earlier distractors as reflecting partially correct responses was supported as the mid response (value of 1) was associated with distinct thresholds with both the incorrect response zero and the fully correct response two. Specifically, for Item 5, the first (0, 1) and second thresholds (1, 2) were −0.451 and 0.045 logits, respectively. For Item 2, the first and second thresholds (0, 1) and (1, 2) were equal to −0.665 and −0.194 logits, respectively. Last, for Item 9 the first threshold (0, 1) was equal to −0.654 logits and the second (1, 2) 0.127 logits. Based on effect size conventions of differences in ability (Wang & Chen, 2004), Item 9 thresholds were associated with a medium size difference (i.e., exceeded 0.5 logits). Figure 5 shows that the three new items modeled under the PCM provided thresholds that were ordered and distinct from each other, suggesting valuable information between the originally correct and incorrect responses that necessitated further modeling. When looked on individually, each of the items that were modeled under the PCM provided improved fit to the data of the Rasch model compared with the original formulation (see Table 1, Models 2, 3, and 4, compared with original model). Furthermore, when combinations of the three distractor-informative items were modeled together, it was the model with Items 2 and 9 modeled as partial credit items, that provided the best fit to the data, χ²(72) = 127.434, CAIC = −497.903, compared with all other models.

Figure 4.

Providing partial credit for Items 5 (upper panel), 2 (middle panel), and 9 (lower panel) of the history of chemistry subscale.

Figure 5.

Partial credit model for estimating the efficacy of the hypothesized “informative” distractors.

Note. The stochastic contribution of each of the distractors of Items 2, 5, and 9 is evident. No disordering was also observed across categories for any item.

Table 1.

Summary of Model Fit for Differently Parameterized Models.

Model description	Chi-square	df	CAIC	AIC	AICc
1. Original 9-item model	151.555	63	−395.615	25.555	29.374
2. Item 2 modeled as partial credit	135.353	72	−489.985	−8.647	−3.649
3. Item 5 modeled as partial credit	139.915	72	−485.422	−4.085	0.194
4. Item 9 modeled as partial credit	131.852	72	−493.485	−12.148	−7.149
5. Items 2 and 9 modeled as partial credit	127.434	72	−497.903	−16.566	−11.567
6. Items 2, 5 and 9 modeled as partial credit	134.298	72	−491.040	−9.702	−4.703
7. Super item for Items 2, 5, and 9	127.874	49	−297.703	29.874	32.179
8. Item split for Items 2, 5, and 9	354.380	96	−479.403	162.380	171.338
9. Deleting low achievers who potentially guessed by choosing erroneous, albeit informative, distractors	123.570	70	−454.568	−16.430	−9.067

Note. Best model is in italic based on the corrected AIC index for evaluating parsimony. AIC = Akaike information criterion; CAIC = consistent AIC (Anderson, Burnham, & White, 1998); AICc = corrected AIC.

Splitting Items Having Informative Distractors

One approach to evaluating the full measure, also in line with modeling the data via the PCM, deals with applying Andrich and Styles’ (2011) resolved design through splitting the items with informative distractors onto separate items. Thus, based on the behavior of the distractors of Items 2, 5, and 9, these items were split, comprising three new items. Results indicated that although the new items fit the Rasch model (no significant misfit was observed for any one of the new items by use of the chi-square statistic), the full model was not supported based on parsimony as both AIC, AICc, and CAIC indices suggested over parameterization with the addition of, respectively, little information compared with their degrees of freedom. Thus, splitting items was not proved to be the most efficient practice for measurement purposes (using parsimony as the driving standard), with the current dataset.

Creating a Polytomous Item From Items With Informative Distractors

Andrich and Styles (2011) proposed that items for which distractors are informative can be combined, particularly if they contain other similar types of information, to form a single item with the number of thresholds equal to the number of correct and partially correct options minus one. As discussed above, Items 2, 5, and 9 were as a testlet significantly different (more difficult) from the remaining items but, content wise, did not seem to share some specific information (through evaluating residual correlations using the first principal component [PC] of the residuals). Thus, they were modeled as a “super item,” which was one of the most difficult items of the measure. Figure 6 displays the threshold probabilities for each of the three combined items, which were −.349 (previously Item 2), .861 (previously Item 9), and 2.045 (previously Item 5). Overall model fit suggested less than optimal fit compared with all other models as albeit having a small chi-square value, the number of degrees of freedom was also substantively smaller compared with all other models. Thus, again with the present data set, this approach did not significantly improve model fit, using parsimony as the golden criterion.

Figure 6.

Creation of a “super item” from combining the correct responses of Items 2, 9, and 5, respectively.

Note. The curves model threshold probabilities at 50% success levels as per the Rasch model.

Deleting Individuals of Low Ability Who Likely Guessed by Selecting Informative, Albeit Erroneous, Distractors: Application of Tailored Testing

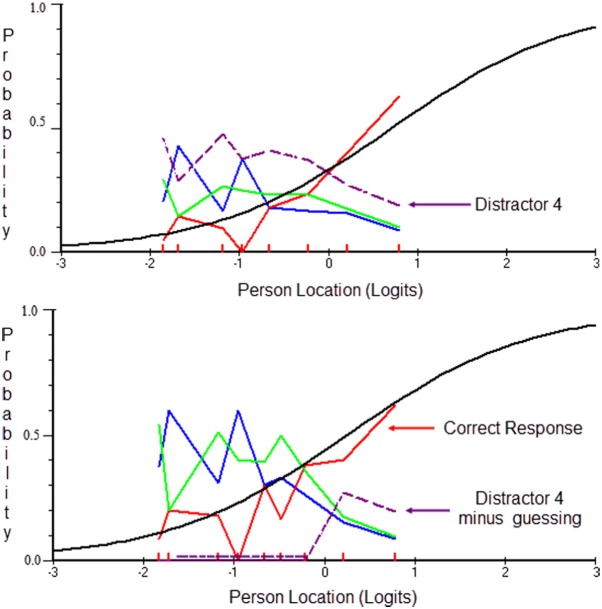
Using the deletion of individuals who likely guessed approach, we selected individuals who were below average competency (i.e., less than 0 logits on the theta scale continuum) who also selected Distractor 4 of Item 9. The number of participants eliminated from the specific option of Item 9 was n = 827 with the analysis for Item 9 involving 1,421, compared with the original 2,248 cases. Figure 7 displays Item 9 with the full data set (upper panel) and after deleting low-ability individuals who likely guessed on the informative distractor (lower panel). Results obtained using this approach indicated excellent model fit, at equivalent levels to that of the PCM of Items 2 and 9. Thus, the elimination of individuals’ responses on the distractor that potentially is a cause of concern essentially eliminates the additional information due to the distractor and results in good model fit for the Rasch model (for which predicted guessing⁵ for specifically low-ability individuals would likely result to misfit due to not modeling the lower asymptote). Thus, this approach was also associated with improved model fit and low levels of measurement error, and was among the best fitted models, but not the most parsimonious based on AIC, AICc, and CAIC.

Figure 7.

Item 9 with original Distractor 4 (upper panel) and corrected Distractor 4 through eliminating individuals of low ability (below 0 logits), who selected Distractor Option 4.

Note. Approximately 36.8 of the participants’ scores on Option 4 were eliminated using that approach. Thus, the full analysis involved the original sample of 2,248 individuals but, specifically Item 9, Option 4 had missing data on n = 827 participants.

Discussion

The purpose of the present article was to illustrate, using an example from a national assessment, the value from analyzing the behavior of the distractors in tests that employ the multiple-choice format. A secondary purpose of the present article was to illustrate remedial actions that can potentially improve the measurement of the construct under study.

The first important finding was the fact that the thorough analysis of the behavior of the distractors in the present national assessment was associated with valuable information for measurement purposes. Among remedial actions, the use of the PCM proved to be the best strategy to improve the fit of the Rasch model and significantly lower measurement error using two potential pathways. The first involves investigating the presence of potentially informative distractors which are then provided credit under the PCM model. The second involves creating super items using the same idea in that a partial credit item is formed using as the number of thresholds the number of the combined items minus one. Using the first parameterization informative distractors are modeled, using the second, informative distractors are ignored, and the items having deleterious, measurement-wise information are modeled in a combined format assuming they share common information (at least across the ability continuum).

A secondary approach, that of splitting items with informative distractors as separate items, may be useful for identifying how well this approach improves measurement. In the present study, the information provided by the distractors did not suggest the need to model them as separate items; however, this finding pertains only to the specifics of the current sample and measure. We cannot predict how successful this strategy may be with other data but we recommend that it can be used heuristically with potentially beneficial effects. In other domains, the splitting of distractors and their use as separate items may prove to be beneficial through tapping an underlying trait, previously unknown.

Last, the post hoc strategy of tailored testing (English, Reckase, & Patience, 1977; Lord, 1971; Urry, 1977) through deleting responses of low achievers on hypothetically guessed distractors, although proved to be efficacious for measurement purposes, is nevertheless associated with the production of missing data and related consequences. For example, differences in personality may represent a salient third variable that may govern responses to some measures. Individuals who guess may be prone to taking chances, compared with those who do not risk or gamble over an item. The above implies the presence of systematic measurement error in that, if the data are not missing completely at random, item parameters may be biased (Wolkowitz & Skorupski, 2013). One potential strategy that may have precluded individuals from guessing is that of providing negative marking for incorrect responses. Although this strategy will be efficacious for guessing without any prior knowledge, it will unfairly penalize individuals who possess some knowledge at that item but, due to uncertainty, will choose not to respond to avoid the penalty of negative marking. In this direction Bond et al. (2013) recently recommended the use of “elimination testing” an alternative form of MCQs for which partial knowledge is encouraged and rewarded. Nevertheless, this approach of tailored testing is recommended with reservations as both the idea of guessing is based on statistical rather than empirical criteria and the fact that persons are eliminated due to model misfit rather than strictly speaking methodological criteria (e.g., exclusionary criteria of a study) warrants further attention.

The recommended procedures and applied findings in the present article may be limited for several reasons. First, the method of estimating the PCM used herein followed the work of Andrich (1978, 2005), which posits that threshold disordering (also termed reversed deltas) is both a nuisance and a problem of measurement (see also Nijsten, Sampogna, Chren, & Abeni, 2006; Nilsson, Sunnerhagen, & Grimby, 2007; Zhu, Timm, & Ainsworth, 2001). The Andrich approach contradicts the ideas of other researchers who do not consider disordering a problem of model misfit (Linacre, 1991; Masters, 1982), or as indicative of a flawed measurement instrument (Adams, Wu, & Wilson, 2012). Furthermore, the Andrich approach is one among several estimation approaches to the difficulty of the items (e.g., Agresti, 1990; Andersen, 1977; Masters, 1980; Molenaar, 1983; Samejima, 1969; Wilson, 1992; Wilson & Adams, 1993, 1995) and places an ordering requirement over the thresholds, which is more in accord with the partial credit formulation, whereas others did not specifically comment on the ordering of the thresholds (see Adams et al., 2012, for a thorough discussion regarding the Andrich derivations).⁶ Under this conceptualization, data that follow the Guttmann pattern (0, 1) in the sample space are automatically eliminated and are treated as missing. Second, model misfit and decision making regarding fit and evaluation could potentially be hindered by the excessive power of the omnibus chi-square statistic given the large sample size. Thus, several significant findings that pointed to misfit could be well attributed to Type I errors.

Overall, the present study adds to the literature that item-based distractor analysis (beyond that related to differential distractor functioning) is an extremely useful practice that may be associated with improved measures. This finding agrees with previous literature that found value to linking instruments through using informative distractors (Kim, 2006). For example, Kim’s study suggested that the number of required items for efficient linking was dramatically reduced when one models the information from distractors.

In the future one may attempt to use an alternative to the PCMs that impose different assumptions in order to evaluate model fit. One such case is the sequential model (Molenaar, 1983) for which there is a dependency of each subsequent threshold on the previous one or one of the few graded response models (e.g., Agresti, 1990; Samejima, 1969), which do not allow for disordering. Other formulations have been recommended by Adams and colleagues and are available via different software (e.g., ConQuest; Wu, Adams, & Wilson, 1997). The number of distractors and their effect on measurement is another venue for future research as fewer options have been associated with enhanced achievement (Schneid, Armour, Park, Yudkowsky, & Bordage, 2014) and practicality (Haladyna, Downing, & Rodriguez, 2002; Tarrant, Ware, & Mohammed, 2009). Furthermore, designing the MCQs to contain the “none of the above” option has been associated with enhanced discrimination through increasing item difficulties, if that is desirable (DiBattista, Sinnige-Egger, & Fortuna, 2014).