Different Approaches to Covariate Inclusion in the Mixture Rasch Model

Abstract

The present study investigates different approaches to adding covariates and the impact in fitting mixture item response theory models. Mixture item response theory models serve as an important methodology for tackling several psychometric issues in test development, including the detection of latent differential item functioning. A Monte Carlo simulation study is conducted in which data generated according to a two-class mixture Rasch model with both dichotomous and continuous covariates are fitted to several mixture Rasch models with misspecified covariates to examine the effects of covariate inclusion on model parameter estimation. In addition, both complete response data and incomplete response data with different types of missingness are considered in the present study in order to simulate practical assessment settings. Parameter estimation is carried out within a Bayesian framework vis-à-vis Markov chain Monte Carlo algorithms.

In a wide variety of empirical studies in behavioral science and education, collateral information is collected in addition to the variables of primary interest to the researchers. This type of collateral information, also referred to as covariates in literature, usually contains background characteristics such as gender, ethnicity, and years of education. Although these types of “outside variables” are sometimes ignored in statistical modeling, it is believed that they may potentially have important relations with the modeled variables of primary interest. The present study is an investigation of the potential benefits and limitations of including such covariate information in mixture item response theory (IRT) modeling, in complete and incomplete response data scenarios.

Mixture IRT models, which combine IRT and latent class analysis (LCA), have been used in psychometric research for analyzing item response data that may violate underlying assumptions of either modeling approach (Rost 1990). Whereas IRT models assume the latent variable, a person’s latent trait, to be continuous, models in LCA framework assume discrete latent classes underlying item responses. As a combination of the two modeling approaches, mixture IRT models estimate both the examinees’ continuous latent trait and latent class membership simultaneously.

The mixture IRT modeling approach has been applied to tackle such psychometric issues in test development as the identification of items with latent differential item functioning (DIF; e.g., Cohen & Bolt, 2005), and the detection of testing speededness (e.g., Bolt, Cohen, & Wollack, 2002). Furthermore, this approach has also been applied to practical situations. For instance, in psychopathological testing (e.g., Finch & Pierson, 2011), researchers and clinicians have applied mixture IRT models to assign subjects to their most likely type of behavior disorders for diagnostic purposes from which an intervention program may be implemented.

As the most commonly used mixture IRT model, the mixture Rasch model (MRM) was first introduced by Rost (1990), Kelderman and Macready (1990), and Mislevy and Verhelst (1990). Basically, the idea of MRM is to incorporate the Rasch model in a discrete mixture of latent subgroups (i.e., latent classes), with the Rasch model fitted to each class but with different item parameters across latent classes (Rost, 1990). As a member of the mixture model family, the MRM shares many similarities with other mixture models (e.g., growth/factor mixture models). Small latent class separation sometimes poses challenges for model parameter estimation and latent class identification. Thus, the inclusion of covariates has been proposed in the mixture IRT, as well as in other mixture modeling frameworks, in order to achieve different purposes such as obtaining more accurate model parameter estimates, latent class assignment, and enumeration of latent classes (e.g., Lubke & Muthén, 2005; Smit, Kelderman, & van der Flier, 1999, 2000).

Mislevy (1987) explored the incorporation of covariates in non-mixture IRT models and found that covariate information may increase the precision of model parameter estimation in the same amount as adding 2 to 6 items, and it accounts for as much as one third of the population variance in educational assessment. This explanatory IRT modeling approach has been elaborated later (e.g., Adams, Wilson, & Wu, 1997; Wilson & De Boeck, 2004). Item or person related covariates are included for different purposes such as explaining estimated effects or improving parameter estimation.

In mixture IRT, covariates have been added to achieve similar goals as those in non-mixture IRT models. For example, Smit et al. (1999, 2000) explored the use of covariates in the mixture Rasch and two-parameter-logistic IRT models by manipulating the association between latent class membership and a dichotomous covariate in terms of bivariate probability. Samuelsen (2005) further explored this issue in the context of DIF. More recently, latent class membership in the MRM was modeled using logistic regression with a dichotomous covariate as the sole predictor of latent class membership (Dai, 2013). Tay, Newman, and Vermunt (2011) conducted a real data analysis using both continuous and dichotomous covariates as predictors of the latent class membership.

All previous studies have demonstrated that incorporating potentially effective covariates may help the recovery of latent class structure, and obtain more accurate model parameter estimates. However, certain important areas still have not been thoroughly explored. First, all relevant simulation work in mixture IRT modeling has exclusively focused on dichotomous covariate related to the latent class membership, and none included continuous covariate. Second, the possibilities of relating dichotomous covariate with other model parameters have not been explored, and no information is available about the comparison among different approaches to including both dichotomous and continuous covariates in the model. Third, none of previous studies provided information about overall model fit and selection with respect to covariate inclusion. Fourth, all previous studies were based on complete item response data.

Therefore, the purpose of the present study is to examine the impact of different approaches to incorporating covariates in mixture IRT models on model parameter estimation based on complete and incomplete item response data sets. Both dichotomous and continuous covariates are included in the present study as predictors for the latent class membership and the person ability parameters. The impact of covariate specification is compared and analyzed in terms of model parameter recovery, latent class identification, and the relative overall model fit among competing models.

Method

The Data Generating Model and Alternative Models

In the present study, the covariates enter the MRM either as predictors of π_jg, the probability of person j belonging to latent class g (i.e., $\sum _{g=1}^G{\pi }_{\mathrm{jg}}=1$), or as predictors of latent trait θ_jg. In the true model, which is used for data generation, a dichotomous covariate enters the model as a predictor of π_jg through a logistic function as follows.

$${\pi }_{\mathrm{jg}}=\frac{\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j)}{\sum _{g=1}^G\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j)},$$

where D_j indicates the dichotomous covariate, such as gender, and β_0g and β_1g are corresponding regression coefficients in the logistic function. For model identification purpose, both β₀₁ and β₁₁ are fixed as 0 for latent class 1. Two latent classes are assumed (G = 2) in the current simulation. Further, a continuous covariate enters the MRM as a predictor of the latent ability through a linear function:

$${\theta }_{\mathrm{jg}}={\alpha }_{0g}+{\alpha }_{1g}{C}_j+e_{\mathrm{jg}},$$

where C_j indicates the continuous covariate (e.g., intelligence or motivation), α_0g and α_1g are the intercept and the slope of the latent regression model corresponding to latent group g, and e_jg is the error term with a distributional assumption of $e_{\mathrm{jg}}~N(0,{\sigma }_{\mathrm{eg}}^2)$. Equation (3) gives the mathematical specification of the complete version of the data generating model:

$$P(X_{ij}=1|{\theta }_{jg},b_{ig})=\sum _g\left(\frac{1}{J}{\displaystyle \sum _J\frac{\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j)}{{\displaystyle \sum _{g=1}^G\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j)}}}\right)\left(\frac{1}{1+\exp \{-[({\alpha }_{0g}+{\alpha }_{1g}{C}_j+e_{jg})-b_{ig}]\}}\right)$$

Five alternative models with misspecified covariate effects are included in the present study to fit the simulated data. Table 1 presents the mathematical functions of all the six models. The model name abbreviations are used in the tables and figures presented in the Simulation Results section.

Table 1.

True Data-Generating Model and Alternative Models.

Model type	Model specification
True model (TM)	the MRM with ${\pi }_{\mathrm{jg}}=\frac{\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j)}{\sum _{g=1}^G\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j)}$ and ${\theta }_{\mathrm{jg}}={\alpha }_{0g}+{\alpha }_{1g}{C}_j+e_{\mathrm{jg}}$ where β01 = β11 = 0
Overspecified model (OM)	the MRM with ${\pi }_{\mathrm{jg}}=\frac{\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j+{\beta }_{2g}{C}_j)}{\sum _{g=1}^G\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j+{\beta }_{2g}{C}_j)}$ and ${\theta }_{\mathrm{jg}}={\alpha }_{0g}+{\alpha }_{1g}{C}_j+{\alpha }_{2g}{D}_j+e_{\mathrm{jg}}$ where β01 = β11 =β21 = 0
Model with mismatch covariates (MISM)	the MRM with ${\pi }_{\mathrm{jg}}=\frac{\exp ({\beta }_{0g}+{\beta }_{1g}{C}_j)}{\sum _{g=1}^G\exp ({\beta }_{0g}+{\beta }_{1g}{C}_j)}$ and ${\theta }_{\mathrm{jg}}={\alpha }_{0g}+{\alpha }_{1g}{D}_j+e_{\mathrm{jg}}$ where β01 = β11 = 0
Underspecified models (UNM)
1. UNM-N	The MRM without covariates
2. UNM-D	The MRM with ${\pi }_{\mathrm{jg}}=\frac{\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j)}{\sum _{g=1}^G\exp ({\beta }_{0g}+{\beta }_{1g}{D}_j)}$ where β01 = β11 = 0
3. UNM-C	The MRM with ${\theta }_{\mathrm{jg}}={\alpha }_{0g}+{\alpha }_{1g}{C}_j+e_{\mathrm{jg}}$

Note. MRM = mixture Rasch model.

Simulation Design

To keep the simulation study manageable, certain factors are held constant in the simulation design. The number of latent classes is set at two according to previous simulations in this line of research (e.g., Smit et al., 1999, 2000). A total of 2,000 respondents responding to 30 dichotomously-scored items are simulated. It is a reasonable test length that is often seen in educational assessments. Also, the number of respondents is fixed at 2,000 to ensure that the model parameters could be accurately estimated so that the analysis of model performance would not be affected by the imprecision in model parameter estimates. The person parameters are simulated from a standard normal distribution, Normal(0, 1), for one latent class and a normal distribution, Normal(1, 1), for the other. The person parameters may be drawn from the same distributions or different distributions, as suggested by previous mixture IRT literature (e.g., Dai, 2013; Li, Cohen, Kim, & Cho, 2009). In the present study, a mean difference of 1 is set for the person parameters of the two latent classes so that the estimation of the MRM can converge more easily. Some previous studies have manipulated test length and the number of respondents. However, because the present study focuses on different approaches to covariate inclusion and their corresponding impacts, these two factors are fixed to make the current simulation study manageable.

Additionally, the proportions of the dichotomous covariate are set to be .30 and .70 based on a previous study (Dai, 2013). In other words, 30% of the respondents are assigned a value of 0 and 70% are assigned a value of 1 on the dichotomous covariate. The values of the continuous covariate are drawn from the standard normal distribution respectively for the two latent classes.

Other factors, including the mixing proportion (i.e., Prop), the average DIF effect size (i.e., DIF), the strength of relations between covariates and model parameters (i.e., OR [odds ratio] and Corr), the response data completeness (i.e., Data), and the types of covariate inclusion approaches for comparison purpose (i.e., Model), are manipulated. The abbreviations of these factors shown in the parentheses are used in the tables and figures presented in later sections.

As for the mixing proportion, two levels, LC1%:LC2% = 50%:50% and 30%:70%, are considered. Extremely unequal mixes of latent classes are not included in the present study so as to ensure that the parameters could be accurately recovered for each latent group. For the strength of relations between covariates and model parameters, odds ratios are used to indicate the magnitude of association between the dichotomous covariate and the latent class membership (Dai, 2013). In the DIF context, the odds ratio indexes the strength of the relation between manifest grouping variables and latent classes:

$$\mathrm{odds\; ratio}(\mathrm{OR})=\frac{(P(g=1|D_j=0)/P(g=2|D_j=0))}{(P(g=1|D_j=1)/P(g=2|D_j=1))}.$$

Specifically, when OR equals 1, the covariate has no effect on the latent class membership; while the OR equals 10, their relation is fairly strong. Regarding the relation between the continuous covariate and the latent trait, α_1g denotes the magnitude of the correlation. The strength of the correlation is also manipulated at two level as either weak (i.e., .20), or strong (i.e., .80).

Item parameters are generated respectively from the standard normal distribution and then two levels of average DIF effect sizes (i.e., the mean of |b_i1-b_i2|) are created. When the average DIF effect size equals 1.5, 80% of the items have a difference in item difficulty greater than 1.0 between the two latent classes; when the average DIF effect size equals 1.0, 40% have a difference greater than 1.0. These two DIF effect size levels are designed based on Zwick and Ercikan’s (1989) standards (i.e., negligible DIF: item difficulty differs less than 0.5; moderate DIF: item difficulty differs by 0.5; and large DIF: item difficulty differs by 1.0) and our preliminary study in consideration of model convergence in both complete and missing data scenarios. The selected average DIF size levels in the present simulation are quite large to ensure that the latent structure and parameters could be accurately recovered. The generated item parameters represent a wide range of parameter values observed in operational settings.

Additionally, both complete and incomplete response data are simulated, because missing data scenarios are prevalent in practical assessment settings, and it is believed that covariate inclusion could compensate for the sparse information in the response data and hence improve the model parameter estimation. The reasons for missing responses may generally be classified into two major categories: missingness by test design such as using matrix-sampled booklets, and nonresponse such as with omitted and not-reached items (Ludlow & O’Leary, 1999). Not-reached items usually occur when examinees fail to complete a test within a given time, whereas omitted items are associated with examinees’ low ability levels or lack of motivation in low-stakes assessments (e.g., De Ayala, Plake, & Impara, 2001). In this study, two types of missing data are of primary interest: the missingness by design through balanced incomplete block spiraling (BIB) which is implemented in many large-scale assessments, such as the National Assessment of Educational Progress (NAEP); and the missingness by omitted items with low-ability individuals omitting difficult items which are essentially conditional missing. The not-reached item scenario is not considered in the present study because it is suggested that not-reached items are not used in item calibration or scaling in practical settings (Lord, 1980). In the current simulation, the missingness by test design is considered as missing completely at random, whereas the nonresponse by omitted items is considered missing not at random (Finch, 2008).

For missingness by the booklet design, one condition is simulated based on previous research (e.g., von Davier, Gonzalez, & Mislevy, 2009) reflecting practical test settings (i.e., NAEP; National Center for Education Statistics, 2009): items are randomly assigned to one of three blocks named A, B, and C, and each person responds to two of these blocks (i.e., a total of 20 items out of 30 items) such that the booklets are organized as AB, BC and CA, to which are responded by 667, 667, and 666 examinees, respectively. The total proportion of missing data is .33. Regarding the other type of missingness, omitted responses, previous literature indicates that this type of missingness usually affects 10% to 50% of the items in a test (e.g., Chen & Jiao, 2012). Thus, the omitted responses are simulated according to the upper bound: a total of 400 respondents with the lowest ability omit 50% of the most difficult items (i.e., 15 items) corresponding to the latent class the person belongs to. This leads to a total proportion of missing data of .10. In both types of missingness, missing data only occur in the item responses but not in the covariate information.

In summary, all the levels of the manipulated factors are carefully chosen based on both the previous literature in this line of research and the preliminary simulation runs. Certain extreme levels, such as a large amount of missing data (e.g., 60%), extremely unequal latent classes (e.g., 15%:85%) and small DIF size (e.g., 0.5), are excluded from the present design because they have been found to result in serious convergence issues (i.e., non-mixing or within chain label switching) in the preliminary study. Table 2 summarizes the fixed and manipulated factors and their corresponding levels. The present study includes 2 × 2 × 2 × 2 × 3 = 48 simulation conditions. With 25 data sets simulated for each study condition, 1,200 data sets are generated. For each data set, 6 models are used to fit the data. Thus, there are a total of 6 × 48 = 288 simulation cells with 25 × 288 = 7,200 replications. In the preliminary study, 100 replications are run in one condition for the data-generating model. The summary statistics show that there is little fluctuation in the standard error and bias of model parameter estimates after the number of replications exceeds 20. Considering the large amount of time required for Bayesian estimation, 25 replications per cell are used in the present study.

Table 2.

Fixed and Manipulated Factors and Their Corresponding Levels in the Simulation.

Factors	Values
Fixed factors
Number of latent classes	2
Test length	30
Sample size	2,000
Distribution of subjects’ latent ability	LC1: N(0,1); LC2: N(1,1)
Distribution of covariates	Dichotomous: 30%:70% Continuous: LC1: N(0,1); LC2: N(0,1)
Manipulated factors
Model type (6 models)	True model Overspecified model Underspecified models (3 models) A model with mismatching covariates
Mixing proportion (LC1%; LC2%)	(50%; 50%) (30%; 70%)
Strength of the relation between Dj and πjg	Strong (OR = 10) Weak (OR = 1)
Strength of the relation between Cj and θjg	LC1: α11 = .2; LC2: α12 = .2 LC1: α11 = .8; LC2: α12 = .8
Average DIF (i.e., the mean of |bi1-bi2|)	1.5 1.0
Response data completeness (3 types)	Complete data Incomplete data with booklet design Incomplete data with conditional omitted response

Note. LC = latent class; OR = odds ratio; DIF = differential item functioning.

Parameter Estimation

In this study, R2WinBUGS package in R 2.15.2 is employed to interface with WinBUGS 1.4 to carry out the Bayesian estimation of model parameters. The starting values for all model parameters are randomly generated by WinBUGS. The estimates of item and person parameters are the means over the sampled iterations starting from the next iteration after the burn-in period (Kim & Bolt, 2007). For the latent class membership, the estimates are the modes of the sampled iterations after burn-in. To derive the posterior distributions for each model parameter, the following prior distributions are used for the estimation of the data generating model:

$$\begin{array}{cc}\hfill b_{i1}~\mathrm{Normal}(0,1)\hfill & \hfill {\beta }_{02}~\mathrm{Normal}(0,1)\hfill \\ \multicolumn{1}{c}{b_{i2}-b_{i1}~\mathrm{Normal}(0,.5)}& \hfill {\beta }_{12}~\mathrm{Normal}(0,1)\hfill \\ \multicolumn{1}{c}{{\tau }_g~\mathrm{Gamma}(.5,1)}& \hfill {\alpha }_{0g}~\mathrm{Normal}(0,1)\hfill \\ \multicolumn{1}{c}{}& \hfill {\alpha }_{1g}~\mathrm{Normal}(0,1)\hfill \end{array}$$

where G = 2. As the person parameter θ_jg is decomposed as shown in Equation (2), the intercept parameter, slope parameter, and variance of the error term are estimated instead of θ_jg. τ_g indicates the precision of the error term with ${\tau }_g=1/{\sigma }_{\mathrm{eg}}^2$. For the MRM without covariates, additional prior distributions are used:

$$\begin{array}{c}{\theta }_{\mathrm{jg}}~\mathrm{Normal}({\mu }_g,{\tau }_g)\hfill \\ {\mu }_g~\mathrm{Normal}(0,1)\hfill \\ ({\pi }_1,{\pi }_2)~\mathrm{Dirichlet}(5,5)\hfill \end{array}$$

These prior distributions are not highly informative. They are selected based on relevant research (e.g., Cho & Cohen, 2010) and the distributions for data generation used in the present study.

Two chains of 31,000 iterations are run, and the burn-in cycle for each chain is 6,000. To reduce serial dependencies across iterations, a thinning of 5 is used. Thus, the final posterior sample size is 10,000 on which model estimates are based. No convergence problems have been observed in any replications.

Model Performance

The model performance is evaluated in terms of three outcomes: (a) the latent group classification accuracy, (b) the parameter recovery accuracy, and (c) the overall model fit as indicated by the proportion of correct model selections.

The accuracy of latent group classification is assessed using the proportion of subjects that are assigned to their true latent class based on their estimated latent class membership. The recovery of model parameters is evaluated in terms of (a) the proportion of replications for which the 95% confidence interval around the item and person parameter estimates captured the true value and (b) the bias, the standard error (SE) and the root mean squared error (RMSE) of the item and person parameter estimates.

The following fit statistics are also obtained for each model under different simulation conditions: Akaike’s information criterion (AIC; Akaike, 1974), Bayesian Information Criterion (BIC; Schwarz, 1978), a correction of AIC based on sample size and the number of parameters (AICc; Burnham & Anderson, 2002), the consistent AIC (CAIC; Bozdogan, 1993), the sample-size adjusted BIC (SABIC; Sclove, 1987) and deviance information criterion (DIC; Spiegelhalter, Best, Carlin, & van der Linden, 2002).

Some research (e.g., Li et al., 2009) has recommended the use of BIC for mixture distribution model selection; however, the choice of model fit indices is still inconclusive because the performance of overall fit indices is sometimes model- and design-specific. In the present study, 6 indices are calculated in R and summarized in order to provide a comprehensive overview of the model fit with regard to different approaches to covariate inclusion in the MRM.

Simulation Results

For all the outcome measures, descriptive statistics are provided in this section. In order to identify statistically significant effects of the manipulated factors on the model performance (except overall model fit), several repeated-measures analyses of variance (ANOVAs) were performed. The manipulated factors, including mixing proportion, strength of the relation between D_j and π_jg, strength of the relation between C_j and θ_jg, DIF, and data completeness, were used as between-replication variables. Model was used as a within-replication variable. The sphericity assumption was checked, and the Huynh–Feldt correction was used to adjust the degrees of freedom if necessary. Considering that the sample size with respect to the repeated variable (i.e., model) was relatively large in the current simulation, the normality assumption was not a big concern for the present study and thus no data transformation was implemented.

Only those statistically significant effects with at least a Cohen’s f value of 0.1 (i.e., small effect size) were reported. The effect size cutting values are negligible (f < 0.1), small (0.1 ≤f < 0.25), moderate (0.25 ≤f < 0.4), and large (f≥ 0.4) in the ANOVA (Cohen, 1988). The proportion of variance accounted for by each main or interaction effects (η²) was provided as well.

Latent Group Classification

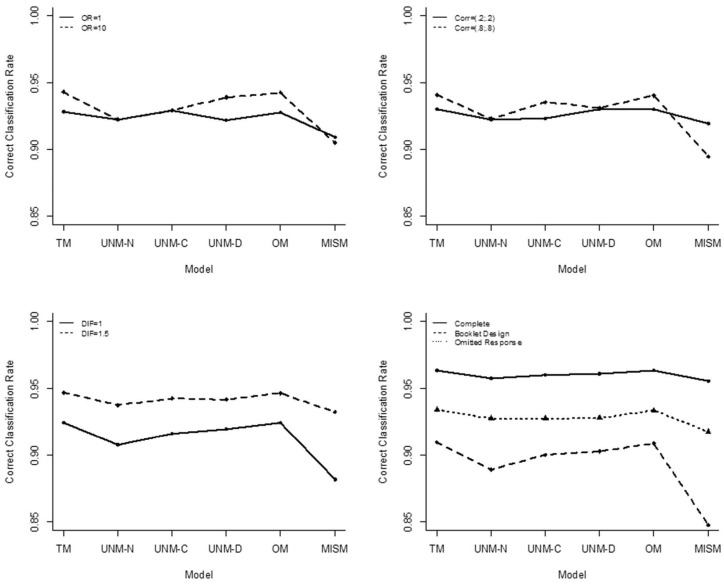
Table 3 presented the descriptive statistics of correct classification rate by six manipulated factors. As expected, the true model with both dichotomous and continuous covariates correctly specified resulted in in the most accurate latent class assignment, although the difference between the true model and the overspecified model was almost negligible. Also, when either of the covariates was correctly specified in the model (i.e., UNM-C and UNM-D), the accuracy of latent group classification was better than the conditions in which no covariates were included (i.e., UNM-N). The model with only the dichotomous covariate resulted in slightly higher correct classification rate than that with only the continuous covariate. The MRM with mismatching covariates resulted in the worst correct classification rate, and it was even worse than not including any covariates.

Table 3.

The Average Correct Classification Rate of Model by Other Manipulated Factors.

		Model
		TM	UNM-N	UNM-C	UNM-D	OM	MISM	Marginal
Data	Complete	0.963	0.958	0.960	0.961	0.963	0.956	0.960
	Booklet design	0.910	0.889	0.900	0.903	0.909	0.848	0.893
	Omitted response	0.934	0.921	0.928	0.928	0.934	0.918	0.927
Prop	.5/.5	0.940	0.929	0.935	0.934	0.939	0.917	0.932
	.3/.7	0.932	0.916	0.924	0.927	0.931	0.897	0.921
OR	1	0.928	0.923	0.929	0.922	0.928	0.909	0.923
	10	0.943	0.923	0.929	0.939	0.943	0.905	0.930
Corr	.2;.2	0.930	0.922	0.923	0.930	0.930	0.919	0.926
	.8;.8	0.941	0.923	0.935	0.931	0.941	0.895	0.928
DIF	1	0.924	0.908	0.916	0.920	0.924	0.882	0.912
	1.5	0.947	0.937	0.943	0.942	0.946	0.932	0.941
Marginal		0.936	0.923	0.929	0.931	0.935	0.907	0.927

Note. TM = true model; OM = overspecified model; UNM = underspecified model; MISM = model with mismatch covariates; OR = odds ratio; DIF = differential item functioning.

The ANOVA results indicated that the estimation model, data completeness, mixing proportion, and DIF size had significant effects on the correct classification rate. The effect sizes were large for data completeness (p < .001, f = 0.853, η² = 0.421), moderate for DIF (p < .001, f = 0.363, η² = 0.116), and small for model (p < .001, f = 0.239, η² = 0.054) and mixing proportion (p < .001, f = 0.131, η² = 0.017). Besides, larger DIF and equal mixing proportion tended to result in higher correct classification rate. Post hoc pairwise comparison showed that all pairwise differences were statistically significant.

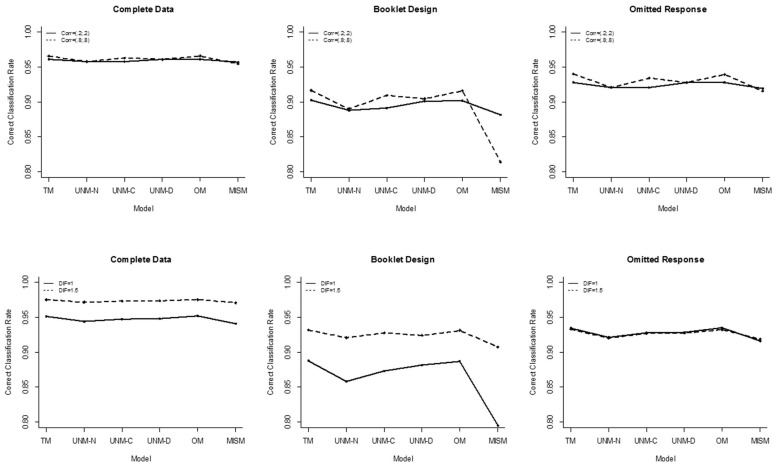
In addition to the main effects, the interaction terms of model by data completeness (p < .001, f = 0.203, η² = 0.040), odds ratio (p < .001, f = 0.102, η² = 0.010), correlation (p < .001, f = 0.151, η² = 0.022), and DIF (p < .001, f = 0.120, η² = 0.014), and the interactions of data completeness by mixing proportion (p < .001, f = 0.178, η² = 0.031) and DIF (p < .001, f = 0.316, η² = 0.091) were also found to be significantly related to the accuracy of latent class assignment. Furthermore, three-way interactions among data completeness, model, and correlation (p < .001, f = 0.148, η² = 0.021), and among data completeness, model, and DIF (p < .001, f = 0.141, η² = 0.019) were also statistically significant. The two-way and the three-way interactions are presented in the appendix.

Parameter Recovery

The recovery of item and person parameters was evaluated separately. As the item parameters were constrained for scale identification and model comparability, on average there was no bias in the item parameter estimates.

Item Parameter Recovery

Table 4 presented the descriptive statistics of item parameter recovery evaluation criteria by manipulated factors. Across all the other factors, the true model resulted in the smallest SE and RMSE, and the highest 95% coverage rate, followed by the overspecified model with negligible differences. Also, when either of the covariates was correctly specified (i.e., UNM-C or UNM-D), the item parameter recovery was better than the MRM with no covariates included. The MRM with only the continuous covariate resulted in slightly better recovery than the MRM with only the dichotomous covariate. Similar to the results of latent group classification, MISM was also the worst in item parameter recovery.

Table 4.

The Descriptive Statistics of Item Parameter by Manipulated Factors.

		Item parameter SE		Item parameter RMSE		95% coverage
Factors	Levels	M	SD	M	SD	M	SD
Model	TM	0.089	0.024	0.136	0.103	0.868	0.103
	UMN-N	0.091	0.024	0.144	0.115	0.849	0.116
	UMN-C	0.089	0.023	0.140	0.107	0.860	0.109
	UMN-D	0.092	0.029	0.142	0.110	0.859	0.112
	OM	0.089	0.024	0.136	0.103	0.867	0.104
	MISM	0.094	0.029	0.158	0.132	0.823	0.145
Prop	.5/.5	0.085	0.020	0.100	0.032	0.892	0.055
	.3/.7	0.097	0.029	0.185	0.142	0.816	0.145
OR	1	0.091	0.026	0.144	0.112	0.850	0.118
	10	0.090	0.025	0.141	0.110	0.859	0.114
Corr	.2;.2	0.091	0.025	0.143	0.113	0.852	0.115
	.8;.8	0.091	0.026	0.142	0.110	0.856	0.117
DIF	1	0.083	0.017	0.121	0.074	0.864	0.088
	1.5	0.098	0.030	0.164	0.136	0.844	0.138
Data	Complete	0.072	0.004	0.073	0.005	0.953	0.005
	Booklet design	0.119	0.025	0.250	0.137	0.749	0.138
	Omitted response	0.082	0.007	0.104	0.020	0.861	0.022

Note. TM = true model; OM = overspecified model; UNM = underspecified model; MISM = model with mismatch covariates; OR = odds ratio; DIF = differential item functioning; SE = standard error; RMSE = root mean squared error.

The ANOVA results indicated that data completeness, mixing proportion, and DIF had statistically significant impacts on the SE of item parameters. Among them, data completeness had a large effect size (p < .001, f = 0.483, η² = 0.189), and mixing proportion (p < .001, f = 0.128, η² = 0.016) and DIF (p < .001, f = 0.187, η² = 0.034), respectively, had a small effect size. In addition, data completeness interacted significantly with DIF with a small effect size (p < .001, f = 0.122, η² = 0.015). Regarding the RMSE of item parameters, data completeness and mixing proportion had statistically significant effects, respectively with a moderate (p < .001, f = 0.327, η² = 0.097) and a small effect size (p < .001, f = 0.172, η² = 0.029). The interaction term of data completeness by mixing proportion was also statistically significant with a small effect size (p < .001, f = 0.172, η² = 0.029). Similar to the results of RMSE, data completeness, mixing proportion and their interactions also had statistically significant effects on the 95% coverage of item parameters. The interaction among data completeness, mixing proportion, and DIF was also statistically significant. The effect size was large for data completeness (p < .001, f = 0.403, η² = 0.140), and small for mixing proportion (p < .001, f = 0.174, η² = 0.029), the two-way interaction (p < .001, f = 0.225, η² = 0.048) and the three-way interaction (p < .001, f = 0.123, η² = 0.015).

Person Parameter Recovery

Table 5 presented the summary statistics of person parameter recovery. Overall, there tended to be a positive bias in the person parameter estimates, indicating an overestimation of the person parameters. However, the marginal bias for the booklet design condition across other manipulated factors was negative, suggesting an underestimation. For the SE of person parameters, there were negligible differences among the true model, the MRM with only the continuous covariate and the overspecified model, and they resulted in smaller SE than the other three models. It indicated that the inclusion of the continuous covariate, rather than the dichotomous covariate, may potentially lead to a reduction in the SE of person parameter estimates. With regard to the RMSE which indicated the overall recovery of person parameters, it was found that the true model and the overspecified model resulted in the best person parameter recovery, followed by the MRM with only the continuous covariate with negligible difference. The MRM with mismatching covariates again performed the worst in terms of person parameter recovery.

Table 5.

The Descriptive Statistics of Person Parameter by Manipulated Factors.

		Person parameter bias		Person parameter SE		Person parameter RMSE		95% coverage
Factors	Levels	M	SD	M	SD	M	SD	M	SD
Model	TM	0.025	0.061	0.144	0.040	0.184	0.056	0.948	0.011
	UMN-N	0.022	0.075	0.162	0.042	0.202	0.065	0.946	0.012
	UMN-C	0.031	0.065	0.143	0.042	0.185	0.059	0.947	0.012
	UMN-D	0.022	0.071	0.163	0.047	0.198	0.066	0.946	0.011
	OM	0.024	0.063	0.145	0.041	0.184	0.058	0.948	0.011
	MISM	0.027	0.080	0.163	0.043	0.207	0.070	0.942	0.014
Prop	.5/.5	0.043	0.035	0.179	0.029	0.217	0.048	0.948	0.010
	.3/.7	0.007	0.087	0.128	0.040	0.170	0.067	0.944	0.013
OR	1	0.026	0.071	0.154	0.044	0.195	0.064	0.946	0.012
	10	0.025	0.067	0.153	0.042	0.191	0.062	0.946	0.011
Corr	.2;.2	0.022	0.072	0.161	0.042	0.199	0.065	0.945	0.012
	.8;.8	0.028	0.065	0.146	0.041	0.188	0.060	0.946	0.012
DIF	1	0.029	0.023	0.135	0.032	0.158	0.035	0.948	0.008
	1.5	0.022	0.095	0.172	0.046	0.229	0.064	0.944	0.014
Data	Complete	0.010	0.003	0.134	0.033	0.146	0.035	0.955	0.001
	Booklet design	−0.016	0.091	0.181	0.046	0.234	0.067	0.950	0.007
	Omitted response	0.082	0.029	0.145	0.034	0.200	0.046	0.933	0.009

Note. TM = true model; OM = overspecified model; UNM = underspecified model; MISM = model with mismatch covariates; OR = odds ratio; DIF = differential item functioning; SE = standard error; RMSE = root mean squared error.

The ANOVA results showed that data completeness had a statistically significant effect on the bias of person parameters with a moderate effect size (p < .001, f = 0.223, η² = 0.047). In addition, data completeness interacted significantly with mixing proportion (p < .001, f = 0.156, η² = 0.024) and DIF (p < .001, f = 0.142, η² = 0.020) with respect to the bias of person parameters. The three-way interaction term of data by mixing proportion and DIF were also found to be statistically significant with a small effect size (p < .001, f = 0.129, η² = 0.016). Regarding the SE and RMSE of person parameters, data completeness (p < .001, f = 0.118, η² = 0.014; p < .001, f = 0.163, η² = 0.026), mixing proportion (p < .001, f = 0.147, η² = 0.021; p < .001, f = 0.104, η² = 0.011), and DIF (p < .001, f = 0.106, η² = 0.011; p < .001, f = 0.159, η² = 0.025) were found to have significant effects on these two measures with small effect sizes. No significant interaction terms were observed. For the 95% coverage, only data completeness was found to be statistically significant with a small effect size (p < .001, f = 0.122, η² = 0.015).

Overall Model Fit Indies

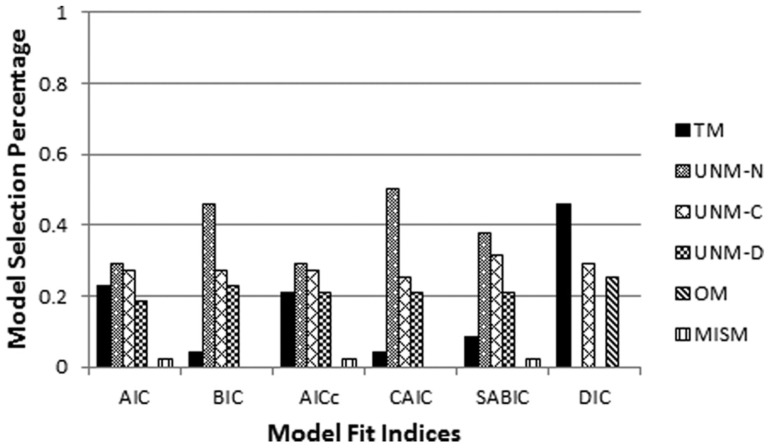
The percentage of each model being selected as the best-fitting model with respect to the six overall model selection indices were graphically displayed in Figure 1. Overall, AIC, BIC, AICc, CAIC, and SABIC did not perform very well. Among them, AIC and AICc performed the worst as they had difficulty differentiating models. On the other hand, BIC, CAIC and SABIC performed similarly and they all tended to choose the most parsimonious model, the MRM without covariates. The only index that successfully identified the MRM with correctly specified covariates was DIC, a Bayesian measure of fit. However, a closer examination of selection frequency showed that the performance of model fit indices tended to vary depending on certain manipulated factors. Thus, the selection decisions were analyzed with respect to data completeness, and the relations between model parameters and the covariates.

Figure 1.

Overall model selection percentage across simulation conditions.

Note. TM = true model; OM = overspecified model; UNM = underspecified model; MISM = model with mismatch covariates; AIC = Akaike’s information criterion; BIC = Bayesian information criterion; AICc = a correction of AIC based on sample size and the number of parameters; CAIC = consistent AIC; SABIC = sample-size adjusted BIC; DIC = deviance information criterion.

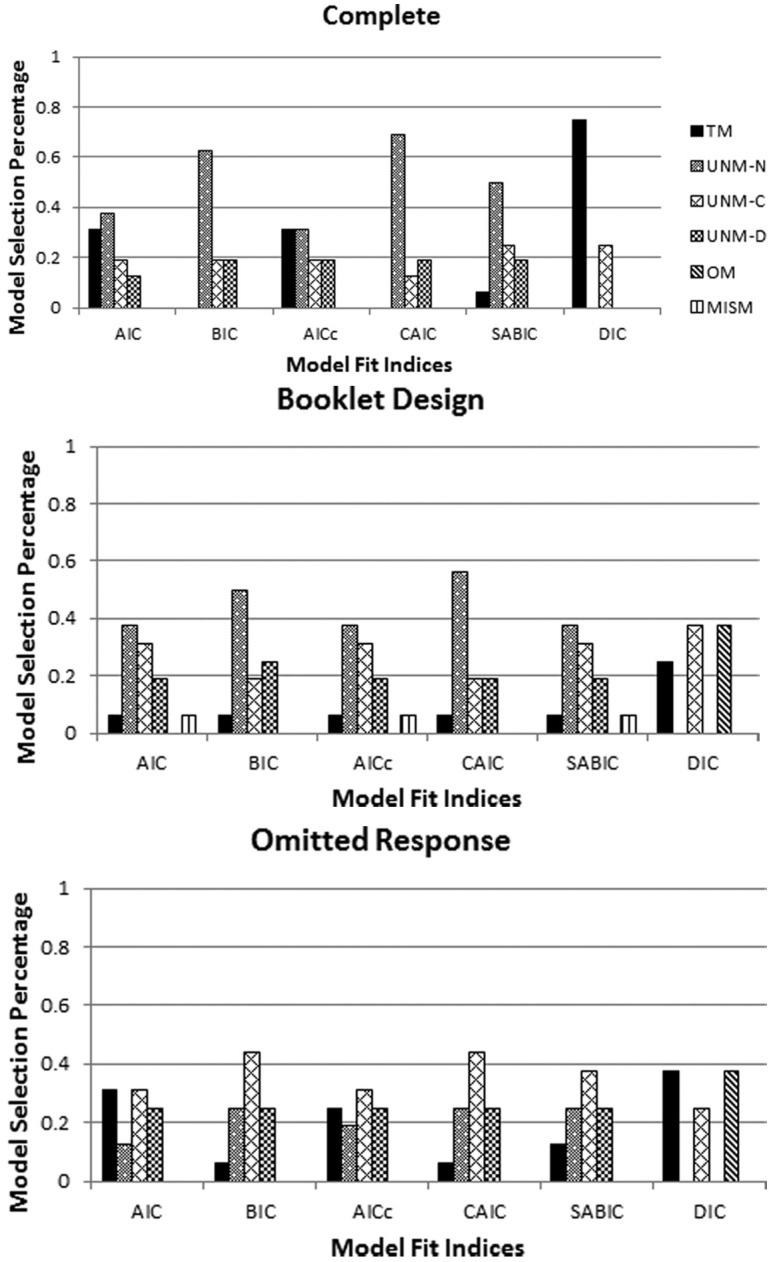
As shown in Figure 2, the ability of differentiating models was stronger for the six indices when the data was complete. In this scenario, BIC, CAIC, and SABIC had a strong tendency of selecting the most parsimonious model. With regard to DIC, it was highly effective in selecting the data-generating model. As for the few cases that DIC chose the MRM with only the continuous covariate, they all occurred when the odds ratio was weak (i.e., OR = 1), so it was reasonable for DIC to select a more parsimonious model without the dichotomous covariate.

Figure 2.

Model selection percentage by data completeness across other manipulated factors.

Note. TM = true model; OM = overspecified model; UNM = underspecified model; MISM = model with mismatch covariates; AIC = Akaike’s information criterion; BIC = Bayesian information criterion; CICc = a correction of AIC based on sample size and the number of parameters; CAIC = consistent AIC; SABIC = sample-size adjusted BIC; DIC = deviance information criterion.

In the booklet design condition, BIC, CAIC, and SABIC still tended to choose the MRM without covariates, yet the tendency was relatively weak. Moreover, DIC was no longer effective when the booklet design was used. It could not distinguish between the overspecified model and the MRM with only the continuous covariate. In addition, for the omitted response condition, none of the indices was effective. DIC had the same selection percentage for the true model and the overspecified model.

Further, the selection decision was examined with respect to odds ratio. When the odds ratio was weak, BIC, CAIC, and SABIC most frequently selected the most parsimonious model. DIC predominantly identified the MRM with only the continuous covariate as the best-fitting model, which was a reasonable choice in consideration of model parsimony when OR = 1. However, as the odds ratio was strong, the decisions were made most often between MRM with only the dichotomous covariate and the MRM without covariates for BIC, CAIC, and SABIC. Again, DIC successfully identified the MRM with correct covariate specification with the highest selection percentage.

Finally, the selection percentage was analyzed by the correlation between the continuous covariate and the person parameter. When the correlation was as weak as 0.2, AIC, BIC, AICc, CAIC, and SABIC all favored the most parsimonious model. Meanwhile, DIC correctly identified the true model as the best-fitting model. However, when the correlation was as strong as 0.8, BIC, CAIC, and SABIC most frequently selected the MRM with only the continuous covariate, whereas DIC still predominantly selected the correct model.

In sum, the above results suggested that DIC was the most successful index in selecting the MRM with correct covariate inclusion, whereas the performances of BIC, CAIC, and SABIC were quite similar and they had a consistent tendency of favoring model parsimony. Another important finding was that their performance tended to be strongly compromised when missing data were present. Also, the tendency of selecting the overspecified model occurred in particular for DIC in both the booklet design and omitted response conditions.

Discussion

Given the potential advantages of covariate inclusion in IRT modeling, the present study explored different approaches to adding covariates into the MRM and the corresponding impacts on model estimation. The results are summarized and relevant implications are addressed in details in this section.

The data generating model, with both the dichotomous and continuous covariates correctly specified, has the best performance in terms of the accuracy of latent class assignment. It also has, on average, the smallest SE and RMSE in item parameter recovery, the smallest RMSE in person parameter recovery and the highest 95% coverage rate for both item and person parameter recovery. Literature (Smit et al., 1999; 2000) suggested that the latent class assignment may substantially benefit from incorporating dichotomous covariates that are moderately or strongly related to the latent class variable. In line with their results, the current study also witnesses a moderate increase in the correct classification rate if both dichotomous and continuous covariates are correctly specified in the MRM. Moreover, if only one covariate, dichotomous or continuous, is correctly specified in the MRM, there is also an improvement in the correct classification rate, but the MRM with only the dichotomous covariate performs slightly better than the MRM with only the continuous covariate. The reason might be that the dichotomous covariate enters UNM-D directly as a predictor of the latent class membership.

As for the parameter recovery, Mislevy and Sheehan (1989a, 1989b) suggested that the incorporation of covariates associated with the latent trait could compensate for the sparse information in the response data and hence reduce the MSE of person parameter estimates and the SE of item parameter estimates in maximum likelihood estimation. The results were further confirmed in Adams et al. (1997) and Smit et al. (1999, 2000). Similarly, in the present study, the descriptive statistics show that the correct covariate inclusion may lead to a reduction in the item parameter SE and RMSE, person parameter RMSE and an increase in the 95% confidence interval coverage rate, although this pattern is not of practical significance in the ANOVA results (i.e., f < 0.1). A plausible explanation for the small effect size is the test length used in the current simulation. Previous studies all used very short tests with no more than 10 items (Mislevy & Sheehan, 1989a, 1989b; Smit et al., 1999; 2000) and indicated that the effects of covariate information could diminish as test length increases. However, in the present study, in order to guarantee the convergence rate in the missing data scenarios, the test length is set to be 30. This could be the major reason why the effect of model is not very pronounced for parameter recovery as shown in the ANOVA results.

Additionally, there is an interesting finding that the improvement in person parameter recovery may be exclusively due to the inclusion of the continuous covariate as a predictor of the person parameter, because the MRM with only the dichotomous covariate does not perform any better than the MRM without covariates in terms of the SE and RMSE of person parameter recovery. Thus, it is possible that the covariate may function differentially in the model estimation and the benefits for the MRM may depend on the approach to covariate inclusion.

In summary, for the different approaches to covariate inclusion, the results in the present study show that the correct specification of both covariates in the MRM could potentially benefit model parameter estimation. Moreover, if only one covariate is correctly specified in the MRM, the model performance could still be improved to some extent, and the continuous covariate tends to influence both the latent group classification and the model parameter recovery whereas the dichotomous covariate seems only to improve the latent class assignment. Furthermore, based on all the model performance criteria mentioned above, it is found that the true model and the overspecified model are almost indistinguishable from each other, indicating that including redundant covariate information may not necessarily worsen the model performance as long as all the necessary covariates are correctly specified in the model. However, the MRM with mismatching covariates results in the worst model performance in terms of most of the criteria considered in the present study, implying that the mismatch between covariates and model parameters may lead to even worse results than not including any covariates at all.

Among the other manipulated factors, DIF, mixing proportion, data completeness, and their interactions tend to strongly impact the accuracy of latent class assignment, as well as item and person parameter recovery. As mixing proportion and DIF have been extensively studied in mixture IRT literature, they are not discussed in detail here. Regarding data completeness, the booklet design tends to lead to the worst result in terms of most of the evaluation criteria used in the present study, with the exception that the omitted response condition results in the largest bias and the lowest 95% coverage for the person parameter estimates. The poor performance of booklet design is within expectation, considering the largest amount of missing data involved; however, it is surprising to find even worse performance of omitted response in two person parameter outcome measures, and one possible reason for that could be the conditional missing data mechanism involved in the omitted response scenario.

The other important aspect of the present study is to provide information about model fit with respect to covariate inclusion, which has not been discussed by other studies in this line of research. Previous research regarding model fit in the mixture IRT context (Li et al., 2009) recommended the use of BIC because of its outstanding performance and consistency in detecting latent class enumeration. It was also suggested that both AIC and DIC had a tendency to select the most complex model (Li et al., 2009). However, different from the previous study, the current simulation provides unique information about the effectiveness of overall model fit indices in the mixture IRT modeling context with covariate inclusion.

In general, among the six indices reported in the study, DIC is the most effective one in identifying the correct covariate inclusion in the MRM. Regarding the other five indices, they are not found to be useful in the current study, yet it is found that AIC and AICc are highly consistent with each other, and BIC, CAIC, and SABIC all have a very strong tendency to select the most parsimonious model. Different from the message provided by previous research that AIC tended to select more complex model, the current simulation indicates that AIC and AICc are highly ineffective in the MRM context when covariates are involved. These two indices may not be good choices for practitioners when mixture IRT models are used. Furthermore, although BIC is proved to be successful in selecting the best latent structure for mixture IRT models in the literature, this index may not be sensitive to the fit of covariate inclusion in the mixture IRT models. Thus, the use of BIC should be implemented with caution as it works well in some contexts but not the others. However, in most commonly-used commercial software programs for mixture IRT model parameter estimation, the use of AIC and BIC is prevalent, and other model fit indices are usually not provided. The lack of choices for model fit indices in the commercial software programs may lead to misfitting models being selected as best-fitting models for practitioners. It is suggested that the calculation of more model fit indices may be implemented in software programs and DIC could also be included if a Bayesian module exists, so that researchers may select which index to use, depending on the purpose of the study and the data structure.

Another important finding in the present study regarding model selection is that the effectiveness of all six indices is highly sensitive to the missing data. Even for DIC, its performance is greatly compromised when missing data are present. To be specific, DIC shows a tendency of selecting the most complicated model no matter the missing data come from omitted responses or booklet design. The other indices also have great difficulty in differentiating the true model and the three underspecified models in missing data conditions. Therefore, one important suggestion to come out of this study for practitioners is to be extremely cautious about overall model selection indices when using them with missing data. As the effectiveness of model fit indices is sometimes model and design specific and could be compromised by missing data, it is recommended that researchers should evaluate the model-data fit from different perspectives, rather than solely relying on overall information-based fit indices to choose models.

As for the practical implications of covariate inclusion approaches, it is expected that the mixture IRT model with correctly specified covariates may help identify latent DIF, explain latent DIF using manifest grouping variables (e.g., dichotomous covariate), and improve model parameter estimation simultaneously. Previously, covariate inclusion has been proved useful in non-mixture IRT context for the purpose of explaining estimated effects (e.g., Wilson & De Boeck, 2004) and improving model parameter estimation (e.g., Adams et al., 1997). The current study incorporates covariates into the MRM via different approaches, and extends the use of covariate information to a broader scenario.

Purely in the perspective of model estimation, covariate inclusion is promising for mixture IRT models with the potential benefit of improving the latent group classification and the estimation of model parameters. However, regarding the practical use, there exists a theoretical debate with respect to the validity of inference drawn about the population if covariate information is used, because covariate inclusion violates the fundamental of equitable measurement and test fairness; namely, the parameter estimation should be independent of any variables beyond the response data per se (Adams et al., 1997). Thus, it is desirable to use covariates to improve the precision of model parameter estimation, yet it is less desirable to draw inference based on the conditional model, especially when high-stakes decisions are involved (Mislevy & Sheehan, 1989a). Additionally, one important methodology, which is closely related to the covariate inclusion approach and also commonly used in large-scale survey assessment, is the plausible value imputation method. Plausible values are imputed values drawn from an empirically derived distribution of latent achievement scores that are conditional on the observed values of respondents’ background variables (i.e., covariates) and item responses (e.g., Mislevy, 1991, 1993; Rubin, 1987; von Davier et al., 2009). As mentioned in Adams et al. (1997), to draw plausible values, NAEP uses an approach very similar to a two-step estimation with covariates. Item parameters are estimated first without the covariates and then the item parameters are fixed in the second phase for the generation of plausible values to better approximate population parameters (Adams et al., 1997). This methodology could be taken as an important extension and practical application based on covariate inclusion approaches.

As with all other studies, certain limitations remain in the present study. First, considering the amount of time required for the model estimation under the Bayesian framework¹, a number of factors and the prior distributions are fixed, so that the results are limited to the manipulated factors under investigation. Future research may manipulate more simulation factors or include more levels of the studied factors, especially for test length and data completeness. Second, previous research suggested that one-step estimation, as used in the present study, is favored than two-step estimation, due to the fact that the latter might greatly underestimate the regression parameters (Adams et al., 1997). However, without a direct comparison, it is unclear how much one-step estimation is better than two-step estimation in terms of recovering the relations between covariates and model parameters in the MRM context. This issue may be explored in future research.

In summary, despite the limitations, the findings from this study definitely add to the literature about different approaches to covariate inclusion in mixture IRT modeling. A proper use of covariate information is of theoretical and practical importance for researchers to achieve more accurate model estimation. The current simulation study provides important theoretical evidence and practical implications about the impact of different covariate inclusion approaches on the accuracy of latent group classification, model parameter recovery, and overall model fit. It complements previous studies and lays a foundation for future explorations.

Appendix

Figure A1.

Statistically significant two-way interaction effects between the model and other between-replication variables on the correct classification rate.

Figure A2.

Statistically significant three-way interaction effects on the correct classification rate.