Differences in Reaction to Immediate Feedback and Opportunity to Revise Answers for Multiple-Choice and Open-Ended Questions

Abstract

There are many reasons to believe that open-ended (OE) and multiple-choice (MC) items elicit different cognitive demands of students. However, empirical evidence that supports this view is lacking. In this study, we investigated the reactions of test takers to an interactive assessment with immediate feedback and answer-revision opportunities for the two types of items. Eighth-grade students solved mathematics problems, both MC and OE, with standard instructions and feedback-and-revision opportunities. An analysis of scores based on revised answers in feedback mode revealed gains in measurement precision for OE items but not for MC items. These results are explained through the concept of effortful engagement—the OE format encourages more mindful engagement with the items in interactive mode. This interpretation is supported by analyses of response times and test takers’ reports.

Introduction

There are many reasons to believe that open-ended (OE) and multiple-choice (MC) items elicit different cognitive demands of students (Bennett & Ward, 1993; Martinez, 1999). However, empirical evidence that supports this view is lacking, especially when the response to the OE items is a number or a few words (e.g., Bridgeman, 1992; Traub & MacRury, 1990; Wainer & Thissen, 1993). In a meta-analysis of the construct equivalence of MC and OE items, Rodriguez (2003) examined 67 empirical studies and found that when the OE and MC items have the same stem (stem equivalent), the disattenuated correlations between the test scores tend to be very high and typically approaches unity. Even when the items are not stem-equivalent, but still tap the same content and cognitive demands, disattenuated correlations are still high, typically larger than .90. Only when the OE items are explicitly designed to tap a different aspect of the content domain and different cognitive demands (e.g., essay items) do we find lower correlations (typically in the low 80s).

However, the research thus far on possible differences between item formats has been conducted in the context of traditional tests. One feature of these tests is that they are administered with no immediate feedback to examinees about item performance. Providing feedback regarding task performance is one of the most frequently applied psychological interventions (Kluger & DeNisi, 1996). Nevertheless, immediate feedback during tests is still rare. This can be attributed both to the technological difficulty of providing immediate feedback on paper-based tests or on tests requiring complex constructed responses, and to the traditional emphasis on summative assessments in educational testing (Attali & Powers, 2010).

In the context of formative assessments (Scriven, 1967; Wiliam & Thompson, 2008), or assessment as and for learning, feedback is essential. Feedback helps learners determine performance expectations, judge their level of understanding, and become aware of misconceptions. It may also provide clues about the best approaches for correcting mistakes and improving performance (Shute, 2008). Bangert-Drowns, Kulik, Kulik, and Morgan (1991) summarized studies examining the instructional effects of feedback during tests and concluded that in order for feedback to be effective, learners should be guided or given the correct answer. In addition, they also conclude that immediate feedback is generally more effective than delayed feedback for complex learning.

Feedback may also be beneficial in the context of tests with no personal consequences to the students. These tests are used for many purposes including assessing teacher effectiveness and assessing district- and state-level performance. The concern is that students in these testing situations may not be highly motivated to try their best, and as a consequence data collected will not be a valid measure of student achievement (Eklof, 2006; Wainer, 1993; Wise & DeMars, 2005). Nevertheless, effective solutions to this problem have not been found. For example, several studies examined the effects of using monetary incentives to motivate students, but have generally found weak effects on performance (Baumert & Demmrich, 2001; Braun, Kirsch, & Yamamoto, 2011; O’Neil, Abedi, Miyoshi, & Mastergeorge, 2005; O’Neil, Sugrue, & Baker, 1996). A different kind of approach may be based on creating a more engaging experience to test takers through different types of feedback. Although feedback in educational contexts may primarily be associated with cognitive processes, it can operate through affective processes, such as increased effort, motivation, or engagement (Hattie & Timperley, 2007).

The Present Study

Whether in the context of formative assessments or low-stakes accountability tests, a basic question is how to design them in order to ensure their intended purposes. The purpose of this study was to examine the reactions of test takers to immediate feedback about their responses and to compare the psychometric effects of these reactions under the MC and OE item formats.

In this study, we used a particular variant of immediate feedback, multiple-try feedback that has a long history in educational technology. Pressey (1926, 1950) was the first to develop a “teaching machine,” which presented an MC question and provided immediate feedback on the correctness of a response (selected by pressing the appropriate key). The student repeatedly selected answers until the correct answer was chosen, hence the term answer-until-correct. Pressey (1950) reviewed several studies that showed positive long-term learning effects of answer-until-correct (see also Epstein, Epstein, & Brosvic, 2001). Answer-until-correct has also been used to improve the psychometric properties of the test by incorporating partial knowledge measurement (Gilman & Ferry, 1972). Attali and Powers (2010) extended the use of this paradigm to OE questions and showed that the reliability of revision scores was significantly higher than the reliability of scores based on no feedback and that test anxiety was significantly lower following a test section with feedback and revision.

In the current study, we conducted a more systematic comparison of multiple-try feedback under the MC and OE item formats. We hypothesized that, because the MC item format allows test takers to produce answers effortlessly, their reactions to feedback could be different from those under the OE format. Bangert-Drowns et al. (1991) used the concept of mindfulness (Salomon & Globerson, 1987) to explain the successful implementation of assessments for learning and feedback in particular. That is, feedback can promote learning if it is received mindfully, but can inhibit learning if it encourages mindlessness. Therefore, the lower effort required in answering MC items may reduce the effectiveness of feedback during assessment. In a multiple-try test in particular, it is possible that students would exert less effort in correcting initial errors in MC items than OE items because of the temptation to simply click on a different option without much thought.

In a recent experimental study of mathematics problem solving, Attali (2015a) found support for this hypothesis in a transfer of learning context. Participants solved mathematics problems that were presented as either MC or OE questions and were provided with one of four types of feedback: no feedback (NF), immediate knowledge of the correct response (KCR), multiple-try feedback with knowledge of the correct response (MTC), or multiple-try feedback with hints after an initial incorrect response (MTH). Participants later solved similar problems that were presented without feedback. Results showed that gains in performance were larger in the OE than MC condition (effect size d = .24). Furthermore, gains under NF and KCR were similar, gains were larger under MTC than KCR (d = .30), and gains were larger under MTH than MTC (d = .21). However, no interaction between item type and feedback type was found.

In another recent study, Attali (2015b) used similar manipulations in a high-stakes setting. GRE candidates were invited, several weeks before their scheduled GRE test, to complete up to seven quantitative practice tests through a web-based application. Participants were randomly assigned to specific testing conditions, determined by item format (MC or OE) and feedback mode. Three modes of feedback were used: standard no-feedback condition with delayed review of results; immediate feedback about correctness; and immediate correctness feedback with two revision opportunities (multiple-try feedback). Results indicated that practice with OE questions and with immediate correctness feedback had a beneficial effect on test practice performance as well as actual GRE test performance.

Whereas the focus of the two studies described above was on learning effects, the focus of the current study was on a comparison of the psychometric properties of the test. Eighth-grade students completed mathematics tests both with and without feedback and under both MC and OE formats. The MC and OE versions of the tests were content-equivalent (i.e., were written to measure the same Common Core standards), and the OE items required test takers to type a whole number, decimal, or fraction. This approach of comparing parallel tests that vary in one systematic dimension (in this case, item format) is sometimes called faceted test design (Snow & Lohman, 1989). As was reviewed above, psychometric research in this tradition on the question of equivalence of item formats has been equivocal (Martinez, 1999; Rodriguez, 2003; Traub, 1993). One content area where format effects have generally not been detected is mathematics and related areas that require analytical thinking. For example, Bennett, Rock, and Wang (1991) examined the factor structure of MC and OE items from the College Board’s Advanced Placement Computer Science examination and could not find meaningful format effects. Wainer and Thissen (1993) examined the correlations between MC and OE sections of several Advanced Placement tests and found disattenuated correlations of .98, .96, and .99 for calculus, computer science, and chemistry, respectively. In an effort to explain these types of findings, Ward, Dupree, and Carlson (1987) suggested that when items require complex cognitive processing (such as mathematics problem solving), the difference between recognition (for MC) and recall (for OE) is no longer important, since test takers have to accomplish considerable processing in order to answer the question, even in the presence of response options.

However, as was discussed above, the introduction of multiple-try feedback that was the focus of this study may change this dynamic following the first attempt. In other words, test takers (particularly in a low-stakes test) may be less willing to invest effort in revising their initial incorrect answers to MC than OE items. This may affect the psychometric properties of scores under the two item formats. Specifically, the different conditions under which participants in this study answered mathematics problems allow a comparison of MC and OE scores under two conditions: when students initially try to answer the questions (before any feedback is provided) and when students revise their answers following feedback. These two conditions give rise to two types of scores: first-attempt scores and revision scores that take into account students’ reaction to feedback.

This double comparison of MC and OE scores (before and after feedback) was performed in terms of performance, reliability coefficients, validity coefficients, and MC–OE correlations. For first-attempt scores, we expected to replicate previous research findings, namely, higher test scores and lower reliability for the MC format because of the guessing effect, but very high MC–OE correlations and similar validity coefficients for the two formats. On the other hand, if students react to feedback with more effort under the OE format, we expected larger gains in performance, reliability, and validity coefficients to be manifested for revision scores in the OE format than the MC format, as well as lower MC–OE correlations for these revision scores.

Method

Participants

A total of 841 eighth-grade students participated in the study. These students were randomly selected from their school grade cohort. A total of 25 schools from the Northeast and Midwest regions of the United States participated in the study. Twelve schools had an NCES classification of suburb, 10 rural, 2 city, and 1 town. Almost all schools were middle schools with a Grade span of 6 to 8. The range for the number of eighth-grade students in the schools was 81 to 417, with a median of 178. Students were compensated with a gift card valued at $20, and schools received $40 per participating student. Students were selected to participate in the study based on whether they had an individualized education program (IEP). The ratio of IEP to non-IEP students in each school was approximately 1:2, but all students had taken their state assessment the previous year. Overall, 312 IEP students (37%) and 530 non-IEP students participated. The entire sample was approximately 50% female, 74% White, 14% Black, 5% Black, and 5% Asian.

Materials

Four test forms, each with 20 items, were developed for this study. Two of the forms were composed of four-choice MC items, and the other two forms were composed of OE items requiring numerical entry. Each form was similar in content and difficulty (but OE and MC items were not versions of the same items), covering the eighth-grade standards of the Common Core State Standards framework. The items were previously piloted with age-appropriate students. Following the pilot, in which each form had 21 items, 4 items that showed lower discrimination or very low performance were removed and several items were switched between forms to make each form similar in difficulty (while maintaining content similarity).

Design

Each participant was administered all four forms, but in different orders and with one form in each format mode administered under standard (no feedback) condition and the other administered under feedback condition. Participants were randomly assigned within IEP group to one of eight conditions that determined which forms were administered with feedback (and which forms without) and the order of forms (see Table 1). These conditions were constrained such that standard or feedback testing was administered in both sections of a single session.

Table 1.

Test Conditions.

		Session 1		Session 2
Condition	n	Section 1	Section 2	Section 1	Section 2
1	106	MC1-ST	OE1-ST	MC2-FR	OE2-FR
2	104	MC1-FR	OE1-FR	MC2-ST	OE2-ST
3	105	MC2-ST	OE2-ST	MC1-FR	OE1-FR
4	106	MC2-FR	OE2-FR	MC1-ST	OE1-ST
5	104	OE1-ST	MC1-ST	OE2-FR	MC2-FR
6	103	OE1-FR	MC1-FR	OE2-ST	MC2-ST
7	106	OE2-ST	MC2-ST	OE1-FR	MC1-FR
8	108	OE2-FR	MC2-FR	OE1-ST	MC1-ST

Note. OE = open-ended; MC = multiple-choice; ST = standard; FR = feedback-and-revision. Test forms are labeled MC1, MC2, OE1, OE2.

Procedures

Participants completed the study on two consecutive days. Each session was limited to 90 minutes (based on estimates obtained from the pilot study). The study was administered as a computerized assessment. Students logged into the web-based system from the school’s computer lab. Test questions were presented sequentially on the screen. For MC questions students selected an option to answer. For OE questions students typed a numeric answer in a text box. In standard condition, students did not receive any feedback after they submitted their answer. In the feedback condition, students received up to three opportunities to answer each question (or two opportunities to correct their initial answer). After each attempt, the student was informed if the answer was correct or not, and after the third attempt, in case the answer was incorrect, the correct answer was displayed.

Each test section was followed by anxiety (where test takers were asked how well adjectives like “calm” and “tense” describe their feelings during the test) and test reaction (where test takers were asked to evaluate effort, engagement, and success in the test) questionnaires. The results of these questionnaires are discussed in a separate article (Laitusis, Attali, & Stone, 2015). A 5-minute break was provided after the first section of each session. Participants were allowed to use any calculator and scratch paper for any question on the test.

Computation of Test Scores

To answer the research questions of this study, two types of test scores were computed. First-attempt scores were computed for both standard and feedback mode, based on awarding full credit (1 point) for a correct answer (in the first attempt) and no credit (0 points) for an incorrect answer. In addition, to capture students’ reaction to feedback in feedback mode revision partial-credit scores were computed. As in previous studies of multiple-try feedback (e.g., Attali & Powers, 2010), revision partial-credit scores were based on the number of attempts needed to reach a correct answer. Specifically, with a maximum of three attempts revision scores were computed by awarding full credit (1 point) for a correct answer in the first attempt, 2/3 of a point for a correct answer in the second attempt, 1/3 of a point for a correct answer in the third attempt, and no credit (0 points) for an incorrect answer after all three attempts were exhausted.

Results

All analyses in this article were performed for the entire group of participants. A separate article (Laitusis, Attali, & Stone, 2015) found little evidence for differential reaction to feedback for students with and without IEP.

Although not the focus of this study, a preliminary analysis of the school effect on scores was performed by estimating variance components between and within schools. In a two-level (students within schools) random-effects model of overall (across all sections) first-attempt scores (percent correct), the estimate of the variance component at the student level (within school) was .0383 and the estimate at the school level (between school means) was .0039 (se = .0019, p = .007). Although the estimated variance between schools was significantly greater than zero, the intraclass correlation (the proportion of variance in test scores attributable to schools) was quite low, .09. Therefore, the school effect was not included in subsequent analyses.

First-Attempt Performance and Internal Consistency

The purpose of this section is to compare first-attempt scores for MC and OE formats in terms of level of performance and internal consistency reliability estimates. For first-attempt scores, we expected higher performance and lower reliability for the MC format because of the guessing effect. The two feedback modes (standard and feedback) should not have an effect on first-attempt scores. However, Attali and Powers (2010) found that in multiple-try testing mode, first-attempt performance was slightly lower than in standard mode, possibly because in multiple-try mode students knew they would get a second chance to answer the questions. Therefore, we expected this result could be replicated both in MC and OE formats.

The first two column sections of Table 2 (labeled Standard and F&R First Attempt) present psychometric properties of first-attempt test performance for the four forms, collapsed across all form orders. The table shows that performance was quite low on average, around 40% correct, or 8 questions out of 20. A preliminary analysis investigated possible order effects. A 4 (form, MC1, MC2, OE1, and OE2) × 2 (session, first or second) × 2 (section, first or second) mixed effects ANOVA was performed on proportion correct in first attempt. A significant form effect was found, F(3, 841) = 105.73, p < .01, with higher performance (as expected from the guessing factor) for MC forms than OE forms (see Table 2). A significant section effect was also found, F(1, 841) = 48.51, p < .01, with higher performance for the first section in a session (M = .428, se = .006) than for the second section (M = .399, se = .005), possibly as a result of fatigue. None of the other main effects or interactions were significant, Fs < 2.43, ps > .06. Because there was no interaction between the section effect and any other factor, analyses below were collapsed across the two sections.

Table 2.

Psychometric Properties of Section Scores (Proportion Correct).

	Standard				F&R first attempt				F&R revision
Form	N	M	SD	α	n	M	SD	α	n	M	SD	α
MC1	424	.455	.201	.749	418	.432	.199	.748	418	.639	.148	.738
MC2	418	.459	.211	.779	424	.435	.200	.750	424	.653	.148	.747
OE1	424	.399	.250	.882	418	.406	.255	.887	418	.468	.265	.912
OE2	418	.370	.244	.878	424	.352	.226	.862	424	.415	.243	.897

Note. F&R = feedback-and-revision; OE = open-ended; MC = multiple-choice. For each item type, participants completed one form in feedback mode and another in standard mode.

Table 2 also shows that the internal consistency of performance was acceptable, with Cronbach’s α coefficients of .75 to .78 for MC forms and .86 to .89 for OE forms. For each item type, internal consistency measures were similar; none of the differences between the measures, using Feldt’s (1969)W¹ statistic, were significant (ps > .10). However, internal consistency measures were higher for OE than MC items (ps < .01), as expected from the lack of the guessing factor in OE items.

To analyze the effects of feedback mode and item type on first-attempt test performance, a 2 (feedback mode) × 2 (item type) within-subjects ANOVA was performed on proportion correct in first attempt. A significant item type effect was found, F(1, 841) = 232.19, p < .01, with higher performance for MC (M = .442, se = .007) than for OE items (M = .378, se = .007). A significant feedback type effect was also found, F(1, 841) = 14.48, p < .01, with higher performance for standard mode (M = .417, se = .007) than for feedback mode (M = .403, se = .007). However, these two main effects should be qualified by a significant interaction, F(1, 841) = 6.76, p < .01. A post hoc Tukey test indicated that for MC, standard mode (M = .453, se = .008) was significantly higher than feedback mode (M = .430, se = .008), but for OE, standard mode (M = .381, se = .008) was not significantly different from feedback mode (M = .375, se = .008).

In summary, as expected from the guessing effect, first-attempt scores in the MC format were higher and less reliable than in the OE format. In addition, first-attempt scores in feedback mode were lower than in standard mode, but only in the MC format.

Test Performance on Later Attempts

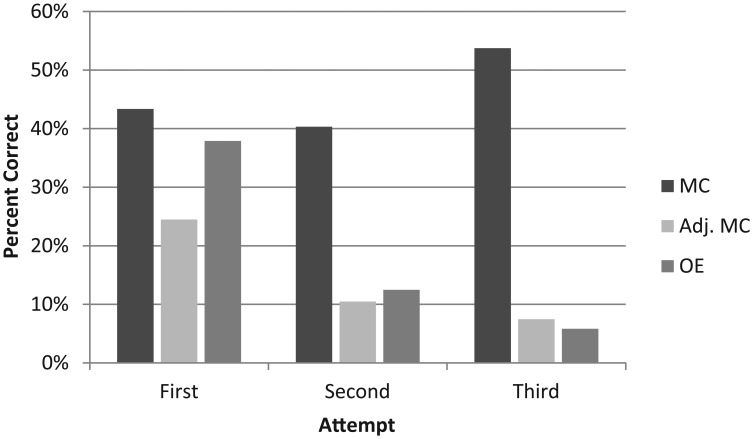
The previous section focused on test performance in the first-attempt answering each question. This section will analyze the success in revising incorrect answers in feedback mode and the psychometric properties of the resulting partial-credit revision scores. First, Figure 1 summarizes overall response correctness in each attempt. In addition to showing the actual percent correct for MC and OE items, it also shows an adjusted percent correct for MC items, taking the guessing factor into account. Adjusted proportion correct (PC) is equal to PC − (1 − PC)/k, where k is the number of options available for each attempt (4 in the first attempt, 3 in the second attempt, and 2 in the third attempt). The figure shows that for OE items, percent correct drops significantly from 38% in the first attempt to 12% and 6% in the second and third attempts. In contrast, for MC items percent correct drops slightly in the second attempt (from 43% to 40%) and then increases to 54% in the third attempt. However, this is mainly due to the decreasing number of available options. The adjusted percent correct for MC items is very similar to percent correct for OE items in the second and third attempts. In summary, Figure 1 shows that for both MC and OE, participants were able to correct a substantial number of initially incorrect responses in the second attempt (12% for OE and 10% for adj. MC) and that even on the third attempt (after two failed attempts) some responses were corrected (6% for OE and 7% for adj. MC).

Figure 1.

Percent correct across attempts and item type (feedback mode only).

The last two column sections of Table 2 compare psychometric properties of first-attempt scores and revision partial-credit scores (based on attempt number) in feedback mode. As expected from the results shown in Figure 1, revision scores are higher than first-attempt scores, especially for MC items. However, for the MC forms, revision scores have lower variability and lower reliability than first-attempt scores, whereas the reverse is true for OE forms. Using the test statistic recommended by Feldt (1980) for comparison of correlated Cronbach’s α coefficients, we find that for the two MC forms the coefficients for first-attempt and revision scores are not significantly different (.748 vs. .738 for MC1 and .750 vs. .747 for MC2, ps > .25) but for the two OE forms they are .887 versus .912 for OE1 and .862 versus .897 for OE2, ps < .01. Applying the Spearman–Brown formula for the two pairs of OE coefficients, we find that the increase in reliability of the revision scores compared with the reliability of first-attempt scores corresponds to an increase in the length of the test forms by a factor of 31% and 39% for OE1 and OE2, respectively. This differential effect on measurement accuracy across item formats is consistent with the main hypothesis of this study, that test takers may be less willing to invest effort in revising their initial incorrect answers in MC compared with OE items.

Correlations Between OE and MC scores

The degree to which OE and MC scores measure the same underlying construct is reflected in the correlation between these scores. Therefore, potential differences in these correlations across modes (standard vs. feedback) may also indicate differences in reactions of test takers to feedback under the two modes. Table 3 presents the correlations between OE and MC scores, both for standard mode and feedback mode (revision scores). For both Forms 1 and 2, raw correlations are higher for standard scores than for revision (feedback) scores, and the differences in these correlated correlations are statistically significant (ps < .01; see Meng, Rosenthal, & Rubin, 1992). This pattern manifests itself for estimates of true-score correlations (computed by dividing raw correlations by the square root of the product of the reliability estimates, presented in previous tables). True-score correlations for standard scores are very high, .97 and .96, but are lower for revision scores (.95 and .90, respectively). These results provide further support for the main hypothesis of this study, namely, that test takers react differently to feedback across testing modes, with more effort invested in revising answers in OE mode. This difference would lower the correlations between MC and OE revision scores, compared with standard no-feedback scores.

Table 3.

OE–MC Correlations.

	Form 1 (N = 418)		Form 2 (N = 424)
Score	Raw	True score	Raw	True score
Standard	.800	.967	.780	.960
Revision	.780	.951	.734	.897

Note. OE = open-ended; MC = multiple-choice.

Validity Coefficients

Correlations with mathematics school grades were used as validity coefficients and were compared across item formats and feedback mode. Table 4 shows that coefficients for standard scores were similar to those for revision scores in all four cases (none of the comparisons was statistically significant), but coefficients were higher for OE scores than MC scores (all ps < .01). In other words, validity coefficients were higher for OE than MC but the differences were not larger for feedback mode than standard mode.

Table 4.

Correlations With School Mathematics Grades.

	Form 1 (N = 418)		Form 2 (N = 424)
Score	MC	OE	MC	OE
Standard	.476	.545	.475	.571
Revision	.480	.537	.458	.587

Note. OE = open-ended; MC = multiple-choice.

Response Time Analysis

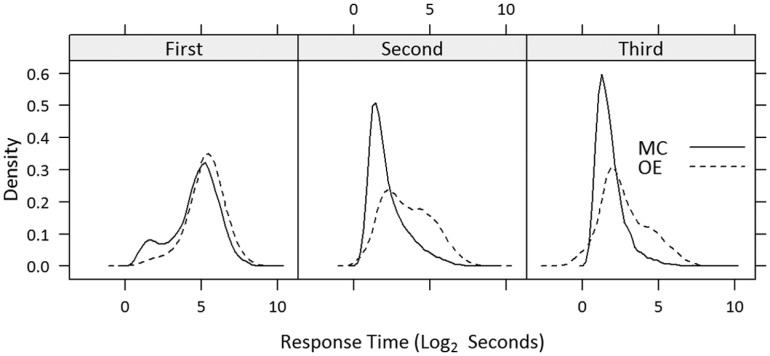
The previous results suggest that in the context of OE items, test takers are able to demonstrate partial knowledge through their revised answers following feedback. However, with MC items revision of answers does not contribute to higher measurement precision. The cause of this difference may be less effort in revising answers in the context of MC items due to the ready availability of alternative answer options. In other words, in the context of MC items test takers are more likely to engage in rapid guessing behavior in response to feedback. Figure 2 shows that response time patterns for the two item types across attempts conform to this expectation. In the first attempt, response time distributions for the two item types are similar. The main difference between types in the first attempt is the slightly higher proportion of rapid responses for MC items, apparent in the figure as a small “bump.” However, in the second and third attempts, the differences in response time distributions of the two item types are more pronounced. For these later attempts, the MC distributions are dominated by rapid responses, much more so than for OE items.

Figure 2.

Density plot of response time across attempts and item type (feedback mode only).

Conclusions

This study found several differences in test takers’ reactions to feedback under MC and OE item formats. First, MC first-attempt scores in standard mode were higher than in feedback mode. This is possibly because of the fact that test takers knew they would have a second chance to answer the question and therefore may have felt less scrupulous about their first response (see also Attali & Powers, 2010). However, this effect was not found for OE, suggesting that when answering OE questions test takers may have been more careful even in the first attempt. More important, large differences in measurement accuracy were found between the item formats. As expected from the lack of a guessing factor in OE items, internal consistency measures were higher for OE than MC items for first-attempt scores. The MC test would need to be lengthened by an estimated (through the Spearman–Brown formula) 144% and 100% (for Forms 1 and 2, respectively) in order to reach the reliability of the OE tests.

But these differences were even larger when revision scores were considered. For MC, revision scores had lower variability and lower reliability than first-attempt scores, whereas the reverse was true for OE. As a consequence, the MC test would need to be lengthened by an estimated 269% and 142% (for Forms 1 and 2, respectively) in order to reach the reliability of the OE test. This result suggests that in the context of OE items, test takers are able to demonstrate partial knowledge through their revised answers following feedback whereas with MC items successful revision of answers does not result in higher measurement precision. Additionally, true-score correlations between OE and MC scores were lower in feedback mode than in standard mode (although quite high in all cases), and validity coefficients were higher in OE format than in MC format (although the differences did not seem to be larger in feedback than standard mode).

The possibility that these results are due to less effort in revising answers in the context of MC items due to the ready availability of alternative answer options was supported by response time analysis that showed that in the context of MC items test takers are more likely to engage in rapid guessing behavior in response to feedback. These results can be explained through the general concept of effortful and mindful problem solving. Multiple-try feedback tries to prime students to reflect on their errors. This reevaluation of the problem after feedback (indicating an incorrect response) involves a greater exertion of effort. OE questions may provide a more conducive context for this effort by forcing the student to generate the response instead of selecting one.

One area where these results may have value is in the design of formative assessments. The interest in formative assessment has been growing in recent years. However, in a critical review of the field, Bennett (2011) argues that the widely cited claims of the effectiveness of formative assessment on student achievement (Black & Wiliam, 1998; Bloom, 1984; Rodriguez, 2004) are not well grounded and that “the magnitude of commonly made quantitative claims for effectiveness is suspect, deriving from untraceable, flawed, dated, or unpublished resources” (p. 5). Moreover, even a basic component of formative assessment, the provision of feedback to learners, is not well understood (Shute, 2008). The results of this study shed more light on the psychometric effects of interactive test items in the context of both MC and OE item formats.

Another area where these results may prove useful is in raising student motivation in low-stakes assessments. Past research supports the assumption that tests with no personal consequences, that is, low-stakes tests, are associated with a decrease in motivation and performance (Wise & DeMars, 2005). Extrinsic rewards (such as monetary incentives) as a way to motivate students in tests have generally found weak effects on performance (Braun, Kirsch, & Yamamoto, 2011; O’Neil, Abedi, Miyoshi, & Mastergeorge, 2005). The use of more engaging item types, including the use of constructed response and interactive item types, may be more effective in motivating students in these types of tests.

Several limitations of this study should be noted. First, this study focused on mathematical problem solving. It is possible that in other content areas that are based on declarative (e.g., vocabulary) rather than procedural knowledge, the effect of feedback and revision in selected-response as well as constructed-response tests might be different. Second, the focus of the study has been on low-stakes testing. The effects of item type in a high-stakes context might be different—specifically, test takers may be more willing to exert effort even in MC tests when the stakes are higher. Finally, the study focused on middle school children because of the potential applications of such low-stakes exams for K-12 test takers. However, it is not clear how adults would respond to the different conditions of testing that were examined in this study.

In summary, advances in computer-based testing makes constructed-response items a more feasible alternative to selected-response items and allows the intriguing possibility of providing immediate feedback to examinees and making assessments into more interactive experiences. The results of this study suggest that this interactivity was more beneficial to the measurement of test-takers’ ability with OE than MC items. These advantages could benefit different types of assessments, including formative and other low-stakes assessments.