The Impact of Ignoring the Level of Nesting Structure in Nonparametric Multilevel Latent Class Models

Abstract

The multilevel latent class model (MLCM) is a multilevel extension of a latent class model (LCM) that is used to analyze nested structure data structure. The nonparametric version of an MLCM assumes a discrete latent variable at a higher-level nesting structure to account for the dependency among observations nested within a higher-level unit. In the present study, a simulation study was conducted to investigate the impact of ignoring the higher-level nesting structure. Three criteria—the model selection accuracy, the classification quality, and the parameter estimation accuracy—were used to evaluate the impact of ignoring the nested data structure. The results of the simulation study showed that ignoring higher-level nesting structure in an MLCM resulted in the poor performance of the Bayesian information criterion to recover the true latent structure, the inaccurate classification of individuals into latent classes, and the inflation of standard errors for parameter estimates, while the parameter estimates were not biased. This article concludes with remarks on ignoring the nested structure in nonparametric MLCMs, as well as recommendations for applied researchers when LCM is used for data collected from a multilevel nested structure.

Introduction

One fundamental assumption underlying latent class models (LCMs; Goodman, 1974; Lazarsfeld & Henry, 1968) is that observed responses are conditionally independent of each other, given latent class memberships. This local independence assumption is often violated because individuals are naturally nested within a higher-level unit, and such a nested structure creates dependency in collected data. This observed dependency in data can be attributed to the communalities that individuals share by belonging to the same higher-level unit, such as a school or an organization. When analyzing data with a nested structure, researchers should consider this additional dependency.

The multilevel latent class model (MLCM; Vermunt, 2003, 2004) is a multilevel extension of the LCM that incorporates possible dependency due to a nested structure. Vermunt (2003) discussed two versions of MLCMs: the parametric MLCM, which is assumed to have a continuous random effect to deal with dependency due to the nested structure, and the nonparametric MLCM, on the other hand, has a discrete latent variable at the higher-level, under the assumption that individuals as well as groups are assigned to latent classes.¹ Several authors have proposed various specifications for MLCMs. For example, Henry and Muthén (2010) presented MLCMs with normally distributed random effects at three different levels, while Di and Bandeen-Roche (2011) introduced an MLCM that assumes a Dirichlet distributed random effect to capture variability among higher-level units. Furthermore, other authors (e.g., Muthén & Asparouhov, 2008; Palardy & Vermunt, 2010; Varriale & Vermunt, 2012) have proposed related multilevel extensions of LCMs with either continuous or discrete random effects at multiple levels.

Ignoring the nested data structure when analyzing data is sometimes unavoidable: for example, when the higher-level data structure cannot be identified appropriately (Moerbeek, 2004); when individuals belong to multiple higher-level units simultaneously, but cannot be reasonably disentangled (Chen, Kwok, Luo, & Willson, 2010); or when a model including a multilevel structure has difficulty reaching convergence (Van Landeghem, De Fraine, & Van Damme, 2005). A number of studies have investigated the consequences of ignoring a higher-level structure within the context of mixture modeling when such a misspecification is unavoidable. For example, Chen et al. (2010) investigated the consequences of ignoring the higher-level structure in a three-level multilevel growth mixture model. The results of their simulation study showed that when the higher-level nesting structure was ignored, the classification of individuals became less accurate. Their findings also revealed that the classification accuracy was mainly affected by the size of variance at the group level (i.e., intraclass correlation [ICC]), as well as the within-class variance-covariance and the distribution of latent classes (i.e., mixing proportion).

Chen et al.’s (2010) results were similar to earlier studies that focused on multilevel regression modeling (e.g., Maas & Hox, 2004; Moerbeek, 2004; Moerbeek, van Breukelen, & Berger, 2003; Tranmer & Steel, 2001; Van Landeghem et al., 2005; Wampold & Serlin, 2000). These studies noted that when the higher-level nesting structure was ignored, the variances of the ignored higher-level structure were relocated to the adjacent level, whereas the estimates of the fixed effects were not biased. On the other hand, ignoring the higher-level structure resulted in overestimated standard errors for the fixed effects at the lower level; however, in general, the standard errors of the fixed effects at the higher-level are only slightly overestimated.

Kaplan and Keller (2011) studied the effects of ignoring the multilevel data in a parametric MLCM. They generated data using moderately separated MLCMs with three different ICC values. The values of ICC were manipulated to adjust the amount of variance among the higher-level units. Their study showed that the ICC and the ratio of higher-level to lower-level sample sizes are two crucial factors that determine the classification quality of latent class membership and relative model fit measures. Specifically, when the amount of variance at the higher-level structure is large (a larger ICC) and the sample sizes at the higher-level structure are small, ignoring the higher-level structure results in a greater likelihood that individuals were misclassified and differences in the Bayesian information criterion (BIC; Schwarz, 1978) between true model (i.e., MLCM) and misspecified model (i.e., LCM) will increase. These results suggested that under such conditions, misspecified models are less likely to be chosen from a set of competing models; in other words, the impact of ignoring the multilevel structure becomes greater. This study explored the impact of misspecified models with parametric MLCMs. The same issue has not been systematically investigated in the context of nonparametric MLCMs, although it is not clear whether the results from the parametric approach would generalize to nonparametric MLCMs.

A number of studies have noted that a choice of underlying latent variables (continuous or discrete) leads to different consequences in model fit and parameter estimates (e.g., Lubke & Neale, 2006, 2008). Therefore, we hypothesized that the different specifications of two MLCMs may result in different scenarios when the multilevel data structure is ignored. The two MLCMs are considerably different in terms of the random effect that accounts for the variations among the higher-level units. Specifically, the higher-level effect is represented as a continuous random effect originating from a normal distribution with estimated variance terms at the higher level, so that the ICC can be used as a typical measure of the higher-level effects (see Hedeker, 2003). In contrast, a finite number of mixture components (latent clusters) were included to represent the higher-level discrete random effects in a nonparametric MLCM. This mixture component at the higher level is formed by marginalizing over the distribution of lower-level mixture components (latent classes). This specification implies that the classes work as indicators of a discrete latent component at the higher level; thus, the state of the classes (e.g., class separations) has a direct impact on the composition of the latent clusters (Lukočienė, Varriale, & Vermunt, 2010).

Moreover, we believe that examining the impacts of ignoring multilevel data structures in nonparametric MLCMs has practical importance because the nonparametric version of an MLCM is preferable under certain empirical applications. One advantage of using the nonparametric MLCM over the parametric version is that it provides classification information for both higher-level units and lower-level units. This additional information about the latent structure and the classification of higher-level units sometimes provides more useful descriptions and explanations about the observed dependency than the typical variance decomposition approach. Examples of applications include the study by Rüdiger and Hans-Dieter (2013), which clustered German students and their universities based on the attitude toward research methods and statistics. Rindskopf (2006) explored the characteristics of individuals at risk for alcoholism by considering their areas of residence. More broadly, some studies have focused on substantive national-level heterogeneity, offering informative segmentation of countries (e.g., Bijmolt, Paas, & Vermunt, 2004; da Costa & Dias, 2014; Onwezen et al., 2012; Pirani, 2011). Other advantages of a nonparametric MLCM in comparison with a parametric MLCM are that the former approach does not introduce unrealistic assumptions about the distribution of the higher-level random effect (Aitkin, 1999) and it is computationally less intensive than the latter approach (Vermunt, 2004).

In the present study, the potential risk of misspecification is empirically assessed to provide general guidelines for applied researchers. Specifically, we investigated the impact of ignoring multilevel data structures when true latent class solutions were either known or unknown. Various nonparametric MLCM structures were created by manipulating factors that are known to influence cluster-class separations (see, Lukočienė et al., 2010), and then the impact of ignoring the nested structure was examined using various criteria.

The rest of this article is organized as follows. The specifications of nonparametric MLCMs are introduced, and the three types of criteria used to evaluate the misspecification—model selection, classification quality, and the accuracy of parameter estimates—are discussed. A simulation study was conducted to evaluate the impact of ignoring a nested data structure, and the results of the simulation study are presented and discussed. This article concludes with remarks on ignoring the nested structure in nonparametric MLCMs, as well as recommendations for applied researchers about the applications of nonparametric MLCMs in empirical studies.

Nonparametric Multilevel Latent Class Models

A nonparametric MLCM assumes a discrete latent variable (H_g) at the higher-level with L latent clusters, and a discrete latent variable at the lower-level ($X_{\mathrm{gi}}$) with M latent classes. Each outcome of the discrete latent variables can be conceptualized as a latent cluster-class consisting of groups-individuals that are internally homogenous within each cluster-class, but distinct between clusters-classes in terms of the response patterns. The clusters-classes are assumed to be mutually exhaustive and exclusive; thus, the latent cluster-class probabilities can be conceptualized as cluster-class sizes. The sum of these probabilities is one.

Let $Y_{\mathrm{gij}}$ be the response to indicator j of individual i in group g, where g = 1, . . ., G; i = 1, . . ., n_g; and j = 1, . . ., J. ${\mathbf{Y}}_{\mathrm{gi}}$ represents the J responses for individual i nested in group g, and Y_g denotes the full responses of all individuals in group g. The nonparametric MLCM is defined by two separate equations for the higher-level and the lower level. For the lower level, the probability of observing a certain response pattern for individual i in group g can be written as

$$P({\mathbf{Y}}_{\mathrm{gi}})=\sum _{m=1}^{M}P(X_{\mathrm{gi}}=m|H_g=l)\underset{j=1}{\overset{J}{\Pi }}f(Y_{\mathrm{gij}}|X_{\mathrm{gi}}=m,H_g=l).$$

The term $P(X_{\mathrm{ig}}=m|H_g=l)={\rho }_{\mathrm{lm}}$ represents the distribution of conditional latent class probabilities given a particular latent cluster. The conditional response density $f(Y_{\mathrm{gij}}|X_{\mathrm{gi}}=m,H_g=l)$ in Equation (1) is the probability of observing a certain response pattern $Y_{\mathrm{gij}}$ for variable j of individual i in group g, given the latent cluster membership (l) and latent class membership (m). To facilitate interpretation of the results, a restricted form of the conditional density $f(Y_{\mathrm{gij}}|X_{\mathrm{gi}}=m)={\pi }_{\mathrm{mj}}$ is preferred in most multilevel extensions of the LCM (e.g., Asparouhov & Muthén, 2008; Vermunt, 2003). This constraint implies that the conditional response density is affected only by the latent class memberships, but no effects from the higher-level latent cluster were assumed.

The probability density of the nonparametric MLCM at the higher level is

$$P({\mathbf{Y}}_g)=\sum _{l=1}^{L}P(H_g=l)\underset{i=1}{\overset{n_g}{\Pi }}P({\mathbf{Y}}_{\mathrm{gi}}|H=l).$$

Equation (2) assumes that each group belongs to only one latent cluster, and conditional densities for each of the individuals n_g within group g are independent of each other, given the latent cluster membership. By combining Equations (1) and (2) with the restricted form of conditional response probabilities, the MLCM is

$$P({\mathbf{Y}}_g)=\sum _{l=1}^{L}P(H=l)(\underset{i=1}{\overset{n_g}{\Pi }}\sum _{m=1}^{M}P(X_{\mathrm{gi}}=m|H_g=l)\underset{j=1}{\overset{J}{\Pi }}f(Y_{\mathrm{gij}}|X_{\mathrm{gi}}=m)).$$

Density $f(Y_{\mathrm{gij}}|X_{\mathrm{gi}}=m)$ depends on the assumed distributions of the responses. It can take the form of a multinomial distribution, or other more general distributions, such as Poisson or normal. In the MLCM, the estimations of the parameters can be obtained through a modified version of an expectation-maximization algorithm (Vermunt, 2003, 2004).

Evaluation of the Impact of Ignoring the Multilevel Structure

We evaluated the impact of ignoring a nested structure using three criteria: model selection accuracy, lower-level classification quality, and parameter estimation accuracy. The first criterion is based on the assumption that the true latent structure is unknown, whereas the other two presume that the true latent structure is given in advance.

The accuracy of identifying a true latent class structure (in terms of the number of latent classes) was used as the criterion for the model selection. In the context of the LCM, the task of model selection is to determine the optimal number of latent components based on the observed responses. A number of prior studies have suggested using BIC as a standard measure to determine the number of latent classes for a single-level LCM (e.g., Collins, Fidler, Wugalter, & Long, 1993; Hagenaars & McCutcheon, 2002). For model selection in the MLCM, BIC has also been reported to be a good criterion in identifying the true number of latent clusters and classes with both an iterative approach (Lukočienė et al., 2010; Lukočienė, & Vermunt, 2010) and a simultaneous approach (Yu & Park, 2014). In the present study, the model selection accuracy was assessed in each replication by calculating the percentages of the correctly recovered latent structures using BIC. The obtained percentages under various MLCMs were compared to identify the condition in which a true latent class structure was better recovered.

The lower-level classification quality was used as a second criterion to evaluate the impact of ignoring the multilevel structure. The lower-level classification quality is usually represented by how well an individual’s latent class membership can be predicted given the observed responses (Vermunt & Magidson, 2013). Two measures—R-square entropy and classification accuracy rates—were used to measure the quality of the classification. For these two measures, the difference between the true model and the misspecified model is considered to be the degree of impact on the classification quality.

R-square entropy is an index representing the degree of latent class separation for a given mixture model. This measure is based on a weighted average of the posterior latent class probability of each individual (Ramaswamy, DeSarbo, Reibstein, & Robinson, 1993), and it measures the degree of uncertainty on the individual’s classification into latent classes. Lukočienė et al. (2010) proposed R-square entropy measures that quantify the classification quality. The higher-level and lower-level measures are defined as $R_{\mathrm{entropy}.\mathrm{high}}^2$ and $R_{\mathrm{entropy}.\mathrm{low}}^2$, respectively:

$$R_{\mathrm{entropy}.\mathrm{high}}^2=1-\frac{\sum _{g=1}^G\sum _{l=1}^L-P(H_g=l|{\mathbf{Y}}_g)\log P(H_g=l|{\mathbf{Y}}_g)}{\sum _{g=1}^G\sum _{l=1}^L-P(H_g=l)\log P(H_g=l)}.$$

$$R_{\mathrm{entropy}.\mathrm{low}}^2=1-\frac{\sum _{g=1}^G\sum _{i=1}^{n_g}\sum _{m=1}^M-P(X_{\mathrm{gi}}=m|{\mathbf{Y}}_g)\log P(X_{\mathrm{gi}}=m|{\mathbf{Y}}_g)}{\sum _{g=1}^G\sum _{i=1}^{n_g}\sum _{m=1}^M-P(X_{\mathrm{gi}}=m)\log P(X_{\mathrm{gi}}=m)}.$$

The R-square entropy measures range between 0 and 1. A higher value (close to 1) for a given latent structure indicates that groups-individuals can be classified into latent clusters-classes with a high degree of certainty. On the other hand, a value close to 0 suggests greater uncertainty for assigning groups-individuals into latent clusters-classes, with a relatively greater likelihood of classification error.

We used the classification accuracy rate, which is the proportion of individuals classified into correct latent classes, as the second measure of classification quality. This measure can provide an understanding of empirical classification accuracy when the higher-level structure is ignored. In the LCM, each individual is assigned to a single class with the highest posterior probability. However, this class assignment is still made with a degree of uncertainty, particularly when the dominant posterior latent class probability is unclear. In such cases, individuals are likely to be incorrectly assigned to a latent class. The classification quality was evaluated by comparing the proportion of individuals correctly classified into latent classes (i.e., classification accuracy rates) between the true and misspecified models.

This present study used two measures to evaluate the impact that ignoring the nested structure had on parameter estimation accuracy: (1) bias in the parameter estimates and (2) bias in the standard error (SE). The relative percentage bias (RPB) of a parameter estimate was used as an index to quantify the relative difference between the population parameter values and the averaged parameter estimates over replications. The RPB was calculated as $[(\hat{\theta }-\theta /\theta )]\times 100$ (Maas & Hox, 2004). An RPB value of 0 indicates that an estimate is unbiased, whereas a negative bias represents an underestimation of the parameter; a positive RPB value indicates that the parameter is overestimated.

Similarly, the RPB of the standard error is defined as $(S{E}_{\mathrm{False}}-S{E}_{\mathrm{True}}/S{E}_{\mathrm{True}})\times 100$, where SE_False is the average standard deviation of each parameter estimate from the misspecified model, and SE_True is the standard deviation of the estimated parameter obtained from the true model. An acceptable RPB for both the parameter and standard error estimates should not exceed 5% (Muthén & Muthén, 2009).

Simulation Study

We conducted a simulation study to investigate the impact of ignoring the level of the nested structure under a variety of conditions. Data with two levels of latent structure were first generated using nonparametric MLCMs, given a correct number of latent clusters and classes. Then, MLCMs from which the data were generated (i.e., the true model) was fitted to the data; a single-level LCM (i.e., a misspecified model), which did not include the higher-level structure (i.e., clusters) in the model, was also fitted to the data.

Manipulated Factors

Seven design factors were manipulated: (1) number of latent clusters, (2) number of latent classes, (3) latent cluster size, (4) higher-level sample sizes, (5) lower-level sample sizes, (6) conditional latent class probability, and (7) conditional response probability. Twelve binary indicators were used across all conditions.

The number of clusters and classes was set to either two or three at both levels (L = 2 or 3 and H = 2 or 3). This specification resulted in four MLCMs with different levels of model complexity, denoted as H2L2, H2L3, H3L2, and H3L3, where the number refers to the number of latent clusters and classes. For example, H2L3 represents the model with two latent clusters and three latent classes.

The latent cluster probabilities $P(H_g=l)$ were used to manipulate the latent cluster sizes. The sizes of the latent clusters were set to be either equal or unequal. In the equal condition, the probabilities of a group belonging to each cluster were set to be equal (1/2 for two clusters and 1/3 for three clusters). The latent cluster probabilities for the unequal cluster sizes were set to .75 and .25 for H2L2 and H2L3, and .7, .2, and .1 for the H3L2 and H3L3 conditions, respectively.

The higher-level sample size (i.e., the number of groups) and the lower-level sample size (i.e., the number of individuals in a group) were manipulated to investigate the sample size effect at both levels. There were 50 or 100 groups (G) with 10, 20, or 50 individuals per group (N_g) to represent small, medium, and large samples.

The values of the conditional latent class probabilities (${\rho }_{\mathrm{lm}}$) and the conditional response probabilities (${\pi }_{\mathrm{mj}}$) were manipulated. In the present study, the term cluster-class distinctness was used to characterize the pattern of ${\rho }_{\mathrm{lm}}$ and ${\pi }_{\mathrm{mj}}$. According to the definition by Yang and Yang (2007), the distinctness of classes can be considered to be factor loadings in an exploratory factor analysis, where only selected indicators are loaded highly on a particular distinct factor. Similarly, if we consider ${\rho }_{\mathrm{lm}}$ and ${\pi }_{\mathrm{mj}}$ as loadings of a particular cluster and class, then patterns close to such a “simple structure” can be regarded as distinct clusters and classes, respectively.

Two sets of ${\rho }_{\mathrm{lm}}$ and ${\pi }_{\mathrm{mj}}$ values were chosen to represent the different levels of distinctness among the latent clusters and classes. The exact values used in the simulation study are summarized in the appendix. For the more distinct clusters, the values of ${\rho }_{\mathrm{lm}}$ differ greatly among the clusters, but the values of ${\rho }_{\mathrm{lm}}$ are more evenly distributed among the clusters in less distinct conditions. Likewise, the values of ${\pi }_{\mathrm{mj}}$ were designed to differ largely across classes in more distinct conditions, whereas the values of ${\pi }_{\mathrm{mj}}$ were more evenly distributed in less distinct conditions. In the analysis, the two levels of class and cluster distinctness were combined, resulting in four levels of cluster-class distinctness. These four levels are referred to as H–H (more distinct clusters and classes), H–L (more distinct clusters and less distinct classes), L–H (less distinct clusters and more distinct classes), and L–L (less distinct classes and clusters).

Data Generation and Analysis

The fully crossed simulation design yields 192 (2 × 2 × 2 × 2 × 3 × 2 × 2) conditions. For each condition, 100 data sets were generated according to the parameter specifications of that particular condition using R 3.11 software (R Development Core Team, 2010). When generating the data, the population class memberships of each subject were recorded for further analysis. Both the true model and the misspecified models (LCM with 2, 3, and 4 classes) were then fitted to the simulated data using the Latent GOLD 5.0 syntax module (Vermunt & Magidson, 2008). Among those four models, the MLCM was the “true” model with the structure (numbers of clusters and classes) identical to the structure from which the data were generated, while the other three LCMs were “wrong” models. The log-likelihood values of each data set fitted to the four models were recorded to compute the BIC. The number of groups (G) was used as the sample size for the penalty term in BIC, since using G consistently showed better accuracy in identifying the true number of latent components at both levels (Lukočienė et al., 2010; Lukočienė & Vermunt, 2010; Yu & Park, 2014). For each replication, the model with the lowest BIC value was chosen as the best fitting model. The percentage of replications correctly identified the true model by BIC was calculated.

The outputs obtained from the true model (MLCM) and from one of the misspecified models (an LCM including the same lower-level structure as the true model) were used to evaluate the classification quality and the parameter accuracy. The lower-level R-square entropy values for both the true and misspecified models were collected from the Latent GOLD outputs over the replications. The classification accuracy rates were calculated empirically by comparing the population class memberships and the class assignment outcomes from the Latent GOLD output. The parameter estimates, as well as the standard errors of conditional response probability (${\pi }_{\mathrm{mj}}$) for the true and misspecified models, were also recorded for further analysis.

A logistic regression was used to decide which factor had a significant effect on the model selection accuracy. The dependent variable was whether BIC correctly identified the true model (MLCM) among the competing models. The seven aforementioned factors and all possible two-way interactions were included as predictors in the logistic regression. The importance of the effects was evaluated on the basis of the odds ratio of the predictors, which represents the constant effects of predictors on the dependent variable.

Analyses of variance (ANOVA) were conducted to study the effects that the manipulated factors had on the classification quality and the parameter estimation accuracy. The RPBs of the measures including the R-square entropy, the classification accuracy rates, parameter estimates, and the standard errors of ${\pi }_{\mathrm{mj}}$ were calculated and then used as the dependent variables. Note that an effect size measure η² ($S{S}_{\mathrm{Effect}}/S{S}_{\mathrm{Total}}$) was used to filter out the trivial effects, and it was used as an index to determine the relative importance of the seven factors. Any effect with η² larger than .01 was considered to be meaningful and was interpreted, further, as was done in similar previous studies (Chung & Beretvas, 2012; Krull & MacKinnon, 1999).

Simulation Results

Model Selection Accuracy

The model selection accuracy using BIC was examined to investigate the impact of ignoring the nested structure. The overall probability of correctly identifying the true model (MLCM) was 86.7% across all the simulation conditions, which shows that BIC correctly identified the true models in the majority of the conditions designed in the simulation.

Table 1 shows the odds ratio (OR) for the main effects and the significant two-way interactions of the seven factors. The results indicated that two factors related to cluster structure, cluster distinctness (OR = 57.497), and cluster size (OR = 7.766), and the number of individuals per group (Ng; OR = 2.044) are the three important factors affecting the model selection accuracy. This represents that the odds of recovering the true model under more distinctive clusters is 57.497 times higher than the odds under less distinctive clusters, while the odds under unequal cluster sizes and larger sample sizes (N_g = 50) are 7.766 times and 2.044 times higher than equal and smaller sample sizes, respectively.

Table 1.

The Odds Ratio of Main Effects and Significant Interaction Effects of the Model Selection Accuracy.

Dependent variables	Cluster size	Cluster# (#H)	Class# (#L)	Cluster distinctness (${\rho }_{\mathrm{lm}}$)	Class Distinctness (${\pi }_{\mathrm{mj}}$)	Ng	G	Two-way interaction
Accuracy by BIC	7.766	0.059	0.187	57.497	0.587	2.044	1.000	Size *${\rho }_{\mathrm{lm}}$(17.926)

Note. BIC = Bayesian information criterion. The * indicates an interaction between two factors. Notable effects appear in bold.

Table 2 lists the average model selection accuracy using BIC for the three significant factors in the logistic regression analysis. The patterns showed that the model selection was more accurate under the conditions in which the clusters were more distinctive, the clusters were unequally distributed, and the sample sizes at the lower-level were larger. These results indicate that the misspecification has a greater impact when more distinct and equal-sized clusters are being ignored under larger lower-level sample sizes.

Table 2.

The Average Model Selection Accuracy Rates Under Different Cluster Distinctness, Cluster Size and Lower-Level Sample Sizes.

Factors	Level	Accuracy rates
Cluster distinctness	Less	0.735
	More	1.000
Cluster size	Equal	0.772
	Unequal	0.943
Lower-level sample sizes	10	0.807
	20	0.852
	50	0.933

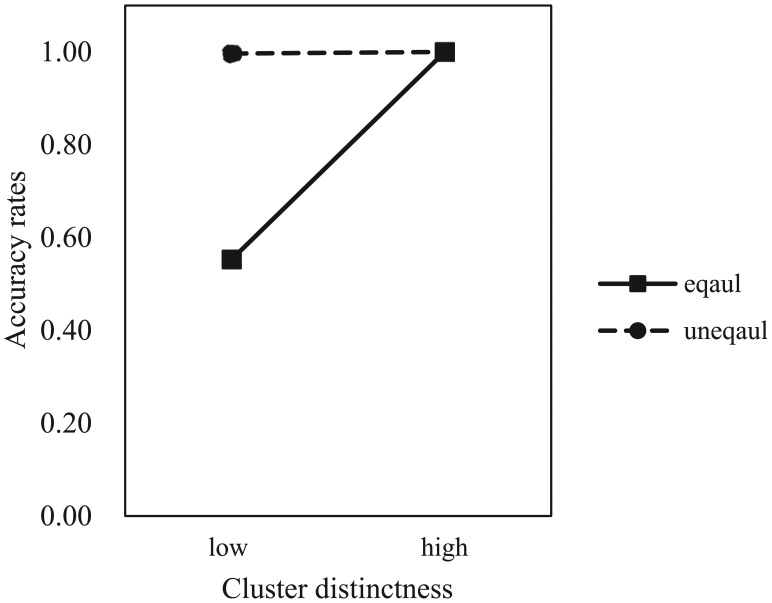
An interaction effect between cluster size and cluster distinctness was found (OR = 17.926). A plot of this interaction is shown in Figure 1. It suggests that the performance of BIC increased rapidly in the condition of more distinctive clusters with equal cluster sizes, while BIC almost perfectly recovered the true latent structure when the clusters are unequally distributed, regardless of whether the clusters were more or less distinctive.

Figure 1.

Interaction between the cluster size and cluster distinctness.

Classification Quality

Table 3 displays the effect sizes (η²) for the main effects and the significant two-way interaction effects that the seven factors had on the measures of classification quality: R-square entropy and the classification accuracy rates.

Table 3.

The Effect Sizes (η²) of Main Effects and Two-Way Interaction Effects of the Two Criteria for Classification Quality.

Dependent variables	Cluster size	Cluster# (#H)	Class# (#L)	Cluster distinctness (${\rho }_{\mathrm{lm}}$)	Class distinctness (${\pi }_{\mathrm{mj}}$)	Ng	G	Two-way interaction
Entropy	0.016	0.027	0.124	0.080	0.107	0.001	0.000	#H * #L (.064)
								${\rho }_{\mathrm{lm}}$*${\pi }_{\mathrm{mj}}$(.048)
Accuracy rates	0.005	0.029	0.026	0.003	0.017	0.000	0.000	#H * #L (.031)
								#H *${\pi }_{\mathrm{mj}}$ (.016)

Note. The * indicates an interaction between two factors. Notable effects (η² > .01) appear in bold

R-Square Entropy

The lower-level R-square entropy for the true and misspecified models was examined. The overall results showed that the R-square entropy for true models ranged from 0.527 to 0.982, whereas the value for misspecified models ranged from 0.152 to 0.981. Furthermore, the mean of R-square entropy for the true models (M = 0.813, SD = 0.122) was slightly higher than it was for the misspecified models (M = 0.745, SD = 0.166). The averaged RPB of R-square entropy across 192 conditions was −5.264 (SD = 11.692). This value indicates that the R-square entropy for the misspecified models (LCM) is, on average, about 5.264% less than it is for the true model (MLCM). In addition, 94% of the conditions created in the simulation study had negative RPB values. Therefore, it is clear that ignoring the higher-level structure decreased the classification quality in the majority of the conditions designed in the simulation.

The significant main effects are presented in Table 4. Two factors related to the lower-level latent structure had substantial effects on the RPB of R-square entropy: the number of latent classes (${\eta }^2=.124$) and the distinctness of the latent classes (${\eta }^2=.107$). The average RPB was higher under the conditions in which the latent class structure was more complex (L = 3) than in conditions with a less complex structure (L = 2). Moreover, the condition of less distinct classes was observed to have a larger average RPB than the condition of more distinct classes.

Table 4.

The Average Relative Percentage Bias (RPB) of R² Entropy Under Different Numbers of Latent Components, Clusters/Classes Distinctness and Cluster Size.

Factors	Level	Average RPB
Cluster#	2	−3.337
	3	−7.192
Class#	2	−1.152
	3	−9.377
Cluster distinctness	Less	−1.965
	More	−8.565
Class distinctness	Less	−9.093
	More	−1.436
Cluster size	Equal	−6.750
	Unequal	−3.780

Although the effects were less substantial, the RPB of R-square entropy was also significantly associated with the factors related to the higher-level structure: the distinctness of the latent clusters (${\eta }^2=.080$), the number of latent clusters (${\eta }^2=.027$), and the cluster sizes (${\eta }^2=.016$). As shown in Table 4, ignoring more complex latent clusters (H = 3), more distinct latent clusters, and equally distributed clusters yielded a substantial increase in the negative average RPB.

In addition to the main effects, significant interaction was observed between the number of classes and clusters (${\eta }^2=.064$). Higher average RPBs were found as both the cluster and class structures became more complex (the number of clusters and classes increased), but this increasing pattern was not observed in the H3L2 model. In addition, the average RPB in the H3L2 model was quite small, and it was close to 0 regardless of the cluster-class distinctness and cluster size, ranging from −0.013 to −0.366.

Another interaction between cluster and class distinctness (${\eta }^2=.048$) was substantially associated with the RPB of the R-square entropy. Table 5 shows that conditions with more distinct clusters and less distinct classes (H–L) had particularly large bias among all possible combinations of cluster and class distinctness, except for the H3L2 conditions. The RPB was even greater under the conditions with equally distributed clusters. In particular, when the true model is H3L3, ignoring equally distributed distinct clusters with less distinct classes yielded the largest average RPB (−64.592), indicating that the classification quality of the misspecified models was inferior to that of the true model in this condition.

Table 5.

The Average Relative Percentage Bias of R² Entropy Under Different Conditions of Latent Classes/Cluster Complexity and Distinctness.

Cluster size	Model	Classes/cluster distinctness
		H–H	H–L	L–H	L–L
Equal	H2L2	−0.845	−7.087	−0.046	−0.436
	H2L3	−2.120	−11.833	−0.741	−4.043
	H3L2	−0.045	−0.366	−0.017	−0.176
	H3L3	−6.417	−64.592	−1.913	−7.315
Unequal	H2L2	−0.698	−5.909	−0.237	−2.144
	H2L3	−1.888	−10.578	−0.758	−4.032
	H3L2	−0.029	−0.255	−0.013	−0.127
	H3L3	−5.271	−19.101	−1.937	−7.497

These patterns suggested that the class structure (i.e., class distinctness and the number of classes) is pivotal in determining the level of classification quality. Although the effects were not substantial as factors related to class structure, ignoring the more complex and more distinct clusters with equal size also had an adverse effect on the RPB.

Classification Accuracy Rates

In general, the overall classification accuracy rates were quite high. The overall classification accuracy rates for both the true and misspecified models was more than 90%, but the accuracy rates in the true models were slightly higher than the misspecified models. The averaged accuracy rate for the true models was 92.5% (SD = 1.64); for the misspecified models the averaged accuracy rates were 90.1% (SD = 2.94).

The number of clusters and classes turned out to have a substantial main effect: ${\eta }^2=.029$ and ${\eta }^2=.026$, respectively. As shown in Table 6, the average RPB increased as both the numbers of clusters and classes increased (H = 3 and L = 3). This pattern implies that the classification of the misspecified models was relatively inaccurate compared with the true model under more complex latent structure, at both levels. Moreover, distinctness among classes was found to have a substantial effect on the RPB, ${\eta }^2=.017$, yielding larger bias under less distinct conditions.

Table 6.

The Average RPB of Classification Accuracy Rates Under Different Numbers of Latent Components and Class Distinctness.

Factors	Level	Average RPB
Cluster#	2	−0.132
	3	−1.963
Class#	2	−0.223
	3	−1.871
Class distinctness	Less	−1.697
	More	−0.397

Note. RPB = Relative percentage bias.

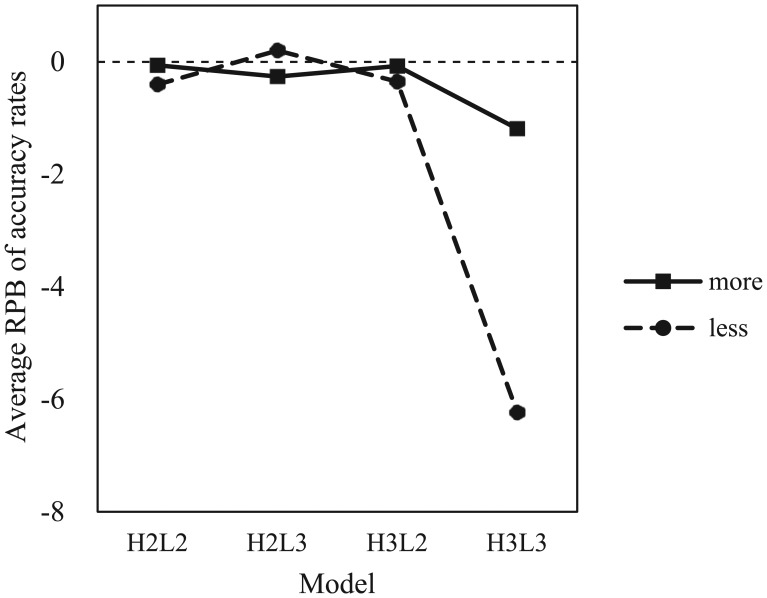
The ANOVA results also revealed that the number of latent clusters significantly interacted with the number of latent classes, ${\eta }^2=.031$, as well as the class distinctness, ${\eta }^2=.016$. Figure 2 shows that negative RPB values increased as both the latent cluster and class structures became more complex (H3L3), while the increase in RPB was particularly prominent when the classes were less distinct, which indicates that the influence of the number of clusters-classes was more evident in the less distinct classes. In summary, the adverse impact of ignoring the multilevel data structure was pronounced when the latent structure was complex, and this effect became more substantial when the classes were less distinct.

Figure 2.

Interaction between the numbers of latent clusters/classes and class distinctness.

Parameter Estimate Accuracy

The parameter estimate accuracy results are summarized in this section. The main effects and the two-way interaction effects that the seven factors had on the parameter estimate bias and the standard error bias are summarized in Table 7.

Table 7.

The Effect Sizes (η²) of Main Effects and Significant Interaction Effects of the Two Criteria for Parameter Estimates Accuracy.

Dependent variables	Cluster size	Cluster# (#H)	Class# (#L)	Cluster distinctness (${\rho }_{\mathrm{lm}}$)	Class distinctness (${\pi }_{\mathrm{mj}}$)	Ng	G	Two-way interactions
Parameter bias	0.002	0.003	0.004	0.007	0.004	0.006	0.000
SE bias	0.001	0.001	0.045	0.026	0.014	0.000	0.000	#L *${\rho }_{\mathrm{lm}}$(.019)
								#L *${\pi }_{\mathrm{mj}}$(.011)

Note. SE = standard error. The * indicates an interaction between two factors. Notable effects (η² >.01) appear in bold face

Parameter Estimation Bias

Ignoring the multilevel data structure did not have a substantial impact on the accuracy of the parameter estimates. The results indicated that both the true and misspecified models almost perfectly recovered the parameters, ${\pi }_{\mathrm{mj}}$. The calculated RPB was extremely small, ranging from 0.000 to 0.806. The ANOVA results indicated that none of the seven factors or their interaction effects were larger than 0.01.

Standard Error Bias

The impact of misspecifying the multilevel data structure on the estimated standard error (SE) of parameter, ${\pi }_{\mathrm{mj}}$, was examined. The SE for true models ranged from 0.071 to 0.428, whereas the SE for the misspecified models ranged from 0.088 to 0.778. The positive RPB of the SE suggests that the SE in the misspecified models was inflated, as compared with the SE in the true models. The calculated average RPB of the SE was 4.92 (SD = 6.878); in general, this indicates that the SE in the misspecified models was 4.92% higher than it was in the true model.

As shown in Table 8, the ANOVA results demonstrated that three main effects were substantially associated with the RPB of the SE: the number of latent classes, ${\eta }^2=.045$; the cluster distinctness, ${\eta }^2=.026$; and the class distinctness, ${\eta }^2=.014$. It appears that having more complex class structure (L=3) led to a sharp increase in the RPB of the SE. In addition, the bias increased as the latent classes became more distinct, but it decreased as the latent clusters became more distinct.

Table 8.

The Average Relative Percentage Bias (RPB) of Standard Error Under Different Numbers of Latent Classes and Cluster/Class Distinctness.

Factors	Level	Average RPB
Class#	2	0.302
	3	5.878
Cluster distinctness	Less	1.871
	More	4.321
Class distinctness	Less	4.931
	More	1.011

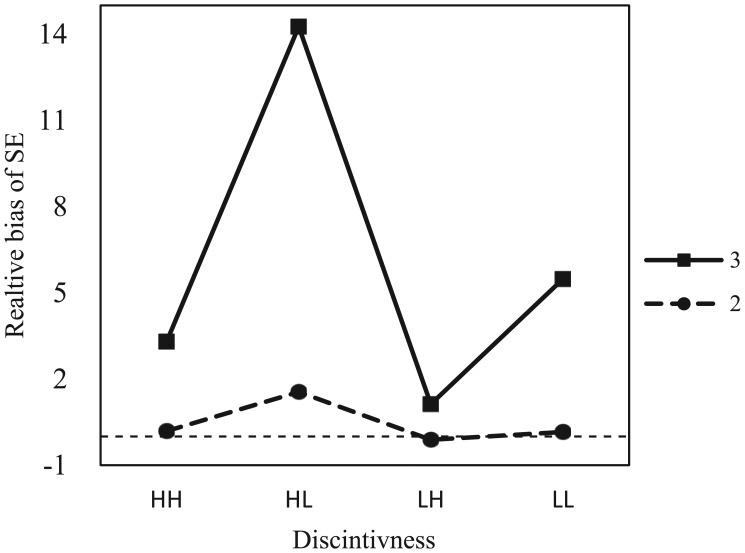
For significant interaction effects, the number of latent classes interacted with the cluster distinctness, ${\eta }^2=.019$, and the class distinctness, ${\eta }^2=.011$. As shown in Figure 3, the highest RPB, ranging from 1.553 to 14.256, was found under the H–L condition, whereas the L–H condition had the lowest RPB, ranging from −0.110 to 1.130. The difference in RPB between the H–L and L–H conditions was particularly large when the class structure was more complex (L = 3). This pattern generally indicates that the RPB of the SE tended to be inflated when class structure was more complex, but it also interacted with cluster and class distinctness, showing larger bias under more distinct clusters and less distinct classes (H–L).

Figure 3.

Interaction between the number of classes and cluster/class distinctness.

Discussion

This study aimed to investigate the impact of ignoring a higher-level nesting structure in a nonparametric MLCM. We conducted a simulation study with seven manipulated factors, using three evaluation criteria: the accuracy of the model selection, the classification quality, and the parameter estimate accuracy. In general, ignoring the higher-level nesting structure in the MLCM resulted in poor performance of BIC in recovering the true latent structure when the true latent class solution was unknown. In the condition in which the true solution is given, individuals were inaccurately classified into latent classes and the standard errors for the parameter estimates were inflated, but the parameter estimates were not affected.

The previous study using parametric MLCM (Kaplan & Keller, 2011) showed that the amount of variation among the higher-level units (size of the ICC) was a crucial determinant for the model fit using BIC and the classification quality. Specifically, the poorer model fit and the less accurate classification of individuals are found when the higher-level structure with larger ICC is ignored.

In general, the results of this study are consistent with the findings from the previous study on a parametric MLCM, although the specification of a nonparametric MLCM is quite different from those of a parametric MLCM. We found that factors related to the variations among the higher-level units (cluster distinctness) as well as the structure of higher-level components (number of clusters) have substantial effects, judging by the three criteria that were chosen. The results suggest that the performance of BIC becomes significantly worse as more distinct clusters are ignored. The larger bias of R-square entropy was associated with ignoring more distinct and more complex clusters, whereas the larger bias of the classification accuracy rates was observed when more complex clusters were ignored. The results also revealed that ignoring the more distinct cluster structure yields inflated standard errors.

One possible explanation for why these patterns occur can be found in whether or not the underlying dependency is well captured. Specifically, the dependency in the responses due to the nested structure cannot be appropriately captured by the single-level latent class structure if the presence of the dependency is evident. Thus, the model selection accuracy, the classification quality, and the parameter estimate accuracy are hindered by this model misspecification (i.e., ignoring the nested structure and fitting only a single-level LCM). As more distinct and complex clusters are ignored—which represent larger amounts of dependency in the data—poorer performance in model selection, less accurate classification, and inflated standard errors for the parameter estimates were observed. This finding led to our recommendation that when applied researchers analyze data with a multilevel structure they should carefully model the dependency in the latent structure using either a parametric MLCM or a nonparametric MLCM.

Moreover, we also found that the three criteria depend heavily on factors related to the lower-level structure (class distinctness, the number of classes, and the lower-level sample sizes). These results suggested that the larger bias of R-square entropy, the classification accuracy rates, and the standard error are associated with conditions in which the classes are more distinct and complex. These findings are not particularly surprising because those measures are based on the properties of lower-level units. A number of prior studies also reported that the class assignments are less accurate and the standard errors of parameter estimates are biased when the classes are poorly separated (Chen et al., 2010; Depaoli, 2012; Tolvanen, 2008).

The results related to the effects of sample size are consistent with the findings presented in Kaplan and Keller’s (2011) study; that is, the model fit by BIC is highly sensitive to changes in sample sizes, while classification quality measured by R-square entropy is not affected by the sample sizes. However, in our study, some of the findings were inconsistent with Kaplan and Keller’s (2011) results. For example, they reported an interaction effect between class size and ICC on both R-square entropy and the BIC measures; however, in the present study, the R-square entropy bias was consistently larger in the equal cluster size than in the unequal cluster size, across other controlled factors, while no interactions were found between cluster size and other factors in terms of the accuracy of the parameter estimates.

One important finding of our study is that the criteria are not only associated with the factors related to cluster and class structure; they are also affected by the interactions of those factors. Specifically, ignoring more distinct clusters with less distinct classes (the H–L condition) produced a larger bias in both R-square entropy and standard error; this pattern became particularly prominent under the complex model (H3L3). On the other hand, smaller bias was found under less distinct clusters and more distinct classes (the L−H condition). This pattern was more evident under simpler latent structures (H2L2), which resulted in the most accurate classification and the lowest bias in standard error among all possible conditions in the simulation study.

Based on the findings in the present article, we recommend that LCM results should be interpreted with caution if a higher-level nesting structure is not incorporated in the analyses, particularly when an obtained LCM (selected number of classes) solution is complex and the classes are not distinct. In such a case, the classification quality and the parameter estimates accuracy can be easily affected by the dependency among the higher-level units. Consequently, if researchers do not account for the dependency by ignoring the higher-level structure, they might misattribute the inaccurate classification and biased SE to the fact that the selected LCM fails to fit the data well.

Conclusion

All the previous results suggest that knowledge about the true latent structure is important to gauge the potential impact of ignoring the multilevel structure, even though the true latent structure of the data is usually “unknown.” We suggest paying careful attention to the literature and gathering substantive knowledge about the topics and the patterns of estimated parameters (e.g., latent class probabilities and conditional response probabilities), as this information can provide clues about the true latent structure of the data.

In addition to substantive understanding of contents and reviewing the findings from previous studies, most software dealing with MLCM, such as Latent GOLD or Mplus (Muthén & Muthén, 2012) provide measures for classification quality that quantify the separation between classes-clusters (such as R-square entropy) in the output. We recommend that researchers regularly check the values of these measures to decide whether or not a higher-level structure should be incorporated in the analysis when LCM is used for multilevel data.

In summary, this study investigated the potential risks of ignoring the higher-level structure in a nonparametric MLCM; it examined and discussed the effects of the factors related to class-cluster separation. The article presented the findings from a simulation study to discuss and evaluate the impact of ignoring the multilevel data structure in a nonparametric MLCM. As MLCMs have been shown to have a variety of possible applications, we hope this study’s findings contribute to promoting the appropriate use of MLCMs in empirical data analysis.

Appendix

Specifications of the Conditional Latent Class Probabilities (${\rho }_{\mathrm{mj}}$) for More Distinct Classes and Less Distinct Clusters.

	More distinct clusters		Less distinct clusters
	H = 2	H = 3	H = 2	H = 3
L = 2	$\left[\begin{array}{cc}\hfill .8\hfill & \hfill .2\hfill \\ \multicolumn{1}{c}{.2}& \hfill .8\hfill \end{array}\right]$	$\left[\begin{array}{ccc}\hfill .8\hfill & \hfill .5\hfill & \hfill .2\hfill \\ \multicolumn{1}{c}{.2}& \hfill .5\hfill & \hfill .8\hfill \end{array}\right]$	$\left[\begin{array}{cc}\hfill .6\hfill & \hfill .4\hfill \\ \multicolumn{1}{c}{.4}& \hfill .6\hfill \end{array}\right]$	$\left[\begin{array}{ccc}\hfill .6\hfill & \hfill .5\hfill & \hfill .4\hfill \\ \multicolumn{1}{c}{.4}& \hfill .5\hfill & \hfill .6\hfill \end{array}\right]$
L = 3	$\left[\begin{array}{cc}\hfill .8\hfill & \hfill .1\hfill \\ \multicolumn{1}{c}{\begin{array}{c}\hfill .1\hfill \\ \multicolumn{1}{c}{.1}\end{array}}& \hfill \begin{array}{c}\hfill .8\hfill \\ \multicolumn{1}{c}{.1}\end{array}\hfill \end{array}\right]$	$\left[\begin{array}{cc}\hfill .8\hfill & \hfill \begin{array}{cc}\hfill .1\hfill & \hfill .1\hfill \end{array}\hfill \\ \multicolumn{1}{c}{\begin{array}{c}\hfill .1\hfill \\ \multicolumn{1}{c}{.1}\end{array}}& \hfill \begin{array}{cc}\hfill \begin{array}{c}\hfill .8\hfill \\ \multicolumn{1}{c}{.1}\end{array}\hfill & \hfill \begin{array}{c}\hfill .1\hfill \\ \multicolumn{1}{c}{.8}\end{array}\hfill \end{array}\hfill \end{array}\right]$	$\left[\begin{array}{cc}\hfill .6\hfill & \hfill .2\hfill \\ \multicolumn{1}{c}{\begin{array}{c}\hfill .2\hfill \\ \multicolumn{1}{c}{.2}\end{array}}& \hfill \begin{array}{c}\hfill .2\hfill \\ \multicolumn{1}{c}{.6}\end{array}\hfill \end{array}\right]$	$\left[\begin{array}{cc}\hfill .6\hfill & \hfill \begin{array}{cc}\hfill .2\hfill & \hfill .2\hfill \end{array}\hfill \\ \multicolumn{1}{c}{\begin{array}{c}\hfill .2\hfill \\ \multicolumn{1}{c}{.2}\end{array}}& \hfill \begin{array}{cc}\hfill \begin{array}{c}\hfill .6\hfill \\ \multicolumn{1}{c}{.2}\end{array}\hfill & \hfill \begin{array}{c}\hfill .2\hfill \\ \multicolumn{1}{c}{.6}\end{array}\hfill \end{array}\hfill \end{array}\right]$

Specifications of Conditional Response Probabilities (${\pi }_{\mathrm{mj}}$) for More Distinct Classes and Less Distinct Classes.

	More distinct classes	Less distinct classes
L = 2	$\left[\begin{array}{c}\hfill \begin{array}{cccccccccccc}\hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill \end{array}\hfill \\ \multicolumn{1}{c}{\begin{array}{cccccccccccc}\hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill \end{array}}\end{array}\right]$	$\left[\begin{array}{c}\hfill \begin{array}{cccccccccccc}\hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill \end{array}\hfill \\ \multicolumn{1}{c}{\begin{array}{cccccccccccc}\hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill \end{array}}\end{array}\right]$
L = 3	$\left[\begin{array}{c}\hfill \begin{array}{cccccccccccc}\hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill \end{array}\hfill \\ \multicolumn{1}{c}{\begin{array}{cccccccccccc}\hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .8\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill \end{array}}\\ \multicolumn{1}{c}{\begin{array}{cccccccccccc}\hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill & \hfill .2\hfill \end{array}}\end{array}\right]$	$\left[\begin{array}{c}\hfill \begin{array}{cccccccccccc}\hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill \end{array}\hfill \\ \multicolumn{1}{c}{\begin{array}{cccccccccccc}\hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .6\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill \end{array}}\\ \multicolumn{1}{c}{\begin{array}{cccccccccccc}\hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill & \hfill .4\hfill \end{array}}\end{array}\right]$