Effect of Purification Procedures on DIF Analysis in IRTPRO

Abstract

Purification of the test has been a well-accepted procedure in enhancing the performance of tests for differential item functioning (DIF). As defined by Lord, purification requires reestimation of ability parameters after removing DIF items before conducting the final DIF analysis. IRTPRO 3 is a recently updated program for analyses in item response theory, with built-in DIF tests but not purification procedures. A simulation study was conducted to investigate the effect of two new methods of purification. The results suggested that one of the purification procedures showed significantly improved power and Type I error. The procedure, which can be cumbersome by hand, can be easily applied by practitioners by using the web-based program developed for this study.

Scientific Software International’s Flexible Item Response Theory Modeling for Patient-Reported Outcomes (IRTPRO) software was first released in 2011, with Version 3 recently released in May 2015 (Cai, Thissen, & du Toit, 2015). IRTPRO has experienced significant proliferation within certain psychometric communities as a software tool, and its convenience of use facilitates the application of item response theory (IRT) by researchers, professionals, and other individuals of varying degrees of theoretical and technological proficiency. Mathematically, IRTPRO is attractive in the application of differential item functioning (DIF) because of its improved estimation of variance–covariance matrices using the supplemental expectation maximization algorithm and also because of the convenience of concurrent calibration of multiple groups. The supplemental expectation maximization algorithm provides estimation advantages, particularly in situations involving missing data (Cai, 2008). Concurrent calibration involves reformatting response data such that anchor items can be estimated on the same scale in one estimation (Kim & Cohen, 1998; Lord, 1980). IRTPRO can be used to calibrate various IRT models and test DIF conveniently using an improved Wald (1943) test, which is an improved Lord’s χ² test (Lord, 1980). If a user already knows which anchor items to use, then the Wald-1 test (option titled “Test candidate items, estimate group difference with anchor items”) can be used very easily. However, if the user does not know the anchor items, then the Wald-2 test (option titled “Test all items, anchor all items”) can be used just as easily. DIF analysis is, as a result, very simple and accessible with IRTPRO.

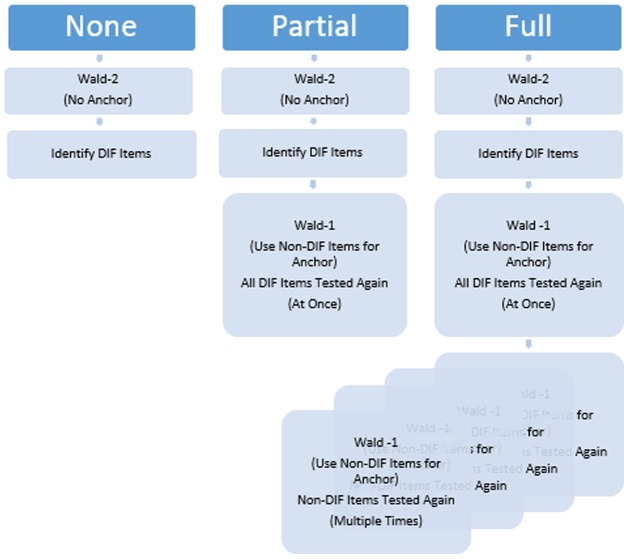
A purification procedure, in which anchor items are “purified” as DIF-free, is a critical step in a DIF analysis. Although the Wald-2 test can benefit from purification procedures, there are currently no options in IRTPRO for purification procedures that are as convenient as the other DIF processes. Various purification procedures have been proposed in the literature with other DIF indices (González-Betanzos & Abad, 2012; Kopf, Zeileis, & Strobl, 2015b; Lee & Ban, 2010; Seybert & Stark, 2012). However, purification procedures for the IRTPRO DIF analysis have not been well established yet, and the effectiveness of those procedures is not known. There are at least two ways to purify anchor items using IRTPRO. One method is to first use Wald-2 to identify “DIF-free” items and then to apply Wald-1 by using those “DIF-free” items as anchor items (hereafter referred to as “partial” purification) to evaluate the remaining candidate items. This two-step process is relatively simple, though tedious, for the end user in IRTPRO. It is a “partial” process because those items found to be “DIF-free” anchor items by the Wald-2 test are not tested for DIF again. This partial purification procedure is straightforward enough to be considered a natural approach to the situation. Another, new approach proposed here is to test all the items again using the “DIF-free” anchor items (hereafter referred to as “full” purification). The latter approach, however, is currently an involved process for the end user because of the additional steps required to evaluate a potential anchor item for DIF. The length of the procedure depends on the number of questions and outcomes of the Wald-2 test. For example, suppose there are five items on a test (Items 1-5), and an initial Wald-2 test identifies Items 1 and 2 as DIF. Next, Items 1 and 2 are tested using Items 3 to 5 as anchor items by the Wald-1 test (partial purification). Afterward, Item 3 can be tested using Items 4 and 5 as anchor items, Item 4 can be tested using Items 3 and 5 as anchor items, and Item 5 can be tested using Items 3 and 4 as anchor items; each anchor item is retested using the other items as anchors to complete the full-purification procedure. Figure 1 illustrates the three methods graphically. The level of detail and the length of the procedure may be prohibitive for end users as the number of items increases, but the complete verification of the proposed model may have attractive qualities. Therefore, the purpose of this study is to evaluate the merits of the full-purification strategy compared with partial purification and no purification and to develop a user-friendly web-based tool to assist with full purification.

Figure 1.

Three types of purification method utilized in IRTPRO.

Linking in the IRT-DIF Analysis

The three-parameter IRT model described by Birnbaum (Lord, 1968) expresses the probability of a correct response for item i as a function of an ability or trait (θ), where an item has difficulty (b), discrimination (a), and pseudo-guessing (c) under the assumption of unidimensionality (Hambleton, Swaminathan, & Rogers, 1991). This assumption creates an understanding that IRT models depict relationships affected only by the specified trait and that the trait operates in the same quantitative way across all individuals and groups (i.e., item invariance). If two participants of equal θ experience differing probabilities of correctly responding to an item owing to some other factor(s), then that item is said to express DIF.

Prior to comparing item parameter estimates from the two groups in a DIF analysis, item parameters need to be on the same scale. The process is called linking, and it is the primary area of focus in this study. Linking is necessary because the distribution of individual θ levels is often constrained to a given mean and standard deviation (commonly 0 and 1, respectively) to avoid problems of indeterminacy in estimation procedures. Two separate groups will generally express differences in observed mean ability levels, resulting in item parameter estimates from those groups that are not directly comparable. One strategy to put item parameter estimates on the common scale is to proceed with two separate calibrations and transform the ability and item parameter estimates of one of the groups. Various procedures have been proposed to obtain linking coefficients for transformation (Haebara, 1980; Stocking & Lord, 1983). Another strategy is to conduct concurrent calibration with multiple groups, which involves estimating parameters using all data simultaneously to obtain a common IRT scale. Comparisons of those two approaches have been conducted, and both methods have been used in conjunction with various DIF techniques proposed in the past few decades (Kim & Cohen, 1998; Lee & Ban, 2010).

Another important aspect of linking is the purification of the test. Lord (1980) states that as the number of DIF items increases, the items are not strictly unidimensional. Then, the ability estimates from two separate groups are not directly comparable. Lord’s purification procedure is conducted as follows:

1. Initially, estimate the DIF.

2. Remove the DIF items, and reestimate θ for both groups combined.

3. With fixed θ, reestimate the DIF for all items.

A more practical iterative linking method for separate calibration was proposed by Candell and Drasgow (1988), as described below:

1. Initially, estimate the DIF.

2. Relink items without the DIF items identified above.

3. Reestimate the DIF for all items. (i.e., “two-stage linking”).

4. Continue Steps 2 and 3 iteratively until no difference in DIF is found at two consecutive times (i.e., “iterative linking”).

Various DIF procedures can be enhanced by using either two-stage linking or iterative linking in the context of separate linking (Park & Lautenschlager, 1990; Seybert & Stark, 2012). DIF procedures with concurrent calibration linking can also be enhanced by purification (González-Betanzos & Abad, 2012; Kopf et al., 2015b; Kopf, Zeileis, & Strobl, 2015a; Wang, 2004; Woods, 2009; Woods, Cai, & Wang, 2013).

The DIF Analysis in IRTPRO

In IRTPRO, the linking for DIF analysis is conducted with concurrent calibration. Figure 2 graphically shows the estimation procedures for the Wald-1 test and the Wald-2 test. The Wald-1 test is a one-step estimation procedure fixing the reference group ability estimates and constraining the anchor item parameter estimates to be the same across groups. The Wald-2 test is a two-step estimation procedure where at the first step the reference group ability estimates are fixed and all item parameters are constrained to be equal, allowing free estimation of the focal group item parameter estimates. Then, with known ability parameter estimates for both groups, all item parameters are estimated. Lord’s statistic, used in the Wald test for DIF, is described in Woods et al. (2013) as (for the two-parameter model)

Figure 2.

Graphic display of estimation procedures for the Wald-1 test and the Wald-2 test in IRTPRO.

$${\chi }_i^2=v_i^T\sum _i^{-1}{v}_i,$$

with $v_i^T=[{\hat{a}}_{F_i}-{\hat{a}}_{R_i},{\hat{b}}_{F_i}-{\hat{b}}_{F_i}],$${\Sigma }_i$ being a matrix of the covariance of the said differences, and the number of such parameters per item is used as the degrees of freedom for a χ² significance test.

When the anchor items are known, the Wald-1 test can be selected. However, when the anchor items are not known (which is often the case in DIF analysis), items can be tested for DIF using χ², without selecting the initial anchor items with the Wald-2 test, attributed by Woods et al. (2013) to Langer (2008). The Wald-2 test, however, has been found to exhibit inflated Type I error (Woods et al., 2013). Such error is to be expected because in the Wald-2 test no purification is applied in estimating the ability parameters (Step 1). Although the Wald-2 test is easy to use in IRTPRO and does not require previous knowledge of item characteristics to identify anchors, this high Type I error can create unexpected challenges for researchers and practitioners.

The use of the Wald-2 test as a way to select anchor items to be used for the Wald-1 test has been suggested (Woods et al., 2013). The initially identified DIF items are tested again by purified anchor items. It is not known, however, to what extent this practice will enhance the DIF analysis. In the current investigation, we take one step further and investigate the effect of “full” purification, where all items (not only the initially identified DIF items) are tested again by the purified anchor items.

Method

The performance of full purification was examined and compared with that of the partial and no purification approaches in IRTPRO’s Wald test. Simulation conditions were selected from a similar study performed by Seybert and Stark (2012), in which the effect of iterative linking on another DIF procedure, differential functioning of items and tests, detailed by Raju, van der Linden, and Fleer (1995), was investigated. A series of scripts and browser-based applications were developed to facilitate the full-purification procedure and the compilation of results (Fikis and Oshima, 2015). This simulation study compared the power and Type I error rates of the Wald test in IRTPRO using three levels of purification: the default Wald-2 test (no purification); a partial, two-phase process; and a full, three-phase process.

Manipulated factors included those typical of field applications of IRT: percent DIF items, sample size, test length, and impact. Table 1 describes the resulting 24 simulation conditions. Each condition was replicated 100 times. The item response data were simulated by using item parameters from Seybert and Stark (2012). Table 2 lists the generating item parameters. Ability θ was generated from the standard normal distribution N(0, 1) for both reference and focal groups for the no-impact condition. For the impact condition, the ability θ for the focal group was taken from an N(−.5, 1) distribution. Sample sizes were equal in all conditions. DIF was embedded by adding .7 on the b parameter onto the focal group item parameters when applicable.

Table 1.

Simulation Conditions.

Condition	Test length	Sample size	% DIF items	Impact
1	15	500	0	0
2	30	—	—	—
3	15	1,000	—	—
4	30	—	—	—
5	15	500	20	—
6	30	—	—	—
7	15	1,000	—	—
8	30	—	—	—
9	15	500	33	—
10	30	—	—	—
11	15	1,000	—	—
12	30	—	—	—
13	15	500	0	−0.5
14	30	—	—	—
15	15	1,000	—	—
16	30	—	—	—
17	15	500	20	—
18	30	—	—	—
19	15	1,000	—	—
20	30	—	—	—
21	15	500	33	—
22	30	.—	—	—
23	15	1,000	—	—
24	30	—	—	—

Note. DIF = differential item functioning.

Table 2.

Item Parameters Using Birnbaum (Lord, 1968) Parameterization.

Item	b	a	c
1	−0.07	0.49	0.19
2a	0.21	0.92	0.15
3	0.54	1.26	0.05
4b	−0.03	0.61	0.18
5	0.01	1.74	0.12
6	1.96	0.5	0.12
7b	0.04	0.96	0.13
8	−0.09	0.59	0.18
9	−1.16	0.82	0.17
10a	0.02	1.26	0.11
11	0.2	0.82	0.07
12	−0.43	0.75	0.15
13b	−0.06	1.49	0.09
14	−0.34	0.97	0.12
15	0.05	1.49	0.12
16	−0.25	0.89	0.15
17a	0.06	1.45	0.07
18	0.31	0.75	0.18
19b	0.04	1.43	0.08
20	0.13	0.6	0.22
21	0.52	0.83	0.09
22b	−0.96	0.56	0.19
23	−0.79	0.67	0.2
24	0.37	0.7	0.18
25a	−0.71	1.03	0.14
26	−0.19	0.89	0.21
27	0.74	1.23	0.06
28b	−0.44	0.9	0.18
29	−0.17	1.23	0.12
30	0.53	0.69	0.17

^aDenotes differential item functioning (DIF) items under 20% and 33% DIF conditions. ^bDenotes DIF items under only 33% DIF conditions. (In those DIF items, .7 was added to the b parameter for the focal group.)

Items were calibrated in IRTPRO with the three-parameter model, with a fixed c parameter (c = .20). For the “no” purification condition, the Wald-2 DIF option (“Test all items, anchor all items”) was selected. For the “partial”-purification condition, the Wald-1 DIF option (“Test candidate items, estimate group difference with anchor items”) followed the Wald-2 DIF option. For the “full”-purification condition, the Wald-1 DIF option was repeatedly applied after the initial Wald-2 DIF option. This process was automated by a web-based computer program, eliminating the need to repeatedly run numerous models and compile results manually. In all phases, an alpha of .05 was used to identify the DIF.

Results

The simulation findings are both consistent with previous research and demonstrate improved analytical capacities with full purification. Table 3 describes the results: The default Wald-2 test exhibited high Type I error as expected based on the findings of Cai (2008). Partial purification improved Type I error, but it reduced power slightly. Full purification both reduced Type I error and improved power. Table 4 details these findings. Generally speaking, the full-purification strategy exhibits superior performance to both partial purification and the default Wald-2 test in IRTPRO.

Table 3.

Simulation Results.

				Purification
				None		Partial		Full
Impact	% DIF items	Sample size	Test length	P	TIE	P	TIE	P	TIE
0	0	500	15	—	0.024	—	0.021	—	0.025
—	—	—	30	—	0.039	—	0.031	—	0.033
—	—	1,000	15	—	0.035	—	0.030	—	0.035
—	—	—	30	—	0.032	—	0.027	—	0.029
—	20	500	15	0.727	0.054	0.713	0.018	0.783	0.020
—	—	—	30	0.717	0.078	0.678	0.027	0.733	0.032
—	—	1,000	15	0.880	0.133	0.870	0.024	0.933	0.033
—	—	—	30	0.900	0.140	0.870	0.029	0.908	0.035
—	33	500	15	0.572	0.185	0.558	0.058	0.698	0.065
—	—	—	30	0.574	0.212	0.495	0.061	0.606	0.063
—	—	1,000	15	0.850	0.394	0.840	0.061	0.914	0.065
—	—	—	30	0.831	0.420	0.803	0.076	0.894	0.077
−0.5	0	500	15	—	0.023	—	0.023	—	0.030
—	—	—	30	—	0.037	—	0.030	—	0.035
—	—	1,000	15	—	0.029	—	0.026	—	0.030
—	—	—	30	—	0.033	—	0.028	—	0.030
—	20	500	15	0.597	0.037	0.587	0.016	0.710	0.025
—	—	—	30	0.618	0.078	0.555	0.030	0.650	0.034
—	—	1,000	15	0.857	0.115	0.857	0.025	0.923	0.030
—	—	—	30	0.863	0.133	0.835	0.025	0.882	0.030
—	33	500	15	0.458	0.141	0.438	0.060	0.588	0.070
—	—	—	30	0.452	0.183	0.415	0.089	0.523	0.097
—	—	1,000	15	0.752	0.357	0.714	0.074	0.848	0.077
—	—	—	30	0.761	0.388	0.745	0.099	0.862	0.100

Note. DIF = differential item functioning.

Table 4.

Simulation Results Relative to the No-Purification Method.

				Purification
				Partial		Full
Impact	% DIF items	Sample size	Test length	P	TIE	P	TIE
0	0	500	15	—	−0.003	—	0.001
—	—	—	30	—	−0.008	—	−0.006
—	—	1,000	15	—	−0.005	—	0.000
—	—	—	30	—	−0.005	—	−0.003
—	20	500	15	−0.014	−0.036	0.056	−0.034
—	—	—	30	−0.039	−0.051	0.016	−0.046
—	—	1,000	15	−0.010	−0.109	0.053	−0.100
—	—	—	30	−0.030	−0.111	0.008	−0.105
—	33	500	15	−0.014	−0.127	0.126	−0.120
—	—	—	30	−0.079	−0.151	0.032	−0.149
—	—	1,000	15	−0.010	−0.333	0.064	−0.329
—	—	—	30	−0.028	−0.344	0.063	−0.343
−0.5	0	500	15	—	−0.001	—	0.007
—	—	—	30	—	−0.007	—	−0.002
—	—	1,000	15	—	−0.003	—	0.001
—	—	—	30	—	−0.004	—	−0.003
—	20	500	15	−0.010	−0.021	0.113	−0.012
—	—	—	30	−0.063	−0.048	0.032	−0.043
—	—	1,000	15	0.000	−0.090	0.067	−0.085
—	—	—	30	−0.028	−0.108	0.018	−0.103
—	33	500	15	−0.020	−0.081	0.130	−0.071
—	—	—	30	−0.037	−0.095	0.071	−0.086
—	—	1,000	15	−0.038	−0.283	0.096	−0.280
—	—	—	30	−0.016	−0.289	0.101	−0.288

Note. DIF = differential item functioning.

Overall, mean power levels were .71, .69, and .78 and Type I error rates were .14, .04, and .05 for the no-, partial-, and full-purification methods, respectively. Using manipulated factors as independent variables, analyses of variance for both power and Type I error were conducted. Table 5 describes the analysis of variance for power.

Table 5.

Analysis of Variance for Power.

Factor	df	F	η2	p
Purification method	2	3.58	.07	<.01
Impact	1	60.60	.07	<.01
% DIF	1	105.92	.12	<.01
Sample size	1	621.55	.69	<.01
Test length	1	4.34	<.01	.05
Method × Impact	2	0.73	<.01	.49
Method × % DIF	2	2.11	<.01	.14
Method × Sample size	2	0.65	<.01	.53
Method × Test length	2	1.74	<.01	.19

Note. DIF = differential item functioning; df = degrees of freedom.

All factors were found to be significant for power and Type I error, with the exception of impact and test length in the case of Type I error. Table 6 describes the analysis of variance for Type I error. All factors were found to be significant for power and Type I error, with the exception of impact and test length in the case of Type I error. Post hoc pairwise comparisons for the purification method factor was conducted using Tukey’s honest significant difference test: In the case of power, full purification showed significant improvements over both alternatives (p < .01 in both cases), whereas the drop in power between partial and no purification was not found to be significant (p = .08). In terms of Type I error, both partial and full purification demonstrated improvements over no purification (p < .01 in both cases), and the increase observed in Type I error for full purification compared with partial purification was not found to be significant (p = .85.).

Table 6.

Analysis of Variance for Type I Error.

Factor	df	F	η2	p
Purification method	2	77.30	.03	<.01
Impact	1	0.04	<.01	.83
% DIF	1	98.50	.33	<.01
Sample size	1	22.57	.04	<.01
Test length	1	3.10	.01	.08
Method × Impact	2	1.04	<.01	.36
Method × % DIF	4	32.84	.22	<.01
Method × Sample size	2	17.26	.06	<.01
Method × Test length	2	0.32	<.01	.73

Note. DIF = differential item functioning; df = degrees of freedom.

Significant interaction effects were found between the method used and the factors of both percent DIF and sample size in relation to Type I error, indicating that the extent of the effect of percent DIF and sample size on Type I error depended on which purification method was used. Large effect sizes were observed in the sample size factor for power analysis and percent DIF factor for Type I error analysis. Figure 3 displays the general findings of this study. Results for test length (15 and 30 items) were collapsed in the graph. For power, the rate was the highest for full purification, and this power advantage is more beneficial with a smaller sample size. For Type I error, the graph clearly shows that the Wald-2 test without purification has serious inflation of Type I error, especially with a larger percentage of DIF items on the test. By applying partial or full purification, the inflation was reasonably controlled.

Figure 3.

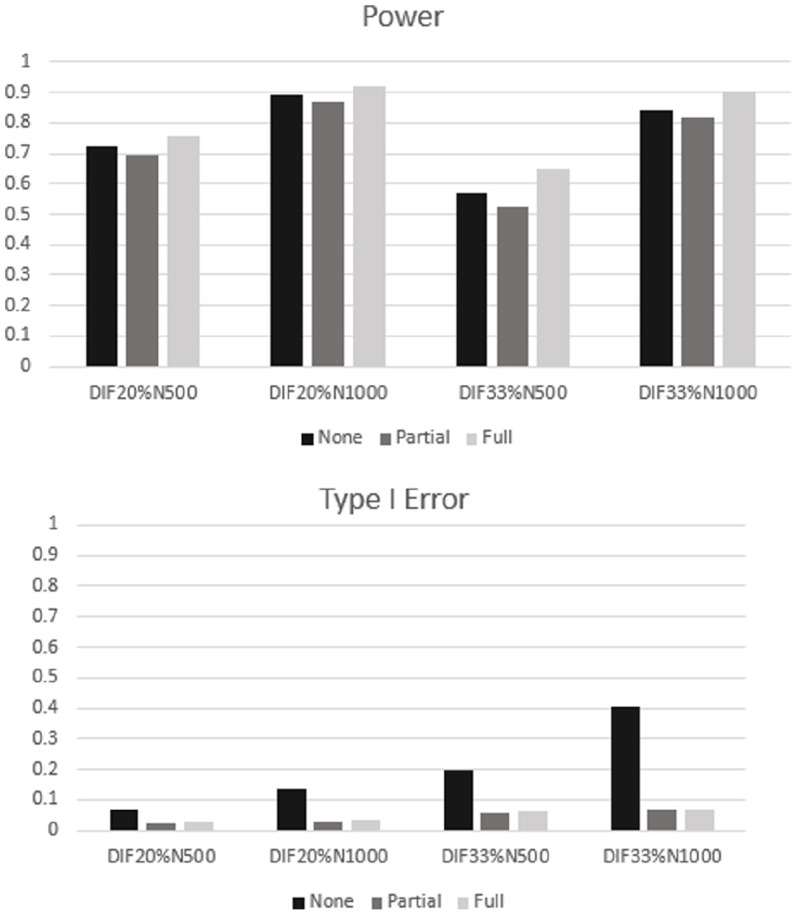
Power and Type I error for the Wald test with “no.”“partial,” and “full” purification by conditions (percent DIF and sample size).

Discussion

Full purification demonstrated improvement in both power and Type I error overall when compared with both no purification and partial purification. Sample size generally exhibited a positive relationship with power. Percent DIF and impact generally exhibited a negative relationship with power. These results conform to expectations.

Type I error was, as discussed in the literature, high in the Wald-2 test, but this inflated Type I error appeared to have been removed through both purification procedures. Full purification did not demonstrate substantial gains in terms of Type I error: An insignificant increase was observed in the simulation when compared with partial purification. Power was found to be highest with full purification, confirming the general hypothesis that reexamining anchor items would result in better identification of DIF items. The rather simple, “commonsense” algorithm of partial purification, which can be accomplished without special software, was able to be confirmed as an improvement on conducting no purification whatsoever, and the new full-purification procedure demonstrated significant merits.

The execution of the various purification methods was simple from an end-user standpoint, but varying computational resources were required. Full purification may not be feasible for very long tests without appropriate hardware resources and software use of them. For widespread adoption, tools such as the one developed for this study may be necessary.

Another consideration for further research is the theoretical impact of using the Wald-2 test as a means of identifying anchor items (i.e., DIF-free items) instead of identifying DIF items from a practical perspective. A “false negative” for a DIF item becomes a “false positive” for an anchor item. This forced paradigm shift of the Wald-2 test may need to be investigated further before this purification procedure is fully advocated. One potential question may be whether the p-value cutoffs in the initial Wald-2 test should be set very high (i.e., a higher α level, e.g., .10) rather than at the traditional level (α = .05) to provide a more sensitive test for choosing potential anchor items. This could significantly reduce the computational time needed to execute full purification as fewer anchors would need to be reexamined with the Wald-1 test in IRTPRO.

Although full purification shows promise as one of multiple potential improvements over the default Wald-2 test in IRTPRO, some of the limitations and findings of this study demonstrate the need for further research and refinement of these methods. In the current study, the full purification was conducted only once. In other words, once the anchor items were identified, they remained as anchor items: A “bad anchor” still held some influence on the evaluation of DIF. Anchor items could be still further refined as some of the anchor items were identified as DIF items. Whether or not the benefit of this iterative purification outweighs the cost and complexities of lengthier iterations and processing time warrants further investigation.