A Comparison of Composite Reliability Estimators

Abstract

Coefficient omega and alpha are both measures of the composite reliability for a set of items. Unlike coefficient alpha, coefficient omega remains unbiased with congeneric items with uncorrelated errors. Despite this ability, coefficient omega is not as widely used and cited in the literature as coefficient alpha. Reasons for coefficient omega’s underutilization include a limited knowledge of its statistical properties. However, consistent efforts to understand the statistical properties of coefficient omega can help improve its utilization in research efforts. Here, six approaches for estimating confidence intervals for coefficient omega with unidimensional congeneric items were evaluated through a Monte Carlo simulation. The evaluations were made through simulation conditions that mimic realistic conditions that investigators are likely to face in applied work, including items that are not normally distributed and small sample size(s). Overall, the normal theory bootstrap confidence interval had the best performance across all simulation conditions that included sample sizes less than 100. However, most methods had sound coverage with sample sizes of 100 or more.

Coefficient omega “captures the notion of the reliability of a test score” (McDonald, 1999, p. 90). As such, it is a measure of composite reliability introduced by McDonald (1970) as an alternative reliability index to coefficient alpha. Coefficient omega is computed using the item factor loadings and uniqueness from a factor analysis whereas coefficient alpha uses the item covariance (or correlation) matrix (Cronbach, 1951; Guttman, 1945). As such, coefficient omega is a more general form of reliability. This is best conveyed via three models based on classical test theory. First, when items are parallel, both coefficient alpha and omega are equal to the composite reliability for the set of items. Second, when items are tau-equivalent or essentially tau-equivalent, coefficient alpha and omega are again equal to the composite reliability for the set of items. However, when items are congeneric, coefficient alpha is less than the composite reliability for a set of items whereas coefficient omega is equal to the composite reliability for the set of items (Graham, 2006; Lord, Novick, & Birnbaum, 1968; McDonald, 1999; Zinbarg, Revelle, Yovel, & Li, 2005). For further details on these three classical test theory based models discussed, see Graham (2006) or Padilla and Divers (2013). It should be noted that there are situations where coefficient alpha can be higher than composite reliability with congeneric items. An example of such a situation is when item errors are correlated (Novick & Lewis, 1967). However, this situation will not be investigated here.

Even though coefficient omega is a more general form of reliability, it has been overshadowed by coefficient alpha in the literature (Hogan, Benjamin, & Brezinski, 2000; Peterson, 1994). Coefficient alpha’s popularity could be attributed to its ease of computation and years trying to understand its statistical properties. However, recent research on coefficient omega is beginning to make it a more viable alternative. In particular, several confidence interval (CI) estimates have been proposed. The objective here is to investigate the performance of CIs in the literature that investigators (a) can implement in a straightforward manner and (b) under conditions they are likely to encounter in applied work.

Raykov (1997) proposed a composite reliability for congeneric unidimensional items and then developed a corresponding percentile bootstrap (PB) CI (Raykov, 1998). Composite reliability is formulated through a structural equation model (SEM) and is equivalent to coefficient omega. An illustration of the PB CI was provided through a small simulation study that included 1,000 bootstrap samples, a sample size of 400, and 6 unidimensional multivariate normal congeneric items.

In a subsequent study, Raykov (2002) derived an analytical standard error via a first-order delta method for composite reliability. This method of estimating the composite reliability standard error will be referred to as the delta method. The method is again formulated through a SEM and illustrated with a small simulation. The simulation included a sample size of 500 and 5 unidimensional multivariate normal congeneric items. In this study, the delta method CI was compared with the PB CI with 2,000 bootstrap samples, and both methods had similar results.

In a parallel study, Raykov and Shrout (2002) formulated a more general form of composite reliability (Raykov, 1997, 1998) through a SEM with a corresponding PB CI. It is more general in that it does not assume the items are unidimensional. The method is again illustrated with a small simulation that assumed two dimensions and included a sample size of 300 and 6 multivariate normal congeneric items. The results provide evidence that the composite reliability estimate is unbiased and the CI contains the population parameter at the specified alpha level.

More recently, Raykov and Marcoulide (2011) added some modifications to the coefficient omega delta method standard error. First, a logit transformation was added to map the reliability parameter from its [0, 1] interval to the real line [−inf, inf]. In addition, the authors noted that the robust maximum likelihood (MLR) estimator should be used with nonnormal items that have at least 5 to 7 response categories. For items with less than 5 response categories, a three-step parceling procedure is discussed. See Little, Cunningham, Shahar, and Widaman (2002) for a discussion on parceling. The delta method and three-step parceling procedure are illustrated using relatively large example data sets (i.e., n≥ 350).

Padilla and Divers (2013) proposed two additional coefficient omega bootstrap CIs: the bias-corrected and accelerated (BCa) and normal theory bootstrap (NTB). They investigated their performance along with the PB CI through a simulation study that varied the number of items, item correlation type, number of item response categories (IRCs), shape of the distribution of items, and sample size. The authors found that the NTB CI had the best performance across the simulation conditions followed by the PB and BCa CIs, respectively. It should be noted that the PB and BCa CIs performed comparably and the differences between them were marginal.

There are five points the literature makes about the coefficient omega CIs from 1997 to 2011. First, the delta method is applicable with (a) approximately continuous items that are “viewed as having (b) a multinormal distribution” (Raykov & Marcoulides, 2011, p. 168). Second, the delta method is applicable by combining it with the MLR estimator with items that are (a) approximately continuous, (b) nonnormally distributed, (c) do not have floor/ceiling effects, and (d) is “. . . applicable in a trustworthy way with items having at least five to seven possible values” (Raykov, 2012, p. 483). Third, for the delta method with binary items, Raykov and Marcoulides (2011) point to combining the MLR estimator with item parceling “as a conceivable alternative to consider . . .” (p. 176). Subsequently, Raykov (2012) indicates that the delta method with MLR/parceling can be used with items with up to 5 to 7 response categories. Fourth, there are no guidelines for deciding which CI to use between the delta and PB method under specific situations (Raykov & Marcoulides, 2011). Lastly, Raykov (2012) indicates that “at present no specific guidelines can be provided with regard to determining [a] necessary sample size . . .” (p. 489) for any of the methods from the above four points.

With these points in mind, interest here is on investigating the relative performance of these coefficient omega CI methods that can be implemented in a straightforward manner. In addition, the BCa and NTB CI methods are included as they are also bootstrap methods but were introduced in the literature after 2011. Furthermore, items are rarely normally distributed (Micceri, 1989) and continuous (Raykov, 2002) in applied work. Therefore, particular interest is on the impact noncontinuous and nonnormally distributed items have on the CIs. We start by defining coefficient omega.

Coefficient Omega and Reliability

Consider a measurement instrument with k items $x_1,x_2,\dots ,x_k$ designed to measure a single construct, factor, or latent variable. In the behavioral/social sciences, it is common to compute the reliability of the composite $x=\sum _{j=1}^k{x}_j.$ This composite reliability is often referred to as the test score reliability or the reliability of the measurement instrument. If the items are congeneric, coefficient omega is the appropriate composite reliability index.

Coefficient omega is defined as

$$\mathrm{\omega }=\frac{{\left(\sum _{j=1}^k{\mathrm{\lambda }}_j\right)}^2}{{\left(\sum _{j=1}^k{\mathrm{\lambda }}_j\right)}^2+\sum _{j=1}^k{\mathrm{\psi }}_j},$$

where λ_j and ψ_j is the jth factor loading and its uniqueness, respectively (McDonald, 1970, 1999). In the definition, ${\left(\sum _{j=1}^k{\mathrm{\lambda }}_j\right)}^2$ is the true-score variance and $\sum _{j=1}^k{\mathrm{\psi }}_j$ is the error variance. Coefficient omega is estimated $\left(\hat{\mathrm{\omega }}\right)$ by using sample estimates ${\hat{\mathrm{\lambda }}}_j$ and ${\hat{\mathrm{\psi }}}_j$ in Equation 1.

Logit Transformation

Some of the CIs are based on the idea of normalizing coefficient omega. As mentioned above, this is done to remove the [0, 1] range constraint on coefficient omega. Normalizing involves transforming the coefficient omega estimate to an approximately normal deviate, which can be used to form a normal theory (NT) CI as follows:

$$\hat{z}\pm z_{\alpha /2}\mathrm{SE}\left(\hat{z}\right),$$

where

$$\hat{z}=\ln \left(\frac{\hat{\mathrm{\omega }}}{1-\hat{\mathrm{\omega }}}\right),$$

$$\mathrm{SE}\left(\hat{z}\right)=\frac{\mathrm{SE}\left(\hat{\mathrm{\omega }}\right)}{\hat{\mathrm{\omega }}(1-\hat{\mathrm{\omega }})},$$

$\mathrm{SE}\left(\hat{\mathrm{\omega }}\right)$ is the standard error for $\hat{\mathrm{\omega }},$ and $z_{\alpha /2}$ is a standard normal deviate corresponding to significance level (α). The key to the above NT CI for $\hat{\mathrm{\omega }}$ is estimating $\mathrm{SE}\left(\hat{\mathrm{\omega }}\right).$ The NT CI bounds are then back transformed to provide the CIs associated with $\hat{\mathrm{\omega }}$ on its original scale.

Non-Bootstrap Coefficient Omega CIs

Two non-bootstrap CI methods were examined. Before discussing these methods the variance estimate that is common to both is first presented. Raykov (2002) first proposed the following delta method based variance estimate for coefficient omega:

$$\mathrm{var}\left(\hat{\mathrm{\omega }}\right)={\hat{D}}_1^2\mathrm{var}\left(\hat{u}\right)+{\hat{D}}_2^2\mathrm{var}\left(\hat{v}\right)+2{\hat{D}}_1{\hat{D}}_2\mathrm{cov}(\hat{u},\hat{v}),$$

where

$$\hat{u}=\sum _{j=1}^k{\hat{\mathrm{\lambda }}}_j,$$

$$\hat{v}=\sum _{j=1}^k{\hat{\mathrm{\psi }}}_j,$$

$${\hat{D}}_1=\frac{2\hat{u}\hat{v}}{{({\hat{u}}^2+{\hat{v}}^2)}^2},$$

$${\hat{D}}_2=\frac{-{\hat{u}}^2}{{({\hat{u}}^2+{\hat{v}}^2)}^2},$$

and var(.) and cov(.) are the variance and covariance operators, respectively. In addition, Raykov presented a corresponding coefficient omega CI where $\mathrm{SE}\left(\hat{\mathrm{\omega }}\right)=\sqrt{\mathrm{var}\left(\hat{\mathrm{\omega }}\right)}.$ Here, two non-bootstrap CIs associated with the above delta variance estimate were examined.

The first non-bootstrap CI method examined is a modification of Rakov’s (2002) original CI. Specifically, Raykov (2012) and Raykov and Marcoulides (2011) modified the original CI by adding the above logit transformation to the standard error of the delta method. From now on, this method will be referred to as the delta with logit transformation (DTLG) method.

The three-step parceling method is the second non-bootstrap method examined. This method is a modification of the first in that it is designed for items with 7 or less response categories and entails (a) parceling the items, (b) estimating the delta variance above via the MLR estimator, and (c) employing the logit transformation. For further details on the three-step parceling procedure, see Rarkov and Marcoulides (2011). In addition, Raykov (2012) points out that the parceling method “will be trustworthy when resulting reliability estimates and confidence intervals do not vary considerably across possible parceling choices” (p. 483). From now on, this method will be referred to as the three-step parceling with logit transformation (PRLG) method.

Bootstrapped Coefficient Omega CIs

Bootstrapping for coefficient omega can be summarized in three steps. Suppose $\mathbf{X}={({\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_n)}^t$ are the observed data where each x_i is a 1×k vector. First, obtain a bootstrap sample ${\mathbf{X}}^{\left(b\right)}={({\mathbf{x}}_1^{\left(b\right)},{\mathbf{x}}_2^{\left(b\right)},\dots ,{\mathbf{x}}_n^{\left(b\right)})}^t,$ which is the bth random resample from X with replacement. Note that X and X^(b) have the same sample size. Second, compute and store the bth bootstrap estimate of coefficient omega $\left({\hat{\mathrm{\omega }}}^{(b)}\right)$ from ${\mathbf{X}}^{\left(b\right)}.$ Lastly, the stored estimates ${\hat{\mathrm{\omega }}}^{(1)},{\hat{\mathrm{\omega }}}^{(2)},\dots ,{\hat{\mathrm{\omega }}}^{(B)}$ represent the empirical sampling distribution (ESD) of $\hat{\mathrm{\omega }}$ for $b=1,2,\dots ,B$ bootstrap samples. The ESD can then be summarized for statistical inference about ω. The bootstrap estimate of SE is

$$\mathrm{SE}\left(\hat{\mathrm{\omega }}\right)={\left[\frac{1}{B-1}\sum _{b=1}^B{({\hat{\mathrm{\omega }}}^{(b)}-\overline{\mathrm{\omega }})}^2\right]}^{1/2},$$

where

$$\overline{\mathrm{\omega }}=\frac{1}{B}\sum _{b=1}^B{\hat{\mathrm{\omega }}}^{(b)}.$$

Four bootstrap CIs were examined. First, Raykov (1998) proposed a percentile based (PB) CI obtained by computing the α/2 and 1 −α/2 percentiles from the $\hat{\mathrm{\omega }}$ ESD where α is the Type I error rate. Second, Padilla and Divers (2013) proposed the BCa and NTB CIs. The BCa CI is an improvement on the PB CI that adjusts the α/2 and 1 −α/2 percentiles in two ways: (a) it makes a correction for bias and (b) a correction for skewness (or acceleration). The NTB CI is estimated as $\hat{\mathrm{\omega }}\pm z_{\alpha /2}\mathrm{SE}\left(\hat{\mathrm{\omega }}\right).$ The fourth CI was formed by using the bootstrap SE with the logit transformation above (BTLG). For technical and theoretical details concerning the bootstrap and the first three bootstrap CIs investigated, see Efron and Tibshirani (1998).

Again, two non-bootstrap (DTLG and PRLG) and four bootstrap (PB, BCa, NTB, and BTLG) methods of estimating coefficient omega CIs are investigated under several simulation conditions.

Method

Simulation Design

Five different simulation factors were investigated in a 4 (# of items) × 3 (corr. type) × 4 (# of IRCs) × 3 (distribution type) × 10 (sample size) Monte Carlo simulation design for a total of 1,440 conditions. All simulated items were nonnormal and binary or Likert-type (ordinal); none of the items were continuous. For each simulation condition, 1,000 replications were obtained.

Binary and Likert-type items were generated using the method used in Maydeu-Olivares, Coffman, and Hartmann (2007). This method is outlined below:

1. Select the structure for the k×k correlation matrix P, where k is the number of items.

2. Select a set of thresholds ν to categorize items to a predetermined skewness and kurtosis.

3. Generate an n×k multivariate data matrix X*~N(0, P), where n is the sample size.

4. Categorize the generated data X* using the thresholds ν to generate the data set X. Each variable x in X is categorized by the thresholds as follows: $x=m$ if ${\nu }_m<x^{*}<{\nu }_{m+1}$ for $m=0,1,\dots ,M-1$ where ${\nu }_0=-\infty$ and ${\nu }_M=\infty ,$ and M is the number of categories.

5. Estimate the coefficient omega CIs from X as outlined above.

6. Compute coefficient omega (ω) from P and the thresholds in ν. See Maydeu-Olivares et al. (2007) for full details.

7. Determine if the CIs contain ω.

Below are the specific simulation conditions investigated.

Number of Items (k)

Past research on coefficient alpha and omega has looked at various numbers of items ranging from 2 to 20 (Duhachek & Iacobucci, 2004; Maydeu-Olivares et al., 2007; Padilla & Divers, 2013). To make the results here comparable to past research and to accommodate even parceling, the following number of items were selected: k = 6, 12, 18, 24.

Item Correlation Type (ρ)

Three different unstructured item correlation matrices P were investigated. All correlation structures were based on a one-factor model with congeneric items. The loadings associated with each correlation structure were as follows: λ₁ = .4, .5, .6, .7, .8, .9; λ₂ = .3, .4, .5, .6, .7, .8; and λ₃ = .4, .4, .4, .8, .8, .8.

Item Response Category

Four IRCs were investigated: 2, 3, 5, and 7. List item number 4 above highlights the item categories that were used; none of the items were continuous.

Distribution Type

Three different distribution types were investigated. When IRC = 2 (i.e., binary items), the thresholds in ν were chosen so that the distributions had the following characteristics:

1. Type 1: skewness = 0 and kurtosis = −2

2. Type 2: skewness = 1.70 and kurtosis = 0.88

3. Type 3: skewness = 0.41 and kurtosis = −1.83

The Type 3 distribution for binary categorization was studied by Maydeu-Olivares et al. (2007). When IRC = 3, 5, 7, the thresholds in ν were chosen so that the distributions had the following characteristics:

1. Type 1: skewness = 0 and kurtosis = 0

2. Type 2: skewness = 0 and kurtosis = 0.88

3. Type 3: skewness = 0.97 and kurtosis = −.20

The Type 2 and 3 distributions for IRC > 2 categorization were studied by Maydeu-Olivares et al. (2007). The combination of number of items, item correlations, and item categorization created a range of .55 to .94 for ω.

Sample Size (n)

The following typical sample sizes in behavioral/social science research were investigated: n = 50, 100, 150, 200, 250, 300, 350, 400, 450, 500. Duhachek and Iacobucci (2004) indicate that n > 200 is a point of diminishing returns for reliability estimates. However, here slightly larger samples sizes were investigated in order to be conservative.

Criteria for Evaluating CIs

In each simulation replication, coefficient omega and corresponding quantities were estimated and evaluated. Here, coefficient omega 100(1 −α)% CIs were estimated with α = .05. For bootstrapping methods, 2,000 bootstraps samples were used. CI coverage is defined as the proportion of estimated CIs that contain ω and was evaluated using Bradley’s (1978) liberal criteria, defined as $1-1.5\alpha \le 1-{\alpha }^{*}\le 1-0.5\alpha ,$ where ${\alpha }^{*}$ is the true Type I error probability. Hence, acceptable coverage is given by [.925, .975].

Results

In terms of coverage, the NTB CI had the most optimal performance. The major impact on the CIs was IRCs combined with Type 2 and 3 distributions. In addition, the results are presented in the context of sample size because it has a noticeable stabilizing effect on the CIs. Therefore, only tables for Type 2 and 3 distributions and sample size of 50 will be presented because most of the CIs began to converge to acceptable coverage beyond this point.

Sample Size of 50

For Type 1 distributions, the NTB CI did not have an instance of unacceptable coverage (0/1,440 = 0). The DTLG CI had one instance of unacceptable coverage with 18 binary items (1/1,440 = .001). The PB CI had the most unacceptable coverage (8/1,440 = .006). In general, most unacceptable coverage occurred with 18 to 24 items.

With Type 2 distributions (see Table 1), the NTB CI had unacceptable coverage in 2 instances for binary items (2/1,440 = .001). The PB CI had the most unacceptable coverage (35/1,440 = .024). Most unacceptable coverage occurred with 18 to 24 items. However, a noticeable characteristic is that the DTLG CI had unacceptable coverage for all binary items (12/1,440 = .008).

Table 1.

95% Coverage Probabilities for a Sample Size of 50 and Type 2 Distribution.

	ρ	.30				.56				Unstructured
IRC	k	6	12	18	24	6	12	18	24	6	12	18	24
2	DTLG	.890	.877	.844	.874	.903	.892	.884	.869	.910	.877	.867	.852
	PRLG	.940	.929	.919	.917	.911	.958	.938	.917	.924	.939	.925	.911
	PB	.948	.927	.888	.896	.960	.918	.907	.887	.964	.923	.914	.883
	BCa	.934	.936	.919	.929	.931	.934	.941	.936	.942	.933	.936	.919
	NTB	.931	.972	.968	.973	.935	.966	.976	.973	.939	.959	.968	.979
	BTLG	.956	.971	.982	.982	.956	.969	.981	.987	.962	.970	.969	.985
3	DTLG	.951	.940	.933	.920	.945	.940	.940	.940	.928	.942	.932	.935
	PRLG	.936	.945	.930	.921	.924	.946	.938	.939	.925	.949	.942	.926
	PB	.943	.931	.906	.908	.941	.907	.914	.911	.930	.918	.918	.905
	BCa	.938	.945	.927	.935	.926	.931	.938	.937	.919	.936	.941	.936
5	NTB	.947	.961	.959	.961	.939	.973	.957	.968	.930	.973	.966	.963
	BTLG	.960	972	.963	.963	.953	.978	.979	.978	.946	.980	.971	.969
	DTLG	.949	.941	.916	.925	.950	.949	.933	.935	.927	.935	.939	.934
	PRLG	.939	.938	.912	.926	.943	.933	.917	.930	.907	.920	.932	.934
	PB	.931	.919	.900	.922	.931	.932	.900	.905	.911	.909	.917	.916
	BCa	.930	.928	.904	.923	.921	.942	.920	.921	.908	.926	.927	.924
	NTB	.951	.949	.939	.950	.944	.958	.951	.947	.927	.949	.944	.948
	BTLG	.954	.950	.935	.947	.958	.978	.959	.944	.933	.952	.950	.948
7	DTLG	.940	.933	.932	.930	.961	.930	.937	.917	.935	.967	.935	.916
	PRLG	.935	.938	.927	.923	.937	.932	.921	.912	.931	.952	.930	.922
	PB	.934	.924	.909	.917	.943	.918	.912	.907	.918	.960	.911	.916
	BCa	.931	.927	.919	.920	.936	.931	.918	.912	.911	.958	.913	.919
	NTB	.948	.950	.946	.947	.961	.955	.956	.934	.934	.962	.947	.948
	BTLG	.953	.945	.942	.938	.972	.965	.957	.944	.943	.977	.948	.940

Note. For IRC = 2: skewness = 1.70 and kurtosis = 0.88. For IRC 3, 5, 7: skewness = 0 and kurtosis = 0.88. DTLG = delta method with logit transformation; PRLG = three-step parceling with logit transformation; PB = percentile bootstrap; BCa = biased-corrected and accelerated bootstrap; NTB = normal theory bootstrap; BTLG = bootstrap SE with logit transformation. Unacceptable coverage is bolded and outside [.925, .975]. All methods based on 2,000 bootstrap samples and 1,000 simulation replications.

For Type 3 distributions (see Table 2), the NTB CI had one instance of unacceptable coverage for 6 items with 5 IRCs (1/1,440 = .001). The PB, PRLG, and DTLG CIs had the most unacceptable coverage (9/1,440 = .006 and 9/1,440 = .006, and 10/1,440 = .007, respectively). As before, most unacceptable coverage occurred with 18 to 24 items.

Table 2.

95% Coverage Probabilities for a Sample Size of 50 With Type 3 Distribution.

	ρ	.30				.56				Unstructured
IRC	k	6	12	18	24	6	12	18	24	6	12	18	24
2	DTLG	.960	.960	.972	.972	.965	.968	.954	.964	.955	.967	.955	.968
	PRLG	.935	.944	.941	.945	.935	.954	.944	.926	.933	.952	.929	.945
	PB	.956	.964	.958	.961	.969	.956	.945	.942	.958	.960	.942	.953
	BCa	.950	.964	.964	.968	.960	.970	.954	.948	.958	.958	.952	.959
	NTB	.959	.956	.965	.967	.955	.969	.960	.959	.941	.962	.954	.958
	BTLG	.971	.974	.977	.982	.970	.987	.977	.975	.962	.977	.972	.976
3	DTLG	.922	.939	.923	.947	.944	.924	.927	.939	.923	.930	.927	.933
	PRLG	.936	.940	.928	.949	.933	.926	.932	.932	.953	.923	.937	.929
	PB	.943	.945	.923	.942	.955	.921	.927	.928	.945	.933	.934	.927
	BCa	.929	.946	.930	.946	.938	.934	.939	.945	.929	.942	.942	.936
	NTB	.942	.957	.948	.961	.943	.955	.967	.958	.936	.940	.952	.952
	BTLG	.958	.969	.952	.965	.956	.969	.974	.968	.956	.964	.956	.960
5	DTLG	.925	.936	.920	.934	.919	.930	.919	.924	.937	.934	.935	.943
	PRLG	.937	.940	.924	.943	.916	.935	.927	.915	.938	.917	.935	.933
	PB	.934	.941	.915	.936	.928	.930	.920	.922	.939	.932	.928	.937
	BCa	.934	.947	.917	.944	.916	.938	.919	.926	.933	.926	.933	.938
	NTB	.944	.952	.944	.957	.923	.951	.954	.952	.937	.943	.953	.959
	BTLG	.953	.960	.938	.957	.946	.968	.966	.953	.950	.951	.952	.951
7	DTLG	.930	.942	.946	.942	.941	.943	.934	.921	.924	.934	.928	.936
	PRLG	.933	.925	.945	.922	.941	.940	.926	.922	.913	.936	.918	.927
	PB	.935	.941	.933	.922	.933	.936	.935	.922	.927	.933	.919	.924
	BCa	.924	.943	.938	.923	.926	943	.934	.932	.914	.934	.919	.929
	NTB	.929	.949	.956	.953	.944	.960	.952	.953	.933	.954	.954	.945
	BTLG	.942	.954	.952	.940	.955	.968	.958	.953	.939	.956	.943	.951

Note. For IRC = 2: skewness = 0.41 and kurtosis = −1.83. For IRC = 3, 5, 7: skewness = 0.97 and kurtosis = −.20. DTLG = delta method with logit transformation; PRLG = three-step parceling with logit transformation; PB = percentile bootstrap; BCa = biased-corrected and accelerated bootstrap; NTB = normal theory bootstrap; BTLG = bootstrap SE with logit transformation. Unacceptable coverage is bolded and outside [.925, .975]. All methods based on 2,000 bootstrap samples and 1,000 simulation replications.

Sample Size of 100

For Type 1 distributions, none of the CIs had an instance of unacceptable coverage.

With Type 2 distributions, the NTB, BTLG, and PRLG CIs did not have an instance of unacceptable coverage. The DTLG CI had the most unacceptable coverage (15/1,440 = .010), most of which occurred with binary items as all coverage was unacceptable in this situation (12/1,440 = .008).

For Type 3 distributions, the PB, BTLG, and PRLG CIs did not have an instance of unacceptable coverage. However, the NTB CI had an instance of unacceptable coverage for 6 items with 7 IRCs (1/1,440 = .001). In addition, the DTLG had the most unacceptable coverage (6/1,440 = .004). Here, most unacceptable coverage occurred with 6 to 12 items.

With the exception of the DTLG CI, the remaining sample sizes (i.e., n≥ 150) had a stabilizing effect on the CIs. Specifically, regardless of the sample size investigated, the DTLG CI had unacceptable coverage for all instances of binary items with Type 2 distributions.

Sample Size of 150

For Type 1 distributions, only the DTLG CI had a single instance of unacceptable coverage with 18 binary items (1/1,440 = .001).

With Type 2 distributions, the NTB, BCa, BTLG, and PRLG CIs had no instances of unacceptable coverage. The DTLG CI had the most unacceptable coverage (16/1,440 = .011), the majority of which occurred with binary items. In fact, it had unacceptable coverage for all binary items (12/1,440 = .008).

For Type 3 distributions, only the DTLG had unacceptable coverage (8/1,440 = .006), most of which occurred with 3 IRCs.

Sample Size of 200

For Type 1 distributions, only the PB and DTLG had an instance of unacceptable coverage that occurred with 24 items (1/1,440 = .001).

With Type 2 distributions, only the DTLG and PRGL CIs had instances of unacceptable coverage (15/1,440 = .010 and 1/1,440 = .001, respectively). The DTLG CI had unacceptable coverage for all instances of binary items (12/1,440 = .008). Furthermore, none of the CIs had unacceptable coverage for 7 IRCs.

For Type 3 distributions, again only the DTLG and PRLG CIs had unacceptable coverage (6/1,440 = .004 and 1/1,440 = .001, respectively). Most of the unacceptable coverage occurred with 18 to 24 items. In addition, neither of the CIs had unacceptable coverage for 7 IRCs.

Sample Size of 250

For Type 1 distributions, only the DTLG CI had instances of unacceptable coverage that tended to occur with 18 to 24 items (4/1,440 = .003).

With Type 2 distributions, only the DTLG CI had unacceptable coverage (14/1, 440 = .010). As before, the DTLG CI had unacceptable coverage for all instances of binary items (12/1, 440 = .008). The remaining two instances of unacceptable coverage were sporadic.

For Type 3 distributions, only the DTLG CI had sporadic instances of unacceptable coverage (5/1,440 = .003).

Sample Size of 300

For Type 1 distributions, only the DTLG CI had two instances of unacceptable coverage with 18 to 24 binary items (2/1,440 = .001).

For Type 2 distributions, only the DTLG CI had unacceptable coverage (16/1,440 = .011). As before, the DTLG CI had unacceptable coverage for all instances of binary items (12/1,440 = .008). The other four instances of unacceptable coverage were sporadic.

For Type 3 distributions, only the DTLG CI had sporadic instances of unacceptable coverage that occurred with 3 to 5 IRCs (4/1,440 = .003).

Sample Size of 350 or More

Regardless of the distribution type, most of the CIs had acceptable coverage here. Only the PRLG and DTLG CIs had instances of unacceptable coverage (4/1,440 = .003 and 96/1,440 = .067, respectively). The PRLG CI unacceptable coverage occurred sporadically. On the other hand, half of the DTLG CI unacceptable coverage occurred with binary items and Type 2 distributions (48/1,440 = .033). The other half of the DTLG CI unacceptable coverage occurred sporadically.

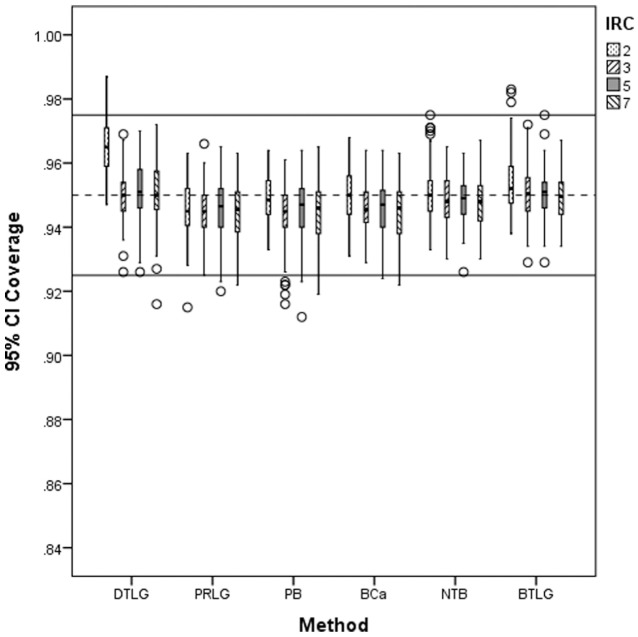
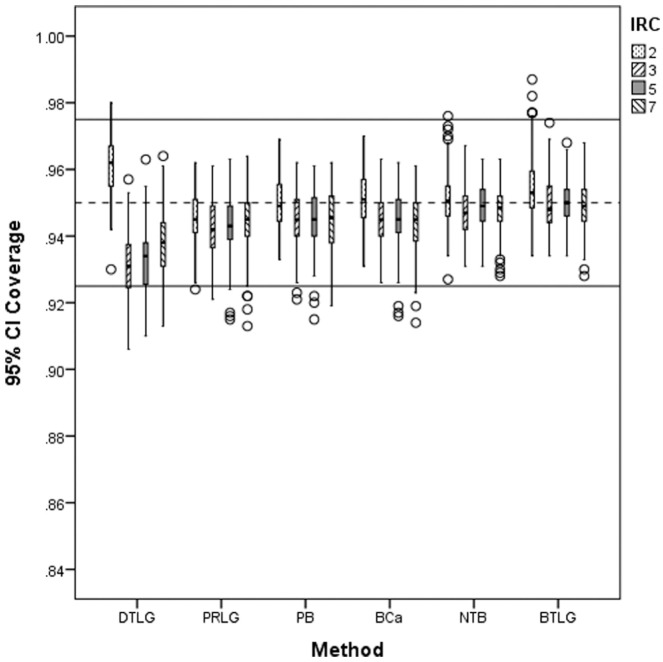
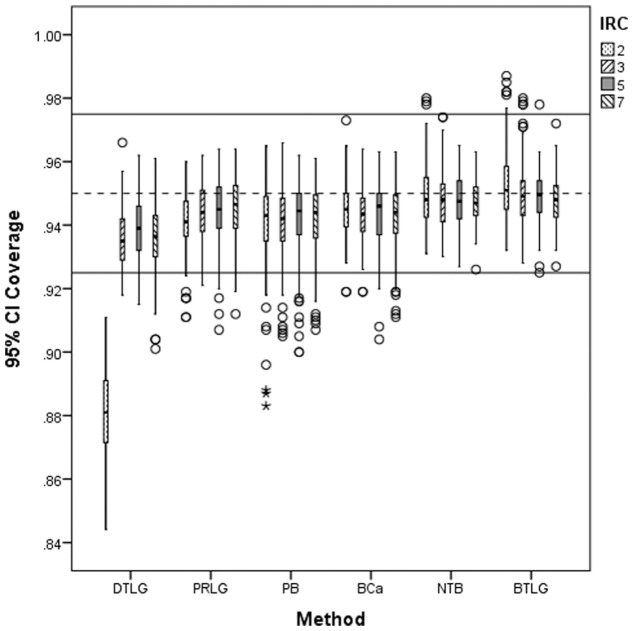
Figures 1 to 3 display the 95% CI coverage for distribution type by item response category. The figures clearly show that the NTB CI had the most consistent coverage within range. In addition, with the exception of the NTB CI, all the CIs were affected by Type 2 distributions as it was the condition with the most unacceptable coverage occurring mostly with the PB and PRLG CIs. A noticeable characteristic is that the DTLG CI was most affected by binary items, and specifically in combination with Type 2 distributions, as it did not have any acceptable coverage here.

Figure 1.

Distribution of 95% CI coverage for item response category (IRC) at Type 1 distribution.

Note. CI = confidence interval; DTLG = delta method with logit transformation; PRLG = three-step parceling with logit transformation; PB = percentile bootstrap; BCa = biased-corrected and accelerated bootstrap; NTB = normal theory bootstrap; BTLG = bootstrap SE with logit transformation; dashed line is at .95 and solid lines at [.925, .975].

Figure 3.

Distribution of 95% CI coverage for item response category (IRC) at Type 3 distribution.

Note. CI = confidence interval; DTLG = delta method with logit transformation; PRLG = three-step parceling with logit transformation; PB = percentile bootstrap; BCa = biased-corrected and accelerated bootstrap; NTB = normal theory bootstrap; BTLG = bootstrap SE with logit transformation; dashed line is at .95 and solid lines at [.925, .975].

Figure 2.

Distribution of 95% CI coverage for item response category (IRC) at Type 2 distribution.

Note. CI = confidence interval; DTLG = delta method with logit transformation; PRLG = three-step parceling with logit transformation; PB = percentile bootstrap; BCa = biased-corrected and accelerated bootstrap; NTB = normal theory bootstrap; BTLG = bootstrap SE with logit transformation; dashed line is at .95 and solid lines at [.925, .975].

Discussion

Six coefficient omega CIs for unidimensional congeneric items proposed in the literature and that can be implemented in a straightforward manner were investigated via a simulation study. Of particular interest was the impact of nonnormality and binary/Likert-type items. To date, no study has compared these CIs. In fact, the literature has called for guidelines between choosing among the investigated CIs that were developed between 1997 and 2011 (Raykov, 2012; Raykov & Marcoulides, 2011). Those developed after 2011 were included for completeness. The results show noticeable variation between the methods. However, the NTB CI had by far the best coverage across all the simulation conditions. Most performance variation was between the remaining methods as they were affected by the type of distribution and IRC.

Most unacceptable coverage occurred with a sample size of 50. In this instance, with the exception of the PB CI, most of the CIs performed fairly well under the Type 1 distribution. However, under the Type 2 distribution there was more noticeable variation and unacceptable coverage between the CIs. Here, the PB CI once again had the most unacceptable coverage. In addition, the DTLG CI did not have a single instance of acceptable coverage with binary items. In fact, only the NTB CI performed well in this situation. The bootstrap CIs were comparable under the Type 1 and 3 distributions. However, while the DTLG performed well with non-binary items, it performed poorly with binary items.

Increasing the sample size had a stabilizing effect. All the CIs had more acceptable coverage as sample size increased. In fact, once the sample increased beyond 100, the CIs had comparable results. The only exception was the DTLG CI under the Types 2 and 3 distributions. Here, the DTLG CI did not start to have comparable results with the other CIs until a sample size of 250 or more. However, regardless of the sample size, the DTLG CI for binary items under the Type 2 distribution did not have a single instance of acceptable coverage.

There are two reasons for the DTLG CI results. First, the parameters are estimated via maximum likelihood, which has large sample size properties. This is why the DTLG CI for nonbinary items did not stabilize and have comparable results with the other CIs until a sample size of 250. Second, the Type 2 distribution binary items had the most positive kurtosis. Distributions with positive kurtosis are narrower with higher peaks. As such, these distributions tend to have less variability which directly affects correlation coefficients. In addition, the range restrictions imposed by binary items affect correlations because they have less variability. These two conditions magnified each other to create the situation where the DTLG CI did not have a single instance of acceptable coverage for binary items with Type 2 distributions. In fact, the Type 2 distribution binary items affected many of the other CIs with a sample size of 50 for the second reason presented here.

Like any study, there are some limitations. Three limitations are noted here. First, the results are limited to the conditions investigated, and therefore there is no suggestion that the results are absolute. Even so, the conditions that were investigated are general in that they can encompass many situations encountered in applied settings. In addition, the results do provide more information about the CIs investigated than there is in the current literature. Second, Raykov, Dimitrov, and Asparouhov (2010) developed a coefficient omega CI method for binary items. However, this method was not included here because it is “rather tedious to apply . . . with more than about 8 to 10 items” (Raykov & Marcoulides, 2011, p. 176). As measurement instruments tend to have more than 10 items, the method could prove to be cumbersome for end users and therefore not straightforward to use. Third, the NTB CI assumes that the ESD for coefficient omega is normal. Padilla and Divers (2013) have discussed this issue and will not be discussed here. However, if one does not want to make the normality assumption about the ESD, the BTLG is a reasonable choice with a sample size of 50 and nonbinary items. The BTLG remains a reasonable choice for sample sizes greater than 50 (see below).

Within the context of the simulation, there is a clear order of performance among the six CIs. The NTB CI had the best performance in that it had acceptable coverage under all but 5 simulation conditions (5/1,440 = .003). The BTLG, BCa, and PRLG CIs had the next best performance (17/1,440 = .012, 32/1,440 = .022, and 33/1,440 = .023, respectively). Note that the BCa and PRLG CIs had nearly equivalent overall performance. This was followed by the PB and DTLG CIs (64/1,440 = .044 and 237/1,440 = .165, respectively). In particular, the NTB CI was the only one that had reasonable performance with a sample size of 50. However, with the exception of the PB and DTLG CIs, the remaining CIs are reasonable choices when the sample size is 100 or larger. If computing power is an issue, a reasonable alternative is the PRLG CI when sample size is 100 or more. Interested readers can obtain a free and easy-to-use R function for the coefficient omega bootstrap CIs through the corresponding author’s website (www.omegalab-padilla.org).