Robust Coefficients Alpha and Omega and Confidence Intervals With Outlying Observations and Missing Data

Abstract

Cronbach’s coefficient alpha is a widely used reliability measure in social, behavioral, and education sciences. It is reported in nearly every study that involves measuring a construct through multiple items. With non-tau-equivalent items, McDonald’s omega has been used as a popular alternative to alpha in the literature. Traditional estimation methods for alpha and omega often implicitly assume that data are complete and normally distributed. This study proposes robust procedures to estimate both alpha and omega as well as corresponding standard errors and confidence intervals from samples that may contain potential outlying observations and missing values. The influence of outlying observations and missing data on the estimates of alpha and omega is investigated through two simulation studies. Results show that the newly developed robust method yields substantially improved alpha and omega estimates as well as better coverage rates of confidence intervals than the conventional nonrobust method. An R package coefficientalpha is developed and demonstrated to obtain robust estimates of alpha and omega.

Introduction

According to classical test theory, an observed score of a test is equal to the true score plus an error score. The reliability coefficient, or reliability, is the ratio of the true score variance to the observed score variance (e.g., Raykov & Marcoulides, 2010). In social, behavioral, and education research, multiple items are often used to measure a construct through a composite score. Therefore, the reliability of a composite is often of great interest. Cronbach’s coefficient alpha (α; Cronbach, 1951, 1988; Cronbach & Shavelson, 2004) and McDonald’s coefficient omega (ω; McDonald, 1999) are probably the most widely used measures of composite reliability. Both alpha and omega bear their own assumptions when measuring reliability (e.g., Raykov & Marcoulides, 2010, 2015). For example, only when the items used are true score equivalent and the error scores are uncorrelated, alpha is equal to reliability (e.g., Raykov, 1997; Raykov & Marcoulides, 2010; Raykov, Marcoulides, & Patelis, 2015). Otherwise, alpha can underestimate or even overestimate the reliability (e.g., Maydeu-Olivares, Coffman, Garcia-Forero, & Gallardo-Pujol, 2010; Raykov, 1997, 2001). The validity of coefficient omega does not require the items to be true score equivalent but needs the items to be homogeneous or unidimentional.¹

In nearly every study involving the measure of a construct through multiple items in psychological research, a reliability coefficient, such as alpha, has been reported. In addition to reporting the sample coefficient alpha and omega, many researchers strongly recommended reporting corresponding standard errors (SE) and/or confidence intervals (CIs; e.g., Fan & Thompson, 2001; Iacobucci & Duhachek, 2003; Raykov & Shrout, 2002). There also exist developments regarding the SEs or the sampling distributions of the sample coefficient alpha and omega under various conditions. For example, under the assumption of parallel items and normally distributed data, Kristof (1963) and Feldt (1965) showed that a transformation of the sample coefficient alpha follows an F distribution. Under the multivariate normal assumption, van Zyl, Neudecker, and Nel (2000) showed that the sample coefficient alpha asymptotically follows a normal distribution without assuming compound symmetry. Yuan and Bentler (2002) further found that the asymptotic distribution given by van Zyl et al. (2000) can still be valid for a large class of nonnormal distributions. Maydeu-Olivares, Coffman, and Hartmann (2007) and Yuan, Guarnaccia, and Hayslip (2003) studied the distributional properties of sample coefficient alpha, and their results are asymptotically valid for all populations with finite fourth-order moments. There are fewer studies on the sampling distribution of omega in the literature (Cheung, 2009; Raykov, 2002; Yuan & Bentler, 2002). For example, Raykov (2002) proposed an analytical procedure that can estimate the SE of sample omega, and Raykov and Marcoulides (2010) illustrated how to get a CI, including the bootstrap interval, of omega (see also Padilla & Divers, 2013a, 2013b; Raykov, 1998). Yuan and Bentler (2002) developed a method that yields a robust standard error for sample omega when data are nonnormal.

However, previous development on the estimation of alpha and omega as well as corresponding SE and CIs rarely accounts for the influence of outlying observations and missing data. The estimation of alpha and omega is typically based on the sample covariance matrix, which is extremely sensitive to outlying observations. Therefore, it is expected that alpha and omega are equally influenced by outlying observations. In fact, previous literature has shown that the sample coefficient alpha can be biased or very inefficient with the presence of outlying observations and nonnormal data (e.g., Christmann, & Van Aelst, 2006; Liu & Zumbo, 2007; Liu, Wu, & Zumbo, 2010; Sheng & Sheng, 2013; Wilcox, 1992). Enders (2004) showed that ignoring missing data in the sample might lead to biased and less accurate estimate of coefficient alpha and proposed an expectation-maximization algorithm to deal with missing data when estimating reliability (see Enders, 2003). Headrick and Sheng (2013) proposed to estimate alpha based on the L-moment to handle nonnormal data. However, methods to deal with both outlying observations and missing data in estimating alpha, especially omega, are desired.

The purpose of this study is twofold. The first is to propose robust M-estimators of alpha and omega. We will obtain the robust estimators as well as their SEs and CIs for alpha and omega to deal with both outlying observations and missing data. The second is to develop easy-to-use software (R package coefficientalpha) that yields robust estimates of alpha and omega as well as corresponding CIs. The robustness of the developed procedure relies on the fact that outlying cases are downweighted in the estimation process. Missing data are handled by an expectation-robust (ER) algorithm (Yuan, Chan, & Tian, 2015), which is a generalization of the EM-algorithm based on a multivariate t distribution (Little, 1988). In the development, we assume that data are missing completely at random (MCAR), missing at random (MAR), or missing not at random (MNAR) but with auxiliary variables (e.g., Little & Rubin, 2002). As we shall see, the unique contributions of the study include the following: (1) the robust estimation of alpha and omega with both outlying observations and missing data, (2) the calculation of the consistent SE, and (3) free software to obtain robust coefficient alpha and omega estimates and their consistent SE. In particular, the developed software also provides diagnostic plots for visually examining cases that are influential to the estimation of alpha and omega. Other desirable features of the software include being free, and being able to run either locally on a personal computer within the statistical software R or remotely on a web server. Notably, our user-friendly web interface does not require researchers to be familiar with R to use the software.

In the next section, we first distinguish two types of outlying observations and show their influence on coefficient alpha. Then, we describe how to obtain robust coefficient alpha estimate and the corresponding CI. Next, we show how to apply the robust procedure to estimate omega and its CIs. After that, we illustrate the influence of outlying observations and missing data on alpha and omega through two simulation studies. Through the simulation studies, we also show that the newly developed robust method yields substantially improved alpha and omega estimates as well as significantly better coverage rates of CIs than the conventional nonrobust method and the bootstrap method. Finally, we demonstrate the use of our software through an example. Some technical details are provided in an appendix.

Outlying Observations and Their Influence

We first illustrate the influence of outlying observations on coefficient alpha through an example.² Using the example, we focus on explaining the different types of outlying observations and their influences on coefficient alpha.

Let y be a vector that denotes a p-variate population with mean $\mathbf{\mu }$ and covariance matrix $\Sigma =({\sigma }_{\mathrm{ij}}).$ The population coefficient alpha for the summation of the scores in y is defined as

$$\alpha =\frac{p}{p-1}(1-\frac{\sum _{i=1}^p{\sigma }_{\mathrm{ii}}}{\sum _{i=1}^p\sum _{j=1}^p{\sigma }_{\mathrm{ij}}}).$$

Let $y_1,\dots ,y_n$ be a random sample of y and $\mathbf{S}=(s_{\mathrm{ij}})$ be the sample covariance matrix. Then the sample coefficient alpha is given by

$$\hat{\alpha }=\frac{p}{p-1}(1-\frac{\sum _{i=1}^p{s}_{\mathrm{ii}}}{\sum _{i=1}^p\sum _{j=1}^p{s}_{\mathrm{ij}}}).$$

The influence of outlying observations on sample coefficient alpha can be clearly illustrated through the analysis of two items. Figure 1 displays a data set of 13 observations on two items $y_1$ and $y_2$ with different types of outlying observations. The coordinates of the nine regular observations are given by

Figure 1.

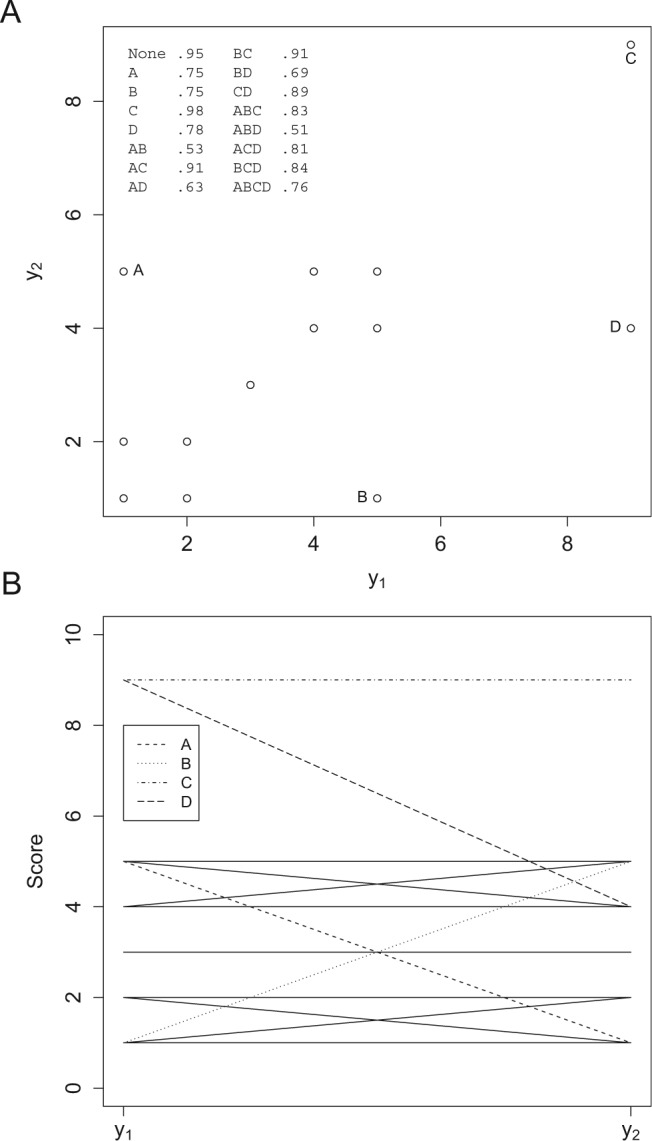
Different types of outlying observations and their influence on coefficient alpha: (A) Scatterplot; (B) Profile plot.

$$\begin{array}{cccccccccc}\hfill y_1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 2\hfill & \hfill 2\hfill & \hfill 3\hfill & \hfill 4\hfill & \hfill 4\hfill & \hfill 5\hfill & \hfill 5\hfill \\ \multicolumn{1}{c}{y_2}& \hfill 1\hfill & \hfill 2\hfill & \hfill 1\hfill & \hfill 2\hfill & \hfill 3\hfill & \hfill 4\hfill & \hfill 5\hfill & \hfill 4\hfill & \hfill 5\hfill \end{array}$$

The coordinates of the four additional observations are A = (1, 5), B = (5, 1), C = (9, 9), and D = (9, 4). Figure 1 also contains the values of coefficient alpha when different combinations of A, B, C, and D are pooled with the nine regular observations. It is clear from the geometry of Figure 1 that A, B, C, and D are outlying observations. The four observations can then be classified according to their locations or geometry relative to the other cases.

We first distinguish between inadmissible outlying observations and admissible outlying observations. Inadmissible outlying observations are typically erroneous observations that do not represent the underlying phenomena to be measured. The scores for inadmissible outlying observations can be either within or out of the range of a test. Errors in data recording and input are the most common cause of inadmissible outlying observations. For example, suppose that $y_1$ and $y_2$ are 5-point Likert-type items. Then, C and D in Figure 1 are obviously erroneous observations because they have scores larger than 5. These observations can be identified by the robust procedure and their effect on the follow-up analysis such as the estimation of reliability can also be controlled. Particularly, when the weight³ is 0, it is equivalent to have such observations removed automatically. After identifying the outlying observations, special attention/treatment by substantive researchers might also be needed to understand the causes behind each.

Admissible outlying observations are different from the majority of the data but carry valid and useful information and truly represent the underlying phenomena. For example, suppose both $y_1$ and $y_2$ are continuous measures of mathematics ability with the maximum possible score 10. For illustration purpose, we further assume that $y_1$ is a measure of addition and $y_2$ is a measure of multiplication. Reasonably, a theory can be hypothesized that the two items are determined by the same unidimensional underlying mathematical ability⁴ and should be positively correlated. In this case, the four observations A, B, C, and D do have valid scores but they also appear different (outlying) from the rest of the observations.

For the four outlying observations, each of them represents a different pattern. First, the observation C has extreme scores on both $y_1$ and $y_2$ but within the limit of maximum scores. Furthermore, the two scores are extreme in the same direction and therefore consistent with the hypothesized theory. The observation is outlying most likely because of the participant’s talent in mathematics that leads to large scores for $y_1$ and $y_2.$ In this study, we refer to such outlying observations that are consistent with the hypothesized theory/relationship as leverage observations (Yuan & Zhong, 2008). In general, leverage observations are “good” in the sense that they lead to enlarged coefficient alpha. For example, when the nine regular observations are considered, the coefficient alpha is .95. With C being included, the alpha increases from .95 to .98.

The observations A, B, and D are also outlying but geometrically different from C. For A, it has a large score on $y_2$ but a small score on $y_1.$ In other words, the observation shows high ability in terms of multiplication but low ability on addition. This is inconsistent with the hypothesized theory on the unidimensional mathematical ability. The pattern of the observation B is the other way around. Although D has a relative large score on $y_1,$ its value is a lot smaller compared to that of $y_2.$ In this study, we refer to such outlying observations that are inconsistent with the hypothesized theory as outliers (Yuan & Zhong, 2008). Outliers typically reduce the value of coefficient alpha. For example, with A or B being included, the coefficient alpha changes from .95 to .75 and with D being included, the alpha changes to .78.

In practice, a data set may contain both outliers and leverage observations; whether the estimated coefficient alpha becomes smaller or larger depends on their combined effects. For example, with all three outliers A, B, and D, the estimated coefficient alpha changes from the original .95 to .51. With outlier A and leverage observation C, the estimated coefficient alpha has a small decrease to about .91. However, in general, we may not want the estimated coefficient alpha to be determined by a few outlying observations, regardless of outliers or leverage observations. This motivates our development of a robust estimator of coefficient alpha.

Although the scatterplot is useful in identifying outlying observations with two items, it can be difficult to use when there are more than two items. Instead, a profile plot can be used to visualize possible outlying observations (e.g., Yuan & Zhang, 2012a). For example, the profile plot in Figure 1B displays the same data as in the scatterplot. It also shows the difference between the regular and outlying observations as well as that between outliers and leverage observations. First, the outlying observations distinguish themselves from the regular observations because their profiles do not mingle together with those of regular observations. Second, for outliers, their profiles usually show atypical patterns. For example, the profiles of A and B show more change than regular ones by having high score on one item but low score on the other item. Third, for leverage observations, all items may have scores noticeably smaller or larger than those of the majority, and their profiles, such as observation C, separate themselves from the profiles of the rest of cases. Note that the profile of D exhibits patterns of both outliers and leverage observations.

Robust Estimation of Covariance Matrix

In this section, we will first review robust estimation of covariance matrix with complete data, and then describe the idea of robust estimation with incomplete data. The idea of robust covariance matrix estimation is to use a formula in which cases that are unusually far from the center of the majority of observations get smaller weights and, therefore, contribute less to the covariance estimates. For complete data, a covariance matrix can be robustly estimated according to

$$\hat{\mathbf{\Sigma }}=\frac{1}{n}\sum _{i=1}^n{w}_{i2}({\mathbf{y}}_i-\hat{\mathbf{\mu }})({\mathbf{y}}_i-\hat{\mathbf{\mu }})\prime ,$$

where

$$\hat{\mathbf{\mu }}=\frac{1}{\sum _{i=1}^n{w}_{i1}}\sum _{i=1}^n{w}_{i1}{\mathbf{y}}_i$$

is the corresponding robust mean estimate; $w_{i1}$ and $w_{i2}$ are weights that are inversely proportional to the deviation between ${\mathbf{y}}_i$ and $\hat{\mathbf{\mu }},$ as measured by the Mahalanobis distance (M-distance; see Yuan & Zhang, 2012b). Because a larger distance corresponds to a smaller weight, cases that are far from the center of the majority of observations (represented by $\hat{\mathbf{\mu }}$) will have a small or tiny contribution to the estimator $\hat{\Sigma }$ in Equation 3. Thus, the effect of outlying observations on $\hat{\mathbf{\Sigma }}$ is limited. Notice that, Equation 3 yields the sample covariance matrix S when $w_{i1}=w_{i2}=1$ for all i. Because outlying cases are treated equally as regular cases in the formulation of S, outlying observations have unlimited influences on S and consequently on the resulting coefficients alpha and omega.

Both outliers and leverage observations will deviate more from the center of the majority of data than other typical observations. Their effect on $\hat{\mathbf{\Sigma }}$ can be controlled when $w_{i1}$ and $w_{i2}$ are properly chosen. Many candidates of weights have been suggested in the robust statistical literature. The Huber-type weights are widely used and are therefore employed in the current study (e.g., Yuan & Zhang, 2012a).⁵ In Huber-type weights, a tuning parameter $\phi (0\le \phi <1)$ is used to practically control the percentage of data to be downweighted. Following the choice of the tuning parameter, a threshold value is obtained to determine how the values of weights are calculated. If the distance of a case from $\hat{\mathbf{\mu }}$ is less than the threshold, the case is not downweighted; and otherwise, the case will be assigned a weight that is smaller than 1 in Equation 3 and its value is inversely proportional to the distance. When $\phi =0,$ no case is downweighted. With the increase of ϕ, more cases will be downweighted and cases are also more heavily downweighted. A larger ϕ would not only make alpha more resistant to outliers but also less efficient when a substantial proportion of the observations that truly represent the population are downweighted. In practice, a weight between 0.01 and 0.1 would work well in controlling the effect of outlying observations on the estimate of coefficient alpha. We will discuss how to choose a proper ϕ with graphs and examples later.

The idea of robust estimation with missing values is the same as robust estimation with complete data. The algorithm for calculating the robust estimates of means and covariance matrix is called the ER algorithm. In the E-step, terms involving missing values in Equation 3 are replaced by their conditional expectations, and the R-step parallels to that in Equation 3, where cases that sit far from the center of the majority of observations will be downweighted. In our R package coefficientalpha, the implementation of the ER-algorithm with the Huber-type weights is based on Yuan et al. (2015).

Robust Coefficient Alpha

With the robust covariance matrix $\hat{\mathbf{\Sigma }}=({\hat{\sigma }}_{\mathrm{ij}})$, the robust alpha estimate is

$$\hat{\alpha }=\frac{p}{p-1}(1-\frac{\sum _{j=1}^p{\hat{\sigma }}_{\mathrm{jj}}}{\sum _{i=1}^p\sum _{j=1}^p{\hat{\sigma }}_{\mathrm{ij}}}).$$

In addition to the point estimator $\hat{\sigma }$, the output of the software also contains the SE of $\hat{\sigma }$ and the corresponding CI for alpha.⁶ The SE is based on the sandwich-type covariance matrix for the robust estimate $\hat{\mathbf{\Sigma }},$ and is consistent regardless of the distribution of the sample (Yuan et al., 2015). It can also provide us the information on the efficiency of the robust method. The details of the ER-algorithm and the sandwich-type covariance matrix for $\hat{\mathbf{\Sigma }}$ are not the focus of the study, and are referred to Yuan et al. (2015) and Yuan and Zhang (2012a). The SE for $\hat{\sigma }$ based on the sandwich-type covariance matrix of $\hat{\mathbf{\Sigma }}$ is provided in Appendix A.

Because the robustness is determined by the tuning parameter ϕ, we next describe three graphs to facilitate its choice and display its effect.

The first one is termed as a diagnostic plot that displays the estimates of coefficient alpha against different values of ϕ. For a given data set, alpha will generally change when ϕ varies. For example, if there are outliers, alpha would first increase quickly and then flatten out with the increase of ϕ. If there are leverage observations, alpha will decline as ϕ increases. When only outliers exist, one may choose an “optimal”ϕ according to the maximum value of alpha or at the place where alpha shows the largest change. When only leverage observations exist, one may choose the tuning parameter ϕ that corresponds to the first substantial drop of alpha to control the effect of leverage observations. When leverage observations and outliers coexist, one may slowly increase the tuning parameter ϕ and choose its value when alpha becomes stabilized.

The second graph is termed as a weight plot where case-level weights $w_{i2}$ against case ID are plotted. We do not include the plot of $w_{i1}$ because it contains the same information as the plot of $w_{i2}.$ In the plot, cases with smallest weights are identified by case numbers. The plot provides the information on which cases are outlying and how heavily they are downweighted.

The third graph is a profile plot in which centered observations $(y_{\mathrm{ij}}-{\hat{\mu }}_j)$ for cases with smallest weights are plotted against the order of the variable j. With such a plot, one can visually examine how the profile of each outlying case is different from the average profile and therefore, why a case is downweighted. The profile plot also provides information on whether an outlying case is an outlier or a leverage observation.

In summary, the three plots together will allow us to select a proper ϕ according to the distribution shape of the data. They also facilitate us to see how coefficient alpha changes when controlling the effect of outliers and/or leverage observations. We will illustrate how to use the graphs in practice later on in an example when introducing our R package coefficientalpha.

Robust Coefficient Omega

The procedure for obtaining robust coefficient alpha estimates can be readily extended to omega for homogenous items. Suppose that p measurements follow a one-factor model

$$y_{\mathrm{ij}}={\mu }_j+{\lambda }_j{f}_i+e_{\mathrm{ij}},$$

where $y_{\mathrm{ij}}$ denotes a score for participant i on item j, ${\mu }_j$ is the intercept for item j, f_i is the common factor score for participant i, ${\lambda }_j$ is the factor loading for item j, and $e_{\mathrm{ij}}$ is the independent unique factor score with variance ${\psi }_{\mathrm{jj}}$. The variance of f_i is fixed at 1.0 for model identification. The population omega (ω) is defined as (McDonald, 1999, Equation 6.20b)

$$\omega =\frac{{(\sum _{j=1}^p{\lambda }_j)}^2}{{(\sum _{j=1}^p{\lambda }_j)}^2+(\sum _{j=1}^p{\psi }_{\mathrm{jj}})}.$$

To estimate ω, the factor model is typically estimated from the sample covariance matrix of y. Therefore, the sample omega, denoted by $\hat{\omega }$, is similarly influenced by outlying observations as the sample coefficient alpha. Actually, α can be viewed as a special case of ω when all the factor loadings are equal ${\lambda }_j\equiv \lambda .$ ⁷ Outliers and leverage observations can also be distinguished using the factor model (see Yuan & Zhang, 2012b). Generally speaking, cases with extreme common factor scores are leverage observations and data contamination leads to cases with large unique factor scores or outliers.

The robust $\hat{\omega }$ can be calculated in three stages. First, a robust covariance matrix $\hat{\mathbf{\Sigma }}$ as in the estimation of robust alpha can be obtained to account for both outlying observations and missing data. Second, the factor model can be estimated by any SEM software based on the robust $\hat{\mathbf{\Sigma }}$ to get ${\hat{\lambda }}_j$ and ${\hat{\psi }}_{\mathrm{jj}}.$ Third, the robust $\hat{\omega }$ is calculated as

$$\hat{\omega }=\frac{{(\sum _{j=1}^p{\hat{\lambda }}_j)}^2}{{(\sum _{j=1}^p{\hat{\lambda }}_j)}^2+(\sum _{j=1}^p{\hat{\psi }}_{\mathrm{jj}})}.$$

In order to get a robust standard error or CI for omega, one first obtains a consistent covariance matrix for $\hat{}\mathbf{\theta }=({\hat{\lambda }}_1,\dots ,{\hat{\lambda }}_p,{\hat{\psi }}_{11},\dots ,{\hat{\psi }}_{\mathrm{pp}})$ and then uses the delta method to get the standard error for $\hat{\omega }$. Both the standard error of $\hat{\omega }$ and CI of omega are available in our R packages and therefore the technical details are omitted here for the sake of space. The robustness of omega is related to the tuning parameter ϕ as for alpha. The same method for determining ϕ for alpha can be applied here.

Simulation Studies

In this section, we present two simulation studies to show the influence of outlying observations and missing data on the estimates of alpha and omega. For the sake of space, we only report the results of a few conditions. To better see the influence of outlying observations and missing data, we investigate their effects separately although in practice they often coexist.

Simulation Study 1: Influence of Outlying Observations

The aim of the study is to demonstrate the influence of outlying observations on the estimates of alpha and omega through simulated data. Consider the one-factor model

$$y_{\mathrm{ij}}={\mu }_j+{\lambda }_j{f}_i+e_{\mathrm{ij}},i=1,\dots ,n,j=1,\dots ,p.$$

Two sets of population parameters are used in this study. One satisfies tau-equivalence with ${\lambda }_j=\sqrt{0.6}$ and ${\psi }_{\mathrm{jj}}=0.4$ for $j=1,\dots ,p$ and $p=6.$ Thus, the population alpha and omega are the same and equal to .9. Another does not conform to tau-equivalence with ${\lambda }_j=\sqrt{0.2}$ and ${\psi }_{\mathrm{jj}}=0.8$ for $j=1,2,3$ and ${\lambda }_j=\sqrt{0.6}$ and ${\psi }_{\mathrm{jj}}=0.4$ for $j=4,5,6.$ The intercept ${\mu }_j$ is set to 0 without losing generality. Under this setting, the population alpha is .777⁸ and the population omega is .789. The alpha is smaller than omega as expected (e.g., McDonald, 1999).

Data are generated as follows. First, 1,000 replications of normally distributed samples with size $n=100$ are generated from populations under tau-equivalence and non-tau-equivalence, respectively. Second, for each of the samples, a new sample with outliers is created by letting $y_{\mathrm{ij}}=y_{\mathrm{ij}}-4$ for $j=1,2,3$ and $y_{\mathrm{ij}}=y_{\mathrm{ij}}+4$ for $j=4,5,6$ with $i=96,97,98,99,100.$ Therefore, each new sample has 5% of outliers. Third, for each of the normally distributed samples, another new sample with leverage observations is created by letting $y_{\mathrm{ij}}=y_{\mathrm{ij}}-6$ for $j=1,\dots ,6$ with $i=96,97,98,99,100.$ Therefore, each sample contains 5% of leverage observations.

Both alpha and omega are then estimated from the generated data with three different levels of downweighting rate $\phi =0,0.05,0.1$. Note that when $\phi =0$, no observations are downweighted and therefore both alpha and omega are estimated by the commonly used nonrobust method.⁹ Because the bootstrap method has been used to obtain the bootstrap CIs for alpha and omega when data are nonnormal, we also obtain the bias corrected and accelerated (BCa) bootstrap CI based on 1,000 bootstrap samples in our simulation study for comparison (e.g., Padilla & Divers, 2013a, 2013b; Raykov & Marcoulides, 2010). Table 1 presents the results as the average of the estimated alpha and omega as well as their empirical SEs and the coverage rates of the 95% CIs.

Table 1.

Average Alpha and Omega Estimates and Empirical Standard Errors and Coverage Rates of 95% Confidence Intervals for Study 1 Under Normally Distributed Data (Normal), Data With Outliers (Outlier), and Data With Leverage Observations (Leverage)^a.

		ϕ	Alpha			Omega
			Est	SE	Coverage	Est	SE	Coverage
Tau-equivalence	Normal	BCa	.898	.016	.931	.899	.016	.933
		0	.898	.015	.934	.899	.016	.939
		.05	.898	.016	.942	.899	.016	.944
		.1	.898	.016	.950	.899	.016	.946
	Outlier	BCa	.663	.112	0	.600	.111	0
		0	.663	.109	.115	.600	.101	0
		.05	.863	.047	1	.862	.049	1
		.1	.872	.033	.991	.873	.033	.995
	Leverage	BCa	.953	.014	.012	.953	.014	.012
		0	.953	.012	.004	.953	.012	.004
		.05	.944	.018	.241	.945	.018	.236
		.1	.940	.019	.348	.941	.019	.337
Non-tau-equivalence	Normal	BCa	.772	.036	.949	.786	.031	.954
		0	.772	.034	.934	.786	.033	.933
		.05	.772	.035	.937	.786	.034	.935
		.1	.772	.036	.939	.786	.034	.930
	Outlier	BCa	.437	.165	.013	.456	.112	.000
		0	.437	.161	.313	.456	.112	.025
		.05	.691	.100	1.00	.691	.102	.988
		.1	.712	.073	.989	.716	.075	.980
	Leverage	BCa	.914	.030	.001	.916	.028	.001
		0	.914	.024	.000	.916	.024	.000
		.05	.885	.047	.314	.889	.045	.346
		.1	.873	.046	.400	.877	.043	.435

Note. Est = estimate; SE = standard error; Coverage = coverage rate of 95% confidence intervals; BCa = bootstrap standard error and confidence interval based on 1,000 bootstrap samples.

^aThe population alpha and omega are both .9 under tau-equivalence; and under non-tau-equivalence, the population alpha is .777 and the population omega is .789.

Results for the analysis of data under tau-equivalence are presented in the upper panel of Table 1. The following can be concluded from the results. First, for the normal data, the average of the estimated alpha and omega are extremely close, with a difference about .001, and are almost the same as the population values. The coverage rates of all the CIs are close to the nominal level .95 for both alpha and omega. Furthermore, robust and nonrobust methods yield essentially the same estimates of alpha and omega. In addition, empirical SEs based on 1,000 bootstrap replications are similar to the sandwich SEs, and the corresponding BCa intervals following the bootstrap provide similar coverage rate. Second, for the data with outliers, the average of the estimated nonrobust alpha is .663 and that of the estimated nonrobust omega is .600, both of which largely underestimate their population values. It seems that omega is influenced even more by outliers than alpha. The coverage rate for alpha is .115 and for omega is 0, both of which are way off from the nominal level .95. Notably, the use of the bootstrap method does not improve the alpha and omega estimates and the BCa intervals do not provide better coverage. In contrast, the robust alpha and omega estimates become much closer to their population values and the estimated SEs become substantially smaller than their nonrobust counterparts. The estimated robust alpha and omega are almost identical to each other. Although the coverage rates are larger than the nominal level .95, they are much better than those from the nonrobust method. Third, for the data with leverage observations, the nonrobust alpha and omega overestimate their population values. After downweighting, the robust alpha and omega estimates become slightly closer to but are still much larger than the population values. However, their SEs become notably larger. This is because leverage observations correspond to more efficient parameter estimates (Yuan & Zhong, 2008) and downweighting minimizes the effect. Before downweighting, the coverage rates are close to 0 and after downweighting, they become greater but are still smaller than .95. The same as for the outlier condition, the use of the bootstrap method does not seem to help.

The lower panel of Table 1 contains the results for the analysis of data under non-tau-equivalence, from which we can conclude the following. First, for the normally distributed data, the average of the estimated omega is slightly larger than the average of the estimated alpha, both are very close to their population values. Similar to the results in the upper panel of Table 1, downweighting data does not play an influential role in the estimated alpha and omega for normally distributed samples. Second, for the data with outliers, the estimated nonrobust alpha and omega are much smaller than their population values. Although the robust alpha and omega estimates are still smaller than their population values, the improvement is substantial. Third, for data with leverage observations under non-tau-equivalence, both nonrobust and robust alpha and omega overestimate their population values. The robust estimates show substantial improvement over the nonrobust ones. The pattern of coverage rates is similar to that for tau-equivalent data. Fourth, as for tau-equivalence, the use of the bootstrap method does not lead to better results than the nonrobust method.

Concluding Remarks

This simulation study shows that, for normally distributed data, there is no substantial difference between alpha and omega estimates regardless of whether the items are tau-equivalent or not. Outliers cause underestimation of alpha and omega whereas leverage observations cause their overestimation. Our robust procedure can effectively control the influence of outlying observations although the procedure seems to work more effectively for outliers than for leverage observations. In particular, the CIs from our robust method have much improved coverage rates.

Simulation Study 2: Influence of Missing Data

This study aims to demonstrate the influence of missing data on alpha and omega through simulated data. Complete normal data are generated from populations satisfying tau-equivalence and non-tau-equivalence as in Study 1. Incomplete data are obtained in the following way. First, there are no missing data in $y_1$ and $y_4.$ Second, missing data in $y_5$ and $y_6$ are related to $y_1$. Specifically, an observation for $y_5$ is missing if $y_1\le q_{0.1}(y_1)$ and an observation for $y_6$ is missing if $q_{0.1}(y_1)<y_1\le q_{0.2}(y_1)$ where $q_p(y)$ is the $100p$th percentile of y. Third, missing data in $y_2$ and $y_3$ are related to $y_4$ so that an observation for $y_2$ is missing if $y_4\ge q_{0.9}(y_4)$ and an observation for $y_3$ is missing if $q_{0.8}(y_4)\le y_4<q_{0.9}(y_4).$ According to the definition of missing data mechanisms (e.g., Little & Rubin, 2002), all the missing values are missing at random. Based on the simulation, there are about 6.7% missing values and approximately 20% to 40% of participants have one or more missing values in each generated data set.

Both alpha and omega are estimated from the generated data with missing values using either listwise deletion or the robust procedure developed in this article that automatically takes care of missing data. Table 2 presents the results as the average of the estimated alpha and omega as well as their empirical SEs and the coverage rates of the 95% CIs.

Table 2.

Average Alpha and Omega Estimates and Empirical Standard Errors and Coverage Rates of the 95% Confidence Intervals for Study 2 Under Listwise Deletion (Deletion) and Maximum Likelihood Method (ML)^a.

		ϕ	Alpha			Omega
			Est	SE	Coverage	Est	SE	Coverage
Tau-equivalence	Deletion	0	.804	.036	.161	.812	.037	.289
		.05	.804	.038	.195	.812	.039	.335
		.1	.804	.039	.221	.812	.039	.354
	ML	0	.898	.016	.938	.899	.016	.939
		.05	.898	.016	.941	.899	.016	.940
		.1	.898	.017	.945	.899	.017	.939
Non-tau-equivalence	Deletion	0	.670	.062	.679	.695	.059	.733
		.05	.670	.065	.714	.694	.062	.764
		.1	.669	.067	.746	.693	.063	.778
	ML	0	.772	.036	.935	.787	.034	.929
		.05	.772	.037	.938	.787	.035	.934
		.1	.771	.038	.938	.787	.036	.935

Note. Est = estimate; SE = standard error; Coverage = coverage rate of 95% confidence intervals.

^aThe population alpha and omega are both .9 under tau-equivalence; and under non-tau-equivalence, the population alpha is .777 and the population omega is .789.

First, it is clear that the alpha and omega estimates following from listwise deletion underestimate their population values whether the items are tau-equivalent or not. Second, the estimated alpha and omega following the robust method are very close to their population values. Third, it is evident that the SEs of the estimated alpha and omega from the robust method are much smaller than those based on listwise deletion. This is because the robust method utilizes more information in the data. Fourth, when listwise deletion is used, the coverage rates are much smaller than the nominal level .95, especially for the tau-equivalent data. Our robust method, on the other hand, yields coverage rates much closer to .95. To separate the influence of nonnormal data and missing data on the reliability estimates, only normal data are investigated in this study. We also have evidences that for nonnormal data, the influence of missing data is similar (Tong, Zhang, & Yuan, 2014).

Software

To facilitate the computation of robust alpha and omega, we developed an R package coefficientalpha. The package is freely available at http://cran.r-project.org/package=coefficientalpha. The package calculates the robust alpha and omega, their SEs, and CIs for a given data set. In addition, the package also generates the diagnostic plot, the weight plot, and the profile plot to assist the selection of the tuning parameter and to visualize outlying observations. To accommodate users who are not familiar with R, an online interface is also developed. The R package includes an example data set with 100 cases and 10 variables. In this section, we illustrate the use of the R package using this data set. The use of its online interface can be found in Appendix B.

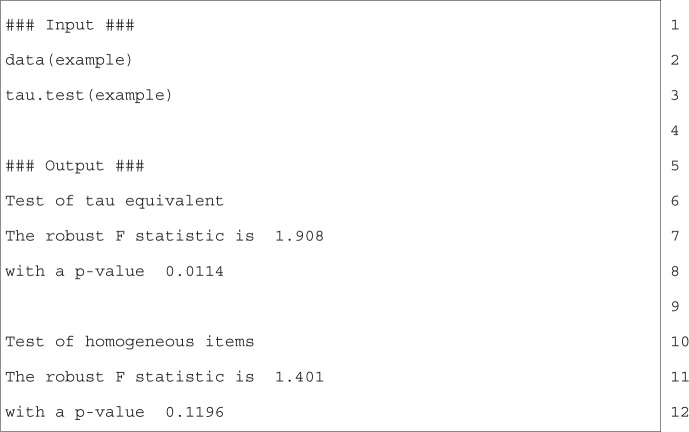
To use the package within R, first install it using the command install.packages (′coefficientalpha′) and then load it using the command library(coefficientalpha). The R package also includes tests of tau-equivalence¹⁰ and homogeneity of items.¹¹ Both tests are based on the robust F statistic proposed by Yuan and Zhang (2012a) and further studied in Tong et al. (2014). The R input and output for the tests are given in Figure 2. Note that the numbers on the right of the figure are the line numbers to facilitate the explanation of the R code, not a part of the code itself. The code on Line 2 loads the example data into R for use. On Line 3, the function tau.test is used to carry out the tests. The output of the analysis is given in Line 6 to Line 12. First, the robust F statistic for the test of tau-equivalence is 1.908 (Line 7) with a p value .0114 (Line 8). Therefore, we have to reject the tau-equivalence assumption. However, the F statistic for the test of homogeneity is 1.401 with a p value .1196, failing to reject the homogeneity assumption.

Figure 2.

Testing tau-equivalence and homogeneity of items.

In addition, when alpha or omega is calculated, the package will produce the test for tau-equivalence or homogeneity unless a user chooses not to perform such a test. Figure 3 shows an example. When estimating alpha for the example data set, the output indicates that tau-equivalence is not met.

Figure 3.

An example showing the tau-equivalence test output.

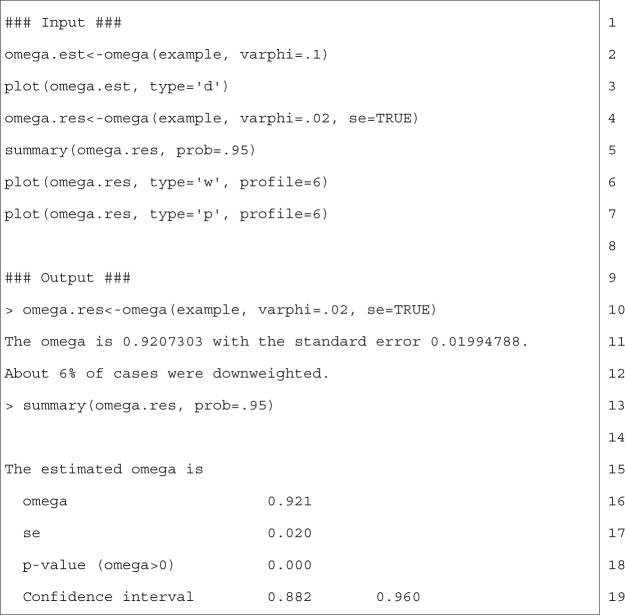
Because we rejected the tau-equivalence but failed to reject the homogeneity assumption, we proceed with the robust method in estimating omega in the following. The same procedure works for robustly estimating alpha. The R code for the analysis as well as the output are given in Figure 4.

Figure 4.

R code and output for computing omega.

In Figure 4, Line 2 uses the function omega to initially obtain the robust estimate of coefficient omega corresponding to the downweighting rate varphi=.1. Note that if the downweighting rate is set at 0, the conventional nonrobust omega with a robust standard error will be calculated. The initial calculation is used for the diagnostic purpose and a relative large downweighting rate is usually specified. Line 3 uses the plot function to generate the diagnostic plot by specifying the plot type through type=′d′. For the example data, the diagnostic plot is shown in Figure 5A, which plots the estimated omega corresponding to ϕ from 0 to 0.1 with an interval of 0.01. As ϕ increases, the estimate of omega first increases and then flattens out when $\phi =0.02$.¹² This indicates that 0.02 is a good choice for the downweighting rate. Therefore, for the rest of the analysis of the data, we let $\phi =0.02$. Line 4 calculates the robust omega estimate by setting $\phi =0.02$. The standard error is requested by setting se=TRUE. The output on Lines 11 to 12 shows that the estimated omega is 0.921 with a robust standard error 0.020. Note that when $\phi =0$, the nonrobust omega is 0.779. To get the 95% CI for omega, the summary function on Line 5 is used with prob=.95. The output on Line 19 gives the CI [0.882, 0.960].

Figure 5.

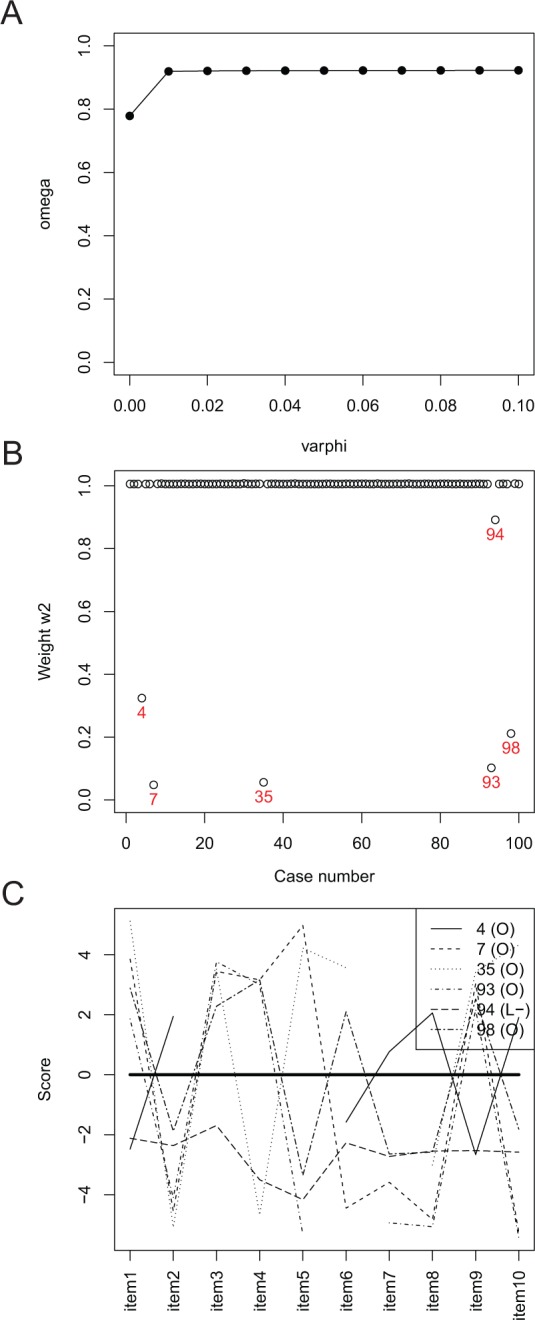
The diagnostic, weight, and profile plots for robustly estimating omega: (A) Diagnostic plot; (B) Weight plot; (C) Profile plot.Note.“O” in the legend indicates an outlier. L+ indicates a leverage observation above average and L− indicates a leverage observation below average.

Lines 6 and 7 generate the weight plot (Figure 5B) and profile plot (Figure 5C), respectively. The option, profile=6 is used to ask the software to Label 6 cases because by default the software only identifies the five most influential cases. According to the weight plot in Figure 5B, six cases with ID 4, 7, 35, 93, 94, and 98 are downweighted. Except for Case 94, whose weight is about .9, each of the other five cases has a weight smaller than .4, indicating that these five cases would have the greatest influence in estimating coefficients omega when using the conventional nonrobust method. In Figure 5C of the profile plot, each variable is centered at the robust estimate of the corresponding mean and plotted against the order of the variable. The profile plot suggests that, for Case 94, it has smaller values than average on all items. Therefore, Case 94 can be viewed as a leverage observation. Cases 4, 7, 35, 93, and 98 show similar patterns where some items have values much larger than average while other items much smaller than average. Therefore, those cases can be viewed as outliers. Note the plot function clearly identifies outlier and leverage observation in the plot by using different legends.

Discussion

In using a test or scale, its reliability is always a primary concern. Cronbach’s alpha is a widely used measure of reliability in the literature. When items are non-tau-equivalent, coefficient omega has been proposed and recommended. Methods for estimating the coefficient alpha and omega are commonly based on the sample covariance matrices or the NML estimates of $\Sigma$ and, therefore, are not robust to outlying observations. In this study, we proposed a robust procedure to estimate alpha and omega as well as their CIs. An R package coefficientalpha together with an online interface is also developed to carry out the proposed procedure.

With outlying observations, alpha and omega can be overestimated or underestimated. Our purpose is not to obtain a larger estimate but one that is closer to the population value without being overwhelmingly affected by a few influential observations. Because alpha and omega commonly estimated using NML are unduly affected by outlying observations, they tend to perform poorly when validating scales across groups (e.g., gender, race, culture). In contrast, robust estimates of alpha or omega will still perform well even if small percentages of the participants in different groups endorse the items differently. In cases where the majority of the participants in different groups endorse the scale differently, the robust alpha and omega can still tell the difference, since they are decided by the majority of the observations as reflected by Equation 3, where only a small percentage of cases lying far from the center are downweighted.

In practice, the mechanisms that lead to outlying observations can be more complex than discussed in the current study. For example, outlying observations can result from different understanding of a scale. It is well known that cultural differences exist between Americans and Chinese in the circumstances evoking pride, shame, and guilt (e.g., Stipek, 1998). Chinese may view expressing pride in public as an improper or unacceptable behavior, contrary to most Americans. Consequently, the recorded data for a Chinese participant in a study with a majority of American participants may be identified as outlying. Although such data might not be viewed as admissible anymore, our robust method can still be applied to identify the participant as outlying and further action, for example, removing such observations, can be taken by a researcher with substantial knowledge of the study. For this purpose, our R package facilitates the identification of peculiar observations and allows a user to drop potentially erroneous ones. On the other hand, if a large number of participants show such a cultural difference, the population cannot be viewed as homogeneous any more. Then, multiple group models or mixture models might be needed for better analysis. Our robust method can be applied as a diagnostic tool to explore such heterogeneous samples.

There are also situations where nonnormality is expected and one would not want to downweight the outlying observations. For example, data on abnormal behaviors in clinical research tend to be skewed and extreme scores in such data are often what a researcher is interested in. In this situation, one can opt not to downweight the extreme scores by setting $\phi =0$ in our R package. However, even for skewed data with heavy tails, robust estimate of alpha and omega may still be more accurate than the traditional ones based on the sample covariance matrix. In particular, the graphs of the R package allow users to identify extreme observations and to examine their profiles as well as to explore how their inclusion or removal affects the evaluation of reliability.

Handling outlying observations inevitably involves making subjective decisions. Our procedure can help identify potential outlying observations and assist the choice of downweighting rate. The estimated alpha and omega using the default procedure can be more resistant to outlying observations than their nonrobust counterparts. However, a researcher can be more involved in the procedure to obtain even better results. For example, the researcher can identify the outlying observations that should be removed directly instead of downweighted.

In summary, data in practice are often nonnormally distributed. When the mechanism of nonnormality is not clear, it is always a safer bet to utilize the robust reliability coefficients than their nonrobust counterparts. At the same time, once outlying observations are identified, special attention might be paid. Especially, robust methods should be preferred in the follow-up statistical data analysis (Yuan & Zhang, 2012a).

In addition to coefficients alpha and omega, other reliability measures have also been proposed in the literature. They include, among others, coefficient β (Revelle & Zinbarg, 2009; Zinbarg, Revelle, Yovel, & Li, 2005), the reliability coefficient for a general structure composite (Raykov & Shrout, 2002), dimension-free and model-based internal consistency reliability (Bentler, 2009, 2010), and model-based reliability that allows nonlinear relationship (Green & Yang, 2009; Yang & Green, 2010). In assessing interrater agreement, reliability coefficients can also be formulated as a form of intraclass correlation coefficients (Shrout & Fleiss, 1979). Under certain conditions, these alternative measures can be better than alpha and omega. However, these reliability measures, typically calculated as functions of the sample covariance matrix, are also influenced by nonnormal and missing data. Future study can investigate how to extend our robust procedure to these reliability measures. Furthermore, although there are other robust methods for alpha with complete data (e.g., Christmann & Van Aelst, 2006; Headrick & Sheng, 2013; Wilcox, 1992), they are not applicable with incomplete data. More work is needed to extend these methods with incomplete data.

Existing literature on missing data analysis typically assumes MCAR and MAR mechanisms. Incomplete data in educational and behavioral research can be MNAR. Although we did not emphasize it, our R package can include auxiliary variables when estimating alpha and omega. With auxiliary variables being included, the overall MAR mechanism becomes a more viable assumption. Methods explicitly modeling nonignorable missing data mechanism might be worth studying when estimating reliability coefficients.

Appendix A

Standard Error of $\widehat{ɑ}$

Notice that $\hat{\mathbf{\Sigma }}$ is a symmetric matrix. Let $\hat{\mathbf{\sigma }}$ be the vector of nonduplicated elements of $\hat{\Sigma }$. Then, under a set of regularity conditions, $\hat{\mathbf{\sigma }}$ is asymptotically normally distributed, which can be written as

$$\sqrt{n}(\hat{\mathbf{\sigma }}-\mathbf{\sigma })\stackrel{\mathcal{L}}{\to }N(0,\mathbf{\Gamma }),$$

where $\mathbf{\sigma }$ is the population counterpart of $\hat{\mathbf{\sigma }}$, $\Gamma$ is the asymptotic covariance matrix of $\sqrt{n}\hat{\mathbf{\sigma }}$, and can be consistently estimated by a sandwich-type covariance matrix $\hat{}\mathbf{\Gamma }$ (see Yuan & Zhang, 2012a). Since α is a function of $\mathbf{\sigma }$, it follows from the delta method that

$$\sqrt{n}(\hat{\sigma }-\alpha )\stackrel{\mathcal{L}}{\to }N(0,{\nu }^2),$$

where ${\nu }^2$ can be consistently estimated by the following:

$${\hat{\nu }}^2=\frac{\partial \hat{\sigma }}{\partial \hat{\mathbf{\sigma }}\prime }\mathbf{\Gamma }\frac{\partial \hat{\sigma }}{\partial \hat{\mathbf{\sigma }}}.$$

It follows from Equation 1 that the elements of the vector $\partial \hat{\sigma }/\partial \hat{\mathbf{\Sigma }}$ of partial derivatives can be evaluated according to

$$\frac{\partial \alpha }{\partial {\sigma }_{\mathrm{ij}}}=\{\begin{array}{cc}\hfill -\frac{p}{p-1}[\frac{1}{\sum _{i=1}^p\sum _{j=1}^p{\sigma }_{\mathrm{ij}}}-\frac{\sum _{i=1}^p{\sigma }_{\mathrm{ii}}}{{\left(\sum _{i=1}^p\sum _{j=1}^p{\sigma }_{\mathrm{ij}}\right)}^2}],\hfill & \hfill i=j\hfill \\ \multicolumn{1}{c}{\frac{2p}{p-1}\left[\frac{\sum _{i=1}^p{\sigma }_{\mathrm{ii}}}{{\left(\sum _{i=1}^p\sum _{j=1}^p{\sigma }_{\mathrm{ij}}\right)}^2}\right],}& \hfill i\ne j\hfill \end{array}$$

SE for $\hat{\alpha }$ and the corresponding CI as implemented in the package coefficientalpha are calculated according to the asymptotic distribution in Equation A2 and the variance estimate in Equation A3.

Appendix B

Using the Online Software

For researchers who may not be familiar with R, a self-explanatory online interface is also developed to robustly estimate alpha and omega. In particular, the use of the online interface does not require previous knowledge of R. To use the online interface, open the web page http://psychstat.org/alpha in a web browser. Figure B1 is a display of the online software interface. To use it, one first uploads a data file in free format (a text file with observations separated by space) with missing data denoted by “NA.” Each column of the data file represents an item. Variable names can be specified in the first line of the data file. Instead of downweighting, users can also choose to remove certain cases by providing the case numbers. A user can choose to deal with missing data using our robust algorithm or just removing missing data through listwise deletion. The default value for the tuning parameter ϕ is .1, which can be modified. If setting ϕ = 0, then coefficient alpha will be estimated using the normal-based-ML. A user can choose whether or not to estimate standard error for alpha. It is recommended but can be slow for large data sets. Finally, a user can choose to generate the three plots discussed in the article. For the weight and profile plots, a user can specify how many cases to be labeled and highlighted and the default is 5.

Figure B1.

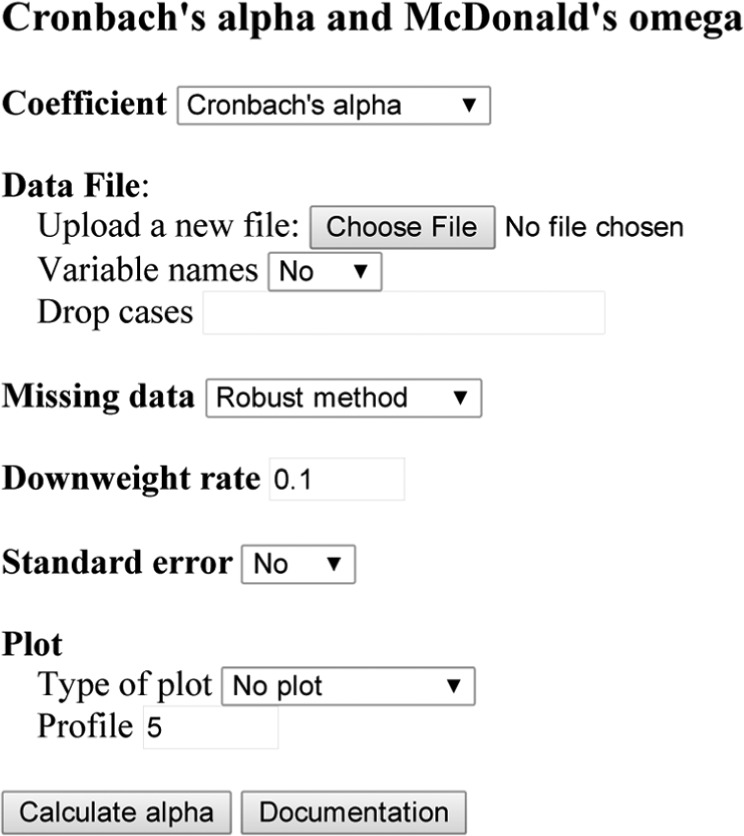
The online interface of the software coefficientalpha.