Abstract
This article proposes a general parametric item response theory approach for identifying sources of misfit in response patterns that have been classified as potentially inconsistent by a global person-fit index. The approach, which is based on the weighted least squared regression of the observed responses on the model-expected responses, can be used with a variety of unidimensional and multidimensional models intended for binary, graded, and continuous responses and consists of procedures for identifying (a) general deviation trends, (b) local inconsistencies, and (c) single response inconsistencies. A free program called REG-PERFIT that implements most of the proposed techniques has been developed, described, and made available for interested researchers. Finally, the functioning and usefulness of the proposed procedures is illustrated with an empirical study based on a statistics-anxiety scale.
Keywords: person-fit, personality measurement, weighted least squares regression, mean-square residual statistics, kernel smoothing
The fact that item response theory (IRT) models have increasingly been used in typical-response (i.e., personality and attitude) measurement in recent decades has made it possible to effectively solve technical and practical issues that could not be easily addressed by more traditional approaches (e.g., Reise & Revicki, 2015). Of these issues, this article is concerned with the assessment of model-data fit at the level of each individual respondent (i.e., person fit). More specifically, in the parametric IRT framework adopted here the issue of interest is to assess the consistency of an individual response pattern given (a) the item parameter values and (b) the respondent’s trait estimate(s) (e.g., Meijer & Sijtsma, 2001; Reise & Flannery, 1996). This type of assessment is important for several reasons (see Ferrando, 2015), but mainly because a trait estimate or test score is meaningful and can be validly interpreted only if the response pattern on which the score is based is consistent with the model (Reise & Flannery, 1996; Smith, 1986; Tendeiro & Meijer, 2014).
At present, person-fit analysis in the typical-response domain is no longer in the stage of being a methodological novelty and is starting to be used in purely applied studies (Conijn, Emons, De Jong, & Sitjsma, 2015; Conijn, Emons, & Sijtsma, 2014; Conrad et al., 2010; Dodeen & Darabi, 2009; Egberink & Meijer, 2011; Ferrando, 2012; Meijer, Egberink, Emons, & Sijtsma, 2008). Furthermore, most of these initial applications use a basic form of analysis in which a practical or nonspecific index is employed as a broad-screening tool for flagging potentially problematic patterns (e.g., Ferrando, 2015). This practice is, indeed, a necessary first step. However, once a pattern has been detected, further information must be obtained so that the practitioner can decide what to do with the pattern in each case (e.g., Smith, 1986).
To date, a variety of procedures have been proposed for collecting auxiliary information about the type and source of misfit in patterns that are flagged as inconsistent. For cognitive measures, Emons, Sijtsma, and Meijer (2004, 2005) have proposed a nonparametric three-step approach in which graphical analysis based on the Person Response Function (PRF) methodology (e.g., Sijtsma & Meijer, 2001) and local analyses based on a test statistic are performed on the patterns detected. For typical-response measures fitted with a parametric model, Conijn et al. (2015) have used two types of follow-up analyses: an “internal” analysis based on item-level residuals and an “external” analysis in which the global person-fit values are used as a dependent variable regarding potentially explanatory variables. In the same context (i.e., parametric IRT and personality content), Ferrando (2015) has proposed a two-step follow-up approach in which PRF-based graphical analysis is used to detect deviation trends, and item-level residual analysis is used for detecting single-item sources of misfit.
This article proposes a new general approach for identifying sources of person misfit in typical-response measures, which, unlike similar existing proposals, is not based on PRF methodology but on weighted-least-squares regression of the vector of individual scaled observed item scores on the vector of scaled model-expected scores. The choice of this type of regression as a basis has three important advantages. First, it is very general and can be used with many unidimensional and multidimensional IRT models intended for different response formats. Second, it is based on standard regression theory, so existing diagnostic procedures can be readily adapted to this particular application. Finally, some results obtained from the approach proposed here can be related to existing person-fit indices and procedures that were derived from an observed–expected residual approach (e.g., Smith, 1986, 1990), thus allowing the results obtained from these existing indices to be extended and complemented. Furthermore, our approach distinguishes between general deviation trends on the one hand, and local and single-response deviations on the other, and proposes different procedures for assessing each of these sources.
Overall, this article has methodological, substantive, and instrumental aims. At the methodological level, we propose a series of procedures intended to assess and clarify the causes of misfit in patterns that have been detected as potentially inconsistent. At the substantive level, we apply these procedures to a real personality data set that has been partly collected for this article. Finally, at the instrumental level, we have developed a user-friendly program that can be used with a variety of IRT models and which we make available at no cost to the interested readers.
The rest of the article is organized as follows. First, a conceptual and technical background is provided. Second, the proposed developments are discussed according to a three-level structure: general trends, local deviations, and single-item deviations. Third, the program REG-PERFIT is described. Finally, the proposal is applied to personality data based on a statistics anxiety measure.
Background
Conceptual Background
The procedures we propose are intended to be used in response patterns that have been flagged as potentially inconsistent by a global, scalar-valued person-fit index. They are based on parametric IRT, so it seems natural to also use a parametric IRT global index at the detection stage. More specifically, as discussed below, many results from the present proposal are closely related to mean-squared person-fit indices. Even so, these reasons are not restrictive in any way, and the follow-up analysis proposed here can be based on any type of parametric or nonparametric global index (see Tendeiro & Meijer, 2014).
As mentioned above, the present proposal is intended for typical-response measurement, and particularly personality measurement, which is the authors’ area of substantive interest. For this reason, the potential results that can be obtained with the procedures, as well as their interpretation, have been linked to the sources of misfit that are features of this domain (Ferrando, 2015). There is no compelling reason why these procedures should not be used with cognitive measures, but we shall not discuss this type of application here.
The procedures we propose aim to detect three levels of inconsistency: (a) general deviation trends, (b) local deviations, and (c) specific-response inconsistencies. General deviation trends refer to inconsistent responding that generalizes across all the test items (e.g., random responding or extreme responding). Local deviations refer to inconsistent responding to specific subsets of items (e.g., inconsistent responding to the reverse-scored items due to acquiescence or to the most socially desirable items due to faking). Finally, specific-response inconsistencies refer to inconsistent responses to single items (e.g., idiosyncratic interpretation of the meaning of this item because of language difficulties).
Technical Background
Consider a typical-response test made up of n items that behaves according to a parametric IRT model. The types of models we shall consider here are unidimensional and multidimensional cumulative models intended for binary, graded, or (approximately) continuous responses.
Let Xij be the response of individual i to item j, and let E(Xj|θ) and σ2(Xj|θ) be the model-expected item score and the conditional variance for fixed θ, respectively. In general, θ will be vector-valued, and will reduce to a scalar in the case of a unidimensional model. Now, for binary items scored as 0 and 1 and fitted by models such as the one-parameter and the two-parameter models, the conditional expectations just defined are given by
where Pj(θ) is the conditional probability of scoring 1 on item j.
For graded-response items scored by successive integers r =1, 2, . . ., and fitted by models such as Samejima’s (1969) graded response model (GRM), they are given by (Chang & Mazzeo, 1994).
where Pjr(θ) is the conditional probability of scoring in category r in item j.
Finally, continuous responses are usually fitted with the linear factor-analytic model. If this is the case, the conditional expectations are (see, e.g., Ferrando, 2015)
where µj is the item intercept, and λjk is the loading of item j on factor k.
If the IRT model is correct, the conditional expectation corresponding to individual i with θ i can be considered as a “true” item score for this individual (e.g., Lord & Novick, 1968), and will be denoted here by τij (i.e., E(Xj|θ i) = τij). Now, let xi be the n× 1 vector containing the scores of individual i on the n items, and let τi be the corresponding vector of model-based true scores. The model-implied regression of xi on τi is
where the elements of the εi vector are the residuals εij with zero expectation and variance σ2(Xj|θ i). So, regression (4) is linear, with zero intercept, unit slope, and residuals that have zero expectation and are independent of one another (by the local independence principle), but which have generally different variances (see Equations 1 to 3).
In order to obtain equal residual variances, we propose to use the following weighted transformation: define the weight and multiply each element of (4) by it:
In vector notation, the transformed regression equation becomes
Again it is linear, with zero intercept, unit slope, zero residual expectations, and independence among residuals. However, the residual variances in (6) are now the same for all the observations.
Detecting General Trends: WLS Regression
Assume that the test considered in the section above has been administered in a sample and satisfactorily fitted according to a given IRT model. Assume further that the calibration results are stable enough for the item parameter estimates to be taken as fixed and known (e.g., Zimowski, Muraki, Mislevy, & Bock, 2003). Finally, assume that a general person-fit index has been computed for each respondent and that a certain proportion of respondents in the sample have been flagged as potentially inconsistent by this index. Define x i as above, and denote by and the vectors corresponding to τ i, y i, and v i but computed using the respondent estimates instead of the unknown θ i. The basic procedure is first to fit for each (potentially) inconsistent respondent i the regression equation:
where 1 is an n× 1 unit vector, ai and bi are the usual intercept and slope estimates obtained by the ordinary least squares (OLS) criterion, and u i is the OLS residual or error term. The scores that are predicted from the fitted regression line (denoted by a prime) are then given in vector and scalar notation as
The OLS estimates obtained from the transformed vectors in (7) are the weighted least squares (WLS) estimates corresponding to the original untransformed vectors x i and (e.g., Draper & Smith, 1966). Under the assumption that the IRT estimates are correct, the WLS regression in (7) fulfils the basic regression requisites of linearity and homoscedasticity for all types of scores considered here, including binary scores (see, e.g., Goldberger, 1964).
General deviation trends are assessed by inspecting the discrepancies between the fitted line (7) and the model-implied line (6). The discrepancies can first be graphically assessed by using standard regression plots in which both lines (fitted and expected) are displayed together with the scatter of points. Analytically, a general significance test at the 1−α level for assessing whether the fitted line departs from the model-expected line can be computed by (e.g., Draper & Smith, 1966)
where F is the upper α point of the F distribution and is an unbiased estimate of the residual variance given by
Significant departures of the fitted line from the model-expected line can provide insight into sources of misfit that generalize over the test items. Thus, a fitted line with a negative slope would suggest a responding trend that is opposite to the normative ordering of the items. This trend, in which the respondent agrees with the most extreme or “difficult” items and disagrees with the “easier” items, has been identified in various data sets and qualified as sabotaging or malingering (Ferrando, 2012). A flat fitted line, on the other hand, would suggest total insensitivity to this ordering and can indicate random responding or a biased type of responding in which a narrow subset of response categories is used regardless of the item content (e.g., middle responding). Finally, a line with a slope that is steeper than the unit model-expected slope would suggest a “polarized” type of responding in which the scores agree with the item ordering, but in which the respondent has a high degree of response extremeness and tends to answer using the extreme points of the response scale (Cronbach, 1950; Ferrando, 2013; Peabody, 1962).
Further information regarding general trends can be obtained by relating the WLS proposal to more general person-fit results. In Rasch modeling, the most common person-fit statistic is the mean-squared outfit index based on the average of the squared observed–expected discrepancies (Smith, 1986, 1990). This statistic can be easily generalized to all the formats and models considered in the article. Using the present notation, the generalized mean-squared outfit index can be written as
The MST statistic ranges from 0 to infinity and has an expectation of 1.0 under the null hypothesis that the IRT model and the trait estimate of respondent i are correct. MST values below the unit expectation indicate that the data are more deterministic than the stochastic IRT model predicts. MST values above 1.0 indicate that the data are less predictable than expected from the model. For interpretation purposes, Wright and Linacre (1994) considered MST values above 1.0 to indicate excess of randomness or noise in the pattern data, and for the case of the Rasch model, they proposed a cut-off value of 1.5 to conclude that the randomness of the data would lead to unproductive measurement. This interpretation, however, can be made more detailed by using the WLS approach proposed here. Define first the identity (see Equation 8):
Squaring both sides of (12), taking the averages, and using well-known regression results, the following orthogonal decomposition is obtained:
We shall interpret decomposition (13) by using related standard results in sampling theory (e.g., Cochran, 1963). First, MST is a measure of general response inconsistency and refers to the size of deviations between the observed scores and the model-expected scores. MSW (within) is a measure of response imprecision and refers to the size of the deviations between the observed scores and the scores predicted from the fitted regression line for this individual. Finally, MSB (between) is a measure of response bias for the deviations between the regression-predicted scores and the model-expected scores. From this result it follows that MST cannot be considered simply as a measure of excess “noise” because a high MST value could also be obtained with a respondent whose response trend deviates substantially from the model-expected regression (i.e., high bias) but whose responses are not too scattered around his/her fitted regression line (i.e., no excess of response imprecision or “noise”).
Under the null hypothesis of consistency, the expected value of MSW is 1.0 and the expected value of MSB is 0.0. Using these values as references the interpretation of the mean-squared values can provide useful insights. Consider, for example, a respondent who systematically uses the central categories of the response scale. This type of bias will produce a flat regression line that differs from the model-expected regression. So, the MSB component will be high. The MSW component, however, will be low, as the responses will all be close to the fitted line. In contrast, consider an individual who responds at random. This inconsistency will also produce a flat fitted line (i.e., high MSB). However, the responses will now be far more scattered around the fitted line, so the expected value of MSW will also be high.
Detecting Local Deviations: Kernel Smoothed Regression
Local deviations can be operationalized as regions or subsets of item responses for which model (6) does not hold. To identify these regions, we propose a graphical approach in which a nonparametric regression curve is fitted to the scatterplot of the and scores. The elements of the proposed graph are, then, (a) the scatter of the n and points, (b) the model-expected regression line with zero intercept and unit slope, (c) the fitted regression line (7), and (d) the empirical nonparametric curve that best fits the points without imposing any particular functional form for the curve. The basic rationale of this approach (Azzalini, Bowman, & Härdle, 1989) is to use the nonparametric curve for assessing the inappropriateness of the model-expected line. Graphical assessment of the discrepancies between the two lines makes it possible to identify the potential subsets of items on which the misfit is mostly localized.
Of the several approaches that can be chosen to fit the nonparametric curve, we propose using kernel smoothing (KS). KS is widely used, relatively simple, and has produced good results in the approaches discussed above which are based on the PRF (Emons et al., 2004; Ferrando, 2015). The basic idea of the KS method in the present application is to obtain a weighted average of the scores around a series of evaluation points defined in v i. If the evaluation point is denoted by v, the Nadaraya–Watson KS estimate (see, e.g., Härdle, 1990) can be written as
where K(x) is the smoothing kernel function, a nonnegative, continuous, bounded, and (usually) symmetric function that assigns its highest values to points near 0.0 and decreases as it gets further away from 0.0. The parameter h is called the bandwidth; it is selected by the user, and controls the amount of smoothing. To help in the graphical comparison, confidence bands on the estimated KS curve can be computed at the evaluation points (Härdle, 1990). These confidence bands indicate the regions at which there are significant discrepancies with respect to the model-derived line. Further details on the KS procedure are provided below.
Detecting Deviations at the Single-Response Level: Scaled Item Residuals
In the KS approach just discussed, a local deviation can be viewed as a region around a set of evaluation points at which the distance between the smoothed line and the model-expected line differ significantly from zero. Consider now the limiting case in which the region on the v i axis reduces to a single point The (signed) distance to be assessed in this case is that between the corresponding single item score and the model-expected regression line, and can be written as
As is written on the right-hand side of (15), the signed distance zij is a scaled or Pearson observed–expected residual index, initially proposed in the context of Rasch analysis (e.g., Smith, 1990), and used in the previous person-fit related proposals by Ferrando (2012, 2015) and Conijn et al. (2015). Item scores with unusually large zij values are therefore potential outliers in the WLS framework adopted here. At the conceptual level they are, indeed, unexpected responses to single items.
The most common approach for interpreting the zij values in (15) is to refer them to the standard normal distribution (Karabatsos, 2000; Smith, 1990). One of the best-known limitations of this practice is that the index is (generally) a transformed discrete variable that cannot be well approximated by a continuous distribution such as the standard normal (Karabatsos, 2000). For practical purposes, however, the interpretation of the residual (15) as a standard variable is generally quite acceptable (see Smith, 1990).
Some Applied Considerations
So far the results and procedures have been discussed as generally as possible. We have considered the multidimensional case, and for discrete responses we have not defined specific models but conditional expectations that can be obtained from different models. Overall, the developments we propose are assumed to be correct and potentially applicable to a wide range of models and situations. In a practical application, however, they are expected to function well only if certain basic conditions are fulfilled.
The first, most basic requirement for good functioning is that the regression lines be well-defined and accurately fitted. From standard regression theory, it follows that this accuracy depends mainly on two factors: the number of items (i.e., the density of the point scatter) and the spread of the values of the regressor (i.e., the elements of the v i vector). This spread, in turn, generally depends on the range of item locations and the discriminating power of the test items. To sum up, the procedures proposed here are expected to work well in general when the test is reasonably long and is made up of items with good discrimination and a wide range of locations. These conditions are the same as those required if person-fit assessment is to be accurate and powerful (e.g., Ferrando, 2015) and, for global indices, have been studied mainly in the unidimensional case. On the basis of our experience and previous related results, for a well-constructed unidimensional test the procedures we propose would begin to function well as from 20 items.
A well-known weakness of global person-fit indices is that, in most cases, the trait estimate is based on the same pattern from which the person-fit index is computed. When this is the case, detection power generally decreases, largely because there is a shift in the estimate due to inconsistent responses (Armstrong, Stoumbos, Kung, & Shi, 2007). In other words, the estimate changes and makes the pattern appear to be more consistent than it really is. This limitation also applies to the procedures proposed here and in some initial studies we have noted that the problem tends to get worse in the multidimensional case. This is because in this case there is more room for the different trait estimates to change and “adapt,” which masks inconsistency.
Because there is a lack of person-fit research based on multidimensional models, we acknowledge the need for further research on this issue. So, our recommendations here, which are based on a previous proposal by Parsons (1983), are only tentative. If the test is multidimensional, but a general factor pervades the responses to the items, then treating the items as essentially unidimensional is expected to increase the power of the person-fit analysis. If this is not the case, then, at the very least, the basic conditions discussed above (a sizeable number of discriminating items with varying locations) should be fulfilled for each dimension.
Implementing the Procedures: The Program REG-PERFIT
While we developed REG-PERFIT in Matlab 2013b release, we compiled it as a user-friendly standalone application for Windows 64-bit operating systems. Users can decide whether to use the advanced Matlab version of REG-PERFIT or the standalone version (which does not require any programming skills). We have tested the program in several computers with different versions of Windows (7/8/8.1) and found that it works correctly.
The input consists of an ASCII format file containing the item scores. In addition, users who are familiar with Matlab can choose to read their data stored in their own mat files. For the moment, REG-PERFIT can fit the following uni-/multidimensional models: the two-parameter model (binary responses), Samejima’s GRM (graded responses), and the linear factor-analysis model (responses treated as continuous). The user must select the model to be fitted, the number of expected latent traits, and the expected relationships between latent variables (orthogonal or oblique). REG-PERFIT first performs the item calibration using a general factor-analytic formulation based on the unweighted least squares criterion and provides the following output: (a) univariate and bivariate descriptive statistics, (b) goodness of model-data fit measures, and (c) item-parameter estimates. In the second, scoring stage, REG-PERFIT provides (a) the individual EAP trait estimates, (b) the indices of precision of these estimates (PSDs and credibility intervals), (c) the global person-fit indices (MST-outfit), and (d) the auxiliary measures proposed in the article (MSB, MSW, intercept and slope estimates, and scaled item residuals). In addition to the numerical outcome, a graphical outcome consisting of the WLS regression plot (expected and fitted straight lines) and the Kernel regression plot are provided for each participant: both the numerical and the graphical outcomes can be stored in ASCII format (numerical outcome) and as editable figures (graphical outcome).
The number of variables, categories, and observations in the data set are not limited. However, when large data sets are analyzed and, depending on the characteristics of the computer (processor chip, memory available, etc.), the computing can take a long time. REG-PERFIT can be freely downloaded from the site http://psico.fcep.urv.cat/utilitats/RegressionPersonFit. The user can download a stand-alone version of the program to be run in Windows, and a toolboox to be run as a Matlab script. In addition, the site offers a manual and some datasets that enable the program to be tested.
REG-PERFIT is by no means fully developed and we are extending the program to make it more flexible and complete. One issue we are working on is to allow the user to input item and person estimates obtained from other programs or other samples and directly carry out the analytical and graphical person-fit analysis on the basis of these estimates.
Empirical Study: Application to the Statistical Anxiety Scale
The Statistical Anxiety Scale (Vigil-Colet, Lorenzo-Seva, & Condon, 2008) is a 24-item narrow-bandwidth instrument intended to measure a specific form of anxiety: that which occurs as a result of encountering statistics in any form at any level (e.g., Onwuegbuzie & Daley, 1999). The SAS item stems are positively worded sentences describing typical situations that can be experienced by students enrolled on a statistics course, and the response format is 5-point Likert-type scale. According to its authors, the SAS can be analyzed either as a multidimensional measure that assesses three related facets or as an essentially unidimensional measure that assesses a more general construct of statistical anxiety. In accordance with the discussion above, the unidimensional solution is that which produces the clearest results in terms of person-fit and is the one that we shall consider here.
As far as item calibration is concerned, the present study used as a basis the unidimensional solution proposed in the original calibration study by Vigil-Colet et al. (2008), which was based on Samejima’s (1969) GRM. So, the GRM-based item estimates obtained by Vigil-Colet et al. (2008) were taken as fixed and known. The analyses in the scoring stage were based on a new sample of 384 undergraduate students enrolled on a statistics courses in psychology and educational faculties which was collected specifically for this article. It should be noted that the sample is somewhat small for an IRT-based calibration study. However, in this study the item parameters are taken as known, so the new sample is solely used for scoring respondents and assessing person fit.
The first-step general person-fit analysis was carried out using REG-PERFIT, and the results can be summarized as follows. Potentially inconsistent respondents were flagged by using the global MST-OUTFIT statistic discussed in Equation (10) with the 1.5 cut-off value. By using this criterion, 35 individuals (9% of the sample) were flagged as potentially inconsistent.
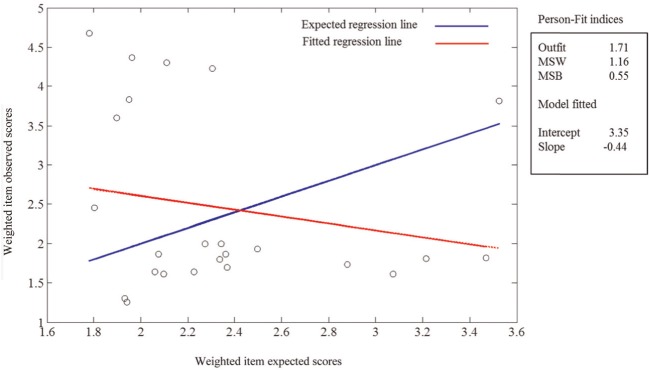
In the second step, the procedures proposed in this article were applied to the potentially inconsistent patterns detected in Step 1. To illustrate the functioning of these procedures, the results of three participants who exhibit different types of misfit will now be discussed. Figure 1 summarizes the analytical and graphical results for Participant No. 331. When interpreting the scatterplot it should be remembered that each one of the 24 points represents an item whose coordinates are the expected item score (X axis) and the observed item score (Y axis).
Figure 1.
Linear assessment for response pattern 331.
Results in Figure 1 show that MSW is only slightly above the expected value but MSB is clearly different from zero, reflecting the fact that the fitted line for this respondent substantially departs from the model-expected line (the departure is statistically significant). The linear graph clearly shows that both lines cross and that the fitted line has a negative slope. The kernel-smoothed regression (not shown in Figure 1) also produced a fitted line which was essentially linear and had a negative slope. As discussed above, this indicates a general trend in which the individual responds opposite to the normative ordering of the items, and suggests some form of sabotaging as the main source of misfit.
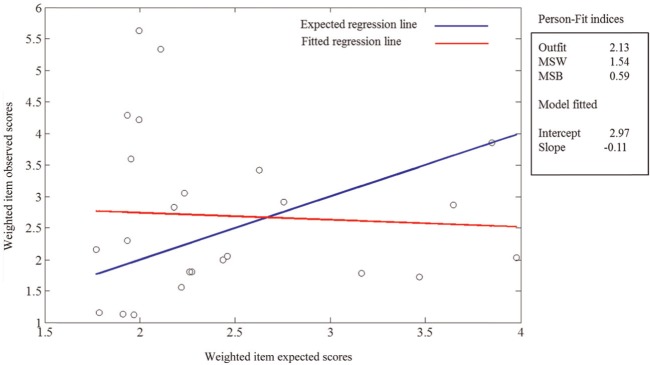
Figure 2 summarizes the results for Participant No. 305. In this case both MSW and MSB are high, which reflects the main graphical results in the figure: the fitted line for this respondent is virtually flat, and the dispersion of the points around this line is rather high. The kernel-smoothing analysis (not shown in the figure) agreed with this general trend of insensitivity to the normative ordering of the items and large dispersion. As discussed above, the most likely source of misfit in this case is random responding.
Figure 2.
Linear assessment for response pattern 305.
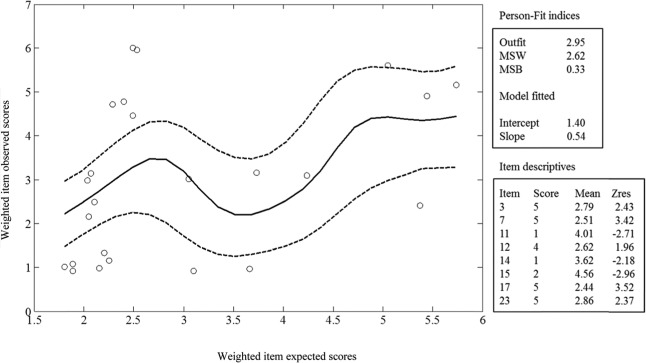
Finally, Figure 3 corresponds to Participant No. 132 and illustrates a type of misfit that is best assessed by using kernel regression and residual analysis. In principle, the mean-squared statistics in this case suggest a large dispersion of points (MSW is very high) and some departure of the fitted line from the model-expected line. Note also that the fitted slope is lower than the expected unit slope.
Figure 3.
Kernel smoothed assessment for response pattern 132.
The graph in Figure 3 provides further interesting information. Note that there is a considerable dispersion of points at the lower end of the graph, which suggests inconsistent responses mainly to the items with low expectation. In this respect, note also that many points at the lower end of the expected scale fall outside the kernel confidence bands, which, in this case, were obtained by using ±1 standard error (i.e., 68% confidence bands under normal assumptions). Furthermore, unexpectedly low responses to items of medium expectation give rise to a “bump” in the center of the kernel-smoothed line. As for the analysis of outliers, 7 of the 24 standardized residuals are greater than 1.96 in absolute value and, in accordance with the graphical results, 4 of these significant residuals are unexpectedly high responses to items with low expectation. In summary, then, the inconsistency in this case does not seem to be due to a general response trend as in the previous examples but to local deviations (inconsistent responses in many low-expectation items) and more specific inconsistencies.
Discussion
This article proposes and implements an integrated approach that combines analytical and graphical procedures and aims to identify the types and sources of misfit in patterns flagged as potentially inconsistent. To the best of our knowledge, our proposal is original. Even so it is based on well-known regression techniques (WLS estimation and Kernel Smoothing), and it is related to existing person-fit developments (mean-squared indices and standardized single-response residuals). Overall, the most remarkable feature of the proposal is, perhaps, its versatility because it can be used with a wide array of IRT models.
The developments we propose have several limitations and, as discussed above, require certain conditions to be met if they are to work properly. We have already provided some advice on this, but we would like to remind the reader that, at present, solid recommendations can only be made for unidimensional applications. So, users should be cautious when applying the present procedures to multidimensional data. At the same time, however, we encourage readers to try multidimensional applications so that they can better understand the usefulness and weaknesses of the procedures proposed.
Provided that the required basic conditions are reasonably met, the procedures we propose should be useful for the applied researcher. In this respect, we made an empirical study that was not a mere “ad hoc” illustration but a real personality application and obtained meaningful results that provided information regarding the response behavior of the respondents. This information is, we believe, useful in itself and should be relevant to the key question discussed at the beginning of the article: what to do with a pattern detected as potentially inconsistent? To discuss this point further, note for example that the patterns of Respondents 331 (malingering) and 305 (random responding) must be considered to be uninterpretable as they reflect general response trends that are expected to lead to an invalid trait estimate. In contrast, the inconsistencies of Respondent 132 are more local and concentrated on a subset of items. So, a valid trait estimate based on the subset of consistent responses might still be obtained in this case.
In conclusion, the present proposal addresses a type of assessment that seems to be of interest and which, if some basic requirements are met, appears to work well. In addition, we provide a free and user-friendly program that effectively implements the proposed procedures. Overall, then, we believe that the contribution is a useful tool for applied researchers and we hope that it will be widely used in the near future.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The research was partially supported by a grant from the Spanish Ministry of Education and Science (PSI2014-52884-P) and by a grant from the Catalan Ministry of Universities, Research and the Information Society (2014 SGR 73).
References
- Armstrong R. D., Stoumbos Z. G., Kung M. T., Shi M. (2007). On the performance of lz statistic in person fit measurement. Practical Assessment, Research & Evaluation, 12. Retrieved from http://pareonline.net/getvn.asp?v=12&n=16
- Azzalini A., Bowman A. W., Härdle W. (1989). On the use of nonparametric regression for model checking. Biometrika, 76, 1-11. [Google Scholar]
- Chang H., Mazzeo J. (1994). The unique correspondence of the item response function and item category response function in polytomously scored item response models. Psychometrika, 59, 391-404. [Google Scholar]
- Cochran W. G. (1963). Sampling techniques. New York, NY: Wiley. [Google Scholar]
- Conijn J. M., Emons W. H. M., De Jong K., Sitjsma K. (2015). Detecting and explaining aberrant responding on the Outcome Questionnaire-45. Assessment. Advance online publication. doi: 10.1177/1073191114560882 [DOI] [PubMed]
- Conijn J. M., Emons W. H. M., Sijtsma K. (2014). Statistic lz-based person-fit methods for noncognitive multiscale measures. Applied Psychological Measurement, 38, 122-136. [Google Scholar]
- Conrad K. J., Bezruczko N., Chan Y., Riley B., Diamond G., Dennis M. L. (2010). Screening for atypical suicide risk with person fit statistics among people presenting to alcohol and other drug treatment. Drug and Alcohol Dependence, 106, 92-100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cronbach L. J. (1950). Further evidence on response sets and test design. Educational and Psychological Measurement, 10, 3-31. [Google Scholar]
- Dodeen H., Darabi M. (2009). Person-fit: Relationship with four personality tests in mathematics. Research Papers in Education, 24, 115-126. [Google Scholar]
- Draper N., Smith H. (1966). Applied regression analysis. New York, NY: Wiley. [Google Scholar]
- Egberink I. J. L., Meijer R. R. (2011). An item response theory analysis of Harter’s self-perception profile for children or why strong clinical scales should be distrusted. Assessment, 18, 201-212. [DOI] [PubMed] [Google Scholar]
- Emons W. H. M., Sijtsma K., Meijer R. R. (2004). Testing hypotheses about the person-response function in person-fit analysis. Multivariate Behavioral Research, 39, 1-35. [DOI] [PubMed] [Google Scholar]
- Emons W. H. M., Sijtsma K., Meijer R. R. (2005). Global, local and graphical person-fit analysis using person-response functions. Psychological Methods, 10, 101-119. [DOI] [PubMed] [Google Scholar]
- Ferrando P. J. (2012). Assessing inconsistent responding in E and N measures: An application of person-fit analysis in personality. Personality and Individual Differences, 52, 718-722. [Google Scholar]
- Ferrando P. J. (2013). A factor-analytic model for assessing individual differences in response scale usage. Multivariate Behavioral Research, 49, 390-405. [DOI] [PubMed] [Google Scholar]
- Ferrando P. J. (2015). Assessing person fit in typical-response measures. In Reise S. P., Revicki D. A. (Eds.), Handbook of item response theory modeling: Applications to typical performance assessment (pp. 128-155). New York, NY: Routledge. [Google Scholar]
- Goldberger A. S. (1964). Econometric theory. New York, NY: Wiley. [Google Scholar]
- Härdle W. (1990). Applied nonparametric regression. London, England: Chapman & Hall. [Google Scholar]
- Karabatsos G. (2000). A critique of Rasch residual fit statistics. Journal of Applied Measurement, 1, 152-176. [PubMed] [Google Scholar]
- Lord F. M., Novick M. R. (1968). Statistical theories of mental test scores. Reading, MA: Addison-Wesley. [Google Scholar]
- Meijer R. R., Egberink I. J. L., Emons W. H. M., Sijtsma K. (2008). Detection and validation of unscalable item score patterns using item response theory: An illustration with Harter’s self-perception profile for children. Journal of Personality Assessment, 90, 1-14. [DOI] [PubMed] [Google Scholar]
- Meijer R. R., Sijtsma K. (2001). Methodology review: Evaluating person fit. Applied Psychological Measurement, 25, 107-135. [Google Scholar]
- Onwuegbuzie A. J., Daley C. E. (1999). Perfectionism and statistics anxiety. Personality and Individual Differences, 26, 1089-1102. [Google Scholar]
- Parsons Ch. K. (1983).The identification of people for whom job descriptive index scores are inappropriate. Organizational Behavior and Human Performance, 31, 365-393. [Google Scholar]
- Peabody D. (1962). Two components in bipolar scales: Direction and extremeness. Psychological Review, 69, 65-73. [DOI] [PubMed] [Google Scholar]
- Reise S. P., Flannery W. P. (1996). Assessing person-fit on measures of typical performance. Applied Measurement in Education, 9, 9-26. [Google Scholar]
- Reise S. P., Revicki D. A. (2015). Handbook of item response theory modeling: Applications to typical performance assessment. New York, NY: Routledge. [Google Scholar]
- Samejima F. (1969). Estimation of latent ability using a response pattern of graded scores. Psychometrika Monograph Supplement, 34(4, Pt 2, Monograph No. 17). [Google Scholar]
- Sijtsma K., Meijer R. R. (2001). The Person Response Function as a tool in person-fit research. Psychometrika, 66, 191-207. [Google Scholar]
- Smith R. M. (1986). Person fit in the Rasch model. Educational and Psychological Measurement, 46, 359-372. [Google Scholar]
- Smith R. M. (1990). Theory and practice of fit. Rasch Measurement Transactions, 3, 78-80. [Google Scholar]
- Tendeiro J. N., Meijer R. R. (2014). Detection of invalid test scores: The usefulness of simple nonparametric statistics. Journal of Educational Measurement, 51, 239-259. [Google Scholar]
- Vigil-Colet A., Lorenzo-Seva U., Condon L. (2008). Development and validation of the statistical anxiety scale. Psicothema, 20, 174-180. [PubMed] [Google Scholar]
- Wright B. D., Linacre J. M. (1994). Reasonable mean-square fit values. Rasch Measurement Transactions, 8, 370. [Google Scholar]
- Zimowski M., Muraki E., Mislevy R. J., Bock R. D. (2003). BILOG-MG 3: Item analysis and test scoring with binary logistic models. Chicago, IL: Scientific Software. [Google Scholar]