Testing the Difference of Correlated Agreement Coefficients for Statistical Significance

Abstract

This article addresses the problem of testing the difference between two correlated agreement coefficients for statistical significance. A number of authors have proposed methods for testing the difference between two correlated kappa coefficients, which require either the use of resampling methods or the use of advanced statistical modeling techniques. In this article, we propose a technique similar to the classical pairwise t test for means, which is based on a large-sample linear approximation of the agreement coefficient. We illustrate the use of this technique with several known agreement coefficients including Cohen’s kappa, Gwet’s AC₁, Fleiss’s generalized kappa, Conger’s generalized kappa, Krippendorff’s alpha, and the Brenann–Prediger coefficient. The proposed method is very flexible, can accommodate several types of correlation structures between coefficients, and requires neither advanced statistical modeling skills nor considerable computer programming experience. The validity of this method is tested with a Monte Carlo simulation.

Introduction

The purpose of this article is to present simple techniques for testing the difference between two or more correlated agreement coefficients for statistical significance. We will confine ourselves to chance-corrected coefficients of agreement for nominal scales. Several such agreement coefficients have been proposed in the literature. Cohen (1960) proposed the kappa coefficient for two raters, and its weighted version (Cohen, 1968). Fleiss (1971) and Conger (1980) extended Cohen’s kappa to the more general situation involving three raters or more. Scott (1955) advocated the pi coefficient for two raters. Although Fleiss (1971) introduced his multiple-rater agreement coefficient as a generalized kappa coefficient, it actually generalizes Scott’s pi coefficient. Conger’s coefficient on the other hand is a genuine extension of kappa to multiple raters. As a matter of fact, Conger’s multiple-rater coefficient reduces to Cohen’s kappa when the number of raters is 2. Many of these coefficients are known to be vulnerable to the paradoxes described by Cicchetti and Feinstein (1990), where agreement coefficients yield a low value when agreement is known to be high. Gwet (2008a) introduced the $\mathrm{AC}{}_1$ coefficient as a paradox-resistant alternative agreement coefficient to remediate this issue. The $\mathrm{AC}{}_1$ and its weighted version known as $\mathrm{AC}{}_2$, as well as many other coefficients are extensively discussed in Gwet (2014). Other interesting agreement coefficients include those proposed by Brennan and Prediger (1981) and Krippendorff (1970).

The motivation behind the study of correlated agreement coefficients stems from various practical situations. As an example, consider a group of raters who must rate the same subjects on two occasions. The two occasions may represent one rating session before the raters receive a formal training, and another rating session after the training. To evaluate the effectiveness of the training program, the researcher may be interested in testing the difference between the two agreement coefficients for statistical significance. If the raters were to rate two distinct groups of subjects on both occasions, then the resulting agreement coefficients would be uncorrelated, and testing their difference for statistical significance would be trivial. In case of uncorrelated agreement coefficients, the variance of the coefficients’ difference equals the sum of the two variances. Therefore, the ratio of the difference to the square root of its variance follows approximately the standard normal distribution, and can be used for significance testing. However, the variance of the difference between two correlated coefficients involves a covariance term that is often problematic.

Other practical situations where the problem of correlated agreement coefficients may arise include the comparison of several raters or groups of raters to an expert whose ratings represent the gold standard. Comparing each rater to the same gold standard based on the same group of subjects will result in a series of correlated coefficients. A researcher may want to know if there is any statistically significant difference among them. If several correlated coefficients are available, one may perform pairwise comparisons, and a global comparison involving all coefficients in a way that is similar to the analysis of variance (ANOVA). Several known studies prompted the investigation of correlated agreement coefficients. For example, Oden (1991) reported ophthalmologic data where two raters rated both eyes of 840 human subjects for the presence or absence of geographic atrophy. Baker, Freedman, and Parmar (1991) describe a study of two pathologists who assessed 27 patients for the presence or absence of dysplasia.

The problem of testing correlated agreement coefficients has already been addressed by several authors, most of whom confined themselves to the kappa coefficient and to the case where the number of raters is limited to 2. McKenzie et al. (1996) proposed a resampling method that uses several bootstrap samples to quantify the variance of the difference between two correlated kappas. This method was later expanded by Vanbelle and Albert (2008) to compare the homogeneity of several correlated kappa coefficients. Williamson, Lipsitz, and Manatunga (2000) recommended an approach based on generalized estimating equations of second order, while Barnhart and Williamson (2002) used the least-squares approach to model correlated kappa coefficients as functions of carefully selected categorical covariates. Resampling methods are computationally intensive, but provide adequate results once a computer program implementing them is made available, and the number of bootstrap samples is sufficiently large. The main drawback of resampling methods is their inability to assist at the planning stage of an interrater reliability experiment aimed at testing correlated coefficients for statistical significance. Data available from prior studies cannot be used. The other approaches based on theoretical models require an adequate statistical model to be built, which is often time-consuming, and requires considerable statistical expertise that many researchers may not have.

In the next section, we propose simple close equations that resolve the problem of correlated coefficients, and which require neither resampling nor the development of theoretical models. The proposed methods are general and versatile, and can be used to analyze correlated coefficients between overlapping groups of raters, or between two rounds of ratings produced by the same group of raters on two occasions. We provide expressions that can also be used to determine the optimal number of subjects required to achieve a desired test power, particularly when information from prior studies is available.

The Proposed “Linearization Method”

The pairwise t test for the mean is one of the most basic statistical tests and involves testing the difference between two correlated sample means for statistical significance. These two sample means are generally evaluated using the same sample of subjects at two different points in time. The simplicity of this test stems from the linear nature of the sample mean, which makes the difference between two means identical to the mean of the differences calculated at the sample unit level. Therefore, computing the variance of the difference between two means obtained from a paired sample amounts to computing the variance of another sample mean using the standard variance formula for means. This is how the pairwise t test is implemented without any need to compute the covariance between two correlated means.

Unfortunately, most agreement coefficients are not linear statistics. The difference between two correlated agreement coefficients does not reduce to a simple expression, and calculating its variance requires the evaluation of a complex covariance term. Our proposed approach, which we will refer to as the “linearization method,” consists of deriving a large-sample approximation of the agreement coefficient with a linear statistic and using the linear approximation in the same way the sample mean is used in the pairwise t test. If the linear approximation includes all the “relevant” terms, then it results in a statistical procedure that is valid even for subject samples of moderate sizes. We will demonstrate the validity of this procedure with a Monte Carlo experiment to be presented later.

To fix ideas, suppose that we want to test the difference $1/{\overline{x}}_2-1/{\overline{x}}_1$ between two inverses of sample means calculated on two occasions based on the same sample of size $n$. Testing this difference for statistical significance requires the knowledge of its sampling distribution. In this particular case, this sampling distribution is unknown. One can assume however that as the sample size $n$ increases, the two sample means ${\overline{x}}_1$ and ${\overline{x}}_2$ converge toward two parameters ${\mu }_1$ and ${\mu }_2$ respectively. Using the first-order Taylor series approximation of the inverse of the sample mean, one can say that for a large sample, $1/{\overline{x}}_1\approx 1/{\mu }_1-({\overline{x}}_1-{\mu }_1)/{\mu }_1^2$, and $1/{\overline{x}}_2\approx 1/{\mu }_2-({\overline{x}}_2-{\mu }_2)/{\mu }_2^2$. Therefore, the difference between both inverses is,

$$1/{\overline{x}}_2-1/{\overline{x}}_1\approx 1/{\mu }_2-1/{\mu }_1+\frac{1}{n}\sum _{i=1}^n{d}_i,$$

where $d_i=(x_i^{(1)}-{\mu }_1)/{\mu }_1^2-(x_i^{(2)}-{\mu }_2)/{\mu }_2^2$. Now, the difference between the two inverse means is expressed as a linear function of the $d_i$‘s, and its approximate variance is that of the sample mean $\overline{d}$. It follows from the central limit theorem that the ratio of the difference between the inverse means to its standard error follows the standard Normal distribution for large sample sizes. Note that in practice, when evaluating $d_i$ one replaces ${\mu }_1$ and ${\mu }_2$ with their respective estimates ${\overline{x}}_1$ and ${\overline{x}}_2$. We will start the description of our method in the following section with Fleiss’s generalized kappa coefficient, followed by Krippendorff’s alpha, Cohen’s kappa, Gwet’s $\mathrm{AC}{}_1$, and the Brennan–Prediger coefficient. A detailed walkthrough example is presented in Appendix B showing step by step how the new method can be implemented with actual data using Gwet’s $\mathrm{AC}{}_1$ coefficient. The reader may repeat the same approach with other agreement coefficients.

Fleiss’s Generalized Kappa Coefficient

Let us consider consider the generalized kappa statistic of Fleiss (1971) often used to quantify the extent of agreement among multiple raters. It is formally defined as follows:

$${\hat{\kappa }}_{\mathrm{F}}=(p_a-p_e)/(1-p_e),$$

where $p_a$ and $p_e$ are respectively the percent agreement, and the percent chance agreement. The percent agreement is defined as,

$$p_a=\frac{1}{n}\sum _{i=1}^n{p_a}_{|i},\mathrm{where}{p_a}_{|i}=\sum _{k=1}^q\frac{r_{\mathrm{ik}}(r_{\mathrm{ik}}-1)}{r(r-1)}$$

with $n$ representing the number of subjects, $r$ the number of raters, $q$ the number of categories, and $r_{\mathrm{ik}}$ the number of raters who classified subject $i$ into category $k$. Likewise, the percent chance agreement is given by

$$p_e=\sum _{k=1}^q{\pi }_k^2,\mathrm{where}{\pi }_k=\frac{1}{n}\sum _{i=1}^n\frac{r_{\mathrm{ik}}}{r}.$$

Note that the percent chance agreement $p_e$ can be rewritten as

$$p_e=\frac{1}{n}\sum _{i=1}^n{p}_{e|i},\mathrm{where}{p}_{e|i}=\sum _{k=1}^q{\pi }_k{r}_{\mathrm{ik}}/r.$$

Let us consider the quantity ${\kappa }_{\mathrm{F}|i}^{\star }$ defined by

$${\kappa }_{\mathrm{F}|\mathrm{i}}^{\star }={\kappa }_{\mathrm{F}|\mathrm{i}}-2(1-{\hat{\kappa }}_{\mathrm{F}})(p_{e|i}-p_e)/(1-p_e),$$

where ${\kappa }_{\mathrm{F}|\mathrm{i}}=(p_{a|i}-p_e)/(1-p_e)$. It appears that Fleiss’s generalized kappa of equation (2) represents the arithmetic mean of the ${\kappa }_{\mathrm{F}|\mathrm{i}}^{\star }$ values. Now suppose that the same group of $r$ raters rate the same group of $n$ subjects on two different occasions labeled as (1) and (2). These two rounds of rating will yield two values for Fleiss’s kappa named ${\hat{\kappa }}_{\mathrm{F}}^{(1)}$ and ${\hat{\kappa }}_{\mathrm{F}}^{(2)}$, the difference of which should be tested for statistical significance. The null and alternative hypotheses considered are expressed as follows:

$$\{\begin{array}{cc}\hfill H_0:\hfill & \hfill {\kappa }_{\mathrm{F}}^{(2)}={\kappa }_{\mathrm{F}}^{(1)}={\kappa }_{\mathrm{F}},\hfill \\ \multicolumn{1}{c}{H_1:}& \hfill {\kappa }_{\mathrm{F}}^{(2)}\ne {\kappa }_{\mathrm{F}}^{(1)}.\hfill \end{array}$$

In Equation (7), ${\kappa }_{\mathrm{F}}$ represents the parameter being estimated by ${\kappa }_{\mathrm{F}}^{(1)}$ and ${\kappa }_{\mathrm{F}}^{(2)}$, and is also referred to as the estimand. Our proposed procedure consists of implementing the following steps:

• Compute the $n$ differences $d_i={\kappa }_{F|i}^{\star (2)}-{\kappa }_{F|i}^{\star (1)}$ associated with the $n$ subjects being rated using Equation (6). Note that the average $\overline{d}$ of the $d_i$ values equals the difference ${\hat{\kappa }}_{\mathrm{F}}^{(2)}-{\hat{\kappa }}_{\mathrm{F}}^{(1)}$ between the two kappa coefficients.

• Compute the variance $v(\overline{d})$ of the mean difference using the following standard formula:

$$v(\overline{d})=\frac{1}{n(n-1)}\sum _{i=1}^n{(d_i-\overline{d})}^2.$$

• Compute the test statistic $T$ given by,

$$T=\frac{{\hat{\kappa }}_{\mathrm{F}}^{(2)}-{\hat{\kappa }}_{\mathrm{F}}^{(1)}}{\sqrt{v(\overline{d})}}.$$

• Under the null hypothesis $H_0$, $T$ follows approximately the standard normal distribution. If the significance level of the test is $\alpha$ then the null hypothesis will be rejected in favor of the alternative $H_1$ if the absolute value of $T$ exceeds the critical value $c_{\alpha }$ representing the $(1-\alpha /2)\mathrm{th}$ percentile of the standard normal distribution.

This procedure is simple and can be used with any agreement coefficient, provided one has its linear approximation based on an expression similar to Equation (6).

Since Fleiss’ coefficient generalizes the pi coefficient proposed by Scott (1955) for two raters, researchers working on correlated Scott’s coefficients for two raters can use the test proposed in this section.

Let us see why this procedure is expected to work. When the number of subjects is large, the agreement coefficients ${\hat{\kappa }}_{\mathrm{F}}^{(1)}$ and ${\hat{\kappa }}_{\mathrm{F}}^{(2)}$ converge to their respective limit values ${\kappa }_{\mathrm{F}}^{(1)}$ and ${\kappa }_{\mathrm{F}}^{(2)}$. Likewise, the two chance agreement probabilities $p_e^{(1)}$, and $p_e^{(2)}$ associated with the two occasions will tend to their limit values. Therefore, $d_i$ can be seen as a variable that solely depends on subject $i$, and the difference ${\hat{\kappa }}_{\mathrm{F}}^{(2)}-{\hat{\kappa }}_{\mathrm{F}}^{(1)}$ can then be written as the average of the $d_i$ values plus a reminder term whose stochastic order of magnitude is smaller than $1/\sqrt{n}$. Consequently, $v(\overline{d})$ can be seen as the large-sample approximation of the variance of ${\hat{\kappa }}_{\mathrm{F}}^{(2)}-{\hat{\kappa }}_{\mathrm{F}}^{(1)}$. The central limit theorem allows us to conclude that the proposed statistic follows the standard normal distribution. A rigorous mathematical treatment of the asymptotics is possible using techniques similar to those discussed by Gwet (2008b).

The Special Case of Two Raters: Scott’s pi Coefficient

As mentioned earlier, Fleiss’s generalized kappa reduces to Scott’s pi coefficient when the number of raters is 2. To test the difference between two correlated Scott’s coefficients for statistical significance Equation (6) is still used with some simplifications. The percent agreement associated with subject $i$ becomes $p_{a|i}={\epsilon }_i$ where ${\epsilon }_i$ is a 0/1 dichotomous variable taking value 1 if both raters agree on subject $i$’s membership category, and 0 otherwise. The percent chance agreement on subject $i$ becomes,

$$p_{e|i}=\sum _{k=1}^q{\pi }_k[{\epsilon }_{\mathrm{ik}}^{(1)}+{\epsilon }_{\mathrm{ik}}^{(2)}]/2,$$

where ${\epsilon }_{\mathrm{ik}}^{(1)}$ is a dichotomous variable that takes value 1 when rater 1 classifies subject $i$ into category $k$, and 0 otherwise. Variable ${\epsilon }_{\mathrm{ik}}^{(2)}$ is defined the same way with respect to rater 2. Moreover, ${\pi }_k=(p_{k+}+p_{+k})/2$ with $p_{k+}$ and $p_{+k}$ representing the percent of subjects classified into category $k$ by raters 1 and 2, respectively.

Krippendorff’s Alpha Coefficient

Another agreement coefficient often used in the field of content analysis is known as Krippendorff’s alpha (see Krippendorff, 1970). This coefficient is similar to Fleiss’s generalized kappa, and is therefore briefly discussed in this section. Assuming that there is no missing ratings (i.e., each rater has rated all subjects),¹ this coefficient is defined as follows:

$${\hat{\alpha }}_K=(p_a^{\star }-p_e)/(1-p_e),\mathrm{where}{p}_a^{\star }=[1-1/(\mathrm{nr})]p_a+1/(\mathrm{nr}),$$

and $p_a$ and $p_e$ are given by equations (3) and (4). For the purpose of testing the difference between two correlated Krippendorff’s alpha coefficients, one could express alpha as the mean of the ${\alpha }_{k|i}^{\star }$ values defined as follows:

$${\alpha }_{K|i}^{\star }={\alpha }_{K|i}-(1-{\hat{\alpha }}_K)(p_{e|i}-p_e)/(1-p_e),$$

where ${\alpha }_{K|i}=(p_{a|i}^{\star }-p_e)/(1-p_e)$, and $p_{a|i}^{\star }=[1-1/(\mathrm{nr})]p_{a|i}+1/(\mathrm{nr})$. Note that $p_{a|i}$ and $p_{e|i}$ are both defined by Equations (3) and (5) respectively.

In the next section, we will show how testing the difference between two correlated kappa coefficients can be done.

The Kappa Coefficient

The kappa coefficient was introduced by Cohen (1960), and later generalized to the case of multiple raters by Conger (1980). Note that unlike Fleiss’s generalized kappa, which reduces to Scott’s pi for two raters, Conger’s coefficient represents a more “natural” generalization of Cohen’s kappa, since it reduces to it when the number of raters is 2. Consequently, we will discuss how the difference between two correlated Conger coefficients can be tested for statistical significance. The proposed test will remain valid for any number of raters, including the case of two raters that was the focus of Cohen (1960).

Consider an interrater reliability experiment where $r$ raters classify $n$ subjects into one of $q$ possible categories. Let $p_{\mathrm{gk}}$ be the proportion of subjects that rater $g$ classified into category $k$, and ${\overline{p}}_{+k}$ the average proportion of subjects classified into category $k$ per rater. Conger’s generalized kappa is defined as follows:

$${\hat{\kappa }}_C=\frac{p_a-p_e}{1-p_e},\mathrm{where}\{\begin{array}{cc}\multicolumn{1}{c}{p_a}& =\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^n}\frac{r_{\mathrm{ik}}(r_{\mathrm{ik}}-1)}{r(r-1)},\hfill \\ \multicolumn{1}{c}{p_e}& ={\displaystyle \sum _{k=1}^q}({\overline{p}}_{+k}^2-s_k^2/r),\hfill \end{array}$$

with $s_k^2$ being the variance of the proportions $p_{\mathrm{gk}}$s within category $k$. More formally, $s_k^2$ is given by:

$$s_k^2=\frac{1}{r-1}\sum _{g=1}^r{(p_{\mathrm{gk}}-{\overline{p}}_{+k})}^2.$$

For the purpose of testing the difference between two correlated Conger’s agreement coefficients for statistical significance, we will use a large-sample linear approximation that expresses Conger’s coefficient as an average of the ${\kappa }_{C|i}^{\star }$ values, where ${\kappa }_{C|i}^{\star }$ is given by

$${\kappa }_{C|i}^{\star }={\kappa }_{C|i}-2(1-{\hat{\kappa }}_C)(p_{e|i}-p_e)/(1-p_e),$$

where

• ${\kappa }_{C|i}=(p_{a|i}-p_e)/(1-p_e)$, $p_{a|i}$ being defined by Equation (3).

• $p_{e|i}$ is defined as follows:

$$p_{e|i}=\frac{1}{r(r-1)}\sum _{g=1}^r\sum _{k=1}^q{\delta }_{\mathrm{gk}}^{(i)}(r{\overline{p}}_{+k}-p_{\mathrm{gk}}),$$

where ${\delta }_{\mathrm{gk}}^{(i)}$ is a dichotomous variable that equals 1 if rater $g$ classifies subject $i$ into category $k$, and equals 0 otherwise.

When testing the difference between two Conger’s coefficients for statistical significance, you would compute ${\kappa }_{C|i}^{\star }$ of Equation (13) for each subject $i$ twice. If the rating of $n$ subjects was performed on two occasions, then ${\kappa }_{C|i}^{\star (1)}$ and ${\kappa }_{C|i}^{\star (2)}$ will be calculated for each subject $i$ before applying the same testing procedure discussed in the previous section. When calculating ${\kappa }_{C|i}^{\star (1)}$ based on Equation (13), you will need to compute ${\hat{\kappa }}_C$ and $p_e$ as shown in Equation (11) using occasion-one data only, and repeat the same process with occasion-two ratings.

The Special Case of Two Raters: Cohen’s Kappa

As previously indicated, Cohen’s kappa (using two raters) is a special case of Conger’s generalized agrement coefficient of Equation (11). Therefore, when testing the difference between two correlated kappa coefficients, you still need to use Equation (13). For two raters, $p_{a|i}={\epsilon }_i$. Moreover, $p_{e|i}$ the percent chance agreement associated with subject $i$, will be expressed as follows:

$$p_{e|i}=\sum _{k=1}^q[{\epsilon }_{\mathrm{ik}}^{(1)}{p}_{+k}+{\epsilon }_{\mathrm{ik}}^{(2)}{p}_{k+}]/2.$$

Gwet’s AC₁ Coefficient

Gwet (2008a) introduced the $\mathrm{AC}{}_1$ coefficient as a paradox-resistant alternative to Cohen’s kappa coefficient. Its weighted version known as $\mathrm{AC}{}_2$ is recommended for analyzing ordinal, interval, and ratio data as discussed in Gwet (2014). Once again, we consider an interrater reliability experiment involving $r$ raters who must rate $n$ subjects by classifying them into one of $q$ possible categories. The $\mathrm{AC}{}_1$ coefficient is defined as follows:

$${\hat{\kappa }}_G=\frac{p_a-p_e}{1-p_e},$$

where the percent agreement $p_a$ is given by Equation (3), and the percent chance agreement $p_e$ given by

$$p_e=\frac{1}{q-1}\sum _{k=1}^q{\pi }_k(1-{\pi }_k).$$

The probability ${\pi }_k$ that a randomly-selected rater classifies a randomly selected subject into category $k$ is defined in Equation (4).

In order to test the difference between two correlated $\mathrm{AC}{}_1$ coefficients for statistical significance, we recommend expressing it as an average of the ${\kappa }_{G|i}^{\star }$’s where ${\kappa }_{G|i}^{\star }$ is given by

$${\kappa }_{G|i}^{\star }={\kappa }_{G|i}-2(1-{\hat{\kappa }}_G)(p_{e|i}-p_e)/(1-p_e),$$

with ${\kappa }_{G|i}=(p_{a|i}-p_e)/(1-p_e)$, and $p_{e|i}$ given by

$$p_{e|i}=\frac{1}{q-1}\sum _{k=1}^q(1-{\pi }_k)r_{\mathrm{ik}}/r.$$

If two $\mathrm{AC}{}_1$ coefficients are correlated due to raters rating the same group of subjects on two occasions, then for each subject $i$ one needs to compute the subject-level differences $d_i={\kappa }_{G|i}^{\star (2)}-{\kappa }_{G|i}^{\star (1)}$ between the $\mathrm{AC}{}_1$ coefficients calculated on each of the two occasions $(1)$ and $(2)$, and use the same procedure previously described for Fleiss’s generalized kappa. Two $\mathrm{AC}{}_1$ coefficients can also be correlated because they were calculated based on two overlapping groups of raters who rated the same subjects. In this case, ${\kappa }_{G|i}^{\star (1)}$ and ${\kappa }_{G|i}^{\star (2)}$ will represent the coefficients associated with each group of raters.

The Special Case of Two Raters

When analyzing two correlated $\mathrm{AC}{}_1$ coefficients based on two raters only, one could use a simplified version of Equation (16). The percent agreement associated with subject $i$ remains the same and given by $p_{a|i}={\epsilon }_i$. As for the percent chance agreement associated with subject $i$, it is given by,

$$p_{e|i}=\frac{1}{q-1}\sum _{k=1}^q(1-{\pi }_k)[{\epsilon }_{\mathrm{ik}}^{(1)}+{\epsilon }_{\mathrm{ik}}^{(2)}]/2$$

One may find a detailed walkthrough example in Appendix B that shows step by step how the linearization method is implemented with actual data.

Brennan–Prediger Coefficient

Brennan and Prediger (1981) proposed a simple chance-corrected agreement coefficient, which generalizes to multiple raters and multiple categories, the G-index previously proposed by Holley and Guilford (1964) for two raters and two categories. What is known as the Holley–Guilford G-index was previously proposed independently by various authors under different names. Among them are Guttman (1945), Bennett, Alpert, and Goldstein (1954), and Maxwell (1977). For an interrater reliability experiment involving $r$ raters who classify $n$ subjects into one of $q$ possible categories, the Brennan-Prediger coefficient is given by

$${\hat{\kappa }}_{\mathrm{BP}}=\frac{p_a-1/q}{1-1/q},$$

where the percent agreement $p_a$ is defined by Equation (3), and the percent chance agreement is a constant representing the inverse of the number of categories.

For the purpose of testing the difference between two correlated Brennan-Prediger agreement coefficients, one would consider ${\hat{\kappa }}_{\mathrm{BP}}$ as the average of ${\kappa }_{\mathrm{BP}|\mathrm{i}}$ values defined for each subject $i$ as

$${\kappa }_{\mathrm{BP}|\mathrm{i}}=(p_{a|i}-1/q)/(1-1/q).$$

Monte Carlo Simulation

In this section, we like to determine the extent to which the proposed procedure works for small to moderately large samples. The linchpin of our linearization method is Equation (8). We will have demonstrated that this method works if under the null hypothesis the test statistic of Equation (8) follows the standard normal distribution. The conventional way of verifying that this test statistic follows the standard normal distribution has been to simulate a large number of samples under the null hypothesis, and to establish that the hypothesized difference of $0$ between the two agreement levels under comparison falls inside the 95% confidence interval of ${\hat{\kappa }}_{\mathrm{F}}^{(2)}-{\hat{\kappa }}_{\mathrm{F}}^{(1)}$ approximately 95% of the times. That is, the following condition is expected to be satisfied about 95% of the times.

$$({\hat{\kappa }}_{\mathrm{F}}^{(2)}-{\hat{\kappa }}_{\mathrm{F}}^{(1)})-1.96\sqrt{v(\overline{d})}\le 0\le ({\hat{\kappa }}_{\mathrm{F}}^{(2)}-{\hat{\kappa }}_{\mathrm{F}}^{(1)})+1.96\sqrt{v(\overline{d})}$$

In our Monte Carlo experiment, we have considered three raters 1, 2, and 3 who must assign subjects into one of $q$ categories with $q$ taking values 2, 3, 4, and 5. Our problem is to test for statistical significance, the difference ${\hat{\kappa }}_{13}-{\hat{\kappa }}_{12}$ between the extent of agreement among raters 1 and 3 on one hand, and the extent of agreement among raters 1 and 2 on the other. These two agreement coefficients are correlated since they have rater 1 in common.

For a given “true” agreement level $\kappa$, and a given sample size $n$, we generated 10,000 data sets (a data set contains 3 columns of $n$ ratings each) under the null hypothesis $H_0:{\kappa }_{13}={\kappa }_{12}=\kappa$, then computed for each dataset the 95% confidence interval associated with the estimated difference ${\hat{\kappa }}_{13}-{\hat{\kappa }}_{12}$ before determining whether or not the confidence interval includes the hypothetical difference 0 as in Equation (19). We expect the coverage rate based on all 10,000 data sets to get closer to 0.95 as the sample size $n$ increases. Our simulation was repeated for 3 “true” agreement levels $\kappa =0.5,0.65,0.85$, for 7 sample sizes $n=10$, 20, 30, 40, 50, 80, 100, and for 4 values of the number of categories $q=2$, 3, 4, and 5. We use a single value for the prevalence rate of $p_r=0.75$. We define prevalence as the propensity for two raters to agree on the first category based solely on subjects where agreement is known to have occurred. Simulations not reported here indicated that the prevalence rate did not affect the interval coverage rate much. Hence, the use of a single prevalence value.

To generate a data set (made up of three series of ratings for the three raters) for a given “true” agreement level $\kappa$, a sample size $n$, and a prevalence rate $p_r$, we proceeded as follows:

• We generated two uniform random numbers $U_1$ and $U_2$ between 0 and 1.

• If $U_1\le \kappa$ then there must be an agreement among all three raters. If $U_2\le p_r$ then all 3 raters are assigned value 1 (the first category); otherwise they are all assigned a randomly chosen category among the remaining $q-1$ categories, $2,\dots ,q$.

• If $U_1>\kappa$ then the ratings from all three raters must be random. In this case, we generated 3 additional uniform random variables $V_1$, $V_2$, and $V_3$ between 0 and 1 for the 3 raters 1, 2, and 3. These variables is used to randomly assign one of the $q$ categories to each rater.

These three steps were repeated $n$ times to obtain one data set, $n$ representing the number of subjects or the sample size. A total of 10,000 such datasets were created to complete the Monte Carlo experiment.

The program implementing this Monte Carlo experiment was written in SAS using the SAS Macro language and some data step programming.

The Results

The two agreement coefficients associated with raters {1, 3} (${\hat{\kappa }}_{13}$) and with raters {1, 2} (${\hat{\kappa }}_{12}$) are correlated. To verify this, we considered two agreement coefficients (Cohen’s kappa, and Gwet’s $\mathrm{AC}{}_1$), and the situation where the number of categories is 3, the “true” agreement coefficient $\kappa =0.65$, and a prevalence rate of 0.95. We then calculated the Monte Carlo variance of the difference between coefficients as well as the sum of variances associated with the individual coefficients for various sample sizes ($n=10$, 20, 30, 40, 50, 60, 70, 80, 90, and 100). The results depicted in Figure 1 show that the variance of the difference is always smaller that the sum of the variances. This proves the existence of a positive correlation between ${\hat{\kappa }}_{13}$ and ${\hat{\kappa }}_{12}$; a clear indication that our Monte-Carlo experiment has created a scenario where two correlated agreement coefficients must be tested. The gap between the continuous and the dotted curves decreases as the sample size increases. It is the case because all variances decrease with larger sample sizes.

Figure 1.

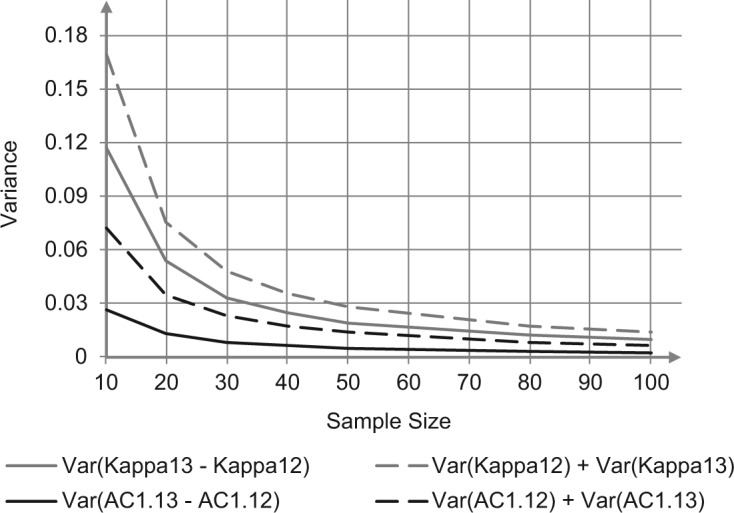
Comparison of the variance of the difference between coefficients and the sum of the coefficient variances for the $\mathrm{AC}{}_1$ and Kappa coefficients for $\kappa =0.65$, $p_r=0.95$, and $q=3$.

Note that each data set $d$ produced an agreement coefficient ${\hat{\kappa }}^{(d)}$, and the Monte Carlo variance is calculated as follows:

$$V_{\mathrm{MC}}(\hat{\kappa })=\frac{1}{10,000}\sum _{d=1}^{10,000}{({\hat{\kappa }}^{(d)}-{\overline{\hat{\kappa }}}^{(·)})}^2,$$

where ${\overline{\hat{\kappa }}}^{(·)}$ is the average of all 10,000 estimated coefficients ${\hat{\kappa }}^{(d)}$, $d=1,\dots ,10,000$. The Monte Carlo based variance of the difference ${\hat{\kappa }}_{13}-{\hat{\kappa }}_{12}$ is calculated the same way.

Tables 1 through 4 show the confidence interval coverage rates for various agreement coefficients, by agreement level and by sample size, when prevalence rate is set to 0.75. Each of the 4 tables is associated with a particular number of categories ($q=2$, 3, 4, and 5 for Tables 1, 2, 3, and 4 respectively).

Table 1.

Coverage Rates of 95% Confidence Intervals When Prevalence Rate is 0.75 and the Number of Categories $q=2$.

		Sample size (n)
$\kappa$ a	Agreement coefficient	10	20	30	40	50	80	100
0.50	Cohen’s kappa	0.864	0.925	0.934	0.943	0.937	0.945	0.943
	Scott’s pi	0.855	0.933	0.936	0.945	0.938	0.946	0.943
	Gwet’s $\mathrm{AC}{}_1$	0.926	0.946	0.945	0.950	0.948	0.951	0.949
	Brennan–Prediger	0.859	0.936	0.928	0.945	0.946	0.948	0.945
	Krippendorff’s alpha	0.872	0.932	0.935	0.944	0.938	0.946	0.942
0.65	Cohen’s kappa	0.796	0.924	0.934	0.941	0.942	0.949	0.942
	Scott’s pi	0.793	0.933	0.935	0.942	0.943	0.949	0.943
	Gwet’s $\mathrm{AC}{}_1$	0.852	0.947	0.948	0.950	0.951	0.954	0.949
	Brennan–Prediger	0.809	0.940	0.932	0.948	0.955	0.951	0.943
	Krippendorff’s alpha	0.808	0.933	0.934	0.942	0.942	0.949	0.942
0.85	Cohen’s kappa	0.521	0.772	0.886	0.924	0.937	0.945	0.946
	Scott’s pi	0.523	0.774	0.887	0.924	0.937	0.946	0.946
	Gwet’s $\mathrm{AC}{}_1$	0.555	0.781	0.895	0.932	0.946	0.952	0.952
	Brennan–Prediger	0.547	0.780	0.887	0.924	0.941	0.952	0.952
	Krippendorff’s alpha	0.542	0.775	0.886	0.924	0.937	0.946	0.947

^a$\kappa$ = hypothesized agreement level, representing the nominal percent of subjects on which the raters agree for cause, as opposed to by chance.

Table 4.

Coverage Rates of 95% Confidence Intervals When Prevalence Rate is 0.75, and the Number of Categories $q=5$.

		Sample size (n)
$\kappa$ a	Agreement coefficient	10	20	30	40	50	80	100
0.50	Cohen’s kappa	0.923	0.935	0.932	0.936	0.940	0.945	0.948
	Scott’s pi	0.931	0.940	0.933	0.937	0.940	0.945	0.948
	Gwet’s $\mathrm{AC}{}_1$	0.976	0.962	0.943	0.946	0.947	0.949	0.952
	Brennan–Prediger	0.786	0.931	0.932	0.948	0.952	0.947	0.949
	Krippendorff’s alpha	0.928	0.937	0.932	0.935	0.938	0.944	0.945
0.65	Cohen’s kappa	0.897	0.948	0.944	0.939	0.937	0.942	0.948
	Scott’s pi	0.903	0.951	0.946	0.940	0.937	0.942	0.948
	Gwet’s $\mathrm{AC}{}_1$	0.946	0.979	0.961	0.953	0.950	0.951	0.953
	Brennan–Prediger	0.678	0.887	0.930	0.946	0.948	0.952	0.952
	Krippendorff’s alpha	0.907	0.951	0.943	0.939	0.935	0.941	0.946
0.85	Cohen’s kappa	0.649	0.901	0.962	0.972	0.973	0.954	0.948
	Scott’s pi	0.653	0.903	0.962	0.973	0.974	0.954	0.949
	Gwet’s $\mathrm{AC}{}_1$	0.685	0.914	0.971	0.982	0.980	0.958	0.953
	Brennan–Prediger	0.388	0.624	0.766	0.848	0.900	0.937	0.946
	Krippendorff’s alpha	0.673	0.904	0.965	0.975	0.972	0.953	0.947

^a $\kappa$ = hypothesized agreement level, representing the nominal percent of subjects on which the raters agree for cause, as opposed to by chance.

Table 2.

Coverage Rates of 95% Confidence Intervals When Prevalence Rate Is 0.75, and the Number of Categories $q=3$.

		Sample size (n)
$\kappa$ a	Agreement coefficient	10	20	30	40	50	80	100
0.50	Cohen’s kappa	0.899	0.921	0.927	0.939	0.941	0.943	0.947
	Scott’s pi	0.907	0.925	0.930	0.940	0.943	0.943	0.947
	Gwet’s $\mathrm{AC}{}_1$	0.958	0.946	0.943	0.947	0.949	0.949	0.951
	Brennan–Prediger	0.849	0.935	0.925	0.944	0.951	0.945	0.950
	Krippendorff’s alpha	0.920	0.928	0.931	0.940	0.942	0.943	0.947
0.65	Cohen’s kappa	0.857	0.930	0.935	0.939	0.940	0.946	0.944
	Scott’s pi	0.863	0.935	0.938	0.942	0.941	0.947	0.945
	Gwet’s $\mathrm{AC}{}_1$	0.916	0.962	0.951	0.952	0.950	0.950	0.950
	Brennan–Prediger	0.775	0.933	0.936	0.950	0.954	0.948	0.946
	Krippendorff’s alpha	0.876	0.938	0.938	0.941	0.940	0.944	0.943
0.85	Cohen’s kappa	0.605	0.859	0.930	0.951	0.956	0.949	0.949
	Scott’s pi	0.607	0.861	0.933	0.952	0.957	0.950	0.950
	Gwet’s $\mathrm{AC}{}_1$	0.647	0.875	0.942	0.959	0.962	0.956	0.957
	Brennan–Prediger	0.500	0.744	0.856	0.915	0.936	0.951	0.955
	Krippendorff’s alpha	0.631	0.863	0.936	0.953	0.957	0.950	0.949

^a$\kappa$ = hypothesized agreement level, representing the nominal percent of subjects on which the raters agree for cause, as opposed to by chance.

Table 3.

Coverage Rates of 95% Confidence Intervals When Prevalence Rate is 0.75, and the Number of Categories $q=4$.

		Sample size (n)
$\kappa$ a	Agreement coefficient	10	20	30	40	50	80	100
0.50	Cohen’s kappa	0.916	0.932	0.930	0.938	0.942	0.941	0.945
	Scott’s pi	0.922	0.935	0.933	0.940	0.944	0.941	0.946
	Gwet’s $\mathrm{AC}{}_1$	0.968	0.959	0.943	0.948	0.950	0.948	0.951
	Brennan–Prediger	0.821	0.942	0.932	0.949	0.955	0.945	0.948
	Krippendorff’s alpha	0.925	0.936	0.933	0.938	0.942	0.940	0.944
0.65	Cohen’s kappa	0.888	0.938	0.938	0.940	0.942	0.945	0.941
	Scott’s pi	0.897	0.942	0.941	0.942	0.942	0.946	0.942
	Gwet’s $\mathrm{AC}{}_1$	0.942	0.971	0.957	0.951	0.952	0.953	0.946
	Brennan–Prediger	0.726	0.914	0.940	0.949	0.953	0.952	0.942
	Krippendorff’s alpha	0.904	0.946	0.942	0.939	0.942	0.944	0.939
0.85	Cohen’s kappa	0.652	0.886	0.948	0.961	0.964	0.949	0.946
	Scott’s pi	0.656	0.888	0.950	0.964	0.965	0.950	0.946
	Gwet’s $\mathrm{AC}{}_1$	0.690	0.901	0.962	0.971	0.970	0.955	0.950
	Brennan–Prediger	0.438	0.685	0.809	0.881	0.919	0.945	0.948
	Krippendorff’s alpha	0.677	0.891	0.954	0.966	0.965	0.950	0.945

^a $\kappa$ = hypothesized agreement level, representing the nominal percent of subjects on which the raters agree for cause, as opposed to by chance.

It appears from all four tables that when the agreement level is low (e.g., $\kappa =0.5$) the simulated interval coverage rate is reasonably close to its nominal value of 0.95 for sample sizes as small as 20. The $\mathrm{AC}{}_1$ coefficient yields a good coverage rate even when the sample is 10. However, when the agreement level increases then a larger sample size becomes necessary to achieve an acceptable coverage rate. For example, if the agreement level is 0.85 and the number of categories is 2, then only a sample size of 40 will produce an acceptable coverage rate.

As the number of categories increases from 2 to 5, the coverage rate of all agreement coefficients for a fixed sample size appears to increase noticeably for smaller sample sizes when the agreement level is high (e.g., 0.85), except the Brenann–Pediger coefficient whose coverage rate deteriorates instead. The considerable decrease of the coverage rate associated with the Brenann-Prediger coefficient is essentially due to a dramatic underestimation of its variance for small and moderately-large samples. The estimated variance of the Brenann-Prediger coefficient equals 0 whenever both pairs of raters (1, 2), and (1, 3) agree or disagree on the exact same subjects. The opportunity of this happening increases with the number of categories. Other authors have found the use of a fixed percent chance agreement $1/q$ as in the Brenann–Prediger coefficient to be problematic (see Cousineau & Laurencelle, 2015). The increase in coverage rate observed with the other coefficients on small sample sizes appears to be the result of an overstatement of their variances due to some categories not always being represented in certain small samples.

Investigating “Systematic” Disagreement

We also investigated the confidence interval coverage rates in situations where there is a “systematic” disagreement among raters. The experiment was set up in such a way that three raters randomly assign subjects to categories according to the predetermined classification probabilities defined in Table 5. For example, when the number of categories is 3 then rater 1 classifies a subject into category 1 with probability 2/3, and into categories 2 or 3 with the same probability of 1/6. It follows that all three raters are expected to classify the majority of subjects into different categories with only a few agreements possibly occurring by pure chance. The classification probabilities associated with the number of categories of 4, and 5 are also defined in Table 5 and will produce similar systematic disagreement among the three raters. The results of this experiment are shown in Table 6.

Table 5.

Raters’ Classification Probabilities for the Systematic Disagreement Experiment.

q a	k b	Rater 1	Rater 2	Rater 3
3	1	2/3	1/6	1/6
	2	1/6	2/3	1/6
	3	1/6	1/6	2/3
4	1	2/4	1/6	1/6
	2	1/6	2/4	1/6
	3	1/6	1/6	2/4
	4	1/6	1/6	1/6
5	1	3/5	1/10	1/10
	2	1/10	3/5	1/10
	3	1/10	1/10	3/5
	4	1/10	1/10	1/10
	5	1/10	1/10	1/10

^a q = number of categories in the experiment.

^b k = category label.

Table 6.

Coverage Rates of 95% Confidence Intervals When There is Systematic Disagreement Among Raters.

		Sample size (n)
(q)a	Agreement coefficient	10	20	30	40	50	80	100
3	Cohen’s kappa	0.966	0.956	0.956	0.952	0.950	0.952	0.948
	Scott’s pi	0.903	0.929	0.940	0.941	0.940	0.946	0.944
	Gwet’s $\mathrm{AC}{}_1$	0.913	0.931	0.942	0.938	0.942	0.945	0.947
	Brennan–Prediger	0.882	0.926	0.936	0.940	0.944	0.946	0.947
	Krippendorff’s alpha	0.925	0.940	0.949	0.946	0.948	0.952	0.952
4	Cohen’s kappa	0.930	0.938	0.944	0.946	0.949	0.948	0.946
	Scott’s pi	0.912	0.934	0.939	0.941	0.944	0.945	0.943
	Gwet’s $\mathrm{AC}{}_1$	0.926	0.933	0.940	0.944	0.946	0.946	0.945
	Brennan–Prediger	0.885	0.928	0.931	0.941	0.947	0.947	0.945
	Krippendorff’s alpha	0.922	0.939	0.943	0.945	0.948	0.950	0.946
5	Cohen’s kappa	0.953	0.948	0.949	0.944	0.944	0.949	0.947
	Scott’s pi	0.914	0.928	0.937	0.941	0.944	0.944	0.948
	Gwet’s $\mathrm{AC}{}_1$	0.936	0.934	0.942	0.940	0.944	0.942	0.943
	Brennan–Prediger	0.858	0.931	0.930	0.937	0.947	0.942	0.942
	Krippendorff’s alpha	0.914	0.928	0.936	0.942	0.944	0.944	0.948

^aq = number of categories.

Table 6 shows a reasonably good interval coverage rate for sample sizes as small as 20. Even when the sample size is 10, most agreement coefficients still yield an interval coverage rate that is over 90%. Therefore, the linearization method for testing correlated agreement coefficients produces satisfactory results when there is systematic disagreement among raters.

Linearization Method Versus the Bootstrap Method

For the sake of comparing our new linearization method to an existing method, we conducted a Monte Carlo experiment where the linearization method and the bootstrap method suggested by McKenzie et al. (1996) are compared. The same five agreement coefficients previously inverstigated are used again in this experiment, which was repeated for each of the three agreement level values 0.5, 0.65, and 0.85. This Monte Carlo simulation is based on 10,000 iterations, and 1,000 bootstrap samples were generated from each of the iterations.

The results are depicted in Figures 2 to 4. It appears from these figures that the linearization and the bootstrap methods produce strikingly similar results. Figure 4 confirms (with the bootstrap method) the poor interval coverage rate of the Brenann–Prediger coefficient for small sample sizes. This provides another indication of the adequacy of the proposed linearization method for testing correlated agreement coefficients for statistical significance.

Figure 2.

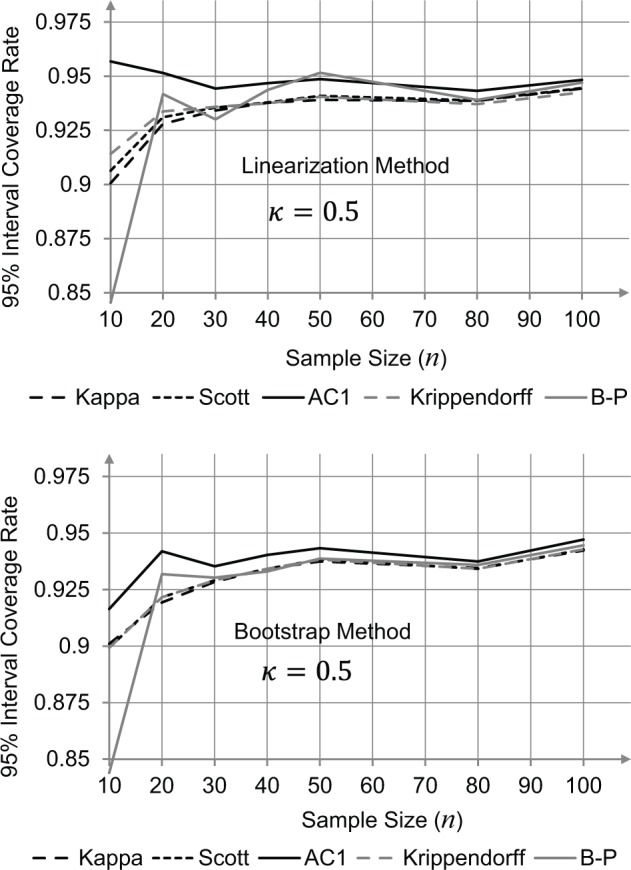
Comparison between the linearization and bootstrap methods with respect to their 95% confidence interval coverage rates, for $\kappa$ = 0.50.

Figure 4.

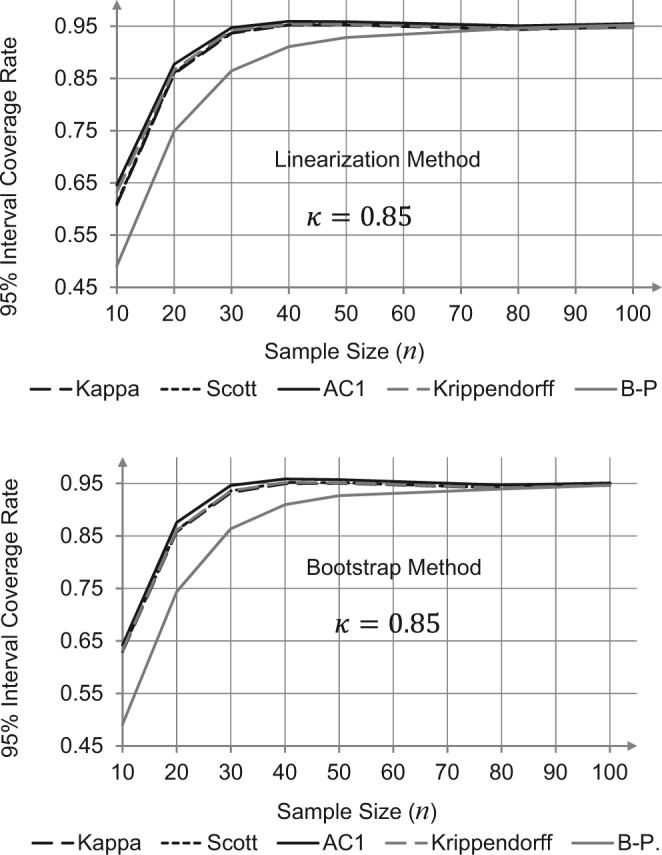
Comparison between the linearization and bootstrap methods with respect to their 95% confidence interval coverage rates, for $\kappa =0.85$.

Figure 3.

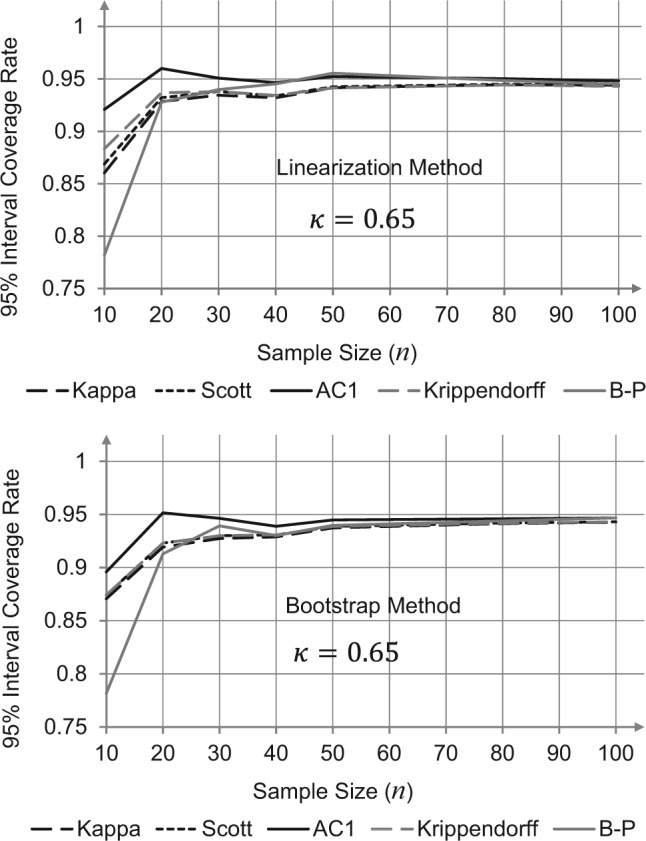
Comparison between the linearization and bootstrap methods with respect to their 95% confidence interval coverage rates, for $\kappa =0.65$.

Discussion

This article addressed the problem of testing the difference between two correlated agreement coefficients for statistical significance. This research was motivated by the complexity of existing procedures and the desire to propose a simpler approach that can be implemented more conveniently and with adequate efficiency (i.e., can provide acceptable coverage rates for smaller samples). While existing approaches rely on statistical modeling or on bootstrapping the existing sample, the procedure recommended in this article is based of the large-sample linear approximation of the agreement coefficients of interest. The Monte Carlo experiment presented in the previous section shows that the proposed procedure works reasonably well for sample sizes as small as 10, provided the agreement level is not too high. For higher agreement levels, a sample size of 30, or 40 may be necessary to obtain satisfactory results.

A key lesson to be learned from our Monte Carlo experiment is that testing the difference between correlated agreement coefficients for statistical significance using the procedure we recommend works well for small sample sizes when the distribution of subjects is not too skewed toward one category, and the agreement level too high. However, the quality of this test for small samples deteriorates when this distribution becomes very skewed (i.e., agreement level $\kappa$ and prevalence rate are simultaneously very high). In this case, increasing the sample size becomes the only remedy. However, a sample size of 40 appears to yield a good coverage rate for all agreement levels and all prevalence rates. Small sizes such as 10 must be avoided if the distribution of subjects is anticipated to be heavily skewed toward one category.

Throughout this article, we have assumed that each rater rated all subjects, yielding a data set with no missing ratings. The situation in practice may be different. We provide in appendix A the formulas that should be used when dealing with missing ratings. These equations and those discussed previously produce identical results if there is no missing rating.

Although the focus of this article was on testing the difference between two correlated agreement coefficients for statistical significance, extending the proposed method to the testing of the equality of several agreement coefficients is straightforward. In fact one can still use the same large-sample linear approximations of the agreement coefficients along with existing statistical tests such as the analysis of variance (ANOVA) or the Friedman test if the nonparametric approach is deemed more appropriate.

Appendix A

Handling Missing Values

In the main part of this article, we provided several equations that can be used as linear approximations to various agreement coefficients. All these equations are valid only when there is no missing rating. That is, each rater is assumed to have rated all subjects. Practitioners know that missing ratings are common in practice for a variety of reasons. Testing the difference between two correlated agreement coefficients in the presence of missing ratings require the use of slightly different equations. Let $n$ be the number of subjects to be rated, and $n\prime$ the number subjects that are rated by 2 raters or more. We also assume that $r$ is the number of raters, and $r_i$ the number of raters who rated a particular subject $i$.

• Fleiss’s generalized kappa coefficient

In the presence of missing ratings, Fleiss’s generalized kappa coefficient can be expressed as average of the ${\kappa }_{\mathrm{F}|\mathrm{i}}^{\star }$ values given by

$${\kappa }_{\mathrm{F}|\mathrm{i}}^{\star }={\kappa }_{\mathrm{F}|\mathrm{i}}-2(1-{\hat{\kappa }}_{\mathrm{F}})(p_{e|i}-p_e)/(1-p_e),$$

where

$${\kappa }_{\mathrm{F}|\mathrm{i}}=\{\begin{array}{cc}\hfill (n/n\prime )(p_{a|i}-p_e)/(1-p_e),\hfill & \hfill \mathrm{if}{r}_i\ge 2,\hfill \\ \multicolumn{1}{c}{0,}& \hfill \mathrm{otherwise},\hfill \end{array}$$

$$p_{a|i}=\{\begin{array}{cc}\hfill \sum _{k=1}^q\frac{r_{\mathrm{ik}}(r_{\mathrm{ik}}-1)}{r_i(r_i-1)},\hfill & \hfill \mathrm{if}{r}_i\ge 2,\hfill \\ \multicolumn{1}{c}{0,}& \hfill \mathrm{otherwise},\hfill \end{array}$$

$$p_{e|i}=\sum _{k=1}^q{\pi }_k{r}_{\mathrm{ik}}/r_i.$$

Note that ${\hat{\kappa }}_{\mathrm{F}}$ and $p_e$ are obtained by averaging the ${\kappa }_{\mathrm{F}|\mathrm{i}}$ and $p_{e|i}$ values respectively over all $n$ sample subjects.

• Krippendorff’s alpha coefficient

Let $\overline{r}$ be the average number of raters who rated a subject (i.e., the mean value of the $r_i$s). In the presence of missing ratings, Krippendorff’s alpha can be expressed as the average of the ${\alpha }_{K|i}^{\star }$ values given by

$${\alpha }_{K|i}^{\star }={\alpha }_{K|i}-(1-{\hat{\alpha }}_K)(p_{e|i}-p_e)/(1-p_e)$$

and,

• ${\alpha }_{K|i}=(p_{a{\epsilon }_n|i}-p_e)/(1-p_e)$

• $p_{a{\epsilon }_n|i}=(1-{\epsilon }_n)[p_{a|i}-p_a(r_i-\overline{r})/\overline{r}]+{\epsilon }_n,\mathrm{and}{p}_{a|i}=\sum _{k=1}^q\frac{r_{\mathrm{ik}}(r_{\mathrm{ik}}-1)}{\overline{r}(r_i-1)},p_a=\frac{1}{n}\sum _{i=1}^n{p}_{a|i}\mathrm{and}{p}_{e|i}=\sum _{k=1}^q{\pi }_k\frac{r_{\mathrm{ik}}}{\overline{r}}-(r_i-\overline{r})/\overline{r}$

Moreover, ${\hat{\alpha }}_K$ and $p_e$ are obtained by averaging the ${\alpha }_{K|i}$s and the $p_{e|i}$s, respectively, over the entire sample of $n$ subjects. Note that only subjects rated by 2 raters or more are considered in the calculation of Krippendorff’s alpha. Subjects rated by a single rater are excluded for the analysis altogether.

• Conger’s generalized kappa coefficient

In the presence of missing ratings, Conger’s generalized kappa coefficient can be expressed as the average of the ${\kappa }_{C|i}$ values given by

$${\kappa }_{C|i}^{\star }={\kappa }_{C|i}-2(1-{\hat{\kappa }}_C)(p_{e|i}-p_e)/(1-p_e),$$

where

$${\kappa }_{C|i}=\{\begin{array}{cc}\hfill (n/n\prime )(p_{a|i}-p_e)/(1-p_e),\hfill & \hfill \mathrm{if}{r}_i\ge 2,\hfill \\ \multicolumn{1}{c}{0,}& \hfill \mathrm{otherwise},\hfill \end{array}$$

where $p_{a|i}$ is defined by Equation (22), and $p_{e|i}$ the percent chance agreement associated with subject $i$ is given by,

$$p_{e|i}=\frac{1}{r(r-1)}\sum _{g=1}^r\sum _{k=1}^q{\delta }_{\mathrm{gk}}^{(i)}(r{\overline{p}}_{+k}-p_{\mathrm{gk}}),$$

with ${\delta }_{\mathrm{gk}}^{(i)}=1$ if rater $g$ classifies subject $i$ into category $k$, and ${\delta }_{\mathrm{gk}}^{(i)}=0$ otherwise. The percent chance agreement is obtained by averaging the $p_{e|i}$ values over all $n$ sample subjects.

• Gwet’ AC₁ coefficient

In the presence of missing ratings, Gwet’s $\mathrm{AC}{}_1$ coefficient can be expressed as the average of the ${\kappa }_{G|i}^{\star }$ values given by

$${\kappa }_{G|i}^{\star }={\kappa }_{G|i}-2(1-{\hat{\kappa }}_G)(p_{e|i}-p_e)/(1-p_e),$$

where

$${\kappa }_{G|i}=\{\begin{array}{cc}\hfill (n/n\prime )(p_{a|i}-p_e)/(1-p_e),\hfill & \hfill \mathrm{if}{r}_i\ge 2,\hfill \\ \multicolumn{1}{c}{0,}& \hfill \mathrm{otherwise},\hfill \end{array}$$

with $p_{a|i}$ defined by Equation (22), and $p_{e|i}$ the percent chance agreement associated with subject $i$ given by

$$p_{e|i}=\frac{1}{q-1}\sum _{k=1}^q(1-{\pi }_k)r_{\mathrm{ik}}/r_i.$$

The percent chance agreement $p_e$ is calculated by averaging the $p_{e|i}$ values over the entire sample of $n$ subjects.

• Brennan–Prediger Coefficient

In the presence of missing ratings, the Brennan–Prediger coefficient can be expressed as the average of the ${\kappa }_{\mathrm{BP}|i}$ values given by:

$${\kappa }_{\mathrm{BP}|\mathrm{i}}=\{\begin{array}{cc}\hfill (n/n\prime )(p_{a|i}-1/q)/(1-1/q),\hfill & \hfill \mathrm{if}{r}_i\ge 2,\hfill \\ \multicolumn{1}{c}{0,}& \hfill \mathrm{otherwise},\hfill \end{array}$$

where $p_{a|i}$ is defined by Equation (22).

Appendix B

Walkthrough Example

This appendix uses a step-by-step approach to illustrate how the proposed linearization method for testing correlated agreement coefficients can be implemented in practice. We confine ourselves to the $\mathrm{AC}{}_1$ statistic, and use the data shown in the first four columns of Table B1. These data summarize the results of an interrater reliability experiment that involves 3 raters who must classify each of the 15 sample subjects into one of 3 categories labeled as 1, 2, and 3.

The main analytic goal is to test the hypothesis that the extent of agreement ${\kappa }^{(1,2)}$ between raters 1 and 2 is identical to the extent of agreement ${\kappa }^{(1,3)}$ between raters 1 and 3. That is,

$$\{\begin{array}{cc}\hfill H_0:\hfill & \hfill {\kappa }^{(1,2)}={\kappa }^{(1,3)},\hfill \\ \multicolumn{1}{c}{H_1:}& \hfill {\kappa }^{(1,2)}\ne {\kappa }^{(1,3)}.\hfill \end{array}$$

We want this walkthrough example to be sufficiently detailed for practitioners to see all the steps involved in the implementation of the linearization method. As a matter of fact, this method may even be implemented manually for small samples by following the steps described here.

The implementation of the linearization method for comparing correlated agreement coefficients is done in four steps:

1. Compute the binary category membership indicators ${\epsilon }_{\mathrm{ik}}^{(g)}$, which take value 1 only if rater $g$ classifies subject $i$ into category $k$, and take value 0 otherwise.

2. Compute the effect ${\kappa }_{G|i}^{\star (1,2)}$ of each subject $i$ on the $\mathrm{AC}{}_1$ coefficient between raters 1 and 2, based on Equation (16).

3. Compute the effect ${\kappa }_{G|i}^{\star (1,3)}$ of each subject $i$ on the $\mathrm{AC}{}_1$ coefficient between raters 1 and 3, based on Equation (16).

4. Compute the subject-level differences $d_i={\kappa }_{G|i}^{\star (1,3)}-{\kappa }_{G|i}^{\star (1,2)}$, and the variance of their mean before computing the T-statistic of Equation (8). This test statistic can then be compared with the critical value before deciding on the rejection or the nonrejection of the null hypothesis.

(a) The Dichotomous Category Membership Indicators ${\epsilon }_{\mathrm{ik}}^{(g)}$

• This first step is described in Table B1, and consists of recoding the initial raw ratings in the form of dichotomous category membership indicators represented by the variables ${\epsilon }_{\mathrm{ik}}^{(g)}$. The variable ${\epsilon }_{\mathrm{ik}}^{(g)}$ takes value 1 if rater $g$ classifies subject $i$ into category $k$, and takes value 0 otherwise.

• The bottom part of Table B1 contains a few summary statistics. $p_{k+}$ represents the relative number of subjects classified into category $k$ by rater 1 and is obtained by averaging the numbers in the associated column. $p_{+k}$ on the other hand, represents the relative number of subjects classified into category $k$ by the second rater whose extent of agreement with rater 1 is being evaluated. The second rater is rater 2 if the pair of raters under consideration is (1, 2), and becomes rater 3 in the pair (1, 3). Moreover ${\pi }_k=(p_{k+}+p_{+k})/2$ is calculated for each of the two pairs of raters (1, 2) and (1, 3) being analyzed. For the (1, 2) pair of raters for example ${\pi }_2=(0.2+0.133)/2=0.167$, and ${\pi }_3=(0.2+0.2)/2=0.2$.

• Adapting Table B1 to the situation where the same pair of raters is compared to itself on two different occasions—as opposed to two overlapping pairs of raters taken out of a group of 3 raters—is straightforward. On any given occasion, each rater must be treated as a distinct entity in its own right.

(b) Subject Effects ${\kappa }_{G|i}^{\star (1,2)}$ on $\mathrm{AC}{}_1$ Coefficient Between Raters 1 and 2

• The primary objective of this step is to compute the contribution ${\kappa }_{G|i}^{\star (1,2)}$ of each subject $i$ to the $\mathrm{AC}{}_1$ coefficient between raters 1 and 2 as given by Equation (16). These quantities are shown in the last column of Table B2. All computations leading to these numbers are described in Table B2, and implement Equation (16) as well as the equations found in the subsection entitled “The Special Case of Two Raters” associated with Gwet’s $\mathrm{AC}{}_1$ coefficient.

• The subject-level percent agreement $p_{a|i}$ is a dichotomous variable taking value 1 when both raters agree, and will take a value of 0 otherwise. Averaging these numbers produces the percent agreement $p_a=0.867$ between raters 1 and 2.

• Columns 3, 4, and 5 use Table B1 results to compute for each subject $i$ the percent chance agreement on subject $i$ and on category $k$ given by $p_{e|\mathrm{ik}}=(1-{\pi }_k)[{\epsilon }_{\mathrm{ik}}^{(1)}+{\epsilon }_{\mathrm{ik}}^{(2)}]/[2(q-1)]$. For subject 2 and category 1 for example, $p_{e|21}=(1-0.633)\times (1+1)/(2\times (3-1))=0.3667/2=0.1833$. Once available, these quantities are summed over all three categories to obtain the percent chance agreement $p_{e|i}$ associated with subject $i$. Averaging the $p_{e|i}$ values produces the percent chance agreement $p_e=0.266$ (see cell defined by the last row of Table B2 and column 6).

• Column 7 of Table B2 is obtained by subtracting $p_e$ from column 2 and by dividing the difference by $1-p_e$. Column 7 on the other hand is calculated according to Equation (16).

(c) Subject Effects ${\kappa }_{G|i}^{\star (1,3)}$ on $\mathrm{AC}{}_1$ Coefficient Between Raters 1 and 3

• The primary objective of this step is to compute the contribution ${\kappa }_{G|i}^{\star (1,3)}$ of each subject $i$ to the $\mathrm{AC}{}_1$ coefficient between raters 1 and 3, as given by Equation (16). These quantities are shown in the last column of Table B3. All computations leading to these numbers are described in Table B3, and are similar to those of Table B2.

(d) Testing the Hypothesis

• Once the ${\kappa }_{G|i}^{\star (1,3)}$ values are calculated, we can compute the subject-level differences $d_i={\kappa }_{G|i}^{\star (1,3)}-{\kappa }_{G|i}^{\star (1,2)}$ (see the last column of Table B3) as well as the variance of mean difference, which is given by $v(\overline{d})=0.009090$.

• We are now in the position to perform the test of hypothesis. The T-statistic of Equation (8) is given by

$$T=\frac{0.728-0.818}{\sqrt{0.009090}}=-0.95209.$$

If we want to test the null hypothesis at the 5% significance level, then the critical value to be used is $c_{0.05}=2.145$. Since the absolute value of the T-statistic is below this critical value, we cannot reject the null hypothesis of equality of the agreement levels between the (1, 2), and (1, 3) pairs of raters.

Table B1.

Computing the Variables ${\epsilon }_{\mathrm{ik}}^{(g)}$, $p_{k+}$, $p_{+k}$, and ${\pi }_k$.

				Rater 1			Rater 2			Rater 3
Subject $(i)$	Rater 1	Rater 2	Rater 3	${\epsilon }_{i1}^{(1)}$	${\epsilon }_{i2}^{(1)}$	${\epsilon }_{i3}^{(1)}$	${\epsilon }_{i1}^{(2)}$	${\epsilon }_{i2}^{(2)}$	${\epsilon }_{i3}^{(2)}$	${\epsilon }_{i1}^{(3)}$	${\epsilon }_{i2}^{(3)}$	${\epsilon }_{i3}^{(3)}$
1	1	1	2	1	0	0	1	0	0	0	1	0
2	1	1	1	1	0	0	1	0	0	1	0	0
3	1	1	1	1	0	0	1	0	0	1	0	0
4	1	1	1	1	0	0	1	0	0	1	0	0
5	3	3	3	0	0	1	0	0	1	0	0	1
6	1	1	1	1	0	0	1	0	0	1	0	0
7	1	1	1	1	0	0	1	0	0	1	0	0
8	1	1	1	1	0	0	1	0	0	1	0	0
9	1	1	1	1	0	0	1	0	0	1	0	0
10	2	2	2	0	1	0	0	1	0	0	1	0
11	1	1	1	1	0	0	1	0	0	1	0	0
12	2	3	1	0	1	0	0	0	1	1	0	0
13	2	2	2	0	1	0	0	1	0	0	1	0
14	3	3	3	0	0	1	0	0	1	0	0	1
15	3	1	1	0	0	1	1	0	0	1	0	0
				$p_{1+}$	$p_{2+}$	$p_{3+}$	$p_{+1}$	$p_{+2}$	$p_{+3}$	$p_{+1}$	$p_{+2}$	$p_{+3}$
Average				0.6	0.2	0.2	0.667	0.133	0.2	0.667	0.2	0.133
							${\pi }_1$	${\pi }_2$	${\pi }_3$	${\pi }_1$	${\pi }_2$	${\pi }_3$
							0.633	0.167	0.2	0.633	0.2	0.167

Table B2.

Computing Subject-Level Agreement Coefficients ${\kappa }_{G|i}^{☆}$ Between Raters 1 and 2 Based on the $\mathrm{AC}{}_1$ Coefficient.

		$(1-{\pi }_k)[{\epsilon }_{\mathrm{ik}}^{(1)}+{\epsilon }_{\mathrm{ik}}^{(2)}]/[2(q-1)]$
Subject $(i)$	$p_{a|i}$	$k=1$	$k=2$	$k=3$	$p_{e|i}$ a	${\kappa }_{G|i}^{(1,2)}$ b	${\kappa }_{G|i}^{☆(1,2)}$ c
1	1	0.1833	0	0	0.1833	1	1.0406
2	1	0.1833	0	0	0.1833	1	1.0406
3	1	0.1833	0	0	0.1833	1	1.0406
4	1	0.1833	0	0	0.1833	1	1.0406
5	1	0	0	0.4	0.4	1	0.9335
6	1	0.1833	0	0	0.1833	1	1.0406
7	1	0.1833	0	0	0.1833	1	1.0406
8	1	0.1833	0	0	0.1833	1	1.0406
9	1	0.1833	0	0	0.1833	1	1.0406
10	1	0	0.4167	0	0.4167	1	0.9253
11	1	0.1833	0	0	0.1833	1	1.0406
12	0	0	0.2083	0.2	0.4083	–0.3616	–0.4322
13	1	0	0.4167	0	0.4167	1	0.9253
14	1	0	0	0.4	0.4	1	0.9335
15	0	0.0917	0	0.2	0.2917	–0.3616	–0.3745
	$p_a$				$p_e$	${\hat{\kappa }}_G$	${\hat{\kappa }}_G$
Average	0.867				0.266	0.818	0.818

^a This is obtained by summing columns 3, 4, and 5. ^bThis is computed as $(p_{a|i}-p_e)/p_e$ (i.e., Col 7 = (Col2 − 0.266)/(1 − 0.266)). ^cThis is computed based on Equation (16): Col8 = Col7 − 2×(1 − 0.818)×(Col6 − 0.266)/(1 − 0.266)

Table B3.

Computing Subject-Level Agreement Coefficients ${\kappa }_{G|i}^{☆}$ Between Raters 1 and 3 Based on the $\mathrm{AC}{}_1$ Coefficient, the Differences $d_i$ From Raters 1 and 2 Extent of Agreement.

		$(1-{\pi }_k)[{\epsilon }_{\mathrm{ik}}^{(1)}+{\epsilon }_{\mathrm{ik}}^{(3)}]/[2(q-1)]$
Subject $(i)$	$p_{a|i}$	$k=1$	$k=2$	$k=3$	$p_{e|i}$	${\kappa }_{G|i}^{(1,3)}$	${\kappa }_{G|i}^{☆(1,3)}$	$d_i$ a
1	0	0.0917	0.2	0	0.2917	–0.3616	–0.3809	–1.42158
2	1	0.1833	0	0	0.1833	1	1.0610	0.02032
3	1	0.1833	0	0	0.1833	1	1.0610	0.02032
4	1	0.1833	0	0	0.1833	1	1.0610	0.02032
5	1	0	0	0.4167	0.4167	1	0.8879	–0.04559
6	1	0.1833	0	0	0.1833	1	1.0610	0.02032
7	1	0.1833	0	0	0.1833	1	1.0610	0.02032
8	1	0.1833	0	0	0.1833	1	1.0610	0.02032
9	1	0.1833	0	0	0.1833	1	1.0610	0.02032
10	1	0	0.4	0	0.4	1	0.9003	–0.02499
11	1	0.1833	0	0	0.1833	1	1.0610	0.02032
12	0	0.0917	0.2	0	0.2917	–0.3616	–0.38092	0.05122
13	1	0	0.4	0	0.4	1	0.9003	–0.02499
14	1	0	0	0.4167	0.4167	1	0.8879	–0.04559
15	0	0.0917	0	0.2083	0.3	–0.3616	–0.3871	–0.01263
	$p_a$				$p_e$	${\hat{\kappa }}_G$	${\hat{\kappa }}_G$
Mean	0.8				0.266	0.728	0.728	$v(\overline{d})$
Variance of mean difference $\mathrm{var}(d_i)/n$								0.009090

^a$d_i={\kappa }_{G|i}^{(1,3)}-{\kappa }_{G|i}^{(1,2)}$, where ${\kappa }_{G|i}^{(1,2)}$ is obtained from Table B2.