Abstract
Observations and ratings of classroom teaching and interactions collected over time are susceptible to trends in both the quality of instruction and rater behavior. These trends have potential implications for inferences about teaching and for study design. We use scores on the Classroom Assessment Scoring System–Secondary (CLASS-S) protocol from 458 middle school teachers over a 2-year period to study changes over time in (a) the average quality of teaching for the population of teachers, (b) the average severity of the population of raters, and (c) the severity of individual raters. To obtain these estimates and assess them in the context of other factors that contribute to the variability in scores, we develop an augmented G study model that is broadly applicable for modeling sources of variability in classroom observation ratings data collected over time. In our data, we found that trends in teaching quality were small. Rater drift was very large during raters’ initial days of observation and persisted throughout nearly 2 years of scoring. Raters did not converge to a common level of severity; using our model we estimate that variability among raters actually increases over the course of the study. Variance decompositions based on the model find that trends are a modest source of variance relative to overall rater effects, rater errors on specific lessons, and residual error. The discussion provides possible explanations for trends and rater divergence as well as implications for designs collecting ratings over time.
Keywords: rater drift, scoring trend, classroom assessment, generalizability theory, B-splines, Classroom Assessment Scoring System–Secondary (CLASS-S), teaching quality
Classroom observations, in which observers rate multiple dimensions of teaching according to established protocols (either live in the classroom or from video recordings of lessons), increasingly are being used for both research and teacher evaluations. However, changes in rater severity over time, and changes in teaching quality over the course of the school year, can lead to time trends in the ratings. Such trends may create challenges for designing measurement systems that avoid bias and excess variance in inferences from ratings of classroom instruction. Given the growing use of these ratings for research and policy purposes, understanding the nature and magnitude of time trends in ratings is critical both for designing measurement systems with desirable properties and for learning about the nature of teaching.
Rater reliability appears to be a persistent problem with ratings of instruction from classroom observations. Across multiple studies, variance among raters observing the same lesson accounted for 25% to as much as 70% of the variance in scores, depending on the study and the protocol (Bill and Melinda Gates Foundation [BMGF], 2012; Casabianca et al., 2013; Hill, Charalambous, & Kraft, 2012). There are multiple sources for discrepancies among raters. These include variation in severity, or the extent to which a rater is strict or lenient in his or her scoring (Kingsbury, 1922); halo effects, which refer to the tendency to apply common scores to multiple measures of performance or behavior based on positive or negative notions about the individual being assessed (Thorndike, 1920); central tendencies, or a rater’s tendency to assign scores in the middle of the score range versus using the full scale when appropriate (Saal, Downey, & Lahey, 1980); and assimilation, a rater’s tendency to assign scores that are influenced by scores assigned to units scored previously (Attali, 2011).
Rater error can also arise because raters’ severity levels change over time (rater severity drift). The literature on scoring written responses including essays, constructed responses, and teacher logs, has revealed such changes in individual raters’ severity levels (Braun, 1988; Congdon & McQueen, 2000; Englehard & Myford, 2003; Harik et al., 2009; Hoskens & Wilson, 2001; McQueen & Congdon, 1997; Myford & Wolfe, 2009; Rowan, Harrison, & Hayes, 2004; Wilson & Case, 2000). Such rater drift may result from a variety of factors, including experience, additional training or calibration, or fatigue that develops during the course of the study. Even when raters receive ongoing training with calibration sessions and frequent feedback, rating severity still can change over time (Congdon & McQueen, 2000; McKinley & Boulet, 2004). While these studies have documented the existence of rater drift, they have not quantified how much this drift contributes to error variance in scores.
Above and beyond rater trends, teaching quality might change during the course of the school year as a result of teachers’ and their students’ growing familiarity with each other, changes in the material being covered, and other external influences such as testing or holidays (Meyer, Cash, & Mashburn, 2012). Identifying such trends is a first step to increasing our understanding of the nature of teaching and developing methods to improve it. Like changes in rater severity, systematic changes in teaching quality over the course of the school year also would have implications for the design of effective measurement systems.
Research Questions
The magnitudes and directions of trends in teaching quality and rater severity remain important questions. Only one study has explored these issues. Casabianca et al. (2013) identified time trends in scores from 82 algebra classrooms observed by five raters using the Classroom Assessment Scoring System–Secondary (CLASS-S; Pianta, Hamre, Haynes, Mintz, & LaParo, 2007). They did not account for other sources of variance when modeling the trends or estimate how much trends contributed to various sources of variability. Given the small size of this study, we aimed to replicate and expand the work of Casabianca et al. (2013) by studying how classroom observation scores vary as a function of both the day on which lessons occurred and the day on which scoring of video recordings of those lessons occurred using data from the Understanding Teaching Quality (UTQ; http://www.utqstudy.org/) project. The UTQ data include scores on lessons taught by 458 middle school math and English language arts (ELA) teachers rated by 12 different observers using four different observation protocols.
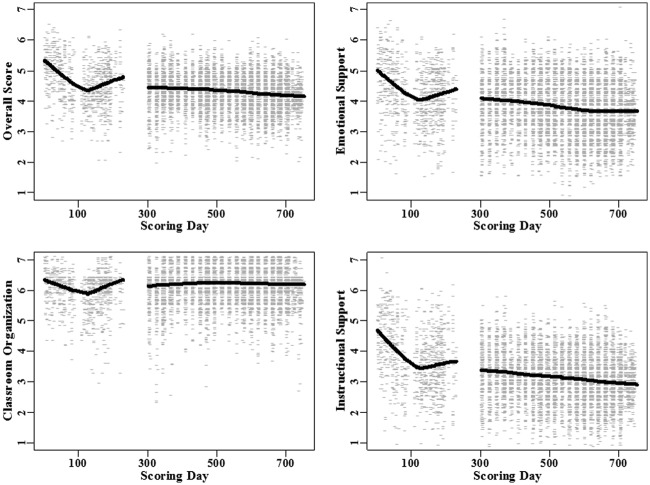
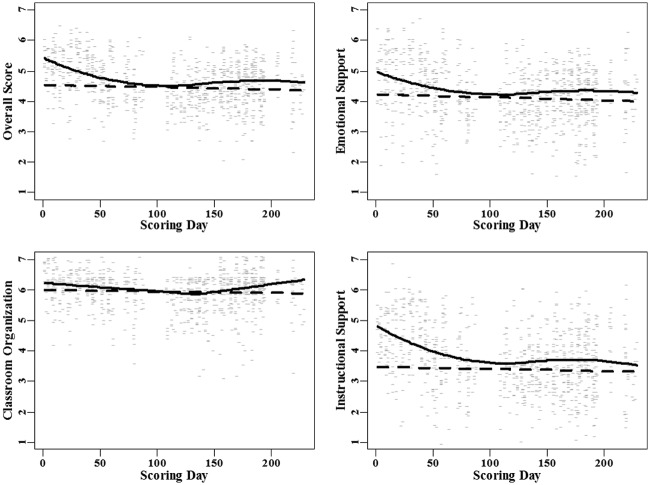
Using UTQ score data from live observations and video recordings of lessons, we found evidence that scores varied as a function of both the day that the observed lesson occurred and the day it was scored. Figure 1 provides an example. It plots the scores on the CLASS-S by the day of the study on which the scoring occurred. From Day 1 to 229, raters conducted live observations. From Day 301 to 752, raters scored video recordings of lessons. The solid lines are smooths of the data. The figure shows that scores drop off precipitously in the early days of live observation and then recover after about the middle of the school year. Scores from video recordings of these same lessons and ones from an additional school year then continue to drift for the duration of video scoring that occurred after raters had completed live observations. Because live observation-based scoring occurred on the same date the lesson occurred, we cannot tell from the figure if the marked trend in live scores is due to drift in rater severity or changes in teaching quality. Also, although the trends are notable and appear large enough to introduce systematic errors into inferences, the figure also demonstrates considerable variability in scores around the trend lines. Identifying the sources of that variability will be important for assessing the reliability of observations from the protocol and for calibrating the contributions of drift in rater severity and teaching quality to the measurement error of scores. We provide additional discussion of the figure and the CLASS-S data in later sections.
Figure 1.
Example of trends in classroom observation scores from the UTQ study. Each panel plots scores from the Classroom Assessment Scoring System–Secondary (CLASS-S) protocol against the day that the scoring occurred. Solid black lines are smooths of the scoring data. CLASS-S measures three domains of classroom interactions and there is one panel for each domain and for the overall score, the average score across dimensions. In the top panel from left to right are plots for the overall score and Emotional Support and in the bottom panel are plots for Classroom Organization and Instructional Support. Scores from day 1 to 229 are from live observations made in the classroom and scores from day 301 to 752 are from video recordings of lessons.
To accomplish the goals of separating the different trends and other sources of variance, and gauging their relative magnitudes, we developed a novel model that we call an “augmented Generalizability Study (G study) model” because it extends the standard G study model (Brennan, 2001) by modeling variation in scores over time via smooth functions of time in addition to modeling the contributions of other facets of the scores (e.g., raters, teachers, classrooms, etc.) to the variability in scores. Although the model was motivated by the data collection design of the UTQ study, features of that design are commonplace in the collection of classroom observation ratings data over time, and so our model is broadly applicable for modeling sources of variability in such data.
We apply our augmented G study model to scores on the CLASS-S from the UTQ study to answer the following research questions:
What are the characteristics of both rater and teaching quality trends in the UTQ study?
How much do raters differ in their severity, and do any such differences change over time?
How much do time trends contribute to overall variability in ratings?
In the next sections, we provide details on the UTQ study design and the CLASS-S observation data. We then develop the augmented G study models and a model-based approach for variance decompositions that can be used to calibrate the contribution of trends in scores to variability in scores. We then present details of our application of these models to the UTQ data and our findings about the research questions. Finally, we discuss implications for classroom observation and scoring in research and practice, as well as ways to mitigate error from rater drift and instructional trends.
The Understanding Teaching Quality Study and CLASS-S Data
Sample
The UTQ study took place in middle schools in three large school systems from the same metropolitan area in southeastern United States. It includes 231 mathematics and 227 ELA teachers of sixth, seventh, or eighth graders. For each teacher, two lessons were studied from each of two classrooms (or sections) of students for a total of 916 classrooms and 1,828 lessons scored.1 Thirty-four percent of the classrooms were Grade 6, 29% were Grade 7, 36% were Grade 8, and the rest were mixed grade. The teacher sample was 83% female, 56% non-Hispanic White, 36% Black, and 8% Hispanic and other race, and teachers in the sample averaged 9.6 years of experience in the district. On average across classrooms, the percentage of students in a classroom who were eligible for free or reduced-price meals was 47%, and the percentages who were non-Hispanic Black, non-Hispanic White, and Hispanic were 44%, 34%, and 11%, respectively.
Measures
The UTQ study included ratings on four protocols: CLASS-S; Framework for Teaching (FFT; Danielson, 2007); Protocol for Language Arts Teaching Observations (PLATO; Grossman et al., 2010); and Mathematical Quality of Instruction (MQI; Hill et al., 2008). As noted previously, our investigation of time trends focuses on CLASS-S but time trends exist in the scores for the other protocols. Those results are available online on http://ows.edb.utexas.edu/site/jodicasa/supplemental-material. The CLASS-S assesses teacher and student interactions in secondary classrooms to produce scores describing levels of Student Engagement and 10 additional dimensions of teaching, each related to one of three domains of classroom interactions: Emotional Support, Classroom Organization or Instructional Support (Table 1). Raters assign a score between 1 and 7 on each dimension according to behavioral indicators of the protocol’s specifications. Domain scores are the average of the associated dimension scores.
Table 1.
Classroom Assessment Scoring System–Secondary Domains and Dimensions.
| Domains | Dimensions |
|---|---|
| Emotional support | • Teacher sensitivity |
| • Regard for adolescent perspectives | |
| • Positive climate | |
| Classroom organization | • Negative climate |
| • Behavior management | |
| • Productivity | |
| Instructional support | • Instructional learning formats |
| • Content understanding | |
| • Analysis and problem solving | |
| • Quality of feedback | |
| Student engagement | • Student engagement |
Rater Demographics, Training, and Calibration
Twelve teachers (6 math; 6 ELA)2 served as raters for the UTQ study. During the 2-year scoring period, the raters’ primary responsibility was observing and rating for the UTQ study. Raters were responsible for rating classrooms on three protocols, CLASS-S, FFT, and a subject-specific protocol (PLATO or MQI, depending on their specialty). Only one rater was male and half of them had a master’s degree or higher.
Raters received multiple days of training on each rubric and proved able to score in agreement with ratings assigned by project staff, or master coders, before starting classroom or video observations.3 Raters also conducted calibration exercises with project staff every third week for the entire study period until all scoring was complete.4 In these exercises, raters scored training videos and compared their results with master codes. Project staff then reviewed the scores with raters and provided additional training when project observers disagreed with the master codes. Feedback provided to raters following the calibration exercises was given via conference call or more often by e-mail, and sometimes, during the later months of the study, no feedback was provided. Raters did not need to maintain a specified level of agreement with the master codes to remain in the study. Across all calibration exercises and dimensions of the CLASS-S rubric, raters agreed with the master codes on 34% of their scores and were within one point of the master codes on 82% of scores. Across the raters, the percentages of scores within one point of the master codes ranged from 76% to 87%.
Data Collection
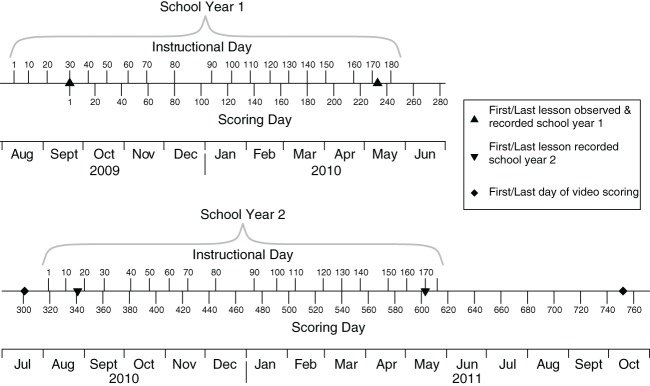
The UTQ data were collected and scored over approximately 2 years, with approximately half of the teachers participating in each year. Figure 2 illustrates the timeline for the UTQ study, which included two full school years. The bottom row of the timeline gives the calendar months and years for the span of the study. Data collection began near the start of the 2009-2010 school year. For the duration of that school year, CLASS-S scores were obtained from live observations of lessons sampled from all Year 1 study teachers. These lessons were also video recorded. For each teacher, two lessons were observed live and the additional two lessons were video recorded without receiving a live observation score.
Figure 2.
Timeline of Understanding Teaching Quality (UTQ) study including relationship between instructional and scoring days. This figure illustrates the 2-year period over which the UTQ study took place. Instructional days were the number of school days between the day the lesson occurred and the first day of school that year. Scoring days were the number of calendar days since the first day of scoring for the study.
During the summer after the first school year, scoring of video recordings of lessons began. This persisted for approximately one more calendar year, during which additional videos of lessons from the 2010-2011 school year were collected and scored for the separate sample of teachers who participated that year (the Year 2 teachers). Project staff recorded four lessons for each of the Year 2 teachers also. The UTQ study had sufficient resources to support double-scoring of 20% of the videos from both years by two separate raters. Rater assignments to live observations and videos were balanced so that all raters scored roughly equal numbers of live observations and scored similar numbers of videos. For video scoring, rater assignments were designed so that typically, four different raters scored the four videos from each teacher. For live observations, each lesson was divided into segments of 22 minutes. Raters observed instruction for about 15 minutes and took detailed notes about teacher and student behaviors and interaction patterns. They used the remaining seven minutes to assign scores for each dimension based on the behavioral anchors provided in the CLASS-S manual. When scoring videos, raters also observed the classroom in 15-minute segments. At the end of each 15 minutes of observation, they paused the video and assigned scores for each dimension before moving on to the next segment. Of the 8,283 segment-level records in the UTQ data, our analysis excludes 31 records because they were incomplete or observation occurred across multiple days.
Instructional Day and Scoring Day
Given our data collection design, there are two dates associated with each score: the day the lesson occurred and the day the scoring occurred; both appear in Figure 2. We measure the day the lesson occurred by the “instructional day.” For both School Year 1 and School Year 2, the instructional day for a lesson is the number of school days between the day the lesson occurred and the first day of school that year. This way, instructional days were on the same scale for both years. For instance, a lesson that occurred on the 50th school day of School Year 1 or School Year 2 would have an instructional day of 50. Instructional day ranged from 30 to 172 (median = 110.5) for School Year 1 and 17 to 170 (median = 104) for School Year 2.
We measure the day the scoring occurred by the “scoring day,” which equals the number of calendar days since the first day of scoring for the study. Regardless of whether the lesson occurred in School Year 1 or School Year 2, all scoring days are on a single continuum from 1, for scores given on the first day of live observation in School Year 1, to 752, for scores given on the day when the last video was scored in the summer after School Year 2. Scoring days ranged from 1 to 229 (median = 135) for the live observations and from 301 to 752 (median = 575) for video ratings.
We designed our assignment of video recorded lessons to calendar dates on which they were to be scored so that instructional day and scoring day were as unrelated as possible. The scoring days of Year 1 lessons were effectively uniformly distributed over the entire window of video scoring. The Year 2 lessons could not have this degree of randomness because they were being collected in real time during the window. However, the assignments were such that the scoring days of Year 2 videos were effectively uniformly distributed on the interval between the date the lesson actually took place, and the end of video scoring.
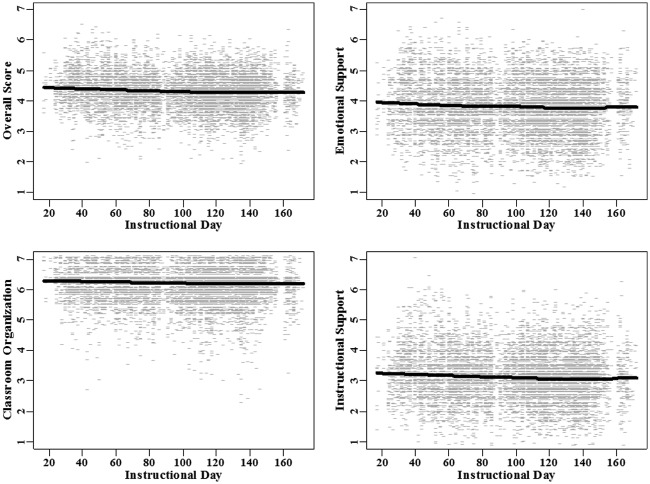
As described previously, Figure 1 plots the scores by scoring day. In contrast, Figure 3 plots them by instructional day. The two figures clearly demonstrate the difference in the two ways we measure time and the distinct differences in the evolution of scores on these two scales. As we describe above, scoring day spans from 1 to 752, and when scores are sorted by scoring day, they show distinctly different trends during the live and video scoring intervals, with large changes during live scoring and continuing drift during video scoring. The instructional days on which lessons occurred span from just 1 to 172, and when video scores are organized by instructional day, scores show a gradual steady decline across the school year. A plot of live scores by instructional day would be essentially identical to the plot of live scores by scoring day since live observations occurred simultaneously with the lesson.
Figure 3.
Plots of raw video scores over instructional day with smoothed trends. In the top panel from left to right are plots for the overall score and Emotional Support and in the bottom panel are plots for Classroom Organization and Instructional Support.
Separating Changes in Instruction From Rater Drift
Because instructional day and scoring day as we have defined them are nearly equivalent during live scoring, with live scores alone we cannot separately estimate the two trends. However, during the video scoring, instructional day is as unrelated as possible to scoring day, so that we can cleanly separate the two types of trends by including both in our model. If we can assume that instructional trends are invariant to whether scoring occurred live or by video, then the instructional trends estimated from video scores can be removed from the live scores and any remaining trends in the live scores can be interpreted as rater drift.
To estimate separate trends for quality of instruction and rater drift during the live and video scoring, we used a sequential strategy for analyzing the data. We began by modeling only the video scores where rater and instructional trends can be separated without the untestable invariance assumption. Also, to improve the precision of the parameter estimates by pooling data across years, our models assumed that the trends in teaching quality were the same function of instructional day for video scores from School Year 1 or 2. We used the models fit to the video data to test whether both types of trends are present and to estimate their magnitudes in terms of contributions to variance in the video scores. We then applied the models to the combined live and video data using the common instructional trend assumption to estimate the degree of rater drift over the entire course of the study. We repeated all our analyses separately for scores from each of the three domains, as well as an overall score that averages scores across the 10 dimensions of the domains and Student Engagement.
We now provide details on the model we used to first fit both trends in the video data, and then to the full data to estimate rater drift in the live scores.
Augmented G Study Models for Time Trends in Classroom Observations
Each score from an observation in the UTQ data (and other studies) depends on the quality of teaching that occurred during the lesson and the errors the rater makes when assessing it. Our goal is to separate these sources of variance from the trends that also may contribute to error variance in scores. To separate the trends from other sources we need a model with flexible specifications for trends in instruction and rater drift, which also models other sources of variability in scores. To make accurate inferences about trends we must account for the dependencies in scores created by other sources of variability (Raudenbush & Bryk, 2002).
G studies (Brennan, 2001) are the standard approach for conducting such decompositions of variance in scores. Hence, embedding the study of trends in the context of G studies will be useful for understanding them as sources of error in inferences about teachers’ classroom interactions. However, drift typically is not part of the basic G study model, so we now extend the traditional G study model. In other traditions, our model would be labeled a cross-classified hierarchical linear or mixed model. The specific terms we include in the augmented G study model are driven by the design of the UTQ data collection, but the basic framework would be applicable to similar designs that are commonly used to collect classroom observation data.
A basic G study model (Brennan, 2001) for score Xiclsr designating a rating assigned according to a rubric based on observation of teacher (i), in a classroom (c) on a lesson (l), for a segment (several minutes) of the lesson (s) by a rater (r) is
where θi is the teacher effect, ηic is the classroom within teacher effect, γicl is the lesson within classroom (within teacher) effect, ωicls is the segment-within-lesson (within classroom, within teacher) effect, βr is the rater effect, δir is the rater-by-teacher effect, ϕiclr is the rater-by-lesson effect, and εiclsr is residual error. The effects are modeled as random and independent of each other and across teachers, classes, lessons, segments, and raters.
Scheduling idiosyncrasies as well as the double scoring of some videos led to a sufficient number of instances of the same rater scoring the same teacher on two different lessons so that the rater-by-teacher variance component is well identified. There were only a very small number of instances where the same rater scored two different lessons from the same classroom, making the rater-by-classroom variance component only weakly identified and we therefore opted to absorb that term into the rater-by-lesson term, possibly inflating that term. This does not prevent us from evaluating the size of drift relative to other sources of variance, but it could limit the utility of our results for designing some studies.
Given the structure of the UTQ data with lessons occurring on the instructional day and ratings occurring on scoring day, the augmented G study models incorporate a teaching quality trend as a function of instructional day and rater scoring trends as functions of scoring day.
We use B-splines to parameterize the trends. A B-spline is a piecewise polynomial function of degree k. Knot points separate the intervals on which each polynomial is defined, or in other words, they are the points at which two polynomials join together, and the function is constrained to be continuous at the knot points (Hastie, Tibshirani, & Friedman, 2009, chap. 5 appendix). B-splines are expressed as a linear combination of basis functions, , where denotes the vector of known basis functions evaluated at a point t, and θ is an unknown vector of parameters. The basis functions depend on the degree of the polynomial and the location of the knot points. A variety of trends may be specified with varying levels of k (e.g., k = 3 is a cubic) and differing numbers of knots. For example, a model using a cubic polynomial with one knot will use two cubic functions, joined by a knot, to represent the trend. Our motivation for using B-splines to model trends is that we do not have strong prior beliefs about what trends should look like and B-splines are flexible enough to capture virtually any shape, including simple linear trends. We can thus investigate whether linear or nonlinear trends are more appropriate for the data all within the B-spline parameterization.
We augment Model 1 to include B-splines for trends as follows. Let ticl equal the instructional day on which lesson l occurred for class c of teacher i and let τiclr equal the scoring day on which rater r scored this lesson. We modeled the common trend in teaching quality for all the teachers as , where is a vector of piecewise-polynomial B-spline basis functions and λ is an unknown vector of parameters. The common trend in rater scoring is represented by , where is also a vector of piecewise-polynomial B-spline basis functions, possibly of a different degree and with different knot points than those used for the teaching quality trend, and µ is an unknown vector of parameters. Adding these terms to Model 1 yields
To simplify model notation, we use the same symbols to denote the facets that appear in both Models 1 and 2, even though the addition of terms to the model potentially changes their definitions. The model allows for a common trend across time in rater severity and variation in severity among raters through the rater main effects, βr, but these deviations from the common trend are assumed to be constant across time in this model.
To capture rater drift that might differ across raters, Model 3 augments Model 2 by adding rater-specific trends, , where is another vector of piecewise-polynomial B-spline basis functions, possibly of a different degree, and with different knot points than those used for the common rater trend, and βr is a random, rater-specific vector of parameters. The rater-specific trend parameters are independent of all the other effects and across raters.
Depending on the complexity of , the model allows for substantial flexibility in the variation across raters in their trends. If is a constant, then raters differ from one another only through a rater-specific but constant deviation from the overall rater trend, and Model 3 is equivalent to Model 2. If contains both a constant and a linear term, the model allows each rater to have his or her own linear deviation from the overall trend which could capture features of the rating process such as raters getting more or less similar to one another over time. More complex allows for more complex rater-specific deviations from the overall trend. The model could include trends in teaching quality for individual teachers, , with random coefficient vectors, θi. As noted below, we tested such models but they did not fit our data well because the small numbers of observations for each teacher. We suspect this will be common in practice because studies typically observe teachers on a small number of occasions.
Model-Based Variance Decomposition for Augmented G Study Models
Among scores from a sample of lessons from a sample of teachers and their classrooms with each lesson scored by a rater on a randomly selected day, var(Xiclsr) equals the sum of the variances of the terms on the right-hand side of Equation 3 (Model 3). The variance components from the random effects determine the variance of the facets other than the trends (i.e., θi, ηic, γicl, ωicls, δir, φiclr, and εiclsr). Because the teaching quality trend, , has fixed coefficients, the variance in it depends only on the variability in when the observed lessons occurred. Similarly, the variability in the common rater trend, , depends only on the variability in when the lessons were scored. That is, and
The variance of the rater-specific trends depends on both the variability in when the lessons were scored and the variability of the coefficients across raters. Our derivations for the variance yielded
where tr(V) denotes the trace, the sum of the diagonal elements, of the matrix V (Searle, 1971) and . Details are in the online supplemental material.5 The variance in rater-specific trends decomposes into a rater-specific term, , which generalizes the notion of variability in rater severity to cases where it varies over time, and the average of the variability in the timing of observations among raters.
We let , , , , , , , equal the variances of the random effects and error term from Model 3 and V1, V2, V3, and Vβ equal the variance–covariance matrices for , , , and Then
In addition to this overall variance decomposition, Model 3 can be used to provide a traditional G study variance decomposition at each possible scoring time. For lessons occurring on all scored on scoring day
since and are common across all the scores. The variance due to rater-specific trends varies with the scoring day and may be decreasing, increasing, or staying roughly constant over time.
Results From Fitting the Augmented G Study Model to the UTQ Data
As noted above when fitting the augmented G study model to the UTQ data, we first fit the model to the video data to separately estimate trends for instructional day and scoring day. We then fit the model to the combined live and video score data assuming invariance in the instructional day trends and using the functional form of the trends selected with the video data. We used the lmer() function in R for linear mixed models to fit all models (Bates, Maechler, & Bolker, 2013). Because our general specification of the augmented G study model includes unspecified splines for the functional form of the trends, fitting the model required both selecting a form for the trend and estimating the model parameters. We first describe our methods for selecting the functional form for trends in the video and live data and then describe our results.
Selection of the Functional Form of the Trends
Video Data
Our general specification of the augmented G study model includes unspecified splines for the functional form of the trends. We used the UTQ data to select the functional form for the trends by fitting a sequence of models that are variants of Models 1 to 3 and used both the Bayesian information criterion (BIC; Schwarz, 1978) and likelihood ratio tests to choose among them. The goals were to test whether both instructional and rating trends were evident in the data, whether those trends appeared to be linear or nonlinear, and whether there was variability among raters in their trends.
After preliminary analyses and experimentation, we considered seven piecewise polynomials for the spline bases for each of , and : a constant (no trend); linear, 0 knots; linear, 1 knot; quadratic, 1 knot; cubic, 0 knots; cubic, 1 knot; and cubic, 2 knots. Importantly, these bases generate trends with complexities ranging from no trends to simple linear to potentially very nonlinear. Therefore our model comparisons address not only whether trends are evident in the data, but also whether those trends demonstrate notable nonlinearities.
We explored 115 different models for the video scoring data that include various combinations of these bases for , and The first 49 models tested all possible combinations of and with set equal to a constant so that there were no random rater-specific trends. The first model, Model 1, set all the bases equal to a constant so that there were no trends. The remaining models in this group are all versions of Model 2. Six models kept equal to a constant and tried the six trend specifications for The next six models kept equal to a constant and tried the six trend specifications for The last 36 of the 49 models tested the remaining combinations of trends for both and This collection of models allows us to test whether the data demonstrate average trends in both teaching quality and rater severity, and if so, whether each of those trends is linear or nonlinear.
We then tested variants of Model 3. First we set equal to a linear, 0 knot spline (a simple linear trend, ) and tested the 36 combinations of trends for both and The final set of 36 models again tested all the combinations of trends for both and but for each of these models we constrained . That is, in the last set of models, the functional form of the rater-specific and the common rater trends were the same but each had separate coefficient values. Some of the models in these two groups of 36 overlap, so in total, we fit 66 variants of Model 3.
The 66 variants of Model 3 combined with the 49 variants of Model 2 and Model 1, give 115 total models that we considered for each outcome. For each outcome we selected the model that minimized the BIC among these 115 variations of the augmented G study models. Smaller values of BIC indicate models that better fit the data.
We also explored models that included teacher-specific teaching quality trends, . However, our analyses found models with these additional trends fit the data less well than Model 2 or 3, so we do not report the results of these models.
Live Observations
When modeling the combined video and live scoring data to test for rater drift in the live observation scores, we retained the chosen models for instructional trends and rater trends for the video scoring selected with the video data and then tested a series of 19 models for rater trends in the live scores. The first seven models fit the seven alternative bases for scoring day for the live scores with rater-specific trends set to constants (i.e., no rater-specific trends). The next six models tested the six specifications of trends for average rater trend in live scores with linear random rater-specific trends such that . The final six models replaced the linear rater-specific trends with random trends that had the same form as the average trend, or Again, for each outcome we selected the model with the smallest BIC.
Results From Fitted Models for Trends in Video Scores
Table 2 presents the degree of polynomial and number of knots of the spline basis from the best-fitting models for the domain and overall scores in the video scoring data. It also provides the BIC for Model 1 (the basic G study model), three variations of Model 2 (instructional trend only, rater trend only, and both trends and ), and the best-fitting Model 3 (rater-specific trends ), and compares the best-fitting version of Model 3 to Model 1 with likelihood ratio tests. In all cases, we find that both instructional and rater trends are present. For each outcome, a model with trends for both instructional day and scoring day fit better (had smaller BIC) than models with no trends or models with trends just for either instructional day or scoring day. These trends were statistically significant (i.e., the likelihood ratio tests comparing the selected models to Model 1 without trends had p values less than .05). Also, in all cases, the best-fitting parameterization for the instructional trend was linear with 0 knots.
Table 2.
Measures of Fit From the Best-Fitting Models Selected by the Sequential Modeling Procedure, by Outcome.
| Outcome | Bayesian information criterion (BIC) |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best-fitting parameterizations for Model 3 |
Model 2 |
Log likelihood |
||||||||||
| p2(τ) | p3(τ) | Model 1 | p1(t) only | p2(τ) only | p1(t) and p2(τ) | Model 3 | Model 1 | Model 3 | χ2 | df | p | |
| Overall | Linear, 0 knots | Linear, 0 knots | 6,897 | 6,874 | 6,845 | 6,828 | 6,749 | −3,408 | −3,317 | 184 | 4 | <.0001 |
| Emotional Support | Linear, 1 knot | Linear, 1 knot | 12,389 | 12,369 | 12,268 | 12,257 | 12,179 | −6,154 | −6,014 | 282 | 8 | <.0001 |
| Classroom Organization | Cubic, 0 knots | Linear, 0 knots | 6,604 | 6,597 | 6,584 | 6,578 | 6,492 | −3,262 | −3,179 | 165 | 6 | <.0001 |
| Instructional Support | Linear, 0 knots | Linear, 0 knots | 12,379 | 12,368 | 12,273 | 12,268 | 12,191 | −6,149 | −6,038 | 223 | 4 | <.0001 |
Note. Sequential modeling procedure using video data tested fit for Model 1 with no trends, Model 2 with a common instructional trend only, p1(t), Model 2 with a common rater trend only, p2(τ), Model 2 with both common trends, p1(t) and p2(τ), as well as Model 3 with rater-specific trends, p3(τ) in addition to both common trends. The table provides BIC values for Model 1 and the best-fitting Model 3, in addition to BICs for the best-fitting models for the three versions of Model 2 (p1(t) only, p2(τ) only, and p1(t) and p2(τ)). The table also provides likelihood ratio test results comparing Model 1 and the best-fitting Model 3.
Consistent with Figure 3, the linear trends for teaching quality were relatively flat and negative for all outcomes. Over the entire range of observations, teaching quality as measured by the overall score dropped by 0.19 points or about 35% of a standard deviation unit in scores. The trend was steepest for Emotional Support. Over the observation period, scores on this domain dropped by 0.25 points (29% of a standard deviation unit). The trend was flattest for Classroom Organization, on which scores dropped by 0.13 points (24% of a standard deviation unit). The drop in scores was 0.19 points for Instructional Support (24% of a standard deviation unit).
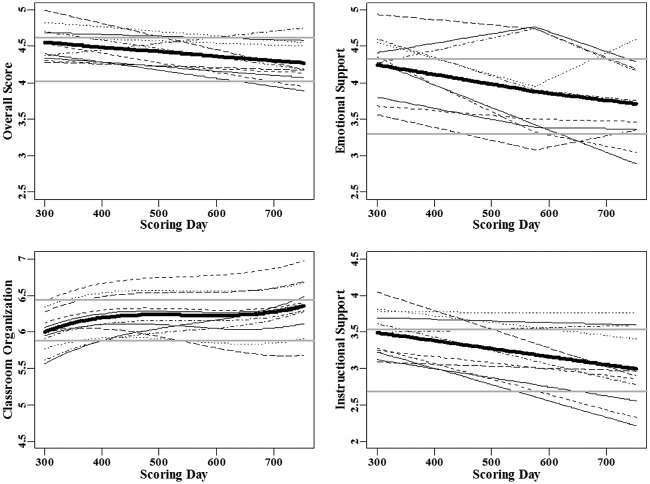
Figure 4 presents the best-fitting rater trends to video scores for all four outcomes. In each of the plots in the figure, the thick black line depicts the common rater trend in scores. The thin lines are the model estimates of the individual rater-specific trends; each rater is distinguished by a different type of line (dashed, etc.). The thin gray horizontal lines indicate the 25th and 75th percentiles of scores. To improve the visibility of the trend lines, the y-axes have a score range of 2.5, but the location of the range is shifted up or down for each outcome. The model separated the teaching quality trend from the rater trend, so that the trend lines represent changes in rater severity only.
Figure 4.
Time trend plots for Classroom Assessment Scoring System–Secondary (CLASS-S) overall and domain scores. In the top panel from left to right are plots for the overall score and Emotional Support and in the bottom panel are plots for Classroom Organization and Instructional Support.
For each outcome, models that included random, rater-specific trends (Model 3) were preferred by BIC over any model with only a common trend for scoring day shared by all raters (Model 2). As shown in the figure, for Instructional Support and the overall score, the common rater trends were linear and decreasing. For Emotional Support the best fit is a piecewise linear trend with one knot at scoring day 575, but the two pieces almost share a common slope. Hence, on average, for each of these outcomes, raters steadily decreased the scores they assigned throughout video scoring. The day-to-day changes were not large but across the entire scoring interval the changes were large, with average scores falling by 0.28, 0.53, and 0.49 points for overall, Emotional Support, and Instructional Support scores, respectively, or from about the 75th percentile of the scores to nearly the 25th percentile for each outcome.
For Classroom Organization, the best-fitting model for the common rater trend was nonlinear (cubic polynomial with 0 knots) with the raters on average increasing their scores for the first 150 or so days, leveling off, and then increasing again for about the last 100 days. Again, the day-to-day change in the average scores assigned by raters is small, but over the 352 days of scoring, these changes reach across much of the interquartile range in scores.
Variation in the individual rater trends around the common trend can also be seen in Figure 4. For Classroom Organization, Instructional Support and the overall score the best-fitting model includes linear, random, rater-specific trends, or . Deviations from the common trends are large and result in large notable variation in rater-specific average scores on every day of scoring. Raters are not converging to the common trends. For the selected model for Emotional Support, the deviations of each rater’s average scores from the common trend were piecewise functions of time with one knot.6 This results in pronounced variation in scores around the common trend. About half of the raters have trends that are similar in form to the common trend but their overall levels of severity differ. However, because the rater-specific trends are linear with one knot, some raters’ trends start with increasing scores over time and then change to decreasing scores after the knot point. Some raters exhibit the opposite trend; their scores start out decreasing and then change to increasing. Again raters are not converging to a common average score.
Changes in Rater Variability Over Study Period
Consistent with the variation in rater-specific trends that is observable in Figure 4, the variance among raters, increased as a function of the scoring day, τ, during video scoring. For all four outcomes, variability increases over the scoring period. The greatest increase is for Instructional Support; the standard deviation in the variance among raters increases monotonically from a little over 0.3 to 0.45. Over the scoring period, the standard deviation among raters’ scores on the Emotional Support domain increased by almost 0.20 and then, at around day 575, decreased but to a level still higher than its starting point.
Share of Error Variance
Using the model-based variance decomposition described above, we estimated the contribution of different sources to the variability in the overall and the domain scores. Table 3 provides the results. The first row of this table gives the amount of variance attributable to the teacher, which is typically the signal of interest in classroom observation scores. The overall score had the largest amount, 17%, attributable to teachers; Emotional Support and Classroom Organization had the second and third highest, and Instructional Support the lowest.
Table 3.
Variance Decomposition Including Instructional and Rater Trends as a Source.
| Variance source | Overall score | Emotional support | Classroom organization | Instructional support |
|---|---|---|---|---|
| Teacher | 17.4 | 12.3 | 11.8 | 9.7 |
| Classroom | 1.4 | 0.4 | 1.2 | 1.4 |
| Lesson | 10.6 | 6.9 | 6.9 | 11.7 |
| Rater | 13.3 | 31.2 | 26.6 | 22.8 |
| Rater × Lesson | 18.1 | 12.3 | 19.7 | 12.6 |
| Rater × Teacher | 6.0 | 5.9 | 0.0 | 4.5 |
| Segment | 10.6 | 5.3 | 7.3 | 11.1 |
| Residual | 17.5 | 18.7 | 22.6 | 20.7 |
| Instructional trend | 0.7 | 0.5 | 0.3 | 0.3 |
| Common Rater Trend | 1.9 | 2.9 | 1.2 | 2.9 |
| Rater-specific trend | 2.5 | 3.6 | 2.5 | 2.3 |
Note. Variance decomposition results are based on video data only.
Variance attributable to a trend in the quality of teaching was minimal; it ranged from 0.3% to 0.7% for all scores. Lesson-to-lesson variability contributed between 7% and 12% to the total variance. The rater trend effects were a larger source of variance for the domains related to instruction (versus classroom organization). Three percent of the variance was attributable to the common rater trend for the Instructional Support and Emotional Support domains. Only 2% and 1% of the variance in the overall score and the Classroom Organization scores, respectively, were attributable to the common rater trend; scores on these domains were relatively stable over time compared with variability from other sources. The variability due to rater drift is driven in part by the long duration of scoring for this study. On a day-to-day basis, rater drift during the video scoring was similar to the change in teaching quality but because scoring stretched over 15 months it had greater share of the variance. If raters had completed their scoring in fewer days, rater drift would have contributed less to overall variance. For example, if raters had completed scoring in the first 180 days, common rater drift would have accounted for less than 1% of the variability in scores. This is comparable to the variability due to changes in teaching quality.
Although there is notable variation in the drift among the raters on the CLASS-S domains, the variance in the rater-specific trend accounts for a relatively small share of the overall variability in scores, 2% to 4%, depending on the outcome. Again, if raters had completed scoring in less time, these trends would contribute even less to the overall variability in scores.
The rater, rater-by-lesson interaction, and residual effects all contributed substantially to the variability in scores. Individually, these sources contributed as much as 31% of the variability in scores. Therefore, while rater drift and time trends in scores are problematic, the persistent difference in raters and the high level of variation due to the rater-by-lesson interaction suggests that above and beyond the time trends, the UTQ raters did not rate consistently when scoring the same lesson and tended to have different levels of severity.
Results From Fitted Models for Trends in Live Scores
Figure 5 presents the best-fitting trends in rater scores (solid line) for all four outcomes for the live observations. For each outcome, we find strong support for drift in the scores. The models with trends in scoring day fit far better than models without trends. The trends were statistically significant for each outcome. For each outcome the selected model was Model 2, which includes random rater effects but no random rater trends. This does not mean there is no variability in the evolution of individual rater scores during the live observations; however, that variation was not substantial enough to warrant the extra model complexity over the selected model, given the limited number of live scores for each rater. A quadratic with one knot trend was the best-fitting parameterization for the rater scoring trend for the overall, Emotional Support and Instructional Support scores, and a linear with one knot trend was the best for Classroom Organization.
Figure 5.
Plots of fitted trends for live data. The solid line is the trend in rater scoring and the dashed line is the trend in instructional day estimated via the video scoring data. In the top panel from left to right are plots for the overall score and Emotional Support and in the bottom panel are plots for Classroom Organization and Instructional Support. The parameterization for the rater scoring trend p2(τ) was quadratic with one knot for the overall, Emotional Support, and Instructional Support scores, and linear with one knot for Classroom Organization scores. The parameterization for the instructional trend p1(t) was linear with zero knots (as determined from the video data modeling procedure).
The selected models reflect the smooth trends in Figure 1. Raters start out giving high scores but rapidly decrease those scores. About midway through the school-year they start to increase scores again. The change in scores is quite large, especially for Instructional Support. Between the start of scoring and the middle of the year, the decrease amounted to 1.3 points on the seven-point scale or 1.5 standard deviation units for the scores. The initial drift is smaller for the other outcomes (0.9, 0.7, and 0.5 for the overall score, Emotional Support, and Classroom Organization, respectively). The figure also includes the fitted trend for instructional days for year 1 (dashed line), based on the video scoring. As noted above, these trends are very flat, especially compared to the very large initial rater drift. The trend in rater scores accounted for 12%, 4%, 5%, and 13% of the variance in the live scores for the overall scores, Emotional Support, Classroom Organization, and Instructional Support, respectively. For Instructional Support, the rater trend accounted for more variance than the teacher or the lesson, but less than rater variance, the remaining rater-by-lesson variance, or the residual variance. The variance explained by trends in teaching quality that occurred on the same days as the live observations explained only from 0.3% to 0.6% of the variance in scores. Hence, in the UTQ live observations, rater drift is a much more substantial source of error than any systematic variation in teaching quality.
Discussion
We found significant rater drift in live observation scores and continued drift across 15 months of video scoring that raters conducted after completing live observations during nearly an entire school year. For all three of the CLASS-S domains, raters initially gave relatively very high scores when they start live observations before rapidly adjusting their scoring downward. The changes were large relative to the scale and the variability in scores. A teacher receiving the average overall score on the first day of scoring would have received a score of about 0.9 points higher than if she had been observed teaching equally well on about the 100th day of scoring. That is a drop from about the 84th percentile of scores to the 43rd. The drift on the individual domain scores was similarly large.
Rater drift continued during the entire interval of video scoring, even after raters had made significant adjustments to their scoring during a school year of live observation. Drift during video scoring was much less pronounced with relatively small day-to-day changes in scores but, because of the long duration, average scores at the end of video scoring were notably lower than at the beginning. Our model was sufficiently flexible to fit trends that leveled off, if indeed scoring had stabilized, but such models did not fit the data well. Instead we chose models with drift throughout the interval. Moreover, the evolution of scoring varied among raters, so that variability among raters actually grew during video scoring. This increase occurred even though raters were substantially divergent at the beginning of video scoring. Raters did not come to a common agreement on scores nor did they each level off at their own stable level of scoring.
Teaching quality also drifted across the school year. For all three CLASS-S domains and the overall score, teaching quality as measured by CLASS-S declined steadily throughout the school year. However, the declines were modest—across the entire year, scores dropped about 0.13 to 0.25 score points depending on the outcome, with the largest decline in Emotional Support and the smallest in Classroom Organization. The date of the observed lesson could affect scores because of variation in teaching but much less so than drift in rater scoring via live observations.
These trends occurred in the context of several other substantial sources variability in scores. For instance, even after accounting for the trends, there was rater-by-lesson variability and substantial rater-to-rater variability in the average scores for all outcomes in both live and video scoring. There was also substantial residual variability which is primarily the result of raters disagreeing on the score given to a segment of a lesson. Correcting drift would not remove all the rater variance.
Our augmented G study model facilitated the assessment of the relative sizes of various sources of error and the contribution of rater drift to them. It also allowed us to distinguish those sources in order to obtain accurate estimates of the trends. By modeling the various sources of error, the model provides more accurate inferences than one that ignored the hierarchical structure in the data and incorrectly treated the scores as independent. The standard G study model would allow for a decomposition of the variance, but without the additional information we learned from modeling trends. By modeling the trends, we can identify possible sources of the variability and potential fixes. For instance, the rapid change in rater scoring at the start of live observations suggests that raters may need more practice before scoring and that studies may need to budget for more rater-training time. We would not know this if we only knew the size of the rater by lesson variance.
By permitting us to estimate the trends and other sources of variance, the model also supports evaluating alternative designs for scoring. The primary concern with drift identified by the model is that teachers who are scored only by raters who are new to rating would be at an advantage relative to other teachers, and teachers observed only by raters at their most severe-level of scoring would be at a notable disadvantage. To avoid this sort of confounding of the rater experience with our inferences about a teacher, we would need a study in which every teacher is observed by multiple raters at different levels of rating experience. The UTQ plan for video scoring, in which all the videos were collected and then scored, allowed for this type of scoring design and in general, might be preferred for research studies that use classroom observations (e.g., Measures of Effective Teaching, BMGF, 2012) or in studies using teacher artifacts such as portfolios and self-report (Martínez, Borko, & Stecher, 2012).
In teacher evaluations, live observations are the standard, often without opportunity for multiple observers. Hence a teacher’s evaluation may be sensitive to the rater’s level of experience with observations and with the rubric. Evaluations may also be somewhat sensitive to the time of year in which the observation occurs. In light of these results, it may be prudent for teachers to be observed at multiple times of the school year. Also, before consequential decisions are made on the basis of observations, school systems might want to corroborate scores from observations using other sources of data or through additional observations made by observers with varying levels of experience.
Consistent with the literature on text scoring (Congdon & McQueen, 2000; McKinley & Boulet, 2004), we observed extensive rater drift in the UTQ study, even though the raters participated in calibration exercises the entire time they were rating live or from videos. They also continued to drift even after an entire year of live scoring experience, and did not become more likely to agree on scores for the same lesson with more scoring experience. We might ask how this can occur. Detailed investigation of the calibration data revealed that several raters consistently disagreed with the master codes. For example, a rater with highly divergent scoring trends for CLASS-S disagreed with the master scores by 2 or more points on nearly 24% of calibration scores and, consistent with the drift, the rater’s errors on calibration exercises were somewhat more common later in the study. It is clear that providing raters with feedback on their performance can be insufficient for improving their accuracy. Our data suggest that calibration could be used to identify raters who are struggling with the protocols, especially if calibration data are tracked across time in a statistical quality control chart (Wang & von Davier, 2014).
An alternative design using the UTQ-like plan would employ a very large number of raters so that after all videos (or artifacts) are collected, the duration of scoring period is not so long that rater drift contributes to error in scores. Still, this would not resolve the trend that we see in the beginning of scoring where raters have a “burn-in” period related to the number of observations they have rated (not necessarily related to scoring days since it depends on how many observations they rated in a day). Given our observed trends, a design where many inexperienced raters each score a relatively small number of observations is likely to yield inflated scores. To avoid the bias in raters’ initial scores, studies may need to allow raters to conduct scoring for a period of a number of ratings before their scores are considered valid for use in research or practice. More extensive practice in training may remove this drift, but we cannot test such a design with our data.
Beyond removing struggling raters, our data do not provide any clear paths to reducing rater drift. Given rater tendency to be lenient at the start it might make sense to include real field ratings as part of training. Raters’ initial leniency also suggests they do not fully comprehend the standards of high-quality classroom interactions used by CLASS-S. It may take them several observations to reorient from their a priori beliefs about quality of instruction to the standards and practices embraced by these protocols. Interviews with raters support this conjecture and indicate that some raters never gain full comprehension of the protocol standards (Bell et al., 2014). This may be indicative of the lack of common understanding of quality instruction among educators noted often in the literature (Gitomer et al., 2014; Goe, Bell, & Little, 2008) and the emphasis of teachers and principals on classroom management which raters observe accurately with less drift and much less variability than almost all other aspects of practice. The problems with rater accuracy may also be due to the cognitive challenges of assessing so many high inference dimensions at the same time. Again, think-aloud rating interviews with the UTQ observers suggest that they struggled with determining the scores for an observation and that their processes for determining a score differed from those used by master coders (Bell et al., 2014).
The trends might be the result of differences in factors other than rater drift that contribute to scores and are confounded with scoring days. One such potential confounder is the demographic composition of participating classes. Classes in the Year 2 sample tended to have lower average prior year test scores, and greater percentages of low-income and minority students than classes from Year 1. These factors are correlated with the observation scores and given that Year 2 classes were more likely to be scored later in the project, they could be contributing to the downward trend in scores that we observe. We decided to test this potential confound by adding the classroom average prior mathematics and language scores and the percentage of students who were Black or eligible for free and reduced-priced lunches to Model 2 and comparing the coefficients for the trends from this model to the corresponding coefficients from Model 2. The results were very similar implying that the trends were not the result of differences in classroom composition. Additionally, we fit our models to the Year 1 and Year 2 data separately and found similar results; therefore we conclude there is essentially no confounding of the effects of demographics and the effects of scoring day within either year.
Care should be taken when generalizing the findings from the UTQ data. The study included only 12 raters. These raters conducted massive amounts of observations (approaching 10,000 scores) over a 2-year period using a rotating system involving different scoring protocols, which may have yielded different scoring trends than if raters were responsible for using a single scoring protocol. Several expressed fatigue with the video scoring. The raters were trained under state-of-the-art training at the time, but training is rapidly evolving since structured observations have become key to many teacher evaluation systems. The raters were part of a research study and did not know the teachers they observed and there were no consequences for any participants (raters or teachers) from the observations. Evaluations by principals are made in a very different context and may not show drift as the scores tend to be less variable and more consistently high than what is found in research studies (Jawahar & Williams, 1997; Lord & Cole, 1961; Weisberg, Sexton, Mulhern, & Keeling, 2009). Nonetheless, the UTQ experience is consistent with other research studies on observations (BMGF, 2012; Casabianca et al., 2013) and the experience with independent text raters. Rater drift is likely with observation protocols and studies should be designed to allow for it. Calibration data should be monitored over time to identify struggling raters and indicate that raters are not coming to a consensus agreement with master codes. Detailed study of the sources of such disagreements may suggest strategies not only to reduce drift in ratings but also to reduce the large rater-by-lesson variance, which profoundly degrades the reliability of the scores as measures of persistent teacher attributes.
Four classrooms were observed only once during the study due to unresolvable scheduling conflicts.
One rater conducted only live scoring and did not participate in video scoring.
Raters were considered able to score if at least 80% of the ratings were within one scale point of the master codes. The standard of being within one scale point of the master codes was, at the time of the UTQ study, the same standard used by the CLASS-S developers.
Raters were using three scoring rubrics on a rotating system; in the first week a rater may use CLASS-S, the second week, FFT, and the subject-specific protocol in the third week. Calibration and retraining for each protocol coincided with this rotating system as well.
For supplemental material, please visit http://ows.edb.utexas.edu/site/jodicasa/supplemental-material
The knot location is chosen by the bs() function in the splines R package. When requesting only one knot, the knot location is the median. For Emotional Support, the knot location is at scoring day 575.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This research was supported by grants from the Bill and Melinda Gates Foundation (52048) and the Institute of Education Sciences, U.S. Department of Education (R305B1000012). The opinions expressed are those of the authors and do not necessarily represent views of these organizations.
References
- Attali Y. (2011). Sequential effects in essay ratings. Educational and Psychological Measurement, 71, 68-79. [Google Scholar]
- Bates D., Maechler M., Bolker B. (2013). lme4: Linear mixed-effects models using S4 classes. R package version 0.999999-2. Retrieved from http://CRAN.R-project.org/package=lme4
- Bell C. A., Qi Y., Croft A. J., Leusner D., Gitomer D. H., McCaffrey D. F., Pianta R. C. (2014). Improving observational score quality: Challenges in observer thinking. In Kane T., Kerr K., Pianta R. (Eds.), Designing Teacher Evaluation Systems: New Guidance from the Measures of Effective Teaching Project. San Francisco, CA: Jossey-Bass. [Google Scholar]
- Bill and Melinda Gates Foundation. (2012). Gathering feedback for teaching: Combining high-quality observations with student surveys and achievement gains. Seattle, WA: Author; Retrieved from http://www.metproject.org/downloads/MET_Gathering_Feedback_Research_Paper.pdf [Google Scholar]
- Braun H. I. (1988). Understanding score reliability: Experiments in calibrating essay readers. Journal of Educational Statistics, 13, 1-18. [Google Scholar]
- Brennan R. L. (2001). Generalizability theory. New York, NY: Springer-Verlag. [Google Scholar]
- Casabianca J. M., McCaffrey D. F., Gitomer D., Bell C., Hamre B. K., Pianta R. C. (2013). Effect of observation mode on measures of secondary mathematics teaching. Educational and Psychological Measurement, 73, 757-783. [Google Scholar]
- Congdon P. J., McQueen J. (2000). The stability of rater severity in large-scale assessment programs. Journal of Educational Measurement, 37, 163-178. [Google Scholar]
- Danielson C. (2007). Enhancing professional practice: A framework for teaching. Alexandria, VA: Association for Supervision and Curriculum Development. [Google Scholar]
- Engelhard G., Myford C. M. (2003). Monitoring faculty consultant performance in the Advanced Placement English Literature and Composition Program with a many-faceted Rasch model (Research Rep. 03-01). Princeton, NJ: Educational Testing Service. [Google Scholar]
- Gitomer D. H., Bell C. A., Qi Y., McCaffrey D. F., Hamre B. K., Pianta R. C. (2014). The instructional challenge in improving teaching quality: Lessons from a classroom observation protocol. Teachers College Record, 116(6). Retrieved from http://www.tcrecord.org/library/abstract.asp?contentid=17460 [Google Scholar]
- Goe L., Bell C. A., Little O. (2008). Approaches to evaluating teacher effectiveness: A research synthesis. Washington, DC: National Comprehensive Center for Teacher Quality; Retrieved from http://www.tqsource.org/publications/EvaluatingTeachEffectiveness.pdf [Google Scholar]
- Grossman P., Loeb S., Cohen J., Hammerness K., Wyckoff J., Boyd D., Lankford H. (2010). Measure for measure: The relationship between measures of instructional practice in middle school English language arts and teachers’ value-added scores (NBER Working Paper No. 16015). Retrieved from http://www.nber.org/papers/w16015
- Harik P., Clauser B. E., Grabovsky I., Nungester R. J., Swanson D., Nandakumar R. (2009). An examination of rater drift within a generalizability theory framework. Journal of Educational Measurement, 46, 43-58. [Google Scholar]
- Hastie T., Tibshirani R., Friedman J. (2009). The elements of statistical learning: Data mining, inference, and prediction (2nd ed.). New York, NY: Springer Science+Business. [Google Scholar]
- Hill H. C., Blunk M., Charalambous C., Lewis J., Phelps G. C., Sleep L., Ball D. L. (2008). Mathematical knowledge for teaching and the mathematical quality of instruction: An exploratory study. Cognition and Instruction, 26, 430-511. [Google Scholar]
- Hill H. C., Charalambous C. Y., Kraft M. A. (2012). When rater reliability is not enough: Teacher observation systems and a case for the generalizability study. Educational Researcher, 41, 56-64. [Google Scholar]
- Hoskens M., Wilson M. (2001). Real-time feedback on rater drift in constructed response items: An example from the Golden State Examination. Journal of Educational Measurement, 38, 121-146. [Google Scholar]
- Jawahar I. M., Williams C. R. (1997). Where all the children are above average: The performance appraisal purpose effect. Personnel Psychology, 50, 905-925. [Google Scholar]
- Kingsbury F. A. (1922). Analyzing ratings and training raters. Journal of Personnel Research, 1, 377-383. [Google Scholar]
- Lord R., Cole D. (1961). Principal bias in rating teachers. Journal of Educational Research, 55, 33-35. [Google Scholar]
- Martínez J. F., Borko H., Stecher B. M. (2012). Measuring instructional practice in science using classroom artifacts: Lessons learned from two validation studies. Journal of Research in Science Teaching, 49, 38-67. [Google Scholar]
- McKinley D., Boulet J. R. (2004). Detecting score drift in a high-stakes performance-based assessment. Advances in Health Sciences Education, 9, 29-38. [DOI] [PubMed] [Google Scholar]
- McQueen J., Congdon P. J. (1997, March). Rater severity in large-scale assessment: Is it invariant? Paper presented at the annual meeting of the American Educational Research Association, Chicago, IL. [Google Scholar]
- Meyer J. P., Cash A. H., Mashburn A. (2012). Occasions and the reliability of classroom observations: Alternative conceptualizations and methods of analysis. Educational Assessment, 16, 227-243. [Google Scholar]
- Myford C. M., Wolfe E. M. (2009). Monitoring rater performance over time: A framework for detecting differential accuracy and differential scale use. Journal of Educational Measurement, 46, 371-389. [Google Scholar]
- Pianta R. C., Hamre B. K., Haynes N. J., Mintz S. L., Paro K. M. (2007). Classroom Assessment Scoring System (CLASS), secondary manual. Charlottesville: University of Virginia Center for Advanced Study of Teaching and Learning. [Google Scholar]
- Raudenbush S. W., Bryk A. S. (2002). Hierarchical linear models: Applications and data analysis methods (2nd ed.). Thousand Oaks, CA: Sage. [Google Scholar]
- Rowan B., Harrison D. M., Hayes A. (2004). Using instructional logs to study mathematics curriculum and teaching in the early grades. Elementary School Journal, 105, 103-127. [Google Scholar]
- Saal F. E., Downey R. G., Lahey M. A. (1980). Rating the ratings: Assessing the psychometric quality of rating data. Psychological Bulletin, 88, 413-428. [Google Scholar]
- Schwarz G. E. (1978). Estimating the dimension of a model. Annals of Statistics, 6, 461-464. [Google Scholar]
- Searle S. R. (1971). Linear models. New York, NY: Wiley. [Google Scholar]
- Thorndike E. L. (1920). A constant error in psychological ratings. Journal of Applied Psychology, 4, 25-29. [Google Scholar]
- Wang Z., von Davier A. A. (2014). Monitoring of scoring using e–rater® and human raters on a writing test (Research Rep.). Princeton, NJ: Educational Testing Service. Advance online publication. DOI: 10.1002/ets2.12005 [Google Scholar]
- Weisberg D., Sexton S., Mulhern J., Keeling D. (2009). The widget effect. Brooklyn, NY: The New Teacher Project; Retrieved from http://widgeteffect.org/downloads/TheWidgetEffect.pdf [Google Scholar]
- Wilson M., Case H. (2000). An examination of variation in rater severity over time: A study of rater drift. In Wilson M., Engelhard G. (Eds.), Objective measurement: Theory into practice (Vol. 5, pp. 113-134). Stamford, CT: Ablex. [Google Scholar]