Abstract
The purpose of this article is to highlight the distinction between the reliability of test scores and the fit of psychometric measurement models, reminding readers why it is important to consider both when evaluating whether test scores are valid for a proposed interpretation and/or use. It is often the case that an investigator judges both the reliability of scores and the fit of a corresponding measurement model to be either acceptable or unacceptable for a given situation, but these are not the only possible outcomes. This article focuses on situations in which model fit is deemed acceptable, but reliability is not. Data were simulated based on the item characteristics of the PROMIS (Patient Reported Outcomes Measurement Information System) anxiety item bank and analyzed using methods from classical test theory, factor analysis, and item response theory. Analytic techniques from different psychometric traditions were used to illustrate that reliability and model fit are distinct, and that disagreement among indices of reliability and model fit may provide important information bearing on a particular validity argument, independent of the data analytic techniques chosen for a particular research application. We conclude by discussing the important information gleaned from the assessment of reliability and model fit.
Keywords: model fit, item response theory, factor analysis, reliability
Psychologists routinely develop tests to measure important theoretical constructs that cannot be observed directly with the goal of using the resulting scores in basic and applied scientific work. Providing evidence of the degree to which test scores are valid for an intended interpretation and/or use is a critical component of the measurement process (American Educational Research Association, American Psychological Association, & National Council on Measurement in Education, 2014; Kane, 2013; Messick, 1989). This often includes (but is not limited to) studying the statistical properties of test scores in a sample of individuals drawn from a population of interest and using psychometric methods to assess reliability and model fit.
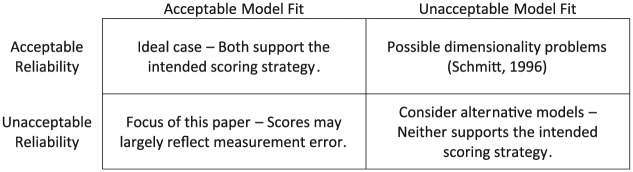
Reliability and model fit are distinct concepts. The former refers to the precision of scores, representing the degree to which scores are expected to be consistent across repeated testing occasions (American Educational Research Association et al., 2014). In the tradition of structural equation modeling (SEM) and confirmatory factor analysis, model fit indices measure discrepancies between observed and model-implied correlation/covariance matrices. In general, model fit indices represent discrepancies between observed and model-implied data. It can be helpful to think of reliability and model fit in terms of the 2 × 2 matrix presented in Figure 1. For the sake of clarity, this problem has been simplified considerably by assuming that a researcher has determined criteria for “acceptable” versus “unacceptable” reliability and model fit appropriate to the research situation. Certainly, these distinctions are not always so clear, and a level of reliability that is considered acceptable for one purpose, such as comparing population average scores, may be considered unacceptable for another, such as comparing individual scores in employee selection.
Figure 1.
Potential implications when reliability and model fit are deemed acceptable versus unacceptable.
Given the assumption that both reliability and fit can be categorized as acceptable or unacceptable, there are four possible outcomes. First, if both reliability and model fit are deemed acceptable for a given purpose, a researcher can reasonably conclude that the scores are precise and consistent with the hypothesized dimensional structure. Second, if both reliability and fit are deemed unacceptable, it is time to consider alternative models, as neither type of evidence supports the intended scoring strategy. The conclusions are not quite so clear for the third and fourth cases, in which the assessment of reliability and model fit appear to provide conflicting evidence about the extent to which the intended scoring strategy is supported by data. If reliability is considered acceptable but model fit is not, it is possible that scores reflect multiple distinct, albeit possibly related, dimensions. Schmitt (1996) illustrated this point, focusing on the popular coefficient alpha (Cronbach, 1951) as a measure of reliability. He demonstrated that a high alpha value alone is not enough to show that a measurement model is supported by data, as alpha does a poor job of detecting underlying multidimensionality. This highlights the point that reliability and model fit are distinct and that it is important for researchers to assess both when they are constructing an argument for a particular interpretation and use of test scores.
The fourth potential outcome illustrated in Figure 1 has not received much attention in the measurement literature and is the focus of the present work. What does it mean when a model fits well but reliability of the resulting scores is poor? Before addressing this question, we first present the results of a small simulation. The primary goal of this simulation is to demonstrate empirically that it is possible to have “good fit” and “bad reliability” simultaneously, as well as to expand on what this can mean when it is encountered in practice. A secondary goal is to demonstrate that this is a broad issue and not specific to any particular measure of reliability (or model fit). Although coefficient alpha is still a widely used measure of reliability, arguments have been made that it is problematic and should be replaced by other methods for assessing reliability (e.g., Sijtsma, 2009). Thus, in addition to alpha, we consider a factor analysis-based reliability index, coefficient omega (McDonald, 1999), as well as incorporating standard error curves from an item response theory (IRT) approach. We also use several fit indices drawn from the SEM framework to assess the fit of corresponding psychometric models.
Method
Simulation Design
Ordinal item response data were simulated using item parameters for a subset of items from the Patient Reported Outcomes Measurement Information System (PROMIS) anxiety item bank (Pilkonis et al., 2011), presented in Table 1. These item parameters were calibrated from data on 29 five-category items using the logistic graded response model, an IRT model commonly fit to ordinal data in psychology. Raw item responses were generated for 10 items and 1,000 simulees in flexMIRT (Cai, 2013). The generating slopes were multiplied by six different scaling factors to represent an increasingly unreliably measured unidimensional construct. Slopes were multiplied by 1, 1/2, 1/3, 1/4, 1/5, or 1/6 with 100 replications for each of these slope scaling factors. There is a well-established analytic relationship between slopes in the logistic graded response model and factor loadings for ordinal factor models (Takane & de Leeuw, 1987; Wirth & Edwards, 2007). Table 2 shows the slopes used to generate the data converted to the traditional factor loading metric, which may be more intuitive to readers than the metric of IRT slopes.
Table 1.
Calibrated Item Parameters From the PROMIS Anxiety Item Bank.
| Threshold |
|||||
|---|---|---|---|---|---|
| Item | Slope | 1 | 2 | 3 | 4 |
| 1. I found it hard to focus on anything other than my anxiety | 3.86 | 0.41 | 1.20 | 2.05 | 2.84 |
| 2. My worries overwhelmed me | 3.64 | 0.29 | 0.96 | 1.71 | 2.56 |
| 3. I felt uneasy | 3.64 | −0.31 | 0.52 | 1.50 | 2.44 |
| 4. I felt fearful | 3.58 | 0.27 | 1.02 | 1.90 | 2.64 |
| 5. I felt like I needed help for my anxiety | 3.53 | 0.47 | 0.98 | 1.80 | 2.32 |
| 6. I felt frightened | 3.43 | 0.42 | 1.26 | 2.09 | 2.82 |
| 7. I felt nervous | 3.38 | −0.29 | 0.56 | 1.58 | 2.67 |
| 8. I felt anxious | 3.34 | −0.27 | 0.53 | 1.51 | 2.38 |
| 9. I felt tense | 3.33 | −0.59 | 0.24 | 1.18 | 2.23 |
| 10. It scared me when I felt nervous | 3.32 | 0.55 | 1.17 | 2.00 | 2.70 |
Note. PROMIS = Patient Reported Outcomes Measurement Information Systems.
Table 2.
Generating Item Factor Loadings.
| Item | Slope scaling factor |
|||||
|---|---|---|---|---|---|---|
| 1 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | |
| 1 | 0.92 | 0.75 | 0.60 | 0.49 | 0.41 | 0.35 |
| 2 | 0.91 | 0.73 | 0.58 | 0.47 | 0.39 | 0.34 |
| 3 | 0.91 | 0.73 | 0.58 | 0.47 | 0.39 | 0.34 |
| 4 | 0.90 | 0.73 | 0.57 | 0.47 | 0.39 | 0.33 |
| 5 | 0.90 | 0.72 | 0.57 | 0.46 | 0.38 | 0.33 |
| 6 | 0.90 | 0.71 | 0.56 | 0.45 | 0.37 | 0.32 |
| 7 | 0.89 | 0.71 | 0.55 | 0.45 | 0.37 | 0.31 |
| 8 | 0.89 | 0.70 | 0.55 | 0.44 | 0.37 | 0.31 |
| 9 | 0.89 | 0.70 | 0.55 | 0.44 | 0.36 | 0.31 |
| 10 | 0.89 | 0.70 | 0.55 | 0.44 | 0.36 | 0.31 |
Analysis
The simulated data sets were analyzed using a variety of statistical techniques in R (R Core Team, 2015), Mplus (Muthén & Muthén, 1998-2012), and flexMIRT. For each data set, coefficient alpha was computed manually in R. Limited-information estimation was performed in Mplus using mean- and variance-adjusted diagonally weighted least squares estimation (WLSMV) on a matrix of polychoric correlations, an estimation technique that tends to work well for ordinal data (Wirth & Edwards, 2007). The estimated item factor loadings were used to compute coefficient omega in R. Three limited-information fit statistics were extracted from the Mplus output using the R package MplusAutomation (Hallquist & Wiley, 2014): the root mean square error of approximation (RMSEA; Steiger & Lind, 1980) and the associated 90% confidence interval, the comparative fit index (CFI; Bentler, 1990), and the Tucker–Lewis index (TLI; Tucker & Lewis, 1973). These indices are commonly reported in SEM and factor analysis, and are reviewed in a simulation study by Hu and Bentler (1999). Full-information estimation was performed in flexMIRT. The development of model fit measures for this type of estimation is an active area of inquiry (see, e.g., Cai & Monroe, 2013; Edwards, 2013; Maydeu-Olivares, 2013; Thissen, 2013). To explore their behavior, we obtained from flexMIRT the Akaike information criterion (AIC; Akaike, 1987) for the fitted model, the ordinal RMSEA (Joe & Maydeu-Olivares, 2010) for the fitted model and the zero-factor null model, and the TLI. Additionally, standard error curves were plotted for each slope scaling factor.
Results
Item parameter recovery results are summarized for each estimation method and each slope scaling factor in Table 3, including the average bias (estimated parameter–generating parameter) and root mean square error (RMSE). Generally, item parameters were recovered well—certainly in line with expectations given existing simulation studies (Forero & Maydeu-Olivares, 2009; Forero, Maydeu-Olivares, & Gallardo-Pujol, 2009). There is a slight trend for the RMSE values to be higher for larger slopes, but as the parameters being estimated are larger this is to be expected to some extent.
Table 3.
Item Parameter Recovery.
| Full-information estimation |
Limited-information estimation |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept |
Loading | Threshold |
|||||||||
| Statistic | Slope scaling factor | Slope | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| Average bias | 1 | .00 | −.01 | −.02 | −.05 | −.10 | −.01 | .00 | .00 | .00 | −.02 |
| 1/2 | .00 | .00 | −.01 | −.02 | −.03 | −.01 | .00 | .00 | −.01 | −.05 | |
| 1/3 | .00 | .00 | −.01 | −.01 | −.02 | −.01 | .00 | .01 | .00 | −.03 | |
| 1/4 | .00 | .00 | .00 | −.01 | −.01 | .00 | .00 | .01 | .01 | .00 | |
| 1/5 | .00 | .00 | .00 | −.01 | −.01 | .01 | .00 | .01 | .02 | .01 | |
| 1/6 | .00 | .00 | .00 | −.01 | −.01 | −.08 | .00 | .01 | .02 | .02 | |
| Root mean square error | 1 | .22 | .17 | .21 | .34 | .57 | .02 | .04 | .04 | .07 | .12 |
| 1/2 | .12 | .10 | .11 | .16 | .25 | .03 | .04 | .04 | .06 | .09 | |
| 1/3 | .10 | .09 | .09 | .11 | .16 | .03 | .04 | .04 | .05 | .07 | |
| 1/4 | .10 | .08 | .08 | .10 | .12 | .04 | .04 | .04 | .05 | .05 | |
| 1/5 | .10 | .07 | .08 | .09 | .10 | .05 | .04 | .04 | .05 | .05 | |
| 1/6 | .11 | .07 | .07 | .08 | .09 | .24 | .04 | .04 | .05 | .05 | |
Note. Data were generated for 10 items and 1,000 simulees in flexMIRT with 100 replications per slope scaling factor.
Table 4 summarizes the estimates of reliability and model fit for the simulated data by slope scaling factor. As expected, the reliability coefficients alpha and omega decreased quickly as the slopes became weaker. At the same time, the average interitem polychoric correlation became weaker, indicating that item responses were less closely linked. This highlights the potential diagnostic utility of the average interitem correlation in reliability assessment because, unlike coefficient alpha, it is not confounded by the number of items on a measure. The correlation metric is also widely used and interpreted by psychologists. The estimated model fit indices (RMSEA, CFI, and TLI) from the limited-information estimation remained stable for the different slope scaling factors. This demonstrates empirically the distinction between the fit of psychometric models and the reliability of test scores. Unlike the reliability estimates, which decreased rapidly as the item responses became weaker indicators of the underlying latent construct, the fit of the unidimensional measurement models remained quite stable.
Table 4.
Means and Standard Deviations of Reliability and Model Fit Statistics.
| Limited-information estimation |
Full-information estimation |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Statistic | Slope scaling factor | α | Average interitem polychoric correlation | ω | RMSEA [90% CI] | CFI | TLI | Fitted model AIC | Fitted model RMSEA | Null model RMSEA | TLI |
| M | 1 | .96 | .79 | .97 | .01 [.00, .03] | 1.00 | 1.00 | 15,612 | .01 | .44 | 1.00 |
| 1/2 | .87 | .50 | .91 | .01 [.00, .02] | 1.00 | 1.00 | 21,896 | .01 | .26 | 1.00 | |
| 1/3 | .77 | .31 | .82 | .01 [.00, .02] | 1.00 | 1.00 | 24,889 | .01 | .15 | 1.00 | |
| 1/4 | .66 | .21 | .73 | .01 [.00, .02] | 1.00 | 1.00 | 26,129 | .01 | .10 | 1.00 | |
| 1/5 | .56 | .15 | .63 | .01 [.00, .02] | .99 | 1.00 | 26,482 | .01 | .06 | 1.00 | |
| 1/6 | .47 | .11 | .55 | .01 [.00, .02] | .99 | 1.01 | 26,376 | .01 | .05 | .92 | |
| SD | 1 | .01 | .01 | .00 | .01 [.01, .01] | .00 | .00 | 234 | .01 | .09 | .00 |
| 1/2 | .01 | .02 | .01 | .01 [.00, .01] | .00 | .00 | 267 | .02 | .06 | .02 | |
| 1/3 | .01 | .01 | .01 | .01 [.00, .01] | .00 | .01 | 249 | .01 | .03 | .04 | |
| 1/4 | .02 | .01 | .02 | .01 [.00, .01] | .01 | .01 | 228 | .01 | .02 | .09 | |
| 1/5 | .02 | .01 | .02 | .01 [.00, .01] | .01 | .02 | 205 | .01 | .02 | .24 | |
| 1/6 | .03 | .01 | .03 | .01 [.00, .01] | .02 | .04 | 188 | .01 | .01 | .48 | |
Note. CFI = comparative fit index; TFI = Tucker–Lewis index; RMSEA = root mean square of error approximation; AIC = Akaike information criterion; CI = confidence interval. Data were generated for 10 items and 1,000 simulees in flexMIRT with 100 replications per slope scaling factor.
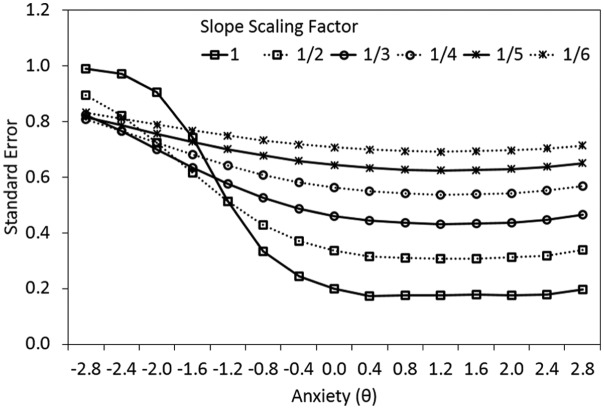
The full-information model fit results tell a similar story. The fitted model RMSEA and TLI behave quite similarly to their limited-information counterparts. The addition of AIC and the null model RMSEA show that, as the explainable covariance decreases, the utility of a model over no model at all decreases. Average standard error curves are plotted in Figure 2. Because the generating location parameters are less concentrated at the lower end of the latent variable continuum, the standard error values in this region tend to be higher. However, as the average slopes become weaker, the measurement of the latent construct becomes less precise (i.e., average standard error increases).
Figure 2.
Test standard error curves for the simulated data sets with six different slope scaling factors, averaged across replications.
Discussion
This study focuses on a mostly undiscussed corner in the relationship between reliability and model fit. While many methodologists are comfortable with the theoretical and functional distinctions between the two concepts, it is our experience that many applied researchers struggle when confronted with a “good fitting” psychometric model that produces scores with below-par reliability. We view these results as complementary to those of Schmitt (1996), who eloquently demonstrated cases where high reliability and poor model fit could coexist. The present work demonstrates empirically (and conceptually) that reliability and model fit assessment provide distinct information about the psychometric properties of scores. Given that these results can occur in practice,1 it is important to consider what this means and what, if anything, should be done when model fit is deemed acceptable and reliability is not.
As mentioned at the outset of this article, given particular decisions about what constitutes acceptable levels of reliability and model fit, a researcher may find himself or herself in any one of the four quadrants of Figure 1. If the model fits well and the score reliability is deemed acceptable, then fortune (or good planning) has smiled on the researcher and life proceeds peacefully. If the model does not fit well and the score reliability is deemed unacceptable, then it seems useful to revisit the basic assumptions underlying the theoretical development of the instrument. If the model fits poorly, but the scores are reliable, this can be a sign that what is being treated as one construct may in fact be multiple constructs. If the model fits well, but the reliability of the scores is unacceptable, there are several possible causes/courses of action. First, it is possible that the scale is simply too short. While researchers may want/need scales to be short for practical reasons, the universe is not always willing to comply. It may be that more items are needed to reach a targeted level of reliability. Second, it seems possible that for some very broad constructs it may be quite difficult to obtain very high levels of reliability. There is a constant tension between the breadth of the construct and the consistency of the responses (as often characterized by alpha in practice). In such contests, alpha usually wins and our scores become more reliable (as judged by alpha), but tell us about a less conceptually broad construct. Finally, we are reminded that while high levels of reliability/precision are always nice, they are not always necessary. When making a high-stakes decision about an individual, one should demand the highest levels of reliability achievable. On the other hand, when trying to further elaborate a theory using a convenience sample of 300 undergraduates, a reliability of .6 or .7 might be just fine.
Indeed, it was the appearance of several such situations over the course of the past few years that motivated us to write this article. The title “Dear psychometrician—my model fits but my scale is terrible!” was toyed with briefly before we settled on the current one.
Footnotes
Declaration of Conflicting Interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) received no financial support for the research, authorship, and/or publication of this article.
References
- Akaike H. (1987). Factor analysis and AIC. Psychometrika, 52, 317-332. [Google Scholar]
- American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (2014). Standards for educational and psychological testing. Washington, DC: American Educational Research Association. [Google Scholar]
- Bentler P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107, 238-246. [DOI] [PubMed] [Google Scholar]
- Cai L. (2013). flexMIRT® version 2: Flexible multilevel multidimensional item analysis and test scoring [Computer software]. Chapel Hill, NC: Vector Psychometric Group. [Google Scholar]
- Cai L., Monroe S. (2013). IRT model fit evaluation from theory to practice: Progress and some unanswered questions. Measurement: Interdisciplinary Research and Perspectives, 11, 102-106. [Google Scholar]
- Cronbach L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16, 297-334. [Google Scholar]
- Edwards M. C. (2013). Purple unicorns, true models, and other things I’ve never seen. Measurement: Interdisciplinary Research and Perspectives, 11, 107-111. [Google Scholar]
- Forero C. G., Maydeu-Olivares A. (2009). Estimation of IRT graded response models: Limited versus full information methods. Psychological Methods, 14, 275-299. [DOI] [PubMed] [Google Scholar]
- Forero C. G., Maydeu-Olivares A., Gallardo-Pujol D. (2009). Factor analysis with ordinal indicators: A Monte Carlo study comparing DWLS and ULS estimation. Structural Equation Modeling, 16, 625-641. [Google Scholar]
- Hallquist M., Wiley J. (2014). MplusAutomation: Automating Mplus model estimation and interpretation (R package version 0.6-3). Retrieved from http://CRAN.R-project.org/package=MplusAutomation
- Hu L.-T., Bentler P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling, 6, 1-55. [Google Scholar]
- Joe H., Maydeu-Olivares A. (2010). A general family of limited information goodness-of-fit statistics for multinomial data. Psychometrika, 75, 393-419. [Google Scholar]
- Kane M. T. (2013). Validating the interpretations and uses of test scores. Journal of Educational Measurement, 50, 1-73. [Google Scholar]
- Maydeu-Olivares A. (2013). Goodness-of-fit assessment of item response theory models. Measurement: Interdisciplinary Research and Perspectives, 11, 71-101. [Google Scholar]
- McDonald R. P. (1999). Test theory: A unified treatment. Mahwah, NJ: Lawrence Erlbaum. [Google Scholar]
- Messick S. (1989). Validity. In Linn R. L. (Ed.), Educational measurement (3rd ed., pp. 13-103). New York, NY: American Council on Education. [Google Scholar]
- Muthén L. K., Muthén B. O. (1998-2012). Mplus user’s guide (7th ed.). Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Pilkonis P. A., Choi S. W., Reise S. P., Stover A. M., Riley W. T., Cella D. (2011). Item banks for measuring emotional distress from the Patient-Reported Outcomes Measurement Information System (PROMIS®): Depression, anxiety, and anger. Assessment, 18, 263-283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. (2015). R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; Retrieved from http://www.R-project.org/ [Google Scholar]
- Schmitt N. (1996). Uses and abuses of coefficient alpha. Psychological Assessment, 8, 350-353. [Google Scholar]
- Sijtsma K. (2009). On the use, misuse, and very limited usefulness of Cronbach’s alpha. Psychometrika, 74, 107-120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steiger J. H., Lind J. C. (1980, June). Statistically based tests for the number of factors. Paper presented at the Annual Meeting of the Psychometric Society, Iowa City, IA. [Google Scholar]
- Takane Y., de Leeuw J. (1987). On the relationship between item response theory and factor analysis of discretized variables. Psychometrika, 52, 393-408. [Google Scholar]
- Thissen D. (2013). The meaning of goodness-of-fit tests: Commentary on “Goodness-of-fit assessment of item response theory models”. Measurement: Interdisciplinary Research and Perspectives, 11, 123-126. [Google Scholar]
- Tucker L. R., Lewis C. (1973). A reliability coefficient for maximum likelihood factor analysis. Psychometrika, 38, 1-10. [Google Scholar]
- Wirth R. J., Edwards M. C. (2007). Item factor analysis: Current approaches and future directions. Psychological Methods, 12, 58-79. [DOI] [PMC free article] [PubMed] [Google Scholar]