A Cautionary Note on the Use of the Vale and Maurelli Method to Generate Multivariate, Nonnormal Data for Simulation Purposes

Abstract

To further understand the properties of data-generation algorithms for multivariate, nonnormal data, two Monte Carlo simulation studies comparing the Vale and Maurelli method and the Headrick fifth-order polynomial method were implemented. Combinations of skewness and kurtosis found in four published articles were run and attention was specifically paid to the quality of the sample estimates of univariate skewness and kurtosis. In the first study, it was found that the Vale and Maurelli algorithm yielded downward-biased estimates of skewness and kurtosis (particularly at small samples) that were also highly variable. This method was also prone to generate extreme sample kurtosis values if the population kurtosis was high. The estimates obtained from Headrick’s algorithm were also biased downward, but much less so than the estimates obtained through Vale and Maurelli and much less variable. The second study reproduced the first simulation in the Curran, West, and Finch article using both the Vale and Maurelli method and the Heardick method. It was found that the chi-square values and empirical rejection rates changed depending on which data-generation method was used, sometimes sufficiently so that some of the original conclusions of the authors would no longer hold. In closing, recommendations are presented regarding the relative merits of each algorithm.

Introduction

With the increasing availability of computer power, Monte Carlo simulations have become one of the most popular methods to explore the robustness of statistical procedures to the less-than-ideal conditions found in applied research (Bandalos & Leite, 2013). In order to be able to properly conduct simulation studies, it is important for the researcher to use algorithms that accurately reflect the conditions being studied or the conclusions from said simulation results would be suspect.

To investigate the effect of violating distributional assumptions (mostly, normality) for multivariate methods, simulation studies usually require the implementation of a data-generating procedures that allow the researcher to control the correlation or covariance structure of the data as well as the degree of nonnormality (Mattson, 1997; Ruscio & Kaczetow, 2008; Vale & Maurelli, 1983). Various methods have been proposed to this effect (e.g., Azzalini & Dalla Valle, 1996; Headrick, 2002, etc.) but, arguably, none have been as widely used within the methodological literature as the Vale and Maurelli (1983) multivariate extension of the Fleishman (1978) power method.

Overview of the Fleishman–Vale–Maurelli Method (Third-Order Polynomial)

The Fleishman method or (third-order polynomial approach) employs a polynomial transformation of standard, normal variables where the polynomial coefficients are used to specify the first four moments of a distribution. Let X ~ N(0,1) and define

$$Y=a+bX+c{X}^2+d{X}^3$$

where a, b, c, and d are the polynomial coefficients that will control the first four-order moments of the new random variable Y. For appropriately chosen coefficients, the researcher can control the skewness and kurtosis of Y taking advantage of the following relationships.

Let us define the first four moments of Y as E(Y) = 0, E(Y²) = 1, E(Y³) = γ₁ and E(Y⁴) = γ₂+ 3 (where γ₁ and γ₂ are the skewness and kurtosis of Y) then it follows that

$$a=-c.$$

$$b^2+6bd+2c^2+15d^2=1.$$

$$2c(b^2+24bd+105d^2+2)={\gamma }_1$$

$$24\left(bd+c^2\left[1+b^2+28bd\right]+d^2\left[12+48bd+141c^2+225d^2\right]\right)={\gamma }_2$$

where Equations (2) to (5) correspond to Fleishman’s Equations (5), (11), (17), and (18), respectively.

Because of its relative ease of implementation, the Fleishman (1978) method was extended by Vale and Maurelli (1983) to the multivariate case by applying the algorithm to each one-dimensional marginal in the multivariate distribution being defined. An undesirable aspect of this process is that it changes the correlation structure intended by the user, so a correction needs to be implemented before proceeding. The solution proposed in Vale and Murelli (1983) is to calculate an intermediate correlation matrix so that the data takes it as the initial “population” correlation matrix and, as one applies the Fleishman (1978) method to each marginal distribution, the correlation matrix is transformed to the originally intended one. Define the vectors x and w and the new variable Y as:

$$\mathbf{x}\mathbf{\prime }=[1,X,X^2,X^3]$$

$$\mathbf{w}\mathbf{\prime }=[a,b,c,d]$$

$$Y=\mathbf{w}\mathbf{\prime }\mathbf{x}$$

where X is defined as above and the vector w′ contains the polynomial weights needed to control the moments of the nonnormal distribution Y. Letting r_Y1Y2 be the correlation coefficient of two nonnormal variables Y₁ and Y₂ generated from the two normally distributed variables X₁ and X₂ (with a correlation coefficient r_X1X2) it follows that

$$r_{Y1Y2}=E\left(Y_1{Y}_2\right)=E\left({\mathbf{w}\mathbf{\prime }}_1{\mathbf{x}}_1{\mathbf{x}\mathbf{\prime }}_2{\mathbf{w}}_2\right)={\mathbf{w}\mathbf{\prime }}_{1}E\left({\mathbf{x}}_1{\mathbf{x}\mathbf{\prime }}_2\right){\mathbf{w}}_2={\mathbf{w}\mathbf{\prime }}_1\mathbf{R}{\mathbf{w}}_2$$

$$R=\left[\begin{array}{cccc}1& 0& 1& 0\\ 0& r_{X1X2}& 0& 3r_{X1X2}\\ 1& 0& 2r_{X1X2}^2+1& 0\\ 0& 3r_{X1X2}& 0& 6r_{X1X2}^3+9r_{X1X2}\end{array}\right]$$

And by collecting the appropriate terms from the matrix R in Equation (10) it can be shown that the correlation between Y₁ and Y₂ is

$$r_{Y1Y2}=r_{X1X2}\left(b_1{b}_2+3b_1{d}_2+3d_1{b}_2+9d_1{d}_2\right)+r_{X1X2}^2\left(2c_1{c}_2\right)+r_{X1X2}^3(6d_1{d}_2)$$

By solving for r_X1X2, it is possible to find the pairwise elements of the intermediate correlation matrix so that the researcher can specify all the elements r_Y1Y2 that will act as the desired and final correlation matrix used to generate the data.

Overview of the Headrick Method (Fifth-Order Polynomial)

Tadikamalla (1980) published one of the first overviews of algorithms to generate nonnormal data that let the user specify the higher order moments of a distribution. As a criticism, he pointed out that the probability density function that arises from implementing the Fleishman (1978) method is not known and that various combinations of skewness and kurtosis are not possible (a boundary exists that relates the values of kurtosis and skewness as γ₂≥γ²₁− 2 and Fleishman’s method can only obtain a subset of the values in it). Nevertheless, he did recommend the third-order polynomial method because of its ease of implementation.

To address some of the previously mentioned limitations, Headrick (2002) proposed an extension of the power method where polynomials of Order 5 (instead of those of Order 3) are implemented to obtain a wider range of values in the skewness–kurtosis parabola. Again, taking X ~ N(0,1) the Headrick (2002) approach defines the new, nonnormal variable Y as

$$Y=c_0+c_{1}X+c_2{X}^2+c_3{X}^3+c_4{X}^4+c_5{X}^5.$$

As expected, the increase in the number of polynomial coefficients also increases both the number and the complexity of the equations that need to be solved in order to obtain the estimates of c₀ to c₅. The general equations (which are quite lengthy) as well as the technical details can be found in Headrick (2002), but the general logic rests on the idea of moment-matching the new distribution of Y to the skewness/kurtosis values defined by the user and needed to solve Equation (12). The more moments one can control, the better the approximation of Y will be. By using the fifth- and sixth-order moments, the user now has the ability to choose from a wider range of skewness and kurtosis values and can better reproduce well-known distributions whose theoretical higher order moments are known.

The fifth-order polynomial approach has been extended to the multivariate case as well, following the same premise of finding an intermediate correlation matrix for the data before the nonnormal transformations are carried out (Headrick, 2002, 2004; Headrick & Kowalchuk, 2007). For two nonnormal variables Y₁ and Y₂ generated from two normally distributed variables X₁ and X₂ with a correlation coefficient r_X1X2, the resulting correlation of the Y variables is

$$\begin{array}{l}{r}_{Y1Y2}=3c_{4\left(1\right)}{c}_{0\left(2\right)}+3c_{4\left(1\right)}{c}_{2\left(2\right)}+9c_{4\left(1\right)}{c}_{4\left(2\right)}+c_{0\left(1\right)}\left(c_{0\left(2\right)}+c_{2\left(2\right)}+3c_{4\left(2\right)}\right)+c_{1\left(1\right)}{c}_{1\left(2\right)}{r}_{X1X2}\\ +3c_{3(1)}{c}_{1(2)}{r}_{X1X2}+15c_{5(1)}{c}_{1(2)}{r}_{X1X2}+3c_{1(1)}{c}_{3(2)}{r}_{X1X2}+9c_{3(1)}{c}_{3(2)}{r}_{X1X2}+45c_{5(1)}{c}_{3(2)}{r}_{X1X2}\\ 15c_{1(1)}{c}_{5(2)}{r}_{X1X2}+45c_{3(1)}{c}_{5(2)}{r}_{X1X2}+225c_{5(1)}{c}_{5(2)}{r}_{X1X2}+12c_{4(1)}{c}_{2(2)}{r}_{X1X2}^2+72c_{4(1)}{c}_{4(2)}{r}_{X1X2}^2\\ +6c_{3(1)}{c}_{3(2)}{r}_{X1X2}^3+60c_{5(1)}{c}_{3(2)}{r}_{X1X2}^3+60c_{3(1)}{c}_{5(2)}{r}_{X1X2}^3+600c_{5(1)}{c}_{5(2)}{r}_{X1X2}^3+24c_{4(1)}{c}_{4(2)}{r}_{X1X2}^4\\ +120c_{5(1)}{c}_{5(2)}{r}_{X1X2}^5+c_{2\left(1\right)}(c_{0\left(2\right)}+c_{2\left(2\right)}+3c_{4\left(2\right)}+2c_2{r}_{X1X2}^2+12c_4{r}_{X1X2}^2)\end{array}$$

So by substituting the desired correlation in r_Y1Y2 and obtaining the appropriate polynomial coefficients, it is possible to solve for r_X1X2 and obtain the intermediate correlation matrix.

Both theoretical and simulation results have shown that the fifth-order polynomial method can, indeed, obtain estimates of skewness and kurtosis that cannot be achieved through the implementation of third-order polynomials (Headrick 2002, 2004). It has also been shown that the range of possible correlation values allowed by using the Headrick (2002) method is much wider than when using the Vale and Maurelli (1983) method (Headrick, 2004). The polynomial coefficients place boundaries on the correlational structure that each method can generate, so it is not unusual to find that certain correlations (particularly on the higher or lower ranges) cannot be reproduced when certain combinations of skewness or kurtosis are present, particularly if one variable is severely skewed and the other one is symmetric (Mair, Satorra, & Bentler, 2012). It is also relevant to point out that since the intermediate correlation matrix is estimated in a pairwise fashion, there is no guarantee that it will be positive definite once it is fully assembled (Fan, Sivo, & Keenan, 2002; Li & Hammond, 1975). Both polynomial methods have this problem, but Headrick (2002) has shown that his method is much more flexible in terms of the values that these correlations may have.

Issues on the Implementation of the Polynomial Methods in Simulation Studies

Because of its ease of implementation, the Vale and Maurelli (1983) multivariate extension of Fleishman’s (1978) method is arguably the most-widely used method in simulation studies for the social sciences. It has more than 130 citation counts on ISI’s Web of Knowledge (and more than 230 on Google Scholar) and has been the default in popular software programs such as EQS and the lavaan and semTools packages in R. In spite of its widespread use, there is not much research documenting its implementation, outside of the fact that other methods can cover a wider range of skewness/kurtosis combinations and ranges of correlation values.

Only two series of studies were found to specifically address the issue of empirically assessing the quality of the nonnormal data generated by both the third-order polynomial and the fifth-order polynomial methods (Kraatz, 2011; Luo, 2011). Kraatz (2011) evaluates the third- and fifth-order polynomial methods (alongside the g- and h- distributions) in terms of the theory behind the method and the quality of the estimates they generate. In her evaluation of the Vale and Maurelli (1983) method (which is directly relevant to the purpose of this article), Kraatz (2011) presents eight combinations of skewness/kurtosis from published articles (0/25, 0/3, 1/1, 1.75/3.75, 2/6, 3/21, −1.25/3.75, and 2/40) at two different sample sizes (40 and 100) and 100,000 replications per condition to empirically estimate their expected values. Overall, she found that the simulation-derived expected values are almost never close to the values specified in the population (and intended by the researcher), sometimes underestimating it them by a substantial amount. She concluded that skewness tends to be better reproduced than kurtosis and that, overall, larger sample sizes were needed to obtain better parameter estimates of skewness and kurtosis, even though they also resulted in larger variability of the estimates.

Luo (2011) focuses on ordinal data in structural equation models but contains two sets of studies where the Fleishman (1978) method, the Vale and Maurelli (1983) extension, the Headrick and Sawilowsky (1999) modification of Vale and Maurelli, the Headrick (2002), and Ruscio and Kaczetow (2008) methods are investigated. In her simulation study, she chose distributions of Dimension 2 (with a skewness of √8 and a kurtosis of 12), 3 (with skewness/kurtosis combinations of 2/6, 0/3, and 0/1.2), and 4 (with skewness/kurtosis combinations of 2/6, 0/0, √8/3, and 0/3) at sample sizes of 10, 20, 100, and 1,000 and 50,000 replications per condition. In her assessment of these methods, she concludes that the Ruscio and Kaczetow (2008) method is preferred in the cases of large sample sizes and that Headrick and Sawilowsky’s (1999) modification is to be preferred at small samples.

One relevant aspect of both Luo and Kraatz’s work touches on the fact that the estimates of higher order moments can be biased and highly variable if the sample sizes are small or moderate. In some of the simulation conditions studied by Kraatz and Luo, the mean of the empirical distributions of the kurtosis values were several units lower than the population-defined ones, sometimes even less than half of their intended value.

Another issue that is raised in both studies is the fact that both the third and fifth order polynomial methods can have more than one set of solutions for the exact same values of skewness and kurtosis. The fact that there is more than one solution can be predicted by the fundamental theorem of algebra so that nonconstant polynomials of degree higher than one are susceptible to have many solutions, especially if nonreal solutions are also taken into account. Aside from the work of Headrick and Kowalchuk (2007) there are no guidelines in the literature that help researchers choose which set of polynomial coefficients are appropriate for data-generation purposes and no studies have yet been done to see whether the conclusions from simulation studies change depending on the use of different sets of polynomial coefficients.

Because very limited literature exists that evaluates the use and quality of the data generated through the previously discussed methods, the series of studies herein aims to address two specific goals. The first goal, and hence the first study, is meant to assess the performance of the third-order polynomial method with high-dimensional data. Although the studies conducted both by Kraatz and Luo investigate correlated data, Kraatz only worked with bivariate distributions and Luo did not consider distributions with more than 4 dimensions. Currently, to our knowledge, no published studies exist where the quality of the data generated by the Vale and Maurelli (1983) method is analyzed in models where the factor structure of the covariance is known in the population. There are also, to our knowledge, no published studies answering the question of whether or not typical factor models used in simulation studies imply nonpositive definite intermediate correlation matrices. This study will look at both issues.

The second goal, and hence the second study, aims to redo the first simulation study in Curran, West, and Finch (1996) using Headrick’s fifth-order polynomial method, in order to discover whether or not some of the conclusions from this published article would change if a different data-generation method had been used. Some of the computational difficulties of implementing the Headrick (2002) method will be discussed as well as general recommendations for quantitative analysts for the use of each algorithm.

Method

Study 1

Four articles were chosen to exemplify the use of the Vale and Maurelli (1983) method in the robustness literature: Curran et al. (1996); Finch, West, and MacKinnon (1997); Flora and Curran (2004); and Skidmore and Thompson (2011). The first three were chosen because of their prominence in the structural equation modeling (SEM) literature, as evidenced by their citation count. The Skidmore and Thompson (2011) article was selected both because it is outside of the field of SEM (hence illustrating the use of the Vale & Maurelli, 1983, method in other types of robustness studies) and because of its relatively recent publication date, hinting toward the fact that the third-order polynomial approach is still very much in vogue.

For the first study, the models and simulation conditions investigated by the authors in the previously mentioned articles were redone, but instead of looking at the impact that nonnormality had on the parameter estimates, the sample estimates of skewness and kurtosis were recorded. All simulations and analyses were done in the R (Version 3.0.3) programming environment, using the lavaan package (Rosseel, 2012, Version 0.5-15), which implements the Vale and Maurelli (1983) method to generate nonnormal data through the simulateData() function. Each combination of sample size and nonnormality condition was replicated 10,000 times. Table 1 summarizes the sample sizes and skewness/kurtosis population values used in the articles. Path diagrams of the models can be found in the appendix.

Table 1.

Sample Sizes and Skewness/Kurtosis Combinations Studied in Each Article.

Article	Sample Size	(Skewness, Kurtosis)
Curran, West, and Finch (1996)	100, 200, 500, 1,000	(0, 0) (2, 7) (3, 21)
Finch, West, and MacKinnon (1997)	150, 250, 500, 1,000	(0, 0) (2, 7) (3, 21)
Flora and Curran (2004)	100, 200, 500, 1,000	(0, 0) (0.75, 1.75) (1.25, 3.75)
Skidmore and Thompson (2011)	10, 20, 40, 60, 100, 200	(0, 0), (1, 1), (−1.5, 3.5)

Note. The Flora and Curran (2004) article used all possible combination of these values. Only a subset of them was used here to make the studies comparable.

In all four articles, the large-sample properties of the skewness and kurtosis estimates were verified by means of generating “empirical” populations of size 10,000 (Curran et al., 1996; Finch et al., 1997); 50,000 (Flora & Curran, 2004); and 100,000 (Skidmore & Thompson, 2011). The same empirical populations were reproduced using lavaan to ensure that the data-generation method was comparable across the different studies (EQS was used in the first three articles to generate data and the SAS macro described in Fan et al., 2002, was used for the last article). Descriptive statistics were calculated to investigate any potential biases of the estimates as well as their variability. Intermediate-correlation matrices were also calculated in each case to verify their positive-definiteness.

Study 2

For the second study, the fifth-order polynomial method as described in Headrick (2002) was implemented in R to compare its sample estimates of skewness and kurtosis to the ones generated by using Vale and Maurelli (1983). To investigate this method further, the first simulation study described in Curran et al. (1996) (“Model 1” on p. 19) was rerun, under the same conditions, but using the newer data-generation algorithm to discover the impact (if any) that it could have on the conclusions from the study.

Headrick, Sheng, and Hodis (2007) provide a Mathematica script that needed to be adapted in R before the main simulation studies could be set up.¹ The nlimnb() function was used to find the roots of the fifth-order polynomial equations instead of the FindRoot routine from Mathematica. To verify the validity of the R implementation of the Mathematica script, some of the simulations done in Headrick (2002) and Headrick and Kowalchuck (2007) were run and results were compared with the tables published in said articles. All answers were within four or five decimal points showing that the R script was accurately implementing the fifth-order polynomial method as it was originally intended.

An initial problem that had to be overcome was the fact that no ranges of potential values for the standardized higher order moments are known if the skewness and kurtosis values are set in advance. Even though Headrick (2002, 2004) provides certain values for the fifth- and sixth-order moments for certain combinations of skewness and kurtosis, no values are available for the combinations of skewness/kurtosis used in the published articles being analyzed. To obtain a solution, a grid search was programmed where the known values shown in Headrick (2002) are used as starting values and then R would attempt different solutions until estimates of the fifth and sixth standardized higher order moments were found. The grid search starts by randomly generating two lists of 50 candidate values (each for one higher order moment) and inspects all first 10 × 10 combinations in search of a solution. If no solution is found, the index for the fifth-order moment is increased to 15 so 5 new combination of values is explored. If all those values are traversed and no solution is found, the index for the sixth-order moment is increased then to allow new candidates and the process is repeated. This method of exhaustively exploring candidate solutions is standard practice for grid search—the interested reader can consult Kruschke (2010, Chap. 6), for a more in-depth explanation. A list of these values was kept in order to use them either to calculate future values of skewness and kurtosis or to go through the data-generation process more efficiently. Once the values for the fifth and sixth standardized order moments are found, the data-generation process is relatively straightforward.

For the purposes of comparing methods, descriptive statistics of the estimated skewness and kurtosis values of the fifth-order polynomial were computed. Headrick (2002) showed in simulation studies that estimates of skewness and kurtosis from his method are superior in terms of less variability and smaller bias, but Luo’s (2011) results seem to contradict this finding. In her simulation studies, she found that the improvement provided by the Headrick (2002) method over Vale and Maurelli (1983) was marginal at the cost of great computational complexity. She also found that in the cases of three- and four-dimensional distributions, the sample estimates of the correlations were biased (even at the sample size of 1,000) making it the least efficient one among the ones she studied. Kraatz (2011) also speculates that the fifth-order polynomial method could become “unpredictable” (p. 61) if used to simulate data in higher dimensional settings (much like the ones being studied here) but provides no evidence of this.

The main purpose of Study 2, however, is to answer the question of whether conclusions derived from simulations using the Vale and Maurelli (1983) method hold when the Headrick (2002) method is chosen instead. Because of the exploratory nature of this study, only the simulations done for Model 1 (properly specified model) described in Curran et al. (1996) were redone to exemplify the uses of the fifth-order polynomial method. The same simulation conditions were implemented with the only exception that instead of 500 replications (as in the original study), 10,000 replications were used to ensure the stability of the results. Portions from table 1 (p. 22) from the Curran et al. (1996) article were reproduced including the estimated chi-square values obtained when the Headrick (2002) method was used. Although not investigated in the original study, the average standard errors in each simulation condition will also be reported to further investigate any differences that may arise by using each data-generation method. To ensure comparability between both simulation studies, the mimic=“EQS” option was specified within the cfa() function of lavaan.

Results

Study 1

Descriptive statistics of the estimates across the 10,000 replications for each sample size are shown in Table 2. Because of the large number of simulation conditions studied in each article, only one SEM model was chosen for Curran et al. (1996); Finch et al. (1997); and the Flora and Curran (2004) to report in the table. For Skidmore and Thompson (2011), only results with population correlation of 0.5 are depicted. For these particular articles, the various types of SEM models and ranges of correlations did not seem to have an impact on the quality of the sample skewness and kurtosis estimates generated by the Vale and Maurelli (1983) algorithm. There was also no evidence found that any of the models or correlational structures implied nonpositive definite intermediate correlation matrices.

Table 2.

Mean (M), Median (Mdn), Standard Deviation (SD) Minimum (Min), and Maximum (Max) of the Skewness and Kurtosis Estimates Generated by Vale and Maurelli (1983).

	N = 100			N = 200			N = 500			N = 1,000
	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max
Curran, West, and Finch (1996)
Skewness = 2	1.70/1.59	0.62	0.62/7.43	1.83/1.72	0.55	0.57/7.58	1.97/1.91	0.33	1.22/7.21	1.99/1.94	0.31	1.35/7.93
Kurtosis = 7	4.26/3.04	4.45	−1.01/63.11	5.32/4.09	4.63	−0.42/102.8	6.57/5.72	3.73	1.57/114.2	6.60/5.74	3.66	1.77/137.21
Skewness = 3	2.21/2.09	1.21	−4.63/8.09	2.48/2.33	1.15	−4.56/11.04	2.74/2.60	1.02	−3.82/13.26	2.86/2.72	0.83	−1.89/14.66
Kurtosis = 21	9.65/7.11	8.51	−0.53/75.68	12.88/9.71	10.60	1.20/136.55	16.44/12.77	12.40	3.12/211.7	18.38/14.83	12.50	4.69/359.73
	N = 150			N = 250			N = 500			N = 1,000
	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max
Finch, West, and McKinnon (1997)
Skewness = 2	1.78/1.67	0.58	0.35/7.95	1.86/1.77	0.51	0.78/8.08	1.93/1.85	0.42	1.00/7.70	1.96/1.90	0.32	1.20/4.02
Kurtosis = 7	4.86/3.59	4.70	−0.61/80.22	5.61/4.35	4.57	−0.12/95.56	6.26/5.16	4.01	0.75/107.7	6.56/5.71	3.65	1.51/132.12
Skewness = 3	2.25/2.12	1.43	−4.29/9.11	2.55/2.42	1.11	−8.36/12.02	2.76/2.58	0.92	−4.33/11.62	2.86/2.73	0.84	−4.78/16.66
Kurtosis= 21	9.74/7.44	9.12	−0.32/93.86	13.71/10.46	11.60	1.36/175.92	16.74/13.11	13.64	4.32/208.9	18.20/14.90	12.10	4.82/390.06
	N = 100			N = 200			N = 500			N = 1,000
	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max
Curran and Finch (2004)
Skewness = 0.75	0.56/0.41	0.36	−1.12 /7.32	0.64/0.59	0.28	−1.06/6.33	0.71/0.68	0.16	−0.98/4.12	0.74/0.71	0.08	0.01/3.12
Kurtosis = 1.25	0.98/0.82	1.13	−0.16/23.18	1.11/0.96	1.64	−0.04/17.44	1.16/1.04	1.78	0.06/19.26	1.22/1.17	2.03	0.09/13.11
Skewness = 1.25	1.06/0.99	0.55	−1.13/6.11	1.14/1.08	0.43	−0.99/5.56	1.21/1.16	0.33	0.13/4.43	1.23/1.20	0.21	0.55/3.04
Kurtosis = 3.75	2.34/1.56	2.93	−0.83/46.72	2.96/2.16	3.11	−0.71/38.83	3.40/2.77	3.96	0.11/81.35	3.59/3.05	4.22	0.65/77.58
	N = 10			N = 40			N = 100			N = 200
	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max	M/Mdn	SD	Min/Max
Skidmore and Thompson (2011)
Skewness = 1	0.18/0.09	0.21	−1.65/1.98	0.36/0.21	0.16	−1.08/1.33	0.78/0.52	0.12	−0.96/1.29	0.91/0.76	0.08	−0.10 /1.06
Kurtosis = 1	0.12/0.06	0.33	−2.34/3.02	0.22/0.16	1.62	−1.04/7.88	0.31/0.25	2.02	−0.86/14.61	0.72/0.64	2.14	−0.88/19.06
Skewness = −1.5	−0.63/0.59	0.52	−2.22/1.36	−1.15/−1.08	0.50	−4.96/0.08	−1.33/−1.26	0.44	−5.20/−.031	−1.41/−1.36	0.37	−4.38/−0.50
Kurtosis = 3.5	−0.68/−0.99	1.00	−2.15/3.39	1.36/0.71	2.31	−1.59/20.44	2.35/1.64	2.58	−1.08/37.93	2.87/2.25	2.48	−0.59/59.67

There is a consistent downward bias of the skewness/kurtosis estimates across all sample size conditions and across all different studies. In general, sample skewness is estimated much more accurately than sample kurtosis and higher levels of kurtosis at smaller sample sizes were generated with a heavily downward bias, which is consistent with the findings from the Luo (2011) and Kraatz (2011). From inspecting the minimum and maximum values, it is possible to see that there is much variability in the estimates, particularly for sample kurtosis. For the population kurtosis value of 21, there were instances where the Vale and Maurelli (1983) algorithm generated estimates more than 10 times larger than what was specified in the population. It is important to point out that the variability in the estimates of skewness and kurtosis (measured by the standard deviation of the empirical distributions) seems to follow different patterns as sample size becomes larger. For skewness estimates, the standard deviations are progressively reduced but for kurtosis estimates, they tend to increase.

To further analyze the nature of the bias in the skewness and kurtosis estimates, Table 3 shows the percentage of the values generated by Vale and Maurelli (1983), which fall below the population values specified by the authors. In general, the majority of the estimates are below the population parameter, particularly for small sample sizes and higher levels of skewness/kurtosis.

Table 3.

Percentage of Sample Estimates Lower Than the Population Estimates Across 10,000 Replications.

	Curran, West, and Finch (1996)
	N = 100	N = 200	N = 500	N = 1,000
Skewness = 2	75.66	71.36	62.06	58.51
Kurtosis = 7	83.35	78.08	68.29	58.61
Skewness = 3	79.81	74.88	72.77	66.54
Kurtosis = 21	91.24	86.40	84.75	76.98
	Finch, West, and MacKinnon (1997)
	N = 150	N = 250	N = 500	N = 1,000
Skewness = 2	72.85	69.82	65.58	59.82
Kurtosis = 7	80.92	77.68	66.93	60.11
Skewness = 3	73.69	72.04	69.23	65.38
Kurtosis = 21	88.74	85.82	81.93	76.04
	Flora and Curran (2004)
	N = 100	N = 200	N = 500	N = 1,000
Skewness = 0.75	62.13	59.48	50.12	46.88
Kurtosis = 1.25	68.11	65.72	61.66	58.16
Skewness = 1.25	70.33	66.34	61.46	60.32
Kurtosis = 3.75	81.54	77.11	70.06	67.82
	Skidmore & Thompson (2011)
	N = 10	N = 40	N = 100	N = 200
Skewness = 1	96.11	88.50	67.95	59.12
Kurtosis = 1	98.12	90.42	74.57	69.16
Skewness = −1.5	6.24	20.85	28.42	34.07
Kurtosis = 3.5	100.00	87.28	78.85	73.49

Note. All values are in percentage.

Even at the largest sample size condition of 1,000, a substantial amount of sample skewness and kurtosis are still below the values intended by the simulation conditions.

Study 2

For Study 2, the same values of skewness and kurtosis used in the Curran et al. (1996) simulation studies were re-calculated using the Headrick (2002) method. Only the correctly specified model condition (“Model Specification 1” in their article) was run. Table 4 shows the average across 10,000 replications for the differing sample sizes and higher order moment conditions. It can be seen that the empirical averages generated by the Headrick (2002) method, although still downward biased, are closer to those specified in the population. The standard deviations for each condition are also consistently lower when compared with the ones calculated from the values generated via the Vale and Maurelli (1983) algorithm, which helps show that the fifth-order polynomial method also generates estimates that are more consistent.

Table 4.

Comparison of the Mean Skewness and Kurtosis Estimates Between the Vale and Maurelli (1983) Method (VM) and the Headrick (2002) Method (H) for the Curran, West, and Finch (1996) Study Across 10,000 Replications.

	N = 100		N = 200		N = 500		N = 1,000
	VM	H	VM	H	VM	H	VM	H
Skewness= 2	1.70 (0.62)	1.92 (0.51)	1.83 (0.55)	1.98 (0.42)	1.97 (0.33)	2.00 (0.31)	1.99 (0.31)	2.00 (0.30)
Kurtosis = 7	4.26 (4.45)	5.85 (2.42)	5.32 (4.63)	6.12 (3.44)	6.57 (3.73)	6.83 (3.11)	6.60 (3.66)	6.96 (3.50)
Skewnes = 3	2.21 (1.21)	2.61 (1.19)	2.48 (1.15)	2.76 (1.06)	2.74 (1.02)	2.79 (0.91)	2.86 (0.83)	2.96 (0.67)
Kurtosis = 21	9.65 (8.51)	12.46 (7.90)	12.88 (10.63)	16.39 (9.58)	16.44 (12.40)	18.02 (10.88)	18.38 (12.55)	20.46 (11.05)

Note. Standard deviations appear within parentheses.

Just as with the estimates shown in Table 2, the kurtosis values obtained via the Headrick (2002) method exhibit an increasing trend in their standard deviations as the sample size grows larger, the opposite of what happens to the skewness estimates, where larger sample sizes are associated with less variability.

In Figure 1, it is possible to see the mean values across replications for each condition of sample size and population skewness and kurtosis. The Headrick (2002) method consistently outperforms the Vale and Maurelli (1983) method in terms of less bias in the parameter estimates, but its overall slope is smaller so it approaches the true population values at a slower rate, particularly in small samples. With the exception of the population skewness of 2, neither method ever reaches their intended value, although the fifth-order polynomial approach is always the closest.

Figure 1.

Plots of means for skewness and kurtosis values across simulation replications as a function of sample size conditions. True population values are shown in black.

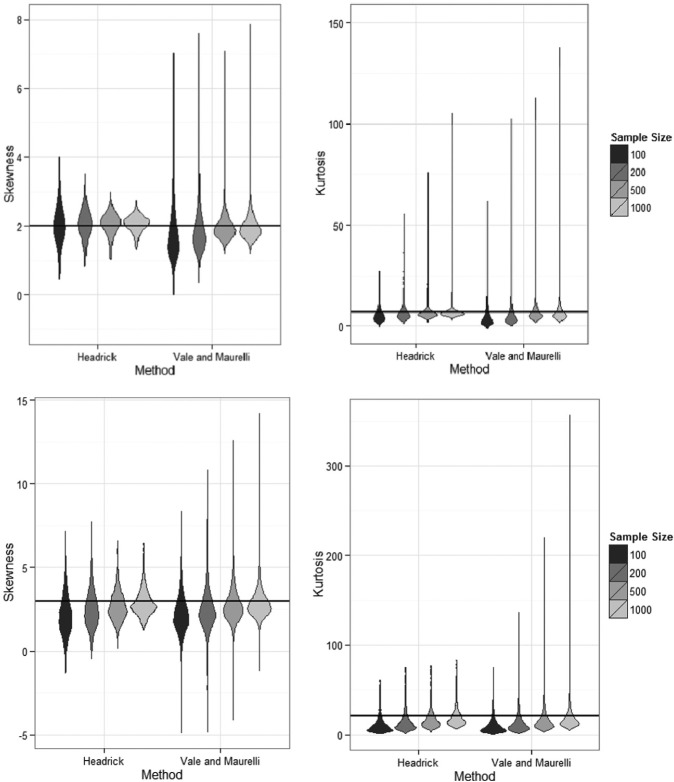
To visually investigate the variability of the estimates, violin plots for each skewness/kurtosis combination and sample size condition are presented in Figure 2. As a hybrid between a boxplot and an empirical density plot, violin plots highlight the areas of highest mass in the distribution of the data as well as the behavior of its furthermost points. It is possible to see that the Vale and Maurelli (1983) method is susceptible to generating extreme points, particularly when the population values of skewness or kurtosis are high. The Headrick (2002) method is much more consistent in generating sample skewness and kurtosis values closer to the true value intended in the population. By comparing the areas of highest density of the data (where the “shoulders” of the violin plot begin to appear) across methods, it becomes apparent that the fifth-order polynomial algorithm consistently outperforms the third-order polynomial approach, particularly with increasing sample size. This fact is most evident in the condition of population kurtosis of 21 where, as sample size increases, the curves of the violin plot for the Headrick (2002) method become wider and closer around the true population value. Although the Vale and Maurelli’s (1983) plot also approaches the intended value, it can be readily seen that the highest density of the data is still below it. Contrary to the plots depicting skewness, where larger sample sizes imply that the largest density of the data concentrates around the population values, kurtosis plots show the same trend of more extreme values being generated at higher sample sizes, reflecting the increases in standard deviation of the estimates shown in Tables 2 and 4.

Figure 2.

Violin plots showing the empirical density of the values of skewness and kurtosis generated by each method. The intended population value is highlighted with a black line. The top two plots correspond to the skewness of 2 and a kurtosis of 7 condition. The bottom two plots show the skewness of 3 and kurtosis of 21 condition.

In terms of whether or not using Headrick’s (2002) method would have influenced the conclusions found in Curran et al.’s (1996) first study on the robustness of the chi-square test of fit, Table 5 compares the values obtained by the authors with the values obtained in this simulation when using both the Vale and Maurelli (1983) approach and the Headrick (2002) approach. The values reported by Curran et al. (1996) differ little from what was found by fitting the model in lavaan. Only the results of the “moderately nonnormal” and “severely nonnormal” conditions are shown, but the normal distribution condition was run to ensure lavaan’s results were comparable.

Table 5.

Chi-Square Values Obtained by the Methods of Maximum Likelihood (ML), Satorra–Bentler (SB) Correction, or Asymptotic Distribution Free (ADF).

N	Method	Moderately nonnormal (skewness = 2, kurtosis = 7)
		Expected	C, W, & F (1996)	VM (1983)	Min/Max VM	H (2002)	Min/Max H
100	ML	24	29.35	29.46	8.59 /72.58	36.19	7.24/61.98
	SB	24	26.06	26.38	8.13/58.76	28.83	6.68/41.51
	ADF	24	38.04	36.85	9.01/64.94	36.16	11.10/47.2
200	ML	24	30.15	29.96	8.93/71.08	34.78	7.41/62.47
	SB	24	25.44	25.18	9.71/47.29	26.36	7.23/40.83
	ADF	24	29.27	28.53	10.11/57.98	31.32	7.36/42.27
500	ML	24	31.26	30.66	10.40/61.01	36.23	10.06/50.76
	SB	24	25.44	24.28	8.33/53.43	25.92	8.11/43.84
	ADF	24	26.42	25.79	10.19/53.73	26.95	8.29/44.48
1,000	ML	24	30.78	30.06	9.94/66.84	36.82	11.77/55.79
	SB	24	24.77	24.32	8.96/55.09	24.16	8.71/42.46
	ADF	24	25.36	25.11	8.79/53.42	24.85	8.04/46.33
N	Method	Severely nonnormal (skewness = 3, kurtosis = 21)
		Expected	C, W, & F (1996)	VM (1983)	Min/Max VM	H (2002)	Min/Max H
100	ML	24	33.54	33.46	10.65/91.09	30.82	7.84/74.38
	SB	24	27.26	27.41	12.17/53.20	28.19	8.31/44.19
	ADF	24	44.82	40.56	11.24/64.14	34.16	11.35/59.43
200	ML	24	34.40	34.78	11.33/104.39	29.86	9.82/97.83
	SB	24	25.80	26.17	11.09/68.59	25.94	9.12/48.94
	ADF	24	31.29	28.66	11.52/52.61	26.80	8.92/41.94
500	ML	24	35.55	34.95	9.46/102.21	31.12	8.57/94.06
	SB	24	24.85	24.62	10.15/52.21	23.62	9.01/46.28
	ADF	24	26.83	25.31	9.37/50.56	25.11	10.09/47.72
1,000	ML	24	37.40	37.10	10.50/94.89	29.73	9.38/95.47
	SB	24	25.01	24.84	8.43/50.16	24.60	8.05/52.96
	ADF	24	25.47	25.20	8.88/48.7	25.12	8.61/49.52

Note. The values reported by Curran, West, and Finch (1996) (C, W, & F) are presented alongside with those obtained using the Vale and Maurelli (1983) (VM) method and the Headrick (2002) (H) method at the various sample size (N) conditions. Minimum and maximum (Min/Max) chi-square values per method and sample size conditions are also presented.

Overall, both the Headrick (2002) and the Vale and Maurelli (1983) methods generated mean chi-square values which were relatively comparable to each other. For the cases of the “moderately nonnormal” condition, the fifth-order polynomial method was consistently associated with higher chi-square values when the model was fitted using likelihood theory. This situation seemed to reverse itself for the “severely nonnormal” condition though, in which the Headrick (2002) method was associated with lower chi-square values (albeit still higher than the expected value for the chi-square distribution). The Satorra–Bentler correction and asymptotic distribution free (ADF) chi-square estimates followed the overall pattern reported by Curran et al. (1996) where the Satorra–Bentler correction yielded the closest values to the expected model chi-square when calculated with nonnormal data, particularly for small sample sizes. No considerable differences were found in the mean chi-square values obtained for the Satorra–Bentler and ADF chi-squares, regardless of whether the Headrick (2002) method or the Vale and Maurelli (1983) method were used. It is important to point out, however, that the Vale Maurelli (1983) method was associated with higher chi-square values, particularly with higher maximums than the Headrick (2002) method.

Table 6 shows the empirical rejection rates published by Curran et al. (1996) and those obtained by generating data through the Vale and Maurelli (1983) and Headrick (2002) method. In general, the Vale and Maurelli (1983) rejection rates appear to be somewhat lower than those reported by Curran et al. (1996; with the exception of chi-squares obtained from the normal theory maximum likelihood), although they are still reasonably close to the ones published in the original study. The empirical rejection rates from the Headrick (2002) method, however, do exhibit some important changes, particularly for the ADF estimator. The Headrick (2002) algorithm yielded empirical rejection rates that were overall higher than those obtained through the Vale and Maurelli (1983) method for the case of the normal-theory maximum likelihood, but they seemed to converge to the nominal alpha of 5% much faster, that is at smaller sample sizes, for the Satorra–Bentler correction and ADF estimator. Although the ADF chi-square still required larger sample sizes to approach the theoretical rejection rate, it did so at smaller sample sizes when the data were generated by the Headrick (2002) method than when the data generated by the Vale and Maurelli (1983) method. For instance, the ADF estimator at a sample size of 200 for the Headrick (2002) method had a better rejection rate than the Satorra–Bentler chi-square calculated from data generated by the Vale and Maurelli (1983) method.

Table 6.

Empirical Rejection Rates Obtained by the Methods of Maximum Likelihood (ML), Satorra–Bentler (SB) Correction, or Asymptotic Distribution Free (ADF) Across 10,000 Replications.

N	Method	Moderately nonnormal (skewness = 2, kurtosis = 7)
		Expected	C, W, & F (1996)	VM (1983)	H (2002)
100	ML	5	20.0	21.7	30.8
	SB	5	8.5	8.6	9.5
	ADF	5	49.0	46.5	26.7
200	ML	5	25.0	20.5	27.9
	SB	5	8.0	7.7	6.7
	ADF	5	19.0	16.1	7.2
500	ML	5	24.0	21.3	29.4
	SB	5	6.9	6.5	6.4
	ADF	5	6.7	6.5	6.0
1,000	ML	5	24.0	23.3	25.6
	SB	5	7.5	6.8	5.8
	ADF	5	7.5	6.6	4.8
N	Method	Severely Nonnormal (skewness = 3, kurtosis = 21)
		Expected	C, W, & F (1996)	VM (1983)	H (2002)
100	ML	5	30.0	33.8	37.9
	SB	5	13.0	12.4	9.3
	ADF	5	68.0	59.4	46.6
200	ML	5	36.0	34.7	38.3
	SB	5	6.5	7.0	5.2
	ADF	5	25.0	19.2	10.3
500	ML	5	40.0	40.0	40.7
	SB	5	8.5	8.4	6.5
	ADF	5	8.5	7.9	4.6
1,000	ML	5	48.0	42.4	42.5
	SB	5	7.0	6.4	4.6
	ADF	5	7.2	6.1	5.9

Note. All values are in percentage. The rejection rates reported by Curran, West and Finch (1996) (C, W, &F) are presented alongside with those obtained using the Vale and Maurelli (1983) (VM) method and the Headrick (2002) (H) method at the various sample size (N) conditions.

Even though it was not initially investigated by Curran et al. (1996), it was of interest to also document whether the choice of data-generation method affects the estimates of standard errors for parameter estimates or not. Percentage reduction of the standard errors was calculated the same way Finch et al. (1997) did by subtracting the estimated standard error from the true parameter and dividing the difference by the true parameter. Table 7 summarizes these results, where it is possible to see that, under the Headrick (2002) method, the shrinkage of the standard errors is higher than when data are generated by the Vale and Maurelli (1983) method.

Table 7.

Percentage Reduction of the Standard Error of the Parameter Estimates at Different Sample Sizes (N) for the Vale and Maurelli (VM) and Headrick (H) Methods.

Skewness = 2 and Kurtosis = 7
N	% Bias (VM)	% Bias (H)
100	35	43
200	31	39
500	33	39
1,000	34	41
Skewness = 3 and Kurtosis = 21
N	% Bias (VM)	% Bias (H)
100	52	61
200	51	58
500	53	58
1,000	52	57

Discussion

As it can be readily seen from the results in Study 1, the quality of the estimates generated by the Vale and Maurelli (1983) algorithm is extremely susceptible to the sample size being chosen, yielding estimates of skewness and kurtosis that can be both moderately to severely downwardly biased and extremely variable. These findings are in line with the ones of Luo (2011) and Kraatz (2011), so it is reasonable to assume that regardless of the dimensionality of the data, the third-order polynomial method can result in suboptimal estimates, unless the sample sizes are moderately large (likely larger than 200, although even at 1,000 one can see some bias when the population kurtosis is large in the population). The estimates of kurtosis were much more biased and variable than those of skewness, possibly because larger sample sizes are needed to estimate more accurately the higher moments of a distribution. In spite of this, even after 10,000 replications the bias was still present. Moderate estimates were generated with more precision than higher estimates of kurtosis, so the Vale and Maurelli (1983) method is still ideal for simulations where either larger sample sizes are used or if lower values of skewness and kurtosis are being inspected. Of particular interest is the seemingly contradictory finding that larger sample sizes are accompanied by increases in the variability of the estimates of kurtosis, as measured by the standard deviation of the sampling distribution. The same trend can be observed in Kraatz’s (2011) work in her tables 20 to 27 (pp. 105-112). A potential explanation for this result is an interplay between the upper bound that the sample size places on the estimates of kurtosis and the tendency of the Vale and Maurelli (1983) algorithm to generate extreme values of it. Dalen (1987) provides the most up to date upper bound to the sample kurtosis as a quadratic function of the sample size. If the sample size grows larger, the bound also becomes higher and the third-order polynomial method has more opportunity to generate values that concentrate toward the extreme of the distribution. Clearly, more research is needed that helps evaluate the quality of the data generated by these algorithms not only in terms of bias but also in terms of the variability of these higher order moments.

Although Li and Hammond (1975) and Headrick (2002) present examples where nonpositive intermediate correlation matrices arose while using the third-order polynomial method, the inspection of the intermediate correlation matrices implied by the models specified in each one of the four articles were all positive definite. A potential explanation as for why this could be the case relies on the fact that the range of correlation values is most restricted when the intended population correlation is high (0.7 and greater) and the variables are either highly skewed in opposite directions or if one variable is skewed and the other one is symmetric (Mair et al., 2012). In all the simulation studies considered here, all the variables had skewness and kurtosis values specified in the same direction, so further research is needed to understand other potential factors that may influence the quality of the data obtained via the Vale and Maurelli (1983) method. Preliminary inspections, for instance, show that if the population correlation coefficients are negative, it is much more likely to obtain a nonpositive definite intermediate correlation matrix.

Study 2 helped understand the use of the fifth-order polynomial algorithm and highlighted many of the advantages and potential problems one may encounter with it. In terms of the quality of the generated data, the results were consistent with those found in Headrick (2002), Kraatz (2011), and Luo (2011), where the newer method outperformed the third-order polynomial method both in terms of less bias and variability. This is, of course, a reasonable expectation because of the fact that the addition of the two higher order moments provides the algorithm with more information to better reproduce the values intended in the population. The use of higher dimensional data (9 dimensions) did not result in unstable estimates and the data-generation procedure was, overall, relatively straightforward once suitable values for the γ₃ and γ₄ values were found. This is, perhaps, one of the biggest drawbacks associated with the Headrick (2002) method. The optimization of these high-dimensional polynomials is not a simple task and there is currently no theory to help potential users choose suitable values of γ₃ and γ₄ for any arbitrary case. Table 2 from Headrick (2002; p. 698) is a good starting point to properly choose some of these values, but most authors use values of skewness and kurtosis well above the range of what is presented there. Experimentation during the process of coding the grid search that currently finds these values in R suggests that there are no specific values but ranges of values of γ₃ and γ₄, which yield acceptable solutions for the polynomial coefficients. Deriving the boundaries of these ranges for given population skewness and kurtosis could be a potential way to expand the results found here.

The comparison of the simulation results from the first model specification in Curran et al. (1996) yielded some very interesting results. Overall, whether one uses the Vale and Maurelli (1983) or the Headrick (2002) method, the results are consistent with the statistical theory surrounding SEM: higher levels of kurtosis inflate the value of the chi-square test of fit (Bollen, 1989). It also supported the general conclusions found in Curran et al. (1996), where the Satorra–Bentler correction is favored over the ADF correction when nonnormality is present. In spite of this, a more nuanced analysis of the results highlights the fact that some of the conclusions the authors arrived at would have changed had the Headrick (2002) method been available to them.

The inflation of the chi-square appeared to be higher with the Headrick (2002) method for the case of moderately nonnormal distributions but somewhat lower for severe nonnormality. This result is slightly counterintuitive given than the third-order polynomial method not only generates values that had lower kurtosis but also that the bulk of these values is on the lower end of the distribution. Further analysis, however, helped show that some of the datasets generated by the Vale and Maurelli (1983) algorithm included pockets of very extreme values of kurtosis, with some having kurtosis values more than 100 for the cases of population kurtosis of 7 and even close to 400 in the cases of population kurtosis of 21, as can be seen in Figure 2. These extreme values of kurtosis generated extreme chi-square values which raised the overall average across simulation repetitions. Because the Headrick (2002) method yields estimates that are more consistent, the inflation of chi-square values is not as severe. Table 5 helps exemplify this by showing the minimum and maximum chi-square values from the 10,000 replications across conditions. In general, the Vale and Maurelli (1983) method had maximum chi-square values that were 10 times higher in the moderately nonnormal condition and around 20 times higher in the severe nonnormal condition, when compared with the Headrick (2002) method.

Table 6 highlights some of the important differences of using the Headrick (2002) versus the Vale and Maurelli (1983) procedures. Even though under normal likelihood theory the Headrick (2002) method resulted in higher rejection rates, it seemed to reach the nominal rate of 5% faster. This case is particularly noticeable for the ADF estimator, where it becomes almost as good as the Satorra–Bentler correction even at samples of 200. This is goes against some of the recommendations found in Curran et al. (1996), where they suggest this estimator should be used in samples of 500 or higher. A working hypothesis of why these differences may have arisen has to do with the fact that because the Vale and Maurelli (1983) method is prone to generating data with very large kurtosis values, the demands it places on the data to estimate the weight matrix needed by the ADF estimator are considerably higher than when the data is generated using the Headrick (2002) method. Under the Headrick (2002) method, the ADF estimator reaches its asymptotic chi-square distribution much faster and obtains a better empirical rejection rate. Regardless of whether one uses the third- or the fifth-order polynomial method, both the Satorra–Bentler correction and the ADF chi-square statistic tended to behave similarly when compared with normal-likelihood chi-square. This comes from the fact that both approaches are specifically designed to handle excess kurtosis and, as sample size grows larger, it is expected that they would behave more and more similarly by returning the Type I error rate to its nominal value. It is important to highlight the fact, however, that when the data is generated by the Headrick (2002) method it appears that the asymptotic properties of the ADF estimator manifest themselves faster. The fact that normal likelihood chi-squares are more different between both data-generating methods could point toward the fact that the multivariate structure implied by both them is not the same. It is important to keep in mind that, when using the power polynomial methods, the multivariate nonnormality is indirectly attained by modifying all the one-dimensional marginal distributions. Neither method offers the researcher any control over what the shape of the joint distribution looks like. An interesting avenue for future research could be to explore different methods that allow the researcher to control the multivariate nonnormality (perhaps by setting a population value of Mardia’s kurtosis or another measure of multivariate nonnormality) and not only the lower dimensional moments.

Table 7 also helps highlight the fact that the shrinkage of standard errors changes depending on whether one uses the Vale and Maurelli (1983) method or the Headrick (2002) method. Future research could look at whether the robust corrections to standard errors require larger sample sizes than what is usually recommended in the published literature, given that standard errors of the parameter estimates tend to be smaller when the data is generated via fifth-order polynomials.

Conclusions and Recommendations

There are two sets of concluding remarks to be made from this article. First, it was the purpose of these studies to start a conversation about the algorithms being used in simulations by highlighting some of the advantages and drawbacks of the Vale and Maurelli (1983) method and looking at the differences in terms of results that can be encountered when another method is used. The third-order polynomial is the status quo in terms of nonnormal data-generation procedures for Monte Carlo studies in the social sciences and, even though it used to be the best alternative available, advances in both computational power and statistical theory have given the quantitative researcher a much wider range of choices, many of which could be better suited to investigate the simulation conditions intended by the researchers. Just a small, and by no means exhaustive list of these methods include the multivariate skew-normal distribution (Azzalini & Dalla Valle, 1996), the multivariate g-and-h distribution (Kowalchuk & Headrick, 2010), Gaussian mixtures (Muthén & Muthén, 2002), copula distributions (Mair et al., 2012), and iterative approaches such as the one described in Ruscio and Kaczetow (2008).

Still, the majority of these methods have received little (if any) attention from researchers in psychometrics and the social sciences, in general. The Headrick (2002) method, for instance, has only been used once within the published SEM literature as the data-generating procedure used in the simulation studies of Tong and Bentler (2013). Most of the citations of the fifth-order polynomial in the social sciences come from researchers commenting on the improvements done by Headrick (2002) and Headrick and Kowalchuk (2007) on the power method, but not many actually use the algorithm itself for the purpose it was intended to (particularly in the multivariate case). Even the overall lack of literature on the empirical properties of the estimates of these algorithms points to the fact that a wide area of study exists which is not seeing much incursion from quantitatively oriented social scientists.

The second concluding remark is that the validity of conclusions in simulation studies depends heavily on the quality of the data-generating procedures, and if these procedures are suspect, the conclusions from simulation studies are suspect as well. For example, the simulation studies done in Lix and Fouladi (2007); Lix, Keselman, and Hinds (2005); and Weathers, Sharma, and Niedrich (2005) use skewness–kurtosis values that imply nonreal polynomial coefficients as solutions to the Fleishman (1978) equations, and a variety of combination of skewness and kurtosis conditions used commonly in the literature can imply odd-shaped (and even bi-modal) distributions on the generated datasets (Kraatz, 2011). There is no published research to document whether different sets of solutions to the Fleishman (1978) and Vale and Maurelli (1983) polynomials influence the results intended by the researchers, yet most people who rely on simulations used this method unsuspectingly.

In conclusion, it is important to raise awareness of a type of “black box” approach to simulation that exists among many quantitative social scientists. Although exceptions do exist where researchers create empirical populations to study the large-sample properties of the data-generating methods they use (all the articles studied here reported doing this as a manner of checking whether the data they generated matches their simulation conditions), there seems to be a general lack of concern or awareness about how exactly many of these algorithms work and, more importantly, their limitations. Being the field traditionally associated with fighting against the “black box” approach to understanding statistics and data analysis, it is crucial that we start taking the necessary steps to not only fully understand the tools of our trade, but also to know which tools work better for which task.

Appendix

Two-factor model for Curran, West, and Finch (1996) with 9 indicators (“Model 1”).

One-factor base model from Flora and Curran (2004) with 10 indicators.

Latent mediation model from Finch, West, and MacKinnon (1997).

Bivariate correlation from Skidmore and Thompson (2011).