Tree-Based Global Model Tests for Polytomous Rasch Models

Abstract

Psychometric measurement models are only valid if measurement invariance holds between test takers of different groups. Global model tests, such as the well-established likelihood ratio (LR) test, are sensitive to violations of measurement invariance, such as differential item functioning and differential step functioning. However, these traditional approaches are only applicable when comparing previously specified reference and focal groups, such as males and females. Here, we propose a new framework for global model tests for polytomous Rasch models based on a model-based recursive partitioning algorithm. With this approach, a priori specification of reference and focal groups is no longer necessary, because they are automatically detected in a data-driven way. The statistical background of the new framework is introduced along with an instructive example. A series of simulation studies illustrates and compares its statistical properties to the well-established LR test. While both the LR test and the new framework are sensitive to differential item functioning and differential step functioning and respect a given significance level regardless of true differences in the ability distributions, the new data-driven approach is more powerful when the group structure is not known a priori—as will usually be the case in practical applications. The usage and interpretation of the new method are illustrated in an empirical application example. A software implementation is freely available in the R system for statistical computing.

Introduction

A major concern in educational and psychological testing is the stability of measurement properties of a test or questionnaire between different groups of subjects, also known as measurement invariance. Violations of this property at the item level are known as differential item functioning (DIF). To assess whether DIF is present, a variety of procedures have been proposed (for a review, see, e.g., Holland & Wainer, 1993).

Nearly all these procedures require an a priori specification of (two or more) groups, which are then analyzed for DIF, such as the likelihood ratio (LR) test (Andersen, 1973), the Mantel-Haenszel test (Holland & Thayer, 1988), logistic regression procedures (Swaminathan & Rogers, 2000), and extensions thereof (De Boeck & Wilson, 2004; Van den Noortgate & De Boeck, 2005), which also allow for hierarchical group structures by means of a flexible mixed model approach.

In practice, the groups are often formed by splitting the sample based on a few standard covariates such as gender, ethnicity, or age. For numeric covariates such as age, the median is often (arbitrarily) used as the split point (like, e.g., in the study of Sauer, Walach, Kohls, & Strobl, 2013, that is, reanalyzed in the section “Application: The Freiburg Mindfulness Inventory”). An advantage of this approach—as opposed to pure mixture distribution (or latent class) approaches (cf., e.g., von Davier & Carstensen, 2007)—is that the usage of observed covariates as splitting variables automatically provides some guidance for the interpretation of detected DIF. However, an obvious disadvantage is that DIF can only be denied for groups explicitly compared by the researcher, leaving the possibility that a later found group difference is only an artifact due to unnoticed DIF.

An approach that combines the benefits of mixture distribution and observed covariate approaches is the extension of logistic regression procedures suggested by Tay, Newman, and Vermunt (2011), which lets the latent class probability depend on concomitant variables (and contains the observed-covariates-only approach as a special case when the number of latent classes is set to one). A strong advantage of this approach is that it is able to incorporate numeric covariates without a priori discretization. As the authors note, “There may be greater sensitivity and power in this approach, as more information is utilized in contrast to a ‘median-split’ approach” (Tay et al., 2011, p.169-172). However, like any parametric model, it requires that the functional form of the association between the covariate and DIF (in this case a logistic regression model for predicting the latent class membership from the observed covariates) be specified in advance. If this specification is wrong, for example, because the true association is nonmonotonic, it might again go unnoticed.

Based on a statistical algorithm called model-based recursive partitioning (Zeileis, Hothorn, & Hornik, 2008), Strobl, Kopf, and Zeileis (2015) proposed an alternative global model testing procedure for dichotomous items, which is sensitive to DIF and requires neither a prespecification of the group structure nor of the specific functional form of the association between covariate and DIF. Given a number of covariates, this procedure identifies groups of persons violating measurement invariance due to DIF in dichotomous Rasch models. This is achieved by means of a recursive, data-driven comparison of all possible groups formed by (combinations of) covariates. Strobl et al. (2015) illustrated this for a variety of complex but realistic group patterns, for example, DIF that is present only between females over a certain age and all other subjects (i.e., DIF associated with an interaction of the two covariates age and gender), groups formed by nonmedian splits in numeric covariates such as age and nonmonotonic patterns (e.g., when both young and old participants are affected). Since the procedure is based on the conditional likelihood and forms a closed testing procedure, it does not lead to an inflation of the Type I error rate even in the presence of true ability differences. Consequently, this approach provides a more thorough and informative basis for further DIF analysis than fixed group or parametric approaches while still maintaining the interpretability of the results.

Besides dichotomous items, polytomous items are often used as an alternative to allow for a more detailed response. As for dichotomous items, various DIF detection procedures exist for polytomous items (for a review, see, e.g., Potenza & Dorans, 1995). Most of these procedures again require a prespecification of the groups or the exact functional form and are therefore susceptible to the same problems as described above. As the model-based recursive partitioning algorithm is not restricted to the dichotomous Rasch model, an extension of this algorithm to polytomous Rasch models can provide a similarly thorough global model test for polytomous items as was provided by Strobl et al. (2015) for dichotomous items. Therefore, the aim of this article is to develop and illustrate an extension of the framework presented by Strobl et al. (2015) to polytomous items.

The extension of the model-based recursive partitioning algorithm to polytomous Rasch models not only provides a global model testing procedure that can identify previously unspecified groups of persons exhibiting DIF. Depending on the underlying model, it also provides a procedure that is sensitive to violations of measurement invariance at the individual score level, a phenomenon termed differential step functioning (DSF; Penfield, 2007). The rationale is the following: Since the model-based recursive partitioning algorithm can detect instabilities in any parameter of a statistical model, and the parameters in polytomous Rasch models most often describe some form of a transition between score levels, a procedure which is sensitive to DIF and DSF is the consequence. In addition, this sensitivity is independent of the sign of the effects and therefore not prone to a cancellation of diverging DSF effects within an item, as some other existing procedures are, for example, the polytomous SIBTEST procedure (Chang, Mazzeo, & Roussos, 1996).

Unlike itemwise tests for DIF and DSF, the framework proposed here offers a global test for DIF and DSF that does not flag individual items or score levels. However, as opposed to other global DIF tests, such as the LR test, our data-driven approach for detecting groups of subjects with different item parameters is much more flexible and the graphical representation of the results can provide additional information about the parameter profiles of these groups, as illustrated below. In summary, the extension of the model-based recursive partitioning algorithm to polytomous Rasch models will provide a global model testing procedure that is able to detect groups of persons violating measurement invariance and is sensitive to both DIF and DSF.

In this article, we present the extension of the model-based recursive partitioning algorithm to two well-known polytomous models from item response theory (IRT), the rating scale model (RSM; Andrich, 1978) and the partial credit model (PCM; Masters, 1982), and thus present a general framework for the detection of groups exhibiting DIF and/or DSF in polytomous items. After an introduction of the RSM and PCM in the next section, a more detailed introduction of the model-based recursive partitioning algorithm, along with an artificial instructive example, follows in the section “Detecting Noninvariant Groups.” The section “Simulation Studies” contains the results of a series of simulation studies to support and illustrate the statistical properties of the proposed procedures together with performance comparisons to the well-established LR test. Finally, an application example with empirical data is presented in the section “Application: The Freiburg Mindfulness Inventory.” A software implementation of the proposed procedures is freely available in the add-on package psychotree (Zeileis, Strobl, Wickelmaier, Komboz, & Kopf, 2015b) for the R system for statistical computing (R Core Team, 2016).

Rating Scale and Partial Credit Model

The RSM and the PCM are two widely applied polytomous Rasch models. The RSM describes the probability that subject $i$ with person parameter ${\theta }_i$ scores in one of the categories $x_{\mathrm{ij}}\in \{0,1,\dots ,p\}$ of item $j$ with item parameter ${\beta }_j$ and a vector of thresholds $\mathbf{\tau }$:

$$P(X_{\mathrm{ij}}=x_{\mathrm{ij}}|{\theta }_i,{\beta }_j,\mathbf{\tau })=\frac{\exp {\displaystyle \sum }_{k=0}^{x_{\mathrm{ij}}}({\theta }_i-({\beta }_j+{\tau }_k))}{{\displaystyle \sum }_{\ell =0}^p\exp {\displaystyle \sum }_{k=0}^{\ell }({\theta }_i-({\beta }_j+{\tau }_k))}$$

with all sums ${\sum }_{k=0}^0$ defined to be $0$.

In the RSM, items are modeled by means of two types of parameters: an item location parameter ${\beta }_j$, describing the overall location of item $j$ on the latent scale and a set of threshold parameters $\mathbf{\tau }=({\tau }_1,\dots ,{\tau }_p{)}^T,$ describing the distance between the overall location ${\beta }_j$, and the transition points from one category to the next category (see Figure 1 for an illustration).

Figure 1.

Category characteristic curves (above) and region plot (below) with regions of most probable category responses of an item with five categories. In addition, the locations of RSM and PCM parameters are depicted.

Note. RSM = rating scale model; PCM = partial credit model.

As becomes clear from Equation 1, the number and values of the threshold parameters ${\tau }_k$ are constant over all items j, which restricts the RSM to a set of items with the same number of categories and also assumes equal distances between the intersections of the category characteristic curves of two adjacent categories over all items.

The PCM relaxes these assumptions by allowing a variable number of categories and spacing of the intersections of the category characteristic curves per item:

$$P(X_{\mathrm{ij}}=x_{\mathrm{ij}}|{\theta }_i,{\mathbf{\delta }}_j)=\frac{\exp {\displaystyle \sum }_{k=0}^{x_{\mathrm{ij}}}({\theta }_i-{\delta }_{\mathrm{jk}})}{{\displaystyle \sum }_{\ell =0}^{p_j}\exp {\displaystyle \sum }_{k=0}^{\ell }({\theta }_i-{\delta }_{\mathrm{jk}})}$$

While ${\theta }_i$ is still the person parameter of subject $i$, each item is now described by a set of threshold parameters ${\mathbf{\delta }}_j=({\delta }_{j1},\dots ,{\delta }_{\mathrm{jk}},\dots ,{\delta }_{j{p}_j}{)}^T$, which mark the intersections between the probability curves of two adjacent categories, that is, the point where the probability of scoring in category $k-1$ is the same as scoring in category k. This is illustrated in Figure 1.

In the upper part of Figure 1, the category characteristic curves of an artificial item with five categories are shown. For given item and person parameters, these curves describe the probability of responding in a category as predicted under the RSM or the PCM. The positions of the RSM and the PCM threshold parameters are depicted, showing their location at the intersection between the category characteristic curves of two adjacent categories.

An alternative illustration that was already used by Van der Linden and Hambleton (1997) in the context of IRT and that is similar to the “effect displays” by Fox and Hong (2009) for ordinal regression models is shown in the lower part of Figure 1. In this illustration, only the regions of the most probable category responses of an item over the range of the latent trait are shown. This type of illustration will be called “region plot” from here on and will be later used as a means of illustrating the results of the new methods.

For ordered threshold parameters, which are increasing in their value with the response categories, the locations of the borders of the regions in the plot directly correspond to the values of the threshold parameters. Otherwise they are given by the mean between two adjacent unordered threshold parameters (Wilson & Masters, 1993). A discussion of the meaning of unordered threshold parameters can be found in Andrich (2013). One possibility to inform the user about the existence of unordered threshold parameters within an item is to depict their locations with dashed lines (see Figure 1) that is employed in all region plots shown here. From the point of view of the proposed procedures, unordered threshold parameters do not pose a problem because only parameter differences between groups and not their order is considered.

Detecting Noninvariant Groups

Similar to the procedure proposed by Strobl et al. (2015), the new framework for polytomous items proposed in the following is based on a statistical algorithm called model-based recursive partitioning (Zeileis et al., 2008). Model-based recursive partitioning is a semiparametric approach that employs statistical tests for structural change adopted from econometrics. The aim is to detect differences in the parameters of a statistical model between groups of subjects defined by (combinations of) covariates.

Model-based recursive partitioning is related to—but by means of modern statistical techniques avoids the earlier weaknesses of—the method of classification and regression trees (CART; Breiman, Friedman, Olshen, & Stone, 1984; see Strobl, Malley, & Tutz, 2009, for a thorough introduction), where the covariate space is recursively partitioned to identify groups of subjects with different values of a categorical or numeric response variable. As an advancement of this approach, in model-based recursive partitioning it is the parameters of a parametric model—rather than the values of a single response variable—that vary between groups. Such parameters could be, for example, intercept and slope parameters in a linear regression model or, as it is the case here, the parameters of a RSM or a PCM that may vary between groups of subjects and thus indicate violations of measurement invariance.

This principle is now first illustrated by means of an artificial instructive example, before the technical details are addressed in the next sections. The data for the instructive example are the responses of 500 hypothetical subjects to 8 items with 3 categories per item simulated under the PCM. These data from a single-case simulation can be thought of, for example, as responses to an attainment test. In addition to the responses, the data set includes three covariates: gender, age, and a motivation score (all discretely uniformly distributed over their respective ranges). The summary statistics of these covariates are reported in Table 1.

Table 1.

Summary Statistics of the Covariates of the Instructive Example (Artificial Data).

Variable	Summary Statistics
Gender	Female: 261			Male: 239
	$x_{\min }$	$x_{0.25}$	$x_{\mathrm{med}}$	$\overline{x}$	$x_{0.75}$	$x_{\max }$
Age(years)	20	35	49	49.69	64	80
Motivation	1	2	3	2.91	4	5

Note. For the categorical variable gender the frequency distribution is displayed, while for the numeric variables age and motivation the minimum $x_{\min }$, the first quartile $x_{0.25}$, the median $x_{\mathrm{med}}$, the mean $\overline{x}$, the third quartile $x_{0.75}$ and the maximum $x_{\max }$ are listed.

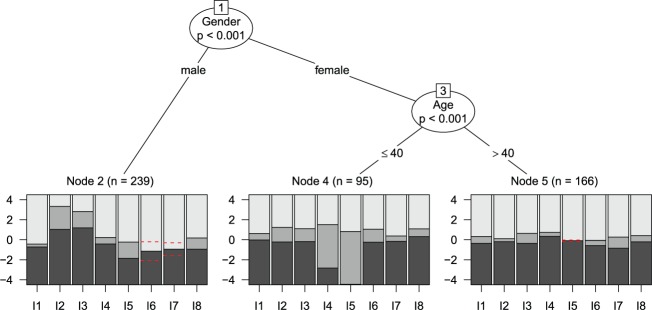
The data of the instructive example were simulated with DIF between males and females in Items 2 and 3: All threshold parameters of these items were higher for males than for females, that is, it was simulated to be more difficult for males to get a higher score on these items. In addition, the threshold parameters of Items 6 and 7 have been reversed for males but not for females to illustrate how unordered threshold parameters are indicated in the graphical output of our procedure. Between females up to the age of 40 and females over the age of 40, DSF was simulated in Items 4 and 5, that is, only the first threshold parameter of these items was different between these two groups such that younger females were simulated to have a lower threshold between the first and second category (see Figure 2 for an illustration of the results). This means that in this example there is no measurement invariance between the groups defined by males, females up to the age of 40 and females over the age of 40 so that these groups should not be compared based on a single measurement model.

Figure 2.

Partial credit tree for the instructive example (artificial data for illustration purposes). In the terminal nodes, region plots are depicted for each item with the estimated threshold parameters of the partial credit model in the corresponding node.

No DIF was simulated with respect to the covariate motivation, so that this variable induces no additional violations of measurement invariance. All ability parameters were drawn from a standard normal distribution.

In order to test whether a single measurement model holds for all persons by means of the model-based recursive partitioning procedure, the item responses are assessed with respect to possible group differences related to the three covariates gender, age, and motivation, as described in detail below. The resulting model, which is partitioned with respect to a combination of the covariates gender and age, is presented in Figure 2 and will be termed a partial credit tree (or a rating scale tree if the RSM is used for partitioning) from here on. In each of the terminal nodes of the tree, a region plot like that in Figure 1 (rotated by 90°) is shown for each item. As in Figure 1, these plots show regions of the most probable category responses over the range of the latent trait, as defined by the estimated threshold parameters of the PCM in the corresponding node.

Overall, the mere fact that there is more than one terminal node in Figure 2 means that the null hypothesis of measurement invariance (i.e., a single PCM would fit for the entire sample) must be rejected. This is how the procedure serves as a global model test for the underlying IRT model. In contrast to standard global model tests, however, we gain much more information from the entire tree structure than from a simple test statistic: The visualization shows the identified subgroups, which did not have to be prespecified but were automatically detected from the data from (combinations of) the available covariates. This structure of noninvariant groups of persons—or, in cases where the tree does not split, the information that no significant violations of measurement invariance were detected in the available covariates—is the main information provided by the model-based recursive partitioning approach.

In addition to the group structure, the visualization of the tree also gives a first impression of the item parameter profiles within the groups. Together, these information can help generate hypotheses about possible underlying sources of the group differences and guide the decision how to proceed.

With respect to the results of the instructive example (Figure 2), we find that the simulated DIF pattern has been correctly recovered: Different threshold parameters have been detected for males and females, and within the group of females for those up to the age of 40 and those over the age of 40. The estimated threshold parameters of Items 2 and 3 have higher values for males (Node 2) than for females (Nodes 4 and 5). In addition, reversed threshold parameters for males in Items 6 and 7 are indicated by dashed lines. Within the group of females, the first threshold parameters of Items 4 and 5 are much lower for females up to the age of 40 (Node 4) than for females above the age of 40 (Node 5). This means that the noninvariant groups and the item parameter profiles within the groups were correctly recovered by the algorithm.

It is important to note that in order to come to this result, all that was passed over to the algorithm was the three covariates age, gender, and the motivation score. Neither the specific subgroups nor the cutpoint within the numeric covariate age were prespecified. Both had to be detected by means of the available data. Especially the data-driven detection of the cutpoint within the numeric covariate age is in contrast to the widely employed approach of arbitrarily splitting a numeric variable at the median (which for the subgroups of females would have been at the value 47 and thus too high). This common practice would not only have concealed the actual age at which the parameter change occurs but may even result in not detecting significant noninvariance in a numeric variable at all, as was shown by Strobl et al. (2015) for the Rasch tree approach and as is further illustrated in the simulation studies below for the extension to polytomous items proposed here. As will be explained in more detail in the section “Selecting the Cutpoints,” the exact value of the empirical cutpoint may vary between random samples from the same population, but on average is very well able to recover the true cutpoint and has a clear advantage over arbitrarily chosen cutpoints such as the median (also illustrated in Strobl et al., 2015).

In addition to the successful recovery of the noninvariant groups, the item parameter profiles within the groups were correctly identified. In particular, besides the general effect of DIF, that is, the shift in all threshold parameters of an item, the fact that in two items only single threshold parameters differ between females up to the age of 40 years and above the age of 40 years (i.e., DSF) was also correctly discovered by the partial credit tree. Moreover, the variable motivation was not selected for splitting, which also correctly replicates the simulated pattern where this variable induced no violation of measurement invariance.

The data-driven identification of the group structure is a key feature of the model-based recursive partitioning framework employed here, which makes it very flexible for detecting noninvariant groups and distinguishes it from other procedures, where DIF can only be detected between those groups or with respect to the functional form that was specified a priori.

Technically, the following consecutive steps are used to infer the structure of a partial credit tree like that depicted in Figure 2 from the data:

1. Estimate the model parameters jointly for all subjects in the current sample, starting with the full sample.

2. Assess the stability of the item or threshold parameters with respect to each available covariate.

3. If there is significant instability, split the sample along the covariate with the strongest instability and in the cutpoint leading to the highest improvement of model fit.

4. Repeat Steps 1 to 3 recursively in the resulting subsamples until there are no more significant instabilities (or the subsample becomes too small).

These four steps are now explained in more detail and the extension of the approach of Strobl et al. (2015) for the polytomous Rasch models is explicitly formulated.

Estimating the Model Parameters

Since the person raw-scores $r_i={\sum }_{j=1}^m{x}_{\mathrm{ij}}$ form sufficient statistics for the person parameters in the family of Rasch models (Andersen, 1977), a conditional maximum likelihood approach can be used. In this approach, the conditional likelihoods given in Equation 3 for the RSM and in Equation 4 for the PCM are maximized by means of iterative procedures to estimate the item and threshold parameters.

$$L_c(\mathbf{\beta },\mathbf{\tau }|r_1,\dots ,r_n)=\underset{i=1}{\overset{n}{\Pi }}{L}_c(\mathbf{\beta },\mathbf{\tau }|r_i)=\underset{i=1}{\overset{n}{\Pi }}\frac{\exp (-{\sum }_{j=1}^m(x_{\mathrm{ij}}·{\mathrm{\beta }}_j+{\sum }_{k=0}^{x_{\mathrm{ij}}}{\tau }_k)}{{\gamma }_{r_i}(\mathbf{\beta },\mathbf{\tau })}$$

$$L_c(\mathbf{\delta }|r_1,\dots ,r_n)=\underset{i=1}{\overset{n}{\Pi }}{L}_c(\mathbf{\delta }|r_i)=\underset{i=1}{\overset{n}{\Pi }}\frac{\exp (-{\sum }_{j=1}^m{\sum }_{k=0}^{x_{\mathrm{ij}}}{\delta }_{\mathrm{jk}})}{{\gamma }_{r_i}(\mathbf{\delta })}$$

In Equation 3 as well as in Equation 4, ${\gamma }_{r_i}$ are the elementary symmetric functions of order $r_i$ (cf. e.g., Fischer & Molenaar, 1995). To fix the origin of the scale, for both equations some constraint has to be applied, leaving $m+p-2$ free parameters in the RSM and ${\sum }_{j=1}^m{p}_j-1$ free parameters in the PCM.

Here, we use the common constraint to set the first threshold parameter of the first item to zero, that is, ${\delta }_{11}=0$ for the PCM and ${\beta }_1=0$ as well as ${\tau }_1=0$ for the RSM. Note, however, that all subsequent analyses are not affected by the choice of this constraint because—unlike itemwise DIF tests, where the selection of anchor items is crucial (Kopf, Zeileis, & Strobl, 2015; Wang, 2004)—in a global test framework like the one employed here, the result is independent of the choice of the constraint because under the global null hypothesis all item parameters are equal, which would hold under any constraint, and any deviation correctly leads to a rejection of measurement invariance.

Testing for Parameter Instability

To test whether the model parameters vary between groups of subjects defined by covariates, we use the approach of structural change tests from econometrics. The rationale of these tests is the following: The model parameters are first estimated jointly for the entire sample. Then the individual deviations from this joint model are ordered with respect to a covariate, such as age. If there is systematic DIF or DSF with respect to groups formed by the covariate, the ordering will exhibit a systematic change in the individual deviations. If, on the other hand, no DIF or DSF is present, the values will merely fluctuate randomly.

Note that, in the case of DIF or DSF, the joint model used in the starting node, which assumes the same parameter values for the entire sample, is actually misspecified and thus misfits. However, the method is not relying on the initial model to fit—to the contrary, it is exactly the misfit that is used by the structural change test approach: The misfit is reflected in the score contributions from the initial model, so that the first split can start resolving the misfit with respect to the variable most strongly associated with DIF. As long as there is still misfit in the resulting models, the splitting will continue. Therefore, at every level of the tree any remaining misspecification of the current model should be considered as a valuable means for quantifying the misfit to recursively resolve it, rather than an erroneous violation of the model assumptions.

The statistical theory behind the structural change tests is explained in detail by Merkle and Zeileis (2013) and in the context of recursive partitioning by Zeileis et al. (2008), Strobl et al. (2015), and Strobl, Wickelmaier, and Zeileis (2011), but is shortly illustrated in Figure 3: In this example, the individual contributions of all subjects to the score function, which is used for the estimation of a parameter, are ordered with respect to the variable age. The score contributions are the derivatives of the individual observations’ contributions to the log-likelihood with respect to the parameter vector and quantify the individual deviations from a joint parameter estimate. By construction the sum over all deviations from the joint estimate is zero (i.e., fulfill the first-order condition of the likelihood maximization), but some subjects will have positive and other subjects will have negative score contributions (that are illustrated as dashed lines in Figure 3).

Figure 3.

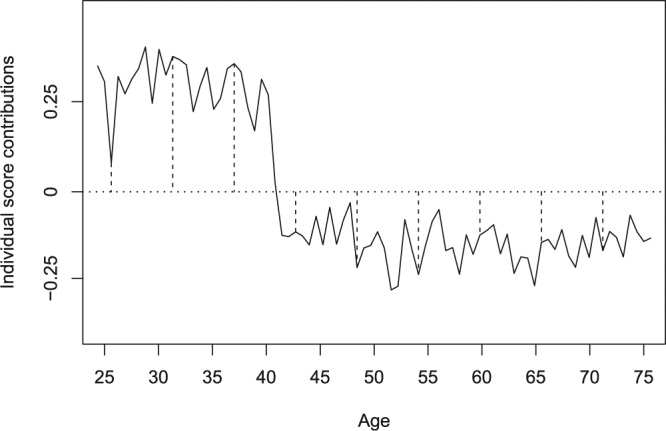
Structural change in the variable age (artificial data for illustration purposes). The individual score contributions are ordered with respect to the variable age. The dashed lines indicate deviations from the overall mean zero, which are positive before the structural change and negative afterward.

When these score contributions are ordered with respect to the variable age, it becomes obvious that they do not fluctuate randomly around the mean zero—which would be the case under the null hypothesis that one joint parameter estimate is appropriate for the entire sample—but there is a systematic change at the age of 40. This systematic change indicates that, instead of one joint parameter estimate for the entire sample, different parameter estimates should be permitted for subjects up to the age of 40 and above the age of 40.

Based on statistical theory described in Zeileis et al. (2008), p values can be provided for each candidate variable. An advantage of the underlying score-based approach is that the model does not have to be reestimated for all splits in all covariates, because the individual score contributions remain the same and only their ordering needs to be adjusted for evaluating the different covariates.

For the RSM and the PCM, the individual score functions can easily be computed from the conditional likelihoods given in Equations 3 and 4 and are provided in Appendix A. Based on the individual score functions, the structural change tests outlined above can be applied straightforwardly. The results of these tests for the instructive example are shown in Table 2.

Table 2.

Summary of the Parameter Instability Test Statistics and Corresponding Bonferroni-Adjusted p Values for the Instructive Example.

		Node 1	Node 2	Node 3	Node 4	Node 5
Age	Statistic	51.031	30.448	76.765	20.716	22.407
	p	.001	.341	<.001*	.911	.904
Gender	Statistic	212.909	—	—	—	—
	p	<.001*	—	—	—	—
Motivation	Statistic	62.941	68.663	47.415	56.068	46.593
	p	.753	.372	.986	.856	.989

Note. Variables whose p values are highlighted with an asterisk are selected for splitting in the respective node.

In the first node, the variable with the smallest p value—in this case gender—is selected for splitting (cf. Table 2 and Figure 2). In each daughter node the splitting continues recursively: Here, the variable age is selected for splitting in the third node, whereas no further splits are found significant in the second and all the following nodes.

Note that the model-based recursive partitioning algorithm performs only binary splits in each step but can capture any type of group structure by means of multiple splits in the same variable, as illustrated in Figure 4, or by using combinations of variables, as was already illustrated in Figure 2 (see also Strobl, 2013; Strobl et al., 2009). Thus, as opposed to parametric approaches, the model-based recursive partitioning framework can approximate any functional form even when it is not known a priori—as will likely be the case in practical applications.

Figure 4.

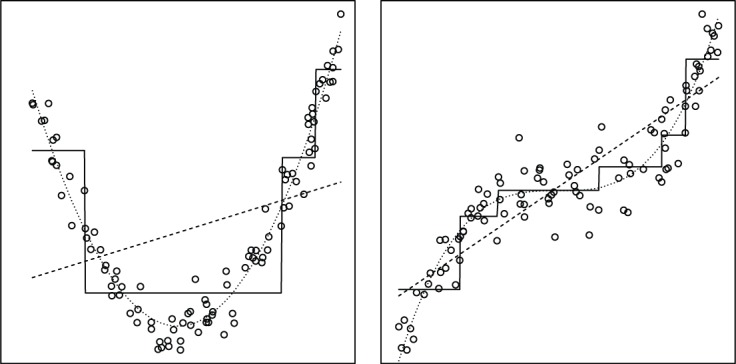
Approximation of unknown functional forms by means of recursive partitioning. The dotted line represents the true functional form (left: quadratic, right: cubic), the dashed line represents a linear model fit and the solid line represents the approximation through recursive partitioning.

Splitting continues until all p values exceeded the significance level (commonly 5%), indicating that there is no more significant parameter instability, or until the number of observations in a subsample falls below a given threshold (see also section “Stopping Criteria”).

Selecting the Cutpoints

After a covariate has been selected for splitting, the optimal cutpoint is determined by maximizing the partitioned log-likelihood (i.e., the sum of the log-likelihoods for two separate models: one for the observations to the left and up to the cutpoint, and one for the observations to the right of the cutpoint) over all candidate cutpoints within the range of this variable.

For the first split in the instructive example, the selection of the cutpoint is trivial—since the binary variable gender only allows for a single split between the subgroups of females and males. In the second split, however, all possible cutpoints in the variable age for the female subsample are considered and the associated partitioned log-likelihood is displayed in Figure 5. The value 40 is selected as the optimal cutpoint, because it shows the highest value of the partitioned log-likelihood, that is, the strongest differences in the item parameters exist between females up to the age of 40 and over the age of 40.

Figure 5.

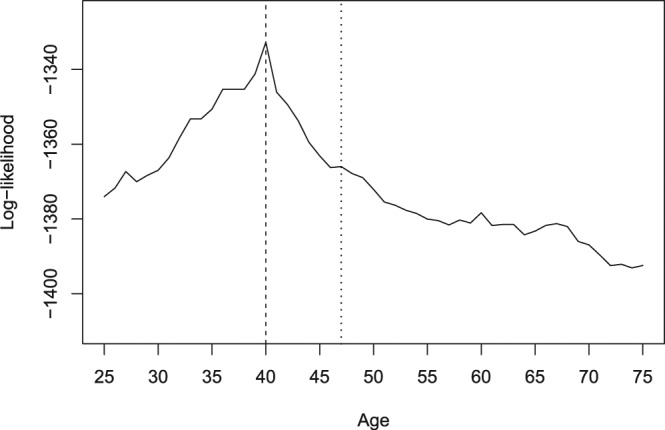
Partitioned log-likelihood for the second split in the covariate age. The dashed line indicates the location of the optimal cutpoint (at the value 40), while the dotted line indicates the location of the median (at the value 47) for the subgroup of females.

Note that other potential cutpoints close to this value also show a high value of the partitioned log-likelihood, so that in different random samples from the same underlying population not always the exact same value for the optimal cutpoint may be detected. However, from Figure 5 it is obvious that the median (dotted line) that is often used for prespecifying the reference and focal groups from a numeric predictor variable such as age may be far off the maximum of the partitioned log-likelihood indicating the strongest parameter change. As opposed to that, the data-driven approach suggested here cannot only reliably detect the parameter instability in the variable age, but it can also identify at what age the strongest parameter change occurs (as was also systematically illustrated by the simulation results of Strobl et al., 2015).

While this approach can be applied to numeric and ordered covariates, for unordered categorical covariates the categories can be split into any two groups in each split. From all these candidate binary partitions, again the one that maximizes the partitioned log-likelihood is chosen. This means that the algorithm can also detect which groups formed by a multicategorical covariate, such as ethnicity, actually show different item parameters—rather than having to specify a priori a reference group (usually the majority group) and a focal group (usually all minority groups combined, even though empirically there might be additional differences between the minority groups, or some of the minority groups may not differ from the majority group while others do).

From a technical point of view, selecting the optimal cutpoint by maximizing the partitioned (log-)likelihood corresponds directly to using the maximum LR statistic of the joint versus the partitioned model. Hence for testing whether there is significant DIF or DSF in a covariate, the computationally cheap score test from the section “Testing for Parameter Instability” is used, while for estimating where the strongest DIF or DSF occurs, the computationally costly LR test is used.

This two-step approach has two important advantages: Not only does it considerably reduce the computational burden but at the same time it also prevents an artifact termed variable selection bias (see Strobl, Boulesteix, & Augustin, 2007, and the references therein), which was inherent in earlier recursive partitioning algorithms.

Stopping Criteria

For creating a rating scale or partial credit tree, the four basic steps outlined above—(1) estimating the parameters of a joint model, (2) testing for parameter instability, (3) selecting the splitting variable and cutpoint, and (4) splitting the sample accordingly—are repeated recursively until a stopping criterion is reached.

Two kinds of stopping criteria are currently implemented: The first is to stop splitting if there is no (more) significant instability with respect to any of the covariates. Thus, the significance level—usually set to 5%—serves as stopping criterion. As a second stopping criterion, a minimum sample size per node can be specified. This minimal node size should be chosen such as to provide a sufficient basis for parameter estimation in each subsample and should thus be adjusted to the number of model parameters. In our examples, we have chosen a significance level of 5% and by default the minimal node size is 10 times the average number of parameters per item (as a simple rule of thumb for assuring reasonable parameter estimates).

Finally, one should keep in mind that when a large number of covariates is available in a data set, and all those covariates are to be tested for measurement invariance, multiple testing becomes an issue—as will be the case for any statistical test. To account for the fact that multiple testing might lead to an increased false-positive rate when the number of available covariates is large, a Bonferroni adjustment for the p value splitting criterion is applied internally.

As explained in detail in Strobl et al. (2009) and Strobl et al. (2015), pruning, a procedure employed in classical algorithms (e.g., CART; Breiman et al., 1984) to avoid overfitting, is no longer necessary in the inference-based approach employed here. Moreover, the model-based recursive partitioning algorithm is not affected by an inflation of chance due to its recursive nature but forms a closed testing procedure (cf., e.g., Hochberg & Tamhane, 1987). This ensures that noninvariance groups are not erroneously detected as an artifact of the recursive nature of the algorithm.

In the following, the statistical properties of rating scale and partial credit trees are further investigated by means of a series of simulation studies.

Simulation Studies

A series of three simulation studies was conducted to illustrate the statistical properties of the new framework and compare them to those of the well-established LR test in the spirit of Andersen (1973) and Gustafsson (1980). This LR test provides a good basis for comparison, because it is also a global model test procedure that is based on an underlying IRT model and uses the conditional maximum likelihood approach.

All simulation studies were conducted in the statistical software R (R Core Team, 2016). To fit rating scale and partial credit models in prespecified subgroups for the LRT the add-on package psychotools (Zeileis, Strobl, Wickelmaier, Komboz, & Kopf, 2015a) is used and for the rating scale and partial credit trees psychotree is employed (Zeileis et al., 2015b), which reuses the psychotools functions. R itself as well as all add-on packages are freely available under the General Public License (GPL) from the Comprehensive R Archive Network (CRAN).

Table 3 gives an overview over the three following simulation studies, indicating the central question addressed in each study as well as the experimental factors and criterion variables.

Table 3.

Overview of the Aims and Settings of the Following Simulation Studies.

Study	Central question	Experimental factors	Criterion variables
I	Are the methods mislead by actual differences in the person parameter distributions (PPD)?	DIF: No/Yes Mean difference in PPD: No/Yes Variance difference in PPD: No/Yes Covariate pattern: Binary/Numeric	Type I error/Power
II	Are the methods sensitive to DIF in groups formed by complex covariate patterns?	DIF: No/Yes Covariate pattern: Categorical/Numeric-80/U-shaped/Interaction	Type I error/power
III	Are the methods also sensitive to DSF?	DSF pattern: Single-level/Convergent/Divergent/Balanced	Power

Note. DIF = differential item functioning; DSF = differential step functioning.

Criterion Variables

In each simulation setting, the percentage of significant test results is recorded. In cases where no DIF is simulated, the percentage of significant test results reflects the Type I error rate, that is, the percentage of simulation runs where the methods indicate noninvariant groups despite the fact that no DIF is simulated. In cases where DIF is simulated, on the other hand, the percentage of significant test results reflects the power, that is, the percentage of simulation runs where the methods indicate noninvariant groups when DIF is actually present. A method performs well when the Type I error rate does not exceed the given significance level and the power is high.

For LR tests, the percentage of significant test results directly corresponds to the percentage of simulation runs where the tests show a significant difference between the prespecified groups. For rating scale and partial credit trees, the percentage of significant test results corresponds to the percentage of simulation runs where the trees made at least one split, forming two or more noninvariant groups.

Note that the terms Type I error rate and power (or hit rate) may be used in a different context in other DIF studies, where itemwise tests are conducted. In those studies, terms such as error rate and hit rate often refer to the percentage of items incorrectly and correctly classified as DIF items. Here, however, the terms Type I error rate and power are used in their statistically precise meaning to describe the performance of the global tests and refer to the percentage of incorrect and correct test decision over all items.

Fixed Experimental Settings

The following settings were the same for all three simulation studies, whereas specific settings are discussed below for each study individually.

• Significance level: α = .05 was used as the significance level.

• Number of replications: 10,000 replications were conducted for each experimental scenario to ensure an appropriate precision of the estimates of the criterion variables.

• Number of observations: n = 1,000 was used as the overall sample size.

• Number of items, categories, and item parameters: To make the simulation studies realistic as well as comparable to previously published simulation studies, we used a set of item parameters that were estimated in a calibration of the 1992 NAEP study (Johnson & Carlson, 1994) by means of the graded response model (GRM; Samejima, 1969). The same parameter values were also used for polytomous items in previous simulation studies by Chang et al. (1996), Camilli and Congdon (1999), and Penfield and Algina (2006). The parameter set consisted of threshold parameters ${\delta }_{\mathrm{jk}}$ and discrimination parameters ${\alpha }_j$ for eight polytomous items with four categories each, which are displayed in Table 4. With this setup, we were able to generate data based on the more general GRM for a preparatory study presented in Appendix B to rule out a potential effect of model misspecification on the following results. For the simulations based on the RSM and the PCM, however, the threshold parameters ${\delta }_{\mathrm{jk}}$ from Johnson and Carlson (1994) were used as described in detail below, while the discrimination parameters ${\alpha }_j$ were all fixed to 1.

• Person parameters: Person ability parameters were drawn from the same baseline distribution (except for those settings of Simulation Study I, where the person parameters were drawn from two different distributions to simulate differences in the person parameter distributions, as described in detail below). The baseline distribution was a normal distribution $N(\mu ,1)$, where $\mu$ is the mean over all item threshold parameters, that is, $\mu =\frac{1}{m·p}{\sum }_{j=1}^m{\sum }_{k=1}^p({\beta }_j+{\tau }_k)$ for the RSM and $\mu =\frac{1}{{\sum }_{j=1}^m{p}_j}{\sum }_{j=1}^m{\sum }_{k=1}^{p_j}{\delta }_{\mathrm{jk}}$ for the PCM.

• Methods: Four methods were compared in all simulation studies that result from the combination of the two underlying models—RSM and PCM—and the two testing frameworks—LR tests and model-based recursive partitioning trees: LR tests based on RSMs (abbreviated as “LRT-RSM” in this entire section to enhance readability of the results), rating scale trees (“TREE-RSM”), LR tests based on PCMs (“LRT-PCM”), and partial credit trees (“TREE-PCM”).

• Data generating models: The data were generated either with the RSM or the PCM. For the RSM, the mean over all item threshold parameters ${\delta }_{\mathrm{jk}}$ of an item $j$ from Table 4 has been used as the item location parameter ${\beta }_j$ and the mean of all differences between successive item threshold parameters ${\delta }_{j(k-1)}$ and ${\delta }_{\mathrm{jk}}$ has been used as the threshold parameter ${\tau }_k$. For the PCM, the item threshold parameters ${\delta }_{\mathrm{jk}}$ listed in Table 4 have been used directly.

• The analysis method was chosen according to the data-generating model in Simulation Studies I and II, whereas Simulation Study III and Appendix B also include cases of model-misspecification.

Table 4.

Item Threshold and Discrimination Parameters of a 1992 NAEP Calibration by Johnson and Carlson (1994) Estimated With the GRM.

Parameter	Item
	1	2	3	4	5	6	7	8
${\delta }_{j1}$	$-0.203$	$-0.342$	$-1.804$	$-0.345$	$-1.559$	$-2.105$	$-2.299$	$-2.449$
${\delta }_{j2}$	$1.344$	$1.008$	$-0.368$	$2.428$	$0.218$	$-0.452$	$-1.060$	$-0.089$
${\delta }_{j3}$	$2.549$	$1.797$	$0.219$	$2.822$	$1.804$	$2.873$	$0.581$	$2.416$
${\alpha }_j$	$1.004$	$1.359$	$0.535$	$0.779$	$1.215$	$0.794$	$0.689$	$0.563$

Note. NAEP = National Assessment of Educational Progress; GRM = graded response model.

Simulation Study I: Mean and Variance Differences in the Person Parameter Distributions

The aim of this study is to investigate how the methods perform in the presence of actual differences in the person parameter distributions. In particular, we will see whether differences in the mean and/or variance of the ability distributions are mistaken for violations of measurement invariance in cases where indeed no DIF is present (Type I error rate) and whether actual violations of measurement invariance can be detected despite differences in the mean and/or variance of the ability distributions in cases where DIF is indeed present (power).

Moreover, through the investigation of a binary covariate (offering only one possible split into two groups) and a numeric covariate (for which the TREE methods search the optimal cutpoint), the results of this simulation study would show any inflating effect that the exhaustive search over all possible cutpoints may have on the Type I error rate of the TREE methods.

Design of Simulation Study I

• Ability mean difference: In settings with no ability mean difference, the person parameters of both reference and focal group were drawn from the baseline $N(\mu ,1)$ distribution (with $\mu$ as defined above). In settings with an ability mean difference, the person parameters of the reference group were drawn from a normal $N(\mu -0.5,1)$ distribution, whereas the person parameters of the focal group were drawn from a normal $N(\mu +0.5,1)$ distribution. Additionally, the mean differences here can be combined with the variance differences described in the next paragraph.

• Ability variance difference: In settings with no ability variance difference, the person parameters of both reference and focal group were drawn from a normal $N(\mu ,1)$ distribution. In settings with an ability variance difference, the person parameters of the reference group were drawn from a normal $N(\mu ,1)$ distribution, whereas the person parameters of the focal group were drawn from a normal $N(\mu ,2)$ distribution.

• DIF: Scenarios where no DIF is simulated represent the null hypothesis that there are no differences in any item parameters between the reference and the focal group. Scenarios where DIF is present, on the other hand, represent the alternative where for the fifth item all item threshold parameters in the PCM (or item location parameters in the RSM, respectively) have been shifted by a constant value of \epsilon = 0.5 for the focal group.

• Covariate pattern: Under the “binary” covariate pattern, covariate values were sampled from a binomial distribution with equal class probabilities. In those scenarios with DIF, it was then simulated between the two groups corresponding directly to the two categories of this binary covariate.

  Under the “numeric” covariate pattern, covariate values were sampled from a discrete uniform distribution over the values 1 to 100. In those scenarios with DIF, it was then simulated between the two groups specified by splitting the observations at the median of the numeric covariate.

Note that, while the TREE methods have to select the optimal cutpoint in all settings with the numeric covariate in a data-driven way, for the LR tests a cutpoint defining reference and focal group has to be specified a priori. In Simulation Study I, the LR tests were given the correct cutpoint, that is, the median, while in Simulation Study II, we will investigate the influence of misspecified cutpoints. This means that in this first simulation study the LR tests have an advantage over the TREE methods, because they are provided with the correct group structure while the TREE methods have to search for it.

Results of Simulation Study I

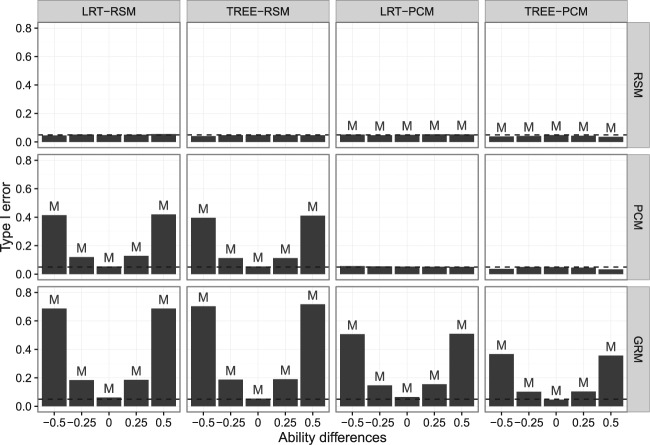
As can be seen from Table 5, all methods roughly respect the given significance level of α = .05 under the null hypothesis of no DIF—both for the binary and for the numeric covariate. This shows that the optimal cutpoint selection over numeric covariates does not lead to an inflated Type I error rate in the model-based recursive partitioning framework.

Table 5.

Results of Simulation Study I: Type I Error Rate of the Four Methods Depending on Ability Mean and/or Variance Differences and Covariate Pattern Under the Null Hypothesis of No DIF.

Type I error rate
Covariate pattern	Mean difference	Variance difference	Method
			LRT-RSM	TREE-RSM	LRT-PCM	TREE-PCM
Binary	No	No	0.053	0.050	0.054	0.047
	Yes	No	0.049	0.045	0.049	0.015
	No	Yes	0.048	0.053	0.052	0.046
	Yes	Yes	0.051	0.050	0.052	0.023
Numeric	No	No	0.051	0.052	0.051	0.050
	Yes	No	0.053	0.048	0.052	0.044
	No	Yes	0.052	0.051	0.054	0.045
	Yes	Yes	0.052	0.047	0.052	0.045

Note. DIF = differential item functioning; LRT-PCM = likelihood ratio test partial credit model; LRT-RSM = rating scale model.

Moreover, we can see that mean and/or variance differences between the person parameter distributions of reference and focal group do not lead to an inflation of the Type I error: None of the methods is mislead to identify differences between the person parameter distributions as violations of measurement invariance. In cases with a binary covariate and ability mean differences, the TREE-PCM procedure even shows a conservative Type I error.

The same trend was already noted by Strobl et al. (2015) for the Rasch tree procedure. A first investigation of this effect (results not shown here for brevity) indicated that in principle all likelihood-based DIF tests—the score test employed in the TREE procedures, but also the LR test and the Wald test (Glas & Verhelst, 1995)—are affected by this phenomenon. However, for the LR test (and similarly for the TREE-RSM) the effect occurs only for larger ability differences than those that were presented in this simulation study. However, the direction of the effect is that all methods behave conservatively rather than showing an inflated Type I error rate in the presence of ability mean differences, so that true ability differences (often termed impact) are not mistaken for DIF.

Table 6 shows the power of the four methods under the alternative of DIF being present. The results illustrate that the TREE methods achieve a lower power for the numeric covariate—where they have to search for the optimal cutpoint, while the LR tests are given the correct cutpoint—as compared to the binary covariate—where for both types of methods the correct cutpoint is specified in advance. This may seem like a disadvantage of the TREE methods at first sight, but we will show in Simulation Study II that the data-driven cutpoint selection of the TREE methods is actually an advantage in the more realistic settings where the true cutpoint is not known.

Table 6.

Results of Simulation Study I: Power of the Four Methods Depending on Ability Mean and/or Variance Differences and Covariate Pattern Under the Alternative Hypothesis of DIF.

Power
Covariate pattern	Mean difference	Variance difference	Method
			LRT-RSM	TREE-RSM	LRT-PCM	TREE-PCM
Binary	No	No	0.997	0.997	0.898	0.892
	Yes	No	0.996	0.995	0.874	0.776
	No	Yes	0.994	0.991	0.883	0.864
	Yes	Yes	0.993	0.988	0.867	0.772
Numeric	No	No	0.997	0.975	0.898	0.723
	Yes	No	0.995	0.969	0.875	0.568
	No	Yes	0.991	0.956	0.878	0.686
	Yes	Yes	0.989	0.950	0.855	0.576

Note. DIF = differential item functioning; LRT-PCM = likelihood ratio test-partial credit model; LRT-RSM = likelihood ratio test-rating scale model.

The results also show that—as a consequence of the higher number of parameters estimated in the PCM as compared to the more parsimonious RSM—the power of those methods based on the PCM is in general lower than the power of those methods based on the RSM. While the higher number of parameters results in a disadvantage for methods based on the PCM in situations with simple DIF like here, we will see that it turns out to be an advantage in situations where DSF is present, as illustrated in Simulation Study III. Note also that in this simulation design the sample size was held constant for brevity, whereas future research should investigate to what degree increasing the sample size can compensate for the higher number of parameters of the PCM methods.

As another general tendency, the presence of ability mean and/or variance differences to some extent reduces the power of all four methods. The power is lower when either one of these effects is present and is lowest when both occur simultaneously—especially for the methods based on the PCM.

In summary, the results of Simulation Study I show that neither of the methods is mislead to identify differences between the person parameter distributions as violations of measurement when no actual DIF is simulated. However, the power for detecting violations of measurement invariance when it is present is alleviated by differences between the person parameter distributions for all methods.

Simulation Study II: Complex Covariate Patterns

In Simulation Study I, the covariate patterns specifying reference and focal groups have been very simple. However, this will not often be the case in empirical data, where the true group structure can result from various more complex covariate patterns. Simulation Study II therefore illustrates how the investigated methods perform when the noninvariant groups are specified by more complex patterns, such as nonmedian splits, U-shaped patterns, and interactions of covariates—none of which would typically be specified in a LR test.

Since in one setting of this simulation study both covariates are presented at a time, another aspect of interest is a potential inflating effect that the multiple testing over more than one covariate may have on the Type I error rate of the methods.

Design of Simulation Study II

• DIF: Again, scenarios where no DIF is simulated represent the null hypothesis of measurement invariance, where there are no differences in any item parameters between the reference and the focal group. Scenarios where DIF is present, on the other hand, represent the alternative where for the fifth item all item threshold parameters in the PCM (or the item location parameter in the RSM, respectively) have been shifted by a constant value of $ϵ=0.5$ for the focal group.

• Covariate pattern: Under the “categorical-4” covariate pattern, the covariate values were sampled from a multinomial distribution with four classes and equal class probabilities. In those scenarios with DIF, it was then simulated between two groups that were each specified by a combination of two levels of the categorical covariate: Levels 1 and 3 for the reference group and Levels 2 and 4 for the focal group. This covariate pattern mimics noninvariance between groups formed by multicategorical covariates, such as ethnicity or language groups, where it is not known in advance which—if any—categories show a significant difference in the item parameter values.

  Under the “numeric-80” covariate pattern, the covariate values were sampled from a discrete uniform distribution over the values 1 to 100. In those scenarios with DIF, it was now simulated between two groups specified by splitting the observations at the value 80. This pattern mimics noninvariance in a numeric covariate such as age, where DIF is present between elderly subjects and the rest of the population.

  Under the “U-shaped” covariate pattern, the covariate values were again sampled from a discrete uniform distribution over the values 1 to 100. In those scenarios with DIF, it was now simulated between two groups specified by those observations with values up to 20 and from 80 onward versus those observations with values between 20 and 80. This patterns mimics noninvariance in a numeric covariate such as age, where DIF is present for young and elderly subjects as compared to middle-aged subjects.

  Under the “interaction” covariate pattern, again numeric covariate values were sampled from a discrete uniform distribution over the values 1 to 100, and binary covariate values were sampled from a binomial distribution with equal class probabilities. In those scenarios with DIF, it was now simulated between two groups specified by those observations with a value of 1 in the binary covariate in combination with a value above the median in the numeric covariate versus all other observations. This pattern mimics a situation where noninvariance is present only with respect to a subgroup of subjects resulting from a combination of two covariates, such as females above the median age.

Due to the more complex covariate patterns, there are now several aspects that are automatically incorporated by the TREE methods, but need to be explicitly specified for the LR tests: Like in the previous simulation study, when confronted with a numeric covariate the TREE methods automatically select the optimal cutpoint, while for the LR tests a cutpoint has to be specified a priori: We used the median as is often found in practice.

A similar issue arises for multicategorical variables: while the TREE methods automatically detect which—if any—categories show a significant difference in the item parameter values, the groups need to be prespecified for the LR tests. An approach often found in practice is to define one class (e.g., an ethnic majority) as the reference group and combine all other classes to form the focal group. This may lead to severe information and power loss if the actual parameter differences do not follow this grouping. Since the LR test can straightforwardly deal with more than two classes, here, we have chosen an approach more favorable for the LR test, namely, to create four separate groups for the four categories of our simulated categorical covariate. This ensures that the power of the LR test is not underestimated—but it also means that a significant test result for the LR tests is not informative as to which categories actually differ.

The last aspect where the TREE and LR test methods differ in their general procedure is the treatment of more than one covariate. In the interaction pattern, two covariates are involved in the data-generating process and thus both covariates were made available to all four methods. This is indicated in the results tables for the LR tests, where for the interaction pattern a result is displayed for both the binary and the numeric variable, while in all other settings only the variable of interest is presented to the methods and the other fields are left blank. In this scenario, the LR tests deal with one variable at a time, while the TREE methods can search over several covariates recursively, so that only one result is listed in the results tables for the TREE methods.

From a statistical point of view, this means that LR tests are limited to detecting DIF associated with the main effect of a single covariate (or interaction effects explicitly specified in advance—but we have never seen this in practice because usually there is no a priori information what interactions should be tested), while the TREE methods can also detect DIF associated with interactions of more than one variable. As pointed out in the section “Stopping Criteria,” however, the TREE methods employ a Bonferroni correction to ensure that their searching over several potential splitting variables does not lead to an inflated Type I error. For a fair comparison, we have therefore applied a Bonferroni correction, that is, adjusting p values from k comparisons to $1-(1-p{)}^k$—to the LR tests as well for the interaction pattern, where both the binary and the numeric variable are presented to the methods.

Results of Simulation Study II

As can be seen from Table 7, again all methods roughly respect the given significance level of α = .05 under the null hypothesis of no DIF. As noted above, in the interaction pattern, where both the binary and the numeric covariate were presented to the methods, we used the Bonferroni adjustment for all methods to make the results comparable. The corresponding Type I error rates for the LR test have to be added for the binary and the numeric splitting variables for comparison with the TREE methods, in which case the LR tests also meet the specified significance level.

Table 7.

Results of Simulation Study II: Type I Error of the Four Methods Depending on the Covariate Pattern Under the Null Hypothesis of No DIF.

Type I error rate
	LRT-RSM			TREE-RSM	LRT-PCM			TREE-PCM
Covariate pattern	Binary	Numeric	Categorical		Binary	Numeric	Categorical
Categorical-4	—	—	0.049	0.050	—	—	0.059	0.048
Numeric-80	—	0.049	—	0.047	—	0.052	—	0.049
U-shaped	—	0.051	—	0.052	—	0.050	—	0.049
Interaction	0.025	0.026	—	0.050	0.026	0.024	—	0.043

Note. DIF = differential item functioning; LRT-PCM = likelihood ratio test-partial credit model; LRT-RSM = likelihood ratio test-rating scale model.

If no Bonferroni adjustment was applied, the results of Strobl et al. (2015) indicate that all methods, but in particular LR tests, show a severe inflation of the Type I error rate, so that some type of adjustment is suggested for any method when more than one covariate is investigated for DIF at the same time, as is done by default for the TREE methods. The TREE-PCM again behaves even slightly conservative in the interaction pattern where both covariates are presented, indicating that the Bonferroni adjustment may be a little strict and less conservative forms of adjustments could be considered in future research.

Table 8 shows the power of the four methods under the alternative of DIF being present. As a general tendency, we see again that—as a consequence of the higher number of parameters and again based on a constant sample size—the power of those methods based on the PCM is lower than the power of those based on the RSM, as already discussed for Simulation Study I.

Table 8.

Results of Simulation Study II: Power of the Four Methods Depending on the Covariate Pattern Under the Alternative Hypothesis of DIF.

Power
	LRT-RSM			TREE-RSM	LRT-PCM			TREE-PCM
Covariate pattern	Binary	Numeric	Categorical		Binary	Numeric	Categorical
Categorical-4	—	—	0.960	0.952	—	—	0.673	0.637
Numeric-80	—	0.325	—	0.810	—	0.168	—	0.430
U-shaped	—	0.051	—	0.677	—	0.054	—	0.284
Interaction	0.389	0.392	—	0.523	0.166	0.174	—	0.222

Note. DIF = differential item functioning; LRT-PCM = likelihood ratio test-partial credit model; LRT-RSM = likelihood ratio test-rating scale model.

More interestingly, however, the results also illustrate that—as compared to Simulation Study I—the power of the LR tests drastically decreases when the true group structure is not known. This effect is especially pronounced in the u-shaped pattern, where the power of the LR tests is only around chance level, whereas the TREE methods pick up the DIF with a notably higher power.

In the interaction pattern, too, the more flexible TREE methods have an advantage: Overall, this is a hard setting where the power for all methods is lower than for the simpler settings. However, while the LR tests can only assess one variable at a time (which in this case still gives them some power, because the main effects account for part of the DIF), the TREE methods again show a notably higher power because they can also pick up the interaction effect formed by the combination of the two covariates. Here, it would also be interesting to investigate to what degree increasing the sample size can compensate for the complexity of this setting.

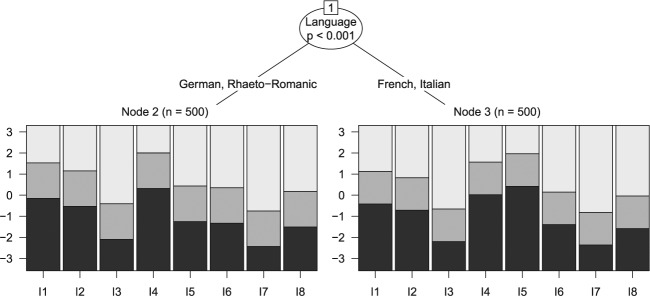
For the categorical covariate pattern (where the LR tests considered the four categories as distinct groups, while the TREE methods searched for the optimal partition of the categories) the power alone is not very informative and gives comparable values for the LR tests and TREE methods. However, it is important to note that the TREE methods have the additional advantage that they provide more information about the group structure, as illustrated in Figure 6.

Figure 6.

Exemplary result for a TREE method in the setting with a multicategorical covariate.

Here, we have labeled the four groups simulated in the categorical covariate pattern with the four language groups present in Switzerland (to provide an invented but plausible illustrative example). In this case, a naive analysis might either treat all four groups separately, like the LR test in our simulation, or divide the four groups into one reference and one focal group, for example, by testing the German-speaking majority against all other languages. Either of these arbitrary specifications would make it impossible to reveal the true group structure that, in this illustrative example, the Rhaeto-Romanic minority should be grouped together with the German majority rather than with the other language minorities. A similar information gain can be expected from the TREE methods for other multicategorical covariates, such as ethnicity, where it is also common in practice to test only the majority group against a combination of all minority groups.

In summary, the results of Simulation Study II show that in complex covariate patterns—that are more realistic and not known a priori—the TREE methods show a comparable to substantially higher power for detecting DIF in the first place and also a better recovery of the group structure, which is of high relevance for interpretability in practical applications.

Simulation Study III: Differential Step Functioning

While Simulation Studies I and II assessed the performance of the methods when DIF (i.e., a constant shift of all score categories) is present, Simulation Study III illustrates the performance under various patterns of DSF (i.e., different combinations of shifts in individual score categories). For brevity only the power is reported as the criterion variable in this simulation study.

Design of Simulation Study III

Due to the parametrization in the RSM (the same distance between two categories is assumed for all items) it is not possible to simulate DSF in a single item with this model. Therefore, the PCM was used in all settings as the data-generating model. This automatically implies a model misspecification for the TREE-RSM procedure and the LRT-RSM procedure.

The model misspecification is not the main focus of this study. However, we have conducted a preparatory study on this issue, which is presented in Appendix B. In this preparatory study, we could show that the results of Bolt (2002) for an itemwise LR test also extend to the global LR tests and TREE methods used here: Both findings indicate that likelihood-based methods for DIF detection in polytomous items can show an increased Type I error rate not when faced with model misspecification alone (like in the following Simulation Study III), but when model misspecification co-occurs with mean differences in the person parameter distributions.

The results of our preparatory study also indicate that this is not an issue when the analysis model contains the actual data-generating model as a special case—so, even in the presence of both model misspecification and mean differences, there is no problem when, for example, TREE-PCM and LRT-PCM are applied to RSM data. However, when the data-generating model is more general than the analysis model, problems arise in the presence of both model misspecification and mean differences if, for example, TREE-RSM and LRT-RSM are applied to PCM data. Due to these findings—and also due to the results we will show for Simulation Study III below—we do not generally recommend RSM trees over PCM trees, as is further elaborated in the discussion section.

The DSF patterns implemented in Simulation Study III were inspired by previous simulation studies (Chang et al., 1996; Penfield, 2007; Su & Wang, 2005; Wang & Su, 2004) and form a combination of the most often used scenarios:

• Single-level: In this setting, the first item threshold parameter of the fifth item of the focal group was shifted by $ϵ=0.5$. This corresponds to DSF in a single category.

• Convergent: In this setting, the first and third item threshold parameter of the fifth item of the focal group were shifted by $ϵ=0.5$ and $ϵ=0.25$, respectively.

• Divergent: In this setting, the first and third item threshold parameter of the fifth item of the focal group were shifted by $ϵ=0.5$ and $ϵ=-0.25$, respectively.

• Balanced: In this setting, the first and third item threshold parameter of the fifth item of the focal group were shifted by $ϵ=0.5$ and $ϵ=-0.5$, respectively. This leads to a cancellation of DSF in Item 5, that is, the region covered by this item on the latent trait gets smaller but the mean of the item threshold parameters remains the same.

In all settings of this simulation study a binary covariate (again sampled from a binomial distribution with equal class probabilities) was used to specify reference and focal groups.

Results of Simulation Study III

The results of Simulation Study III are reported in Table 9. Overall, the power is notably lower than in the previous simulation studies, because now only one or two threshold parameters (as opposed to all threshold parameters) of one item were shifted. This is a very tough setting, but still the results show that all four methods are sensitive to DSF, even if it affects only a single parameter. In contrast to other existing DIF detection procedures for polytomous items, such as the polytomous SIBTEST procedure (Chang et al., 1996), this is also the case when the DSF effects are balanced. (We did not include any of these other procedures in the simulation study, because they are itemwise and not directly comparable to the global procedures compared here.)

Table 9.

Results of Simulation Study III: Power of the Four Methods for a Selection of DSF Patterns.

Power
DSF pattern	Method
	LRT-RSM	TREE-RSM	LRT-PCM	TREE-PCM
Single-level	0.143	0.130	0.199	0.191
Convergent	0.261	0.256	0.257	0.254
Divergent	0.083	0.085	0.258	0.230
Balanced	0.102	0.091	0.443	0.421

Note. DSF = differential step functioning; LRT-PCM = likelihood ratio test-partial credit model; LRT-RSM = likelihood ratio test-rating scale model.

The power of the TREE methods is comparable or only slightly lower than the power of the corresponding LR tests. Because of the comparable power of the two types of methods, we only distinguish between methods based on the RSM and methods based on the PCM in the following.

Please note again that the overall power in this simulation study is lower than in the previous studies because less parameters differed between the groups. Of course, in a simulation study the power could be increased by increasing the effect size or the number of affected parameters. However, even the small effects simulated here for comparison with the previous studies are well suited for showing the general pattern of how the power depends on both the DSF pattern and the underlying model:

Most important, it should be noted that in contrast to the results of Simulation Studies I and II, it now becomes obvious that methods based on the RSM are not always more powerful than methods based on the PCM. For example, for the balanced DSF pattern, the results in Table 9 show that the power of the PCM methods is more than four times the power of the RSM methods. As explained in the following, these effects can be attributed to the different parametrization of the two models.

In the PCM, where each transition between two categories is modeled by an individual item threshold parameter ${\delta }_{\mathrm{jk}}$, DSF in a single response category can—independently of its sign—be captured directly by an individual model parameter. In the RSM, however, there is no individual parameter for each transition, but one overall location parameter for each item and a set of threshold parameters ${\tau }_k$ that are assumed to be the same for all items. Therefore, shifts in one or more threshold parameters of a single item cannot directly be captured in the RSM.

In summary, the results of Simulation Study III show that, in the presence of DSF, methods based on the PCM can be substantially more powerful than methods based on the RSM.

Application: The Freiburg Mindfulness Inventory

The Freiburg Mindfulness Inventory (FMI, Walach, Buchheld, Buttenmüller, Kleinknecht, & Schmidt, 2006) is a self-report questionnaire to measure mindfulness, “ . . . a concept originally derived from Buddhist psychology” (Walach et al., 2006, p. 1543). In the following, we focus on the subscale “presence” of a short version of the FMI. Each of the five items has six response categories (1 = completely disagree to 6 = completely agree) and is reported in Table 10.

Table 10.

Items of the Subscale “Presence” of a Short Version of the Freiburg Mindfulness Inventory (Walach et al., 2006).

Item	Label
1	I am open to the experience of the present moment.
2	I sense my body, whether eating, cooking, cleaning, or talking.
3	When I notice an absence of mind, I gently return to the experience of the here and now.
4	I pay attention to what’s behind my actions.
5	I feel connected to my experience in the here and now.

To investigate potential violations of measurement invariance in the subscale “presence,”Sauer et al. (2013) analyzed the responses of 1,059 subjects. The following four covariates have been used to define reference and focal groups: age (with the median as cutpoint), gender, mode of data collection (online/offline), and previous experience with mindfulness meditation (yes/no). Table 11 reports the summary statistics for these covariates based on a slightly reduced data set (n = 1,032, where subjects below the age of 16 years, and those who scored either in the lowest or in the highest category in every single item were removed) that will be used in the following analysis.

Table 11.

Summary Statistics of the Four Considered Covariates.

Covariate	Summary statistics
Gender	Female: 694			Male: 338
Experience	Yes: 420			No: 612
Mode	Online: 952			Offline: 80
	$x_{\min }$	$x_{0.25}$	$x_{\mathrm{med}}$	$\overline{x}$	$x_{0.75}$	$x_{\max }$
Age	16	26	33	35.10	44	77

Note. For the categorical variables gender, experience, and mode the frequency distribution is displayed, while for the numeric variable age the minimum $x_{\min }$, the first quartile $x_{0.25}$, the median $x_{\mathrm{med}}$, the mean $\overline{x}$, the third quartile $x_{0.75}$, and the maximum $x_{\max }$ are listed.

According to the results reported by Sauer et al. (2013) for the global LR test, the null hypothesis of measurement invariance has to be rejected for the covariates previous experience with mindfulness meditation $({\chi }^2(8)=78.71)$ and mode of data collection (with Item 5 excluded due to a null category: $({\chi }^2(7)=19.71,p=.006)$, which is marginally significant when correcting for multiple testing as in Sauer et al., 2013), but not for the covariates age $({\chi }^2(8)=11.59,p=.171)$ and gender $({\chi }^2(8)=12.89,p=.116)$. Besides slightly different numerical results, the conclusions for the LR test would remain the same in the slightly reduced data set used here.

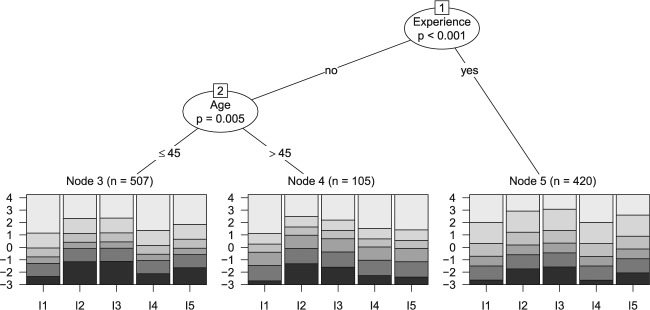
However, as it is common in DIF analysis, Sauer et al. (2013) only compared groups defined by a single covariate at a time. This leaves noninvariances between groups resulting from interactions of two or more covariates unidentified. Also, for numeric covariates such as age, noninvariance groups may result from cutpoints other than the median that was used for creating the reference and focal groups by Sauer et al. (2013). To overcome these drawbacks and examine whether there are groups resulting from interactions of covariates or nontrivial cutpoints, the slightly reduced data set is reanalyzed by means of model-based recursive partitioning, where all four covariates can be presented to the method at the same time and without previous discretization. Since, based on a variety of statistical and content based criteria, Sauer et al. (2013) have chosen the RSM rather than the PCM for their analysis, we also use the rating scale tree method for the reanalysis. The resulting rating scale tree is reported in Figure 7.

Figure 7.

Resulting rating scale tree for the subscale “presence” of a short version of the Freiburg Mindfulness Inventory after providing the four covariates age, gender, experience, and mode of data collection.

As a very first result, we see that there is more than one terminal node in Figure 7 so that the global null hypothesis of measurement invariance with respect to the four available covariates has to be rejected. Similar to the results of Sauer et al. (2013), the rating scale tree identified the covariate previous experience with mindfulness meditation to be most strongly associated with violations of measurement invariance. The covariate mode of data collection, which was marginally significant in Sauer et al. (2013), is not selected by the rating scale tree—and for a good reason: When each of the two variables experience and mode of data collection are considered individually, both are associated with violations of measurement invariance, but the association with experience is stronger, as already observed by Sauer et al. (2013). What goes unnoticed when treating each variable individually, however, is that there is also a strong association between the two covariates themselves (the percentage of subjects having previous experience with mindfulness meditation is higher among those questioned offline than among those questioned online). Therefore, once experience has been selected for splitting in the rating scale tree, the mode of data collection does not provide enough additional information to be selected for further splitting.

Interestingly, however, in contrast to the results of Sauer et al. (2013), where age showed no significant violation, in the rating scale tree, we find that age is in fact significantly associated with violations of measurement invariance when considered in an interaction with the covariate experience and at a nontrivial cutpoint of 45, which is notably higher than the previously used median.

This more complex group pattern resulting from an interaction of two covariates could only have been detected with the LR test if the interaction was explicitly provided in the specification of the test—together with the correct (or a nearly correct) cutpoint. In practice, this will hardly ever be possible, leaving violations of measurement invariance in numeric covariates with nonmedian splits and more complex group structures unnoticed, like in this example.

The region plots in the terminal panels of the rating scale tree illustrated in Figure 7 can be used as a first descriptive evidence concerning specific items or categories affected by DIF. For example, it can be seen that over all items the region of the second highest Category 5, shaded in the second lightest gray, is much wider for subjects with previous experience with mindfulness meditation (Node 5) than it is for subjects without previous experience with mindfulness meditation (Nodes 3 and 4), especially those above 45 years (Node 4). The characterization of the noninvariant groups can thus help content experts to generate hypotheses about the underlying sources of the observed DSF, for example, that subjects with previous experience in mindfulness meditation can distinguish more subtly between the highest response categories than subjects without any previous experience in mindfulness mediation.

Note that for the region plots we currently use a constraint where the sum of all item parameters is set to zero within each node. This constraint highlights differences in the profile of item difficulties over all items. Alternatively, one or more anchor items could be selected to align the scales across nodes. While this is easily implemented from a technical point of view, the selection of anchor items itself is by no means trivial. It is usually performed by a content expert or by means of a heuristic anchor selection approach (cf. e.g., Kopf et al., 2015). However, all these strategies have certain drawbacks, including the lack of a straightforward generalization to multiple groups. Therefore, this issue is beyond the scope of this article and will be explored in future research.

Discussion and Outlook

We have proposed a framework for detecting noninvariant groups of persons in tests with polytomous items, which is based on a model-based recursive partitioning approach.

As was shown in a series of simulation studies and several examples, this framework is equally powerful as the established LR test in simple settings with known reference and focal groups but can be substantially more powerful and more informative in settings where the true group structure is not known a priori, as will often be the case in practice.

With this framework, noninvariant groups of subjects are detected in a data-driven way, but remain directly interpretable with respect to their covariate values. In particular, for numeric covariates it is not necessary to specify a cutpoint a priori as the cutpoint associated with the strongest parameter differences is detected automatically. Similarly, the specific combination of levels of a categorical covariate, which determine reference and focal groups, do not have to be prespecified but are detected based on the empirical data. Moreover, by means of a sequence of binary splits model-based recursive partitioning methods can capture any number of categories and approximate any functional shape in a data-driven way. This makes them more flexible than previous approaches and offers a methodological advantage especially for the detection of violations of measurement invariance that should not go unnoticed because a wrong group structure or functional form was assumed in the statistical test.

As has been pointed out throughout the article, the framework in its current form is not an itemwise but a global procedure that does not flag individual items or score levels but focuses on the identification of noninvariant groups. In future research, we will further enhance the means for interpretation by investigating different anchoring approaches for the graphical displays as well as the possibility of post hoc tests for individual items.

Of course, like any covariate-based approach, the model-based recursive partitioning framework is only able to detect noninvariant groups when the relevant covariates are observable and available for the analysis. Moreover, as with all observational data, a covariate used for splitting cannot simply be interpreted as the causal source of the violation, because the observed splitting variable may only serve as a proxy for the unobserved (and potentially unobservable) true cause.

To keep this first publication of the extension to polytomous models as compact as possible while still covering all fundamental statistical properties, the simulation studies presented here have been limited to a small range of settings highlighting the particular features of the proposed framework. However, as already pointed out in the simulation results, there are several additional aspects that should be investigated in further research, such as the effect of different sample sizes (especially on the methods based on the PCM that require many more parameters than those based on the RSM) and the effects of different proportions of DIF items and different DIF effect sizes.

In particular, our simulations have been limited to eight items to be able to use a set of parameter values for polytomous items that had already been used in several previous simulation studies. However, the model-based recursive partitioning framework is of course not limited to this low number of items. Future research should therefore include scenarios with an increased number of items, where the sample size is varied while the percentage of DIF/DSF items is kept constant, to see how the methods perform in these situations.

Another interesting aspect, which would be worth further investigation, is that no general recommendation can be made as to whether the model-based recursive partitioning method based on the RSM or based on the PCM should be preferred. Our results not only indicate that the higher number of parameters in the PCM reduces the power in many simple DIF settings but also strongly increases the power in certain DSF settings that are entirely missed by the RSM. Moreover, our extensions of the findings of Bolt (2002) imply that in the presence of true ability differences using an underparameterized model can lead to Type I error inflation, while using an overparameterized model is “safe”. Therefore, for now our cautious recommendation would be to perform model-based recursive partitioning trying both models and then compare the results, as long as no theoretical considerations strongly call for one or the other model.

Finally, note that the methods presented here and in Strobl et al. (2015) are based on Rasch models, which can be estimated by means of conditional maximum likelihood estimation. Future research will investigate the possibility to extend the model-based recursive partitioning approach to a greater class of IRT models.

Computational Details

Our results were obtained using the R system for statistical computing (R Core Team, 2016), Version 3.2.2, and the add-on packages psychotools (Zeileis et al., 2015a), Version 0.4-0, and psychotree (Zeileis et al., 2015b), Version 0.15-0. R itself and all packages are freely available at http://CRAN.R-project.org/.

In addition to the functionality presented here, the psychotree package also contains functions for fitting Rasch trees for binary item response data (Strobl et al., 2015) and Bradley-Terry trees for paired comparison data (Strobl et al., 2011).

Appendix A

Individual Score Contributions

In the following, the individual score contributions of the RSM and the PCM are derived. For both models, the objective function used for parameter estimation is the conditional log-likelihood. The individual contributions to the conditional log-likelihood can be easily computed as $\log L_c(\mathbf{\beta },\mathbf{\tau }|r_i)$ (cf. Equation 3) and $\log L_c(\mathbf{\beta },\mathbf{\tau }|r_i)$ (cf. Equation 4), yielding for the RSM

$$\mathrm{\Psi }({\mathit{x}}_i,\mathbf{\beta },\tau )=-{\displaystyle \sum }_{j=1}^m(x_{\mathrm{ij}}·{\beta }_j+{\displaystyle \sum }_{k=0}^{x_{\mathrm{ij}}}{\tau }_k)-\log {\gamma }_{r_i}(\mathbf{\beta },\tau )$$

and for the PCM

$$\mathrm{\Psi }({\mathit{x}}_{\mathit{i}},\mathbf{\delta })=-{\displaystyle \sum }_{j=1}^m{\displaystyle \sum }_{k=0}^{x_{\mathrm{ij}}}{\delta }_{\mathrm{jk}}-\log {\gamma }_{r_i}(\mathbf{\delta })$$

The individual contributions to the score function are derived from Equation 5 and Equation 6. For the RSM, the contribution of the ith subject to the jth item location parameter is given by

$$\mathrm{\psi }({\mathit{x}}_{\mathit{i}},\mathbf{\beta },\mathbf{\tau }{)}_j=\frac{\partial \mathrm{\Psi }({\mathit{x}}_{\mathit{i}},\mathbf{\beta },\mathbf{\tau })}{\partial {\beta }_j}=-x_{\mathrm{ij}}-\frac{1}{{\gamma }_{r_i}(\mathbf{\beta },\mathbf{\tau })}·\frac{\partial {\gamma }_{r_i}(\mathbf{\beta },\mathbf{\tau })}{\partial {\beta }_j}$$

and the contribution of the ith subject to the kth threshold parameter is given by

$$\mathrm{\psi }({\mathit{x}}_{\mathit{i}},\mathbf{\beta },\mathbf{\tau }{)}_k=\frac{\partial \mathrm{\Psi }({\mathit{x}}_i,\mathbf{\beta },\mathbf{\tau })}{\partial {\tau }_k}=-n_k-\frac{1}{{\gamma }_{r_i}(\mathbf{\beta },\mathbf{\tau })}·\frac{\partial {\gamma }_{r_i}(\mathbf{\beta },\mathbf{\tau })}{\partial {\tau }_k}$$

with n_k as the number of times subject i has chosen category k or higher. Similarly for the PCM, the contribution of the ith subject for the kth threshold parameter of the jth item is given by

$$\mathrm{\psi }({\mathit{x}}_i,\mathbf{\delta }{)}_{\mathrm{jk}}=\frac{\partial \mathrm{\Psi }({\mathit{x}}_i,\mathbf{\delta })}{\partial {\delta }_{\mathrm{jk}}}=-I_{[x_{\mathrm{ij}}\ge k]}(x_{\mathrm{ij}})-\frac{1}{{\gamma }_{r_i}(\mathbf{\delta })}·\frac{\partial {\gamma }_{r_i}(\mathbf{\delta })}{\partial {\beta }_{\mathrm{jk}}}$$

with $I_{[x_{\mathrm{ij}}\ge k]}$ as an indicator function returning one if subject i has chosen category k or higher on item j and zero otherwise.

The derivatives of the elementary symmetric functions ${\gamma }_{r_i}$ are again elementary symmetric functions with certain terms omitted (cf., e.g., Fischer & Ponocny, 1995). In our implementation of the rating scale and partial credit trees, the summation algorithm is used (by default) for computing these derivatives (cf. Fischer & Ponocny, 1995).

Appendix B

Preparatory Study on Model Misspecification

As parametric procedures, both the TREE methods and the LR tests that are investigated in the main article assume that the data-generating process follows a specific IRT model. This assumption is sometimes mentioned as a disadvantage of this class of procedures (see, e.g., Potenza & Dorans, 1995), but, to our knowledge, so far only Bolt (2002) has systematically examined the consequences of violations of this assumption (i.e., model misspecification or model misfit, as it is termed in Bolt, 2002). Although Bolt (2002) used only 100 replications per setting, a Type I error inflation was found for an itemwise LR test under model misspecification—however, only when the model misspecification co-occurred with mean differences in the person parameter distributions. Thus, the results of Bolt (2002) indicate that the earlier postulated robustness of the itemwise LR test to ability differences (Ankenmann, Witt, & Dunbar, 1999) seems to be valid only when there is no additional model misspecification.

The preparatory simulation study presented here examines whether the results of Bolt (2002) extend to the global LR tests and TREE methods employed here.

Design of the Preparatory Simulation Study

• Ability mean difference: In settings with no ability mean difference, the person parameters of both reference and focal group were drawn from the baseline $N(\mu ,1)$ distribution (with $\mu$ defined like in the simulation studies in the main article). In settings with an ability mean difference, ability differences of $\mathrm{\Delta }\in \{-0.5,-0.25,0.25,0.5\}$ have been simulated. For these settings, the person parameters of the reference group were drawn from a normal distribution $N(\mu -\frac{\mathrm{\Delta }}{2},1)$, whereas the person parameters of the focal group were drawn from a normal distribution $N(\mu -\frac{\mathrm{\Delta }}{2},1)$.

• Data generating model: The data were generated, as explained in detail in the main article, based on different IRT models: the RSM, the PCM, or the GRM (in order of increasing generality). When the data-generating model is different from the model used for the analysis (e.g., when the TREE-RSM method is applied to data generated with the PCM or GRM), this corresponds to a setting with model misspecification. When the data-generating model is equal to the model used for the analysis (e.g., when the TREE-RSM method is applied to data generated with the RSM), this corresponds to a setting without model misspecification.

In all settings of this simulation study a binary covariate (again sampled from a binomial distribution with equal class probabilities) was used to specify reference and focal groups. No item parameter differences have been simulated because the emphasis of this study is on the Type I error.

Results of the Preparatory Simulation Study

Figure 8 shows the Type I error rates of the four methods (columns) conditional on ability mean differences between reference and focal groups (x axis) and the data generating IRT model (rows). The results indicate, as one would expect, that no Type I error inflation occurs in settings without model misspecification, where the analysis model is equal to the actual data-generating model. Interestingly, this is still the case in some settings with model misspecification, as long as the analysis model contains the actual data-generating model as a special case, for example, when TREE-PCM and LRT-PCM are applied to RSM data.

In settings with model misspecification, however, where the analysis model does not contain the actual data-generating model as a special case, the Type I error is inflated when the model misspecification co-occurs with mean differences in the person parameter distributions. This Type I error inflation is more pronounced with increasing level of model misspecification and ability mean differences (regardless of the direction of the ability mean differences).

Figure 8.

Results of preparatory simulation study: Type I error of the four methods (columns) conditional on ability mean differences between reference and focal groups (x axis) and the data-generating item response theory model (rows). Settings with model misspecification are marked by the capital letter “M.” The dashed line indicates the nominal significance level of α = .05.

In summary, this preparatory study shows that the results of Bolt (2002) extend to the global LR tests and TREE methods investigated here and restrict earlier claims of the robustness of LR tests to ability differences (Ankenmann et al., 1999) to settings where no additional violations of the model assumptions are present.

With respect to Simulation Study III in the main article, where a model misspecification but no mean differences in the person parameter distribution are simulated, the results of this preparatory study show that no Type I error inflation is to be expected. Therefore, the power of the four methods under various DSF patterns can safely be compared.