ATS-PD: An Adaptive Testing System for Psychological Disorders

Abstract

The clinical assessment of mental disorders can be a time-consuming and error-prone procedure, consisting of a sequence of diagnostic hypothesis formulation and testing aimed at restricting the set of plausible diagnoses for the patient. In this article, we propose a novel computerized system for the adaptive testing of psychological disorders. The proposed system combines a mathematical representation of psychological disorders, known as the “formal psychological assessment,” with an algorithm designed for the adaptive assessment of an individual’s knowledge. The assessment algorithm is extended and adapted to the new application domain. Testing the system on a real sample of 4,324 healthy individuals, screened for obsessive-compulsive disorder, we demonstrate the system’s ability to support clinical testing, both by identifying the correct critical areas for each individual and by reducing the number of posed questions with respect to a standard written questionnaire.

List of abbreviations: ARP: Admissible Response Pattern; BLIM: Basic Local Independence Model; CAT: Computerized Adaptive Testing; DFA: Doingnon and Falmagne’s algorithm; DSM-IV-TR: Diagnostic and Statistical Manual of Mental Disorders, fourth edition, text revision; FCA: Formal Concept Analysis; FPA: Formal Psychological Assessment; IRT: Item Response Theory; KST: Knowledge Space Theory; MOCQ-R: Maudsley Obsessional-Compulsive Questionnaire-Reduced; OCD: Obsessive-Compulsive Disorder.

Introduction

Clinical psychology is concerned with psychological disorders, namely patterns of behavioral or psychological symptoms that involve several life areas and/or create distress for the person experiencing them (American Psychiatric Association [APA], 2000; Groth-Marnat, 2009). The set of this kind of disorders is very broad and includes, for instance, obsessive-compulsive disorder (OCD), mood disorders, eating disorders, psychotic disorders, personality disorders and developmental disorders (APA, 2000; Groth-Marnat, 2009). A psychological disorder is often egodystonic, that is, its symptoms are recognized by the subject as real problems; in other cases, the problem is mainly perceived by the affected person’s family and/or the collectivity (Groth-Marnat, 2009).

The specificity and peculiarity of mental health problems lead to the need to perform time-consuming investigations before a diagnosis is reached (Salmon, Dowrick, Ring, & Humphris, 2004); in this context, an automated support tool could improve both the accuracy and the effectiveness of the whole assessment procedure, resulting in a more specific and case-oriented diagnosis formulation.

In this article, we propose a novel, adaptive computerized system for supporting an essential part of the clinical assessment: the testing.

Clinical assessment can be described as an intelligent procedure the clinician carries out with the aim of collecting information about a patient, in order to formulate the diagnosis and propose a therapeutic work. The investigation proceeds through a sequence of hypothesis formulations and validations (Spoto, 2010). Any diagnostic hypothesis that can not be falsified represents a potential diagnosis to be further investigated; the process iterates until the number of plausible diagnoses is sufficiently low. Errors in the assessment could lead to a wrong diagnosis and case formulation, causing ruinous therapeutic interventions and patient disappointments (Spoto, 2010).

In the present clinical practice the main procedures used to perform the clinical assessment are the questionnaires, that is, sets of items submitted to the patient, the semistructured interviews and the clinical interview. Psychological tests are generally less time-consuming than interviews, but the result of a test is simply one or more numeric scores. The score of a questionnaire is an undoubtedly useful tool to distinguish individuals presenting critical clinical elements from nonclinical individuals. Nevertheless, such score may often be insufficient to actually help the psychologist in distinguishing among different symptoms configurations. For instance, when considering OCD, and in particular the washing subtype, it has to be noted that despite almost all washing/cleaning patients report obsessions related to dirtiness and subsequent cleaning compulsions or avoidance of feared stimuli (H. Kaplan & Sadock, 2003), washing rituals may be driven by fears of becoming contaminated/ill or rather they may be performed to seek feelings of perfect cleanliness or sensory rightness (Cougle, Goetz, Fitch, & Hawkins, 2011; Pietrefesa & Coles, 2009); therefore, identifying the most adequate treatment strategies according to the mainly involved motivational factors is essential to achieve successful therapeutic outcomes. Thus, the opportunity to have a tool able to provide a clinician with this kind of information, may be of high relevance in everyday clinical practice.

Semistructured interviews, on the other hand, are more informative than questionnaires and consist in a problem-solving and decision-making process, in which the clinician, through logical inferences, formulates hypotheses and then checks if correspondences in the patient exist. The problem in this case is the possibility of having wrong inferential decisions due to the large amount of information that could mislead the assessment, resulting in wasted time and risk of planning wrong interventions. In general, clinical assessment includes both interviews and tests and may take up to 4 hours to identify a diagnosis and to formulate the case (Camara, Nathan, & Puente, 2000). Time consumption is clearly a critical issue from the ethical perspective. In fact, using 4 hours for assessing the clinical picture of an individual means to postpone the beginning of the treatment phase. A time reduction, preserving the accuracy, is thus an important objective to achieve.

Increasing attention has been also recently devoted to the use of biomarkers in the early evaluation of clinical disorders. A number of projects are in progress, for example, the MONitoring treAtment and pRediCtion of bipolAr disorder episodes (MONARCA; Faurholt-Jepsen et al., 2013), trying to jointly use self report information and biomarkers. However, self reports still play a major role in the assessment of clinical disorders, as indicators of what the patient subjectively feels.

In order to provide a contribution for both reducing the time consumption of the testing phase and improving its accuracy, we propose an Adaptive Testing System for Psychological Disorders (ATS-PD). The system is based on a formal representation of psychological disorders, the formal psychological assessment (FPA; Spoto, Bottesi, Sanavio, & Vidotto, 2013), and exploits the FPA representation in an adaptive knowledge assessment algorithm. The latter can be considered and extension and adaptation to the clinical domain of an algorithm originally designed for the Adaptive Knowledge Assessment of a subject (AKA algorithm from now on; Falmagne & Doignon, 2011), with the novel adoption of a Bayesian updating rule in the adaptive testing process, taking into account false-positive and false-negative answers, and with a novel compound stopping criterion.

Taking into account false-positive and false-negative answers while selecting the questions for a patient is essential for extending the original AKA algorithm to the clinical domain. In fact, in the AKA algorithm, due to the kind of questions asked, the false-positive (usually called lucky guess) rate is often assumed to be 0, while the false-negative (usually named careless error) rate is expected to be low. In the clinical context none of these assumptions may hold. An incorrect answer to items may be due to problems with item formulation, as well as to problems with patient’s insight, as well as problems with social desirability, and so on. For this reason, false-negative and false-positive rates may not be irrelevant. Thus, the opportunity of taking into account step by step these parameters represents not only a technical improvement introduced by ATS-PD but also, from the authors’ point of view, a sort of prerequisite to apply AKA-like procedures in the clinical context.

The ATS-PD system can perform logically correct inferences on the basis of the whole information collected during the testing. The system is adaptive, in the sense that the question posed by the system at a given moment depends on the previously collected answers of the patient. The main advantage of ATS-PD over the traditional clinical practice is its ability to return the clinical state¹ of a patient, rather than a simple score. In this manner, patients with the same score—for example, because of the same number of positively answered questions—can be mapped to different sets of symptoms, thus facilitating the diagnosis.

The adaptivity of our system lets it dynamically choose the best sequence of questions to be posed, in order to maximize the information content of each answer. This way, the system can often avoid posing the entire set of questions by inferring the answers to logically connected questions, thus saving experimental time.

The remainder of the article is organized as follows: The next section summarizes related work from the literature. The subsequent section presents the theoretical and mathematical foundations of our system, that is, the FPA theory and the original AKA algorithm, which is followed by a section that presents our extension of the AKA algorithm to the clinical domain through the FPA theoretical framework. The fourth section presents experimental results of the application of the ATS-PD to real patient data. The penultimate section provides a discussion of the results and the final section provides conclusions along with future works.

Related Work

Clinical assessment and clinical testing are not among the usual fields of application for computerized assessment systems and only few technologies form the state of the art.

Several examples of expert systems for clinical diagnosis can be found in literature. Spiegel and Nenh (2004) developed an expert system for the diagnosis in clinical psychology based on the relation between symptoms and mental disorders. The psychologist enters the symptoms and the system calculates possible symptom combinations and returns all possible diagnoses with a degree of risk. DECES (Yong, Rambli, Rohaya, & Anh, 2007) is an interactive self-help online expert system for depression diagnosis that provides advice to lower the patients’ levels of depression. ESDAP (Seong-in, Hyun-Jung, Jun-Oh, & Seong-Hak, 2006) is concerned with diagnosis in art psychology; it provides a web-based interface such that parents and teachers can control their children’s psychological problems simply by posting children’s drawings. Also, hybrid approaches are exploited: for example, Nunes, Pinheiro, and Pequeno (2009) combined an expert system with MACBETH (Measuring Attractiveness by a Categorical Based Evaluation Technique; Bana e Costa & Vansnick, 1999), a system for multicriteria decision analysis, for diagnosing OCD (Nunes et al., 2009). Furthermore, PsyDis (Casado-Lumbreras, Rodríguez-González, Álvarez Rodríguez, & Colomo-Palacios, 2012) is a decision support system that merges the ontologies technology with the classic logic inference mechanisms for psychological disorders diagnosis.

However, none of the aforementioned expert systems can be considered adaptive according to the definition above. Adaptive assessment can be found in the literature on knowledge assessment systems: the computerized systems that assess a subject’s knowledge are the so-called computerized adaptive testings (CATs; Segall, 2013), that is, computer-based tests that adapt to the examinee’s ability level. The theoretical framework on which CATs are based is provided by item response theory (IRT; Lord, 1980) and Bayesian statistical techniques. This system has been applied in different clinical settings, for instance in developing adaptive classification tests by means of stochastic curtailment in clinical screening of depression (Finkelman, Smits, Kim, & Riley, 2012; Smits, Finkelman, & Kelderman, 2016). CAT systems, however, are not based on a formal representation of the domain of interest as ATS-PD is.

SIETTE (Conejo et al., 2004) is a IRT-based CAT, web-based, used to assist teachers in the assessment process in educational settings. Eggen and Straetmans (2000) combined IRT with statistical procedures, like sequential probability ratio test and weighted maximum likelihood, for classifying examinees into categories (Eggen & Straetmans, 2000). Following IRT but moving in the field of psychological assessment, (Chien et al., 2011) developed a Web-based CAT for collecting data regarding workers’ perceptions of job satisfaction in the hospital workplace. Simms et al. (2011) started the CAT-PD (CAT for Personality Disorders) project aimed at realizing a computerized adaptive assessment system, IRT-based, for personality disorders. EDUFORM (Nokelainen et al., 2001) and PARES (Marinagi, Kaburlasos, & Tsoukalas, 2007) are adaptive systems for the assessment of students’ knowledge, based on Bayesian statistical techniques instead of IRT.

In the field of knowledge assessment ALEKS (http://www.aleks.com/; Falmagne & Doignon, 2011; Reddy & Harper, 2013; Grayce, 2013) is a system able to adaptively assess a subject’s knowledge and provide a learning path to that subject. The AKA assessment algorithm, at the core of the ALEKS system, is based on knowledge space theory (KST; Falmagne & Doignon, 2011; Doignon & Falmagne, 1999). The next section will present the algorithm in detail and the section “An Example of Testing” will explain how we customized and extended the algorithm to the clinical psychology domain.

Finally, the Cognitive Behavioural Assessment 2.0 battery (CBA 2.0; Bertolotti, Zotti, Michielin, Vidotto, & Sanavio, 1990) is a wide-spectrum tool for the assessment of the main psychological disorders, and it was developed with the aim of supporting the clinician who is highlighting the aspects (or areas) on which the analysis is being deepened.

As far as we know, our system is unique in its conjugating adaptivity, formal definition of the investigation field and item response theory elements like parameter estimation procedures and a mathematical verification of the relations among items. Such a verification is assured by FPA, which guarantees that the relations among items are strictly related to the set of attributes each item satisfies.

Theoretical Foundations

In this section, we present the theoretical background on which ATS-PD is based. The idea is to formalize each psychological disorder as a particular mathematical lattice, with a methodology called formal psychological assessment (FPA; Spoto et al., 2013; Spoto, Stefanutti, & Vidotto, 2010), and then exploit an assessment algorithm to make probabilistic inferences through such a lattice.

The Formal Psychological Assessment

FPA is a formal theory developed by Spoto and colleagues (Spoto et al., 2010; Spoto et al., 2013), which consists in the clinical joint application of two mathematical theories: knowledge space theory (KST; Doignon & Falmagne, 1999; Falmagne & Doignon, 2011) and formal concept analysis (FCA; Ganter & Wille, 1999; Wille, 1982). Particularly, FPA derives a mathematical lattice from a questionnaire investigating a particular psychological disorder. As pointed out by Heller, Stefanutti, Anselmi, and Robusto (2015, 2016), both the KST and the FCA methodologies have a common rationale with the cognitive diagnosis models (CDMs; de la Torre, 2009, 2011): above all, even this methodology analyze mastered and nonmastered attributes by different examinees/ items by means of a matrix that in the CDM approach is the so-called Q matrix (Heller et al., 2015, 2016; M. Kaplan, de la Torre, & Barrada, 2015). In what follows, we will use OCD as a running example to illustrate the FPA model.

In clinical psychology, a question on a questionnaire is called an item. Each clinical item is concerned with one or more clinical symptoms that have to be investigated to diagnose a specific disorder. In FPA, the items of a questionnaire are called objects, while the symptoms investigated by each item are defined attributes. Objects and attributes are referred to as the theoretical framework chosen by the researcher. In our running example, the items investigating the OCD belong to the Maudsley Obsessional-Compulsive Questionnaire–Reduced (MOCQ-R; Sanavio & Vidotto, 1985), and the attributes are the diagnostic criteria that the Diagnostic and Statistical Manual of Mental Disorders, fourth edition, text revision (DSM-IV-TR; APA, 2000) defines for the OCD. The MOCQ-R is composed of three subscales: cleaning, checking, and doubting-ruminating, that is, three specific typologies of OCD. In our example, two items taken from the cleaning subscale could be i3: “I am not excessively concerned about cleanliness” and i5: “My hands feel dirty after touching money.” Item i3 involves the set of attributes $\{a2,a3,a8\}$, where $a2$: “Thoughts, impulses, or images are experienced as intrusive and inappropriate, cause marked anxiety and distress, and are not simply excessive worries about real-life problems,”$a3$: “The person recognizes that the obsessional thoughts, impulses, or images are a product of his/her own mind,” and $a8$: “At some point during the course of the disorder, the person has recognized that the obsessions or compulsions are excessive or unreasonable”. Item $i5$, on the other hand, involves the set $\{a1,a3,a13\}$, where $a1$: “Recurrent and persistent thoughts, impulses, or images,”$a3$ as above and $a13$: “Money (contamination).” A patient who answers “true” to $i5$ will thus present the corresponding set of attributes. As it can be noted, the sets of attributes are not mutually exclusive.

Starting from a set of objects Q (the MOCQ-R’s items), a set of attributes S (the DSM-IV-TR criteria for OCD) and the relation I between items and attributes, a Boolean matrix called formal context$(Q,S,I)$ is built (Ganter & Wille, 1999). The matrix contains a 1 whenever an item investigates the specific symptom and a 0 otherwise.

The whole set $Q$ of items is the domain of the formal context and the clinical state$K\subseteq Q$ of a patient is the subset of the domain he or she affirmatively answered. Each clinical state is uniquely associated with a subset of attributes (Spoto et al., 2010; Spoto et al., 2010). This way, even if two different clinical states score the same (two different patients affirmatively answer the same number of items), their attribute configurations differ. This means that the only case in which two response patterns are considered equivalent in FPA is when they contain positive answers to exactly the same items.

From the formal context $(Q,S,I)$ it is possible to build the clinical structure$\mathcal{K}$ of a specific psychological disorder (Spoto et al., 2010). A clinical structure is a lattice representing the implications among the items of $Q$. It includes all of the so-called admissible response patterns (ARPs; i.e., the clinical states) with their respective sets of attributes. An ARP is a set of items that are consistent with the implications postulated by the selected theoretical framework.

To summarize, the FPA theory maps sets of items to sets of attributes and allows one to adaptively collect the same information of a clinical interview through the administration of self-report questionnaires (Bottesi, Spoto, Freeston, Sanavio, & Vidotto, 2015; Serra, Spoto, Ghisi, & Vidotto, 2015). Up to now, all of the presented considerations refer to a deterministic situation. Such an approach is inadequate in clinical practice: in fact, it is very likely to observe response patterns that do not correspond to the actual clinical state of the patient, and not all clinical states have the same probability of occurring.

For these reasons, FPA exploits a probabilistic framework to manage the conditional probabilities of response patterns given a clinical state. Such a theoretical background was inspired by a similar probabilistic framework developed in KST (Doignon & Falmagne, 1999; Falmagne & Doignon, 1988, 2011). A probabilistic clinical structure is a triple $(Q,\mathcal{K},p)$, where $p$ is a probability distribution for $\mathcal{K}$, assigning to every clinical state $k\in \mathcal{K}$ the probability of occurrence in the population. This value can be estimated from a sample of patients (Spoto et al., 2010). In this model, given a state, the responses to the items are assumed to be locally independent. Moreover, given a probabilistic clinical structure $(Q,\mathcal{K},p)$ and a specific response pattern $R\subseteq Q$, the response function$r:2^Q\times \mathcal{K}\to \mathbb{R}$ assigns to $R$ its conditional probability given that a subject is in state $K$ (for all states $K\in \mathcal{K}$). Thus, it is possible to compute for each response pattern $R$ a probability distribution:

$$\rho (R)=\sum _{K\in \mathcal{K}}r(R,K)p(K).$$

Because the response function satisfies local independence for each item $q\in Q$, the conditional probability $r(R,K)$ is determined by the probabilities $\beta$, $\eta$ related to each item $q$, where ${\beta }_q$ is the probability of a false-negative answer and ${\eta }_q$ the probability of a false-positive answer to $q$. Formally,

$$\begin{array}{c}r(R,K)=\left(\underset{q\in K\backslash R}{\Pi }{\beta }_q\right)(\underset{q\in K\cap R}{\Pi }(1-{\beta }_q))\hfill \\ \left(\underset{q\in R\backslash K}{\Pi }{\eta }_q\right)(\underset{q\in \overline{R\cup K}}{\Pi }(1-{\eta }_q)).\hfill \end{array}$$

Equation (2) represents the basic local independence model (BLIM; Doignon & Falmagne 1999; Falmagne & Doignon, 1988). In the running example, the model parameters $\beta$, $\eta$, and the probability distribution for $\mathcal{K}$ have been estimated from a sample of 33 patients with a diagnosis of OCD (Spoto et al., 2010) with the expectation-maximization algorithm (Dempster, Laird, & Rubin, 1977). The reliability of the adopted parameter estimates is confirmed by some papers that used the same questionnaire, estimated such parameters on larger samples (Bottesi et al., 2015; Spoto et al., 2013), and obtained similar estimates.

The Original Adaptive Knowledge Assessment Algorithm

The AKA algorithm was proposed by Doignon and Falmagne for the adaptive assessment of a subject’s knowledge (Falmagne & Doignon, 2011). The algorithm takes as input a knowledge structure$\mathcal{K}$, that is, a mathematical structure developed in KST (Doignon & Falmagne, 1999; Falmagne & Doignon, 2011) that is very similar to a clinical structure. Given a knowledge domain $Q$, a knowledge structure is formed by knowledge states$K\subseteq Q$, that is the subsets of $Q$ that contain questions (or problems) that a subject masters or is able to solve. A probabilistic knowledge structure can further be defined by appending to every knowledge state $K\in \mathcal{K}$ the probability $p(K)$ that a subject is in that state. The objective of the algorithm is to focus the knowledge assessment as quickly as possible on some knowledge state that is capable of explaining the subject’s responses.The pseudocode of the procedure is presented in Algorithm 1.

Algorithm 1.

The AKA algorithm.

Require: $Q$, $\mathcal{K}$, ${\mathbf{L}}_1$  $n\leftarrow 1$  while$\mathrm{stopCondition}({\mathbf{L}}_n)$do    $\mathrm{question}\leftarrow \mathrm{questioningRule}(\mathcal{K},{\mathbf{L}}_n)$    ask $\mathrm{question}$    append in $D$    $\mathrm{question}$ and user’s answer    ${\mathbf{L}}_{n+1}\leftarrow \mathrm{updatingRule}(D,{\mathbf{L}}_n,\mathcal{K},\zeta )$    $n\leftarrow n+1$  end while  return the state $K_0$ with the highest likelihood ${\mathbf{L}}_n(K_0)$

The AKA algorithm requires a probabilistic knowledge structure $(Q,\mathcal{K},L)$, where for every state $K\in \mathcal{K}$, ${\mathbf{L}}_1=L(K)$ represents the initial probability of $K$. At step $n$, the algorithm considers as a plausibility function of every state $K$ its current likelihood ${\mathbf{L}}_n$, based on all of the information accumulated so far. Now, the procedure questioning rule selects the next question to ask, i.e. the item $q$“maximally informative,” such as the sum of the likelihoods of all of the states containing $q$ has to be as close as possible to the sum of the likelihoods of all of the states not containing $q$. If several items are equally informative, one of them is chosen at random. We indicate the set of possible questions as $S({\mathbf{L}}_n)\subseteq Q$, so we can formalize the rule as

$$S({\mathbf{L}}_n)=\underset{q}{\arg \min }(|2{\mathbf{L}}_n({\mathcal{K}}_q)-1|),$$

where

$${\mathbf{L}}_n(\mathcal{F})=\sum _{K\in \mathcal{F}}{\mathbf{L}}_n(K)$$

and ${\mathcal{K}}_q$ indicates the set of all knowledge states $K\in \mathcal{K}$ containing a given question $q$.

The subject’s response is collected by the system and the procedure updating rule updates the likelihood ${\mathbf{L}}_{n+1}(K)$ of every state $K$. If a subject answers correctly to $q$, the likelihoods of the states containing $q$ are increased and, correspondingly, the likelihoods of the states not containing $q$ are decreased. A wrong response has the opposite effect. If we indicate a correct response with $r=1$ and a wrong one with $r=0$, we can formalize the rule as

$${\mathbf{L}}_{n+1}(K)=\frac{{\zeta }^K{\mathbf{L}}_n(K)}{\sum _{K\prime \in \mathcal{K}}{\zeta }^{K\prime }{\mathbf{L}}_n(K\prime )},$$

where

$${\zeta }^K=\{\begin{array}{cc}\hfill 1\hfill & \hfill \mathrm{if}{i}_K(q)\ne r\hfill \\ \multicolumn{1}{c}{\zeta }& \hfill \mathrm{if}{i}_K(q)=r,\hfill \end{array}$$

$\zeta >1$ is a parameter that increases the likelihood, and

$$i_K(q)=\{\begin{array}{cc}\hfill 1\hfill & \hfill \mathrm{if}q\in K\hfill \\ \multicolumn{1}{c}{0}& \hfill \mathrm{if}q\notin K.\hfill \end{array}$$

It is worth noting that the value of the $\zeta$ parameter influences the efficiency of the adaptive assessment process. In fact, the higher its value, the more reliable are considered the answers provided by the subject. It has been observed (Falmagne & Doignon, 2011) that $\zeta$ values less than 2 make the system extremely redundant in completing the assessment, since a higher number of answers are needed to reach a reliable conclusion about the actual state of the patient. On the other hand, the efficiency of the system reaches a maximum at a specific value of $\zeta$ (depending on many variables) and it makes no sense to further increase its value. Notice that it has been proven that the system, even with high values of the parameter $\zeta$, tends to converge to the “correct state”. Thus, the selected value of this parameter does not affect algorithm efficacy.

The algorithm stops when a stopping condition is satisfied. For the experiments reported in Falmagne and Doignon (2011), the authors suggest to stop the algorithm as soon as ${\mathbf{L}}_n({\mathcal{K}}_q)$ lies outside the interval $[.2,.8]$ for all $q$. In the previous section, the mathematical structure with which FPA formalizes a psychological disorder and the AKA algorithm for the adaptive knowledge assessment have been shown. This section presents how ATS-PD was developed by extending the assessment algorithm and adapting it to the FPA mathematical model. Specifically, we explain the adoption of a Bayesian rule for updating the likelihood of each state in each step, taking into account false-positive and false-negative answers, and a compound stopping criterion, based on both the likelihood of the states and the entropy of the clinical structure.

The Algorithm

Because of the clinical relevance of false-positive and false-negative answers in the psychological assessment process, we decided to take into account the response pattern $R$ during the assessment, through a Bayesian rule for updating the posterior state probabilities in the form

$$P(K_i|R)=\frac{P(R|K_i){\mathbf{L}}_n(K_i)}{\sum _{j=1}^{|\mathcal{K}|}P(R|K_j){\mathbf{L}}_n(K_j)},$$

where $P(R|K_i)=r(R,K_i)$ is given by Equation (2) of the previous subsection.

The updated states are used by our algorithm for a novel stopping criterion, based on the combination of two criteria. The first criterion stops the computation as soon as the updated likelihood of a state ${\mathbf{L}}_n(K)$ surpasses a threshold ${\theta }_L$. The second criterion is based on the entropy of the clinical structure, defined as

$$H({\mathbf{L}}_n)=-\sum _{k\in \mathcal{K}}{\mathbf{L}}_n(K){\log }_2{\mathbf{L}}_n$$

and stops the assessment as soon as the entropy gets below a second threshold ${\theta }_H$. Careful tuning on experimental data revealed us that the values 0.7 for ${\theta }_L$ and 1 for ${\theta }_H$ and a compound criterion stopping the assessment as soon as at least one of the two criteria was satisfied are optimal choices, in the sense that they lead to the smallest minimum distance between nonadmissible response patterns, that is, patterns induced by false-positive and false-negative answers, and the real patterns assigned to them by the system.

The pseudo-code of our novel testing algorithm, ATS-PD, is presented in Algorithm 2.

Algorithm 2.

The ATS-PD system.

Require: a file containing the formal representation of a given psychological disorder  import data $Q,\mathcal{K},{\mathbf{L}}_1,\beta ,\eta ,S,I$ from file  $n\leftarrow 1$  $\mathrm{tmpL}\leftarrow {\mathbf{L}}_1$  while$\mathrm{stopCondition}(\mathrm{tmpL})$do   $\mathrm{question}\leftarrow \mathrm{questioningRule}(\mathcal{K},{\mathbf{L}}_n)$   ask $\mathrm{question}$   append in $D$$\mathrm{question}$ and user’s answer   ${\mathbf{L}}_{n+1}\leftarrow \mathrm{updatingRule}(D,{\mathbf{L}}_n,\mathcal{K},\zeta )$   $\mathrm{tmpL}\leftarrow \mathrm{bayesianUpdate}(\mathcal{K},{\mathbf{L}}_{n+1},D,\overrightarrow{\beta },\overrightarrow{\eta })$   $n\leftarrow n+1$  end while  $(\mathrm{state},\mathrm{symptoms})\leftarrow \mathrm{report}(\mathrm{tmpL},\mathcal{K},Q,S,I)$  return the patient’s clinical $\mathrm{state}$ and his/her $\mathrm{symptoms}$

For a given psychological disorder, ATS-PD imports its clinical structure, the diagnostic criteria $S$ and their relation $I$ with the items; moreover, the false-positive and the false-negative rates of each item are used. Then, the system starts the assessment algorithm, counting the number of questions posed. For a given psychological disorder, the system selects the question that is maximally informative (i.e., the item that splits in two equivalent parts the mass of the probability of the states that include or not include it) to pose with the questioning rule (see Equation 3). The system then stores the answer and updates the likelihood ${\mathbf{L}}_n$ into ${\mathbf{L}}_{n+1}$ using the updating rule given by Equation (5). At this point of the procedure, ATS-PD performs the Bayesian updating rule (Equation 8) on the likelihoods ${\mathbf{L}}_{n+1}(K)$ for every $K\in \mathcal{K}$ and stores them in a temporary list. Such a function allows one to extract the response pattern $R$ from the data structure that stores the patient’s answers. If the temporary list satisfies the stopping criterion the system stops the testing and returns the clinical state with the corresponding attributes.

Implementation Considerations

With further formalization, it is possible to show that the testing algorithm used is a Markovian process (Falmagne & Doignon, 2011); this fact gives us the advantage of storing only the vector ${\mathbf{L}}_n$ to compute ${\mathbf{L}}_{n+1}$.

Furthermore, we chose the uniform probability distribution, $L_1=1/|\mathcal{K}|$, as the initial likelihood. This distribution was considered because it formulates fewer a priori assumptions; indeed, it gives us the maximum entropy at the beginning of the testing (Harremoës, 2009). The system is implemented in the Python language, version 2.7.

An Example of Testing

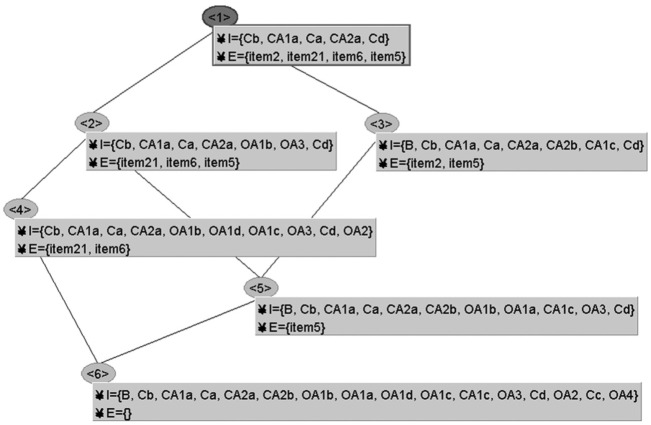
Let us show an example of testing performed by ATS-PD, using the running example of OCD, in particular, the clinical structure of the doubting-ruminating subscale (see Figure 1).

Figure 1.

The clinical structure of the doubting-ruminating subscale.

Table 1 shows the initial likelihood of every state at Step 1 ($n=1$), following the uniform probability distribution. The system, using the questioning rule (Equation 3), selects the more discriminative items; in this case, they form the set $S({\mathbf{L}}_1)=\{6,21\}$. The system will randomly choose between this two items since they have, cumulatively, the same mass probability to be present or absent among the states.

Table 1.

Initial likelihood of the states.

$\mathbf{L}$	[ ]	[5]	[2, 5]	[6, 21]	[5, 6, 21]	[2, 5, 6, 21]
${\mathbf{L}}_1$	0.1667	0.1667	0.1667	0.1667	0.1667	0.1667

Let us suppose the system, between Item 6 and Item 21, randomly chooses the former: “I frequently have disagreeable thoughts and I cannot get rid of them.” It is important to stress that in this case the selection of the first item to be asked is random because of the fact that the starting distribution is uniform: In the case in which theoretical prior knowledge or previous parameters estimates (e.g., the probability of the states in a population) are taken into account, the starting point may not be randomly chosen. Now suppose that the user answers “True.” The system now, using the updating rule (Equation 5), increases the likelihood of the states containing Item 6 and decreases the others (see Table 2). As we can see, the likelihoods do not satisfy the threshold stopping criterion, and if the system performs the Bayesian update (Equation 8) on the response pattern observed, [6], it does not satisfy the entropy stopping criterion.

Table 2.

Initial likelihood of the states at Trial 2.

$\mathbf{L}$	[ ]	[5]	[2, 5]	[6, 21]	[5, 6, 21]	[2, 5, 6, 21]
${\mathbf{L}}_2$	0.0278	0.0278	0.0278	0.3056	0.3056	0.3056

ATS-PD is now at trial 2 ($n=2$) and, again, using the questioning rule (Equation 3), selects the more discriminative items. In this case, they form the set $S({\mathbf{L}}_1)=\{2,5\}$. We suppose ATS-PD randomly selects Item 2: “Usually, I have serious doubts about simple things I do every day,” and we suppose that the user answers again “True.” The system now, using the updating rule (Equation 5), increases the likelihoods of the states containing Item 2 and decreases the others (see Table 3).

Table 3.

Initial likelihood of the states at Trial 3.

$\mathbf{L}$	[ ]	[5]	[2, 5]	[6, 21]	[5, 6, 21]	[2, 5, 6, 21]
${\mathbf{L}}_3$	0.0064	0.0064	0.0705	0.0705	0.0705	0.7756

We can see that the likelihood of state [2, 5, 6, 21] is greater than 0.7, satisfying the first stopping criterion. Moreover, if the system performs the Bayesian update (Equation 8) on the response pattern observed, [6, 2], and then calculates the entropy, it obtains a value of 0.1883. Thus, ATS-PD returns as output the state [2, 5, 6, 21] with the corresponding attributes {Cb, CA1a, Ca, CA2a, Cd}, where

• CA1a: repetitive behaviors or constrained mental acts;

• CA2a: behaviors are designed to reduce or prevent discomfort;

• Ca: marked discomfort;

• Cb: waste of time;

• Cd: interference with social and working life.

Analysing the output, the users responded only to Questions 6 and 2 and the system inferred, in a probabilistic way, that the clinical state is [2, 5, 6, 21]. That is, everyone who responds to items 6 and 2 automatically will respond positively to the other questions. This strong inference is the core of testing algorithms based on clinical structures. Furthermore, in this case, the number of items asked is $n=2$ of four possible questions; thus, we have an items saving of 50%.

Experimental Results

In this section, we first assess the performance of the ATS-PD system on real patient data. Subsequently, we focus our analysis on the system’s behavior in the presence of nonadmissible response patterns.

Performance of the System

As stated in the introduction, we expect that ATS-PD

• identifies a patient’s precise critical areas supporting the clinician’s decisions during the assessment (effectiveness);

• asks a smaller number of questions with respect to the standard written version questionnaires (efficiency).

To this aim, we reproduced the clinical testing in an adaptive way using real data. We executed several testing using a sample of 4,324 subjects taken from normal population tested on OCD. The subjects answered the questions of the written version of the MOCQ-R, the questionnaire on which FPA built the mathematical lattice representing the OCD used by ATS-PD. Furthermore, subjects answered the questions of the MOCQ-R in a nonadaptive way—that is, they responded to all items sequentially.

Before giving performance results, we provide some definitions. A response pattern is a list of items, for example [1, 4, 7], containing the items to which a subject answered “True” in the written version of the MOCQ-R. Different subjects can have the same response pattern to a certain subscale. The set $\mathcal{R}$ includes all the different response patterns, that is, it lists each pattern independently from its frequency in the sample one time. We say that a response pattern $R$ is assigned to a state $K$ if the system outputs $K$ with input $R$. Moreover, we need a method to measure the similarity between response patterns and states; thus, we assigned to every response pattern a distance$d(R,K)$ to a state $K$ expressed as the following cardinality:

$$d(R,K)=|(R\cup K)\backslash (R\cap K)|,$$

with $d(R,K)=0$ if and only if $R$ corresponds with the clinical state $K$, that is, $R=K$. We say that a response pattern $R$ has a minimum distance to a state $K$ if a state $K\prime$, such as $d(R,K\prime )<d(R,K)$, does not exist.

The goal of reproducing the testing phase of clinical assessment was to test whether ATS-PD could generate the same response pattern of a subject who answered the written version of the MOCQ-R (system efficacy), but with a smaller number of questions (system efficiency). That is, given a response pattern $R$, we want to assess if the system assigns it a clinical state $K$ such as $d(R,K)=0$, with a smaller number of questions.

ATS-PD returns only states in the clinical structure, and we assume that the clinical structure is a good model of the reality. This datum is supported by a good fit index of the clinical structure (Spoto et al., 2010; Spoto et al., 2013). Thus, a response pattern $R$, with an assigned clinical state $K$ such as $d(R,K)\ne 0$, indicates that $R$ is affected by false-positive or false-negative errors. The reproduction of the testing proceeds as follows: the system imports the clinical structures of the subscales and the response patterns of 4,324 subjects. For every response pattern $R$, ATS-PD performs the testing by asking a question, answering automatically, and updating the likelihood until it uncovers the latent state $K$. After some empirical observations, the parameter $\zeta$ used for the updating rule was set to 11. This value allowed the algorithm to be as less redundant as possible, and preserved its accuracy. The system, then, calculates the distance $d(R,K)$.

Following the structure of the MOCQ-R questionnaire (see section “The Formal Psychological Assessment”), we focused on the cleaning and checking subscales. The considered subscales contain the same number of items, 8, and are thus both a collection of 256 possible total states; however, the two differ in the number of admissible states (92 and 20, respectively) and have a different topology, thus allowing us to test the behavior of ATS-PD under two different conditions. Moreover, the number of different response patterns, that is $|\mathcal{R}|$, is 220 in the cleaning subscale and 185 in the checking subscale.

Results show that the response patterns corresponding to a state $K\in \mathcal{K}$ and not assigned to $K$ are 0 in both cases. Thus, as expected, all the response patterns corresponding to a state $K$ are assigned to it.

Furthermore, analysing the number of questions posed (Figure 2), we observed it to be significantly lower than 8 in both cases, with 95% confidence intervals $[6.88;6.91]$ for the cleaning scale and $[4.34;4.39]$ for the checking scale. The average saving in terms of question posed is thus statistically significant and around 14% for the cleaning subscale and 45% for the checking subscale.

Figure 2.

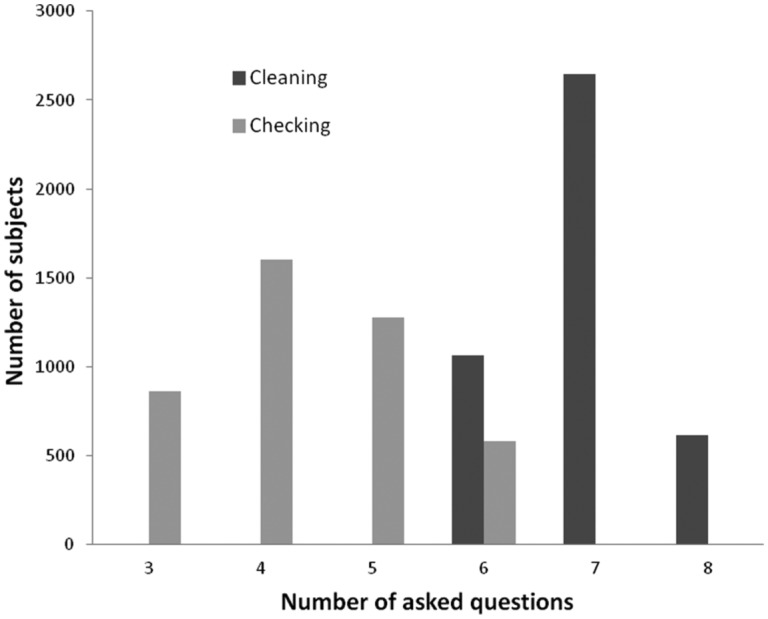
Distribution of the number of asked items for the cleaning and checking subscales.

Concerning computational time, the system always requires less than 75 milliseconds for the checking subscale and 250 milliseconds for the cleaning subscale to update all likelihoods after an answer and to pose the subsequent question. Finally, the amount of memory required is always less than 10 megabytes, thus making the system suitable for a desktop application.

Nonadmissible Response Patterns

During a clinical testing, a subject can also provide a nonadmissible pattern; for example, he/she could provide wrong answers due to poor introspection capabilities or for showing social desirability, so his or her response pattern is not a state of the clinical structure. Such patterns can be explained through false-negative or false-positive errors and we want to study the ATS-PD behavior with these patterns. As the system returns only states present in the clinical structure, we study the distance between nonadmissible response patterns and their assigned states (Figure 3).

Figure 3.

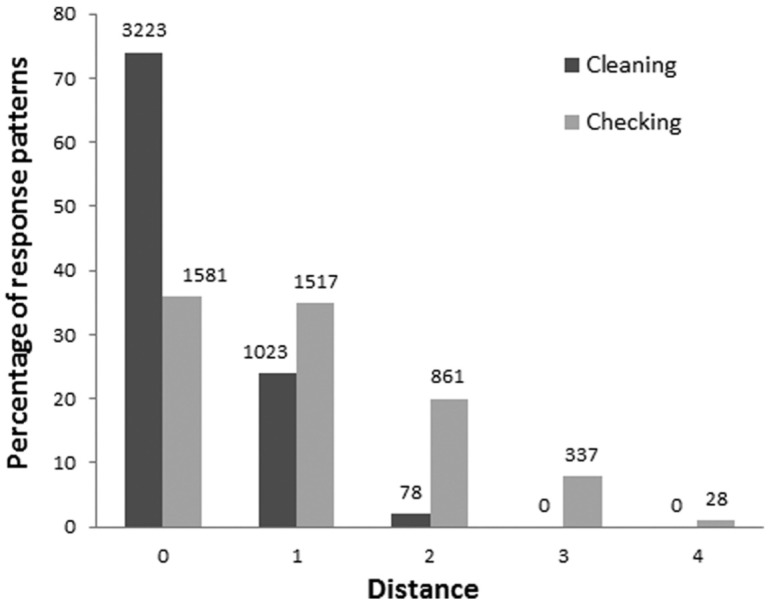
Cleaning and checking subscales: distribution of the response patterns according to the distances. The x-axis represents the distances, the y-axis the percentage of response patterns over the total 4,324 subjects. The values above every column represents the number of subjects with that distance.

As it can be seen from the figure, in the cleaning subscale the distances $d(R,K)$ of the response patterns not included in the clinical structure are at most 2. The 78 subjects with $d(R,K)=2$ represents only the 2% of the response patterns, while a large majority of subjects (74%) are gathered at distance $d(R,K)=0$. The checking subscale, instead, presents a critical situation; the number of response patterns with $d(R,K)=0$ is low, only the 36%, and the distance measure reaches 4.

Focusing on the patterns with a nonminimum distance, we observed for the cleaning subscale that every response pattern with $d(R,K)>1$ is assigned to its nearest state, the state with the minimum distance. For the checking subscale, on the other hand, 392 response patterns are assigned to a state with a nonminimum distance. This result could be explained as the combination of the smaller cardinality of the checking structure and the system behavior. Indeed, as already said, ATS-PD asks question in an adaptive way and outputs a clinical state containing questions that are also purely inferred. In the checking case, ATS-PD makes inferences on a small number of states, and this behavior could be a plausible explanation for the different results between the subscales considered.

Nevertheless, with these considerations, as seen above, both the cleaning and the checking clinical structures present good results regarding the means of the distances.

Discussion

The objective of the present work was to build an adaptive testing system to support the clinician in the diagnosis of psychological disorders. We aimed at a system that is

• able to individualize a patient’s precise critical areas and

• efficient, that is, a system that poses fewer questions than the standard written questionnaire does.

To this aim, we presented an Adaptive Testing System for Psychological Disorder (ATS-PD). Such a system performs inferences that are logically correct thanks to the formal model on which the testing algorithm is based.

The performance results reported in the previous section showed that all of the response patterns that are states are assigned to that state, so the system is able to correctly reproduce the patient’s admissible response pattern of a questionnaire.

It is worth noting some crucial differences between a classical questionnaire administration and the assessment through ATS-PD. As mentioned in the introduction, the classical questionnaires used to perform the clinical testing return only a numeric score. The score can be defined as the number of positively answered items and defines a “clinical label” for the individual, that is, clinical subject or nonclinical subject. Such a score does not allow to distinguish between different response patterns with the same score. For example, in our dataset, Subjects 7 and 15 achieved the same score for the cleaning subscale, 5, and this is the only information provided by classical questionnaires. ATS-PD returns the individuals’ clinical states and the related symptoms: the states of Subjects 7 and 15 are [10, 13, 16, 17, 20] and [3, 8, 10, 16, 20], respectively. This information permits one to distinguish the individuals showing, for example, different critical areas and, thus, leading to different diagnoses.

Another important point to be stressed is the reduction of the number of questions posed together with the improvement of the quality and quantity of information collected. In the classical paper and pencil form of the MOCQ-R, each participant has to answer all 16 items and the output of the questionnaire is a score, either clinically significant or not. In ATS-PD only a percentage ranging between 50 and 75% of the items are asked and the clinician is provided with the clinical state of the individual, including the diagnostic symptoms presented by the patient.

Concerning computational time, the system was shown to require some milliseconds to process an answer and choose the next question. Such a task, if accomplished by a clinician during a semistructured interview, would require the time for considering the answer, choosing the next question, accessing the correct page in the MOCQ-R booklet and finding the question in the page, for a total estimated time of around a minute. Our system, thus, is clearly competitive.

The strong assumption exploited by ATS-PD (but supported by the fit of the model) is that the admissible response patterns are the states of the structure, so the system will always complete its evaluation in one of these states. However, the pattern observed is affected by errors and could differ from the assigned state. Indeed, the response patterns that are not states are assigned to states at a close distance from them. Such response patterns are explained through false-positive and false-negative answers.

In the presence of nonadmissible response patterns, the system was shown to exhibit different behaviors for the cleaning and checking subscales, with the latter exhibiting a larger average distance between response patterns and assigned clinical states. This fact can be explained by considering the number of states of the checking structure: only 20 clinical states and 185 admissible patterns exist, so the states cover only 11% of the possible patterns. This structure could be affected by an overfitting problem: It is a good representation of the structure concerning subjects affected by OCD, but it does not have enough states to fit a nonclinical population. It could be interesting to reformulate the structure using alternative methods, such as the extraction of the structure from the response patterns (Schrepp, 1999).

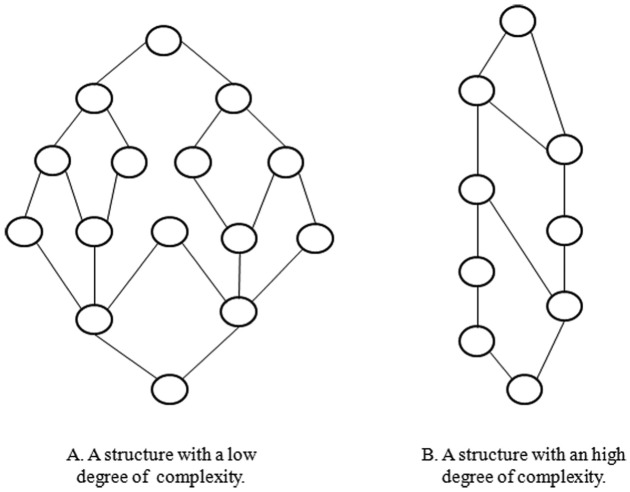
A greater or smaller cardinality of the states is directly linked to a property of such structures—the ordering of a structure. A clinical structure (or ordered set) is more ordered if fewer states are in the structure, i.e. if it is more similar to the total order. In our case, the cleaning structure has 92 states of 256 total possible states, so it is similar to Figure 4A, while the checking structure has only 20 states of 256 (see Figure 4B). Thus, the higher percentage of response patterns with distance $d(R,K)>0$ can be explained considering that the checking structure is more ordered than the cleaning structure is. Moreover, the concept of the ordering of a clinical structure can also explain the difference in the number of items posed; indeed, we hypothesize that a more ordered clinical structure will converge more quickly than a less ordered one will. It has to be further stressed that, as shown by Albert, Kickmeier-Rust, and Matsuda (2008), a size-fit trade-off exists. Thus, the larger the structure, the lower the distance between response patterns and states. It would be crucial to identify, even through simulation data, the structure size that both maximizes the fit of the model and allows an acceptable level of meaning of the clinical model.

Figure 4.

Diverse kinds of ordering of the ordered sets.

The major innovation of the ATS-PD system, with respect to the standard assessment questionnaires, is that our system does not return a simple numeric score, but rather a relation between a set of items of a questionnaire and a set of symptoms of the subject. Thus, the numeric score is no more the focus of the testing procedure and it can be read in terms of diagnostic attributes. Indeed, ATS-PD indirectly uses diagnostic criteria to proceed in the identification of questions to ask and returns a description of the patient that is readable on the basis of the attributes.

ATS-PD is based on an extension of an algorithm for the adaptive assessment of knowledge (Falmagne & Doignon, 2011). Several new features are added to the procedure: first, the definition of the reference structure for the algorithm is performed through the application of FPA; second, the parameters estimates are carried out by referring to the IRT framework; third, the algorithm updates the states’ probabilities through a Bayesian rule step by step in the testing; finally, two different criteria, one likelihood based and one entropy based, are jointly exploited in a compound stopping criterion.

Conclusions and Future Work

Few computerized diagnostic systems have been introduced in clinical psychology and none of them is able to accomplish an adaptive assessment, reproducing the logical inferences of the clinician.

The aim of this work was to fill this gap with a system, called ATS-PD, that can execute the process of clinical testing in an adaptive and logically correct manner, in order to assist the clinician in the diagnosis formulation. ATS-PD innovation lies in its theoretical framework, combining a formal model of a psychological disorder, generated by the formal psychological assessment theory, with the extension of an algorithm for the assessment of knowledge (Falmagne & Doignon, 2011).

The results fit our expectations. The system, tested on a sample of 4,324 patient’s response patterns and verified for two subscales of the OCD (cleaning and checking), converges correctly to the latent state of every response pattern. ATS-PD outputs the patient’s clinical state with the corresponding set of diagnostic criteria; such criteria individualize the critical area where the clinician should concentrate his or her attention to formulate the diagnosis. Furthermore, the adaptivity of the system results in a consistent reduction of the number of asked questions: ATS-PD has thus the power of a clinical interview but is faster than a standard questionnaire.

As future work, we intend to extend ATS-PD to the other main psychological disorders and to develop a software product that can assist the clinician with the assessment and based on a solid formal representation of the disorders. We imagine a scenario where the patient, with a tablet, for example, fills out a questionnaire in an adaptive manner, and in a second moment, the clinician controls the response of the system. The response could be a pie chart, where every slice represents a psychological disorder and has a probability that indicates how likely the patient can fall in that clinical diagnosis. In order to achieve this goal, it is necessary to calculate the attributes’ probabilities (Spoto et al., 2013) and to apply FPA to the other main psychological disorders. A simple graphical user interface will provide the clinician with a helpful way to interact with the system.

There can be several improvements of our system, for example we would investigate the possibility of simplifying the updating rule, as in Augustin et al. (2013), useful for real-time application as ATS-PD is. Another foreseen extension will be to treat items with more than two answer alternatives. This further development of both ATS-PD and FPA will represent a crucial strategic improvement, since it will allow to adopt the most widely used response format in psychological testing, that is, the Likert scale. Two main solutions are under evaluation to solve this issue: on the one hand we have the fuzzy logic approach; on the other hand we have an IRT oriented solution. In both cases, the possibility to take into account the case in which the answering format is not dichotomous is ensured. The implementation of either of these proposals would allow FPA to construct structures by using all the questionnaires available in psychological testing; at the same time it would allow ATS-PD to become much more usable in clinical practice.

Finally, the issues of authoring of the structures as well as the potentially harmful constraints in terms of computational efforts in real-time computing for large clinical structure with a great number of items may deserve some further considerations. All the FPA methodology is, at present, a work in progress. The authoring process is at present one of the core elements under evaluation for identifying an efficient and accurate procedure to end up with reliable and valid structures. The analysis item by item of the presence/absence of a set of clinical attributes is the presently used approach. Further research is in progress with respect to the construction of the structure and of the clinical context from a given database of answers to questionnaires. This approach seems to be promising and would represent a strong improvement of the authoring part. With regard to the constraints in terms of computational efforts, the construction of several substructures on which to perform in parallel the assessment seems, at present, the most interesting perspective.