Type I and Type II Error Rates and Overall Accuracy of the Revised Parallel Analysis Method for Determining the Number of Factors

Abstract

Traditional parallel analysis (T-PA) estimates the number of factors by sequentially comparing sample eigenvalues with eigenvalues for randomly generated data. Revised parallel analysis (R-PA) sequentially compares the kth eigenvalue for sample data to the kth eigenvalue for generated data sets, conditioned on k− 1 underlying factors. T-PA and R-PA are conceptualized as stepwise hypothesis-testing procedures and, thus, are alternatives to sequential likelihood ratio test (LRT) methods. We assessed the accuracy of T-PA, R-PA, and LRT methods using a Monte Carlo approach. Although no method was uniformly more accurate across all 180 conditions, the PA approaches outperformed LRT methods overall. Relative to T-PA, R-PA tended to perform better within the framework of hypothesis testing and to evidence greater accuracy in conditions with higher factor loadings.

In the context of exploratory factor analysis (EFA), data analysts often use empirical criteria to suggest the number of factors that should be extracted to explain covariation among a set of measures. A number of methods have been recommended in the literature, including the eigenvalues-greater-than-one criterion (Guttman, 1954; Kaiser, 1960), the scree test (Cattell, 1966), parallel analysis (PA; Horn, 1965), and the MAP test (Velicer, 1976). The use of PA has been advocated by many methodologists because PA has been shown to outperform other methods (e.g., Fabrigar, Wegener, MacCallum, & Strahan, 1999; Lance, Butts, & Michels, 2006; Preacher & MacCallum, 2003).

A number of variations of PA have been described and evaluated (e.g., see Crawford et al., 2010), including the traditional method that compares sequentially the eigenvalues of the sample data with eigenvalues for data that are computer-generated completely at random. However, it has been argued that the use of comparison data sets based on completely random data is theoretically problematic (Green, Levy, Thompson, Lu, & Lo, 2012; Harshman & Reddon, 1983; Ruscio & Roche, 2012; Turner, 1998). Green, Levy, et al. (2012) proposed and evaluated via simulation methods a revised approach to PA that compares sequentially the kth eigenvalue for sample data to the kth eigenvalue for computer generated data given k− 1 factors; the data are simulated using the k− 1 factor loadings estimated with the sample data. This revision to the traditional PA approach tended to perform better than traditional PA methods across a range of factor structures.

Alternatively, researchers may choose to use sequential likelihood ratio test (LRT) methods for determining the number of factors to extract. One LRT method assesses sequentially models with zero factors, one factor, and so on, based on chi-square tests, whereas another LRT method sequentially compares models with k− 1 and k factors using a chi-square difference test. The traditional and revised PA methods can be viewed as stepwise hypothesis-testing approaches for assessing the number of factors and, thus, are alternatives to the sequential LRT methods.

The objective of our study was to assess the relative accuracies of three sequential methods for determining the number of factors to extract in the context of EFA: traditional PA, revised PA, and LRT. Distinctive from previous investigations, a goal of this study was to gain understanding of their accuracies by examining the Type I and Type II error rates of the tests making up the PA and LRT methods. We evaluated their accuracies by using computer-generated data with known factor structures and design characteristics to examine systematic variation in factor structure, number of factors, number of variables, size of factor loadings, sample size, and correlation between factors.

Before presenting our study in greater detail, we describe previous research on PA. We will keep our review relatively brief in that (a) others have recently presented detailed descriptions of this literature (e.g., Crawford et al., 2010) and (b) we can make better use of our allocated space by exploring in the “Results” section the accuracies of PA and LRT methods within the framework of hypothesis testing.

Modifications to Parallel Analysis

Although there are a number of variations of PA, perhaps the most common approach involves the following steps: (a) Calculate eigenvalues obtained from the sample correlation matrix (i.e., the unreduced matrix with 1s along the diagonal). These are the eigenvalues that are obtained in conducting a principal components analysis (PCA). (b) Generate multiple comparison data sets (e.g., 100 data sets) with the same number of variables and sample size as the sample data. The data are generated such that the variables are uncorrelated and multivariate normally distributed in the population. (c) Calculate eigenvalues for correlation matrices for these comparison random data sets. (d) Calculate the mean eigenvalue for each of the sequential components extracted for these comparison data sets. (e) Determine the assessed number of dimensions, which is equal to the number of eigenvalues for the sample data that exceed the respective means of eigenvalues for the comparison data sets.

A number of researchers have suggested how PA might be modified to improve its accuracy. First, psychometricians have argued against the use of eigenvalues obtained with PCA and in favor of calculating eigenvalues of reduced correlations matrices, that is, the eigenvalues obtained in conducting a principal axes analysis (e.g., Ford, MacCallum, & Tait, 1986). This perspective is based on the rationale that the common factor model underlying principal axes analyses is more appropriate for educational and psychological data because assessments of constructs in these disciplines are measured with error (e.g., Fabrigar et al., 1999). To be consistent, researchers then should substitute eigenvalues based on a common factor analysis method for those computed with PCA when conducting a PA. Second, because PA can result in overextraction of factors (Zwick & Velicer, 1986), psychometricians have encouraged the use of a more stringent criterion than the mean eigenvalue of the comparison data sets; most frequently, the recommendation has been the 95th percentile (e.g., Glorfeld, 1995).

Crawford et al. (2010) evaluated the use of principal axis factoring (PAF) and the 95th percentile eigenvalue rule by comparing the following four PA methods: (a) PA with PCA and the mean eigenvalue rule, (b) PA with PCA and the 95th percentile eigenvalue rule, (c) PA with PAF and the mean eigenvalue rule, and (d) PA with PAF and the 95th percentile eigenvalue rule. None of these methods were uniformly best across conditions. Also, none of the PA methods were well behaved across conditions. As described by the authors, a method is well behaved if its accuracy increases with increases in sample size, factor loadings, and number of variables per factor and with decreases in the magnitude of correlation between factors.

Turner (1998) suggested one reason why PA methods may not work optimally. He argued it is appropriate to reference an empirical eigenvalue distribution based on comparison data sets in which variables are uncorrelated in the population in assessing the first eigenvalue, that is, in evaluating whether at least one factor underlies a correlation matrix. However, it is inappropriate to reference the same empirical distribution in assessing the kth eigenvalue, that is, in evaluating whether at least k factors underlie a correlation matrix. Instead, the proper reference distribution for assessing the kth eigenvalue should be based on comparison data sets in which k− 1 factors are modeled based on the sample data.

Green, Levy, et al. (2012) proposed a revised PA method that incorporated Turner’s idea. With the revised method, the kth eigenvalue for the sample data is compared with the kth eigenvalues for the generated comparison data sets taking into account k− 1 prior factors. Ideally, the comparison data sets should be generated based on population factor loadings of the k− 1 factors. Because the population factor loadings are unknown, the sample factor loadings are substituted for the population values. They conducted a Monte Carlo study to evaluate the revised and traditional PA methods. The traditional and revised PA methods were conducted using either PCA or PAF extraction methods and either the mean or the 95th percentile eigenvalue rule. Overall, Green, Levy, et al. (2012) demonstrated that the revised PA method using PAF and the 95th percentile rule (referred to as R-PA in this article) had relatively high accuracy and behaved better than traditional PA methods. However, the traditional PA method using PAF and the 95th percentile rule (referred to as T-PA in this article) generally performed quite well in conditions except those with highly correlated factors.

Concurrent with the work of Green and his colleagues (Green, Levy, et al., 2012; Green, Lo, Thompson, & Levy, 2012), Ruscio and Roche (2012) independently proposed and evaluated an alternative sequential PA approach based on Turner’s (1998) recommendations. In each step in their sequential approach, a large data set is generated with 10,000 cases such that the correlation matrix associated with these data can be reproduced by k underlying factors and, given this restriction, is as similar as possible to the sample correlation matrix. Five hundred random samples are then drawn from this larger data set, factored, and eigenvalues computed. Root mean square residuals (RMSRs) are computed between all the eigenvalues for each of these random samples and all the eigenvalues for the sample data set. The 500 RMSRs with k factors are compared with 500 RMSRs based on comparably generated data with k− 1 factors. The decision rule for the number of factors is based on sequential comparisons of the RMSRs for k factors and RMSRs with k− 1 factors (beginning with k = 2) using the Mann–Whitney U test with alpha set at .30. When the null hypothesis is not rejected, the number of estimated factors is equal to k− 1, as defined at that step. Generally, they found their proposed method tended to produce more accurate estimates of the number of factors in comparison with traditional PA as well as other approaches. Although the Ruscio and Roche method uses a similar general approach to PA as the revised PA method by Green and colleagues, it differs in multiple specific ways (e.g., data generation, RMSRs across all eigenvalues, Mann–Whitney U test, and alpha of .30). It would be interesting in the future to compare the revised PA and the Ruscio–Roche methods to understand how and why they differ. However, in this article, we chose to conduct an in-depth evaluation of the revised PA method using a hypothesis-testing framework. This framework allowed us to gain a more fundamental understanding of the strengths and weaknesses of PA as a method to determine the number of factors.

Rethinking Parallel Analysis as a Stepwise Hypothesis-Testing Approach

Green, Levy, et al.’s (2012) revised PA method (i.e., R-PA) can be reconceptualized as a series of tests of null hypotheses that k− 1 factors are sufficient to reproduce the population correlation matrix associated with the sample data. If the 95th percentile rule is used, the implication is that the hypotheses are tested at the .05 level. More specifically, if the kth eigenvalue for the sample data exceeds the 95th percentile of kth eigenvalues for the comparative data sets, the null hypothesis of k− 1 underlying factors is rejected at the .05 level, and the conclusion is that at least k factors underlie the variables in the population. With the revised PA method, k initially is set to 1; that is, the hypothesis is that the variables in the population are uncorrelated. If the hypothesis is rejected, k is increased by 1; that is, the hypothesis is evaluated that one factor is sufficient to explain the covariation among variables in the population. If this hypothesis is rejected, k is again increased by 1. This stepwise process is continued until the hypothesis is not rejected. At this point, the process is discontinued, and the researcher may conclude that the number of underlying factors is equal to k− 1 of the current step. One additional rule must be introduced in this process to avoid a nonsensical result. At any step, if the kth eigenvalue for the sample data is nonpositive, the number of factors is assessed to be k− 1.

It may be helpful to examine in greater detail the hypothesis tests involved in a revised PA. In the framework of EFA, we want to evaluate whether P, an N_I×N_I correlation matrix among the N_I indicators, can be reproduced on the basis of Λ, an N_I× (k− 1) factor loadings matrix, and Ψ, an N_I×N_I diagonal matrix of unique variances:

$$\mathbf{P}=\mathbf{\Lambda }\mathbf{\Lambda }\mathbf{\prime }\mathbf{+}\mathbf{\Psi }\mathbf{.}$$

Within revised PA, the null hypothesis at any step is that (k− 1) factors are sufficient to reproduce P. The alternative hypothesis is that the kth factor is necessary to reproduce P. It should be noted that the null hypothesis allows for fewer factors than (k− 1) to reproduce P, and that the alternative hypothesis allows for more than k factors to reproduce P. The null hypothesis is assessed by examining the kth eigenvalue of the reduced correlation matrix, which has communalities (variances of the indicators explained by the factors) rather than 1s along the diagonal. If the number of factors underlying the indicators is k− 1, then the kth eigenvalue of the population reduced correlation matrix is 0. However, the kth eigenvalue of a sample reduced correlation matrix will differ from 0 due to sampling error and biased estimates of the communalities (e.g., squared multiple correlations). With revised PA, an empirical sampling distribution of the kth eigenvalue is generated that is conditioned on the presence of (k− 1) factors. The null hypothesis is assessed by evaluating the kth eigenvalue in the sample to this empirical sampling distribution.

Overall, the reconceptualization of PA as a series of hypothesis tests is advantageous in that it allows for a nuanced assessment of accuracy in terms of Type I and Type II errors associated with each step in the evaluation of eigenvalues. At the same time, the reconceptualization of PA as a series of hypothesis tests raises a few concerns: (a) The decision concerning the number of assessed factors involves accepting the null hypothesis based on a nonsignificant test. In practice, this decision rule may yield incorrect conclusions due to a lack of power. Accordingly, it is important to understand the power of the tests used in the revised PA method. (b) In general, effect size statistics should be considered in conjunction with hypothesis tests in making data analytic decisions. In the context of factor analysis, trivial factors, as well as psychometrically important factors, are likely to underlie any set of variables in the population. A variety of statistics could be computed, such as the eigenvalue of a factor divided by the sum of the eigenvalues for all factors selected using the revised PA method. Alternatively, one could compare fit indices typically used in structural equation modeling (e.g., Akaike information statistic and root mean square error of approximation [RMSEA]) for models with k− 1 and k factors. (c) The tests in the stepwise process are not independent of each other, and consequently the error rate associated with a series of tests is not well defined.

Parallel Analysis Versus Maximum Likelihood Tests

The revised PA method can be viewed as an alternative to the use of the more traditional maximum likelihood (ML) tests to assess the number of factors in EFA. As discussed by Hayashi, Bentler, and Yuan (2007), two types of ML tests can be conducted. The model goodness-of-fit test assesses the null hypothesis that the correlation matrix among measures can be reproduced based on k− 1 factors. The statistic for this test is approximately distributed as a chi-square. If the hypothesis is rejected, it can be concluded that at least k factors are necessary to reproduce the correlation matrix. The alternative ML method involves comparing a model with k factors to a model with k− 1 factors. The difference in the test statistics associated with the two models is referred to a chi-square distribution to assess the null hypothesis that k− 1 factors are sufficient to reproduce the correlation matrix among measures. Geweke and Singleton (1980) and Hayashi et al. (2007) presented analytical and Monte Carlo results to demonstrate that the difference test statistic is not distributed as a chi square and too often rejects the null hypothesis when evaluating more factors than the true number of factors.

These ML tests are most often applied in a sequential fashion to assess the number of factors. Initially, the hypothesis is assessed whether zero factors are sufficient to explain the data. If this initial null hypothesis is rejected, then the hypothesis of whether one factor underlies the data is evaluated. This process continues until the null hypothesis can no longer be rejected. The number of factors equals the number specified by the null hypothesis in the final step. It should be noted that the concerns discussed with the revised PA method (i.e., power, effect size, and dependency among tests) are also applicable to these approaches.

We investigated in our study the first ML method along with PA approaches, but excluded the second ML method involving chi-square difference tests after some initial analyses. The problem of overfactoring with the second ML method is serious in that researchers must evaluate more than the correct number of factors to determine when to stop extracting factors. For example, for data with one underlying factor, the correct number of factors is obtained if the chi-square test for zero factors is rejected, the chi-square difference test for zero versus one factor is rejected, and the chi-square difference test for one versus two factors is not rejected. The last analysis based on two extracted factors exceeds the true number of factors, and the results too frequently suggest that two or more factors are required to reproduce the correlation matrix.

To illustrate the problem, we generated 1,000 data sets, each containing 400 observations. The data sets had a single factor underlying eight variables; the factor loadings were uniformly .5, and the error variances were all .75. The chi-square test evaluating a single factor yielded relatively valid results. The mean chi square of 19.97 was very close to its expected value of 20, the degrees of freedom for the model. The chi-square test evaluating two factors yielded out-of-bound estimates (Heywood cases) in 43.9% of the cases. The mean chi squares were similar for the replications with in-bound and out-of-bound estimates: 8.92 and 9.86, respectively. Both were much smaller than their expected value of 13. As a consequence, the chi-square difference test comparing chi square for two factors with the chi square for one factor was too large. The alpha for this test was inflated in comparison with the nominal alpha of .05: .19 for replications with in-bound estimates and .18 for those with out-of-bound estimates.

We will no longer consider the second ML method, which results in estimation problems and overfactoring. For simplicity, we will refer to the first ML method involving a series of chi-square, goodness-of-fit tests as the LRT method.

Objective of Study

The objective of our study was to determine the accuracy of the revised and traditional PA sequential methods using PAF and the 95th percentile eigenvalue rule. For comparison purposes, we also assessed the accuracy of the LRT method. We evaluated their accuracies using computer-generated data with known factor structures and design characteristics. We varied the factor structure, number of factors, number of variables, size of factor loadings, sample size, and correlation between factors (if more than one factor). To maximize understanding of the findings, we assessed three interrelated aspects of the sequential methods: Type I error rate of tests, power of tests, and overall accuracies of the sequential methods involving these tests.

In the first part, we examined the empirically determined Type I error rates ($\hat{\mathrm{\alpha }}$) and compared them to the nominal alpha of .05. For generated data based on a model with N_F factors, we calculated $\hat{\mathrm{\alpha }}$ for the null hypothesis that N_F factors are sufficient to reproduce the population correlation matrix. For example, $\hat{\mathrm{\alpha }}$ was computed for the test of H_o: N_F≤ 2 for generated data with two factors.

In the second part, we considered the empirically determined power (1 −$\hat{\mathrm{\beta }}$) for the sequential methods test with the lowest power: the test of the null hypothesis that N_F− 1 factors are sufficient to reproduce the population correlation matrix with N_F underlying factors. For example, 1 −$\hat{\mathrm{\beta }}$ was computed for the test of H_o: N_F≤ 1 for generated data with two factors.

In the third part, we considered the overall accuracies of PA and LRT methods across the same generation conditions examined in the first two parts. The Type I and Type II error rates of particular hypotheses comprising the sequential methods are useful in explaining the overall accuracies of these methods. For two reasons, however, the overall accuracies are not simply a function of the presented error rates. First, to avoid an overly complex results section, we do not present the power of all possible hypotheses making up these methods. For example, we do not discuss the power to reject H_o: N_F = 0 for generated data with two factors. Second, the results of the individual hypotheses making up a method are, to some degree, dependent on each other.

Method

In the following sections, we describe the data generation design, the steps used to generate the data, and the methods conducted to analyze these data. All data were created and analyzed using SAS.

Data Generation Design

Data were generated using four different types of models: (a) models with no factors have indicators that share no common variance (i.e., unique indicators); (b) models with single-factor indicators may have one, two, or three factors, but each indicator is a function of one and only one factor; (c) models with unique and single-factor indicators may have one or two factors, but some indicators are a function of one and only one factor, and others share no common variance; (d) bifactor models have a general factor and one or two group factors. For these models, some indicators are a function of only a general factor, and others are a function of a general factor and one group factor. These four different types of models were chosen in that they were viewed as prototypes of models that are found in research practice.

For each model type, data were generated with a sample size (N_O) of 100, 200, or 400. Other aspects of the data generation design—number of factors (N_F), number of total indicators (N_I), size of factor loadings (λ), and magnitude of factor correlations $({\mathrm{\rho }}_{\mathrm{FF}\prime })$—varied depending on the type of model, as described next:

1. Models with no factors differed in terms of the number of indicators: 4, 6, or 8.

2. Models with single-factor indicators had 1, 2, or 3 factors. For those with one factor, the number of indicators was 4, 6, or 8. For those with two or three factors, any indicator had a nonzero loading on one and only one factor, and all factors had the same number of indicators with nonzero loadings. For two-factor models, the number of indicators with nonzero loadings for a factor was 4 or 6. For three-factor models, the number of indicators with nonzero loadings per factor was 4. The nonzero factor loadings for any one model were the same: .3, .5, or .7. For two- and three-factor models, the correlations between factors were the same for any one model: 0, .5, or .8.

3. For models with unique and single-factor indicators and a single underlying factor, four indicators were a function of one factor, and the remaining four indicators were unique. For models with unique and single-factor indicators and two underlying factors, four indicators were a function of one factor, four other indicators were a function of the other factor, and the remaining four indicators were unique. All nonzero factor loadings were .3, .5, or .7 for any one of these models. For two-factor models, the correlations between factors were set at 0 or .5.

4. For bifactor models with one general factor and one group factor, four indicators were a function of only a general factor, and the other four indicators were a function of a general factor and a group factor. For bifactor models with a general factor and two group factors, four indicators were a function of only a general factor, four other indicators were a function of a general factor and a group factor, and the remaining four indicators were a function of a general factor and the other group factor. For any one bifactor model, all loadings were .3, .5, or .7 on the general factor, and the loadings were either .3 or .5 for all indicators on group factors. The correlations between factors were always zero.

The total number of conditions across all manipulations was 180. We initially designed a study with 54 conditions and included additional conditions based on the results of this initial study and those subsequently obtained. We chose conditions carefully because analyses were numerically intensive. Any one condition required generating as many as two thirds of a trillion random numbers and conducting as many as 600,000 factor analyses.

Data Generation

Generation of Sample Data Set

One thousand data sets were generated for each condition using SAS. For conditions with correlated factors, scores on a factor, F_GRP, were a function of scores on a single second-order factor, F_H, and a disturbance, D_GRP:

$$F_{\mathrm{GRP}}={\mathrm{\lambda }}_{\mathrm{H}}{F}_{\mathrm{H}}+\sqrt{(1-{\mathrm{\lambda }}_{\mathrm{H}}^2)}{D}_{\mathrm{GRP}},$$

where ${\mathrm{\lambda }}_{\mathrm{H}}$ is a loading on a second-order factor and is equal to the square root of the design-specified ${\mathrm{\rho }}_{\mathrm{FF}\prime }$ (i.e., ${\mathrm{\rho }}_{\mathrm{FF}\prime }$= 0, .5, or .8). F_H and D_GRP were generated using RANNOR, a SAS random normal number generator with a mean of zero and a unit variance. The weight for the disturbance was specified such that the variance of F_H was 1.0. It should be noted that the use of the second-order factor was a convenient method to produce factor scores with design-specified correlations; accordingly, the scores on the second-order factor were subsequently deleted and not analyzed.

Scores on an indicator, X_j, were created based on the following equation:

$$X_j={\mathrm{\lambda }}_{\mathrm{GEN}}{F}_{\mathrm{GEN}}+{\mathrm{\lambda }}_{\mathrm{GRP}}{F}_{\mathrm{GRP}}+\sqrt{\left(1-{\mathrm{\lambda }}_{\mathrm{GEN}}^2-{\mathrm{\lambda }}_{\mathrm{GRP}}^2\right)}{e}_j,$$

where ${\mathrm{\lambda }}_{\mathrm{GEN}}$ and ${\mathrm{\lambda }}_{\mathrm{GRP}}$ are the design-specified loadings for a general factor F_GEN and a group factor F_GRP, respectively, and e_j is the error for X_j. ${\mathrm{\lambda }}_{\mathrm{GEN}}$ was zero for all conditions except for those with a bifactor model. F_GRP was created following Equation (1) for conditions with correlated factors. Errors were generated using RANNOR, and the weight associated with the errors was specified so that the variance of X_j was 1.0.

Generation of Comparison Data Sets for T-PA and R-PA

For traditional PA (i.e., T-PA), 100 comparison data sets were generated for each of the 1,000 sample data sets for a condition. These comparison data sets had the same number of variables and observations as the sample data. The variables were normally distributed and uncorrelated with each other and generated using RANNOR. For revised PA (i.e., R-PA), 100 comparison data sets were generated to assess each successive eigenvalue obtained in factoring each of the 1,000 sample data sets for a condition. As with traditional PA, the comparison data sets had the same number of variables and observations as the sample data set. However, the variable scores were not just error scores, but a weighted combination of factor and error scores. For the 100 comparison data sets associated with any one sample data set and test of a null hypothesis, variable scores were generated using the weights of the unrotated standardized factor loadings for this sample data set. Both the factor and error scores were generated using RANNOR. The weights for errors were constructed such that the variances for the variables were 1.0. When evaluating the first eigenvalue for R-PA, variable scores are solely a function of error, as they are with T-PA. Accordingly, the same 100 comparison data sets were used to evaluate the first eigenvalue for T-PA and R-PA.

Analyses

The 1000 sample data sets for each condition were analyzed with the traditional and revised PA methods using PAF and the 95th percentile eigenvalue rule. In addition, the sequential LRT method was conducted using chi-square tests. The nominal alpha level for the LRTs was set at .05, which was consistent with the use of the 95th percentile eigenvalue rule with the PA methods.

For any sequential method, we conducted a series of tests to evaluate the hypotheses that zero factors is sufficient, one factor is sufficient, and so on. For conditions with N_F factors, the last test in a series evaluated the hypothesis that N_F factors are sufficient. The assessed number of factors was determined based on the first hypothesis test that was not rejected; that is, it was equal to the number of factors hypothesized by this test. If all N_F+ 1 hypotheses were not rejected, we concluded that the assessed number of factors was greater than N_F.

We evaluated the quality of a sequential method for a condition by computing its overall accuracy, which was equal to the number of times a method yielded the correct number of factors divided by the number of sample data sets for a condition. To gain insights into the results for the overall accuracies, we also examined the accuracies/error rates of the individual hypothesis tests making up these methods. In more traditional language, we computed the Type I error rates and powers of the individual hypothesis tests. For any hypothesis assessing N_F factors or more, the focus was on alpha; for any hypothesis assessing N_F− 1 factors or fewer, the focal concern was power.

We were interested in the empirical alphas for testing the null hypothesis that N_F factors are sufficient to reproduce a population correlation matrix with N_F underlying factors. These tests should provide the crucial stopping rule in the assessment of the number of factors in that nonrejection implies additional factors beyond the correct number of factors are unnecessary. We also focused on the empirical powers for evaluating the null hypothesis that N_F− 1 factors are sufficient to reproduce the population correlation matrix with N_F underlying factors. In terms of power, this is the crucial test in that it will have less power than any other test in the sequence (e.g., in comparison with the test of the hypothesis that N_F− 2 factors are sufficient).

We were concerned that the empirical powers could be inflated if the alphas for these tests exceeded the nominal level of .05. Accordingly, we also examined the empirical alphas associated with these tests. To this end, we factored the population correlation matrix for a condition, extracted N_F− 1 factors (i.e., consistent with the null hypothesis tested when investigating empirical powers), and generated sample data based on these factor loadings. We then applied PA and LRT methods to assess the empirical Type I error rate for the hypothesis that N_F− 1 factors are sufficient.

Results

In this section, we initially evaluate the Type I error rates and powers of the critical tests in the described sequential methods for determining the number of factors. We then present the overall accuracies of these methods, taking into account the Type I and Type II error rates of the tests they comprise. We summarize the differences among methods graphically by focusing on the most consequential manipulated factors, but describe additional difference in the text.

It is important to note that Heywood cases were encountered frequently in some conditions with the LRT method. Regardless of whether we included or excluded the replications with Heywood cases, the empirical alphas, powers, and accuracies were very similar, as we describe in each subsection of the Results section.

Empirical Type I Error Rates

We will refer to tests as “markedly conservative” or “markedly liberal” if empirical Type I error rates fall outside the lower and upper limits, respectively, of Bradley’s (1978) liberal criterion, ${\mathrm{\alpha }}_{\mathrm{nominal}}\pm .5{\mathrm{\alpha }}_{\mathrm{nominal}}$ = [.025, .075].

Heywood cases were most frequently encountered using the LRT method when the factor loadings and the number of observations were small. For example, the mean percentage of replications with Heywood cases was 53.7 for conditions with λ = .3 and N₀ = 100 observations and 1.6 for conditions with λ = .7 and N₀ = 400. More important, the difference between alphas based on all replications and those without Heywood cases were very similar. The absolute differences in alphas were less than .004 in 88% of the conditions and never exceeded .009. Thus, we present alphas based on all replications.

Models With No Factors

For models with zero factors, the empirical alpha levels had to be the same for T-PA and R-PA methods because they used the same comparison data sets. In addition, these methods had to be close to the nominal alpha level of .05 due to the use of the 95th percentile eigenvalue rule. Across the 9 conditions (N_O = 100, 200, 400 and N_I = 4, 6, 8), the empirical alphas for the PA methods ranged from .043 to .057. In comparison, the empirical alphas for the LRT method ranged from .040 to .052 across these conditions.

Models With One Factor

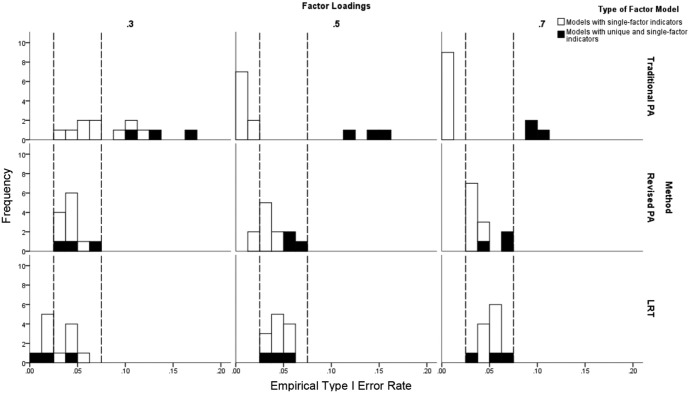
In Figure 1, we present results for Type I error rates for one-factor models. For the T-PA method, the empirical Type I error rates differed markedly from the nominal alpha level of .05 in a majority of conditions. The error rates were conservative for some conditions and liberal in others. For one-factor models with single-factor indicators and loadings of .5 or .7, the Type I error rates were markedly conservative; the null hypothesis was not rejected once (out of 1,000 replications) for 12 of the 18 conditions. In contrast, the empirical alphas were liberal when λ = .3 and N_O≤ 200. For three of these six conditions, they were markedly liberal: .105 (λ = .3, N_O = 100, and N_I = 6), .116 (λ = .3, N_O = 100, and N_I = 8), and .090 (λ = .3, N_O = 200, and N_I = 8). For all models with unique and single-factor indicators, the empirical alphas for T-PA were markedly liberal (.089 to .174). The inflation was greatest when factor loadings were small.

Figure 1.

Empirical Type I error rates for conditions with models having one factor. The pairs of lines at .025 and .075 represent the lower and upper limits of an acceptable alpha using Bradley’s (1978) liberal criterion.

In contrast, the alphas for the R-PA and LRT methods were much closer to the nominal alpha level of .05 and never exceeded the upper limit of Bradley’s liberal criterion. The alphas were markedly conservative for the R-PA method for the two conditions with models having single-factor indicators, λ = .5, and N_I = 4 (.024 and .016 when N_O = 100 and 400, respectively). The empirical alphas for the LRT method were markedly conservative (.011 to .022) for six of the conditions in which the data were generated for models with single-factor indicators or models with unique and single-factor indicators; these findings were limited to those conditions with N_O = 100 or 200 and λ = .3. In terms of the percent of conditions that had empirical alphas that fell between the limits defined by Bradley’s liberal criterion, R-PA performed somewhat better than LRT (94.4% vs. 83.3%), both of which outperformed T-PA (16.7%). On the other hand, the means of the absolute differences between the empirical alphas and .05 were almost the same across conditions for LRT (.012) versus R-PA (.013); the mean absolute difference was much greater for T-PA (.049).

Models With Two or More Factors

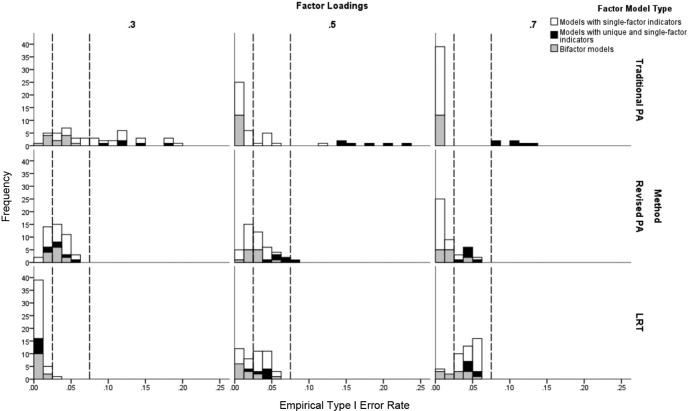
In Figure 2, we present results for Type I error rates for models with two or more factors. Similar to the results for models with one factor, the traditional PA method yielded empirical alphas that differed most dramatically from the nominal alpha level of .05. The empirical Type I error rates for T-PA were more likely to be conservative for models with single-factor indicators with higher factor loadings and for bifactor models with higher factor loadings on the general factor. In contrast, the empirical alphas were markedly liberal for all conditions in which the data were generated with models with single-factor indicators, factor loadings of .3, and uncorrelated factors, and with all models with unique and single-factor indicators.

Figure 2.

Empirical Type I error rates for conditions with models with two or more factors. For bifactor models, the factor loadings are those for the general factors, not the group factors. The pairs of lines at .025 and .075 represent the lower and upper limits of an acceptable alpha using Bradley’s (1978) liberal criterion.

For R-PA, the alphas exceeded the upper limit of Bradley’s liberal criterion only once (.077). The empirical alphas for the R-PA method tended to be more conservative for models with single-factor indicators with higher factor loadings and bifactor models with higher factor loadings on the general factor. For 25 out of the 27 conditions, alphas for models with unique and single-factor indicators were within the limits defined by Bradley’s liberal criterion.

The pattern of results for alphas with the LRT method was quite different from those for the other two methods. The alphas never exceeded the upper limit of Bradley’s liberal criterion and became more conservative with lower factor loadings, regardless of the model used to generate the data. When λ = .3, the alphas were markedly conservative for 44 of the 45 conditions (.000 to .023). For conditions with λ≥ .5, the empirical alphas were markedly conservative for 26 of the 90 conditions.

In terms of the percent of conditions with two or more factors that had empirical alphas that fell within the limits defined by Bradley’s liberal criterion, LRT performed slightly better than R-PA (48.1% vs. 47.5%), both of which outperformed T-PA (18.5%). The mean of the absolute differences between the empirical alphas and .05 was essentially the same across conditions for R-PA and LRT (.026) and was much greater for T-PA (.049).

Empirical Powers

In this section, we focus on the powers of tests to reject the hypothesis that N_F− 1 factors are sufficient to reproduce the correlation matrix with N_F underlying factors. A standard practice in Monte Carlo studies is not to report powers of tests in which the alphas are inflated in that the powers for these tests would be spuriously high. Accordingly, we assessed for each condition the alphas as well as the powers for the tests of interest. For example, for a model with three factors, we assessed the power of rejecting the null hypothesis that two factors are sufficient. To determine the alpha level for this test, we extracted two factors from the population correlation matrix with three underlying factors, generated sample data based on the factor loadings for these two factors, and then computed the proportion of replications in which the null hypothesis that two factors are sufficient was rejected with the PA and LRT methods.

The empirical alphas previously reported are different from those considered in this section, except if N_F = 1. The previously presented alphas were for tests evaluating the hypothesis that N_F factors are sufficient to reproduce the correlation matrices with N_F underlying factors, whereas the alphas in this section were for tests assessing the hypothesis that N_F− 1 factors are sufficient to reproduce the correlation matrices with N_F− 1 factors. We do not report in detail the alphas considered in this section in that they follow a pattern comparable to those previously described and thus contribute little additional information.

Heywood cases were less common using the LRT method for the power analyses than for the Type I error rates. Heywood cases occurred more often for the power analyses when the factor loadings and the number of observations were small. The mean percentage of replications with Heywood cases was 17.4 for conditions with λ = .3 and N₀ = 100 and 1.6 for conditions with λ = .7 and N₀ = 400. The absolute differences between powers based on all replications and those without Heywood cases were less than .004 in 91% of the conditions and never exceeded .011 in the remaining conditions. Thus, we present the powers for all replications.

Power of LRT Versus PA Methods

For 26.3% of conditions with models having one or more factors, the powers were 1.0 for all methods and thus insensitive to differences between methods. In 92.1% of the remaining conditions, the R-PA method yielded substantially higher powers than the LRT method, with the mean differences in powers in these conditions averaging .103. The powers for the T-PA method also tended to be greater than those for the LRT method in more than two thirds of the conditions with at least one non-1.0 power, although some of the advantage of the T-PA method was due to inflated alphas.

Power of the T-PA and R-PA Methods

For models with one factor, the T-PA and R-PA methods have identical powers to evaluate the hypothesis that zero factors are sufficient in that both invoke comparison data sets assuming no underlying factors. In addition, the alpha levels are accurate for these methods, as demonstrated in the previous section on Type I error rates. The powers for one-factor models with single-factor indicators were substantial (.98 or higher) as long as the factor loadings were .5 or greater. In contrast, for models with factor loadings of .3, the powers were as low as .35 (N₀ = 100 and N_I = 4), but increased dramatically with increases in N₀ and N_I. Similar results were obtained for single-factor models with unique and single-factor indicators. The powers were all greater than .95 when λ≥ .5, but dipped to as low as .17 when λ = .3 and N₀ = 100.

In considering power for the 135 conditions with two or more factors, we took into account the degree that the alpha levels for the focal tests were inflated (i.e., greater than the nominal value of .05). The alphas were markedly liberal for 63 conditions for the T-PA method, but only one condition for the R-PA method; in this one condition the T-PA method was more liberal than the R-PA method. Alphas for T-PA were inflated more often for particular types of models; for example, all alphas were markedly inflated for models with unique and single-factor indicators. Across the remaining conditions, the alphas for T-PA method were markedly conservative in 54 conditions. In comparison, the alphas for the R-PA method were markedly conservative in 17 conditions, respectively. These results mimic those reported in the previous section on Type I error rates.

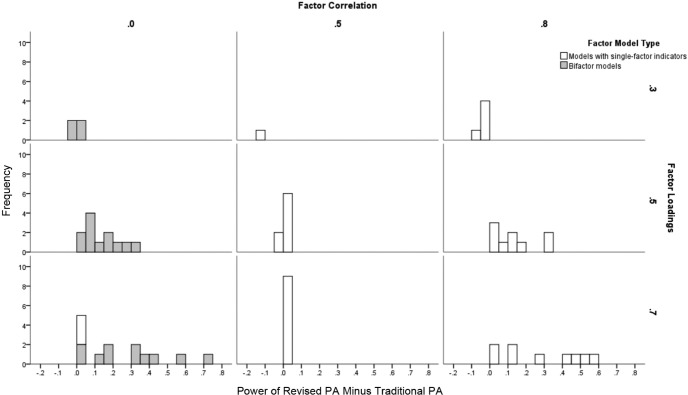
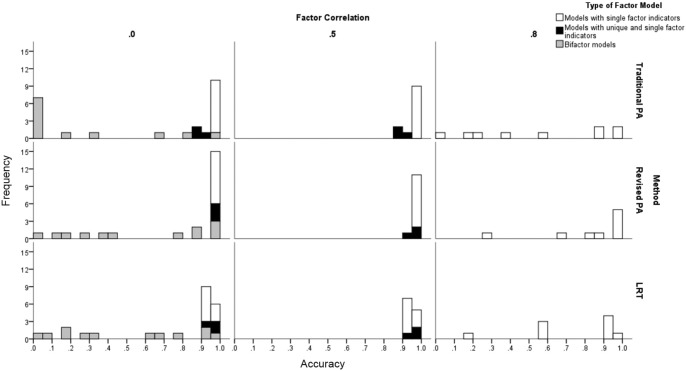
In Figure 3, we present the relative powers of the two PA methods for conditions with two or more factors when the alphas were not markedly inflated. For models with single-factor indicators, the differences in power between the two PA methods were minimal when the correlations among factors were 0 or .5. When the factor correlations were .8, the power tended to be higher for R-PA (i.e., positive values along the abscissa) when the factor loadings were high. For bifactor models, T-PA and R-PA methods produced relatively similar results with low factor loadings, but R-PA tended to produce greater power as the factor loadings on the general factor increased in magnitude. In summary, for conditions with two or more factors, the R-PA method yielded higher powers than the T-PA method in 86% of the conditions. Excluding the 13 conditions in which the powers for both methods were 1.0, the mean difference in powers in favor of R-PA was relatively large (.196) for the 49 conditions in which R-PA yielded greater powers, whereas the mean difference in powers in favor of T-PA was rather small (.036) for the 10 conditions in which T-PA yielded higher values.

Figure 3.

Relative power of revised parallel analysis (R-PA) and traditional parallel analysis (T-PA) to reject the null hypothesis of N_F− 1 factors for conditions with two or three factors (N_F = 2 or 3) and noninflated alphas (<.075). For bifactor models, the factor loadings are those for the general factors, not the group factors.

In Figure 4, we present the results for power when the alphas were markedly inflated for T-PA. The three columns in the figure are for results when the inflated alphas for T-PA were somewhat greater, much greater, and very much greater than the alphas for R-PA. These results indicate that the empirically determined powers tended to be greater for the T-PA method (i.e., negative values along the abscissa) to the extent that the alphas for T-PA were inflated in comparison with R-PA. The differences were most profound when the factor loadings were small. These findings support the conclusion that differences in empirical power in favor of T-PA are due to inflated alphas.

Figure 4.

Relative power of revised parallel analysis (R-PA) and traditional parallel analysis (T-PA) to reject the null hypothesis of N_F− 1 factors for conditions with two or three factors and inflated alphas (>.075). For bifactor models, the factor loadings are those for the general factors, not the group factors.

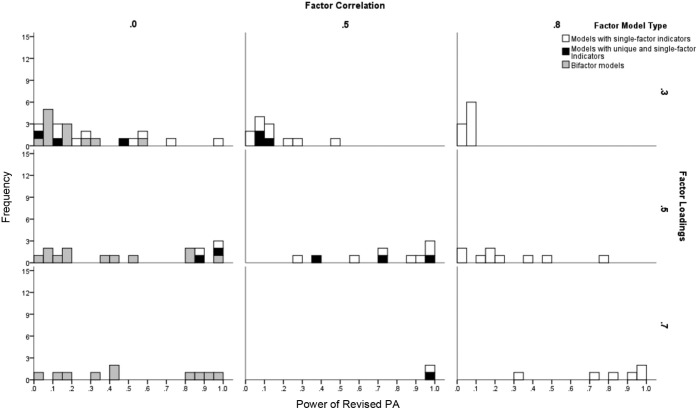
Given the results in favor of R-PA, powers are presented for this method in greater detail in Figure 5. Power increased systematically as factor loadings increased (on the general factor for the bifactor models) and factor correlations decreased. Although not shown in the graphs, power also increased with decreases in the number of factors and increases in sample size and, for bifactor models, increases in factor loadings on the group factors.

Figure 5.

Power of the revised parallel analysis (R-PA) method for models with two or more factors.

Overall, the revised PA method tended to demonstrate substantially greater powers than the traditional PA method for models with highly correlated factors and bifactor models. On the other hand, there was some tendency for the revised PA method to have slightly less power than the traditional PA method for models with low factor loadings.

Accuracies

In this section, we examine the overall accuracies of these methods to detect the correct number of factors. We interpret the differences in accuracies between methods by considering the alphas and powers for the methods. For example, for conditions with a single underlying factor, accuracies of methods are a function of Type II errors in testing the hypothesis of zero factors and of Type I errors in testing the hypothesis of one or fewer factors. Differences in accuracies are just not a function of the error rates of the individual tests in that there is dependency between tests across steps.

Heywood cases occurred in tests used to make a decision about the number of factors using the LRT method. As one would expect, the conditions with higher percentages of Heywood cases for the accuracy analyses were similar to those for the Type I error rates and power analyses. The highest percentages were for conditions with low factor loadings and small sample sizes. The accuracies for these conditions were minimally affected by the presence of out-of-bound estimates in a large majority of conditions. The absolute differences in accuracies were less than .004 in 91.7% of the conditions, between .003 and .015 in 5.6% of the conditions, and between .016 and .049 in 2.8% of the conditions. In conditions with the greatest discrepancies in accuracies, higher accuracies were found based on all replications in comparison with those based on replications without Heywood cases. Given these results, we chose to present accuracy results for the LRT method based on all replications.

Models With No Factors

For conditions with no underlying factors, the accuracies of the methods are equivalent to one minus the previously reported Type I error rates for assessing whether zero factors are sufficient. For LRT, the accuracies ranged from .943 to .962. Accuracies for the T-PA and R-PA methods had to be equivalent and ranged from .943 to .957.

Models With One Factors

For models with one underlying factor, the accuracies were .90 or greater for all three methods in 22 of the 36 conditions. Overall, accuracies were higher for conditions with no unique indicators and with larger factor loadings, sample sizes, and numbers of indicators. Next, we consider differences in accuracies between methods for conditions with single-factor models.

Overall, the PA methods yielded higher accuracies than the LRT approach for conditions with single-factor models and no unique indicators. Relative to the LRT approach, the accuracies for the R-PA method were greater in all conditions except one (.003 mean difference for the one exception). The accuracies for the T-PA method were greater than those for the LRT approach in 25 of the 27 conditions, and essentially the same (within .001) in the remaining two conditions.

Neither PA method was uniformly superior for conditions with single-factor models and no unique indicators. The accuracies of the R-PA method were greater than those for the T-PA method (.001 to .052) when factor loadings were .3. When factor loadings exceeded .3, the accuracies for the T-PA method were greater than those for the R-PA approach (.013-.047). The differences in accuracy between the two PA methods reflected the differences in their alphas for the test of one or fewer factors; the correlation between the accuracy differences and alpha differences was −.98. Alphas for the T-PA method were overly liberal when factor loadings were .30 and N₀ < 400, and overly conservative when factor loadings were greater than .30 regardless of N_0. In contrast, alphas for the R-PA method generally were close to the nominal level of .05. Ironically, the greater accuracy of the T-PA method for conditions in which factor loadings exceeded .30 was due to their overly conservative alphas. All accuracies for these conditions exceeded .98 for the T-PA method, whereas the maximal accuracy should be .95 given α = .05.

For conditions with models with unique and single-factor indicators, the accuracies for the R-PA method were uniformly superior to those for the T-PA approach (.021 to .088). The relative inaccuracy of the T-PA method can be attributed to the inflated alphas for the test that one factor is sufficient; these alphas ranged from .089 to .174.

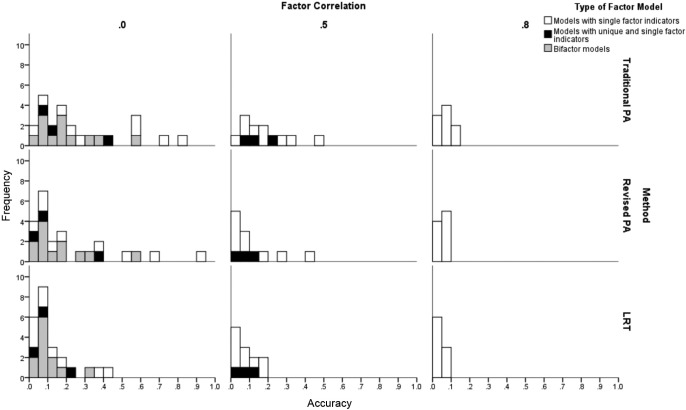
Models With Two or More Factors

We present the accuracies for conditions with two or more factors when factor loadings were .3 in Figure 6 and .7 in Figure 7. Regardless of method, accuracy increased most dramatically as a function of the factor loadings and sample size. In addition, accuracy increased for models with single indicators to the extent that factors were less correlated. Although not shown in the figures, accuracy also increased as the number of indicators associated with a factor became greater.

Figure 6.

Overall accuracies of revised parallel analysis (R-PA), traditional parallel analysis (T-PA), and likelihood ratio test (LRT) methods for conditions with two or more factors and with factor loadings of .30. For bifactor models, the factor loadings are those for the general factors, not the group factors.

Figure 7.

Overall accuracies of revised parallel analysis (R-PA), traditional parallel analysis (T-PA), and likelihood ratio test (LRT) methods for conditions with two or more factors and with factor loadings of .70. For bifactor models, the factor loadings are those for the general factors, not the group factors.

Overall, the R-PA method outperformed the LRT approach for 79 of the 81 conditions with models having only single-factor indicators and for 33 of the 36 conditions with bifactor models. The T-PA approach yielded higher accuracies than those for the LRT method for 66 of the 81 conditions with models having only single-factor indicators and for 17 of the 36 conditions with bifactor models.

For the six conditions with unique and single-factor indicators and λ = .3, the accuracies for the T-PA method were greater than those for the R-PA method, and the accuracies for R-PA were essentially equivalent to (within .005) or greater than those for the LRT method. The greater accuracy of the T-PA method in these conditions was not due to the precision of the stopping rule for determining the number of factors; alphas for these tests were inflated (.088 to .262). Rather, the greater accuracy of T-PA in these conditions was a function of the greater power of the test in the prior step in the sequential process, although this greater power was aided by the inflated alphas for these tests (.099 to .194). In contrast, for the six conditions with unique and single-factor indicators and λ = .7, the accuracies for the R-PA and LRT methods were very similar (.917 to .969) and uniformly higher than those for the T-PA method (.859 to .924). The powers for the relevant tests for these conditions were very high for all three methods (.97 to 1.00), and thus the lower accuracy of the T-PA method was because of its inflated alphas (.076-.126). For the remaining six conditions with unique and single-factor indicators (λ = .5), the accuracy results fell between conditions with λ = .3 and λ = .7. Given the PA methods tended to outperform the LRT approach in a majority of conditions with two or more factors, we focused next on differences in accuracies of the T-PA and R-PA methods.

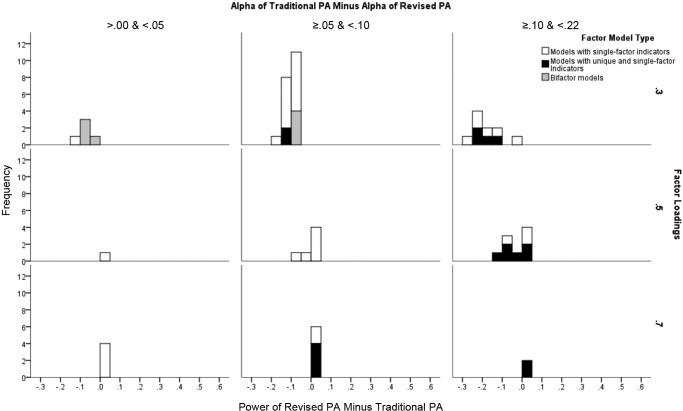
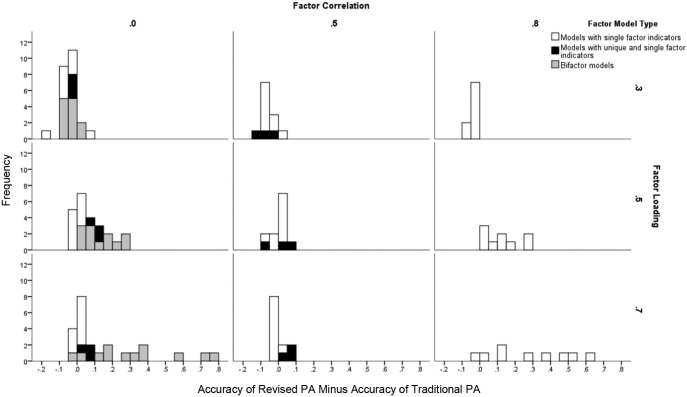
In Figure 8, we present the differences in accuracies between the two PA methods. For conditions with generation models that have single-factor indicators, the accuracies for R-PA tended to be (a) similar or lower when λ = .3; (b) similar when λ > .3 and ${\mathrm{\rho }}_{\mathrm{FF}\prime }$≤ .5; and (c) higher—in some conditions dramatically higher—when λ = .7 and ${\mathrm{\rho }}_{\mathrm{FF}\prime }$ = .8. For bifactor models, the R-PA method tended to perform similarly or somewhat poorer when models had λ for the general factor of .3, but much better when λ for the general factor became larger. These results are consistent with those presented in the section on power for testing the null hypothesis that N_F− 1 factors are sufficient. R-PA yielded poorer power than T-PA with weaker factor loadings, but tended to yield greater power with stronger factor loadings. However, in many conditions, the Type II error rates for T-PA were spuriously low because of inflated alphas.

Figure 8.

Relative accuracies of revised parallel analysis (R-PA) and traditional parallel analysis (T-PA) for conditions with two-factor or three-factor models. For bifactor models, the factor loadings are those for the general factors, not the group factors (which were either .3 or .5).

Discussion

Although none of the examined methods was uniformly better than the other approaches across all conditions, the results overall best supported the revised PA method. The R-PA and LRT approaches tended to yield alphas that were closer to the nominal level than the T-PA method. Both the R-PA and the LRT approaches produced conservative alphas under some conditions. In terms of power, the two PA methods were generally more powerful than the LRT approach. The T-PA method performed better with lower factor loadings, whereas the R-PA approach produced better results for models having single-factor indicators with higher factor loadings, particularly those with highly correlated factors, and with bifactor models. In terms of accuracy, the two PA methods outperformed the LRT approach in a majority of conditions. The pattern of accuracies for the two PA methods generally mimicked those for their power.

R-PA outperformed T-PA in conditions with the following types of models: models with unique and single-factor indictors, single-factor indicator models with higher factor loadings and highly correlated factors, and bifactor models with a general factor having higher factor loadings. It is not surprising that the latter two types of models produced similar results. The two- and three-factor models with single-factor indicators are equivalent to hierarchical models with a second-order general factor, which is nested within a bifactor model (Rindskopf & Rose, 1988). As the correlations between first-order factors increase, the loadings of the general factor in the equivalent bifactor model become increasingly strong. Thus, R-PA performed better relative to T-PA to the extent that underlying models had a stronger general factor. From a slightly different perspective, R-PA detected more accurately group factors in the presence of a strong general factor.

As a method to evaluate null hypotheses, R-PA tended to behave better than T-PA in most conditions. The only real advantage for T-PA was in terms of power for conditions with weak factor loadings, particularly with smaller sample sizes. This advantage was expected given the R-PA method uses factor loadings from the sample data. Under these conditions, the factor loadings are likely to be less stable, so R-PA would offer little advantage over the T-PA approach. Importantly, these conditions in which T-PA exhibited a power advantage over R-PA tended to be those in which T-PA also yielded compromised empirical alphas. It is also important to note that the LRT approach suffered poor power relative to the PA methods. Based on our results, the R-PA method appears to work well in comparison with more traditional methods, although it is likely to yield less accurate results for poorer designed measures (i.e., those with low factor loadings and fewer numbers of indicators) and studies (i.e., those with small sample sizes).

The overall superior performance of R-PA over T-PA in our research and the work by Ruscio and Roche (2012) are consistent with the argument that it is inappropriate to assess the kth eigenvalue by referring it to a distribution based on comparison data sets in which variables are uncorrelated in the population (Green, Levy, et al., 2012; Harshman & Reddon, 1983; Turner, 1998). Instead, the proper reference distribution is one based on comparison data sets in which k− 1 factors are modeled based on the sample data.

In the current work, we reconceptualized the traditional and revised PA methods as a series of sequential hypothesis tests and interpreted the relative accuracies of these methods in terms of the Type I and Type II errors of the tests making up these methods. In so doing, we were able to better understand why the accuracies were higher for R-PA in some conditions, T-PA in other conditions, and LRT in still others. Using the framework of hypothesis testing, we gained a deeper and more coherent understanding of these accuracies. For example, we demonstrated that T-PA evidenced higher accuracies because of overly conservative Type I error rates in some conditions and overly liberal Type I error rates in other conditions. In addition, based on our results, it would appear that the revised PA method provides a better method to test the null hypothesis about a specific number of factors than the traditional ML test in that it tends to have greater power across a wide range of conditions.

Comparison data sets with PA methods in our study were generated using a multivariate normal generator, and thus these PA methods assume normality. The robustness of this assumption was not evaluated in that we also generated the sample data using a multivariate normal generator. Past research has indicated that traditional PA methods are surprisingly robust to violations of the normality assumption (Buja & Eyuboglu, 1992; Dinno, 2009; Hayton, 2009). In fact, Dino (2009) stated that

Given the computational costs of the more complicated distributions for random data generation (e.g., rerandomization takes longer to generate than uniformly distributed numbers), and the insensitivity of PA to distributional form, there appears to be no reason to use anything other than the simplest distributional methods such as uniform (0, 1) or standard normal distributions. (p. 383)

Future research is required to ensure that the revised PA method is also robust to violations of the normality assumption.

In the future, it would be useful to investigate how to augment hypothesis testing with R-PA using fit indices. For example, we might choose to include an additional factor if it would improve fit to the correlation matrix based on fit indices (Preacher, Zhang, Kim, & Mels, 2013), even if we cannot reject the null hypothesis at the .05 level. It is important to use multiple approaches in the assessment of the number of factors, including the interpretability of factor analytic results with different numbers of factors (Preacher & MacCallum, 2003). By doing so, we can better take into account the complexities associated with these decisions. For example, underextraction is likely to lead to more serious errors in interpretation than overextraction (Fava & Velicer, 1992; Wood, Tataryn, & Gorsuch, 1996). At the same time, smaller factors are likely to underlie the correlation matrix that are inherent in the measures, but have little or no theoretical meaning (Fabrigar et al., 1999). It also would be informative to evaluate the relative accuracies of the revised PA method and the modified PA approach presented by Ruscio and Roche (2012) in that the methods used to assess the accuracies of the two methods differ dramatically. If differences in accuracies are found, it would be important to assess why they differ, given that the statistical steps required by the two methods are quite dissimilar. Finally, it would be interesting to investigate particular applications of the R-PA approach, such as methods for handling missing data or for accommodating polychoric correlation matrices with discrete data.