Data Integration Approaches to Longitudinal Growth Modeling

Abstract

Synthesizing results from multiple studies is a daunting task during which researchers must tackle a variety of challenges. The task is even more demanding when studying developmental processes longitudinally and when different instruments are used to measure constructs. Data integration methodology is an emerging field that enables researchers to pool data drawn from multiple existing studies. To date, these methods are not commonly utilized in the social and behavioral sciences, even though they can be very useful for studying various complex developmental processes. This article illustrates the use of two data integration methods, the data fusion and the parallel analysis approaches. The illustration makes use of six longitudinal studies of mathematics ability in children with a goal of examining individual changes in mathematics ability and determining differences in the trajectories based on sex and socioeconomic status. The studies vary in their assessment of mathematics ability and in the timing and number of measurement occasions. The advantages of using a data fusion approach, which can allow for the fitting of more complex growth models that might not otherwise have been possible to fit in a single data set, are emphasized. The article concludes with a discussion of the limitations and benefits of these approaches for research synthesis.

Research synthesis involves collecting, combining, and summarizing research for a specific study question (Cooper & Patall, 2009) in an attempt to come to an overarching conclusion regarding the direction and magnitude of an effect of interest. Synthesizing results from multiple studies is a daunting task, that is, even when studies have the same goals, they may differ in the sampling of participants, the measurement of the independent and dependent variables, covariates included in the analysis, study design, and analytic techniques (e.g., ANOVA, structural equation modeling). The exponential growth in the amount of data collected on individuals has created numerous opportunities for examining new theories and developing new methods of analysis. At the same time, the number of different sources over which this information is divided continues to grow, creating potential obstacles for effectively combining such data before it can be explored.

At its most basic level, the process of combining data is one in which information from different data sets, sharing at least some common variables or constructs, is merged. The whole process for combining and analyzing such data from multiple sources is often referred to as data fusion (Wilderjans, Bernal, Galindo-Villardón, & Ceulemans, 2015). The main objective of data fusion can be considered the creation of a new data set that allows for more flexibility in the analysis than the separate analysis of each individual available data set. Different terms have been used to describe data fusion, including statistical matching, data matching, file concatenation, data integration, multisource imputation and ascription, and data merging (Cooper & Patall, 2009; McArdle & Horn, 2002, 2005; Piccinin & Hofer, 2008); however, the most commonly used term across the various disciplines is data fusion.

Data Fusion of Longitudinal Studies

Longitudinal studies create additional challenges for data fusion, and research synthesis more generally, particularly when the focus is on within-person change. In addition to varying on all of the dimensions of a cross-sectional study (e.g., sampling, measurement protocol, population), longitudinal studies vary in the number and timing of assessments, which creates a potential confound when attempting to summarize research findings focused on within-person changes.

Given the varied study designs inherent in longitudinal studies, analyses of longitudinal data are similarly varied even when they share the goal of studying within-person change and its determinants. The first challenge to synthesize results of longitudinal studies that vary in the number and timing of the measurements is the fitted model. For example, some longitudinal studies may afford the ability to fit curvilinear growth models (e.g., quadratic, logistic), whereas other studies may be limited to a linear growth model. Combining results about within-person change can be challenging when different growth models are fit across studies (Grimm, Zhang, Hamagami, & Mazzocco, 2012) because the within-person rate of change is a combination of multiple model parameters (e.g., linear and quadratic components in the quadratic growth model) in certain models and a single model parameter (e.g., linear) in others.

The second challenge to synthesizing results from longitudinal studies deals with the rate of change as the construct of interest. When studying within-person change across studies, the measurement of the rate of change must be equivalent across studies. This means that the time metric used to track change and the scaling of the outcome must be equivalent. The first part of this challenge involves the time metric, and different studies, depending on the original goals of the study, may use different time metrics (e.g., age, measurement occasion, grade, time since the beginning of the study, time since puberty) to track change against. The second part of this challenge is the scaling of the outcome measure, which must also be equivalent across studies. Studies may use different scales (tests, surveys) to measure the same construct, and this makes the results of longitudinal studies more difficult to synthesize because there is no good way to alter the rate of change to be scale-free—akin to using a standardized effect size in cross-sectional studies.

Data fusion approaches to research synthesis may be able to face some of the challenges brought about by longitudinal studies when the goal is to summarize results related to individual rates of change and the determinants of those changes. Specifically, by combining data from multiple sources, design differences that are inherent in longitudinal studies can be taken into consideration during the analysis phase.

Purpose

The purpose of this article is to illustrate the data fusion approach to longitudinal data analysis and compare its conclusions with an alternative approach, termed parallel analysis (Piccinin & Hofer, 2008), where raw data from multiple studies are separately analyzed using the same, or as similar as possible, analytic model. The results of these analyses are then synthesized, often using meta-analytic techniques. In the parallel analysis of longitudinal data, we consider different approaches to synthesizing the results. To accomplish these goals, we have compiled six longitudinal studies of mathematics ability in children with a goal of examining individual changes in mathematics ability and to determine differences in the trajectories based on sex and socioeconomic status. These studies vary slightly in their assessment of mathematics ability and vary significantly in the timing and number of measurement occasions. We conclude with a discussion of the limitations and benefits of these approaches for research synthesis with longitudinal data.

Method

Data

Data for this project come from six longitudinal studies: The National Institute of Child Health and Human Development’s (NICHD) Study of Early Child Care and Youth Development (SECCYD; NICHD Early Child Care Research Network, 2002); National Center for Early Development and Learning’s (NCEDL) Multi-State Pre-K Study (LoCasale-Crouch et al., 2007); NCEDL’s Study of State-Wide Early Education Programs (SWEEP; LoCasale-Crouch, et al., 2007); Morrison’s Longitudinal Study (MLS; Connor, Morrison, & Slominski, 2006); Welfare, Children, Families: A Three City Study (WCF; Winston et al., 1999); and the Panel Study of Income Dynamics Child Development Supplement (PSID; Hill, 1992).

NICHD Study of Early Child Care and Youth Development

The NICHD SECCYD provided detailed, repeated, and comprehensive assessments of child outcomes in multiple domains for 1,364 children from 10 sites across the United States. The children in the NICHD study were predominately White (80%), with fewer percentages of African American (13%) and Hispanic (5%) children. Children were assessed at 54 months of age, and in the spring of Grades 1, 3, and 5. Additional details about recruitment, selection procedures, public use data sets, variable selection, and variable information are available in prior publications (see NICHD Early Child Care Research Network, 2002, 2005) and from the study websites (http://secc.rti.org).

NCEDL Multi-State Pre-K Study

The NCEDL Multi-State Study took place in six states (California, Illinois, Georgia, Kentucky, New York, and Ohio) selected from states serving more than 15% of their 4 year olds in their pre-K programs in 2001. States were selected to maximize diversity with regard to geography, program location (in a public school building or not), program length (full-day vs. part-day programs), and educational requirements for teachers (bachelor’s vs. not). Forty centers/schools per state were randomly selected to participate in the study. A single classroom per site was randomly selected and four children were randomly selected per classroom. Data were collected on a total of 1,015 students residing in 246 classrooms. The sample was diverse with 24% African American, 25% Hispanic, and 41% White children. The sample was also economically diverse with an average maternal education of 12.5 years, and 57% of the families have an income-to-needs ratio less than 1.5. Children were assessed in the fall and spring of the pre-kindergarten and kindergarten years.

Study of State-Wide Early Education Programs

SWEEP took place in five states (Maine, New Jersey, Texas, Washington, and Wyoming) chosen to complement the six states selected for the NCEDL Multi-State Pre-K Study by including additional funding and service models. One hundred centers/schools per state were randomly selected via a stratified random sampling. A single classroom per site was randomly selected with a total of 465 classrooms, and four children were randomly selected per classroom for a total of 1,583 study children. As in the NCEDL Multi-State Study, the sample was diverse with 15% African American, 27% Hispanic, and 42% White children, and the average education for mothers was 12.7 years. Children were assessed in the fall and spring of their pre-kindergarten year.

Morrison’s Longitudinal Study

These data were collected as part of a larger study examining the effects of preschool instruction on academic gains. This longitudinal study included 383 children (195 girls, 188 boys) from an economically and ethnically diverse community in Michigan. Two hundred and thirteen children were recruited in Year 1 (2002-2003), 151 additional 4 year olds were recruited during the second year of the study, and an additional 18 five year olds were recruited during the third year of the study. The majority were White (80%), with fewer percentages of African American (4%), Asian/Indian (5%), Hispanic (1%), and multiracial (5%) children. Children were assessed twice per year for 5 years in the fall and spring of each school year from preschool through second grade.

Welfare, Children, Families: A Three City Study

This study took place in Boston, Chicago, and San Antonio. For the first wave of the study, between March 1999 and December 1999, a random sample of about 2,400 households with children in low-income neighborhoods were selected for interviews. Forty percent of the families included were receiving cash welfare payments at the time of the interview. Each household interviewed had a child aged 0 to 4 or aged 10 to 14. The second wave took place from September 2000 through June 2001, and the third wave took place between February 2005 and January 2006. The racial distribution was 42% Hispanic, 40% African American, and 18% non-Hispanic White.

Panel Study of Income Dynamics, Child Development Supplement

The Child Development Supplement to the PSID began in 1997 with a sample of 3,563 children. All PSID families with a child aged 0 to 12 in the 1997 calendar year were eligible to participate, with up to two children chosen per family. Subsequent waves of interviews were carried out in 2002-2003 including only children who remained under the age of 18 at the time of the study wave. This data set contains three waves of data. The first wave contains 3,563 children between the ages of 0 and 12 years. The follow-up wave was conducted in 2002-2003 with 2,908 children whose families remained active in the PSID panel. The children in Wave 2 were between 5 and 18 years of age. Last, a third measurement occasion took place in 2007, when the participants were between 9 and 22 years old. The racial distribution was 46.96% White, 40.83% African American, 7.33% Hispanic, 1.31% Asian or Pacific Islander, 0.38% American Indian or Alaskan Native, and 2.96% other.

Measures

Mathematics ability was measured using the Applied Problems (AP) subtest of the Woodcock–Johnson Psycho-Educational Battery–Revised (WJ-R; Woodcock & Johnson, 1990) in the NICHD-SECCYD, PSID, and WCF studies and using the AP subtest of the Woodcock–Johnson Psycho-Educational Battery–III (WJ-III; Woodcock, McGrew, & Mather, 2001) in the NCEDL, SWEEP, and MLS. The AP subtest measures early math reasoning and problem-solving abilities, which requires children to analyze and solve math problems while performing simple calculations. The AP test from the WJ-R contains 60 items, the AP test from the WJ-III contains 63 items, and the two versions share 39 items.

Analytic Techniques

Longitudinal data from each study were analyzed individually (in accordance with the parallel analysis approach) and then as a combined data set (in accordance with the data fusion approach), focusing specifically on individual change across time. Prior to these analyses and to address the issue of different versions of the AP subtest, we used an item response model to estimate a latent variable score that was not dependent on the version of the subtest. A one-parameter logistic model (1PL) was fit to the item-level data from the AP subtest as though they formed a single test (items that were not administered because the items only appeared on one version of the subtest were considered missing). The 1PL can be written as

$$P(X_{in}=1|{\mathrm{\theta }}_n,{\mathrm{\beta }}_i)=\frac{exp({\mathrm{\theta }}_n-{\mathrm{\beta }}_i)}{1+exp({\mathrm{\theta }}_n-{\mathrm{\beta }}_i)}$$

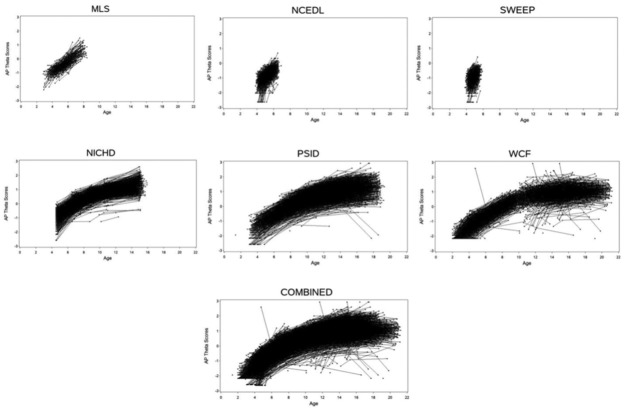
where $P(X_{in}=1|{\mathrm{\theta }}_n,{\mathrm{\beta }}_i)$ is the probability of getting item $i$ correct given person n’s ability level, ${\mathrm{\theta }}_n$, and item i’s difficulty, ${\mathrm{\beta }}_i$. In this specification, the items that were common to both versions have the same item parameters, which places the latent ability, ${\mathrm{\theta }}_n$, on the same scale regardless of the version of the Woodcock–Johnson. Expected a posteriori estimates of the latent ability scores were then output and used as observed data in subsequent analyses. Longitudinal plots of the estimated mathematics ability scores are contained in Figure 1 for each of the six studies. Mathematics ability showed relatively strong increases as the children got older, and the rate of change appeared to vary both within children over time (nonlinear changes) and between children at any particular point in time.

Figure 1.

Longitudinal plot of the individual trajectories of theta scores on the Applied Problems section of the Woodcock–Johnson for each of the six studies as well as the fused data.

Once a common metric for the scores on the AP subtest was established, various growth models were fit to each data set (parallel analysis) as well as the combined data set (data fusion) to account for the individual changes in math ability. A general form of the growth model, from the mixed-effects modeling framework, can be written as

$${\widehat{\theta }}_{tn}=f(t,{\mathbf{b}}_{\mathit{n}})+u_{tn}$$

where ${\hat{\mathrm{\theta }}}_{tn}$ is the estimated mathematics ability score at time t for individual n, $f(t,{\mathbf{b}}_{\mathit{n}})$ is a linear or nonlinear function of time t with random coefficients ${\mathbf{b}}_{\mathit{n}}$, and $u_{tn}$ is the residual at time t for individual n. The random coefficients in ${\mathbf{b}}_{\mathit{n}}$ were assumed to follow a normal distribution with means and covariances, ${\mathbf{b}}_{\mathit{n}}~N(\mathit{\beta },\mathit{\Psi })$, and the residuals were assumed to follow a normal distribution with a mean of 0 and constant variance, $u_{tn}~N(0,{\mathrm{\sigma }}_u^2)$.

In terms of modeling the structure of change, $f(t,{\mathbf{b}}_{\mathit{n}})$, we fit several different growth models including the linear, exponential, and Gompertz models. Detailed descriptions of each fitted growth model can be found in the appendix. Once the structure of change was determined, covariates were entered into the models as predictors of the random coefficients. The covariates included sex (0 = female, 1 = male) and socioeconomic status, which was based on an income-to-needs ratio of 1.5 (0 = income-to-needs > 1.5, 1 = income-to-needs ≤ 1.5).

Mplus (Muthén & Muthén, 1998-2010) with maximum likelihood estimation was used to fit the one-parameter logistic model and estimate latent ability scores. PROC NLMIXED (Littell, Milliken, Stroup, Wolfinger, & Schabenberger, 2006) in SAS v. 9.3 was used to fit the linear and nonlinear growth models to the estimated latent ability scores. All of the input scripts can be found on the second author’s website.

Results

The results are organized by research synthesis approach. First, we present results from the parallel analysis and then we present results from the data fusion approach. Within each section we discuss the results of fitting several growth models and describe the results of including socioeconomic status and sex as predictors of the random coefficients. The resulting parameter estimates and model fit information for the various tested models can be found in the appendix. Model comparisons were made through commonly used likelihood-based fit indexes including the Akaike’s information criterion and the Bayesian information criterion.

Parallel Analysis

Growth Analysis

Three different growth models (linear, exponential, and Gompertz) were fit to the longitudinal mathematics data from each of the six studies. Given the differences in the number and age at assessment, the same growth model was not preferred in all of the studies. Furthermore, several models did not converge because they were too complex given the number and timing of the assessments in certain data sets. For the NCEDL, SWEEP, and MLS studies, the linear growth model was the chosen model, and the exponential and Gompertz models failed to converge. For the NICHD, PSID, and WCF, the exponential growth model fit significantly better than the linear growth model, and the Gompertz model failed to converge.

Based on the linear growth model fit to the MLS, NCEDL, and SWEEP studies, the average mathematics ability score for a 5-year-old in each data set was −0.58, −0.94, and −0.89 and the mean annual rate of change was 0.41, 0.47, and 0.45 points per year, respectively. Examining the intercept and slope variances for each of these three studies, children significantly differed in their mathematics ability at age 5 and in their rate of growth over time, with the exception of the SWEEP study where the slope variance was nonsignificant. The lack of significant slope variance in the SWEEP study was likely a result of only having two measurement occasions.

The exponential growth model was the best fitting model in the NICHD, PSID, and WCF studies. Based on the analyses of the data from these studies, the average mathematics ability score for a 5-year-old was −0.73, −0.92, and −0.88, respectively. The mean amount of change from the intercept to the asymptotic level for the data from the NICHD, PSID, and WCF studies was 2.22, 2.42, and 2.13, respectively, and the rate of approach to the asymptote from each study was 0.22, 0.20, and 0.19, respectively. The intercept and the amount of change to the asymptotic level significantly varied over children indicating true variation in math ability at age 5 and true variation in total predicted growth.

As a way to summarize the results from the growth analyses, we plotted the predicted mean trajectory from the best fitting model for each study in Figure 2. The mean trajectories showed a good amount of overlap across studies, but there were some noticeable differences as well. Most notably, the mean trajectory for the MLS was higher than the other studies, which was due to having a higher intercept than the other studies. Although the mean rate of change was not much different in the MLS compared to the other studies, the mean trajectory in the MLS stands out because it was not predicted to slow when the longer-term studies showed signs of deceleration. This may be due to when the MLS concluded (i.e., second grade) because this appeared to be when the mean trajectories from the NICHD, PSID, and WCF studies began to slow. Thus, the changes observed in the MLS study may just be starting to slow and the fitted growth models were unable to capture the beginning of this deceleration. If data collection continued in this study, a growth model that allowed for deceleration in change (e.g., exponential) may have been more reasonable.

Figure 2.

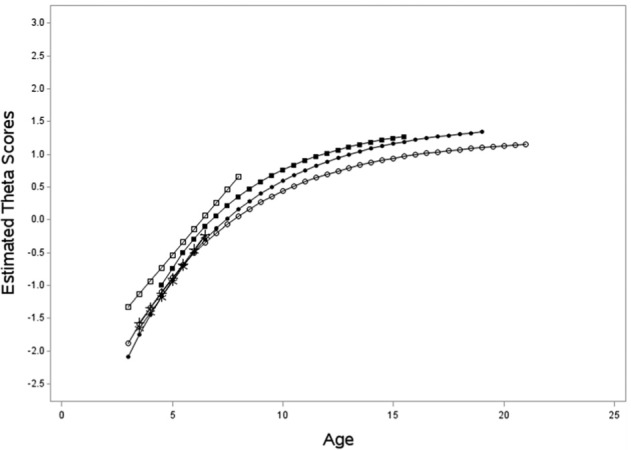
Predicted mean trajectory for the theta scores on the Applied Problems section of the Woodcock–Johnson for each of the six studies.

Note. MLS = open square; NCEDL = star; SWEEP = plus; NICHD = solid square; PSID = solid circle; WCF = open circle.

Socioeconomic and Gender Effects

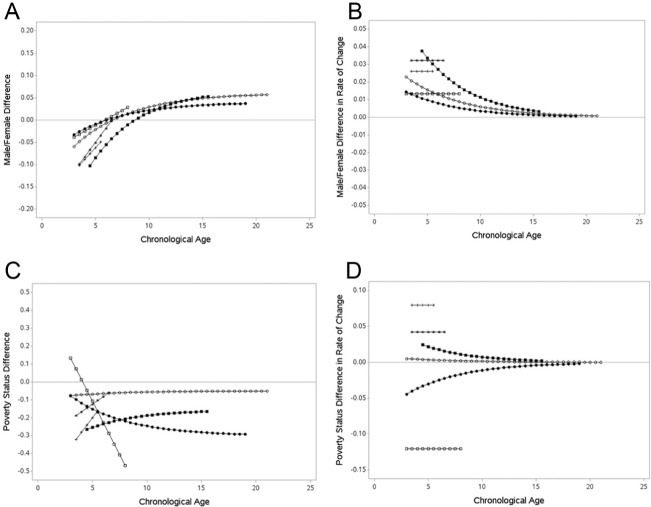
Gender and poverty status were included as predictors of the random coefficients in the best fitting model for each study. Figure 3 graphically presents the effects of sex and poverty status for each dataset. Figure 3A is a plot of the sex differences (male minus female) in the predicted scores at each age. In this plot, negative values indicate that females were predicted to have higher predicted scores, and positive values indicate that males were predicted to have higher predicted scores. Figure 3B is a similar plot, but the y-axis now represents sex differences in the rate of change with negative values indicating ages where females were predicted to have a faster mean rate of change than males, and positive values indicating ages where male were predicted to have a faster mean rate of change. Figure 3C and D contains similar plots based on poverty status with the difference (lower income minus higher income) in predicted scores appearing in Figure 3C and the difference in the predicted rates of change appearing in Figure 3D.

Figure 3.

Socioeconomic and gender effects for parallel analysis performed on the Applied Problems section of the Woodcock–Johnson for each of the six studies.

Note. MLS = open square; NCEDL = star; SWEEP = plus; NICHD = solid square; PSID = solid circle; WCF = open circle.

For the studies where change in mathematics ability was modeled with a linear growth model, gender and poverty status were found to be significant predictors of the intercept and slope in the NCEDL and SWEEP studies, but not in the MLS. In the NCEDL and SWEEP studies, males had lower math ability at age 5 compared to females; however, males had a slightly faster rate of change. Therefore, the difference in math ability scores between males and females decreased over time. Low-income students were found to have lower math ability at age 5 compared to students from higher income families; however, low-income students had a slightly faster rate of growth. Therefore, the difference in math ability between low-income and higher income students tended to decrease over time in these studies.

In the PSID, gender was not a significant predictor of either aspect of the exponential growth model. In the WCF, gender was not a significant predictor of mathematics ability at age 5, but was a significant predictor of the total amount of growth in mathematics ability with males showing more overall positive growth. For the NICHD study, males had lower mathematics ability at age 5, but showed more overall growth. Although not always significant, across the three studies, females tended to have higher mathematics ability at age 5, but this difference between male and female mathematics ability decreased, and then increased such that males were predicted to have higher mathematics ability in late elementary school and into junior high school.

The effects for poverty status on the intercept and slope of the exponential model were also study dependent. In all studies, low-income students had significantly lower mathematics ability scores at age 5, but the association with the overall growth in mathematics ability was study dependent. Low-income students had a slower rate of change than higher income students in the PSID study, whereas low-income students in the NICHD and WCF studies had a faster rate of change than higher income students.

Data Fusion

Growth Analysis

The same growth models were fit to the fused data set. The Gompertz growth model was found to be the best fitting model for the fused data set as it fit better than both the linear and exponential growth models based on fit information criteria. The predicted mean trajectory for the Gompertz model fit to the fused data is displayed in Figure 4. Parameter estimates from the Gompertz model indicate that the lower asymptote was −3.72, the predicted mean amount of change in mathematics ability from the lower to the upper asymptote was 5.01 points, the average relative rate of change to the asymptote was 0.28, and the mean maximum growth rate was predicted to occur at 7.90 years of age. We fixed the variance of the lower asymptote and relative rate of change to be 0, which forced these parameters to be equal across children. However, the amount of change from the lower to the upper asymptote and the time at which the maximum growth rate occurred were allowed to vary across children. Examining the variance in these two parameters indicates that children significantly differed in their amount of change from the lower to the upper asymptote and the time at which their maximum growth rate occurred.

Figure 4.

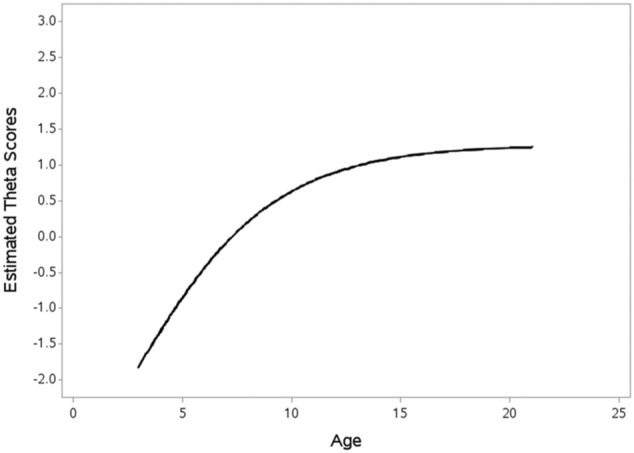
Predicted mean trajectory for the theta scores on the Applied Problems section of the Woodcock–Johnson for the combined data set.

Socioeconomic and Gender Effects

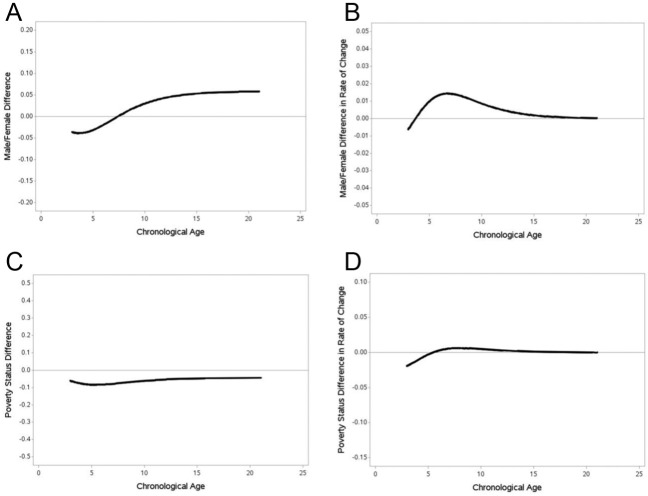
As was done with the parallel analysis approach, we included gender and poverty status as predictors of the two random coefficients in the Gompertz growth model. The results of these analyses can be seen in Figure 5 where the differences between males and females (Figure 5A and B) as well as between low-income and higher income students (Figure 5C and D) are displayed. Gender and poverty status were included as predictors of the amount of change from the lower to the upper asymptote and the timing of the maximum rate of growth, but they were not included as predictors of the lower asymptote or the relative rate of change because these parameters were fixed to be equal across individuals. As can be seen by examining Figure 5A, there were small sex differences in the predicted scores as well as in the rate of change. Females were predicted to outperform males in early childhood; however, males were predicted to outperform females after age 7. In terms of the rate of change (see Figure 5B), males were predicted to have a faster rate of change during childhood; however, sex differences in the rate of change were near zero in adolescence and into adulthood. Overall, lower income students were predicted to have lower scores over the observation period (see Figure 5C); however, there were near zero differences in the rate of change between lower and higher income students (see Figure 5D).

Figure 5.

Socioeconomic and gender effects for the data fusion analysis performed on the theta scores on the Applied Problems section of the Woodcock–Johnson for the combined data set.

Discussion

Synthesizing results from multiple studies is an important task during which researchers must tackle a number of challenges. The task is more demanding when studying processes longitudinally and when different measurement tools are used to measure the same construct. Data integration methodology remains an emerging field, particularly when dealing with multivariate and longitudinal data, where researchers pool data drawn from multiple existing studies and attempt to summarize results potentially from different methodology. To date, such methods are not commonly utilized in the psychological sciences, even though it has been suggested that these methods are useful for studying developmental processes that are difficult to model (Cooper & Patall, 2009; Curran & Hussong, 2009). For example, in studying obesity in children as an outcome of environmental and genetic influences, researchers frequently collect detailed longitudinal measurements involving multiple sources of information (Boyd et al., 2013). By applying integrative data analysis methods to multiple sources of information, greater flexibility in the exploration of observed outcomes can be accomplished. Additionally, more complex modeling and insight into the underlying sources of variability resulting in more accurate predictions is possible. However, determining the most appropriate integration method to use is not a trivial decision. Thus, although multisource data form an extremely rich resource for research, extracting meaningful and integrated information remains challenging.

The primary approach to research synthesis in psychology has been meta-analysis, which involves the aggregation and analysis of results from different but related studies (Alemayehu, 2011; Glass, 1976). While meta-analysis is commonly utilized, there remains a number of challenges facing this approach, particularly when aggregating research findings from longitudinal (and multivariate) studies. For example, a standardized measure of effect size (Cohen’s d or r), which is commonly aggregated in meta-analysis (Glass, McGaw, & Smith, 1981), is more difficult to define in longitudinal studies because of the span of the longitudinal study, the fitted (growth) model, and the utilized timing metric. With reference to the fitted model, certain growth models (e.g., quadratic) have multiple latent variables (linear and quadratic components) that contribute to the within-person rate of change, which can make it difficult to understand how the within-person rate of change is associated with covariates. Furthermore, with growth models that are nonlinear with respect to time (e.g., logistic, quadratic) the association between covariates and the within-person rate of change varies as a function of time.

Additionally, combining standardized effect sizes from studies with different sampling procedures is inappropriate because unstandardized effects (e.g., unstandardized regression coefficients) are expected to generalize across studies and standardized effects (e.g., correlation, standardized regression coefficients) are not. The challenge with longitudinal studies is that their sampling procedures tend to be quite different. Furthermore, attrition in longitudinal studies can serve to change the composition of the sample. In light of the challenges to using meta-analytic approaches with longitudinal studies that focus on within-person change, parallel analysis (Piccinin & Hofer, 2008) and data fusion (Cooper & Patall, 2009; White, 1987; Wilderjans et al., 2015) methods may be able to fill this gap.

This study demonstrated the use of two different integrative methods for the analysis of longitudinal data from multiple studies: the parallel analysis and data fusion approaches. Six longitudinal studies of mathematics ability in children were compiled with the goal of modeling individual changes in mathematics ability and determining differences in the trajectories based on sex and socioeconomic status. Although the studies varied slightly in their assessment of mathematics ability as well as in the timing and number of measurement occasions, these issues were dealt with by utilizing an item response model to estimate latent variable scores that were not dependent on the measurement instrument and by utilizing different growth models. The primary goal was to highlight some of the many advantages of using these alternative methods for the research synthesis of multiple longitudinal studies and to bring new challenges to the forefront.

Parallel Analysis Approach

To evaluate the results of the parallel analysis, we plotted the effects across studies. By plotting the mean trajectories for each study, we were able to examine the similarity of the trajectories and gain insight into the overall trajectory. We also plotted differences in predicted mean trajectories and rate of change for males and females as well as for children from lower and higher income families to examine how these participant characteristics were related to the developmental process of mathematics. Interestingly, the effects of these participant characteristics were not stable and depended on the age of the participants.

There are, of course, alternative approaches to examining the effects across studies, such as calculating the average effect, or the weighted average effects (weighted by sample size and/or the reliability of the intercept/change). One challenge to these alternative approaches is how to consider sample size as well as the number and timing of the assessments. In longitudinal studies, sample size varies over time and the number, spacing, and timing of the assessments affect the reliability of the individual rate of change. How best to account for this information when combining results from multiple studies remains unknown. Furthermore, determining appropriate standard errors of the effects of interest also requires further study.

Data Fusion Approach

When the six data sets were combined into a single data set, the Gompertz growth model, which was too complex for any individual study, was the best fitting model. The Gompertz model has been previously utilized in modeling changes in mathematics and reading behaviors from early elementary school through junior high (Cameron, Grimm, Steele, Castro-Schilo, & Grissmer, 2015; Grimm, Ram, & Estabrook, 2010). Additionally, the shape of the Gompertz curve is more typical of the expected growth in these skills as initially slow changes lead to rapid changes, which is followed by continued slow increases in performance. Given that this model could only be fit to the fused data and was not estimable in any of the individual data sets is one of the benefits of the data fusion approach to data integration.

A second advantage of the data fusion approach is that each data set contributes proportionally to the amount of data provided. In longitudinal modeling, each data point counts equally. Thus, we do not need to think about how to weight each data set based on the number of participants or the number and timing of data points. A third advantage is the handling of covariates that may be missing completely (see Widaman, Grimm, Early, Robins, & Conger, 2013). In the parallel analysis approach, such variables may not be included in the model if they are unmeasured in certain studies, or these variables may be removed from all of the analyses for consistency. In the data fusion approach, full information maximum likelihood can be utilized, and in such a situation, the missing data mechanism is truly missing completely at random.

Fourth, by combining multiple data sets, we create a more heterogeneous sample, which can increase generalizability of results (Curran & Hussong, 2009). Combining data from multiple sources also increases sample size so that more precise estimates of effects can be obtained. Furthermore, the larger and more heterogeneous sample increases the likelihood of having appropriately powered tests of moderating effects (Fritz & MacKinnon, 2007) compared to a single study, where moderating effects are typically underpowered (Hedges & Pigott, 2001; Sansone, Morf, & Panter, 2008).

Limitations

In spite of the many benefits of the data fusion and parallel analysis approaches for integrating data, there are limitations that must be kept in mind. The first major obstacle is the need to obtain raw data from the multiple studies, which can be problematic if researchers are not willing to share their data. We expect this limitation to be minimized in the future because researchers are becoming more willing to share their data and several granting agencies require researchers to deposit their data in a public repository. The second challenge, specific to parallel analysis, is determining the best way in which to summarize the longitudinal results from a parallel analysis. We have proposed some approaches, but questions remain about the optimal way to summarize and take into account sample size as well as the number and timing of the assessments.

The third challenge, specific to data fusion (but one that parallel analysis should also consider), is that a common measure of the outcome must be available or created because the actual data are being combined and collectively analyzed. This can be problematic whenever studies use different measurement tools to measure the same construct. As a consequence, some researchers have criticized any attempts to link data that are from different studies. For example, Feuer, Holland, Green, Bertenthal, and Hemphill (1999) questioned if is even possible to link data obtained from various studies when some might involve low stakes (where perhaps scores do not accurately represent individuals), whereas others involve high stakes (where respondents are usually more motivated and try harder). However, whenever data that involve measurements obtained with similar stakes are used, this criticism is not valid. What can be problematic is when the examined studies use different measurement tools to measure the same construct of interest. If different measurement tools are used to measure the same construct, then researchers must find a way to scale the outcome variables to a common metric. Here, we were able to use an item response model to create an appropriate scale (see Curran et al., 2008, McArdle, Grimm, Hamagami, Bowles, & Meredith, 2009), but acknowledge that our use of studies that administered a version of the Woodcock–Johnson was a limiting factor. If many scales of the same construct need to be scaled, creating a common metric for the construct of interest is challenging unless there are common items across scales or if some participants were administered multiple scales. We note that is it possible to have multiple scales administered to a set of participants outside of the longitudinal studies used in the data integration. This calibration sample may be a necessary and reasonable approach. A fourth limitation is the assumption that the studies have sampled from the same population. In any data integration study, main effects are often studied (unless moderating hypotheses are made and appropriately tested), which makes the assumption that a single effect characterizes the association. If the effect varies over participant characteristics, it is necessary to account for these differences through the incorporation of product terms to examine moderation. As we noted, data fusion may be a good approach if these moderating hypotheses are expected.

Concluding Remarks

In conclusion, we believe that data integration methods are very valuable approaches that help researchers address important questions with more power and accuracy than any single study. The approaches are undoubtedly beneficial for examining the replication of research findings across independent longitudinal data and for enhancing the validity of conclusions obtained from different studies. With these approaches we feel that researchers can stand on the shoulders of the researchers that have come before to build a cumulative science. At the same time, we acknowledge that more work and thinking needs to be done regarding when these approaches are most useful and when we should shy away from such approaches (e.g., if there are strong cohort effects). We look forward to continued evolution of these methods.

Appendix

Specification of Growth Models

The linear growth model can be written as

$${\mathrm{\theta }}_{tn}=b_{1n}+b_{2n}\left(\frac{age-5}{12}\right)+u_{tn}$$

where θ_tn is the outcome of interest (AP score) measured at time t for individual n, b_1n is the intercept or the predicted score for individual n when age = 5 years, b_2n is the slope or the annual rate of change for individual n.

The exponential growth model can be written as

$${\mathrm{\theta }}_{tn}=b_{1n}+b_{2n}(1-\exp (-\mathrm{\alpha }·\frac{age-5}{12}))+u_{tn}$$

where b_1n is the intercept or the predicted score for individual n when age = 5 years, b_2n is the amount of change from the intercept to the asymptotic level for individual n, and α is the rate of approach to the asymptotic level.

Finally, the Gompertz model can be written as

$${\mathrm{\theta }}_{tn}=b_{1n}+b_{2n}·\exp (-\exp (-b_3(\frac{age}{12}-b_{4n})))+u_{tn}$$

Model Fit Information for the Models Tested

	Linear	Exponential	Gompertz
Parallel Analysis
MLS
−2 Log likelihood	−4.9	—	—
Akaike (AIC)	7.1	—	—
Bayesian (BIC)	28.6	—	—
NCEDL
−2 Log likelihood	207.3	—	—
Akaike (AIC)	219.3	—	—
Bayesian (BIC)	248.5	—	—
SWEEP
−2 Log likelihood	1038.3	—	—
Akaike (AIC)	1050.3	—	—
Bayesian (BIC)	1083.0	—	—
NICHD
−2 Log likelihood	—	266.9	—
Akaike (AIC)	—	280.9	—
Bayesian (BIC)	—	316.3	—
PSID
−2 Log likelihood	8079.1	4126.9	—
Akaike (AIC)	8091.1	4140.9	—
Bayesian (BIC)	8127.5	4189.3	—
WCF
−2 Log likelihood	—	5759.5	—
Akaike (AIC)	—	5771.5	—
Bayesian (BIC)	—	5806.1	—
Data Fusion
Combined
−2 Log likelihood	30,849	14,629	14,186
Akaike (AIC)	30,861	14,643	14,202
Bayesian (BIC)	30,904	14,693	14,259

Note. AIC = Akaike’s information criterion; BIC = Bayesian information criterion.

where b₁ is the lower asymptote, b_2n is the amount of change from the lower asymptote to the upper asymptote for individual n, b₃ is the rate of change, and b_4n is the time at which the maximum growth rate occurs for individual n. In order for the model to converge, the lower asymptote and rate of change must be fixed for everyone. The upper asymptotic level and the time at which the maximum growth rate occurs were allowed to vary.