Using Cluster Bootstrapping to Analyze Nested Data With a Few Clusters

Abstract

Cluster randomized trials involving participants nested within intact treatment and control groups are commonly performed in various educational, psychological, and biomedical studies. However, recruiting and retaining intact groups present various practical, financial, and logistical challenges to evaluators and often, cluster randomized trials are performed with a low number of clusters (~20 groups). Although multilevel models are often used to analyze nested data, researchers may be concerned of potentially biased results due to having only a few groups under study. Cluster bootstrapping has been suggested as an alternative procedure when analyzing clustered data though it has seen very little use in educational and psychological studies. Using a Monte Carlo simulation that varied the number of clusters, average cluster size, and intraclass correlations, we compared standard errors using cluster bootstrapping with those derived using ordinary least squares regression and multilevel models. Results indicate that cluster bootstrapping, though more computationally demanding, can be used as an alternative procedure for the analysis of clustered data when treatment effects at the group level are of primary interest. Supplementary material showing how to perform cluster bootstrapped regressions using R is also provided.

Clustered or nested data are a common occurrence in educational and psychological research (e.g., students within schools, patients within clinics). Standard parametric analytic techniques (e.g., regression, analysis of variance, t tests) which ignore this nesting effect violate the well-known assumption of observation independence (Cohen, Cohen, West, & Aiken, 2003). As a result of the violation, the standard errors for the point estimates are misestimated which may result in erroneous conclusions resulting from increased Type I errors (Arceneaux & Nickerson, 2009; Clarke, 2008; Hahs-Vaughn, 2005; Musca et al., 2011). Accounting for the clustered nature of the data is especially important in cluster randomized trials (CRTs) in which a treatment is applied at the group level (e.g., at the school or classroom level) instead of the individual level (e.g., at the student level; Donner & Klar, 2004).

With CRTs, treatment effects are investigated by recruiting intact groups (e.g., schools), randomly assigning groups to a treatment or a control (e.g., business as usual) condition, and individual-level outcomes are evaluated. From a practical perspective, recruiting and retaining groups to participate in CRTs can be financially and logistically challenging. In practice, a large number of groups may not be needed to reach the conventionally acceptable level of power for some CRTs. Conducting power analysis specifically dealing with clustered data using software such as Optimal Design (Spybrook et al., 2011) or PowerUp! (N. Dong & Maynard, 2013) indicates that with an alpha of .05, an intraclass correlation coefficient (ICC) of .05, and a moderate effect size of 0.40, as little as 14 groups with 100 individuals per group (which is not unusual in whole school CRTs) would be needed to achieve a desired power level of .80. The number of clusters needed yielding an acceptable level of power may decrease even further if additional covariates are included in the model which results in improved model precision and power. Recruiting a few groups with a large number of subjects per group (e.g., 10 schools with 100 students each) is generally easier than recruiting more groups with a fewer number of subjects per group (e.g., 100 schools with 10 students each), though power is maximized in the latter condition (Murnane & Willett, 2011; Musca et al., 2011).

Although a large number of clusters may be desirable in CRTs (especially if subgroup analysis is desired), a low number of clusters is at times seen in practice (Flynn & Peters, 2004; Moerbeek & van Schie, 2016). For example, in a health-related CRT, Curtis et al. (2011) recruited 12 hospitals with 822 individuals in total and randomly assigned 6 hospitals each to the treatment and control groups. In an educational setting, Coyne et al. (2010) described a reading intervention assigned at the classroom level involving 121 students within 8 classrooms. To test interventions designed to increase the uptake of children’s vegetable consumption, Hanks, Just, and Brumberg (2016) conducted a CRT and randomly assigned 10 elementary schools to control and treatment groups. A review of 285 CRTs in the health sciences indicated that the median number of clusters used was 21 (Ivers et al., 2011).

A common way of analyzing clustered data is to use a hierarchical linear model (Raudenbush & Bryk, 2002) also commonly referred to as a mixed model, a random coefficient model, or simply a multilevel model (MLM). MLMs have increased in popularity over the years as a means to properly analyze clustered data sets. However, researchers have often expressed concern using MLMs when the number of clusters or groups is low (e.g., groups < 20; e.g., Curtis et al., 2011; Gehlbach et al., 2016; McCoach & Adelson, 2010). Often, this reluctance stems from a concern that standard error estimates for group-level point estimates may continue to be negatively biased even if the clustering is accounted for using MLM (Maas & Hox, 2005). The analysis of CRTs with a low number of clusters thus continues to be of both a practical and statistical concern.

Although various techniques have been suggested in dealing with nested data apart from the use of MLM (see Huang, 2016), one alternative method, that has seen little use in educational and psychological research is cluster bootstrapping (Cameron, Gelbach, & Miller, 2008; Fox, 2016). Since point estimates (e.g., regression coefficients) in a properly specified regression model are generally unbiased when analyzing clustered data (Moulton, 1990; Mundfrom & Schultz, 2001), cluster bootstrapping provides an alternative method for dealing with nested data to estimate standard errors (Dedrick et al., 2009; Maas & Hox, 2005). A full text search on the PsycNET database of the American Psychological Association (APA) for peer-reviewed APA journal articles from 2011 to 2016 using the keywords “cluster* bootstrap*” resulted in only four articles that made use of bootstrapping specifically to account for the clustered nature of the data analyzed (Gehlbach et al., 2016; Ifcher & Zarghamee, 2014; Kizilcec, Bailenson, & Gomez, 2015; van den Bos & Michiel, 2016).¹ Of the four, two of the articles indicated using cluster bootstrapping due to the small number of clusters (Gehlbach et al., 2016; Ifcher & Zarghamee, 2014). In the current article, we describe the issues with analyzing clustered data, provide an overview of cluster bootstrapping, and compare standard error estimates across different methods using a Monte Carlo simulation to analyze data with a low number of clusters.

The Problem With Analyzing Clustered Data

As observations within the same cluster tend to be more alike with each other compared with observations in other clusters (e.g., students in the same class have a common teacher), observations exhibit some degree of interdependence (Hox & Kreft, 1994). This interdependence is a result of the sampling design typically found in CRTs where all students in one group or cluster are assigned to a condition which then affects the variance of the outcome which in turn affects the estimates of the standard errors (McCoach & Adelson, 2010). Although point estimates derived using standard ordinary least squares (OLS) regression with continuous outcomes will generally yield unbiased point estimates when using nested data (Clarke, 2008; Harden, 2011; Maas & Hox, 2005; Moulton, 1986), the greater concern when dealing with clustered data revolves around the standard errors. As standard errors are used in computing t-statistics, standard errors that are too small or biased downward, will yield results that are statistically significant more often increasing the probability of making a Type I, much more than the nominally stated alpha of .05. The ICC (or ρ) is a commonly used measure to indicate the degree of violation of the observation independence assumption, indicates how similar individuals are within clusters, and also measures the proportion of variance in the outcome that is attributable to the group level.

To calculate the ICC, an unconditional MLM is run which partitions the amount of variance at the group level (τ_oo) and the amount of variance within clusters (σ²). The ICC is the group-level variance divided by the overall variance (i.e., τ_oo/[σ²₊τ_oo]). A simple way to estimate the ICC is to run an OLS regression model predicting the outcome of interest and only including J− 1 dummy codes for the cluster variables as predictors, where J is the total number of groups. The resulting adjusted R² estimates the proportion of variance in the outcome variable that is attributable to the grouping variables (Huang, 2016). In education, a review of several national data sets using reading and math outcomes for K-12 students within schools indicated that the average unconditional ICC was .22 (Hedges & Hedberg, 2007).

The violation of observation independence is indicated by the degree in which the ICC is greater than zero, with an ICC of zero indicating complete observation independence. In early studies, some have suggested that clustering may be ignored when ICCs are low (e.g., $\rho <.05$) and data may be analyzed using standard analytic procedures (e.g., OLS regression; Heck & Thomas, 2008). However, more recent studies have shown that even minimal departures from zero can result in increased Type I errors (Lai & Kwok, 2015; Musca et al., 2011) when group-level predictors are of interest. Apart from the ICC, the probability of making a Type I error is also influenced by the average number of observations per cluster and the cluster size is used in estimating what is referred to in the survey sampling literature as the design effect (Kish, 1965).

Kish (1965) defined the design effect (or DEFF) for a sample statistic (e.g., the mean) as the “ratio of the actual variance of a sample to the variance of a simple random sample of the same number of elements” (p. 258). For nested models, DEFF can be estimated by DEFF = 1 +ρ (m− 1; Kish, 1965) where ρ is the ICC and m is the average number of observations per cluster (for unbalanced cluster sizes, the harmonic mean may also be used). The square root of DEFF is known as DEFT (Hahs-Vaughn, 2005) and DEFT can be used as a variance inflation factor to adjust standard errors to account for the clustering effect (i.e., adjusted standard errors = DEFT × standard errors). For example, with a DEFT of 2, standard errors should be twice as large compared with a model that ignores the clustering effect.

Given the equation, the standard error corrections are a factor of both the ICC and the number of observations within a cluster such that DEFT increases if either the ICC and/or the cluster size increases. So even if the ICC is held constant, DEFT may increase if the number of observations within a cluster increases. In cases where $\rho =0$ or m = 1 (i.e., there is one individual per cluster), then no adjustments are necessary. In the field of applied economics, the design effect was rediscovered by Moulton (1986, 1990) and the correction factor has popularly come to also be known as the Moulton factor (Angrist & Pischke, 2014). The design effect can also be used in power analyses to compute the effective sample size such that effective sample size is the nominally stated sample size divided by DEFF (Snijders & Bosker, 2012; Taljaard, Teerenstra, Ivers, & Fergusson, 2016).

Various approaches have been discussed in the literature that can be used in the analysis of clustered data (Huang, 2016; McNeish & Stapleton, 2016). However, when the number of clusters is low (e.g., J < 30), certain approaches may not be suitable if Level 2 regression coefficients are of interest. An example of this is the commonly used cluster robust standard errors, widely used by economists (Cameron & Miller, 2015). Although relatively easy to implement, the use of cluster robust standard errors or similar standard error adjustment technique such as using Taylor series variance estimation can still underestimate Level 2 standard errors with a low number of clusters (R. Bell & McCaffrey, 2002; Harden, 2011; Huang, 2016). Another common method to analyze clustered data is through the use of fixed effects models. Fixed effects models are a powerful, flexible, and straightforward way to account for the nesting effect though may not be of use if the variable of interest is at the cluster level (Murnane & Willett, 2011) which is the case when CRTs are analyzed. In education and psychological sciences, MLM is a commonly used technique for the analysis of clustered data though some may refrain from using MLM when the number of groups is low due to potentially biased estimates (Coyne et al., 2010; e.g., Curtis et al., 2011; McCoach & Adelson, 2010).

Sample Size Guidelines for the Number of Clusters

The most widely cited rule of thumb for minimum sample sizes based on a recent review of MLM studies (Tonidandel, Williams, & LeBreton, 2014) can be attributed to Kreft’s (1996) unpublished manuscript² and coined the 30/30 sample size requirement indicating that 30 groups with 30 individuals per group was sufficient for MLM studies. However, Tonidandel et al. pointed out that Kreft’s study was based on a review of other unpublished manuscripts and findings were applicable only to studies with ICCs < .25,³ focused on fixed effects estimation, and sample size recommendations were for obtaining sufficient power to detect cross-level interactions. However, researchers should not rely heavily on rules of thumb—which ignore important components of power analyses such as considering minimum detectable effect sizes—especially when software for multilevel power analyses (N. Dong & Maynard, 2013; Spybrook et al., 2011) are readily available and take out the unnecessary guesswork for calculating required sample sizes.

Another often cited reference for minimum sample sizes in MLM studies is the Monte Carlo simulation of Maas and Hox (2005), which focused not on power but on potentially biased estimates.⁴ Simulating two-level models varying the number of clusters, observations per cluster, and ICCs (.10 to .30), Maas and Hox concluded that both the regression coefficients and the standard errors were estimated without bias in all the conditions investigated. Only with an extremely small sample size of 10 clusters with 5 observations per cluster (an extra condition investigated) did the standard errors for the regression coefficients become slightly underestimated (~9%). Other simulations though using more conditions and a low number of clusters have indicated that using MLM may not necessarily result in biased point estimates or standard errors (B. A. Bell, Morgan, Schoeneberger, Kromrey, & Ferron, 2014; Huang, 2016; McNeish & Stapleton, 2016). Although Maas and Hox (2005) indicated that the variance components may be underestimated to a larger extent, often the focus of MLM studies are on the fixed effects and their associated significance tests (Dedrick et al., 2009). However, as MLM and OLS point estimates are generally unbiased, studies have suggested the use of bootstrapping which may not be as sensitive to a small number of Level 2 clusters (Dedrick et al., 2009; Maas & Hox, 2005; McNeish & Stapleton, 2016).

The Cluster Bootstrapping Procedure

Bootstrapping as an analytic technique is not new and has been around for decades (Efron, 1979). The term itself is said to be derived from the phrase to “pull oneself up by one’s bootstrap, widely thought to be based on one of the 18th century Adventures of Baron Munchausen, by Rudolph Erich Raspe” where the baron finds himself at the bottom of a lake but manages to get out by pulling himself up only using his bootstraps (Efron & Tibshirani, 1994, p. 5).

Bootstrapping is a resampling technique which involves computing a statistic of interest repeatedly based on a large number of random samples drawn from the original sample. In such a manner, the variability of the statistic of interest can be calculated as a result of the repeated sampling. Operationally, from an existing original sample of size n, bootstrapping involves taking a random sample (simply referred to as a bootstrap replicate) from the existing sample (with replacement) also of size n and computing a statistic of interest (e.g., a regression coefficient which we can denote as θ_b) using the bootstrapped sample b. Since the sampling is done with replacement, observations may appear more than once and some observations will also not be selected.⁵ The process of drawing a new sample and computing the statistic of interest is performed B times and will result in collecting B number of θs (i.e., θ₁, θ₂, . . ., θ_B). For a large number of θ_b estimates, the standard deviation of the θs can be referred to as the bootstrapped standard error of $\hat{\theta }$, the estimated statistic of interest, or

$$S{E}_{\hat{\theta }}={\left(\frac{1}{B-1}{\sum }_{b=1}^B{({\theta }_b-\overline{\theta })}^2\right)}^{\frac{1}{2}},$$

where $\overline{\theta }$ is the mean of the collected θs.

The standard error, along with the mean of the vector of θs, can be used to construct the bootstrapped normal-approximation confidence intervals (CIs) and used for inferential statistics such as t tests (e.g., $\hat{\theta }/S{E}_{\hat{\theta }}$). Nonparametric confidence intervals (e.g., a 95% CI) using the α/2 and 1 − (α/2) quantiles (i.e., 2.5% and 97.5%) of the ordered distribution of θs can also be used which does not make any distribution assumptions for $\hat{\theta }$. Although $\overline{\theta }$ is used to estimate the standard error, it is not used to estimate the statistic itself and instead, the original statistic $\hat{\theta }$ is used which is computed using the original sample and is the best point estimate of the statistic (StataCorp, 2015). Although guidelines have been suggested as to the number of replications required for the optimal number of bootstrapped replications (see Poi, 2004), 1,000 replications is generally considered acceptable for standard error estimates (Chernick & LaBudde, 2011).

Bootstrapping is relatively straightforward, can be used with a wide variety of statistics, but is a computationally intensive task which requires sampling and computing the statistic of interest repeatedly (i.e., B times). However, given the speed of modern computers, that is less of an issue and with relatively simple multiple regression models (e.g., 5 variables and 1,000 observations), results using 1,000 replications can be generated in a few seconds. The logic of bootstrapping is that a random sample drawn from a random sample from the population is also a random sample of the population itself (Murnane & Willett, 2011). Fox (2016, p. 651) indicates that the key bootstrap analogy is that the population is to the sample as the sample is to the bootstrap samples.

However, with nested data, the standard bootstrapping procedure is modified to reflect the sampling design used in a CRT (Fox, 2016). Standard bootstrapping procedures though still require identically distributed responses which is not the case with clustered data (Goldstein, 2011). Cluster bootstrapping, which has been referred to using various names such as the cases bootstrap, the block bootstrap, and the pairs bootstrap (Cameron et al., 2008; Van der Leeden, Meijer, & Busing, 2008), slightly modifies the standard bootstrapping procedure with regard to the resampling process. Instead of drawing a random sample of n observations, the sampling is based on the total number of J clusters. With cluster bootstrapping, the first step is to randomly select J number of clusters with replacement (Davison & Hinkley, 1997). For each cluster selected (with some clusters selected more than once and others not selected at all), all observations within that cluster are included in the bootstrapped sample. Then the desired statistics are computed using the bootstrapped sample and the process is repeated B number of times. Standard errors and confidence intervals can be derived using standard bootstrapping procedures.

For CRTs with a low number of clusters and a binary predictor at Level 2 (i.e., a treatment indicator where treat = 1 or 0) an additional modification to the standard cluster bootstrapping procedure is necessary. Because of the low number of clusters (e.g., 10) and the random selection of clusters with replacement, it is possible to have a bootstrapped sample with clusters that are either all from the treatment condition or all from the control condition. In such a case, the treatment effect for that bootstrapped sample becomes inestimable as a result of a lack of variation in the treatment variable. To remedy this, a modified bootstrap procedure is possible where the treatment and control clusters are separated into two groups and in each resampling step, clusters are sampled independently within the treatment and control groups and then combined to form the complete bootstrapped sample, ensuring the presence of both treatment and control groups in every bootstrapped sample. For example, with an overall sample made up of 10 clusters with 5 clusters in a treatment group and 5 clusters in a control group, in each resampling step, 5 clusters are randomly selected (with replacement) from the treatment group and 5 clusters are randomly selected from the control group (with replacement). All the observations within those clusters from both sets of random samples are combined to form the 10 clusters where the analysis will be performed. This is repeated B number of times. Statistical software such as R and Stata can perform this modified cluster bootstrapping procedure without the need of any statistical programming.⁶

The Present Study

The objective of the current study was to investigate the performance of cluster bootstrapped standard errors (CBSE) in the presence of a low number of Level 2 clusters, a situation found in a number of CRTs (Flynn & Peters, 2004; Ivers et al., 2011). As point estimates (i.e., the regression coefficients) using MLM and OLS are generally unbiased (Moulton, 1986), the current study focuses on the potential bias in standard errors using OLS, MLM, and CBSE.

Previous studies have investigated bootstrapping within a multilevel framework but have not specifically used cluster bootstrapping as an alternative to MLM (e.g., Roberts & Fan, 2004; Thai, Mentré, Holford, Veyrat-Follet, & Comets, 2013; Vallejo Seco, Ato García, Fernández García, & Livacic Rojas, 2013). Other studies have investigated the use of cluster bootstrapping (Cameron et al., 2008; Harden, 2011) but have not used ICCs typically found in an educational setting, have not used a dichotomous Level 2 predictor which is of interest in CRTs, nor compared results with those derived using MLM. To summarize, the current study specifically:

1. Investigated results using cluster bootstrapping using both continuous and dichotomous Level 2 predictors

2. Compared the CBSE with standard error estimates using MLM and OLS regressions

3. Investigated results using a low number of clusters

4. Used unconditional ICC conditions commonly found in educational settings.

Prior studies have suggested that bootstrapping may be a good alternative to standard MLMs (Dedrick et al., 2009; Maas & Hox, 2005; McNeish & Stapleton, 2016). However, cluster bootstrapping has not been specifically investigated with a focus on both continuous and dichotomous Level 2 predictors and comparing estimates with those derived using MLMs, a technique used predominantly in the education and psychological sciences when clustered data are analyzed.

Although bootstrapping as a procedure has been around for decades, barriers that may have slowed its adoption by applied researchers is that the literature on bootstrapping may be dense and in previous years, performing the procedure itself may have involved some statistical programming which may be a daunting task for applied researchers (Fox, 2016; Roberts & Fan, 2004). An additional objective was to use a bootstrapping procedure that was readily available and easily implemented in free software such as R or commercial software such as Stata. To illustrate the process of cluster bootstrapping with an applied data set, a complete example is shown in the online appendix.

Method

Data Generating Process

To assess the various procedures in addressing potentially underestimated standard errors at Level 2, we used a Monte Carlo simulation in R (R Core Team, 2016). We simulated a linear model with dependent variable Y_ij, for observation i in group j, with two uncorrelated predictors at Level 2 (the group level). The first group-level predictor, T_j, was a dichotomous predictor often found in CRTs where entire clusters are assigned to either a treatment and control group. The second group-level predictor, W_j, was a continuous variable, also commonly found in multilevel studies (e.g., group-level socioeconomic status). Both variables were specified to be uncorrelated with another predictor, X_ij, at Level 1 (the individual level), resulting in the following combined model:

$$Y_{\mathrm{ij}}={\beta }_0+{\beta }_1{T}_j+{\beta }_2{W}_j+{\beta }_3{X}_{\mathrm{ij}}+u_{0j}+r_{\mathrm{ij}}.$$

The model is defined such that ${\beta }_0=0.00$, ${\beta }_1=0.30$, ${\beta }_2=0.30$, and ${\beta }_3=0.80$. Approximately half of the participants were assigned to be in the “treatment” (T = 1) or the control (T = 0) groups and assignment was done at the group level. The set of W and X variables were generated from a standard normal distribution and two error terms were included: a cluster-level error term, u_0j, and an individual-level error term, r_ij. Both the error terms were assumed to be independent of each other, followed a normal distribution such that $u_{\mathrm{oj}}~N(0,{\tau }_{\mathrm{oo}})$ and $r_{\mathrm{ij}}~N(0,{\sigma }^2)$, and were not correlated with the independent variables (which is a reasonable assumption in a CRT). Although centering is a commonly used technique when estimating MLMs (Enders & Tofighi, 2007), centering was not done to allow for comparability of results across models.

As we were interested in the level of bias of the standard errors under various small group conditions, we manipulated the number of clusters (i.e., J = 10, 20, 30 clusters), the average number of observations within each cluster (i.e., nJ = 10, 30, 50), and the unconditional ICCs that may typically be found in educational and psychological research (i.e., ICC = .05, .10, .20, .30; Hedges & Hedberg, 2007; Kreft & Yoon, 1994). To estimate the unconditional ICCs, the Level 1 variance for the error term, σ², was set to 2.25 and variance of the group-level error term, τ_oo, was modified accordingly. To simulate an unbalanced number of observations per cluster, we estimated 10% more observations per cluster than specified (e.g., 33 vs. 30 observations in 20 clusters) and then randomly excluded an appropriate number of observations (e.g., 60) to arrive at the specified average number of observations per condition (e.g., 30). The probability of excluding an observation within each cluster was not uniform (i.e., some clusters had no cases removed and others had more excluded) creating an unbalanced design condition often found in CRTs. As a result, we tested 36 conditions (i.e., 3 number of clusters × 3 average observation per cluster conditions × 4 ICCs) with 1,000 replications per condition (i.e., 36,000 data sets).

Analytic Strategy

Each simulated data set was analyzed using three techniques. To establish a baseline, each data set was analyzed using standard OLS regression, not accounting for the clustering. A second method used was multilevel modeling using the lme4 package (Bates, Mächler, Bolker, & Walker, 2015) in R. As standard errors are generally more accurate using restricted maximum likelihood (REML) when the number of groups is small (Goldstein, 2011; Huang, 2016; Meijer, Busing, & Van der Leeden, 1998), REML estimation was used. In addition, a Kenward–Roger (Kenward & Roger, 1997) correction using the pbkrtest package (Halekoh & Højsgaard, 2014) in R was used to adjust standard errors which has shown to result in less-biased standard errors when analyzing data with a low number of clusters (B. A. Bell et al., 2014; McNeish & Stapleton, 2016). As a specification check, MLMs using full maximum likelihood (ML) were also tested. The third technique assessed, which was of primary interest, used cluster bootstrapping using the bootcov function in the rms: Regression Modeling Strategies package (Harrell, 2016) in R. One thousand bootstrap replicates were created by first dividing the sample into two groups (i.e., T = 1 and T = 0) and then within each group, sampling with replacement at the cluster level and then moving all the observations within the clusters to the bootstrap replicate. Each replicate was analyzed using OLS regression as point estimates for properly specified models are unbiased (Moulton, 1990; Mundfrom & Schultz, 2001). To estimate the CBSEs, the standard deviation of the point estimates of the 1,000 bootstrap replicates was used. Because of the resampling required in bootstrapping, the current study analyzed 36 million data sets in total (36,000 data sets × 1,000 bootstrap replicates).⁷

To assess the relative bias of the standard errors, we generated the empirical standard errors (i.e., θ) which was the standard deviation of the point estimates per condition using a specific estimation method. Relative bias was computed using the estimated standard errors (i.e., $\hat{\theta }$) per data set, where bias = $[(\hat{\theta }-\theta )/\theta ]\times 100$ (e.g., Clarke, 2008). The relative bias of the standard errors indicated whether, on average, the expected standard errors were under- or overestimated. Underestimated standard errors result in increased Type I errors while overestimated standard errors result in increased Type II errors. Although there is no generally agreed-upon threshold of what is acceptable bias, we used a ±10% mean bias threshold for standard errors (Muthén & Muthén, 2002).

Results

Convergence Rates

Rates of nonconvergence resulting in inadmissible solutions were first assessed. Out of the 36,000 data sets simulated, only 8 in total (0.02%) had convergence problems when analyzed using MLM, most of which were in the cluster size of 10 condition. As in other studies, convergence was not an issue (B.A. Bell et al., 2014; Maas & Hox, 2005).

Level 2 Standard Errors for the Dichotomous Predictor

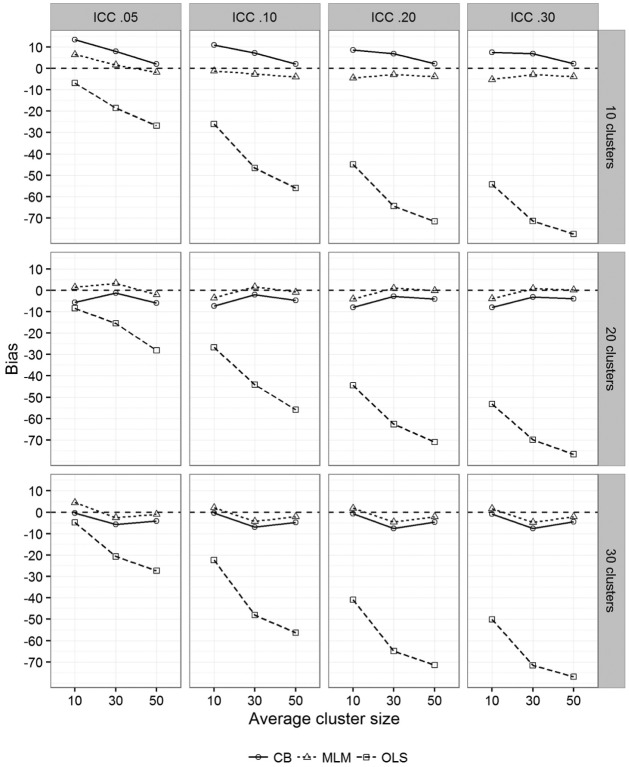
When analyzing CRTs, dichotomous predictors (e.g., treatment = 1 or 0) are often of primary interest. As expected, the Level 2 OLS standard errors (see Table 1) were consistently underestimated, even with a low ICC (i.e., .05). All OLS standard errors were underestimated, with underestimation ranging from 5% to 78%. Apart from underestimation worsening as ICCs increased, the bias worsened when the number of Level 1 units increased. This pattern is more clearly seen in Figure 1, which presents the bias in standard errors visually. In contrast, both CBSE and MLM standard errors performed well when the number of clusters was at least 20, regardless of the number of observations within each cluster and ICC. The average bias when the number of groups was at least 20 was <10% for both MLM and CBSE, regardless of ICC or cluster size.

Table 1.

Mean Bias in Level 2 Standard Errors Across Varying Simulated Conditions for Continuous and Dichotomous Predictors by Analytic Technique (1,000 Replications Each).

Number of clusters	Cluster size	ICC = .05						ICC = .10
		Continuous			Dichotomous			Continuous			Dichotomous
		OLS	MLM	CB	OLS	MLM	CB	OLS	MLM	CB	OLS	MLM	CB
10	10	−10.3	2.0	47.7	−6.8	6.5	13.3	−27.7	−4.1	43.4	−26.0	−1.3	10.9
	30	−23.3	−4.4	31.7	−18.6	1.6	7.9	−50.1	−9.0	28.7	−46.7	−2.7	7.1
	50	−27.2	−2.3	26.9	−26.8	−1.8	2.1	−56.9	−6.2	24.5	−55.9	−4.1	2.0
20	10	−10.6	−1.0	−3.7	−8.4	1.3	−5.7	−27.2	−4.3	−3.7	−26.7	−3.5	−7.4
	30	−22.5	−5.7	−5.4	−15.5	3.2	−1.3	−47.6	−5.2	−3.8	−44.2	1.6	−2.1
	50	−29.7	−4.4	−4.1	−28.0	−2.1	−6.0	−57.6	−4.9	−4.8	−55.8	−0.9	−4.7
30	10	−9.6	−0.7	−4.1	−4.7	4.6	−0.4	−26.6	−3.3	−4.6	−22.3	2.2	−0.4
	30	−17.4	1.7	−0.9	−20.7	−2.6	−5.6	−45.5	0.6	−1.4	−48.0	−4.2	−7.0
	50	−28.7	−3.1	−4.5	−27.3	−1.0	−4.1	−56.8	−3.0	−4.1	−56.3	−2.1	−4.8
Number of clusters	Cluster size	ICC = .20						ICC = .30
		Continuous			Dichotomous			Continuous			Dichotomous
		OLS	MLM	CB	OLS	MLM	CB	OLS	MLM	CB	OLS	MLM	CB
10	10	−45.4	−5.9	39.0	−44.9	−4.5	8.6	−54.3	−6.0	36.7	−54.2	−5.2	7.4
	30	−66.9	−9.7	26.7	−64.4	−3.0	6.9	−73.5	−10.0	26.0	−71.4	−2.9	6.8
	50	−72.5	−7.2	23.1	−71.6	−3.9	2.1	−78.3	−7.5	22.6	−77.5	−3.9	2.2
20	10	−44.7	−4.9	−4.1	−44.5	−4.0	−8.0	−53.4	−5.1	−4.3	−53.2	−3.9	−8.1
	30	−64.3	−4.0	−2.6	−62.6	1.0	−2.8	−71.0	−3.5	−2.2	−69.8	0.7	−3.1
	50	−72.4	−5.1	−5.2	−71.0	−0.2	−4.1	−77.9	−5.2	−5.3	−76.6	0.1	−3.9
30	10	−43.7	−2.7	−4.1	−40.9	1.9	−0.7	−52.2	−2.2	−3.6	−50.1	1.7	−0.8
	30	−63.2	0.2	−1.6	−64.9	−4.6	−7.5	−70.1	0.0	−1.7	−71.5	−4.7	−7.6
	50	−71.7	−3.0	−3.8	−71.4	−2.1	−4.6	−77.2	−3.0	−3.7	−76.9	−2.0	−4.4

Note. OLS = ordinary least squares; MLM = multilevel model estimated with restricted maximum likelihood using a Kenward–Roger (Kenward & Roger, 1997) standard error adjustment; CB = cluster bootstrapped standard errors using 1,000 replicates; ICC = intraclass correlation coefficient.

Figure 1.

Mean bias in standard errors for the Level 2 dichotomous predictor by number of clusters, cluster size, intraclass correlation coefficient (ICC), and analytic technique.Note. CB = cluster bootstrap; MLM = multilevel model estimated with restricted maximum likelihood using a Kenward–Roger (Kenward & Roger, 1997) standard error adjustment; OLS = ordinary least squares regression.

However, in two conditions when ICCs were ≤.10 and the sample size consisted of 10 clusters and an average of 10 observations per cluster, the bias of Level 2 CBSEs were on average slightly greater than 10% (see Table 1). In contrast, MLM standard errors were slightly underestimated when ICCs were >.05 but not to a large extent (i.e., mean bias < 10%). In general though, with 10 clusters, the mean bias of CBSEs were generally positive (i.e., more conservative) while the mean bias of MLM standard errors were more often negative (i.e., more liberal).

Level 2 Standard Errors for the Continuous Predictor

Mirroring with the pattern of underestimation of standard errors for the Level 2 dichotomous predictor using OLS, the OLS standard errors for the continuous Level 2 predictor were consistently underestimated for all conditions. The MLM standard error mean bias on the other hand for the continuous Level 2 predictor was no greater than 10% for any of the conditions. CBSE mean bias was acceptable when the number of clusters was at least 20 or more but showed consistently large overestimation (i.e., >20%) when the cluster size was only 10. The mean bias in CBSE though decreased as the cluster size increased.

Level 1 Standard Errors

For Level 1 standard errors, for OLS and MLM regression analyses, mean bias was never greater than 5% regardless of number of clusters, sample size, and ICC (Table 2) . The average bias over all conditions for OLS and MLM was −0.2% and 0.4%, respectively.

Table 2.

Mean Bias in Level 1 Standard Errors Across Varying Simulated Conditions by Analytic Technique (1,000 Replications Each).

Number of clusters	Cluster size	ICC = .05			ICC = .10
		OLS	MLM	CB	OLS	MLM	CB
10	10	−4.2	−2.8	−16.5	−3.4	−2.6	−16.2
	30	0.5	0.7	−12.0	0.2	0.5	−12.9
	50	1.9	2.2	−11.5	1.5	2.0	−12.5
20	10	−0.2	0.3	−6.1	−0.4	−0.3	−6.7
	30	−1.2	−1.2	−7.4	−1.8	−1.2	−8.5
	50	−1.0	−0.8	−7.0	−1.3	−0.8	−7.8
30	10	3.3	2.9	−1.4	2.8	2.2	−2.1
	30	1.2	1.0	−3.7	1.1	1.0	−4.2
	50	2.2	2.3	−1.2	1.4	2.6	−2.5
Number of clusters	Cluster size	ICC = .20			ICC = .30
		OLS	MLM	CB	OLS	MLM	CB
10	10	−2.2	−2.8	−16.3	−1.3	−2.8	−16.8
	30	−0.1	0.6	−14.8	−0.5	0.7	−16.7
	50	1.0	1.9	−14.5	0.6	1.9	−16.5
20	10	−0.5	−0.6	−7.9	−0.5	−0.7	−9.2
	30	−2.5	−1.1	−10.5	−3.0	−1.1	−12.2
	50	−1.8	−0.8	−9.4	−2.2	−0.9	−11.0
30	10	2.0	1.8	−3.7	1.4	1.7	−5.1
	30	0.7	1.0	−5.2	0.4	1.0	−6.2
	50	0.4	2.7	−4.7	−0.4	2.7	−6.6

Note. OLS = ordinary least squares; MLM = multilevel model estimated with restricted maximum likelihood using a Kenward–Roger (Kenward & Roger, 1997) standard error adjustment; CB = cluster bootstrapped standard errors using 1,000 replicates; ICC = intraclass correlation coefficient.

However, CBSE on average had consistently underestimated Level 1 standard errors for all conditions, with underestimation more pronounced when the number of clusters was low (i.e., 10). When the number of clusters was 10, CBSEs were underestimated from 12% to 17%. However, only in 3 out of the 24 other conditions (i.e., number of clusters > 10) did the underestimation of CBSEs exceed 10%.

Discussion

Revisiting Sample Size Guidelines

As seen by the simulation results, estimating MLMs using 30 or fewer clusters is not only possible but can result in models with relatively unbiased standard error estimates. As indicated by McNeish and Stapleton (2016), the popularly used 30-cluster/30-unit recommendation of Kreft (1996) is “being rendered obsolete, outdated, and inaccurate” (p. 510). This is important since the 30/30 rule is an often-cited guideline for required sample sizes for MLMs (Tonidandel et al., 2014). As indicated by Scherbaum and Ferreter (2009), “following the 30/30 rule may lead to high levels of power but is probably excessive for most organizational research” (p. 354).

The current study, as well as various recent studies, has shown that researchers may estimate unbiased MLMs with fewer than 30 clusters (B. A. Bell et al., 2014; Huang, 2016; McNeish & Stapleton, 2016) and evaluators do not necessarily require a large number of clusters for a successful CRT. Although estimates may be unbiased with a small number of clusters, CRT evaluators should perform the necessary power analyses using free and readily accessible software such as Optimal Design (Spybrook et al., 2011) or PowerUp! (N. Dong & Maynard, 2013) rather than relying on rules of thumb, prior simulations, or conventional wisdom. Also, despite unbiased results, there may be other risks associated with conducting CRTs with a small number of clusters (see Taljaard et al., 2016, for a review).

MLM With a Small Number of Clusters Should Consider REML

When the number of clusters was low (i.e., 10), the use of REML with the Kenward–Roger (1997) adjustment in MLM models is an important consideration as this results in less biased standard errors compared with an MLM estimated using ML (results were estimated but not shown using ML). This finding has been discussed in other studies and recent simulations (Hox & Kreft, 1994; Huang, 2016; McNeish & Stapleton, 2016) but should be reemphasized. In a review of 96 MLM studies (Dedrick et al., 2009), the majority of studies (84%) did not indicate the estimation method use but of those studies that did indicate what was used, only 20% used REML.

Whether to Use MLM or Cluster Bootstrapping?

In cases where a CRT is being analyzed and a Level 2 dichotomous predictor is of interest, both MLM and cluster bootstrapping can be effective in evaluating CRT data with a low number of clusters. When the number of clusters was at least 20, there was no particular advantage in evaluating group-level treatment effects using either MLM or cluster bootstrapping (see Table 1). When the number of clusters was low (i.e., 10) and ICCs were moderate to large (i.e., .10 to .30), standard errors for the Level 2 coefficient estimated using MLM were on average slightly underestimated and the CBSEs were slightly overestimated. In other words, with only 10 clusters, standard errors from MLM were slightly more liberal and CBSEs were slightly more conservative. Researchers though should keep in mind that with only 10 clusters, an intervention’s minimum detectable effect size would need to be large (i.e., ≥.80) to even have an acceptable level of power (i.e., .80).

From a practical perspective, researchers can estimate models using both techniques. If Type I errors are of primary concern, cluster bootstrapping could be used and conversely, if Type II errors are of concern, MLM can be used as well. The choice of procedure to use is not an “either/or” question when researchers can readily perform robustness checks using both methods.

For example, two recent experimental psychology studies indicated using cluster bootstrapping because of a small number of clusters (Ifcher & Zarghamee, 2014) or were worried that MLM may provide underestimated standard errors (Gehlbach et al., 2016), both concerns warranted by prior research. Studies though may use cluster bootstrapping with another analytic technique to compare results as a robustness check and provide additional support for their findings (Gehlbach et al., 2016; Ifcher & Zarghamee, 2014). Providing study results using different model specifications or alternative estimation strategies is a practice often performed by econometricians to lend further support for study findings (Huang, 2016).

However, if a continuous Level 2 predictor is of interest, simulation findings indicate that for the 10 cluster condition, CBSEs will be too conservative (i.e., standard errors will be too high). This is in contrast to Harden’s (2011) simulation using CBSEs which showed unbiased standard error estimates for cluster bootstrapping using only 10 clusters. In an earlier version of this article, which did not include a dichotomous predictor, initial results were similar to Harden’s study but changed once the dichotomous predictor at Level 2 was included.

Simulation results though clearly indicate that OLS regression, without some form of standard error adjustment such as using DEFT, should not be used to evaluate CRTs even if ICCs may be considered low (e.g., .05). The underestimation of standard errors at Level 2 is not merely a factor of the ICC but the number of observations within the cluster. As the number of observations within a cluster increases, so do the resulting design effects (see, Lai & Kwok, 2015). The underestimation of standard errors using OLS when the ICC was .05 still resulted in biased Level 2 standard errors that were not negligible and the bias only worsened when number of observations per cluster increased. At times, studies may indicate low ICCs as a reason for not accounting for the clustering effect (Heck & Thomas, 2008) but even when the ICC in the current study was .05 and the number of observations per cluster were 30 or more, Level 2 standard errors were underestimated by more than 15%.

The findings that OLS and MLM standard errors are relatively unbiased at Level 1 for a properly specified model have been shown in other simulations (Harden, 2011; Huang, 2016). However, CBSEs at Level 1 were generally underestimated, though not to a large extent and certain methodologists may not consider the bias practically meaningful (Clarke, 2008; Muthén & Muthén, 2002) except in the low number of clusters condition. In addition, with CRTs, the primary concern is the effect of the treatment condition which is randomly assigned at the group level and not at the individual level.

Some Other Bootstrapping Considerations

Although bootstrapping is generally a straightforward procedure, why is it not more commonly used? Fox (2016) provided several reasons why this may be the case: lack of familiarity, reliance on common practice, and the necessity of some form of statistical programming. Of the three reasons, the last concern may be greater than the other two. To address the need for statistical programming, a basic tutorial using the bootcov function in R, which does not require any statistical programming, is available in the online appendix. In addition, the code to perform the simulation and analysis in the article are also available upon request. Of the commercially available statistical software packages, Stata may provide the simplest way to run bootstrapped regressions with the built-in bootstrap command which also has both cluster and strata (i.e., can be used to specify treatment groups) options.

Apart from the cluster bootstrapping procedure presented in this article, other bootstrap variants are available. For example, after randomly selecting clusters with replacement, it is also possible to randomly sample within those clusters the observations with replacement as well (referred to as Strategy 2 by Davison & Hinkley, 1997, p. 100). Field and Welsh (2007) also call this a two-stage bootstrap and discuss a variety of cluster bootstrapping strategies (see also, Cameron et al., 2008). Others may skip the first stage of randomly selecting the clusters but instead include all clusters and then randomly sample with replacement observations within every cluster (Roberts & Fan, 2004).

Although we used bootstrapped estimates based on an OLS regression model, it is also possible to bootstrap the estimates derived using an MLM as well (e.g., Thai et al., 2013). For example, the lme4 package in R, which is commonly used in multilevel modeling, specifically does not provide p values for the fixed effects estimates and the developers of the package suggest, among other strategies, bootstrapping to generate the confidence intervals of the MLM point estimates (Bates et al., 2015). When bootstrapping MLMs, bootstrapped estimates of the random effects, not just fixed effects, may also be done though a prior study has shown that bootstrapped higher level random effects may be biased (Vallejo Seco et al., 2013). These other bootstrapping variations though require additional programming expertise when bootstrapping already remains “procedurally difficult for most research practitioners” (Roberts & Fan, 2004, p. 24).

In addition, accounting for missing data may be slightly more challenging if users want to use some form of multiple imputation (Y. Dong & Peng, 2013). However, an alternative procedure is to perform each regression using full information maximum likelihood (FIML), which is considered another modern way of accounting for missing data (Enders, 2010). In R, regressions using FIML may be performed using the lavaan package (Rosseel, 2012) and regression coefficients, which account for the missing data, can then be pooled to estimate the empirical standard errors.

Limitations

As with other simulations, several limitations must be kept in mind when interpreting results. First, models tested were relatively simple though conditions were varied. However, treatment and control groups in CRTs, as a result of randomization to conditions, are generally assumed to be equal on both observed and unobserved characteristics and can be evaluated using simpler statistical procedures that do not necessarily require more complicated models nor control variables if randomization was successful (Murnane & Willett, 2011). In CRTs, the primary interest generally is the treatment condition variable at Level 2 and covariates are included in CRT models in order to increase precision resulting in greater power to detect effects. In other words, even though the models simulated were relatively simple, these are models often used when evaluating CRTs. Second, we used a continuous outcome variable and results may differ if a binary outcome was investigated. Binary outcomes are more challenging to estimate using small samples and are known to experience more convergence issues (Cohen et al., 2003). Third, fully nonparametric confidence intervals can also be estimated (as well as bias corrected bootstraps, see Chernick & Labudde, 2011) though since we generated the data using normally distributed variables and wanted to allow for the comparability of standard errors across different methods, we used the standard deviation of the estimates as the empirical standard errors. However, results support the use of cluster bootstrapping as a viable alternative procedure in analyzing clustered data sets.

Conclusion

Focusing on bias and putting power issues aside (which can be computed using readily available free software instead of using rule-of-thumb guidelines), generally unbiased point estimates and standard errors can be obtained using either MLM or cluster bootstrapping. Although prior studies have suggested that MLM may not be suitable with only 10 clusters (Maas & Hox, 2005), the current study, along with more recent studies (e.g., B.A. Bell et al., 2014; Huang, 2016; McNeish & Stapleton, 2016), suggests otherwise if researchers are interested in fixed effect estimates along with their standard errors. Even though cluster bootstrapping has not seen much use in educational and psychological research, we hope that this article, together with the tutorial in the online appendix, may help applied researchers use cluster bootstrapping as an additional robustness check when dealing with clustered data.