Evaluation of Two Methods for Modeling Measurement Errors When Testing Interaction Effects With Observed Composite Scores

Abstract

Path models with observed composites based on multiple items (e.g., mean or sum score of the items) are commonly used to test interaction effects. Under this practice, researchers generally assume that the observed composites are measured without errors. In this study, we reviewed and evaluated two alternative methods within the structural equation modeling (SEM) framework, namely, the reliability-adjusted product indicator (RAPI) method and the latent moderated structural equations (LMS) method, which can both flexibly take into account measurement errors. Results showed that both these methods generally produced unbiased estimates of the interaction effects. On the other hand, the path model—without considering measurement errors—led to substantial bias and a low confidence interval coverage rate of nonzero interaction effects. Other findings and implications for future studies are discussed.

Testing interaction effects is an important and common practice in social and behavioral research, as researchers are interested in determining whether the relationship between two variables stays the same or changes depending on the level of a third variable (i.e., the moderator). In practice, both the predictor and the moderator are measured by either a single item (e.g., socioeconomic status, age, or gender) or a scale containing multiple items. For the applications of testing interaction effects with multiple-item exogenous variables, methodologists have proposed several statistical methods within the structural equation modeling (SEM) framework to test this type of interaction effects. These statistical methods are capable of modeling the latent interaction effects while simultaneously taking into account any measurement errors in the items (Jöreskog & Yang, 1996; Kenny & Judd, 1984; Klein & Moosbrugger, 2000; Klein & Muthén, 2007; Lin, Wen, Marsh, & Lin, 2010; Little, Bovaird, & Widaman, 2006; Marsh, Wen, & Hau, 2004; Moulder & Algina, 2002; Wall & Amemiya, 2001).

Despite methodological advancements in recent years, however, applied researchers still generally use observed composites (e.g., the mean or sum from a multiple-item scale) for both the predictor and the moderator when testing interaction effects. For example, a review of the articles (N = 120) published in the Journal of Applied Psychology in 2015 identified 22 (18.3%) articles testing at least one interaction effect using observed composites.¹ Of these 22 articles, only 2 corrected for the measurement errors of the exogenous variables, but in neither study did the authors consider measurement errors in the interaction terms (Eby, Butts, Hoffman, & Sauer, 2015; Mitchell, Vogel, & Folger, 2015). In the remaining 20 (90.9%) articles, all the manifest variables and the corresponding interaction effects were assumed to be measured accurately (i.e., without any measurement errors). These findings echo those of Cole and Preacher (2014), who reviewed 44 issues of seven American Psychological Association journals published in 2011, and found that more than one tenth of the studies conducted path analyses without correcting for measurement errors in the manifest variables. Thus, ignoring measurement errors of the manifest variables and the corresponding interaction effects in path analyses is still quite common. Yet, perfectly reliable manifest variables rarely exist in real data (Cohen, Cohen, West, & Aiken, 2003) and, as a result, path analyses with observed variables uncorrected for measurement errors could result in biased (either under- or overestimated) path coefficients (e.g., Aiken & West, 1991; Busemeyer & Jones, 1983; Cole & Preacher, 2014) and lead to reduced statistical power (e.g., Marsh, Wen, Nagengast, & Hau, 2012).

Given the potential problems raised by failing to properly address measurement errors when observed composites are used, in this study, two alternative methods were reviewed and evaluated: the latent moderated structural equations (LMS) method and the reliability-adjusted product indicator (RAPI) method, both of which can properly take into account measurement errors when testing interaction effects based on observed composite measures. The LMS method, developed by Klein and Moosbrugger (2000), originally focused on testing interaction effect with multiple-indicator exogenous variables. In the present study, we illustrated how to impose error variance constraints on the exogenous variables while using the LMS method to estimate interaction effects based on observed composite variables. With regard to the RAPI method, even though it can be traced back to the 1980s (Bohrnstedt & Marwell, 1978; Busemeyer & Jones, 1983), it has seldom been used in applied research.

To our knowledge, the performance of these two alternative approaches in terms of the estimation accuracy of interaction effects with observed composites has yet to be investigated. Therefore, in the present study, we compared the LMS and the RAPI methods with the commonly used path analysis approach, which assumes no measurement error for all the observed composites and the corresponding interaction effect, under conditions of varying sample sizes, reliability levels, and magnitudes of the interaction effects.

Methods for Estimating Interaction Effect With Composite Scores

As mentioned, the most common way to estimate interaction effects with observed composite scores is by using the traditional path models, assuming that all variables in the model are measurement-error free. Thus, under the traditional path model (see Figure 1), both the predictor and the moderator are presented as observed variables and are assumed to be measurement-error free. On the contrary, the distribution analytic method (see Figure 2) and the reliability-adjusted product indicator (RAPI) method (see Figure 3) can take into account the measurement errors of the exogenous variables while estimating interaction effects. A key feature of these alternative approaches is the application of a reliability adjustment of each observed composite by constraining the corresponding error variance. Below we first discuss how to impose the error-variance constraint with the use of reliability. We then present examples of applying these reliability adjustments to both LMS and RAPI methods.

Figure 1.

The path model for estimating one interaction effect with single predictor variable (X) and single moderator (M). Both X and M are composites from multiple items; XM is the product term of X and M.

Figure 2.

The latent moderated structural equations (LMS) method (Klein & Moosbrugger, 2000) for estimating one interaction effect with single predictor variable (X) and single moderator (M). Both X and M are composites from multiple items. The equations for defining the variances of ${\delta }_X$ and ${\delta }_M$ are cited from Bollen (1989).

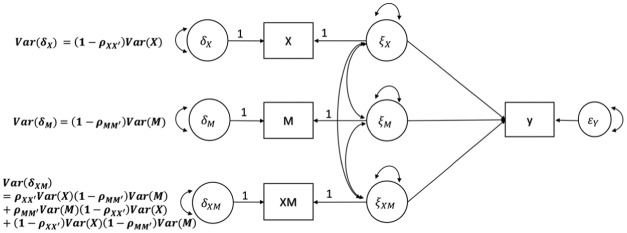
Figure 3.

The reliability adjusted product indicator (RAPI) method for estimating one interaction effect with single predictor variable (X) and single moderator (M). Both X and M are composites from multiple items; XM is the product term of X and M. The equations for defining the variances of ${\delta }_X$ and ${\delta }_M$ are cited from Bollen (1989). The proof for defining $\mathrm{Var}\left({\delta }_{\mathrm{XM}}\right)$ is described in Appendix A.

Reliability Adjustment for the Interaction Effect Between Observed Composites

In the classical testing theory (CTT) framework (Crocker & Algina, 1986; Lord & Novick, 1968), score reliability of a composite variable, X, is defined as the proportion of variance in X that can be attributed to the true score. Multiple approaches have been proposed to estimate reliability coefficients under conditions where the true-score variance cannot be directly obtained (Crocker & Algina, 1986). Among these approaches, structural equation modeling (SEM) is one of the techniques that yield more precise estimation of reliability coefficients (Raykov, 1997; Yang & Green, 2010). Let X_i be the ith observed item of a scale measuring the latent construct, ${\xi }_X$, with the measurement model written as below:

$$X_i={\tau }_X+{\lambda }_{X_i}{\xi }_X+{\delta }_{X_i},$$

where ${\tau }_X$ is the intercept, ${\lambda }_{X_i}$ is the (unstandardized) loading of the ith indicator on ${\xi }_X$, and ${\delta }_{X_i}$ is the corresponding random measurement error term. Under the SEM framework, the factor structure reliability formula for this scale is written as (Bollen, 1989; Kline, 2011; Raykov, 1997; Raykov & Shrout, 2002):

$${\rho }_{\mathrm{XX}\prime }=\frac{{(\sum {\lambda }_{X_i})}^2\mathrm{Var}\left({\xi }_X\right)}{[{(\sum {\lambda }_{X_i})}^2\mathrm{Var}\left({\xi }_X\right)+\sum \mathrm{Var}\left({\delta }_{X_i}\right)]},$$

where $\mathrm{Var}\left({\xi }_X\right)$ is the variance of the latent variable ${\xi }_X$ and $\mathrm{Var}\left({\delta }_{X_i}\right)$ represents the variance of the measurement error for the ith indicator.

If information about the individual item is unknown or unavailable (e.g., use of secondary data), one can only use the composite score, X = ΣX_i, as the single indicator for the latent variable, ${\xi }_X$. Thus, the corresponding reliability formula for X based on Equation (2) can then be rewritten as:

$${\rho }_{\mathrm{XX}\prime }=\frac{\mathrm{Var}\left({\xi }_X\right)}{[\mathrm{Var}\left({\xi }_X\right)+\mathrm{Var}\left({\delta }_X\right)]},$$

given that the only factor loading between X and ${\xi }_X$ (i.e., ${\lambda }_X$) is constrained to 1.0 for identification purpose. Hence, the latent score ${\xi }_X$ is equal to the true score in CTT (Borsboom, 2005). The error variance, $\mathrm{Var}\left({\delta }_X\right)$, can be estimated by using Equation (3), in which the reliability of a measure is the function of true-score variance and error variance as (Bollen, 1989):

$$\mathrm{Var}\left({\delta }_X\right)=(1-{\rho }_{\mathrm{XX}\prime })\mathrm{Var}\left(X\right).$$

Given the reliability coefficient, ${\rho }_{\mathrm{XX}\prime }$, the error variance of X is a function of $(1-{\rho }_{\mathrm{XX}\prime })$, which is the proportion of the variance due to measurement error in X. The true score variance, $\mathrm{Var}\left({\xi }_x\right)$, can be rewritten as a function of the reliability coefficient and the observed variance, namely,

$$\mathrm{Var}\left({\xi }_X\right)={\rho }_{\mathrm{XX}\prime }\mathrm{Var}\left(X\right).$$

Equations (4) and (5) are the key elements in specifying the error variance constraints for the interaction effects under the RAPI method. Note that the discussion is equally applicable to mean composite scores, which is simply a rescaled version of the sum composite score.

Distribution Analytic Approach

Researchers can apply the distribution analytic approach to estimate interaction effects by either the LMS method (Klein & Moosbrugger, 2000) or the quasi-maximum likelihood (QML) method (Klein & Muthén, 2007) under the SEM framework with specific data distributional assumptions. Figure 2 shows the simplest scenario in which a one-indicator predictor composite and a one-indicator moderator composite predict a single outcome. By using Equations (4) and (5) to constrain the error variances of the observed composites according to the corresponding reliability coefficient such as Cronbach’s alpha (Bollen, 1989) or factor structure reliability (Raykov, 1997), one can estimate the latent interaction effect with the observed composite scores via the distribution analytic approach, which takes into account the measurement errors for the observed composites (Figure 2).

Based on Equations (4) and (5), $\mathrm{Var}\left({\delta }_X\right)$ and $\mathrm{Var}\left({\delta }_M\right)$ can, respectively, be defined as

$$\begin{array}{c}\mathrm{Var}\left({\delta }_X\right)=(1-{\rho }_{\mathrm{XX}\prime })\mathrm{Var}\left(X\right),\hfill \\ \mathrm{Var}\left({\delta }_M\right)=(1-{\rho }_{M{M}^{\prime }})\mathrm{Var}\left(M\right),\hfill \end{array}$$

while $\mathrm{Var}\left({\xi }_X\right)$ and $\mathrm{Var}\left({\xi }_M\right)$ can be defined as

$$\begin{array}{c}\mathrm{Var}\left({\xi }_X\right)={\rho }_{\mathrm{XX}\prime }\mathrm{Var}\left(X\right),\hfill \\ \mathrm{Var}\left({\xi }_M\right)={\rho }_{\mathrm{MM}\prime }\mathrm{Var}\left(M\right).\hfill \end{array}$$

Although this is a very powerful approach, access to both the LMS and QML methods is quite limited. For example, the LMS method is exclusively built into Mplus (Muthén & Muthén, 1998-2013) whereas the QML method is a stand-alone program available only from the developer Andreas Klein (Kwok, Im, Hughes, Wehrly, & West, 2016). Additionally, the overall model chi-square test and the commonly used model fit indices (e.g., comparative fit index [CFI], root mean square error of approximation [RMSEA], and standardized root mean square residual [SRMR]) are not available in these methods.

Reliability-Adjusted Product Indicator Method

Researchers can also create a latent interaction effect factor by having the observed interaction effect term (i.e., the product of the predictor and the moderator) loaded on it (see Figure 3). Similar to the distributional analytic approach, the reliability-adjusted constraints can be directly applied to the exogenous variables (i.e., the predictor X and moderator M) under the RAPI approach, with the use of the same error-variance constraints as presented in Equations (4) and (5).

As for the observed interaction variable, XM, which is the product term of X and M, the variance of this interaction effect can be defined as the following equation (reproduced from Equation A7 in Appendix A), under the assumption of independent measurement errors and double mean-centered variables (Lin et al., 2010):

$$\begin{array}{l}\mathrm{Var}\left(XM\right)=\left[E\left({{\xi }_{XM}}^2\right)-{\left(E\left({\xi }_{XM}\right)\right)}^2\right]+E\left({{\xi }_X}^2)E({{\delta }_M}^2\right)+E\left({{\delta }_X}^2)E({{\xi }_M}^2\right)+E\left({{\delta }_X}^2)E({{\delta }_M}^2\right)\\ =\mathrm{Var}({\xi }_{XM})+\mathrm{Var}\left({\xi }_X\right)\mathrm{Var}\left({\delta }_M\right)+\mathrm{Var}\left({\xi }_M\right)\mathrm{Var}\left({\delta }_X\right)+\mathrm{Var}\left({\delta }_X\right)\mathrm{Var}\left({\delta }_M\right),\end{array}$$

The procedure to create the double mean centered variable is straightforward. First both X and M are mean-centered, then the product term of the mean-centered X and M are mean-centered. The variance of the observed interaction variable, $\mathrm{Var}\left(\mathrm{XM}\right)$, can be decomposed into (a) the true- score variance, $\mathrm{Var}({\xi }_{\mathrm{XM}})$, and (b) the error variance, $\mathrm{Var}\left({\delta }_{\mathrm{XM}}\right)$, which equals the last three components of Equation (6), or

$$\mathrm{Var}\left({\delta }_{\mathrm{XM}}\right)=\mathrm{Var}\left({\xi }_X\right)\mathrm{Var}\left({\delta }_M\right)+\mathrm{Var}\left({\xi }_M\right)\mathrm{Var}\left({\delta }_X\right)+\mathrm{Var}\left({\delta }_X\right)\mathrm{Var}\left({\delta }_M\right).$$

The corresponding derivations are described in Appendix A. Accordingly, in Equation (6), we can substitute the measurement error variances and the true-score variances of X and M with their corresponding reliability estimates and observed variances. Hence, the error variance of the latent interaction effect is (Bohrnstedt & Marwell, 1978; Busemeyer & Jones, 1983) as follows:

$$\mathrm{Var}\left({\delta }_{\mathrm{XM}}\right)={\rho }_{\mathrm{XX}\prime }\mathrm{Var}\left(X\right)(1-{\rho }_{M{M}^{\prime }})\mathrm{Var}\left(M\right)+{\rho }_{\mathrm{MM}\prime }\mathrm{Var}\left(M\right)(1-{\rho }_{\mathrm{XX}\prime })\mathrm{Var}\left(X\right)+(1-{\rho }_{\mathrm{XX}\prime })\mathrm{Var}\left(X\right)(1-{\rho }_{M{M}^{\prime }})\mathrm{Var}\left(M\right).$$

Equation (8) is the key equation to set up the nonlinear constraint for the error variance of the latent interaction effect when using the RAPI method.

Purpose of the Study

This study compared three methods of examining the interaction effects with observed composite scores to determine the estimation accuracy of the interaction effects. A Monte Carlo simulation study was conducted to compare methods with and without the consideration of measurement errors of the manifest variables. Both the LMS and RAPI methods were compared with the conventional path model. We chose the LMS method because it is currently the only distributional analytic approach that is feasible in a general SEM program (i.e., Mplus).

Method

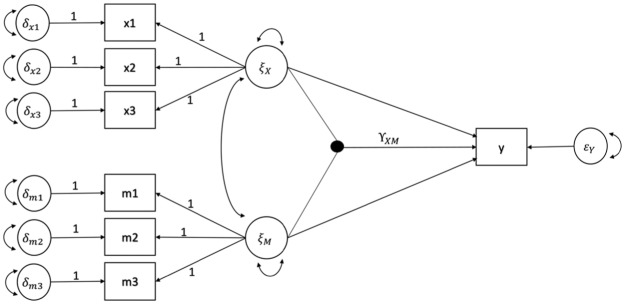
In this Monte Carlo study, we compared different methods for estimating the magnitude of the interaction effect ${\mathrm{\Upsilon }}_{\mathrm{XM}}$, with the use of the data generation model shown in Figure 4. Specifically,

Figure 4.

The pseudo population model for generating simulation data sets.

$$X_i={\tau }_{X_i}+{\lambda }_{X_i}{\xi }_X+{\delta }_{X_i},$$

$$M_i={\tau }_{M_i}+{\lambda }_{M_i}{\xi }_M+{\delta }_{M_i},$$

$$Y={\tau }_Y+{\Upsilon }_X{\xi }_X+{\Upsilon }_M{\xi }_M+{\Upsilon }_{\mathrm{XM}}{\xi }_{\mathrm{XM}}+{ϵ}_Y,$$

where $X_i=X_1,X_2,X_3$ and $M_i=M_1,M_2,M_3$ were observed indicators, as shown in Figure 4. ${\tau }_{X_i}$, ${\tau }_{M_i}$, and ${\tau }_Y$, respectively, represented the intercepts for $X_i$, $M_i$, and Y; all these intercepts were assumed to be zero. ${\lambda }_{\mathrm{Xi}}$ and ${\lambda }_{\mathrm{Mi}}$ were the factor loadings for the ith indicator on the two latent variables, ${\xi }_X$ and ${\xi }_M$, respectively. ${\delta }_{x_i}$ and ${\delta }_{m_i}$ were the unique factors of the ith indicator on $X_i$ and $M_i$, respectively. ${\xi }_{\mathrm{XM}}$ was the latent interaction variable between ${\xi }_X$ and ${\xi }_M$. Finally, ${\Upsilon }_X$, ${\Upsilon }_M$, and ${\Upsilon }_{\mathrm{XM}}$ were the path coefficients from the corresponding latent variables to the observed outcome Y, and ${\epsilon }_Y$ was the error term for Y. We chose a situation where mean composite scores were used in estimating the latent interaction effect. The results from this study are expected to be applicable to other forms of composite methods such as sum scores.

Monte Carlo Simulation Study

The model shown in Figure 4 was used to generate the population data. The two latent variables, ${\xi }_X$ and ${\xi }_M$, and the two unique factors, ${\delta }_{X_i}$ and ${\delta }_{M_i}$, were assumed to follow a standard normal distribution (i.e., mean equals to 0 and variance equals to 1.0) in the population. Both ${\xi }_X$ and ${\xi }_M$ were latent predictors with variance set at 1 and $\mathrm{Corr}({\xi }_X,{\xi }_M)=0.5$. ${\Upsilon }_X$ and ${\Upsilon }_M$ were fixed to 0.3 (Evans, 1985). $\mathrm{Var}\left({ϵ}_Y\right)$ was defined to make the variance of Y equal to 1 under the ${\Upsilon }_{\mathrm{XM}}=0$ condition. Therefore, $\mathrm{Var}\left({ϵ}_Y\right)=1-(2*{0.3}^2+2*0.5*{0.3}^2)=0.73$, indicating that the predictors as a whole explained 27% (large effect size; Cohen, 1988) of the variance in Y.

The items corresponding to ${\xi }_X$ and ${\xi }_M$ were assumed to be tau-equivalent items. Tau-equivalent items are defined as having equal loadings but possibly unequal error variance across items (Lord & Novick, 1968). Raykov (1997) showed that, if all the items (e.g., $X_i$ and $M_i$ in Figure 3 of the present study) under the common factor are tau-equivalent items, the estimated factor structure reliability equals Cronbach’s alpha coefficient (Cronbach, 1951). In the present study, both ${\lambda }_{\mathrm{Xi}}$ and ${\lambda }_{\mathrm{Mi}}$ were fixed to 1.0. In terms of error variance of the exogenous variables, based on Equation (2), the sum of the error variances for the three items for each latent factor was 3.85 and 1.00, corresponding to .70 and .90 reliability, respectively. To achieve tau-equivalent items, we varied the error variances of the three items proportionally for both ${\xi }_X$ and ${\xi }_M$. The error variance of the first item covered 55% of the total error variances in each latent predictor, followed by 33% of the second item, and 12% of the third item.² In other words, we manipulated the error variances as (2.12, 1.27, 0.46) for .70 reliability, and (0.55, 0.33, 0.12) for .90 reliability. The design factors were described below.

Sample Size, N

Based on the conditions used in past simulation studies (Cham, West, Ma, & Aiken, 2012; Chin, Marcolin, & Newsted, 2003; Lin et al., 2010; Marsh, Wen, & Hau, 2004; Maslowsky, Jager, & Hemken, 2015), we chose 100, 200, and 500 to represent small, medium, and relatively large sample sizes.

Reliability, $\mathit{\rho }$

We manipulated the reliability, $\rho$, for both X and M to be either .70 or .90. A reliability of .70 represents 49% of the total variance being the true score variance and has been viewed as the acceptable lower boundary of reliability for group comparison in clinical research. Low reliability conditions (i.e., ρ < .70) were not considered in our simulation setting.

Interaction Effect, ${\Upsilon }_{\mathrm{XM}}$

We manipulated the magnitude of the interaction effect ${\Upsilon }_{\mathrm{XM}}$ to be either 0 (no interaction effect) or 0.50. The value of zero was designed to test the methods’ performance when the null hypothesis was true (Cham et al., 2012). The value of .50 was used in a previous simulation study (cf. Chin et al., 2003).

Mplus 7.11 (Muthén & Muthén, 1998-2013) was used to generate 2,000 data sets for each condition. Given that the data were generated at the item level (i.e., three items per latent factor), we computed the mean composite scores for X and for M by averaging the corresponding items. Hence, we had three new observed composite scores; namely, the two observed composite variables X and M, and the corresponding product (or observed interaction effect) term XM. The data sets were then analyzed by fitting the three methods as shown in Figures 1, 2 and 3, respectively. For all three methods, double-centering strategy (Lin et al., 2010) was applied. Therefore, before analyzing the data using the three methods, X and M were first mean-centered; the product term XM was first computed using the mean-centered X and M and then mean-centered afterward. The annotated Mplus syntax for specifying the models with these three methods is presented in Appendix B.

Path Model

The first method tested was the conventional path model (see Figure 1), with one predictor, one moderator, and the product term predicting one outcome variable. The measurement errors of the manifest exogenous variables were assumed to be zero. The three exogenous variables were allowed to be correlated.

Latent Moderated Structural Equations Method

For the second method, the LMS method, no product indicator was created, as depicted in Figure 2. Instead, a maximum likelihood estimator with robust standard errors using numerical integration was used to estimate the latent interaction effect, based on the information of X and M. The measurement error variances for both X and M were constrained by using Equations (4) and (5). The two latent factors, ${\xi }_X$ and ${\xi }_M$, were correlated. Both the common factor loadings were fixed to 1 for model identification purpose while the factor variances were freely estimated.

Reliability-Adjusted Product Indicator Method

In the RAPI method, we utilized the reliability of each composite to constrain the corresponding measurement error. These non-linear constrains are shown in Figure 3. All the common factor loadings were fixed to 1 for model identification purposes whereas the factor variances were freely estimated. All the latent factors were allowed to be correlated.

Evaluation Criteria

Four criteria were applied to evaluate the performance of the three methods in examining the interaction effects with observed composite scores. The first two criteria, a 95% confidence interval (CI) coverage rate and the standardized bias, were used to evaluate bias—the average difference between the estimator and the true parameter. For the 95% CI coverage, the Wald interval was obtained, with a coverage rate >91% considered acceptable (Muthén & Muthén, 2002). The standardized bias was the ratio of the average raw bias over parameter standard errors. Therefore, the standardized bias can be interpreted in a standard deviation unit, like Cohen’s d. The standardized bias of the latent interaction effect estimates was compared with the cutoff value of 0.40. An absolute value <0.40 was regarded as acceptable (Collins, Schafer, & Kam, 2001).

The third criterion was the relative standard error (SE) bias of the interaction effect estimates; it was designed to evaluate the precision of the interaction estimators. Estimators with smaller relative SE bias show less variability across simulation replications. As recommended by Hoogland and Boomsma (1998), relative SE bias values <10% were considered acceptable.

Finally, the root mean square error (RMSE) was calculated to evaluate both the accuracy and precision of the parameter estimations for the three methods. The smaller the RMSE values, the more accurate the parameter estimations were across the 2,000 replications.

Results

The results of the conventional path model (without considering any measurement errors of the exogenous variables) and the models applying the RAPI and the LMS methods were compared in terms of the 95% CI coverage rate of the interaction effect, the standardized bias, relative standard error bias, and RMSE of the interaction effect estimates. The simulation results for ${\Upsilon }_{\mathrm{XM}}=0$ are displayed in Table 1 and the results for ${\Upsilon }_{\mathrm{XM}}=0.50$ are shown in Table 2.

Table 1.

95% Confidence Interval (CI) Coverage Rate, Standardized Bias, Relative Standard Error (SE) Bias, and Root Mean Square Error (RMSE) for ${\Upsilon }_{\mathrm{XM}}$ (=0).^a

N	ρ	95% CI Coverage (95%)			Standardized Bias			Relative SE Bias (%)			RMSE
		PM	RAPI	LMS	PM	RAPI	LMS	PM	RAPI	LMS	PM	RAPI	LMS
100	.70	93.7	97.0	91.5	−0.02	−0.01	−0.03	−3.69	−2.48	−9.7	0.07	0.19	0.12
	.90	94.0	94.1	91.0	−0.03	−0.03	−0.03	−4.57	−5.13	–11.13	0.08	0.10	0.10
200	.70	94.2	96.1	92.8	−0.03	−0.01	−0.03	−0.66	−2.56	−5.3	0.05	0.10	0.08
	.90	94.7	94.7	93.1	−0.03	−0.03	−0.04	−1.97	−2.21	−5.77	0.06	0.07	0.07
500	.70	94.6	94.1	93.8	−0.04	−0.03	−0.04	0.72	−0.91	−2.27	0.03	0.05	0.05
	.90	94.4	94.6	93.6	−0.04	−0.03	−0.03	−0.29	−0.49	−3.67	0.03	0.04	0.04

Note. N = sample size; ρ = reliability estimate; PM = path model; RAPI = reliability-adjusted product indicator method; LMS = latent moderated structural equations method.

^aValues exceeding the recommended cutoffs are in boldface.

Table 2.

95% Confidence Interval (CI) Coverage Rate, Standardized Bias, Relative Standard Error (SE) Bias, and Root Mean Square Error (RMSE) for ${\Upsilon }_{\mathrm{XM}}$ (=0.5).^a

N	ρ	95% CI Coverage (95%)			Standardized Bias			Relative SE Bias (%)			RMSE
		PM	RAPI	LMS	PM	RAPI	LMS	PM	RAPI	LMS	PM	RAPI	LMS
100	.70	13.4	97.1	90.0	–2.80	0.30	−0.13	–14.82	1.14	−8.58	0.24	0.33	0.14
	.90	79.2	93.7	91.4	–0.91	0.07	−0.07	−9.63	−7.73	–10.29	0.12	0.11	0.11
200	.70	0.0	97.1	93.8	–4.19	0.26	−0.12	–11.50	0.28	−1.47	0.24	0.15	0.09
	.90	67.9	93.9	94.6	–1.35	0.05	−0.06	−6.48	−5.09	−2.88	0.10	0.07	0.07
500	.70	0.0	94.8	93.4	–6.50	0.16	−0.07	–13.96	−1.38	−1.60	0.23	0.08	0.06
	.90	37.5	93.3	93.8	–2.11	0.03	−0.04	−7.65	−6.26	−2.51	0.09	0.05	0.04

Note. N = sample size; ρ = reliability estimate; PM = path model; RAPI = reliability-adjusted product-indicator method; LMS = latent moderated structural equations method.

^aValues exceeding the recommended cutoffs are in boldface.

Convergence and Inadmissible Solutions

All the simulation replications were converged without any issues. Only 12 inadmissible solutions occurred with the RAPI method under the condition of non-zero interaction effect (${\Upsilon }_{\mathrm{XM}}=0.50$), low reliability value ($\rho =.70$), and small sample size ($N=100$). All 12 (out of 2,000 replications) nonpositive definite matrices were due to the non-significant negative error variance in Y, accompanied with an inflated interaction effect ${\Upsilon }_{\mathrm{XM}}$. These 12 inadmissible solutions were excluded from the subsequent analyses. No inadmissible solution was found for either the conventional path model or the model using the LMS method.

Coverage of 95% Confidence Interval of ${\Upsilon }_{\mathrm{XM}}$

As shown in Table 1, for conditions with interaction effect (${\Upsilon }_{\mathrm{XM}}$) equal to zero, the coverage rate for the three methods were adequate, with a range from 93.7% to 94.7% for the conventional path model, from 94.1% to 97.0% for the RAPI method, and from 91.0% to 93.8% for the LMS method, regardless of sample size and the magnitude of reliability.

When the interaction effect was nonzero, the conventional path model without taking measurement errors into account generally resulted in lowest coverage rate. For example, as shown in Table 2, coverage rates were considerably low for the conventional path model, with a range from 0% to 79.2%. By comparison, under the same conditions, the coverage rates for the RAPI method continued to range from 93.3% to 97.1%. Similarly, the coverage rates for the LMS method were higher than those for the conventional path model, ranging from 90.0% to 94.6%. In other words, when the true interaction effect existed, the model that did not directly take measurement errors into account (i.e., the conventional path model) had the lowest chance of identifying the true effect.

Standardized Bias of ${\Upsilon }_{\mathrm{XM}}$

When the true interaction effect, ${\Upsilon }_{\mathrm{XM}}$, was set to zero, all three methods resulted in unbiased parameter estimates. That is, regardless of sample size and the magnitude of reliability, the standardized biases were adequate (i.e., |standardized bias| < 0.40): ranging from −0.04 to −0.02 for the path model, from −0.03 to −0.01 for the model utilizing the RAPI method, and from −0.04 to −0.03 for the model using the LMS method.

When the true interaction effect was not zero (=0.50), the standardized biases of the interaction effects differed for the three methods across simulation conditions. For the conventional path model, substantial underestimations of the interaction effects were observed, with a range from −6.50 to −0.91 across all the conditions. By contrast, interaction effects were slightly overestimated for the RAPI method. These overestimations, however, were still within the acceptable criteria across all conditions. Standardized biases were larger (ranged from 0.16 to 0.30) under the low reliability (.70) condition, compared with those (ranged from 0.03 to 0.07) under the high reliability (.90) condition when using the RAPI method. On the other hand, slightly underestimated interaction effects were found for the LMS method, with standardized biases ranging from −0.13 to −0.07 under the low reliability (.70) condition, and from −0.07 to −0.04 under the high reliability (.90) condition.

Relative Standard Error Bias of ${\Upsilon }_{\mathrm{XM}}$

As shown in Table 1, the absolute values of relative SE bias when ${\Upsilon }_{\mathrm{XM}}=0$ were all below 10% across all the simulation conditions for the conventional path model (ranged from −4.57% to 0.72%) and the model with the RAPI method (ranged from −5.13% to −0.49%). A negative SE bias indicates that the sample-estimated SE is, on average, smaller than the empirical standard error. Compared with the other two methods, the relative standard error biases were relatively higher for the LMS method. Additionally, under the high reliability (.90) and low sample size (100) conditions, the relative SE bias for the interaction effect estimates was the largest: −11.13% (i.e., underestimated by 11.13%). The relative SE biases for the other conditions from the LMS method ranged from −9.70% to −1.47%.

When ${\Upsilon }_{\mathrm{XM}}=0.50$, results of the relative SE biases varied among the three methods. As shown in Table 2, for the conventional path model, the relative SE biases were over 10% in absolute value (ranged from −14.82% to −11.50%) under the low reliability (.70) conditions regardless of sample size. The relative SE biases were below 10% in absolute value for all the conditions with high reliability (.90). For the RAPI method, all the relative SE biases were below 10% in absolute value. For the LMS method, the relative SE bias for the interaction effect estimates was −10.29% under the high reliability (.90) and small sample size (100) condition. For other conditions, the relative SE biases were all below 10% in absolute value (ranged from −8.58% to −1.47%). Although most of the SE biases for the RAPI and LMS methods were negligible, a trend of smaller SE bias in absolute value occurred for lower reliability (.70) conditions.

Root Mean Square Error in Estimating ${\Upsilon }_{\mathrm{XM}}$

Generally, the RMSE values decreased as sample size or reliability increased. Under the condition of ${\Upsilon }_{\mathrm{XM}}=0$, the RMSE values were the highest with the RAPI method (ranged from 0.04 to 0.19), followed by the LMS (ranged from 0.04 to 0.12) method and the path model (ranged from 0.03 to 0.08).

On the other hand, different RMSE patterns were observed when ${\Upsilon }_{\mathrm{XM}}=0.5$, in which the RMSEs of the PM method were overall the highest across all three methods. One exception was when the sample size was small (100) and the reliability was low (.70), here the RMSE of the parameter estimates under the RAPI methods (RMSE = 0.33) was higher than that of the path model (RMSE = 0.24). For all the other simulation conditions, the RMSEs for both RAPI and LMS methods were lower than those from the path model. Overall, the parameter estimates yielded from the LMS method were the most precise and accurate (i.e., RMSE ranged from 0.04 to 0.14) among the three methods. Finally, sample size had less influence on the RMSE values of the path model.

Discussion

Despite the existence of the SEM approach for decades, applied researchers still commonly test interaction effects with the presumably measurement error–free observed composite scores. In this study, we reviewed two alternative methods, namely, the RAPI and the LMS methods, and compared their performance with that of the conventional path model through a Monte Carlo study.

Our simulation results showed a substantial negative standardized bias and considerably low coverage rate when the conventional path model (without adequately taking into account measurement errors of the observed composites) was employed in testing interaction effect. Thus, the interaction effect under the conventional path model is more likely to be underestimated from the true population value when measurement errors are not adequately taken into account in the analysis. These findings reaffirm past research, which has shown biased results due to imperfect (reliability) measurement when testing interaction effects (Dunlap & Kemery, 1988; Evans, 1985; Feucht, 1989). Thus, the conventional path models, which do not adjust for measurement errors of the manifest predictors, are not recommended for testing interaction effects.

On the other hand, the two alternative methods discussed here, namely, the RAPI and LMS methods, can directly adjust the measurement errors of the observed composites by using either the factor structure reliability calculated from the measurement model or the conventional coefficient alpha. The major difference between these two methods is how the interaction effect is specified/captured: RAPI requires the creation of a product indicator for the latent interaction effect, whereas LMS does not. Results from the present study have shown that the RAPI method performed comparably well to the LMS method in estimating the interaction effects. Additionally, when the true interaction effects were nonzero, RAPI yielded slightly overestimated (but still acceptable) coefficients, whereas LMS yielded slightly underestimated coefficients. Hence, the LMS method may be more preferable for applied researchers who aim to be more conservative by preventing overestimated effects.

Both sample size and the magnitude of reliability played important roles in estimating the non-zero interaction effect. The standardized biases became smaller as sample size increased for both RAPI and LMS methods, suggesting that the reliability-adjusted measurement error constraints worked better with larger sample sizes. Reliability had a similar effect on standardized biases. With the same sample size, higher reliability (.90) produced more accurate interaction effect estimates than those from lower reliability (.70). Additionally, the RAPI method yielded less stable estimates than the LMS method under the low reliability and small sample size condition. Hence, the LMS method is more preferable when the exogenous variables are less reliable along with a small sample (e.g., N = 100).

Although our simulation results showed the benefits of controlling for measurement errors when testing interaction effects, this step sometimes comes at the price of increasing variability. For example, comparing four latent interaction modeling approaches, Cham et al. (2012) found that latent variable models can correct for bias but sometimes lose statistical power. When estimating the nonzero interaction effects in our simulation, the relative SE biases of the interaction effects from RAPI and LMS were higher than those from the path model under the high reliability (.90) condition. Given the reciprocal relationship between measurement error and reliability, these results suggest that constraining measurement errors for highly reliable variables may lead to over-correction, especially when the sample size is small. However, if we consider precision and bias together, the RMSE results showed that both the RAPI and LMS methods in general outperformed the conventional path model. Hence, these measurement error adjustment methods are recommended for testing interaction effects with composites, with the recognition that the RAPI method may produce less precise or less accurate estimates than the LMS method under conditions with small sample and less reliable measures.

Practically speaking, there are several situations where researchers will find both the RAPI and LMS methods more preferable than the multiple-item latent factor model in empirical data analyses. For example, if the predictors or the moderators are measured by a large number of items, fitting the hypothesized structural model at the item level may lead to convergence issues due to the complexity of the model.

Another example would be when researchers analyze secondary data and have limited or no access to the original items. As mentioned earlier, the factor structure reliability in SEM is comparable to the conventional internal consistency reliability (i.e., Cronbach’s alpha or coefficient alpha) with tau-equivalent items (i.e., items with equal factor loadings and possibly unequal error variances). Hence, as long as the reliability information of the composites is available, we advocate the use of this information to constrain the error variances for the observed composites and conducting the analyses with either the RAPI or LMS method to obtain interaction effect estimates.

Limitations and Future Research Directions

Two limitations in the present study must be addressed. First, since the interaction effect is the product term of the predictor and moderator, having a low reliability on either or both variables can amplify the measurement error of the interaction effect (Aiken & West, 1991). It is, therefore, worth investigating how changes in the reliability of the interaction term influence the interaction effect estimation. Second, the scope of this study was the traditional single-level interaction effect. Future study is needed to investigate the impact of ignoring measurement errors when testing interaction effect with observed composites under more complex data structures, such as multilevel data.

Conclusions

When examining an interaction effect based on the observed composite scores without properly taking measurement errors into account, the result may be a considerable underestimation in the interaction effect. Thus, we encourage researchers to apply either the LMS or the RAPI method, which can directly take into account the measurement errors in the manifest variables. For researchers who have very limited access to SEM programs, the RAPI model is by far the most feasible way (i.e., can be implemented in most of the SEM programs) to generate unbiased interaction estimates. Moreover, the overall model chi-square test and other commonly used model-fit indices are only available for the RAPI method. On the other hand, the LMS method produces relatively more conservative interaction effect estimates. Additionally, for those who have small data sets (with low sample sizes) or less reliable measures, the LMS method would be more preferable.

Appendix A

Error Variance of the Latent Interaction Effect

The following is a summary of the derivation based on Bohrnstedt and Marwell (1978) and Busemeyer and Jones (1983). Let X (predictor) and M (moderator) be observable random variables with true scores ${\xi }_X$ and ${\xi }_M$ and error random variables ${\delta }_X$ and ${\delta }_M$. We assume the following measurement models for X and M, respectively:

$$X={\tau }_X+{\lambda }_X{\xi }_X+{\delta }_X,$$

$$M={\tau }_M+{\lambda }_M{\xi }_M+{\delta }_M.$$

Both X and M are mean-centered variables so that $E\left(X\right)=E\left(M\right)=0$. For identification purpose, both $E\left({\xi }_X\right)$ and $E\left({\xi }_M\right)$ are fixed to zero. Thus, the two intercepts, ${\tau }_X$ and ${\tau }_M$, would be equal to zero. ${\lambda }_X$ and ${\lambda }_M$ are factor loadings that are constrained to one for identification purpose; these constraints allow the observed variables and the true scores to share the same metric. ${\delta }_X$ and ${\delta }_M$ are assumed to be independent from each other as well as independent from ${\xi }_x$ and ${\xi }_M$, with $E\left({\delta }_X\right)=E\left({\delta }_M\right)=0$. The variance of ${\xi }_X$ is defined as:

$$\mathrm{Var}\left({\xi }_X\right)=E\left({{\xi }_X}^2\right)-{\left(E\left({\xi }_X\right)\right)}^2=E\left({{\xi }_X}^2\right),$$

and the variances of ${\xi }_M$, ${\delta }_X$, and ${\delta }_M$ can all be, respectively, found using the definition in Equation (A3): $\mathrm{Var}\left({\xi }_M\right)=E\left({{\xi }_M}^2\right)$, $\mathrm{Var}\left({\delta }_X\right)=E\left({{\delta }_X}^2\right)$, and $\mathrm{Var}\left({\delta }_M\right)=E\left({{\delta }_M}^2\right)$.

The observed interaction variable, XM, is defined as the product term of the two observed composite variables X and M. The corresponding latent true score of XM, ${\xi }_{\mathrm{XM}}$ is defined as the product term of ${\xi }_X$ and ${\xi }_M$, so ${\xi }_{\mathrm{XM}}={\xi }_X{\xi }_M$. As Lin et al. (2010) pointed out, the use of double-mean-centering strategy can produce more accurate results when estimating latent interaction effect. Therefore, we adopted the double-mean-centering strategy; XM is also a mean-centered variable. The variance of this observed interaction variable XM is defined as:

$$\mathrm{Var}\left(\mathrm{XM}\right)=E\left(X^2{M}^2\right)-{\left(E\left(\mathrm{XM}\right)\right)}^2,$$

in which,

$$\begin{array}{c}E\left(X^2{M}^2\right)=E\left({({\xi }_X+{\delta }_X)}^2{({\xi }_M+{\delta }_M)}^2\right)\hfill \\ =E\left(({{\xi }_X}^2+2{\xi }_X{\delta }_X+{{\delta }_X}^2)({{\xi }_M}^2+2{\xi }_M{\delta }_M+{{\delta }_M}^2)\right)\hfill \\ =E\left({{\xi }_X}^2{{\xi }_M}^2\right)+E\left({{\xi }_X}^2{{\delta }_M}^2\right)+E\left({{\delta }_X}^2{{\xi }_M}^2\right)+E\left({{\delta }_X}^2{{\delta }_M}^2\right)\hfill \\ +2E\left({\delta }_M\right)E\left({{\xi }_X}^2{\xi }_M\right)+2E({\delta }_X)E({\xi }_X{{\xi }_M}^2)+2E\left({\delta }_X\right)E\left({\xi }_X{{\delta }_M}^2\right)+2E({\delta }_M)E\left({\xi }_M{{\delta }_X}^2\right)\hfill \\ +4E\left({\delta }_X\right)E\left({\xi }_X{\xi }_M{\delta }_M\right)\hfill \\ =E\left({{\xi }_{\mathrm{XM}}}^2\right)+E({{\xi }_X}^2)E({{\delta }_M}^2)+E({{\delta }_X}^2)E({{\xi }_M}^2)+E({{\delta }_X}^2)E({{\delta }_M}^2)+0+0+0+0+0\hfill \end{array},$$

and

$$\begin{array}{c}{\left(E\left(\mathrm{XM}\right)\right)}^2={\left(E\left(({\xi }_X+{\delta }_X)({\xi }_M+{\delta }_M)\right)\right)}^2\hfill \\ ={(E({\xi }_X{\xi }_M)+E({\xi }_M{\delta }_X)+E({\xi }_X{\delta }_M)+E({\delta }_X{\delta }_M))}^2\hfill \\ ={(E\left({\xi }_{\mathrm{XM}}\right)+0+0+0)}^2\hfill \end{array}.$$

In Bohrnstedt and Marwell (1978) and Busemeyer and Jones (1983), the derivations of both Equations (A5) and (A6) are based on the assumptions of bivariate normality in X and M. However, when applying the double-mean-centering strategy (Lin et al., 2010), Equations (A5) and (A6) may be derived without any distribution assumption on X and M (other than the assumption that the variances of ${\xi }_X$, ${\xi }_M$, ${\delta }_X$, and ${\delta }_M$ are finite). When substituting Equations (A5) and (A6) back into Equation (A4), we get

$$\begin{array}{l}\mathrm{Var}\left(XM\right)=\left[E\left({{\xi }_{XM}}^2\right)-{\left(E\left({\xi }_{XM}\right)\right)}^2\right]+E\left({{\xi }_X}^2)E({{\delta }_M}^2\right)+E\left({{\delta }_X}^2)E({{\xi }_M}^2\right)+E\left({{\delta }_X}^2)E({{\delta }_M}^2\right)\\ =\mathrm{Var}({\xi }_{XM})+\mathrm{Var}\left({\xi }_X\right)\mathrm{Var}\left({\delta }_M\right)+\mathrm{Var}\left({\xi }_M\right)\mathrm{Var}\left({\delta }_X\right)+\mathrm{Var}\left({\delta }_X\right)\mathrm{Var}\left({\delta }_M\right).\end{array}$$

Appendix B

Mplus Syntax of the Path Model, the Latent Moderated Structural Equations (LMS) Method, and the Reliability Adjusted Product Indicator (RAPI) Method

B1: Path Model

TITLE:

Estimate interaction effect with the path model

DATA:

File=exrep1996.dat;

VARIABLE:

Names = y xc mc;

Usevariables=y xc mc xm;

!xc and mc are the mean-centered composites;

!The creation of xc and mc should be conducted outside the Mplus program;

DEFINE:

!xm is the product term of xc and mc;

!grand mean center strategy apply to xm;

xm=xc*mc;

center xm (grandmean);

ANALYSIS:

MODEL:

y ON xc mc xm;

OUTPUT:

STDYX;

B2: Latent Moderated Structural Equations (LMS) Method.

TITLE:

Estimate interaction effect with the

latent moderated structural equations (LMS) method

DATA:

File=exrep1996.dat;

VARIABLE:

Names = y xc mc;

Usevariables=y xc mc;

!xc and mc are the mean-centered composites;

!The creation of xc and mc should be conducted outside the Mplus program;

ANALYSIS:

Type=Random;

Algorithm=integration;

MODEL:

fx BY xc;

fm BY mc;

!Mplus default function for LMS method;

fxm | fx xwith fm;

y ON fx fm fxm;

!give labels for latent factor variance;

fx (vxc);

fm (vmc);

!give labels for error variance;

xc (v_exc);

mc (v_emc);

Model Constraint:

! define v_ox and v_om to be the sum of the latent factor variance and error variance, or the total variance;

new (v_ox v_om);

v_ox = vxc + v_exc;

v_om = vmc + v_emc;

!define the error variance to be the function of reliability and total variance

!in this example, reliability is assumed to be .7;

v_exc = v_ox*(1-.7);

v_emc = v_om*(1-.7);

OUTPUT:

STDYX;

B3: Reliability-Adjusted Product Indicator (RAPI) Method

TITLE:

Estimate interaction effect with the

reliability-adjusted product indicator (RAPI) method

DATA:

File=exrep1996.dat;

VARIABLE:

Names = y xc mc;

Usevariables=y xc mc xm;

!xc and mc are the mean-centered composites;

!The creation of xc and mc should be conducted outside the Mplus program;

DEFINE:

!xm is the product term of xc and mc;

!grand mean center strategy apply to xm;

xm=xc*mc;

center xm (grandmean);

MODEL:

!specify the model as shown in Figure 3;

fx BY xc;

fm BY mc;

fxm BY xm;

y ON fx fm fxm;

!give labels for latent factor variance;

fx (vxc);

fm (vmc);

fxm (vxm);

!give labels for error variance;

xc (v_exc);

mc (v_emc);

xm (v_exm);

Model Constraint:

! define v_ox, v_om, and v_oxm to be the sum of the latent factor variance and error variance, or the total variance;

new (v_ox v_om v_oxm);

v_ox = vxc + v_exc;

v_om = vmc + v_emc;

v_oxm = vxm + v_exm;

!define the error variance to be the function of reliability and total variance

!in this example, reliability is assumed to be .7;

v_exc = v_ox*(1-.7);

v_emc = v_om*(1-.7);

v_exm = v_ox*.7*v_om*(1-.7)+ v_om*.7*v_ox*(1-.7)

+v_ox*(1-.7)*v_om*(1-.7);

OUTPUT:

STDYX;