Cluster signal-to-noise analysis for evaluation of the information content in an image

Abstract

Objectives:

(1) To develop an observer-free method of analysing image quality related to the observer performance in the detection task and (2) to analyse observer behaviour patterns in the detection of small mass changes in cone-beam CT images.

Methods:

13 observers detected holes in a Teflon phantom in cone-beam CT images. Using the same images, we developed a new method, cluster signal-to-noise analysis, to detect the holes by applying various cut-off values using ImageJ and reconstructing cluster signal-to-noise curves. We then evaluated the correlation between cluster signal-to-noise analysis and the observer performance test. We measured the background noise in each image to evaluate the relationship with false positive rates (FPRs) of the observers. Correlations between mean FPRs and intra- and interobserver variations were also evaluated. Moreover, we calculated true positive rates (TPRs) and accuracies from background noise and evaluated their correlations with TPRs from observers.

Results:

Cluster signal-to-noise curves were derived in cluster signal-to-noise analysis. They yield the detection of signals (true holes) related to noise (false holes). This method correlated highly with the observer performance test (R² = 0.9296). In noisy images, increasing background noise resulted in higher FPRs and larger intra- and interobserver variations. TPRs and accuracies calculated from background noise had high correlation with actual TPRs from observers; R² was 0.9244 and 0.9338, respectively.

Conclusions:

Cluster signal-to-noise analysis can simulate the detection performance of observers and thus replace the observer performance test in the evaluation of image quality. Erroneous decision-making increased with increasing background noise.

INTRODUCTION

The image quality of cone-beam CT (CBCT) images can be evaluated by taking one of two approaches. One approach is physical evaluation based on the analysis of physical parameters, such as spatial resolution, contrast and noise.^1–3 The other is to conduct an observer performance test, such as a detection task for a low-contrast signal against a noisy background.^1,4 These two approaches have their inherent merits and demerits. Physical evaluation allows the quantitative comparison of efficiency between different imaging systems^2,3,5 and is considered to be a part of quality control,^3,6,7 but it cannot be directly applied to a clinical evaluation because it does not include observer performance measures, such as detectability, or perception information.^1,8 However, observers’ data have their own inherent uncertainty. A sufficient number of observers is required to make the data more reliable, resulting in a time-consuming and elaborate procedure.^9,10

It can be expected that a combination of the two approaches will yield further merits and reduce demerits. It may be less time consuming and more reliable if a new method excluding observers can be developed to simulate observer performance. Takeshita et al¹¹ introduced a new observer-free method of evaluating image quality. However, they used a limited number of threshold gray values. The use of more threshold or cut-off values might allow the simulation of observer performance.

Because a large and flat object seems to have no appreciable effect on the perception of mass changes, the modulation transfer function of the system and spatial frequency of the object can be neglected.^8,10 Thus, physical evaluation regarding contrast and noise, and the observer performance test regarding the detectability of low contrast against a noisy background were concomitantly evaluated in the present study.

The aims of the present study were (1) to develop an observer-free method of analysing image quality related to the observer performance in a detection task using CBCT images and (2) to analyse observer behaviour patterns in the detection of small mass changes in CBCT images with this method.

METHODS AND MATERIALS

Test object

A Teflon (polytetrafluoroethylene) plate phantom of 1-mm thickness simulating bone¹¹ was used in this study (Figure 1a). The phantom contained 84 holes that are arranged in 7 rows by 12 columns. The diameter of each hole was 1 mm. The depth of the seven holes in each column decreased from 0.7 to 0.1 mm from top to bottom. Each row had intervals of 0.5 mm and each column had intervals of 1 mm.

Figure 1.

Teflon phantom with holes of decreasing depth (a) attached to a half mandible and immersed in water (b).

The phantom was attached to the molar region of a half mandible and immersed in water to simulate clinical conditions (Figure 1b).

Image acquisition

We placed the phantom perpendicular to the X-ray beam direction. Its centre was positioned at the intersection of positioning light beams, such that the phantom was at the centre of the field of view. The purpose was to minimize image distortion. Afterward, CBCT images were obtained using the Dental (D) mode of a CB MercuRay (Hitachi Medical Corporation, Japan).¹² The field of view was a cube having length of 51.2 mm. The voxel length was 0.1 mm. Images were scanned with a full 360° rotation. The exposure parameters were set at 15 mA, four different tube voltages (60, 80, 100 and 120 kV) and 9.6 s.

Image preparation

We received all images from Takeshita’s study.¹¹ The images were prepared in that study as follows. All CBCT image series in axial planes were reconstructed onto new planes that were parallel to the surface of the phantom. They were then cropped to cover the phantom. Two types of CBCT images were prepared for the observer performance test. One type was serial images and the other was superimposed images (Figure 2a,b). For analysis using the newly developed method, the background was subtracted from all superimposed images (Figure 2c) so that the intensities of the images were suitable for analysis with the FindFoci plugin of ImageJ.

Figure 2.

An example of a serial image (a), superimposed image at thickness of 0.3 mm (b) and superimposed image with background subtraction (c).

There were four sets of serial images, corresponding to the four tube voltages of 120, 100, 80 and 60 kV. Each set comprised contiguous slices that covered the entire thickness of the Teflon phantom. These serial images allowed observers to scroll through the series before scoring the number of detected holes.

The superimposed images were overlaid images that could not be scrolled. In this study, they were reconstructed by merging 1 (no superimposition), 3, 5, 7 and 10 contiguous slices from the surface with holes. The slice thicknesses of the images were therefore 0.1, 0.3, 0.5, 0.7 and 1.0 mm, respectively. When the slices were merged, their image intensities were automatically adjusted by averaging the intensity within merging voxels for a given thickness. These five slice thicknesses were reconstructed for each tube voltage, and there were thus 20 sets of superimposed images.

Observers

13 observers, who were oral and maxillofacial radiologists, were asked to score the number of detected holes in the two types of CBCT images: four sets of serial images and 20 sets of superimposed images. The observation was performed under dim lighting.

Analysis

Relationship between superimposed images and serial images

The following procedures were performed to evaluate the correlation between superimposed images and serial images and to determine the optimum superimposed thickness.

13 observers scored the number of detected holes for all images of the two types. The true positive rate (TPR) was then calculated by dividing the number of detected holes by the total number of true holes (84 holes):

$$TPR=\frac{Numberofdetectedholes}{Totalnumberoftrueholes}$$

For each slice thickness of superimposed images, the correlation between superimposed images and serial images was analysed. The slice thickness that had the highest correlation was chosen as the optimum superimposition thickness.

Table 1 gives average TPRs of 13 observers for superimposed images at four different tube voltages and five different slice thicknesses, and for serial images at four different tube voltages. The highest correlation (R² = 0.91353) was found between superimposed images with a 0.3 mm slice thickness and serial images. The optimum superimposed thickness was thus 0.3 mm.

Table 1.

True positive rates (TPRs) of superimposed images and serial images

Tube voltage (kV)	Superimposed images					Serial images
Thickness
1 mm	0.7 mm	0.5 mm	0.3 mm	0.1 mm
120 kV	0.848	0.862	0.870	0.890	0.907	0.904
100 kV	0.817	0.885	0.890	0.902	0.900	0.907
80 kV	0.763	0.832	0.862	0.856	0.870	0.880
60 kV	0.508	0.519	0.566	0.543	0.470	0.553

Differences among used tube voltages were statistically significant (p ≤ 0.0001), except for differences between 120 and 100 kV (p = 0.6383), in the case of superimposed images, while statistically significant differences were only observed against 60 kV at 120, 100, and 80 kV (p ≤ 0.0001), in the case of serial images.

Cluster signal-to-noise analysis

A new method, which is called cluster signal-to-noise analysis and evaluates the image quality related to the observer performance task, was performed according to the following procedures.

20 superimposed images were analysed using the FindFoci plugin,¹³ which allows the identification of holes within an image by applying a cut-off value or threshold gray value (ΔG) as a background parameter and setting the minimum size of the detected hole. A search is made within pixels that have intensity greater than or equal to the cut-off value. Pixels that have intensity higher than that of surrounding pixels are identified as potential peaks. If an area that consists of a potential peak and its surrounding pixels is larger than or equal to the minimum size of the detected hole, it is identified as a hole.

For each image, the cut-off values were varied among at least 20 numbers such that there was enough data to plot a graph. The cut-off values were determined as follows:

• Cut-off values included all one-digit numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9.

• A cut-off value that produces no false positives (FPs).

  For example, in condition 1, we applied a cut-off value of 45 in the FindFoci plugin and there were 10 FPs and 40 true positives (TPs), while in condition 2, we applied a cut-off value of 50 in the FindFoci plugin and there were no FPs and 35 TPs; we thus choose condition 2 (with a cut-off value of 50).

• Cut-off values are obtained from an arithmetic sequence.

  (3.1) Find the cut-off value that produces both zero FPs and zero TPs and define it as the minimum ΔG (min ΔG). For example, in condition 1, we applied a cut-off value of 50 in the FindFoci plugin and there were no FPs and 35 TPs, while in condition 2, we applied a cut-off value of 70 in the FindFoci plugin and there were no FPs or TPs; we thus choose condition 2 (with a cut-off value of 70 to be min ΔG).

  (3.2) The common difference (d), a constant difference or an interval between two numbers, is then calculated by the following equation:

$$d=\left(\frac{min\mathrm{\Delta }G-1}{10}\right)$$

(3.3) d is rounded up to the nearest integer.

(3.4) The cut-off values are then calculated from the arithmetic sequence:

$${\displaystyle a_n=a_1+\left(n-1\right)d}$$

where a_n is the nth term of the sequence (i.e. the cut-off value in this study), a₁ is the first term of the sequence and is equal to 1, and n is the number of terms to find. In this study, n ranged from 1 to 11. d is the common difference. If the value of the 11th term exceeds the minimum ΔG value, it is changed to the minimum ΔG.

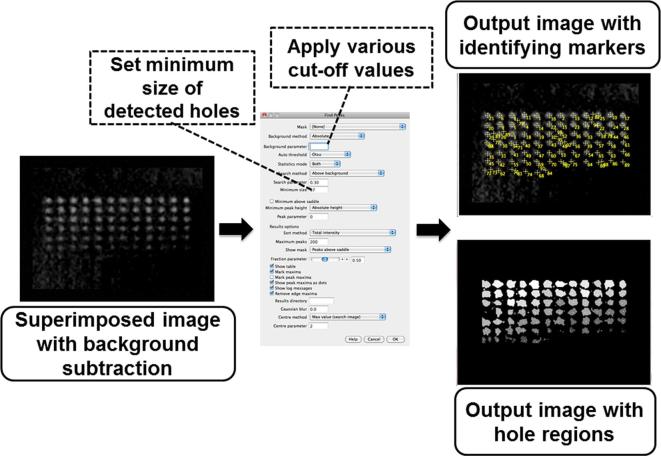
We applied all cut-off values for each image and set the minimum size of a detected hole at 0.3 mm² in the FindFoci plugin of ImageJ to reconstruct the new images for counting holes (Figure 3). For each image, the holes were counted and the data were put into two categories: TPs and FPs. TPs are the true holes detected (i.e. signal) while FPs are the false holes detected (i.e. noise) (Figure 4).

Figure 3.

How to find holes within an image. The FindFoci plugin of ImageJ was used to find holes within a superimposed image. A cut-off value was applied as a background parameter and the minimum size of detected holes was set as 0.3 mm² in the dialog box. After image processing, two output images were obtained. One had identifying markers that indicate the potential peak of holes and the other showed hole regions.

Figure 4.

Categories of detected holes: true positive and false positive.

The total number of true holes was 84. The total number of false holes was calculated as 208 from the analysing area where there were no true holes using the following equation:

$$\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{a}\mathrm{l}\mathrm{s}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{s}=\frac{\mathrm{W}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{o}\mathrm{f}\mathrm{a}\mathrm{n}\mathrm{a}\mathrm{l}\mathrm{y}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}-\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{o}\mathrm{f}84\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{e}\mathrm{s}}{\mathrm{A}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{o}\mathrm{f}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{e}},$$

where the analysing area had the dimensions 23 × 10 mm =230 mm², the area of one hole is πr² = 3.14 × (0.5 mm)² = 0.785 and the area of 84 holes is 0.785 × 84 = 65.94 mm².

The TPR was calculated by dividing the number of TPs by the total number of true holes (84) and the false positive rate (FPR) was calculated by dividing the number of FPs by the total number of false holes (208). TPR values were then plotted against FPR values to construct a cluster signal-to-noise curve in Microsoft Excel.

After varying the cut-off values applied in the FindFoci plugin and categorizing types of detected holes (Figure 7), cluster signal-to-noise curves were derived (Figure 8) to detect the true hole contours (signals) together with noise. It is implied that there was poor discrimination between the signal and noise at 60 kV as the curve at a low FPR made an angle with the vertical axis. Better discrimination was found for 120 and 100 kV as the curves at a low FPR ascended along or nearly along the vertical axis. The maximum TPR was highest at 120 kV, followed by 100 and 80 kV. The TPR at 60 kV was lower than TPRs at other tube voltages.

Figure 7.

An example of the numbers of true positives and false positives after applying various cut-off values.

Figure 8.

Cluster signal-to-noise curves at the optimum superimposed thickness for four tube voltages. Maximum true positive rates (TPRs) of each tube voltage were found at low false positive rates; the maximum TPR was highest at 120 kV, followed by 100 and 80 kV. The maximum TPR was lowest at 60 kV.

Relationship among cluster signal-to-noise analysis, Takeshita’s method11 and observer performance

In cluster signal-to-noise analysis, FPRs of observers corresponding to the detected signals (TPRs) were obtained using cluster signal-to-noise curves and observers’ data. First, each detected signal from observers’ data was converted into the corresponding FPR one by one using cluster signal-to-noise curves as conversion graphs. The detected signal values that exceeded the curves were not converted. Afterward, the mean FPR for each image was obtained by averaging the corresponding FPRs within one superimposed image, and all mean FPRs were then averaged again to obtain the mean FPR of all images. Using this mean FPR of all images, TPRs were recalculated for each tube voltage and superimposed thickness using cluster signal-to-noise curves (Figure 5). If the mean FPR of all images exceeded the curve, the maximum TPR of that curve was used as the calculated TPR instead of recalculating.

Figure 5.

Calculation of false positive rates (FPRs) and true positive rates (TPRs) corresponding to the observers’ data. First, FPRs were converted from observers’ data or TPRs using cluster signal-to-noise curves as a conversion graph (see the direction of the gray arrow in the upper graph). These FPRs were then averaged to be the mean FPR of all images. Similar to the calculation of FPRs corresponding to observers’ data, TPRs were recalculated from the mean FPR of all images using cluster signal-to-noise curves as a conversion graph (see the direction of the gray arrow in the lower graph).

In Takeshita’s method,¹¹ cut-off values (ΔG) are determined for each column of holes in the image. These 12 cut-off values were applied in the FindFoci plugin of ImageJ in the same way as for cluster signal-to-noise analysis. However, in contrast to the case of cluster signal-to-noise analysis that all holes were counted for each cut-off value, the holes of each column were counted when its own cut-off value was applied in the FindFoci plugin. For example, if the cut-off values for the first and second columns were 11 and 9, respectively, the number of holes in the first column would be counted when a cut-off value of 11 was applied in the FindFoci plugin and the number of holes in the second column would be counted when a cut-off value of 9 was used. TPs from each column were then summed and the TPR was calculated.

Correlation between calculated TPRs from cluster signal-to-noise analysis and actual TPRs from observation (detected signals) was analysed. Correlation between calculated TPRs from Takeshita’s method¹¹ and actual TPRs from observation was also evaluated.

Table 2 gives an example of corresponding FPRs converted from detected signals at a slice thickness of 0.3 mm. The mean FPRs of all images for the calculation of TPRs was 0.072. Correlation of the calculated TPRs to observer performance data obtained by cluster signal-to-noise analysis was higher (R² = 0.9296) than that obtained by Takeshita’s method¹¹ (R² = 0.7926) (Figure 9a,b).

Table 2.

An example of detected signals (TPRs) and corresponding FPRs at a slice thickness of 0.3 mm

Observer	120 kV		100 kV		80 kV		60 kV
TPR	Corresponding FPR	TPR	Corresponding FPR	TPR	Corresponding FPR	TPR	Corresponding FPR
1	0.905	0.094	0.905	0.077	0.857	0.067	0.548	0.075
2	0.881	0.077	0.893	0.063	0.857	0.067	0.464	0.049
3	0.881	0.077	0.869	0.045	0.857	0.067	0.560	0.077
4	0.881	0.077	0.917	0.101	0.857	0.067	0.583	0.079
5	0.881	0.077	0.917	0.101	0.857	0.067	0.464	0.049
6	0.917	0.102	0.905	0.077	0.857	0.067	0.524	0.070
7	0.881	0.077	0.869	0.045	0.845	0.067	0.500	0.053
8	0.893	0.086	0.869	0.045	0.857	0.067	0.560	0.077
9	0.881	0.077	0.881	0.054	0.857	0.067	0.476	0.050
10	0.893	0.086	0.905	0.077	0.833	0.067	0.643	0.137
11	0.881	0.077	0.905	0.077	0.857	0.067	0.417	0.035
12	0.905	0.094	0.952		0.869		0.631	0.125
13	0.893	0.086	0.940	0.135	0.869		0.690	0.184
Mean	0.890	0.084	0.902	0.075	0.856	0.067	0.543	0.082
SD	0.012	0.008	0.026	0.027	0.009	0.000	0.080	0.042

FPR, false positive rate; TPR, true positive rate.

Figure 9.

Correlation between calculated true positive rates (TPRs) from cluster signal-to-noise curves and TPRs from 13 observers (a) and correlation between calculated TPRs obtained from Takeshita’s method and TPRs from 13 observers (b). Calculated TPRs obtained from cluster signal-to-noise curves had higher correlation (R² = 0.9296) with TPRs from observers than those obtained from Takeshita’s method (R² = 0.7926).

Observer behaviour patterns for the detection of small mass changes in CBCT images

The relationship between background noise and the observers’ decision levels for detection (mean FPRs) and relationships between the levels (mean FPRs) and intra- and inter-observer variations were evaluated.

First, the background noise of an image was obtained by averaging 12 standard deviations (SDs) of background intensities that were measured on each column of holes with a rectangular (0.8 × 3 mm) region of interest. Mean FPRs of observers in each image were then plotted against background noise. A linear regression equation and R² value were obtained.

The intraobserver variation was the SD of detection (SD of FPRs) within one observer. The inter-observer variation was the SD of detection among observers within one image. These SDs were plotted against their mean FPRs. A linear regression equation and R² value were obtained.

There was not strong but meaningful correlation between background noise and mean FPRs from observers. Mean FPRs increased as the background noise increased; the linear regression equation was y = 0.0052x, where y is the mean FPR of the observers and x is background noise (Figure 10). In addition, correlations were found between mean FPRs and intra- and interobserver variations. The two correlations were similar. The graphs show that intra- and interobserver variations increased with an increasing mean FPR, with the slopes of linear regression equation being 0.3825 and 0.3786, respectively (Figure 11a,b).

Figure 10.

Correlation between background noise and mean false positive rates from observers. The linear regression equation was y = 0.0052x, where y is the mean false positive rate of the observers and x is background noise.

Figure 11.

Correlation between mean false positive rates and intraobserver variation (a) and interobserver variation (b). Mean false positive rates had positive correlation with intra- and interobserver variations; slopes of linear regression equations were 0.3825 and 0.3786, respectively.

Relationship between calculated TPRs from background noise and actual TPRs from observers

From the linear regression equation of the correlation between background noise and the mean FPR, new mean FPRs were calculated from the background noise of each image. TPRs were then calculated from these new mean FPRs using cluster signal-to-noise curves as conversion graphs (Figure 6). Afterward, correlation between TPRs calculated from background noise and TPRs from 13 observers was analysed.

Figure 6.

Calculation of true positive rates from background noise. The background noise of each image was first obtained by measuring standard deviations within 12 regions of interest and averaging them. Mean false positive rates (FPRs) were then calculated from background noise using the linear regression equation of correlation between background noise and FPRs. Afterward, FPRs were converted into true positive rates using cluster signal-to-noise curves.

Calculated TPRs from background noise had high correlation with actual TPRs from 13 observers; R² was 0.9244 (Figure 12a). In the analysis of statistical differences among used tube voltages based on TPRs from background noise, overlaps of 95% CIs were found between 120 and 100 kV and between 120 and 80 kV. Differences among the used tube voltages were thus statistically significant, except for the difference between 120 and 100 kV and the difference between 120 and 80 kV.

Figure 12.

Correlation between calculated true positive rates (TPRs) from background noise and TPRs from 13 observers (a) and correlation between calculated accuracies from background noise and TPRs from 13 observers (b). Both calculated TPRs and accuracies from background noise had strong correlation with TPRs from observers; R² was 0.9244 and 0.9338, respectively.

Relationship between accuracies from background noise and actual TPRs from observers

We used both FPRs and TPRs calculated from background noise to calculate accuracies. As we postulated that the data were unbiased, the accuracy can be expressed as the following equation:¹⁴

$${\displaystyle Accuracy=\frac{TPR+1-FPR}{2}}$$

Correlation between accuracies from background noise and TPRs from 13 observers were then analysed.

Accuracies from background noise had high correlation with actual TPRs from 13 observers; R² was 0.9338 (Figure 12b). In the analysis of statistical differences among used tube voltages based on accuracies from background noise, no overlap of 95% CIs was found. There were thus statistically significant differences among all used tube voltages.

Statistical analysis

For the observer performance test, statistical analysis among used tube voltages was performed with the software RStudio (Version 1.0.136 © 2009–2016 RStudio, Inc., Boston, MA, USA). The variance of data was analysed in a Bartlett test. Statistical differences were analysed in a Tukey honest significant difference test or Steel–Dwass test when the variance was insignificant or significant, respectively. Values under 0.05 are statistically significant.

For comparison with results from previous work,¹¹ we conducted correlation analysis using Microsoft Excel (Version 14.7.0). The differences among used tube voltages were evaluated by considering the overlap of 95% confidence intervals (CIs).

RESULTS

Relationship between superimposed images and serial images

Table 1 gives average TPRs of 13 observers for superimposed images at four different tube voltages and five different slice thicknesses, and for serial images at four different tube voltages. The highest correlation (R² = 0.91353) was found between superimposed images with a 0.3 mm slice thickness and serial images. The optimum superimposed thickness was thus 0.3 mm.

Differences among used tube voltages were statistically significant (p ≤ 0.0001), except for differences between 120 and 100 kV (p = 0.6383), in the case of superimposed images, while statistically significant differences were only observed against 60 kV at 120, 100, and 80 kV (p ≤ 0.0001), in the case of serial images.

Cluster signal-to-noise analysis

After varying the cut-off values applied in the FindFoci plugin and categorizing types of detected holes (Figure 7), cluster signal-to-noise curves were derived (Figure 8) to detect the true hole contours (signals) together with noise. It is implied that there was poor discrimination between the signal and noise at 60 kV as the curve at a low FPR made an angle with the vertical axis. Better discrimination was found for 120 and 100 kV as the curves at a low FPR ascended along or nearly along the vertical axis. The maximum TPR was highest at 120 kV, followed by 100 and 80 kV. The TPR at 60 kV was lower than TPRs at other tube voltages.

Relationship among cluster signal-to-noise analysis, Takeshita’s method11 and observer performance

Table 2 gives an example of corresponding FPRs converted from detected signals at a slice thickness of 0.3 mm. The mean FPRs of all images for the calculation of TPRs was 0.072. Correlation of the calculated TPRs to observer performance data obtained by cluster signal-to-noise analysis was higher (R² = 0.9296) than that obtained by Takeshita’s method¹¹ (R² = 0.7926) (Figure 9a,b).

Observer behaviour patterns for the detection of small mass changes in CBCT images

There was not strong but meaningful correlation between background noise and mean FPRs from observers. Mean FPRs increased as the background noise increased; the linear regression equation was y = 0.0052x, where y is the mean FPR of the observers and x is background noise (Figure 10). In addition, correlations were found between mean FPRs and intra- and interobserver variations. The two correlations were similar. The graphs show that intra- and interobserver variations increased with an increasing mean FPR, with the slopes of linear regression equation being 0.3825 and 0.3786, respectively (Figure 11a,b).

Relationship between calculated TPRs from background noise and actual TPRs from observers

Calculated TPRs from background noise had high correlation with actual TPRs from 13 observers; R² was 0.9244 (Figure 12a). In the analysis of statistical differences among used tube voltages based on TPRs from background noise, overlaps of 95% CIs were found between 120 and 100 kV and between 120 and 80 kV. Differences among the used tube voltages were thus statistically significant, except for the difference between 120 and 100 kV and the difference between 120 and 80 kV.

Relationship between accuracies from background noise and actual TPRs from observers

Accuracies from background noise had high correlation with actual TPRs from 13 observers; R² was 0.9338 (Figure 12b). In the analysis of statistical differences among used tube voltages based on accuracies from background noise, no overlap of 95% CIs was found. There were thus statistically significant differences among all used tube voltages.

DISCUSSION

We developed an observer-free method of evaluating image quality that overcomes the disadvantages of an observer performance test, namely the required time and elaborateness of using observers.^9,10 We compared our new method with the observer performance test and another observer-free method used by Takeshita.¹¹

In the observer performance test, there was high correlation between superimposed images with optimum superimposed thickness and serial images (R² = 0.91353). Superimposed images with optimum superimposed thickness, instead of serial images, can therefore be used for the observer performance test. This will decrease observer fatigue resulting from the long observation time. There were fewer significant differences among used tube voltages in the case of serial images than in the case of superimposed images. An observation using serial images will compensate for image degradation due to the low exposure dose, which was found in the observation of superimposed images, to some extent. The reason may be that the serial images can be scrolled through to look at several images for evaluation, such that they provide more information than superimposed images for the observers to make a final decision.

Cluster signal-to-noise analysis using the FindFoci plugin is a combined approach of physical image quality evaluation and an observer performance test. Unlike physical evaluation that focuses on the performance of the imaging system, cluster signal-to-noise analysis can simulate visual perception; i.e. the detection of signal from noise. In addition, this method was mainly employed as an application program, and there was thus no need to include observers.

Indeed, cluster signal-to-noise curves resemble receiver operating characteristic curves (ROC curves)^4,15–17 except for endpoint (1, 1). We reconstructed the curves from operating points but did not end with point (1, 1) because the information between the rightmost operating point and endpoint (1, 1) is erroneous. Our data were on the left side of the curves. To avoid confusion, we referred to our new method as cluster signal-to-noise analysis.

This new method had higher correlation to observer performance than Takeshita’s method.¹¹ The reason might be that Takeshita’s method used a limited number of cut-off values [threshold gray values (ΔG)] while the cluster signal-to-noise curve used several cut-off values. In Takeshita’s method, only one cut-off value was used for each row; and moreover, the same cut-off value could be used for more than one row. Even a minor change in cut-off values affects the number of TPs. A lower cut-off value results in a higher number of TPs.^4,17 It was therefore difficult to determine a suitable cut-off value that perfectly simulated observer performance. Unlike Takeshita’s method, cluster signal-to-noise curves were reconstructed using several cut-off values, which overcomes this problem.⁴

Variation in detection has three main sources: sample variance (noise) and intra- and interobserver variations.¹⁸ Many studies have analysed the relationship between a variation in detection and each source by evaluating correct detection. Kanal et al¹⁹ and Precht et al²⁰ found better detection when noise decreased. Huda et al²¹ found this effect when a lesion was smaller than 1 mm; otherwise, there was no significant difference in detection. Agreement among observers decreases as noise increases.¹⁹ In our study, we analysed observer behaviour patterns by evaluating error in the detection of small mass (noise) changes in CBCT images. Observers' decision levels for detecting small mass changes became less strict with an increasing level of background noise, leading to larger FPRs. Intra- and interobserver variations increased with increasing FPRs. The two regression equations for the linear approximation of correlation between FPRs and intra- and interobserver variations had similar positive slopes (approximately 0.38) (Figure 11a,b). These results imply that observers tend to loosen their decision levels to detect signals in noisy images at the expense of increasing the number of FP responses.

A low R² value of correlation between background noise and the mean FPR may be due to the widening of intra- and interobserver variation with increasing noise as described above. However, the regression equation in Figure 10 is obviously highly appropriate owing to the high R² value for Figure 12a,b. TPRs and accuracies that were calculated from background noise in the process including the regression equation presented in Figure 10 had high correlation with actual TPRs from observers. In addition, the existence of unrecognized FP signals seems to affect the detection of TP signals because the accuracies, consisting of both TPRs and FPRs from background noise, were a little more correlated with TPRs from observers than with calculated TPRs from background noise (Figure 12a,b). In actual diagnoses, the contribution of FPRs may be even higher than those found in this study because we knew the position of the holes in the phantom used in this study. Further diagnostic study may be needed to confirm this.

There are several statistical differences between the observer performance test and cluster signal-to-noise analysis. However, most statistical results were similar. A higher number of statistical differences in accuracies may suggest that FP signals play an important role in detection, while a lower number of statistical differences in the observer performance test may be due to interobserver variation.

We can calculate the TPR and accuracy from the background noise level and use them in analysis. This method would be sufficiently accurate to simulate the detection performance of observers because calculated TPRs (R² = 0.9244) and accuracy (R² = 0.9338) from background noise had high correlation with actual TPRs from observers.

This study showed that the cluster signal-to-noise analysis can be used for evaluation of the image quality related to observer performance. However, as it didn’t show any direct relationships with diagnostic performance, the further study should be taken to clarify their relationships. If we can confirm that they are related to each other, we can use the cluster signal-to-noise analysis to evaluate the image quality directly related to diagnostic accuracy. Moreover, we can also use it to evaluate the effects of the imaging conditions, such as exposure parameters and pixel sizes on the diagnostic image quality.

CONCLUSION

A new method, cluster signal-to-noise analysis, can simulate the detection performance of observers and thus replace the observer performance test in the evaluation of image quality. The number of erroneous decisions increased with increasing background noise.