Bispectrum Inversion with Application to Multireference Alignment

Abstract

We consider the problem of estimating a signal from noisy circularly-translated versions of itself, called multireference alignment (MRA). One natural approach to MRA could be to estimate the shifts of the observations first, and infer the signal by aligning and averaging the data. In contrast, we consider a method based on estimating the signal directly, using features of the signal that are invariant under translations. Specifically, we estimate the power spectrum and the bispectrum of the signal from the observations. Under mild assumptions, these invariant features contain enough information to infer the signal. In particular, the bispectrum can be used to estimate the Fourier phases. To this end, we propose and analyze a few algorithms. Our main methods consist of non-convex optimization over the smooth manifold of phases. Empirically, in the absence of noise, these non-convex algorithms appear to converge to the target signal with random initialization. The algorithms are also robust to noise. We then suggest three additional methods. These methods are based on frequency marching, semidefinite relaxation and integer programming. The first two methods provably recover the phases exactly in the absence of noise. In the high noise level regime, the invariant features approach for MRA results in stable estimation if the number of measurements scales like the cube of the noise variance, which is the information-theoretic rate. Additionally, it requires only one pass over the data which is important at low signal–to–noise ratio when the number of observations must be large.

I. Introduction

We consider the problem of estimating a discrete signal from multiple noisy and translated (i.e., circularly shifted) versions of itself, called multireference aligment (MRA). This problem occurs in a variety of applications in biology [1], [2], [3], [4], radar [5], [6], image registration and super-resolution [7], [8], [9], and has been the subject of recent theoretical analysis [10], [11]. The MRA model reads

$${\xi }_j=R_{r_j}x+{\epsilon }_j,j=1,\dots ,M,$$ (I.1)

where ε_j are i.i.d. normal random vectors with variance σ² and the underlying signal x is in ℝ^N or in ℂ^N. Operator R_rj rotates the signal x circularly by r_j locations, namely, (R_rjx)[n] = x[n − r_j], where indexing is zero-based and considered modulo N (throughout the paper). While both x and the translations {r_j} are unknown, we stress that the goal here is merely to estimate x. This estimation is possible only up to an arbitrary translation.

A chief motivation for this work arises from the imaging technique called single particle Cryo-Electron Microscopy (Cryo-EM), which allows to visualize molecules at near-atomic resolution [12], [13]. In Cryo-EM, we aim to estimate a three dimensional (3D) object from its two-dimensional (2D) noisy projections, taken at unknown viewing directions [14], [15]. While typically the recovery process involves alignment of multiple observations in a low signal-to-noise ratio (SNR) regime, the underlying goal is merely to estimate the 3D object. In this manner, with the unknown shifts corresponding to the unknown viewing directions, MRA can be understood as a simplified model for Cryo-EM.

Existing approaches for MRA can be classified into two main categories. The first class of methods aims to estimate the set of translations {r_j} first. Given this set, estimating x can be achieved easily by aligning all observations ξ_j and then averaging to reduce the noise. The second class, which we favor in this paper, consists of methods which aim to estimate the signal directly, without estimating the shifts.

Considering the first class, one intuitive approach to estimating the translations is to fix a template observation, say ξ₁, and to estimate the relative translations by cross-correlation. This is called template matching. Specifically, r_j is estimated as

$${\widehat{r}}_j=arg\underset{k}{max}\mathfrak{R}\left\{\sum _{n=0}^{N-1}{\xi }_1[n]\overline{{\xi }_j[n+k]}\right\},j=2,\cdots ,M,$$

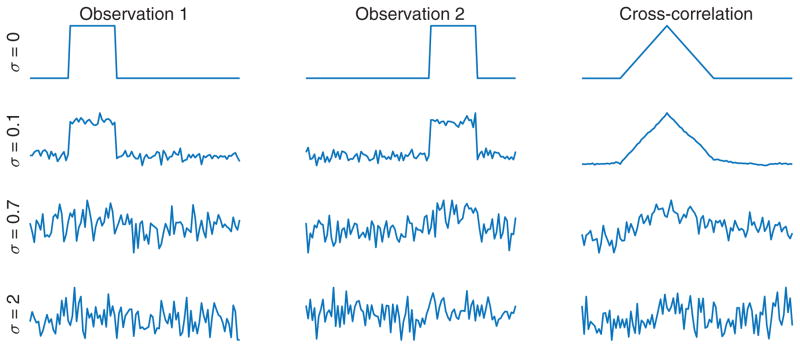
where ℜ{z} and z̄ denote the real part and the conjugate of a complex number z. This approach requires only one pass over the data: for each observation, the best shift can be computed in O(N log N), and the aligned observations can be averaged online. This results in a total computational cost of O(MN log N), see Table I. While this approach is simple and efficient, it necessarily fails below a critical SNR—see Figure I.1 for a representative example.

Table I.

Comparison of main MRA approaches. F(N) denotes the complexity of inverting the bispectrum. For instance, for the FM algorithm, F(N) = O(N²). Storage requirements include the possibility of streaming computations where possible.

Method	Computational complexity	Storage requirement	Comments
Template alignment	O(MN log N)	O(N)	Fails at moderate SNR (see Figure I.1)
Angular synchronization	O(M2N log N)	O(M2)	Fails at low SNR
Expectation maximization	O(TMN log N)	O(MN)	Empirically accurate; #iterations T grows with noise level
Invariant features (this paper)	O(MN2 + F(N))	O(N2)	Under mild conditions, accurate estimation if M grows as σ6

Figure I.1.

Alignment of two translated versions of the same signal in the presence of i.i.d. Gaussian noise with various standard deviations σ. The true signal in ℝ¹⁰⁰ is a window of length 22 and height 1. Each row presents two observations and their cross-correlation. Importantly, beyond a certain threshold, noise makes pairwise alignment impossible.

The issue with template matching is that we rely on aligning each observation to only one template: this is error prone at low SNR. Instead, to derive a more robust estimator, one can look for the most suitable alignment among all pairs of observations. The M² relative shifts thus computed must then be reconciled into a compatible choice of M shifts for the individual observations. This is a discrete version of the angular synchronization problem, see [16], [17], [18], [19], [20], [21]. The computational complexity of aligning all pairs individually is O(M²N log N), while storing the results uses O(M²) memory.

Alternative algorithms for estimating the translations are based on different SDP relaxations [22], [23], iterative template alignment [24], zero phase representations [5] and neural networks [6]. The statistical limits of alignment tasks were derived for a variety of setups and noise models, see for instance [25], [26], [27], [28]. For example, for a continuous, 2D version of the MRA model, it was shown that the Cramér–Rao lower bound (CRLB) for translation estimation is proportional to the noise variance σ² [25]; crucially, it does not improve with M, even if the underlying signal is known. This is motivation to consider the second category of MRA methods, where shifts are not estimated.

Section VI elaborates on expectation maximization (EM) which tries to compute the maximum marginalized likelihood estimator (MMLE) of the signal—marginalization is done over the shifts. This method acknowledges the difficulty of alignment by working not with estimates of the shifts themselves, but rather with estimates of the probability distributions of the shifts. As a result, EM achieves excellent numerical performance in practice. However its computational complexity is high and its performance is not understood in theory.

It has been shown recently that the sample complexity of MRA, under assumption that shifts are distributed uniformly, is proportional to σ⁶ in the low SNR regime. In other words, the number of measurements M needs to scale like σ⁶ to retain a constant estimation error [11].

In this work, we propose a framework which achieves this sample complexity by estimating the sought signal x directly using features that are invariant under translations. For instance, the mean of x is invariant under translation and can be estimated easily from the mean of all observations. We further use the power spectrum and the bispectrum of the observations—which are Fourier-transform based invariants— to estimate the magnitudes and phases of the signal’s Fourier transform, respectively.

For any fixed noise level (which may be arbitrarily large), these features can be estimated accurately provided sufficiently many measurements are available. Hence, our approach allows to deal with any noise level. Besides achieving the sample complexity, the computational complexity and memory requirements of the methods we describe are relatively low. Indeed, the only operations whose computational cost grows with M are computations of averages over the data. These can be performed on-the-fly and are easily parallelizable. We mention that a recent tensor decomposition algorithm also achieves this estimation rate [29].

Given estimators for the mean and power spectrum of x, estimating the DC component and Fourier magnitudes of x is straightforward. In this paper, we thus focus on the task of recovering the Fourier phases of x from an estimator of its bispectrum. We propose two non-convex optimization algorithms on the manifold of phases for this task, which we call bispectrum inversion. We also discuss three additional algorithms which do not require initialization (and hence could be used to initialize others), based on frequency marching, SDP relaxation and integer programming. The first two methods recover the phases exactly in the absence of noise.

Beyond MRA, the bispectrum plays a central role in a variety of signal processing applications. For instance, it is a key tool to separate Gaussian and non-Gaussian processes [30], [31]. It is also used to investigate the cosmic background radiation [32], [33], seismic signal processing [34], image deblurring [35], feature extraction for radar [36], analysis of EEG signals [37], MIMO systems [38] and classification [39] (see also [40], [41], [42], [43], [44] and references therein). In Section III, we review previous works on bispectrum inversion [45], [46], [34]. Reliable algorithms to invert the bispectrum, as studied here, may prove useful in some of these applications.

The paper is organized as follows. Section II discusses the invariant feature approach for MRA. Section III presents the non-convex algorithms on the manifold of phases for bispectrum inversion. Section IV is devoted to additional algorithms that can be used to initialize the non-convex algorithms. Section V analyzes one of the proposed non-convex algorithm. Section VI elaborates on the EM approach for MRA, Section VII shows numerical experiments and Section VIII offers conclusions and perspective.

Throughout the paper we use the following notation. Vectors x in ℝ^N or ℂ^N and y ∈ ℂ^N denote the underlying signal and its discrete Fourier transform (DFT), respectively. In the sequel, all indices are understood modulo N, namely, in the range 0, …, N −1. The phase of a complex scalar a, defined as a/|a| if a ≠ 0 and zero otherwise, is denoted by phase(a) or ã. The conjugate-transpose of a vector z is denoted by z^*. We use ‘∘’ to denote the Hadamard (entry-wise) product, 𝔼 for expectation, Tr(Z) for the trace and ||Z||_F for the Frobenius norm of a matrix Z. We reserve T(z) for circulant matrices determined by their first row z, i.e., T(z)[k₁, k₂] = z[k₂−k₁], and ℋ^N for the set of Hermitian matrices of size N × N.

II. Multireference Alignment via Invariant Features

We propose to solve the MRA problem directly using features that are invariant under translations. Unlike pairwise alignment, this approach fuses information from all M observations together—not just of pairs—and it only aims to recover the signal itself—not the translations. The essence of this idea was discussed as a possible extension in [22, Appendix A]. The invariant features can be understood either as auto-correlation functions or as their Fourier transform. In this work, we make use of the first three invariants defined as

$$\begin{gathered} c_1={\mu }_x=\frac{1}{N}\sum _{n=0}^{N-1}x[n], \\ {c}_2[n_1]=\frac{1}{N}\sum _{n=0}^{N-1}x[n]\overline{x[n-n_1]}, \\ {c}_3[n_1,n_2]=\frac{1}{N}\sum _{n=0}^{N-1}x[n]\overline{x[n-n_1]}x[n+n_2], \end{gathered}$$ (II.1)

for n₁, n₂ = 0, …, N−1. It is clear that c₁, c₂, c₃ are invariant under circular shifts of x. For higher-order invariants based on auto-correlations, see for instance [47].

The first feature is the mean of the signal which is the auto-corrleation function of order one (i.e., c₁ in (II.1)). The distribution of the mean of ξ_j is then given by ${\mu }_{{\xi }_j}~\mathcal{N}\left({\mu }_x,\frac{{\sigma }^2}{N}\right)$ and we can estimate μ_x as

$${\widehat{\mu }}_x=\frac{1}{M}\sum _{j=1}^M\left(\frac{1}{N}\sum _{n=0}^{N-1}{\xi }_j[n]\right)~\mathcal{N}\left({\mu }_x,\frac{{\sigma }^2}{NM}\right).$$ (II.2)

Estimating the signal’s mean supplies only limited information about the signal itself. Thus, we consider also the auto-correlation function of order two (i.e., c₂ in (II.1)). Its Fourier transform, the power spectrum, is explicitly defined as

$$P_x[k]={\mid y[k]\mid }^2,$$

for all k, where y is the DFT of x. An alternative way to understand the invariance of the power spectrum under shifts is through the effect of shifts on the DFT of a signal:

$$\text{DFT}(R_{s}x)[k]=y[k]·e^{-2\pi \mathit{iks}/N}.$$ (II.3)

Thus, shifts only affect the phases of the DFT, so that P_Rsx = P_x for any shift R_s. Furthermore, owing to independence of the noise with respect to the signal itself and to the shift,

$$\mathbb{E}\{P_{{\xi }_j}[k]\}=P_x[k]+N{\sigma }^2,$$

where the second term is the power spectrum of the noise ε_j. Therefore, we estimate the power spectrum of x as:

$${\widehat{P}}_x[k]=\frac{1}{M}\sum _{j=1}^M(P_{{\xi }_j}[k]-N{\sigma }^2).$$ (II.4)

It can be shown that P̂_x is unbiased and its variance is dominated by $\frac{{\sigma }^4}{M}$ for large σ. Hence, P̂_x → P_x as M → ∞. In particular, accurate estimation of the power spectrum requires M to scale like σ⁴. In the sequel, we assume that σ is known.¹

Recovering a signal from its power spectrum is commonly referred to as phase retrieval. This problem received considerable attention in recent years, see for instance [48], [49], [50], [51], [52], [53], [54]. It is well known that almost no one-dimensional signal can be determined uniquely from its power spectrum. Therefore, we use the power spectrum merely to estimate the signal’s Fourier magnitudes. As explained next, we use the auto-correlation of third order and its Fourier transform, the bispectrum, to estimate the Fourier phases.

Since phase retrieval is in general ill posed, we use the auto-correlation function of order three (that is, c₃ in (II.1)) through its Fourier transform, the bispectrum, to estimate the Fourier phases of the sought signal. The bispectrum is a function of two frequencies k₁, k₂ = 0, …, N −1 and is defined as [55]:

$$B_x[k_1,k_2]=y[k_1]\overline{y[k_2]}y[k_2-k_1].$$ (II.5)

Note that, if y[0] ≠ 0, the power spectrum is explicitly included in the bispectrum since P_x[k] = B_x[k, k]/y[0]. The fact that the bispectrum is invariant under shifts can also be deduced from (II.3). Indeed, for any shift R_s,

$$\begin{gathered} B_{R_{s}x}[k_1,k_2]=\left(y[k_1]e^{-2\pi i{k}_{1}s/N}\right)\left(\overline{y[k_2]}{e}^{2\pi i{k}_{2}s/N}\right)·\left(y[k_2-k_1]e^{2\pi i(k_1-k_2)s/N}\right) \\ =B_x[k_1,k_2]. \end{gathered}$$

In matrix notation, we express this as

$$B_x=y{y}^{\ast }\circ T(y),$$ (II.6)

where T(y) is a circulant matrix whose first row is y, that is, T(y)[k₁, k₂] = y[k₂ − k₁]. Observe that if x is real, then $y[k]=\overline{y[-k]}$ so that T(y) and B_x are Hermitian matrices. Simple expectation calculations lead to the conclusion that

$$\mathbb{E}\left\{B_{{\xi }_j}\right\}=B_x+{\sigma }^2{N}^2{\mu }_{x}A,$$ (II.7)

where A = A_ℝ or A = A_ℂ depending on x ∈ ℝ^N or x ∈ ℂ^N and

$$A_{ℝ}=\left[\begin{array}{cccccc}3& 1& 1& 1& \dots & 1\\ 1& 1& 0& 0& \dots & 0\\ 1& 0& 1& 0& \dots & 0\\ 1& 0& 0& 1& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& 0& 0& 0& \dots & 1\end{array}\right],A_{ℂ}=\left[\begin{array}{cccccc}2& 1& 1& 1& \dots & 1\\ 0& 1& 0& 0& \dots & 0\\ 0& 0& 1& 0& \dots & 0\\ 0& 0& 0& 1& \dots & 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& 0& \dots & 1\end{array}\right].$$

Since the bias term is proportional to μ_x, we propose to estimate B̂_x−μx by averaging over B_ξj−μx for all j. This estimator is unbiased and its variance is controlled by $\frac{{\sigma }^6}{M}$ for large σ. Therefore, M is required to scale like σ⁶ to ensure accurate estimation. In practice, μ_x is not known exactly. Thus, we estimate the bispectrum by

$${\widehat{B}}_{x-{\mu }_x}=\frac{1}{M}\sum _{j=1}^M{B}_{{\xi }_j-{\widehat{\mu }}_x},$$ (II.8)

which is asymptotically unbiased. For finite M and large σ, bias induced by the approximation μ̂_x ≈ μ_x is significantly smaller than the standard deviation of (II.8).

The bispectrum contains information about the Fourier phases of x because, defining ỹ[k] = phase(y[k]) and B̃_x[k₁, k₂] = phase(B_x[k₁, k₂]) where phase extracts the phase of a complex number (and returns 0 if that number is 0), we have

$${\stackrel{\sim }{B}}_x[k_1,k_2]=\stackrel{\sim }{y}[k_1]\overline{\stackrel{\sim }{y}[k_2]}\stackrel{\sim }{y}[k_2-k_1].$$ (II.9)

In matrix notation, the normalized bispectrum takes the form B̃_x = ỹ ỹ^* ∘ T(ỹ).

Contrary to the power spectrum, the bispectrum is usually invertible. Indeed, in the absence of noise, the bispectrum determines the sought signal uniquely under moderate conditions:

Proposition II.1

For N ≥ 5, let x ∈ ℂ^N be a signal whose DFT y obeys y[k] ≠ 0 for k = 1, …, K, possibly also for k = 0, and zero otherwise. Up to integer time shifts, x is determined exactly by its bispectrum provided $K\ge \frac{N+1}{2}$.

For N ≥ 5, let x ∈ ℝ^N be a real signal whose DFT y obeys y[k] ≠ 0 for k = 1, …, K and k = N −1, …, N − K, possibly also for k = 0, and zero otherwise. Up to integer time shifts, x is determined exactly by its bispectrum provided $\frac{N}{3}\le K\le \frac{N-1}{2}$.

Proof

This is a direct corollary of Lemmas V.1 and B.1.

We stress that the bispectrum estimator in (II.8) is not a bispectrum itself, since the set of bispectra is not a linear space: B̂_x−μx is not invertible as such [42]. Algorithms we propose aim to find a stable inverse, in the sense that the recovered signal will have a bispectrum which is close to the estimated bispectrum in ℂ^N×N. The following propositions combined argue formally that this can be done in the MRA model. The proofs in Appendix A are constructive.

Proposition II.2 (Stable bispectrum inversion)

There exists an estimator x̂ with the following property. For any signal x in ℝ^N or ℂ^N whose DFT is non-vanishing, there exist a precision δ = δ(x) > 0 and a sensitivity L = L(x) < ∞ such that if an estimator B̂_x of B_x satisfies ||B̂_x−B_x||_F ≤ δ, then x̂ = x̂ (B̂_x) satisfies min_r=0…N−1 ||x − R_r x̂||₂ ≤ L||B̂_x − B_x||_F.

Proposition II.3 (Bispectrum estimation)

For any signal x in ℝ^N or ℂ^N whose DFT is non-vanishing, for any required precision δ > 0 and for any probability p < 1, there exists a constant C = C(x, p, δ) < ∞ such that, for any noise level σ > 0, if the number of observations M exceeds C·(σ²+σ⁶), the estimator

$${\widehat{B}}_x=\frac{1}{M}\sum _{j=1}^M{B}_{{\xi }_j}-{\sigma }^2{N}^2{\widehat{\mu }}_{x}A$$

satisfies ||B̂_x − B_x||_F ≤ δ with probability at least p.

We mention that uniqueness in the continuous setup was considered in [56]. The more general setting of bispectrum over compact groups was considered in [57], [58], [59], [60].

The MRA model here assumes i.i.d. Gaussian noise. However, the estimation is performed by averaging in the bispectrum domain, where noise affecting individual entries is correlated. Consequently, one may want to use a more robust estimator, such as the median. Yet, computing the median of complex matrices is computationally expensive, while computing the average can be performed efficiently and on-the-fly, that is, without requiring to store all observations. For Gaussian noise, we have noticed numerically that using the mean or the median for bispectrum estimation leads to comparable estimation errors (experiments not shown). In other noise models, e.g., with outliers, it might be useful to consider the median or the median of means method, see for instance [61].

Algorithm 1.

Outline of the invariant approach for MRA

Input: Set of observations ξj, j = 1, …, M according to (I.1) and noise level σ

Output: x̂: estimation of x

Estimate invariant features: Compute μ̂x according to (II.2) Compute P̂x according to (II.4) Compute B̂x−μx according to (II.8)

Estimate the signal’s DFT: Estimate y[0] from μ̂x. For other frequencies: Estimate the magnitudes of y from P̂x Estimate the phases of y from B̂x−μx (e.g., Algorithm 2)

Return: x̂: inverse DFT of the estimated y

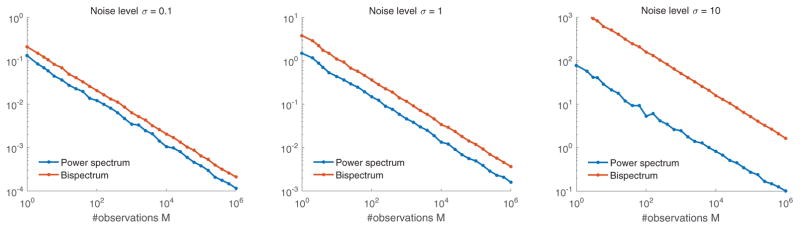
Figure II.1 presents the relative estimation error of the power spectrum and bispectrum as a function of the number of observations M. For the bispectrum, the relative error is computed as

Figure II.1.

Relative error of estimating the power spectrum and bispectrum for different noise levels as a function of the number of observations M. Results are averaged over 10 repetitions for each value of M on a fixed real signal of length N = 41 with i.i.d. normal random entries. The signal-to-noise ratio is then 1/σ². Importantly, the relative error decreases as $1/\sqrt{M}$ regardless of noise level.

$$\text{relative}\text{error}:=\frac{{\Vert B_{x-{\mu }_x}-\frac{1}{M}{\sum }_{j=1}^M{B}_{{\xi }_j-{\widehat{\mu }}_x}\Vert }_{\mathrm{F}}}{{\Vert B_{x-{\mu }_x}\Vert }_{\mathrm{F}}},$$

and similarly for the power spectrum. As expected, the slope of all curves is approximately 1/2 in logarithmic scale, implying that the estimation error decreases as $O(1/\sqrt{M})$. The invariant features approach for MRA is summarized in Algorithm 1.

Consider the case in which the number of samples M may be very large whereas the size of the object is fixed, namely N ≪ M. This case is of interest in many applications, such as cryo-EM [14], [15]. In this regime, the invariant features approach has two important advantages over methods that rely on estimating the translations. First, in the invariant features approach, we average over the M observations (which is computationally cheap), and then apply a more complex algorithm (say, to recover a signal from its bispectrum) whose input size is a function of N but is independent of M. Hence, the overall complexity of this approach can be relatively low. Second, the alignment-based method requires storing all M observations, namely, MN samples, which is unnecessary in the invariant features approach. There, for each observation, we just need to compute its invariants, to be averaged over all observations: this can be done online (in streaming mode) and in parallel.

III. Non-convex Algorithms for bispectrum inversion

After estimating the first Fourier coefficient y[0] as Nμ̂_x, our approach for MRA by invariant features consists of two parts. We use the power spectrum to estimate the signal’s Fourier magnitudes and the bispectrum for the phases. The first part is straightforward: |y[k]| can be estimated as $\sqrt{{\widehat{P}}_x[k]}$ if P̂_x[k] ≥ 0, and as 0 otherwise. Hereafter, we focus on estimation of the phases of the DFT, ỹ.

In the literature, two main approaches were suggested to invert the discrete bispectrum. The first is based on estimating the frequencies one after the other by exploiting simple algebraic relations [45], [46]. The second approach suggests to estimate the signal by least-squares solution and phase unwrapping [46], [34]. We improve these methods and suggest a few new algorithms. The algorithms are split into two sections. This section is devoted to two new non-convex algorithms based on optimization on the manifold of phases. Both of these algorithms require initialization. While experimentally it appears that random initialization works well, for completeness, in the next section we propose three additional algorithms which do not need initialization and hence could be used to initialize the non-convex algorithms.

A. Local non-convex algorithm over the manifold of phases

In this section, similarly to (II.9), we let B̃ denote our estimate of the phases of B_x. Since B̃ ≈ ỹ ỹ^* ∘ T(ỹ), one way to model recovery of the Fourier phases ỹ is by means of the non-convex least-squares optimization problem

$$\underset{z\in {ℂ}^N}{min}{\Vert W\circ \left(\stackrel{\sim }{B}-z{z}^{\ast }\circ T(z)\right)\Vert }_{\mathrm{F}}^2\text{subject}\text{to}\mid z[k]\mid =1,\forall k.$$ (III.1)

The matrix W ∈ ℝ^N×N is a weight matrix with nonnegative entries. These weights can be used to indicate our confidence in each entry of B̃. Expanding the squared Frobenius norm yields

$${\Vert W\circ \left(\stackrel{\sim }{B}-z{z}^{\ast }\circ T(z)\right)\Vert }_{\mathrm{F}}^2={\Vert W\circ \stackrel{\sim }{B}\Vert }_{\mathrm{F}}^2+{\Vert W\circ z{z}^{\ast }\circ T(z)\Vert }_{\mathrm{F}}^2-2\langle W\circ \stackrel{\sim }{B},W\circ z{z}^{\ast }\circ T(z)\rangle ,$$

where

$$\langle U,V\rangle =\mathfrak{R}\{\text{Tr}(U^{\ast }V)\},$$ (III.2)

is the real inner product associated to the Frobenius norm. Under the constraints on z, the first two terms are constant and the inner product term is equivalent to

$$\langle W\circ \stackrel{\sim }{B},W\circ z{z}^{\ast }\circ T(z)\rangle =\langle z,M(z)z\rangle ,$$

with

$$M(z):=W^{(2)}\circ \stackrel{\sim }{B}\circ \overline{T(z)},$$ (III.3)

where we use the notation W⁽²⁾:= W ∘ W. One possibility is to choose $W=\sqrt{\mid {\widehat{B}}_{x-{\mu }_x}\mid }$, where the absolute value and the square root are taken entry-wise, so that $M(z)={\widehat{B}}_{x-{\mu }_x}\circ \overline{T(z)}$. Hence, optimization problem (III.1) is equivalent to

$$\underset{z\in {ℂ}^N}{max}f(z)=\langle z,M(z)z\rangle \text{subject}\text{to}\mid z[k]\mid =1,\forall k.$$ (III.4)

We can also impose z[0] = phase(μ̂_x). If x is real, we have the additional symmetry constraints $z[k]=\overline{z[-k]}$.

Algorithm 2.

Non-convex optimization on phase manifold

Input: The normalized bispectrum B̃[k1, k2] and a weight matrix W ∈ ℝN×N

Output: ŷ: an estimation of ỹ

Compute: Using RTR [62], [63], approximately solve: $$\widehat{y}=arg\underset{z\in {ℂ}^N}{max}\mathfrak{R}\{z^{\ast }M(z)z\}\text{subject}\text{to}\mid z[k]\mid =1,\forall k,(\text{if}x\text{is}\text{real})z[k]=\overline{z[-k]},\forall k,$$

where $M(z):=(W\circ W)\circ \stackrel{\sim }{B}\circ \overline{T(z)}$.

Since the cost function f is continuous and the search space is compact, a solution exists. Of course, the solution is not unique, in accordance with the invariance of the bispectrum under integer time-shifts of the underlying discrete signal. This is apparent through the fact that the cost function f is invariant under the corresponding (discrete) transformations of z. This is true independently of the data B̃ and W. The proof is in Appendix C.

Lemma III.1

The cost function f is invariant under transformations of z that correspond to integer time-shifts of the underlying signal.

To solve this non-convex program, we use the Riemannian trust-region method (RTR) [62], whose usage is simplified by the toolbox Manopt [63]. RTR enjoys global convergence to second-order critical points, that is, points which satisfy first- and second-order necessary optimality conditions [64] and a quadratic local convergence rate. Empirically, in the noiseless case it appears that the algorithm recovers the target signal with random initialization, all local minima are global (with minor technicality for even N in the real case) and all second-order critical points have an escape direction, that is, saddles are “strict”. Numerical experiments demonstrate reasonable robustness in the face of noise. This algorithm is summarized in Algorithm 2 and studied in detail in Section V.

B. Iterative phase synchronization algorithm

In this section we present an alternative heuristic to the non-convex algorithm on the manifold of phases. This algorithm is based on iteratively solving the phase synchronization problem. Suppose we get an estimation of ỹ, say ŷ_k−1. If ŷ_k−1 ≈ ỹ is non-vanishing, then this estimation should approximately satisfy the bispectrum relation:

$$\stackrel{\sim }{B}\circ \overline{T({\widehat{y}}_{k-1})}\approx {\widehat{y}}_{k-1}{\widehat{y}}_{k-1}^{\ast }.$$

The underlying idea is now to push the current estimation towards ỹ by finding a rank-one approximation of $\widehat{B}\circ \overline{T({\widehat{y}}_{k-1})}$ with unit modulus entries. This problem can be formulated as:

$$arg\underset{z\in {ℂ}^N}{max}\mathfrak{R}\left\{z^{\ast }\left(\stackrel{\sim }{B}\circ \overline{T({\widehat{y}}_{k-1})}\right)z\right\}\text{subject}\text{to}\mid z[\ell ]\mid =1,\forall \ell ,$$ (III.5)

where we treat the matrix $\stackrel{\sim }{B}\circ \overline{T({\widehat{y}}_{k-1})}$ as a constant. This problem is called phase synchronization. Many algorithms have been suggested to solve the phase synchronization problem. Among them are the eigenvector method, SDP relaxation, projected power method, Riemannian optimization and approximate message passing [16], [20], [17], [18], [19]. Notice that the solution of (III.5) is only defined up to a global phase, namely, if z is optimal, then so is ze^iϕ for any angle ϕ. To resolve this ambiguity, we require knowledge of the phase of the mean, ỹ[0] (which is easy to estimate from the data) and we pick the global phase of ŷ_k such that ŷ_k[0] = ỹ[0].

The kth iteration of our algorithm thus (tries to) solve the phase synchronization problem with respect to the matrix $M_{k-1}:=\stackrel{\sim }{B}\circ \overline{T({\widehat{y}}_{k-1})}$, where ŷ_k−1 is the solution of the previous estimation. Assuming the signal is real, we also impose at each iteration the conjugate-reflection property of ${\widehat{y}}_k[\ell ]=\overline{{\widehat{y}}_k[-\ell ]}$ for all ℓ so that M_k is Hermitian. In the numerical experiments in Section VII, we solve (III.5) by the Riemannian trust-region method described in [17]. Empirically, the performance of this algorithm and Algorithm 2 is indistinguishable. The algorithm is summarized in Algorithm 3.

Algorithm 3.

Iterative phase synchronization algorithm

Input: The normalized bispectrum B̃, initial estimation ŷ0, phase of the mean ỹ[0]

Output: ŷ: estimation of ỹ

Set k = 0

while stopping criterion does not trigger do: k ← k + 1 Compute ŷk as a solution of (III.5) Fix the global phase: ${\widehat{y}}_k\leftarrow {\widehat{y}}_k·\frac{\stackrel{\sim }{y}[0]}{{\widehat{y}}_k[0]}$ If x is real, symmetrize: ŷk ← phase ((ŷk)↓↑), see (B.1)

end while

Return: ŷ ← ŷk

IV. Initialization-free Algorithms

The previous section was devoted to non-convex algorithms to invert the bispectrum. In this section we present three additional algorithms based on frequency marching (FM), SDP relaxation and phase unwrapping. These algorithms do not require initialization and therefore could be used to initialize the non-convex algorithms.

We prove that FM and the SDP recover the Fourier phases exactly in the absence of noise under the assumption that we can fix ỹ[1]. If the signal has non-vanishing DFT, ỹ[1] can be estimated from the bispectrum using the fact that ỹ[1]^N equals

$$\text{phase}(B_x[N-1,1]B_x[1,2]·B_x[1,2]\cdots B_x[1,N-1]).$$

(Any Nth root can be used for ỹ[1], corresponding to the N possible shifts of x.) In all cases, we argue that forcing ỹ[1] = 1 is acceptable if N is large. Indeed, recall that a shift by ℓ entries in the space domain is equivalent to modulating the kth Fourier coefficient by e^{−2πiℓk/N}. In particular, it means that the phase ỹ[1] can be shifted by e^−2πiℓ/N for an arbitrary ℓ ∈ ℤ. Thus, for signals of length N ≫ 1, the phase ỹ[1] can be set arbitrarily with only small error. In the numerical experiments of Section VII, we give the correct value of ỹ[1] to the algorithms in order to assess their best possible behavior.

We begin by discussing the FM algorithm, which is a simple propagation method: it is exact in the absence of noise. Notwithstanding, its estimation for the low-frequency coefficients is sensitive to noise. Because of its recursive nature, error in the low frequencies propagates to the high frequencies, resulting in unreliable estimation. The other two algorithms are more computationally demanding but appear more robust.

A. Frequency marching algorithm

The FM algorithm is a simple propagation algorithm in the spirit of [45], [46] that aims to estimate ỹ one frequency at a time. This algorithm has computational complexity O(N²) and it recovers ỹ exactly for both real and complex signals in the absence of noise, assuming ỹ[1] is known.

Let us denote B̃[k₁, k₂] = e^{iΨ[k₁,k₂]} and ỹ[k] = e^iψ[k]. Accordingly, we can reformulate (II.5) as

$$\mathrm{\Psi }[k_1,k_2]=\psi [k_1]-\psi [k_2]+\psi [k_2-k_1]mod2\pi ,$$

where the modulo is taken over the sum of all three terms. Using this relation, we can start to estimate the missing phases. The first unknown phase, ψ[2], can be estimated by:

$$\begin{gathered} \mathrm{\Psi }[1,2]=\psi [1]-\psi [2]+\psi [1]mod2\pi \\ \Rightarrow \widehat{\psi }[2]=2\psi [1]-\mathrm{\Psi }[1,2]mod2\pi , \end{gathered}$$

where ψ̂[2] refers to the estimator of ψ[2] (defined modulo 2π). We can estimate the next phase in the same manner:

$$\begin{gathered} \mathrm{\Psi }[1,3]=\psi [1]-\psi [3]+\psi [2]mod2\pi \\ \Rightarrow \widehat{\psi }[3]=\psi [1]+\widehat{\psi }[2]-\mathrm{\Psi }[1,3]mod2\pi . \end{gathered}$$

For higher frequencies, we have more measurements to rely on. For the fourth entry, we now can derive two estimators as follows:

$$\begin{gathered} \mathrm{\Psi }[1,4]=\psi [1]-\psi [4]+\psi [3]mod2\pi \\ \Rightarrow {\widehat{\psi }}^{(1)}[4]=\psi [1]+\widehat{\psi }[3]-\mathrm{\Psi }[1,4]mod2\pi , \end{gathered}$$

and

$$\begin{gathered} \mathrm{\Psi }[2,4]=\psi [2]-\psi [4]+\psi [2]mod2\pi \\ \Rightarrow {\widehat{\psi }}^{(2)}[4]=2\widehat{\psi }[2]-\mathrm{\Psi }[2,4]mod2\pi . \end{gathered}$$

In the noiseless case, it is clear that ψ[4] = ψ̂⁽¹⁾[4] = ψ̂⁽²⁾[4]. In a noisy environment, we can reduce the noise by averaging the two estimators, where averaging is done over the set of phases (namely, over the rotation group SO(2)) as explained in Appendix D. Specifically,

$$e^{i\widehat{\psi }[4]}=\text{phase}\left(e^{i{\widehat{\psi }}^{(1)}[4]}+e^{i{\widehat{\psi }}^{(2)}[4]}\right).$$

We can iterate this procedure. To estimate phase q, we want to consider all entries of $\stackrel{\sim }{B}[k,\ell ]=\stackrel{\sim }{y}[k]\overline{\stackrel{\sim }{y}[\ell ]}\stackrel{\sim }{y}[\ell -k]$ such that exactly one of the indices k, ℓ, or ℓ − k is equal to q and all other indices are in 1, …, q − 1, so that all other phases involved have already been estimated. A simple verification shows that only entries B̃[p, q], p = 1, …, q − 1, have that property. Furthermore, because of symmetry in the bispectrum (V.4), half of these entries are redundant so that only entries B̃[p, q], $p=1,\dots ,\lfloor \frac{q}{2}\rfloor$ remain. As a result, estimation of the kth phase relies on averaging over $\lfloor \frac{k}{2}\rfloor$ equations, as summarized in Algorithm 4, with the following simple guarantee. The above construction yields the following proposition.

Proposition IV.1

Let B̃ = B̃_x be the normalized bispectrum as defined in (II.9) and assume that ỹ[1] is known. If y[k] ≠ 0 for k = 1, …, K, then Algorithm 4 recovers the Fourier phases ỹ[k], k = 1, …, K exactly.

We note in closing that, if the signal x is real, symmetries in the phases ỹ and B̃ can be exploited easily in FM.

B. Semidefinite programming relaxation

In this section we assume that the DFT y is non-vanishing so that the bispectrum relation can be manipulated as

$$\stackrel{\sim }{B}=\stackrel{\sim }{y}{\stackrel{\sim }{y}}^{\ast }\circ T(\stackrel{\sim }{y})\equiv \stackrel{\sim }{B}\circ \overline{T(\stackrel{\sim }{y})}=\stackrel{\sim }{y}{\stackrel{\sim }{y}}^{\ast },$$

where $\overline{T(\stackrel{\sim }{y})}$ is its entry-wise conjugate. The developments are easily adapted if the signal has zero mean. Similarly to the FM algorithm, we assume that ỹ[0] and ỹ[1] are available. We aim to estimate ỹ by a convex program. As a first step, we decouple the bispectrum equation and write the problem of estimating ỹ as the following non-convex optimization problem:

$$\begin{gathered} \underset{Z\in {\mathscr{H}}^N,z\in {ℂ}^N}{min}{\Vert W\circ \left(\stackrel{\sim }{B}\circ \overline{T(z)}-Z\right)\Vert }_{\mathrm{F}}^2 \\ \text{subject}\text{to}Z=z{z}^{\ast }, \\ \text{diag}(Z)=1, \\ z[0]=\stackrel{\sim }{y}[0],z[1]=\stackrel{\sim }{y}[1], \\ (\text{if}x\text{is}\text{real})z[k]=\overline{z[-k]},\forall k, \end{gathered}$$ (IV.1)

where ℋ^N is the set of Hermitian matrices of size N and W ∈ ℝ^N×N is a real weight matrix with positive entries. In particular, in the numerical experiments we set W = |B|.

Algorithm 4.

Frequency marching algorithm

Input: Normalized bispectrum B̃[k1, k2] = eiΨ[k1,k2], ỹ[0] and ỹ[1] ≠ 0

Output: ŷ: estimation of ỹ Set ŷ[0] = ỹ[0] and eiψ̂[1] = ỹ[1] For k = 2, …, N do: Average the phase measurements: $$u=\text{phase}\left({\displaystyle \sum _{\ell =1}^{\lfloor \frac{k}{2}\rfloor }}{e}^{i\left(\widehat{\psi }[\ell ]+\widehat{\psi }[k-\ell ]-\mathrm{\Psi }[\ell ,k]\right)}\right)$$ Estimate ψ̂[k] through: $$e^{i\widehat{\psi }[k]}=\{\begin{array}{ll}u,\hfill & u\ne 0,\hfill \\ 1,\hfill & u=0,\hfill \end{array}$$

Return: ŷ ← eiψ̂

In the absence of noise, the minimizers of (IV.1) satisfy the bispectrum equation. However, in general these cannot be computed in polynomial time. In order to make the problem tractable, we relax the non-convex coupling constraint Z = zz^* to the convex constraint Z ⪰ zz^* (that is, Z − zz^* is positive semidefinite). The convex relaxation is then given by

$$\begin{gathered} \underset{Z\in {\mathscr{H}}^N,z\in {ℂ}^N}{min}{\Vert W\circ \left(\stackrel{\sim }{B}\circ \overline{T(z)}-Z\right)\Vert }_{\mathrm{F}}^2 \\ \text{subject}\text{to}Z\succcurlyeq z{z}^{\ast }, \\ \text{diag}(Z)=1, \\ z[0]=\stackrel{\sim }{y}[0],z[1]=\stackrel{\sim }{y}[1], \\ (\text{if}x\text{is}\text{real})z[k]=\overline{z[-k]},\forall k, \end{gathered}$$ (IV.2)

Upon solving (IV.2), which can be done in polynomial time with interior point methods, the phases ỹ are estimated from phase(z). In practice, we use CVX to solve this problem [65]. The algorithm is summarized in Algorithm 5. We note that problem (IV.2) is not a standard SDP, in that its cost function is nonlinear.

In the noiseless case, the SDP relaxation (IV.2) recovers the missing phases exactly. Interestingly, the proof is not so much based on optimality conditions as it is on an algebraic property of circulant matrices. The proof of the following property is given in Appendix E.

Algorithm 5.

Semidefinite relaxation algorithm

Input: The normalized bispectrum B̃, ỹ[0] and ỹ[1]

Output: ŷ: estimation of ỹ

Solve the SDP with nonlinear cost function (IV.2), for example using CVX [65]

Return: ŷ ← phase(z)

Lemma IV.2

Let û be the DFT of a vector u ∈ ℂ^N obeying $u[k]=\overline{u[-k]}$, so that û is real. If u[0] = u[1] = 1 and û is non-negative, then u[k] = 1 for all k.

The following theorem is a direct corollary of Lemma IV.2. The main proof idea is as follows. Consider $u=\overline{\widehat{y}}\circ z$ where (Z, z) is optimal for the SDP; then, the constraints ensure u[0] = u[1] = 1. Furthermore, one can see via the Schur complement that the constraints force T(u) to be positive semidefinite. Since the eigenvalues of T(u) are the DFT of u, it follows that û is non-negative, so that the lemma above applies and u ≡ 1, or, equivalently, z = ỹ. Details of the proof are in Appendix F.

Theorem IV.3

For a real signal with non-vanishing DFT y, if all weights in W are positive, ỹ[0] and ỹ[1] are known and the objective value of (IV.2) attains 0 (which is the case in the absence of noise), then the SDP has a unique solution given by z = ỹ and Z = zz^*.

We close with an important remark about the symmetry breaking purpose of constraint z[1] = ỹ[1] in the SDP. Because the signal x can be recovered only up to integer time shifts, even in the noiseless case, without this constraint there are at least N distinct solutions (z, Z) to the SDP. Because SDP is a convex program, any point in the convex hull of these N points is also a solution. Thus, if the symmetry is not broken, the set of solutions contains many irrelevant points. Furthermore, interior point methods tend to converge to a center of the set of solutions, which in this case is never one of the desired solutions.

C. Phase unwrapping by integer programming algorithm

The next algorithm is based on solving an over-determined system of equations involving integers. Let us denote ỹ[k] = e^iψ[k] and B̃[k₁, k₂] = e^{iΨ[k₁,k₂]} so the normalized bispectrum model is given by

$$e^{i\mathrm{\Psi }[k_1,k_2]}=e^{i(\psi [k_1]-\psi [k_2]+\psi [k_2-k_1])}.$$

By taking the logarithm, we get the algebraic relation

$$\mathrm{\Psi }[k_1,k_2]+2\pi \chi [k_1,k_2]=\psi [k_1]-\psi [k_2]+\psi [k_2-k_1],$$ (IV.3)

where, as a result of phase wrapping, χ takes on integer values. Let Ψ_vec and χ_vec be the column-stacked versions of Ψ and χ, respectively. Then, the model reads

$${\mathrm{\Psi }}_{\text{vec}}+2\pi {\chi }_{\text{vec}}=A\psi ,$$ (IV.4)

where the sparse matrix A ∈ ℝ^N2×N encodes the right hand side of (IV.3). It can be verified that A is of rank N − 1 (see for instance [66]), with null space corresponding to the time-shift-induced ambiguity on the phases (II.3). Note that both the integer vector χ_vec and the phases ψ are unknown. Given χ_vec, the phases ψ can be obtained easily by solving

$$\underset{\psi \in {ℝ}^N}{min}{\Vert {\mathrm{\Psi }}_{\text{vec}}+2\pi {\chi }_{\text{vec}}-A\psi \Vert }_p,$$ (IV.5)

for some ℓ_p norm. Observe that any error in estimating χ may cause a big estimation error of ψ in (IV.5). These errors can be thought of as outliers. Hence, we choose to use least unsquared deviations (LUD), p = 1, which is more robust to outliers. The more challenging task is to estimate the integer vector χ_vec ∈ ℤ^N2. To this end, we first eliminate ψ from (IV.4) as follows. Let C ∈ ℝ^{(N2 − (N−1))×N2} be a full rank matrix such that CA = 0, that is, the columns of C^T are in the null space of A^T. Matrix C can be designed by at least two methods. One, suggested in [67], exploits the special structure of A to design a sparse matrix composed of integer values. Another, which we use here, is to take C to have orthonormal rows which form a basis of the kernel of A^T. Numerical experiments (not shown) indicate that the latter approach is more stable. Next, we multiply both sides of (IV.4) from the left by C to get

$$C\{{\mathrm{\Psi }}_{\text{vec}}+2\pi {\chi }_{\text{vec}}\}=CA\psi =0.$$

Therefore, the integer recovery problem can be formulated as

$$\underset{{\chi }_{\text{vec}}\in {\mathbb{Z}}^{N^2}}{min}{\Vert \frac{1}{2\pi }C{\mathrm{\Psi }}_{\text{vec}}+C{\chi }_{\text{vec}}\Vert }_2,$$ (IV.6)

where we minimize over all integers. Note that CΨ_vec is a known vector. The problem is then equivalent to finding a lattice vector with the basis C which is as close as possible to the vector −CΨ_vec/(2π). While the problem is known to be NP-hard, we approximate the solution of (IV.6) with the LLL (Lenstra–Lenstra–Lovasz) algorithm, which can be run in polynomial time [68]. The LLL algorithm computes a lattice basis, called a reduced basis, which is approximately orthogonal. It uses the Gram–Schmidt process to determine the quality of the basis. For more details, see [69, Ch. 17].

We note that (IV.6) is under-determined as the matrix C is of rank N² − rank(A) = N² − (N − 1). While the LLL algorithm works with under-determined systems, in our case we can solve it for a determined system since we can fix the first N − 1 entries of χ_vec to be zero.² Once we have estimated χ_vec, we solve (IV.5) with p = 1. This approach is summarized in Algorithm 6.

Algorithm 6.

Phase unwrapping by integer programming

Input: The normalized bispectrum B̃[k1, k2] = eiΨ[k1,k2]

Output: ŷ: estimation of ỹ (integer programming) Apply the LLL algorithm to estimate the integer vector χvec from $$\underset{{\chi }_{\text{vec}}\in {\mathbb{Z}}^{N^2}}{min}{\Vert C{\mathrm{\Psi }}_{\text{vec}}/(2\pi )+C{\chi }_{\text{vec}}\Vert }_2,$$ where A is given in (IV.4), CA = 0 and Ψvec ∈ ℝN2 is a column-stacked version of Ψ, e.g., using code from [70]. (least-unsquared minimization) Let χ̂vec be the solution of stage 1. Then, solve $$\widehat{\psi }=arg\underset{\widehat{\psi }\in {ℝ}^N}{min}{\Vert {\mathrm{\Psi }}_{\text{vec}}+2\pi {\widehat{\chi }}_{\text{vec}}-A\psi \Vert }_1.$$

Return: ŷ ← eiψ̂

V. Analysis of optimization over phases

In this section, we study the non-convex optimization problem (III.4) and give more implementation details to solve it, since numerical experiments identify this as the method of choice for MRA from invariant features among all methods compared. We start by considering the general case of a complex signal x ∈ ℂ^N and consider the real case in Appendix B. Recall that we aim to maximize

$$f(z)=\langle z,M(z)z\rangle ,M\langle z\rangle :=W^{(2)}\circ \stackrel{\sim }{B}\circ \overline{T(z)},$$

where the inner product is defined by (III.2), W is a real weighting matrix and W⁽²⁾:= W ∘ W. The optimization problem lives on a manifold, that is, a smooth nonlinear space. Indeed, the smooth cost function f(z) is to be maximized over the set

$$\mathcal{M}=\{z\in {ℂ}^N:\mid z[0]\mid =\cdots =\mid z[N-1]\mid =1\},$$

which is a Cartesian product of N unit circles in the complex plane (a torus). Theory and algorithms for optimization on manifolds can be found in the monograph [71]. We follow this formalism here. Details can also be found in [17], which deals with the similar problem of phase synchronization, using similar techniques. For the numerical experiments below, we use the toolbox Manopt which provides implementations of various optimization algorithms on manifolds [63].

Under mild conditions, the global optima of (III.4) correspond exactly to ỹ up to integer time shifts. This fact is proven in Appendix G.

Lemma V.1

For N ≥ 3, let x ∈ ℂ^N be a signal whose DFT y is nonzero for frequencies k in {1, …, K}, possibly also for k = 0, and zero otherwise. Up to integer time shifts, x is determined exactly by its bispectrum B provided $K\ge \frac{N+1}{2}$. Furthermore, the global optima of (III.4) correspond exactly to the relevant phases of y—up to the effects of integer time shifts—provided W[k, ℓ] is positive when B[k, ℓ] ≠ 0.

The problem at hand is

$$\underset{z\in \mathcal{M}}{max}f(z).$$ (V.1)

This is smooth but non-convex, so that in general it is hard to compute the global optimum. We derive first- and second-order necessary optimality conditions. Points which satisfy these conditions are called critical and second-order critical points, respectively. Known algorithms converge to critical points (e.g., Riemannian gradient descent) and even to second-order critical points (e.g., Riemannian trust-regions) regardless of initialization [71], [62], [64]. Empirically, despite non-convexity, the global optimum appears to be computable reliably in favorable noise regimes.

As we proceed to consider optimization algorithms for (III.4), the gradient of f will come into play:

$$\nabla f(z)=M(z)z+M{(z)}^{\ast }z+M^{\text{adj}}(z{z}^{\ast }),$$

where M^adj: ℂ^N×N → ℂ^N is the adjoint of M with respect to the inner product 〈·, ·〉. Formally, the adjoint is defined such that, for any z ∈ ℂ^N, X ∈ ℂ^N×N,

$$\langle z,M^{\text{adj}}(X)\rangle =\langle M(z),X\rangle .$$

Specifically, in Appendix H we show that

$$M^{\text{adj}}(X)[k]=\text{Tr}\left(T_k^{\top }\left(W^{(2)}\circ \stackrel{\sim }{B}\circ \overline{X}\right)\right),$$ (V.2)

where T_k is a circulant matrix with ones in its kth (circular) diagonal and zero otherwise, namely,

$$(T_k)[{\ell }^{\prime },\ell ]=\{\begin{array}{ll}1\hfill & \text{if}{\ell }^{\prime }=\ell -k,\hfill \\ 0\hfill & \text{otherwise.}\hfill \end{array}$$ (V.3)

As it turns out, under the symmetries of the problem at hand, there is no need to evaluate M^adj explicitly. Indeed, B̃ obeys

$$\stackrel{\sim }{B}[k_2-k_1,k_2]=\stackrel{\sim }{y}[k_2-k_1]\overline{\stackrel{\sim }{y}[k_2]}\stackrel{\sim }{y}[k_1]=\stackrel{\sim }{B}[k_1,k_2].$$ (V.4)

This property is preserved when B̃ is obtained by averaging bispectra of multiple observations, as in (II.8). Assuming the same symmetry for the real weights W, we find below that M^adj(zz^*) = M(z)z. See Appendix I.

Lemma V.2

If B̃[k₂ − k₁, k₂] = B̃[k₁, k₂] and W[k₂ − k₁, k₂] = W[k₁, k₂] for all k₁, k₂, then M^adj(zz^*) = M(z)z for all z ∈ ℂ^N.

Thus, under the symmetries assumed in Lemma V.2, the gradient of f simplifies and we get a simple expression for the Hessian as well:

$$\begin{gathered} \nabla f(z)=2M(z)z+M{(z)}^{\ast }z, \\ {\nabla }^{2}f(z)[\stackrel{.}{z}]=2M(\stackrel{.}{z})z+2M(z)\stackrel{.}{z}+M{(\stackrel{.}{z})}^{\ast }z+M{(z)}^{\ast }\stackrel{.}{z}. \end{gathered}$$ (V.5)

For unconstrained optimization, the first-order necessary optimality conditions are ∇f(z) = 0. In the presence of the constraint z ∈ ℳ, the conditions are different. Namely, following [71, eq. (3.37)], since ℳ is a submanifold of ℂ^N, first-order necessary optimality conditions state that the orthogonal projection of the gradient ∇f(z) to the tangent space to ℳ at z must vanish. The result of this projection is called the Riemannian gradient. Formally, the tangent space is obtained by linearizing (differentiating) the constraints |z[k]|² = 〈z[k], z[k]〉 = 1 for all k, yielding

$${\mathrm{T}}_z\mathcal{M}=\{\stackrel{.}{z}\in {ℂ}^N:\langle z[k],\stackrel{.}{z}[k]\rangle =0,\forall k\}.$$

Orthogonal projection of u ∈ ℂ^N to the tangent space T_zℳ can be computed entry-wise by subtracting from each u[k] its component aligned with z[k]. Let Proj_z: ℂ^N → T_zℳ denote this projection. This operation admits a compact matrix notation as

$$\begin{gathered} u\mapsto {\text{Proj}}_z(u)=u-\mathfrak{R}\{u\circ \overline{z}\}\circ z \\ =u-\mathfrak{R}\{\text{ddiag}(u{z}^{\ast })\}z, \end{gathered}$$

where ddiag: ℂ^N×N → ℂ^N×N sets all non-diagonal entries of a matrix to zero. Equipped with this notion and the expression for ∇f(z) (V.5), it follows that the Riemannian gradient of f at z on ℳ is

$$\text{grad}f(z):={\text{Proj}}_z(\nabla f(z))=\nabla f(z)-D(z)z,$$

with

$$D(z):=\mathfrak{R}\{\text{ddiag}(\nabla f(z)z^{\ast })\}=\mathfrak{R}\{\text{diag}(\nabla f(z)\circ \overline{z})\}.$$

Lemma V.3

If z ∈ ℳ is optimal for (V.1), then grad f(z) = 0; equivalently, diag(∇f(z)z^*) = ∇f(z) ∘ z̄ is real.

Proof

See [72, Rem. 4.2 and Cor. 4.2]. For the equivalence, notice that Proj_z(u) = 0 if and only if $u[k]=\mathfrak{R}\{u[k]\overline{z[k]}\}z[k]$ for all k, and multiply by $\overline{z[k]}$ on both sides using |z[k]| = 1.

A point z which satisfies these conditions is called a critical point. Likewise, we can define a notion of Riemannian Hessian as the linear, self-adjoint operator on T_zℳ which captures infinitesimal changes in the Riemannian gradient around z. Without getting into technical details, we follow [71, eq. (5.15)] and define (with D the directional derivative operator):

$$\begin{gathered} \text{Hess}f(z)[\stackrel{.}{z}]:={\text{Proj}}_z(\mathrm{D}(z\mapsto \text{grad}f(z))(z)[\stackrel{.}{z}]) \\ ={\text{Proj}}_z({\nabla }^{2}f(z)[\stackrel{.}{z}]-D(z)\stackrel{.}{z}-(\mathrm{D}D(z)[\stackrel{.}{z}])z), \end{gathered}$$

where DD(z)[ż] is a real, diagonal matrix. Its contribution to the Hessian is zero, since (DD(z)[ż])z vanishes under the projection Proj_z. Hence,

$$\text{Hess}f(z)[\stackrel{.}{z}]={\text{Proj}}_z({\nabla }^{2}f(z)[\stackrel{.}{z}]-D(z)\stackrel{.}{z}).$$

The Riemannian Hessian intervenes in the second-order necessary optimality conditions as follows.

Lemma V.4

If z ∈ ℳ is optimal for (V.1), then grad f(z) = 0 and Hess f(z) ⪯ 0, that is, for all ż ∈ T_zℳ we have

$$\langle \stackrel{.}{z},\text{Hess}f(z)[\stackrel{.}{z}]\rangle =\langle \stackrel{.}{z},{\nabla }^{2}f(z)[\stackrel{.}{z}]\rangle -\langle \stackrel{.}{z},D(z)\stackrel{.}{z}\rangle \le 0.$$

Proof

See [72, Rem. 4.2 and Cor. 4.2]. In the equality, we used the fact that Proj_z is self-adjoint and ż ∈ T_zℳ.

A point z which satisfies these conditions is called a second-order critical point. With unit weights, the following lemma shows that second-order critical points z, in the noiseless case, cannot have an arbitrarily bad objective value f(z). This result is weak, however, since empirically it is observed that in the noiseless case local optimization methods consistently converge to global optima whose value are N², suggesting that all second-order critical points are global optima in this simplified scenario. While we do not have a proof for this stronger conjecture, we provide the lemma below because it is analogous to [17, Lemma 14] which, in that reference, is a key step toward proving global optimality of second-order critical points.

Lemma V.5

In the absence of noise and with unit weights, a second-order critical point z of (V.1) satisfies

$$\nabla f(z)\circ \overline{z}\ge 2(\sqrt{3}-1)>0.$$

In particular, this implies

$$f(z)=\frac{1}{3}\langle z,\nabla f(z)\rangle \ge \frac{2(\sqrt{3}-1)}{3}N.$$

Proof

See Appendix J for the proof of the inequality. It follows from two key considerations. First, because z is a critical point, Lemma V.3 indicates that ∇f(z) ∘ z̄ is real. Second, because z is second-order critical, the Riemannian Hessian at z must be negative semidefinite by Lemma V.4. Applied to all tangent directions at z which perturb only one phase at a time implies the desired inequality. The fact that 3f(z) = 〈z,∇f(z)〉 follows from (V.5).

One final ingredient that is necessary to optimize f overℳ is a means of moving away from a current iterate z ∈ ℳ to the next by following a tangent vector ż. A simple means of achieving this is through a retraction [71, Def. 4.1.1]. For ℳ, an obvious retraction is the following:

$${\text{Retr}}_z(\stackrel{.}{z})=\text{phase}(z+\stackrel{.}{z})\in \mathcal{M}.$$ (V.6)

With the formalism of (V.1) and the above derivations, we can now run a local Riemannian optimization algorithm. As an example, the Riemannian gradient ascent algorithm would iterate the following:

$$\begin{gathered} z^{(t+1)}={\text{Retr}}_{z^{(t)}}\left({\eta }^{(t)}\text{grad}f(z^{(t)})\right) \\ =\text{phase}\left(z^{(t)}+{\eta }^{(t)}\text{grad}f(z^{(t)})\right), \end{gathered}$$

where η^(t) > 0 is an appropriately chosen step size and z⁽⁰⁾ ∈ ℳ is an initial guess. It is relatively easy to choose the step sizes such that the sequence z^(t) converges to critical points regardless of z⁽⁰⁾, with a linear local convergence rate [71, §4]. In practice, we prefer to use the Riemannian trust-region method (RTR) [62], whose usage is simplified by the toolbox Manopt [63]. RTR enjoys global convergence to second-order critical points [64] and a quadratic local convergence rate.

In this section, the analysis focused on complex signals. For real signals, we can follow the same methodology while taking the symmetry in the Fourier domain into account. This analysis is given in Appendix B.

VI. Expectation maximization

In this section, we detail the expectation maximization algorithm (EM) [73] applied to MRA. As the numerical experiments in Section VII demonstrate, EM achieves excellent accuracy in estimating the signal. However, compared to the invariant features approach proposed in this paper, it is significantly slower and requires many passes over the data (thus excluding online processing).

Let X = [ξ₁, …, ξ_M] be the data matrix of size N × M, following the MRA model (I.1). The maximum marginalized likelihood estimator (MMLE) for the signal x given X is the maximizer of the likelihood function L(x; X) = p(X|x) (the probability density of X given x). This density could in principle be evaluated by marginalizing the joint distribution p(X, r|x) over the unknown shifts r ∈ {0, …, N−1}^M. This, however, is intractable as it involves summing over N^M terms.

Alternatively, EM tries to estimate the MMLE as follows. Given a current estimate for the signal x_k, consider the expected value of the log-likelihood function, with respect to the conditional distribution of r given X and x_k:

$$Q(x\mid x_k)={\mathbb{E}}_{r\mid X,x_k}\{logp(X,r\mid x_k)\}.$$ (VI.1)

This step is called the E-step. Then, iterate by computing the M-step:

$$x_{k+1}=arg\underset{x}{max}Q(x\mid x_k).$$ (VI.2)

For the MRA model, this can be done in closed form. Indeed, the log-likelihood function follows from the i.i.d. Gaussian noise model:

$$logp(X,r\mid x)=-\frac{1}{2{\sigma }^2}\sum _{j=1}^M{\Vert R_{r_j}x-{\xi }_j\Vert }_2^2+\text{constant}.$$ (VI.3)

To take the expectation with respect to r, we need to compute $w_k^{\ell ,j}$: for each observation j, this is the probability that the shift r_j is equal to ℓ, given X and assuming x = x_k. This also follows easily from the i.i.d. Gaussian noise model:

$$w_k^{\ell ,j}\propto exp\left(-\frac{1}{2{\sigma }^2}{\Vert R_{\ell }{x}_k-{\xi }_j\Vert }_2^2\right),$$ (VI.4)

(with appropriate scale so that ${\sum }_{\ell =0}^{N-1}{w}_k^{\ell ,j}=1$). This allows to write Q down explicitly:

$$Q(x\mid x_k)=-\frac{1}{2{\sigma }^2}\sum _{j=1}^M\sum _{\ell =0}^{N-1}{w}_k^{\ell ,j}{\Vert R_{\ell }x-{\xi }_j\Vert }_2^2+\text{constant}.$$

This is a convex quadratic expression in x with maximizer

$$x_{k+1}=\frac{1}{M}\sum _{j=1}^M\sum _{\ell =0}^{N-1}{w}_k^{\ell ,j}{R}_{\ell }^{-1}{\xi }_j.$$ (VI.5)

In words: given an estimator x_k, the next estimator is obtained by averaging all shifted versions of all observations, weighted by the empirical probabilities of the shifts. Considering all shifts of all observations would, in principle, induce an iteration complexity of O(MN²), but fortunately, for each observation, the matrix of its shifted versions is circulant, which makes it possible to use FFT to reduce the overall computational cost to O(MN logN). See the available code for details. We note that Matlab naturally parallelizes the computations over M.

In practice, we set x₀ ~ 𝒩(0, I_N) to be a random guess. Furthermore, for M ≥ 3000, we first execute 3000 batch iterations, where the EM update is computed based on a random sample of 1000 observations (fresh sample at each iteration). This inexpensively transforms the random initialization into a ballpark estimate of the signal. The algorithm then proceeds with full-data iterations until the relative change between two consecutive estimates drops below 10⁻⁵ (in ℓ₂-norm, up to shifts).

VII. Numerical Experiments

This section is devoted to numerical experiments, examining all proposed algorithms. Code for all algorithms and to reproduce the experiments is available online.³ The experiments were conducted as follows. The true signal x of length N = 41 is a fixed window of height 1 and width 21. With this signal, the signal-to-noise ratio is $\frac{{\Vert x\Vert }^2}{{\Vert \epsilon \Vert }^2}\approx \frac{1}{2{\sigma }^2}$. We generated a set of M shifted noisy versions of x as

$${\xi }_j=R_{r_j}x+{\epsilon }_j,$$

where each shift was randomly drawn from a uniform distribution over {0, …, N − 1} and ε_j ~ 𝒩(0, σ²I) for all j. The relative recovery error for a single experiment is defined as

$$\text{relative}\text{error}(x,\widehat{x})=\underset{s\in \{0,\dots ,N-1\}}{min}\frac{{\Vert R_s\widehat{x}-x\Vert }_2}{{\Vert x\Vert }_2},$$

where x̂ is the estimation of the signal. All results are averaged over 20 repetitions. While we present here results for a specific signal, alternative signal models (e.g., random signals) showed similar numerical behavior.

The following figures compare the recovery errors for all proposed algorithms, with random initialization for those that need initialization. The non-convex algorithm on the manifold of phases, Algorithm 2, runs the Riemannian trust-region method (RTR) [62] using the toolbox Manopt [63]. Algorithm 3 runs 15 iterations with warm-start using the same toolbox. For the phase unwrapping algorithm, Algorithm 6, we use an implementation of LLL available in the MILES package [70]. The SDP is solved with CVX [65]. The EM algorithm is implemented as explained in Section VI. We compared the algorithms with an oracle who knowns the random shifts r_j and therefore simply averages out the Gaussian noise. Experiments are run on a computer with 30 CPUs available. These CPUs are used to compute the invariants in parallel (with Matlab’s parfor), while the EM algorithm benefits from parallelism to run the many thousands of FFTs it requires efficiently (built-in Matlab). The algorithms that need ỹ[0] and ỹ[1] are given the correct values.

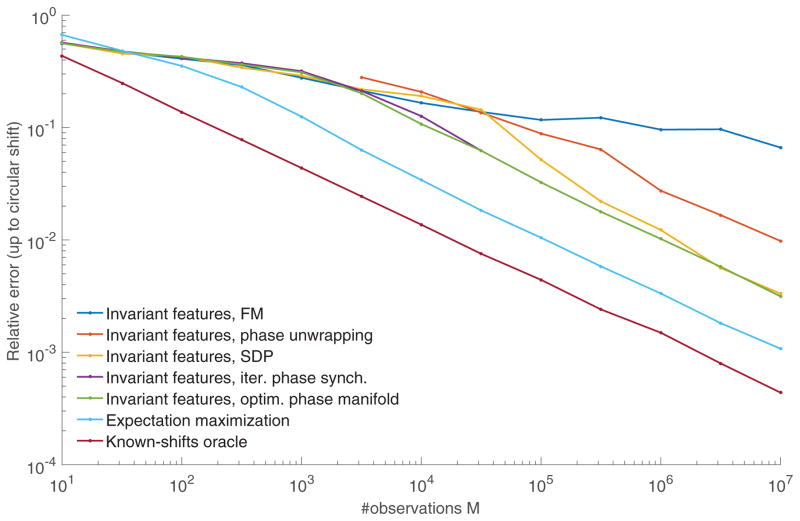
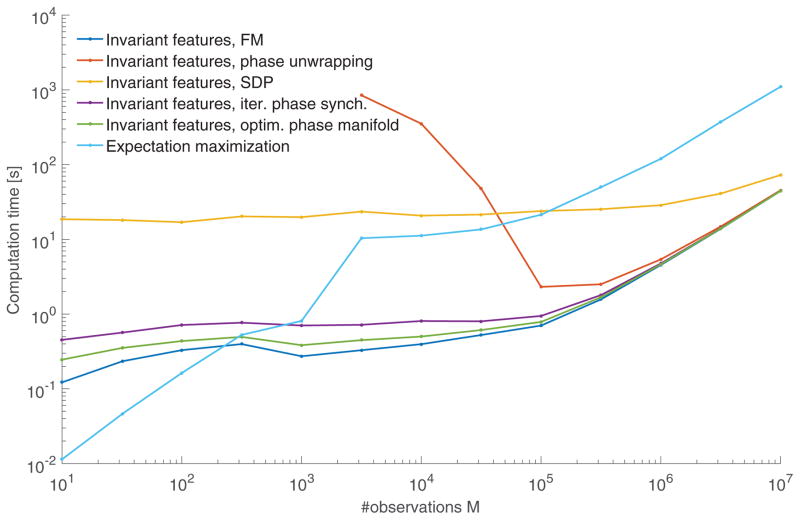
Figures VII.1 and VII.2 present the recovery error and computation time of all algorithms as a function of the number of observations M for fixed noise level σ = 1. Of course, the oracle who knows the shifts of the observations is unbeatable. Algorithms 2 and 3 outperform all invariant approach methods. The inferior performance of the SDP might be explained by the fact that we are minimizing a smooth non-linear objective. This is in contrast to SDPs with linear or piecewise linear objectives which tend to promote “simple” (i.e., low rank) solutions [74], [75, Remark 6.2]. Additionally, while this is not depicted on the figure, we note that for σ = 0 all methods get exact recovery up to machine precision. EM outperforms the best invariant features approaches by a factor of 3, at the cost of being significantly slower. For large M, the best invariant features approaches are faster than EM by a factor of 25. Note, however, that for M up to about 300, EM is faster than the other algorithms. For invariant features approaches (aside from the SDP), almost all of the time is spent computing the bispectrum estimator, while inverting the bispectrum is relatively cheap.

Figure VII.1.

Relative recovery error for the signal x as a function of the number of observations M for fixed noise level σ = 1. The curves corresponding to the optim. phase manifold (Algorithm 2) and the iter. phase synch. (Algorithm 3) overlap.

Figure VII.2.

Average computation times corresponding to Figure VII.1.

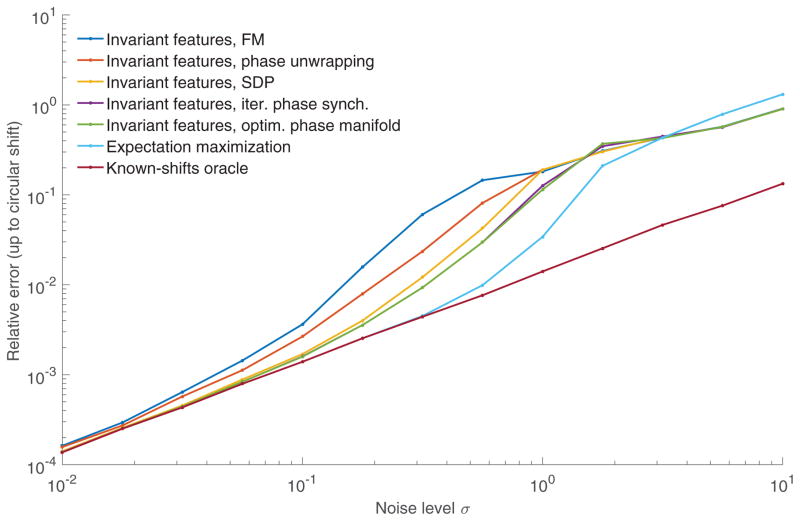
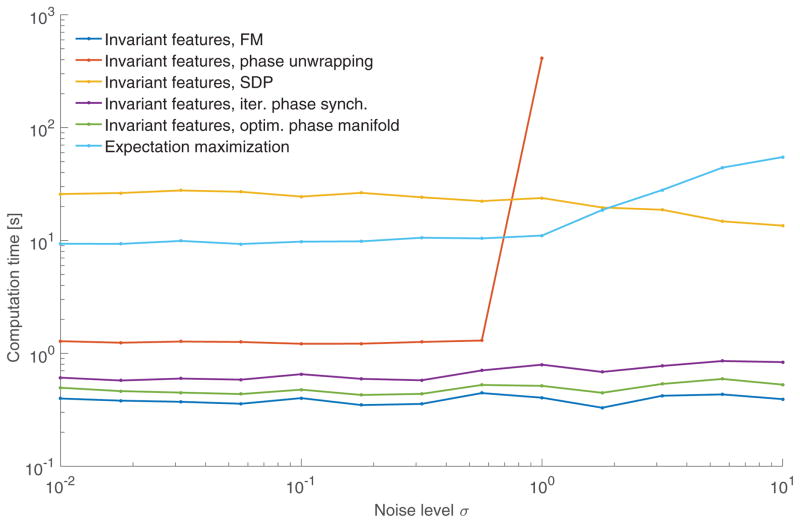
Figures VII.3 and VII.4 show the recovery error and computation time as a function of the noise level σ with M = 10,000 observations. Surprisingly, for high noise level σ ≳ 3, the invariant features algorithms outperform EM.

Figure VII.3.

Relative recovery error for the signal x as a function of the noise level σ with M = 10,000 observations. The curves corresponding to the optim. phase manifold (Algorithm 2) and the iter. phase synch. (Algorithm 3) overlap.

Figure VII.4.

Average computation times corresponding to Figure VII.3.

VIII. Conclusions and perspective

The goal of this paper is twofold. First, we have suggested a new approach for the MRA problem based on features that are invariant under translations. This technique enables us to deal with any noise level as long as we have access to enough measurements and particularly it achieves the sample complexity of MRA. The invariant features approach has low computational complexity and it requires less memory with respect to alternative methods, such as EM. If one wants to have a highly accurate solution, it can therefore be used to initialize EM.

A main ingredient of the invariant features approach is estimating the signal’s Fourier phases by inverting the bispectrum. Hence, the second goal of this paper was to study algorithms for bispectrum inversion. We have proposed a few algorithms for this task. In the presence of noise, the non-convex algorithms on the manifold of phases, namely, Algorithms 2 and 3, perform the best. Empirically, these algorithms have a remarkable property: despite their non-convex landscape, they appear to converge to the target signal from random initialization. We provide some analysis for Algorithm 2 but this phenomenon is not well understood.

Our chief motivation for this work comes from the more involved problem of cryo-EM. In cryo-EM, a 3D object is estimated from its 2D projections at unknown rotations in a low SNR environment. One line of research for the object recovery is based on first estimating the unknown rotations [76], [77], [78]. However, the rotation estimation is performed in a very noisy environment and therefore might be inaccurate. An interesting question is to examine whether the 3D object can be estimated directly from the acquired data using features that are invariant under the unknown viewing directions [79].