Multi-environment fitness landscapes of a tRNA gene

Abstract

A fitness landscape (FL) describes the genotype-fitness relationship in a given environment. To explain and predict evolution, it is imperative to measure the FL in multiple environments because the natural environment changes frequently. Using a high-throughput method that combines precise gene replacement with next-generation sequencing, we determine the in vivo FL of a yeast tRNA gene comprising over 23,000 genotypes in four environments. Although genotype-by-environment interaction (G×E) is abundantly detected, its pattern is so simple that we can transform an existing FL to that in a new environment with fitness measures of only a few genotypes in the new environment. Under each environment, we observe prevalent, negatively biased epistasis between mutations (G×G). Epistasis-by-environment interaction (G×G×E) is also prevalent, but trends in epistasis difference between environments are predictable. Our study thus reveals simple rules underlying seemingly complex FLs, opening the door to understanding and predicting FLs in general.

The fitness landscape (FL) of a gene in a given environment maps each mutational variant of the gene to the fitness of the organism carrying the variant. FLs allow explaining as well as predicting evolutionary trajectories, and are therefore of fundamental biological importance¹. Because fitness is expected to vary by environment, which frequently changes in nature, characterizing FLs in multiple environments offers not only more relevant and accurate evolutionary explanations and predictions but under certain circumstances also insights that are otherwise impossible to gain. For example, a gene that seems harmful to an organism in one environment is nonetheless retained in its genome, because it is beneficial in other environments². Two alleles at a locus may be respectively favored in two environments, resulting in a stable genetic polymorphism if the population switches sufficiently frequently between these environments^3,4. A population trapped at a suboptimal local fitness peak under one environment may escape upon an environmental shift, even if the environment later shifts back^5,6. Differences in FL between two environments may also lead to ecological speciation⁷. Notwithstanding, due to the huge genotype space (4ⁿ genotypes for a gene with n nucleotides), even the characterization of a small fraction of the FL of a gene under one environment had been a formidable challenge until recently^8-13. As a result, past quantifications of FLs typically probe only one environment. Adopting a recently developed high-throughput method⁹ with minor modifications, we map the in vivo FL of a tRNA gene in four environments in order to study the environmental impact on FLs. Of particular interest are genotype-by-environment interactions (G×E) and epistasis-by-environment interactions (G×G×E). In humans, G×E has been implicated in numerous diseases such as cancer and mental disorders^14,15. Epistasis, or interaction between mutations (G×G), has multiple important functional and evolutionary implications¹⁶ and is known to vary among environments^17-22. Because the method employed can measure the fitness of tens of thousands of genotypes⁹, the collected data permit the quantification of G×E and G×G×E at an unprecedentedly large scale, providing opportunities for identifying general principles of these interactions.

Results

Mapping multi-environment FLs of a tRNA gene

${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ is a transfer RNA that uses its anticodon 5′-CCU-3′ to bind to the arginine codon AGG in translation. It is encoded by a single-copy gene (HSX1) in the budding yeast Saccharomyces cerevisiae. Deleting this gene is nonlethal, because ${\text{tRNA}}_{\text{UCU}}^{\text{Arg}}$, another tRNA for arginine, can wobble-pair with AGG. We synthesized the 72-nucleotide ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene with a 3% per-site mutation rate (1% to each alternative nucleotide) at 69 sites; the remaining three sites were kept invariant for technical reasons⁹ (Fig. 1; see Methods). This mutation rate was chosen to maximize the representation of genotypes carrying two mutations for the purpose of studying epistasis between mutations (see Methods). We constructed a library of more than 100,000 yeast strains, each carrying a ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene variant at its native genomic location. Three to five parallel competitions of this strain pool were conducted in each of four environments: 30°C in the rich medium YPD (hereafter Env₃₀), 23°C in YPD (Env₂₃), 37°C in YPD (Env₃₇), and 30°C in YPD with 3% dimethyl sulfoxide (DMSO) added (Env_DMSO) (Fig. 1). Among them, Env₃₀ is the optimal growth condition for the wild-type yeast strain used, with the other environments imposing cold, heat, and oxidative stresses²³, respectively. The selection of these four environments was based on previous studies showing that tRNA folding and decay are temperature-dependent^24-26 and RNA structure and function are affected by DMSO²⁷.

Figure 1. Determining the fitness landscape of the yeast ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene in multiple environments.

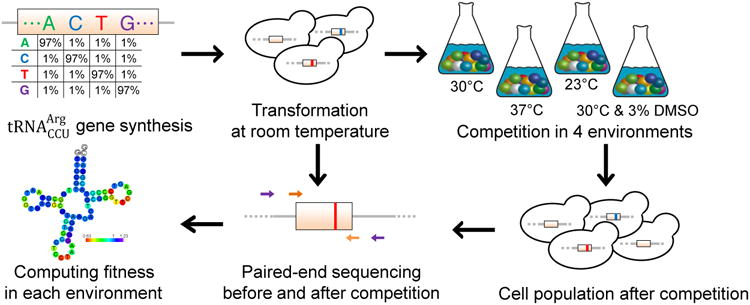
Chemically synthesized ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene variants are incorporated at the native genomic locus of the gene. Transformation is conducted at room temperature to ensure comparatively equal representation of mutant strains. The tRNA variant-carrying cells compete for ∼13 generations in each environment at log phase, and the tRNA gene variants are sequenced before and after the competition. The fitness of each ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ genotype relative to wild-type is calculated from the relative frequency change of paired-end sequencing reads covering the tRNA gene variant during competition.

The wild-type yeast growth rates (GR) in these four environments show GR(Env₃₀) > GR(Env_DMSO) > GR(Env₃₇) > GR(Env₂₃), while the gene importance (GI) to growth, measured by the fractional reduction in growth rate caused by deleting the tRNA gene, shows GI(Env₃₇) > GI(Env_DMSO) > GI(Env₃₀) > GI(Env₂₃) (Supplementary Fig. S1). The ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene is more important to cell growth at higher temperatures probably because the probability that ${\text{tRNA}}_{\text{UCU}}^{\text{Arg}}$ is correctly folded decreases with temperature, reducing its ability to compensate the loss of the ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene.

After the competition, the ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene amplicons from each replicate competition (T₁) under each environment, as well as those from the common starting population (T₀; with two technical repeats), were sequenced with 125-nucleotide paired-end Illumina sequencing (Fig. 1). The sequences provide the ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ genotype as well as genotype frequency information. A total of 881 million read pairs were generated. Read numbers per genotype are highly correlated between technical repeats (Pearson's correlation r =0.994; Supplementary Fig. S2a) and between biological replicates (r =0.9911-0.9999; Supplementary Fig. S2b). The technical repeats are combined in subsequent analysis. The fitness of each genotype relative to the wild-type (fitness hereafter) in an environment was estimated using the genotype frequencies at T₀ and T₁ as well as the number of wild-type generations in the competition (see Methods). We analyzed 23,284 genotypes with read counts ≥100 at T₀. Because the ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene is nonessential, mutations in the gene are unlikely to be lethal. When an estimated fitness is < 0.5 (likely due to stochasticity), we set it at 0.5, meaning that the genotype has no growth⁹.

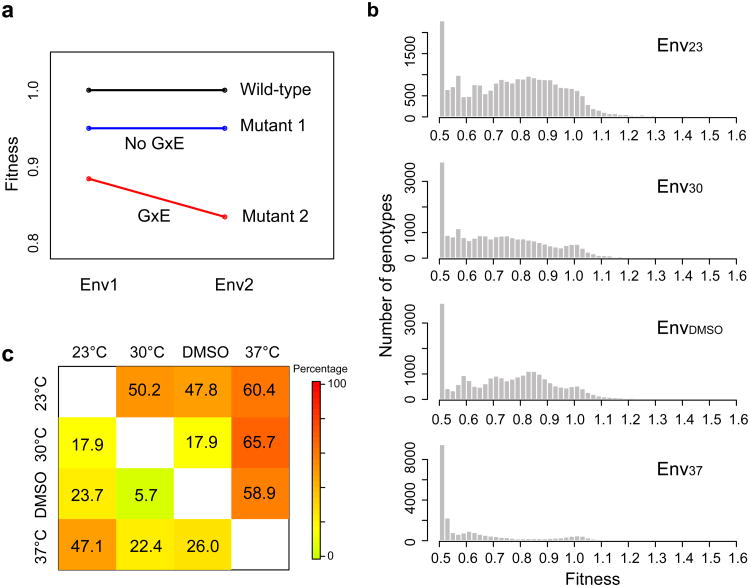
G×E is pervasive

We previously reported the FL of the yeast ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene in Env₃₇ and its reliability, consistency with evolutionary data, and potential mechanistic basis⁹. With the FL data in four environments, we here focus on the impact of the environment on the FL rather than describing the FL under each environment. Specifically, we study whether the same mutation has different fitness effects in different environments, formally known as genotype-by-environment interaction²⁸ (G×E) in fitness (Fig. 2a). Under the null hypothesis of no G×E, the fitness effect of a mutation is environment-independent, and hence the mutant fitness distribution should be identical across environments. In stark contrast to this null expectation, the mutant fitness distribution differs drastically among each pair of the four environments (P < 10^-300, Kolmogorov-Smirnov test; Fig. 2b), suggesting pervasive G×E in our data. Mean mutant fitness (F̄) shows F̄(Env₂₃) > F̄(Env₃₀) > F̄(Env_DMSO) > F̄(Env₃₇), exactly opposite to the aforementioned order of GI in the four environments. That is, mean mutant fitness decreases as gene importance in the environment rises. Although testing G×E for individual genotypes has a much-reduced statistical power, a substantial fraction showed significantly different fitness values between environments (nominal P < 0.05, t-test; lower left triangle in Fig. 2c). This fraction generally increases with the extent of environmental difference that can be gauged (e.g., temperature difference). It also increases for genotypes carrying a single point mutation (N1 mutants; upper right triangle in Fig. 2c), owing to their relatively high genotype frequencies in the strain pool that lead to relatively high numbers of sequencing reads, which empower the statistical test. Because only 5% of genotypes are expected by chance to show significantly different fitness values between any pair of environments under the null hypothesis of no G×E, our findings establish the prevalence of G×E. In some studies, G×E is defined by a between-environment variation in the growth rate difference between a genotype and the wild-type^28-31. Pervasive G×E is also found when growth rate difference instead of relative fitness is used in the definition of G×E (Supplementary Fig. S3; see Methods).

Figure 2. The yeast ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene fitness landscape in each of the four environments examined.

a, Definition of G×E based on mutant fitness relative to the wild-type in two environments. b, Frequency distribution of the fitness of all 23,284 genotypes in each environment. Note the different scales on the Y axis for different environments. c, Fraction of mutants exhibiting significant G×E. The lower left triangle shows the fraction of all genotypes whose fitness values differ significantly between the two environments compared (nominal P < 0.05, t-test), whereas the upper right triangle shows the corresponding fraction of N1 mutants.

Quantitative relationship in genotype fitness between environments

Despite the abundance of G×E, the fitness of a genotype in one environment exhibits a strong linear correlation with that in another environment (r = 0.78 - 0.94; lower left triangle in Fig. 3a), especially for N1 mutants (r = 0.94 - 0.99; upper right triangle in Fig. 3a), which generally have more precise fitness estimates than mutants carrying two or more mutations. The correlation is confirmed by individually measuring the fitness of 55 mutants across the four environments on the basis of growth curves (r = 0.85 - 0.96; Supplementary Fig. S4).

Figure 3. A piecewise linear model predicts fitness landscape in one environment from that in another environment.

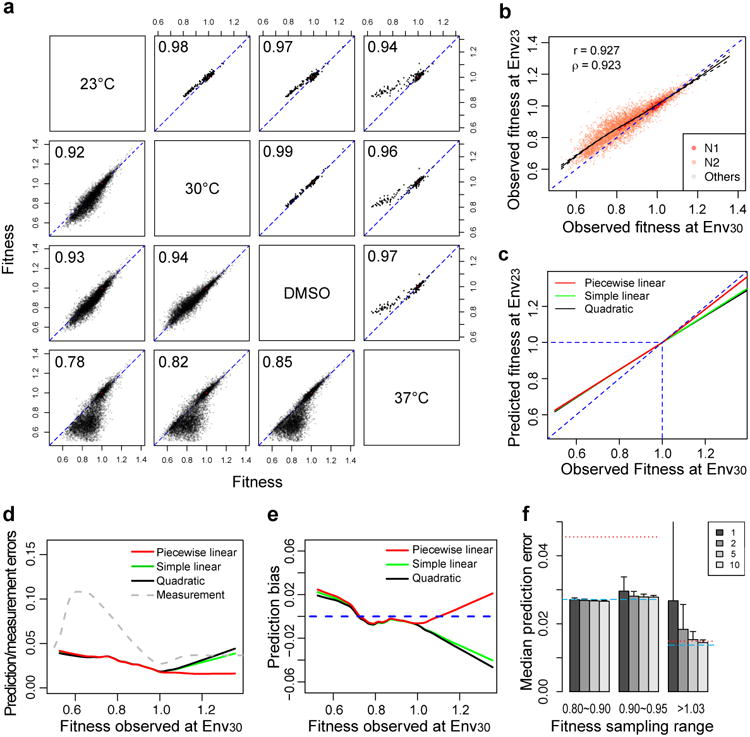
a, Fitness values from two environments are highly correlated among all mutants (lower left triangle), especially N1 mutants (upper right triangle). Pearson's correlation coefficient is presented for each environment pair. b, LOESS curve (black solid curve) describing the relationship between genotype fitness in Env₃₀ and Env₂₃, with 95% confidence intervals indicated (black dashed curves). In a and b, each dot is a genotype, and the diagonal is indicated by a blue dashed line. c, A piecewise linear model, a simple linear model, and a quadratic model are respectively plotted to capture the relationship between genotype fitness in Env₃₀ and Env₂₃. The blue dashed lines show Y=X, X=1, and Y=1, respectively. d, Prediction error and measurement error of fitness at Env₂₃. The three solid curves respectively show prediction errors under three different prediction models when fitness at Env₂₃ is predicted from that in Env₃₀, whereas the grey dashed curve shows the measurement error based on one measurement at Env₂₃. e, Prediction bias of fitness at Env₂₃. The three solid curves respectively show prediction bias under three different models when predicting fitness at Env₂₃ from that in Env₃₀. The blue dashed line shows zero bias. f, Measuring fitness of only a few mutants in Env₂₃ is sufficient for deriving the (piecewise) linear model used in predicting the fitness landscape in Env₂₃ from that in Env₃₀. When 1, 2, 5, or 10 N1 mutants (indicated by different shades of grey) chosen for fitness measurement at Env₂₃ have fitness in Env₃₀ (f₃₀) < 1, median prediction errors shown are for all mutants with f₃₀ < 1. When N1 mutants chosen for fitness measurement at Env₂₃ have f₃₀ > 1, median prediction errors shown are for all mutants with f₃₀ > 1. The x-axis shows the f₃₀ range in which mutants are randomly picked for fitness measurement at Env₂₃. Blue dashed lines show median prediction errors when all genotypes are measured for fitness at Env₂₃. Red dotted lines show median prediction errors assuming no G×E.

To more accurately describe the relationship of genotype fitness in two environments, we plotted a local regression (LOESS) of the fitness in Env₃₀ (f₃₀) and the fitness in Env₂₃ (f₂₃) across all genotypes (Fig. 3b). As expected, the regression goes near the point of (f₃₀ = 1, f₂₃ = 1) because of a large number of genotypes showing similar fitness as the wild-type. The regression suggests that the data can be described approximately by a piecewise linear model of f₂₃-1 = k(f₃₀-1), with one slope (k_a) for genotypes of f₃₀ < 1 and a different slope (k_b) for genotypes of f₃₀ >1 (see Supplementary Table S1 for other environment pairs). In other words, the fitness effect of a mutation in Env₂₃ (i.e., f₂₃-1) is proportional to that in Env₃₀ (i.e., f₃₀-1). We observed a general trend that k_b is closer to 1 than is k_a (i.e., |k_b-1| < |k_a-1|) across all environment pairs (Fig. 3b; Supplementary Table S1). This pattern may reflect different properties of deleterious and beneficial mutations other than their effect size differences, because the same trend holds even for deleterious and beneficial mutations of comparable fitness effect sizes. We also respectively tested a simple linear model with only one parameter and a quadratic model in describing the between-environment fitness relationships. Although the quadratic model generally outperforms the simple and piecewise linear models, the coefficient of the quadratic term is small. Also, the advantage of the quadratic model over the piecewise linear model, measured by the difference in the fraction of variance explained, is small (Supplementary Table S2). Furthermore, this advantage arises from the fact that the vast majority of genotypes are less fit than the wild-type (Fig. 2b) and that the quadratic model allows one more parameter than the piecewise linear model to describe these genotypes. When equal numbers of genotypes that are fitter and less fit than the wild-type are considered, the piecewise linear model generally performs the best (Supplementary Table S3). Because of the distinct biological meanings and evolutionary roles of deleterious and beneficial mutations, the piecewise linear model, which has equal weights for these two types of mutations in fitting, appears more appropriate.

Predicting the FL under new environments

To evaluate how well the piecewise linear model (Fig. 3c) predicts the f₂₃ of a genotype from its f₃₀ estimate, we focused on 6319 genotypes that have relatively precise experimental estimates of f₃₀ and f₂₃ (with ≥ 500 reads at T₀ and ≥ 1 read at T₁ in each of the five replicates under each of the two environments). Such restriction is necessary because of the difficulty in judging whether a prediction is good or not by comparing it with an actual measurement that is imprecise. We treated the f₂₃ of a genotype estimated from the mean of five biological replicates as the observed value. The predicted and observed f₂₃ values are highly correlated (Spearman's ρ = 0.908, Pearson's r = 0.915, P < 10^-300 in both tests). We define prediction error by the absolute difference between the observed and predicted f₂₃. By contrast, measurement error is the mean absolute difference between the observed f₂₃ and that estimated from one biological replicate. Remarkably, the prediction error is no greater than the measurement error across the entire range of f₃₀ in our data (Fig. 3d), and this pattern holds for four of the 12 environment pairs (Supplementary Fig. S5). In addition, we quantified the prediction bias by the median difference between the predicted and observed f₂₃, and found it to be minimal except when f₃₀ < 0.6 (Fig. 3e), which is expected (see Methods). For comparison, we respectively tested a linear model with one k and a quadratic model (Fig. 3c). These two models have larger biases and errors when f₃₀ > 1 but are otherwise similar in performance to the piecewise linear regression (Fig. 3d, e). These observations hold in all 12 pairwise predictions from one environment to another (Supplementary Fig. S5). Another performance indicator of our prediction is the fraction of predictions that deviate significantly from the observation. Only 0.51% of the 6319 predictions of f₂₃ from f₃₀ belong to this category (FDR = 0.05).

In the above exercise, the prediction model is determined by comparing the FLs respectively measured in Env₃₀ and Env₂₃. In practice, we would measure the FL in Env₃₀ and then predict it in Env₂₃. Because the piecewise linear model involves only two parameters (k_a and k_b), in principle we need to measure the fitness of only two genotypes, respectively fitter and less fit than the wild-type, in Env₂₃ to parameterize the model. This is indeed the case, as long as the f₃₀ of the genotypes chosen for fitness measurement in Env₂₃ is not too close to 1 (Fig. 3f). This pattern holds for most of the 12 environment-to-environment fitness predictions (Supplementary Fig. S6).

Epistasis between mutations is negatively biased

We estimated epistasis between mutations in the tRNA gene using the fitness estimates of all 207 N1 mutants and 8,101 double mutants (N2 mutants) (see Methods). In each environment, a large fraction of mutation pairs show significant epistasis and the epistasis is strongly biased toward negative values (Fig. 4a; Supplementary Fig. S7) except at paired sites (Supplementary Fig. S8), similar to observations in other molecules^8,12,32. Furthermore, the average fitness of all genotypes carrying the same number (≥ 2) of mutations is lower than expected under the multiplicative model, again indicating pervasive negative epistasis (Fig. 4b).

Figure 4. Epistasis-by-environment interaction is prevalent.

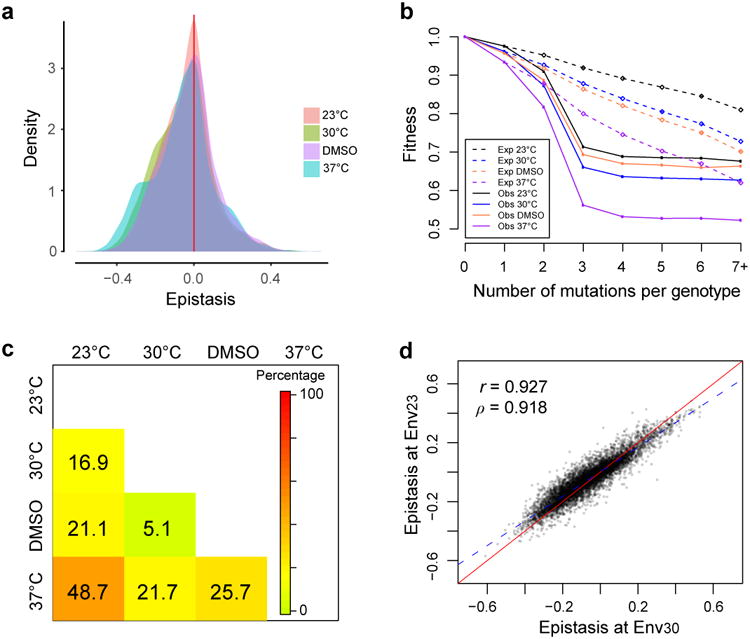
a, Frequency distributions of 8,101 epistasis between mutations in four environments. b, Observed mean fitness of mutants carrying a given number of mutations (solid dots) is lower than expected under no epistasis (open diamonds) in each environment. c, Fractions of mutation pairs that exhibit significant G×G×E for each environment pair (nominal P < 0.05, t-test). d, Epistasis measured in Env₂₃ and that measured in Env₃₀ are highly correlated. Pearson's correlation (r) and Spearman's correlation (ρ) are indicated. The red solid line shows the diagonal, whereas the blue dashed line shows the linear regression.

Epistasis by environment interaction is prevalent

Except for the pair of Env₃₀ and Env_DMSO in which mutant fitness values are similar (Fig. 2c), a substantial fraction of epistasis varies between environments (Fig. 4c), revealing prevalent epistasis-by-environment interactions (G×G×E). G×G×E is also abundantly observed under a commonly used alternative definition of epistasis (Supplementary Fig. S9).

Given that the fitness of a genotype in one environment can be predicted from that in another environment and that epistasis is estimated from the fitness values of three relevant genotypes, it is possible to predict epistasis in one environment from the fitness data in another environment (see Methods). Nevertheless, epistasis prediction is expected to be less precise than fitness prediction, because each epistasis prediction relies on three fitness predictions. Not with standing, predicting the general trend in epistasis changes upon an environmental shift may be sufficiently reliable, because errors in individual epistasis predictions are random and do not alter the general trend. Our prediction of epistasis at Env₂₃ from the fitness data at Env₃₀ suggests a strong, positive correlation in epistasis between the two environments (Supplementary Fig. S10), which is confirmed by a comparison of epistasis respectively measured in the two environments (Fig. 4d; Supplementary Fig. S11). We also predict that epistasis holds the same direction across environments for most albeit not all mutation pairs (Supplementary Fig. S10), as is observed (Supplementary Table S4). We further predict that, when the mean fitness effect of mutation enlarges upon an environmental shift (e.g., from Env₃₀ to Env₃₇), switches from positive to negative epistasis outnumber the opposite switches, which is confirmed by our data (Supplementary Table S4). Nevertheless, none of the predicted epistasis sign switches show significant epistasis in each of the two environments concerned and exhibit an epistasis sign switch, likely due to the relatively large error in predicting the epistasis of specific mutation pairs.

Discussion

In summary, we detected widespread G×E in the FLs of the yeast ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene across four environments, echoing accumulating reports of G×E in humans and model organisms^14,15,29,33 and supporting the importance of mapping FLs in multiple environments. Our discovery of a simple rule of G×E provides a convenient and reliable computational means to transform the FL from one environment to another with minimal additional experiments. Our observation that the fitness effect of a mutation can be linearly transformed between environments is equivalent to the statement that the ratio between the fitness effects of any two deleterious (or beneficial) mutations (say A and B) in a gene is roughly constant irrespective of the specific environment. When mutation B is a null mutation, the ratio measures the fraction of the gene's fitness contribution impacted by mutation A. The constancy of this ratio among environments leads to the interpretation that, while a gene's fitness contribution may vary among environments^2,34, a mutation in the gene influences the gene's fitness contribution by a fixed proportion that is independent of the environment. The above interpretation does not depend on the specific mechanism by which a mutation affects fitness. One critical question is whether our discovery in a yeast tRNA gene applies to other genes (especially protein-coding genes) and other organisms. To address this question, we analyzed the local FLs of a segment of the yeast heat shock protein Hsp90 gene in four environments³⁵ and found that the observed patterns (Supplementary Fig. S12) resemble those in the tRNA gene. Further verifications, especially in other organisms, are needed when more multi-environment FLs become available in the future. Note that because the fitness contribution of one gene may rise while that of another may decrease upon an environmental shift, the between-environment transformation of FL is expected to be gene-specific.

We also detected widespread G×G×E, which were previously reported at much smaller scales^17-22. Because of the broad functional and evolutionary implications of epistasis, between-environment differences in epistasis cannot be ignored, especially in those rare cases where an environmental shift reverses the sign of epistasis.

In previous studies, we and others provided evidence that FLs of RNA genes under a given environment can be explained to a significant extent by RNA folding^8,9. In the present work, our FL mapping across environments suggests that a mutation in the ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene influences the gene's fitness contribution by a fixed proportion that is independent of the environment. We also explained mechanistically why the tRNA gene has a larger fitness contribution at a higher temperature, at least qualitatively. Together, they suggest that FLs of RNA genes can be understood from a molecular mechanistic perspective and hence predicted from relevant information without exhaustive or extensive experimental mapping. Further endeavors toward this goal for both RNA and protein genes are likely to be highly rewarding.

Methods

Measuring genotype fitness in multiple environments

The chemical synthesis of the yeast ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene with random sequence variation was previously described⁹. Briefly, because IDT (https://www.idtdna.com/site) could not synthesize oligonucleotides longer than 100 nucleotides that require manual mixing of nucleotides and because there is a need for constant regions at the two ends of the oligonucleotides for polymerase chain reaction (PCR), we could only allow 69 variable sites in the tRNA gene. Hence, the first nucleotide and last two nucleotides (counting from the 5′ end) of the 72-nucleotide tRNA gene were invariant and synthesized according to the wild-type sequence. At each variable site, the probability of incorporating each of the three non-wild-type nucleotides was set at 0.01. This “mutation” rate was chosen to maximize the fraction of variants carrying two mutations in order to study pairwise epistasis. In the pool of tRNA gene variants synthesized, the fractions of molecules with 0, 1, 2, 3, 4 and >4 mutations are expected to be 12%, 26%, 27%, 19%, 10%, and 6%, respectively, while the possible numbers of variants with 0, 1, 2, 3, and 4 mutations are 1, 207, 2.1×10⁴, 1.4×10⁶, and 7.0×10⁷, respectively. Hence, the expected genotype frequency for a given genotypes with 0, 1, 2, 3, and 4 mutations is 0.12, 1.26×10^-3, 1.29×10^-5, 1.36×10^-7, and 1.43×10^-9, respectively. Previous sequencing data verified these expectations⁹.

Strain construction, competition assay, and library preparation were conducted as previously described⁹ except that KAPA HiFi HotStart DNA Polymerase instead of AccuPrime™ Pfx DNA polymerase was used for PCR amplification to further increase the accuracy of genotyping. In short, we collected over 100,000 BY4742 yeast strains carrying ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene variants at its native genomic location and mixed them as the starting strain pool. Cells derived from the same starting population were cultured in four separate environments and were transferred every few hours to grow in log phase for ∼13 generations. The exact number of generations for the whole population was computed by tracking optical density at 660 nm (OD660) over time, and the number of generations for the wild-type was then inferred from its frequency change in the population. Five parallel competitions were conducted in Env₂₃ and Env₃₀, respectively, whereas three parallel competitions were conducted in Env_DMSO and Env₃₇, respectively. Cells were then harvested and lysed to extract DNA. Two rounds of PCR amplification were conducted to amplify the ${\text{tRNA}}_{\text{CCU}}^{\text{Arg}}$ gene incorporated at the correct genomic location and to add adaptors for sequencing, respectively⁹. We sequenced the common population before the competition in two technical repeats and the population after each competition.

Only perfectly matched fully overlapping paired-end reads were used in estimating genotype frequencies. The change in relative genotype frequency during the competition was used to estimate the fitness of each genotype relative to the wild-type. The fitness of a genotype is calculated by averaging the fitness among biological replicates. To ensure relatively accurate fitness estimation, we focused on 23,284 genotypes with read counts ≥ 100 before the competition unless otherwise mentioned. The reliability of genotype fitness estimation using en masse competition followed by sequencing was previously demonstrated by comparing with three other methods⁹. In the present study, the biological replicates allow the assessment of estimation error.

Quantifying growth rates and fitness of selected genotypes

The growth rates of selected yeast strains were measured using Bioscreen C OD reader in the specific environment considered. Cells were first grown overnight until saturation, and then diluted by a factor of 50 to roughly OD600 = 0.1. OD measurements at the wide band (450-580 nm) were taken every 20 minutes for 48 hours. The maximum growth rate was calculated following standard procedures³⁶. At least two biological replications in growth measurement were performed per genotype per environment. The fitness (f) of a genotype relative to the wild-type was calculated by $2^{(R/R_0-1)}$, where R and R₀ are the maximum growth rates of the genotype and wild-type, respectively. The above formula was derived the following way. After one generation of exponential growth of a population of wild-type cells, we have e^R₀T = 2, where T is the generation time of the wild-type. Similarly, we have e^RT = 2f for the genotype concerned. Combining the above two equations, we obtain $f=2^{(R/R_0-1)}$.

Quantifying G×E and G×G×E

Based on fitness estimates in multiple biological replicates, a t-test is used to examine if the fitness of a genotype (relative to the wild-type) is significantly different between two environments at a nominal P-value of 0.05, which constitutes G×E. In addition to the G×E definition used in the main text (i.e., the fitness of a genotype relative to the wild-type differs between environments), we also used an alternative definition of G×E that the growth rate difference between a genotype and the wild-type varies between environments^28,29.

Epistasis is defined by ε = f_AB – f_Af_B, where f_A and f_B are the fitness values of two single mutants and f_AB is the fitness of the corresponding double mutant. We similarly tested G×G×E by examining if epistasis is significantly different between two environments, using a t-test at a nominal P-value of 0.05. We also tested G×G×E using an alternative definition of epistasis: ε′ = ln f_AB –ln f_A –ln f_B³⁷.

Piecewise robust linear regression between fitness values in two environments

Local regression (LOESS) with a span of 0.5 was used to visualize the general trend in the relationship between mutant fitness measured in two environments. Using the rlm function of the MASS package in R, we conducted a piecewise robust linear regression between the fitness at one environment and that at another for genotypes with ≥ 500 reads at T₀ and ≥ 1 read at T₁ in each biological replicate of the two environments concerned. Compared with the ordinary least squares linear regression, the robust linear regression reduces the potential impact of outliers. The model is fitted separately for genotypes fitter than the wild-type and those less fit than the wild-type. The regression is forced to go through (1, 1), because the relative fitness is defined as 1 for the wild-type in each environment. Specifically, our regression model is

$$\{\begin{array}{cc}{f}_2-1=k_a(f_1-1),& \text{if}{f}_1\le 1\\ f_2-1=k_b(f_1-1),& \text{if}{f}_1>1\end{array},$$

where f₁ and f₂ are the fitness values of a genotype in environment 1 and 2, respectively.

In addition, we tried two alternative models to regress the fitness estimates from two environments. The first alternative model is a simple robust linear model that goes through (1, 1) without separate slopes for genotypes fitter than the wild-type and those less fit than the wild-type. The second alternative model is a quadratic model that goes through (1, 1). We calculated adjusted R² to represent the fraction of variance in fitness explainable by each model. None of the above models would be accepted if correlations between observations and predictions are weak, prediction errors are large, or genotypes with significant prediction errors are numerous.

Evaluating fitness predictions

We can treat the regression line between fitness values in two environments as predictions of fitness in environment 2 from those in environment 1. Two metrics were used to evaluate these predictions. The first metric is prediction error, which is the absolute difference between the predicted and observed fitness in environment 2. Here the observed fitness is the mean of the measured fitness across all biological replicates. As a comparison, we compute measurement error, which is the absolute difference between the fitness estimated from one biological replicate and that averaged across all biological replicates in environment 2. The second metric is prediction bias, which is the difference between the predicted and observed fitness in environment 2. A LOWESS (local polynomial regression) curve fitting is used to acquire a general trend of the prediction error, measurement error, and prediction bias across different fitness ranges (with the smoother span =0.2). As shown in Fig. 3e, we observed a relatively large positive bias for the prediction of f₂₃ at the low fitness end (f₃₀< 0.6). This bias is expected for the following reason. When f₃₀ < 1, f₂₃ is generally higher than f₃₀ (Fig. 3a). Because here we analyze only those genotypes that have ≥1 read at T₁ in both Env₂₃ and Env₃₀, f₃₀ is more likely to be overestimated than f₂₃, which led to a positive prediction bias of f₂₃. In identifying outliers, fitness at Env₂₃ was individually predicted from the fitness values of five biological replicates at Env₃₀ using the piecewise linear model. A t-test was then used to compare the five predicted and five observed fitness values at Env₂₃, followed by a correction for multiple testing with a cutoff of FDR = 0.05.

To predict the FL in a new environment using FL in an old environment and the fitness measures of a few genotypes in the new environment, we randomly picked (without replacement) various numbers of N1 mutants whose fitness values in the old environment are within designated ranges. We used the fitness measures of these mutants in both environments to construct a robust linear model, which was then used to predict the FL in the new environment. We repeated this process 1000 times and computed the prediction bias and error as aforementioned from each repeat. Note that a mutant may be used in multiple replicates.

Expected fitness under no epistasis

Under the assumption of no epistasis, the expected fitness of a genotype carrying n mutations is the product of the fitness of the n constituent N1 mutants or 0.5 whichever is larger.

Predicting epistasis in a new environment

For two N1 mutants and the corresponding double mutant, we first predict their fitness in environment 2 from their measured fitness in environment 1. We then use the definition of epistasis to predict the epistasis between the two mutations in environment 2 from the three predicted fitness values in environment 2. This predicted epistasis in environment 2 is compared with the corresponding epistasis in environment 1.

Let the fitness of two N1 mutants and the corresponding N2 mutant be f_A, f_B, and f_AB in environment 1 and f'_A, f'_B, and f'_AB in environment 2, respectively. Because the vast majority of N1 and N2 mutants are less fit than the wild-type, we assume that formula (f′-1) = k(f-1) holds for all three genotypes considered here. It can be shown that the difference in epistasis between the two environments is

$$\begin{array}{c}{\varepsilon }_2-{\varepsilon }_1=(f_{AB}^{\text{'}}-f_A^{\text{'}}{f}_B^{\text{'}})-(f_{AB}-f_A{f}_B)\\ =-(k-1)[k(1-f_A)(1-f_B)+k{f}_A{f}_B-{\varepsilon }_1].\end{array}$$

When the mean fitness effect of mutations enlarges upon an environmental shift, k > 1. Thus, when ε₁ < 0, which occurs to most pairs of mutations, ε₂ – ε₁ is negative. This result explains why negative epistasis rarely becomes positive upon an environmental shift that enlarges the mean fitness effect of mutations.

Analysis of a previously published fitness landscape

For most FL mapping in the past, the exact number of generations in the competition was not reported, and hence the data cannot be used to estimate the fitness per generation. Here, we focused on a dataset that allowed estimation of fitness per generation. The dataset contains 189 mutants, representing all 20 amino acids and a stop codon at each of nine examined positions of yeast Hsp90 ³⁵. The fitness data were collected in four environments: low salinity in 30°C (30L), high salinity in 30°C (30H), low salinity in 36°C (36L), and high salinity in 36°C (36H). Because no mutant showed a fitness > 1.01 at 30L or 36L, we fitted a simple linear model with a single slope k for prediction of FL in one environment from that in another. If the predicted fitness was < 0.5, the lower bound value of 0.5 was assigned.

Data availability

The NCBI accession number for the sequencing data is GSE111508. Other data are available upon request.

Code availability

The computer code is available on github.com/lichuan199010/tRNAMultiEnv.