Local interactions underlying collective motion in human crowds

Abstract

It is commonly believed that global patterns of motion in flocks, schools and crowds emerge from local interactions between individuals, through a process of self-organization. The key to explaining such collective behaviour thus lies in deciphering these local interactions. We take an experiment-driven approach to modelling collective motion in human crowds. Previously, we observed that a pedestrian aligns their velocity vector (speed and heading direction) with that of a neighbour. Here we investigate the neighbourhood of interaction in a crowd: which neighbours influence a pedestrian's behaviour, how this depends on neighbour position, and how the influences of multiple neighbours are combined. In three experiments, a participant walked in a virtual crowd whose speed and heading were manipulated. We find that neighbour influence is linearly combined and decreases with distance, but not with lateral position (eccentricity). We model the neighbourhood as (i) a circularly symmetric region with (ii) a weighted average of neighbours, (iii) a uni-directional influence, and (iv) weights that decay exponentially to zero by 5 m. The model reproduces the experimental data and predicts individual trajectories in observational data on a human ‘swarm’. The results yield the first bottom-up model of collective crowd motion.

1. Background

Striking displays of collective motion are observed in a variety of species, from flocks of starlings and schools of herring to crowds of pedestrians in public spaces [1,2]. Under certain conditions, groups of individuals coordinate their speed and heading (direction of travel) to yield patterns of coherent motion. A better understanding of the dynamics of human crowds is of particular importance considering the incidence of casualties in stampedes and emergency evacuations [3].

It is commonly believed that global patterns of collective behaviour emerge from local interactions between individuals in a process of self-organization [4–6]. The key to explaining collective motion thus lies in characterizing these local interactions and how they give rise to global patterns. Numerous mathematical and computational models have been proposed within this local-to-global framework [7]. These ‘microscopic’ models describe behavioural ‘rules’ that govern an individual's interactions with neighbours, as well as other entities such as goals and obstacles. In particular, they assume that an individual is influenced by multiple neighbours in a zone of influence, or neighbourhood of interaction. Once local rules are formalized, agent-based simulations are used to test whether the model reproduces characteristic patterns of collective motion and, ideally, to predict behaviour in novel situations.

Such microscopic models have proliferated in recent years. Early models of fish schooling led to the dominant attraction–repulsion approach [8,9]. This class of models is predicated on three basic rules, (i) attraction: move toward neighbours in a far zone, (ii) repulsion: move away from neighbours in a near zone, and (iii) alignment: match the velocity (speed and heading) of neighbours in an intermediate zone.¹ Couzin et al. [10] showed that, by adjusting parameters for the radii of alignment and attraction zones, such a model can generate qualitatively distinct patterns, including unaligned aggregation (shoaling), strongly aligned translational motion (schooling) and coherent rotational motion (mills).

The self-propelled particle model [11] assumes only a minimal alignment rule, in which each individual adopts the mean heading direction of all neighbours within a zone of fixed radius. This rule alone can generate coherent translational motion [12]. Conversely, the influential social force model [13] eschews an alignment term, such that collective motion emerges from position-based attraction and repulsion forces. This, too, generates plausible global patterns, but local trajectories tend to resemble particle motion more than human locomotion [14].

Recently, ‘cognitive heuristic’ or ‘vision-based’ models have been proposed [15,16], which employ simple rules based on the distance or time-to-contact with objects to steer toward the goal while avoiding collisions. Although we are sympathetic with this approach, behavioural experiments are necessary to justify the proposed heuristics.

There is thus a plethora of theoretical models of collective motion. With recent advances in motion tracking of bird flocks and human crowds, they are beginning to be compared against empirical data [1,17–20]. However, successfully simulating observational data is insufficient to confirm a model, for different local rules can give rise to the same motion patterns [2,21]. To decipher the local rules, experimental manipulation at the level of individual behaviour is necessary [7,22].

We have been pursuing such an experiment-driven, bottom-up approach, called behavioural dynamics [23,24], with the aim of building a pedestrian model that can explain emergent behaviour. Elementary locomotor behaviours are studied individually and modelled with simple attractor/repeller dynamics; these models are analogous to behavioural ‘rules’ but emphasize their dynamical rather than logical form. Related experiments identify visual control laws, incorporating the optical information that regulates each behaviour. The resulting pedestrian model has five components: (i) steering to a goal, (ii) obstacle avoidance, (iii) moving target interception, (iv) moving obstacle avoidance, and (v) braking to avoid collision, analogous to a local ‘repulsion’ rule [24–26]. Linearly combining these components successfully predicts trajectories in more complex environments [24,27].

To understand the basis of collective motion, we recently studied binary pedestrian following. We found that a pedestrian p aligns with a neighbour n directly ahead (the leader) by accelerating to match the leader's speed 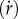and heading direction (ϕ) [28–30]. These results allowed us to specify a simple model of the alignment dynamics for binary interactions:

1.1

and

1.2

where are linear and angular acceleration, and c, k are gain parameters that depend on the leader's distance. To explain collective motion, however, requires determining how a pedestrian is influenced by multiple neighbours.

The present paper thus aims to characterize the neighbourhood of interaction underlying collective motion in human crowds. In particular, we ask which neighbours visually influence a pedestrian's behaviour (i.e. are visually coupled), how the degree of influence (coupling strength) depends on neighbour position, and how the influences of multiple neighbours are combined.

We experimentally test three hypotheses about the neighbourhood of interaction. (i) Superposition hypothesis. Most models of collective motion assume that binary interactions between a pedestrian and each neighbour are linearly combined. That is, the response of a pedestrian in a crowd is the combination of individual responses to each neighbour, a property known as superposition. This hypothesis predicts that as a greater number or percentage of neighbours change direction or speed, the pedestrian's response should increase proportionally. (ii) Distance hypothesis. Many models assume a constant coupling strength within an alignment zone with ‘hard’ boundaries [8–11]. However, Fajen & Warren [25] found that attraction or repulsion strength decreases exponentially with the distance of a goal or obstacle, leading us to expect that the coupling strength for alignment will also decay with distance. (iii) Eccentricity hypothesis. There are numerous reports of an elliptical ‘personal space’ for walking pedestrians [13,25,31]. This implies that, for a given distance, coupling strength should decrease with a neighbour's lateral position or eccentricity, the horizontal angle from the current heading direction.² Neighbours directly ahead should exert the greatest influence, while the influence of those to the left and right should decrease symmetrically to the edges of the field of view.

The results reveal that a pedestrian is strongly coupled to neighbours within a local neighbourhood, that their influence is linearly combined, consistent with the superposition hypothesis, and that coupling strength decreases exponentially with distance out to 4–5 m, consistent with the distance hypothesis. In contrast, we find little evidence that coupling strength depends on eccentricity within the field of view. The results enable us to specify a model of the local neighbourhood that reproduces the experimental data and predicts individual trajectories in motion capture data on a human ‘swarm’. We thus formulate the first bottom-up model of collective motion in human crowds, providing a basis for realistic models of crowd dynamics.

2. Experiments: walking with a virtual crowd

To probe the visual coupling between a pedestrian and their neighbours experimentally, we created a novel paradigm in which a human participant actively walks with a virtual crowd. This allowed us to manipulate the behaviour of virtual neighbours and measure their influence on the participant's trajectory. To determine the alignment response, we suddenly changed (perturbed) the heading direction or walking speed of a subset (S) of the virtual neighbours (N), and recorded the participant's adjustment in lateral position or walking speed.

Experiment 1 tested the superposition hypothesis by varying the number of neighbours in the perturbed subset; Experiment 2 tested the distance hypothesis by selectively perturbing neighbours in a near zone and/or a far zone; and Experiment 3 tested the eccentricity hypothesis by varying the lateral position of the perturbed neighbours.

(a). Experimental methods

(i). Participants

Separate groups of 10 volunteers participated in Experiment 1 (5F, 5M), Experiment 2 (6F, 4M) and Experiment 3 (6F, 4M). Participants were recruited through announcements posted on the Brown University campus. None reported any visual or motor impairment.

(ii). Apparatus

The experiments were conducted in the Virtual Environment Navigation Laboratory (VENLab) at Brown University. Participants walked in a 12 × 14 m tracking area while wearing a stereoscopic head-mounted display (HMD, Oculus Rift DK1, 640 × 800 pixels per eye, 90°H × 65°V field of view, 60 Hz frame rate). Head position and orientation were recorded with an ultrasonic/inertial tracking system (Intersense IS-900, 60 Hz sampling rate) and used to update the display (50–67 ms latency).

(iii). Displays

The virtual environment consisted of a granite-textured ground plane with a green start pole and a red orienting pole (3 m high, 0.2 m radius, 12.7 m apart) and blue sky. The virtual crowd was generated using 3D human models (WorldViz Complete Characters) (figure 1a), animated with a walking gait at a randomly varied phase. Thirty virtual humans were positioned on two circles (radius 1.5 m, 3.5 m) with the participant at the centre (figure 1b) to enhance the sense of immersion. Twelve of them (N = 12) were experimentally manipulated, and appeared on two 90° arcs centred on the initial walking direction, within the typical field of view. Five of these neighbours were placed at equal intervals on the 1.5 m radius arc (near zone), and seven on the 3.5 m radius arc (far zone); their positions were then subjected to Gaussian jitter in polar coordinates (distance Δr: s.d. = 0.15 m; eccentricity Δθ: s.d. = 8°). The remaining 18 were also placed at equal intervals and similarly jittered. A different configuration was generated for each trial; all participants received the same set of configurations, but virtual humans were randomly assigned to the positions.

Figure 1.

(a) Virtual crowd display from participant's view, and (b) an aerial view. (c) Diagram of a heading perturbation with S = 3 (from Experiment 2).

During a trial, all virtual humans accelerated from a standstill (0 m s⁻¹) to a speed of 1.3 m s⁻¹ over a period of 3 s in the participant's walking direction, following an ogive function (μ = 0, σ = 0.5 s) fit to previous data. On perturbation trials, after 2 s a subset (S) of the 12 neighbours then changed their heading direction (±10° left or right) or speed (±0.3 m s⁻¹) over a period of 0.5 s, following another ogive function (μ = 0, σ = 0.083 s).

(iv). Procedure

Participants were instructed to walk as naturally as possible, to treat the virtual pedestrians as if they were real people, and to stay together with the crowd. On each trial, the participant walked to the start pole and faced the orienting pole. After 2 s, the poles disappeared and the virtual crowd appeared; 1 s later, a verbal command (Begin) was played and the virtual crowd began walking. The display continued until the participant had walked about 12 m; a verbal command (‘End’) signalled the end of the trial. In each experiment, there were eight heading trials and eight speed trials per condition, presented in a randomized order, with 80 trials in each 1-hour session.

(v). Data processing

For each trial, the time series of head position in the horizontal X–Y plane were filtered using a forward and backward fourth-order low-pass Butterworth filter to reduce occasional tracker error and oscillations due to the step cycle. Time series of walking speed, heading direction, and their rates of change, were then computed from the filtered position data. A 1.0 Hz cut-off was used for computing speed to reduce anterior–posterior oscillations on each step [30], while a 0.6 Hz cut-off was used for computing heading to reduce lateral oscillations on each stride [25]. To eliminate ‘endpoint error’, the time series were extended by 2 s using linear extrapolation based on the last 0.5 s of data for filtering only [32].

Dependent measures were the participant's change in heading or walking speed in response to a perturbation. Change in heading was measured by computing the lateral deviation, subtracting the participant's final lateral position on a perturbation trial (1 s before the end of the trial) from their mean final lateral position on all control trials. Right and left turn trials were then collapsed by multiplying the lateral deviation on left turns by −1. Change in speed was computed by subtracting the participant's mean final speed on a perturbation trial (1.5 to 0.5 s before the end of the trial) from their mean final speed on all control trials in the corresponding distance condition. Slow and fast trials were collapsed by multiplying the final speed on slow trials by −1. However, we noted a small asymmetry, with a greater speed change in response to neighbours decelerating (for Exp. 2, S = 12, M = 0.31 m s⁻¹, s.d. = 0.09) than accelerating (M = 0.20 m s⁻¹, s.d. = 0.13; t₁₉ = 3.11, p < 0.01) from the same initial distance; Rio et al. [30] attributed this to Euclid's law of perspective, which produces a higher rate of optical expansion than contraction. The collapsed data were analysed in R statistical software using one-way repeated measures (RM) ANOVA in Exp. 1 (main effect of number of perturbed neighbours) and two-way RM ANOVA in Exp. 2 (main effects of number and distance of perturbed neighbours) and Exp. 3 (main effects of eccentricity and distance of perturbed neighbours), with generalized eta squared () as a measure of effect size.

(b). Experiment 1: number of perturbed neighbours

Experiment 1 tested the superposition hypothesis by manipulating the number of neighbours in the perturbed subset (S = 0,3,6,9,12); their positions in the crowd were varied randomly on each trial. Superposition predicts that, as the number (or proportion) of perturbed neighbours increases, the participant's response should increase linearly. There were thus five subset conditions and a total of 80 trials.

(i). Results

There was a significant effect of the number of perturbed neighbours on the participants' lateral deviation, (F_4,36 = 95.33, p < 0.001, ), consistent with a linear combination of neighbour influences (figure 2a). Similarly, there was a significant effect of number of perturbed neighbours on the participants’ change in speed (F_4,36 = 22.17, p < 0.001, ) (see electronic supplementary material, figure S1). Indeed, the mean response increased linearly with the size of the perturbed subset for both heading and speed (r = 0.99).

Figure 2.

Results of Experiment 1: (a) heading perturbations. Mean absolute lateral deviation as a function of the number of neighbours in the perturbed subset S. Results of Experiment 2: (b) heading perturbations. Mean absolute lateral deviation as a function of the number and distance of perturbed neighbours. (c) Speed perturbations. Mean absolute change in speed as a function of same. Error bars = s.e. of mean. (Online version in colour.)

The results of Experiment 1 demonstrate that velocity alignment is consistent with the superposition hypothesis. That is, the participant's heading and speed response is a linear combination of responses to each neighbour. Given that the total number of neighbours was constant (N = 12), the response could depend on either the absolute number or the proportion of neighbours perturbed; subsequent research (in preparation) suggests the latter.

(c). Experiment 2: distance of perturbed neighbours

Experiment 2 tested the distance hypothesis by perturbing neighbours in the near zone and/or the far zone (figure 1c). The distance hypothesis predicts that perturbing neighbours in the near zone should elicit a greater response from the participant than perturbing those in the far zone. The design of Experiment 2 was thus 2 distances (approx. 1.5 m and 3.5 m) × 5 subsets (S = 0,3,6,9,12), yielding 10 conditions and a total of 160 trials.

(i). Results

We found a significant effect of the distance of perturbed neighbours on the participants' lateral deviation (F_1,9 = 71.57, p < 0.001, ), consistent with the hypothesis that neighbour influence decreases with distance (figure 2b). Once again, there was a significant effect of subset size on lateral deviation (F_4,36 = 244.66, p < 0.001, ), consistent with superposition.

Because there were only five neighbours in the near zone and seven in the far zone, larger subsets actually perturbed neighbours in both zones. Thus, for a stronger test of the distance hypothesis, we performed a sub-analysis of the smaller subsets alone (S = 0,3,6, left side of figure 2b). The results confirmed a significantly greater response to perturbed neighbours in the near zone than the far zone (F_1,9 = 69.99, p < 0.001, ), as well as a significant effect of subset size (F_2,18 = 90.93, p < 0.001, ), and a significant interaction (F_2,18 = 45.58, p < 0.001, ).

Similarly, we found a significant effect of neighbour distance on the participants' change in speed (F_1,9 = 22.93, p < 0.001, ), as well as a significant effect of subset size (F_4,36 = 34.28, p < 0.001, ) (figure 2c). A sub-analysis of the smaller subsets (S = 0,3,6) confirmed a significantly greater response to neighbours in the near zone than the far zone (F_1,9 = 60.15, p < 0.001, ), a significant effect of subset size (F_2,18 = 50.67, p < 0.001, ), and a significant interaction (F_2,18 = 2.70, p < 0.001, ).

The results of Experiment 2 demonstrate that coupling strength decreases with neighbour distance for both heading and speed, consistent with the distance hypothesis. Visually, this decrease might be attributed to lower angular velocities due to the laws of perspective, to greater occlusion of far neighbours, or both—a question we are currently pursuing. In sum, the local neighbourhood can be characterized by the superposition of binary interactions, with a coupling strength that decreases with distance.

(d). Experiment 3: eccentricity of perturbed neighbours

In Experiment 3, we tested the eccentricity hypothesis by selectively perturbing neighbours in 30° horizontal sectors of the display. There were five overlapping sectors (centred on −30°, −15°, 0°, +15°, and +30°, left to right). The eccentricity hypothesis predicts that neighbours in the central sector (0°) should elicit the greatest response, while responses to neighbours in more peripheral sectors (±15°, ±30°) should progressively decrease. We also repeated the distance manipulation by perturbing neighbours in the near zone (M = 1.23 neighbours, s.d. = 0.73) or the far zone (M = 2.18 neighbours, s.d. = 0.81) of a given sector. Given that only one to two neighbours were perturbed on average, responses were expected to be smaller. The design was thus 5 eccentricity × 2 distance conditions, plus a no-perturbation control, yielding 11 conditions and a total of 176 trials.

(i). Results

There was no overall effect of eccentricity on the participants' mean lateral deviation (F_4,36 = 1.94, p > 0.05, ; figure 3a). We again observed a significant effect of neighbour distance (F_1,9 = 20.19, p < 0.01, ), but there was also a significant interaction (F_4,36 = 3.65, p < 0.05, ). A simple effects analysis revealed a significant eccentricity effect in the Far condition (F_4,36 = 3.63, p < 0.05, ), but not in the Near condition (F_4,36 = 1.22, p > 0.05, ). Moreover, the distance effect was only significant at eccentricities of −30° and +30° (p < 0.01).

Figure 3.

Results of Experiment 3: (a) heading perturbations. Mean absolute lateral deviation as a function of the eccentricity and distance of perturbed neighbours. (b) Speed perturbations. Mean absolute change in speed as a function of same. Error bars = s.e. of mean. (Online version in colour.)

Similarly, we found no overall effect of eccentricity on the participants' change in speed (F_4,36 = 0.86, p > 0.05, ; figure 3b). There was again a significant effect of distance (F_1,9 = 14.15, p < 0.01, 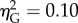), but no interaction (F_4,36 = 0.95, p > 0.05, 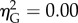); responses were greater to near neighbours than far neighbours at all eccentricities. Simple effects tests did not reveal an eccentricity effect in either the near or the far zone (both p > 0.05, ).

The results do not provide convincing evidence for the eccentricity hypothesis. The only consistent effect occurs with heading perturbations of far neighbours at larger eccentricities (red curve in figure 3a). We suggest this effect may be due to the laws of perspective, similar to one we observed in binary following [33]. If a neighbour straight ahead (0° eccentricity) turns 10° left or right, they drift laterally in the field of view with a given angular velocity; a neighbour at a 30° eccentricity would have a smaller mean angular velocity, which would decrease even further with distance. The reduced response in the Far condition may thus be attributable to reduced optical motion. In contrast, speed perturbations produce optical expansion/contraction that appears to be similar over this range of eccentricities, although it too decreases with distance (figure 3b). These visual effects might explain the pattern of results in Experiment 3.

Taken together, the experimental findings are consistent with the superposition of multiple neighbours, with a coupling strength that decreases with distance but not eccentricity.

3. Observational data on a human ‘swarm’

To compare these experimental results with observations of crowd behaviour, we collected motion capture data on collective motion in a human ‘swarm’ scenario. We recorded three groups of participants walking together for periods of 2 min. To investigate the distance and eccentricity hypotheses, we computed pairwise statistics between a central participant and each neighbour as a function of their relative spatial positions.

(a). Methods

(i). Participants

One group of 16 participants (6F, 10M) and two groups of 20 participants (10F, 10M) were tested in separate sessions as part of a larger study.

(ii). Apparatus

The groups were tested in a large hall with a 14 × 20 m tracking area marked on the floor with red tape. Each participant wore a bicycle helmet with a unique constellation of five reflective markers on 30–40 cm stalks. Head position was recorded at 60 Hz with a 16-camera infrared motion capture system (Qualisys Oqus).

(iii). Procedure

Participants were instructed to walk about the tracking area at a normal speed, veering randomly left and right, while staying together as a group. They began each trial in random positions in a 7 × 7 m start box marked on the floor (approx. 2 m interpersonal distance (IPD)) or a 4 × 4 m start box (approx. 1 m IPD). At a verbal ‘go’ signal, they started walking for 2 min, until a ‘stop’ signal.

(iv). Data processing

We analysed three 2 m IPD trials in detail, a total of 6 min of data. 3D head positions were successfully recovered on 88% of frames, and the time series for each participant was processed as before. Walking speed did not vary appreciably, and was not analysed further. To measure local coordination, we computed the absolute value of the difference in heading direction between the ‘central participant’ nearest the centre of the swarm and each neighbour on each frame, thereby minimizing edge effects [34]. To estimate response times, windowed cross-correlations (1 s travelling window) and optimal delays between the central participant and each neighbour were also computed. These measurements were averaged across all frames and plotted in heat maps with the central participant at the origin (0,0) heading upward; each cell thus represents the mean statistic for all participants occupying that relative spatial location in 6 min of data.

(b). Results

A heat map of mean absolute heading difference appears in figure 4a. It is immediately apparent that the neighbourhood is circularly symmetric, not elliptical. The mean heading difference is quite small, 15–25°, within a 2 m radius, but increases to 30–40° at a radius of 3–4 m. There is thus close coordination with near neighbours that decreases with distance.

Figure 4.

Mean results for 6 min of human ‘swarm’ data. (a) Heat map of mean absolute heading difference between each neighbour and central participant (at origin, heading upward; cell = 0.5 × 0.5 m). (b) Heat map of time delay, positive values indicate neighbours turn before central participant (cell = 0.33 × 0.33 m). (c) Coupling strength (scaled heading difference) as a function of radial distance, from data in a; curve is fit to equation 3.1 (r² = 0.98).

To estimate the decay in coupling strength with distance, we computed the mean heading difference at each radius in the heat map, scaled it (range 0 to 1) and subtracted it from 1, and plotted the result as a function of radial distance (figure 4c). The coupling strength w_i to each neighbour decays exponentially with distance, closely fit by the equation

3.1

where d_i is the distance of neighbour i, ω = 1.3 is the decay rate, and a = 9.2 is a constant (r² = 0.98).

Given that the human field of view is about 180°, however, a pedestrian is visually coupled only to neighbours in front of them. This uni-directional coupling is apparent from the heat map of mean time delay for the same 6 min of data (figure 4b). Time delays in the upper half of the map are positive, indicating that the neighbours ahead turned before the central participant, whereas those in the lower half are negative, indicating that the central participant turned before the neighbours behind. Mean time delays are about 1 s within a 1.5–2 m radius, increasing to 1–3 s at 3–4 m. For binary following, Dachner & Warren [28] reported mean delays of 0.98 s to a neighbour who turns 2 m ahead, and 1.33 s to a neighbour 4 m ahead. This suggests that the central participant's response to some (possibly occluded) far neighbours may be mediated by an intervening neighbour, yielding a chain of response times.

4. Modelling the neighbourhood of interaction

The present findings enable us to formulate a model of the local neighbourhood of interaction (figure 5a). Specifically, given superposition, we propose that a pedestrian's linear (or angular) acceleration is a weighted average of the difference between their current speed (heading) and that of each neighbour. By substituting the alignment dynamics (equations (1.1) and (1.2)) into this neighbourhood model, we can derive the local interactions that generate collective motion,

4.1

and

4.2

where n denotes the number of neighbours in the pedestrian's neighbourhood (within a 5 m radius, ±90° from current heading). The weight w_i has a value of 1 at 0 m and decays exponentially with the neighbour's radial distance, in accordance with equation (3.1). To estimate the gain parameters c, k at a theoretical distance of 0 m, we fit our previous data on binary following separately for distances of 1, 2, and 4 m, and linearly extrapolated to 0 m, obtaining c = 3.61 and k = 3.15.

Figure 5.

(a) Diagram of neighbourhood model. Simulation of Experiment 2: (b) heading perturbations. Mean absolute final heading as a function of number and distance of perturbed neighbours. (c) Speed perturbations. Mean absolute final speed as a function of same. Shaded regions = 95% CI for human data. (Online version in colour.)

To test this ‘soft radius’ model, we first determined how closely it reproduces the data from Experiments 1 and 2, and then how well it predicts individual trajectories in the more variable human swarm, with fixed parameters.

(a). Simulation methods

Each trial from Experiments 1 and 2 was simulated by taking the virtual neighbours' distance and speed (or heading) as input at each time step, and computing a time series of the model's speed (heading) in accordance with equation (4.1) (equation (4.2)). To reduce the effects of gait oscillations and tracker error on individual trials, a mean time series was computed for each participant in each condition and compared with the mean model time series in the corresponding condition, using the correlation coefficient (Pearson's r) and the root of the mean squared error (RMSE).

The same model was used to simulate individual trajectories in the human swarm data. First, we identified 10 s segments in which a participant had ≥7 neighbours in their neighbourhood who were continuously tracked at speeds ≥0.2 m s⁻¹; this yielded 14 segments of 2 m IPD data and 17 segments of 1 m IPD data. At the start of each segment, the model was initialized with the participant's position, speed and heading. The distance, speed, and heading of every neighbour was treated as input, and the model computed the participant's speed, heading, and change in position on each time step. We computed the correlation and RMSE between the individual model and human time series, and the mean position error (distance between model and human), over the 10 s segment.

(b). Results

The correlations between the model and human in Experiment 1 were strong, with means of r = 0.88 (RMSE = 0.05 m s⁻¹) for speed and r = 0.81 (RMSE = 1.94°) for heading in the perturbation conditions. In Experiment 2, the mean correlations were even higher, with r = 0.90 (RMSE = 0.06 m s⁻¹) for speed and r = 0.88 (RMSE = 2.06°) for heading. The model thus closely reproduces the temporal evolution of a pedestrian's response to their neighbours (electronic supplementary material, figures S2 and S3). Moreover, model predictions of the final stabilized heading and speed (mean of last 2 s in time series) were virtually identical to the mean human data, as shown in figure 5b,c for Experiment 2. The predicted value is contained within the 95% confidence interval for the human data, indicating that the data do not differ significantly from the model.

The model also predicts individual trajectories in the human swarm. A sample trajectory from a 10 s segment of swarm data appears in figure 6 (also electronic supplementary material, figure S4). For the 2 m IPD, the mean correlations between model and human time series were r = 0.90 (RMSE = 31.16°) for heading, and r = 0.65 (RMSE = 0.19 m s⁻¹) for speed.³ Position error accumulated from a mean of 0.27 m during the first 3 s to a mean of 0.93 m for the 10 s segments. The model also generalized to the 1 m IPD, with mean correlations of r = 0.93 (RMSE = 27.56°) for heading and r = 0.60 (RMSE = 0.16 m s⁻¹) for speed; mean position error increased from 0.21 m during the first 3 s to 0.70 m over 10 s.

Figure 6.

Simulation of sample segment from the human ‘swarm’ (IPD = 1 m). (a) Path in space, mean position error = 0.13 m (dots at 1 s intervals). (b) Time series of speed, r = 0.95, RMSE = 0.10 m s⁻¹. (c) Time series of heading, r = 0.99, RMSE = 11.84°. Participant = solid grey curve (red), model = dashed curve (blue), neighbours = thin black curves O = starting positions, X = final positions. (Online version in colour.)

In sum, the neighbourhood model accounts for the coordination of heading and speed between individuals in a crowd, and consequently the emergence of collective motion.

5. Discussion

The experimental results demonstrate that a pedestrian's interactions with multiple neighbours are linearly combined, in accordance with superposition. At the same time, neighbour influence decreases with distance, going to zero by 5 m. On the other hand, influence does not appear to depend on eccentricity within the field of view. In contrast to prey species with nearly panoramic vision, yielding bi-directionally coupled flocks and schools, humans typically have a 180° field of view and are uni-directionally coupled to neighbours ahead. This has implications for the causal network in human crowds.

These findings led us to model the local neighbourhood as a weighted average of neighbours (equations (4.1) and (4.2)), in which the weights decrease exponentially with radial distance (equation (3.1)). Together with our previous results on alignment dynamics (equations (1.1) and (1.2)), this enabled us to simulate the local interactions underlying collective crowd motion. The model not only reproduces participant responses in a virtual crowd, but generalizes to individual trajectories in a human swarm. Despite the fact that swarm motion was more variable and some neighbour data were missing, leading to an accumulation of position error, the heading correlation was highly robust.

The model neighbourhood decays exponentially with radial distance, creating a ‘soft’ radius. This neighbourhood structure contrasts with previous theoretical models that presume an alignment zone with a constant coupling strength and a hard radius. Our empirical model agrees with the theoretical equation of Cucker & Smale [35], who showed that a weighted-average model with a sufficiently gradual decay converges to collective motion.

A number of further questions remain. First, the present data do not resolve the issue of whether the neighbourhood is defined by metric distance (e.g. metres), or topological distance (number of neighbours) as suggested by some analyses of bird flocks ([17]; but see [36]). Second, although an ‘attraction’ rule appears to play a role in flocking [18,19], an analogue for moving crowds has not yet been investigated. Finally, at present, physical distance is a proxy for visual information that depends on perspective or occlusion; we are currently incorporating optical variables into the model. We plan to address these questions in future reports.

6. Conclusion

We conclude that the local neighbourhood of interaction in human crowds is circularly symmetric, with a uni-directional coupling to multiple neighbours within ±90° of the current heading. Their influences are superposed as a weighted average, where the weight decays exponentially with distance. Combining this ‘soft’ neighbourhood with the alignment dynamics yields the first experiment-driven, bottom-up model of collective motion in human crowds. This behavioural dynamics model accounts for individual trajectories in virtual and real crowds, and generates collective motion, consistent with principles of self-organization. It is thus possible to experimentally decipher the local interactions that underlie collective crowd behaviour.

Ethics

The research protocol was approved by Brown University's Institutional Review Board, in accordance with the principles expressed in the Declaration of Helsinki. Informed consent was obtained from all participants, who were paid for their participation.

Data accessibility

The data supporting this article may be accessed from the Brown University Digital Repository: https://repository.library.brown.edu/studio/item/bdr:735090/.

Authors' contributions

K.W.R. contributed to the conception and design of the experiments, created the visual displays, collected the data, performed the data analysis, and co-wrote the manuscript. G.C.D. performed the model simulations and contributed to the data analysis. W.H.W. contributed to the conception and design of the experiments and the data analysis, and co-wrote the manuscript. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

The research was supported by National Institutes of Health (USA) grant R01EY010923 and National Science Foundation (USA) grant BCS-1431406 to W.H.W., and a Link Foundation fellowship to K.W.R.