Contribution of action potentials to the extracellular field potential in the nucleus laminaris of barn owl

Abstract

Extracellular field potentials (EFP) are widely used to evaluate in vivo neural activity, but identification of multiple sources and their relative contributions is often ambiguous, making the interpretation of the EFP difficult. We have therefore analyzed a model EFP from a simple brainstem circuit with separable pre- and postsynaptic components to determine whether we could isolate its sources. Our previous papers had shown that the barn owl neurophonic largely originates with spikes from input axons and synapses that terminate on the neurons in the nucleus laminaris (NL) (Kuokkanen PT, Wagner H, Ashida G, Carr CE, Kempter R. J Neurophysiol 104: 2274–2290, 2010; Kuokkanen PT, Ashida G, Carr CE, Wagner H, Kempter R. J Neurophysiol 110: 117–130, 2013; McColgan T, Liu J, Kuokkanen PT, Carr CE, Wagner H, Kempter R. eLife 6: e26106, 2017). To determine how much the postsynaptic NL neurons contributed to the neurophonic, we recorded EFP responses in NL in vivo. Power spectral analyses showed that a small spectral component of the evoked response, between 200 and 700 Hz, could be attributed to the NL neurons’ spikes, while nucleus magnocellularis (NM) spikes dominate the EFP at frequencies ≳1 kHz. Thus, spikes of NL neurons and NM axons contribute to the EFP in NL in distinct frequency bands. We conclude that if the spectral components of source types are different and if their activities can be selectively modulated, the identification of EFP sources is possible.

NEW & NOTEWORTHY Extracellular field potentials (EFPs) generate clinically important signals, but their sources are incompletely understood. As a model, we have analyzed the auditory neurophonic in the barn owl’s nucleus laminaris. There the EFP originates predominantly from spiking in the afferent axons, with spectral power ≳1 kHz, while postsynaptic laminaris neurons contribute little. In conclusion, the identification of EFP sources is possible if they have different spectral components and if their activities can be modulated selectively.

INTRODUCTION

Identification of the sources of extracellular field potentials (EFP) is important for interpreting in vivo neural activity. Difficulties in differentiating among EFP sources typically stem from complex patterns of neural activity and multiple neuron types with dispersed and asynchronous inputs (Mazzoni et al. 2013). The low-frequency (≲500 Hz) components of the EFP are usually attributed to synaptic currents [Gold et al. (2006, 2007); Mitzdorf (1985); Nunez and Srinivasan (2006); see also Buzsáki et al. (2012) and Einevoll et al. (2013) for reviews], while contributions of spiking activity have been traditionally observed and modeled in the high-frequency (>500 Hz) part of the spectrum (Galindo-Leon and Liu 2010; Kajikawa and Schroeder 2011; Logothetis et al. 2001; Pettersen et al. 2008). Recent work suggests, however, that spikes may also contribute to frequencies as low as 20 Hz (Belluscio et al. 2012; Denker et al. 2011; Kuokkanen et al. 2013; Reimann et al. 2013; Ray and Maunsell 2011; Schomburg et al. 2012; Waldert et al. 2013). Furthermore, the degree to which currents at different spatial distances (ranging from tens of micrometers to millimeters) contribute to the EFP depends on their spatiotemporal activity (Buzsáki et al. 2012; Gawne 2010; Henrie and Shapley 2005; Katzner et al. 2009; Kreiman et al. 2006; Mineault et al. 2013; Xing et al. 2009). The more synchronous the population activity, the more visible it is far from the recording site (Kuokkanen et al. 2010; Lindén et al. 2011). However, high-frequency components are expected to attenuate faster than those at lower frequencies (Pettersen and Einevoll 2008).

To identify which sources underlie the EFP, we exploited a model system with a strong EFP, an anatomically simple circuit, and separable pre- and postsynaptic components. The barn owl’s auditory brainstem nucleus laminaris (NL) detects interaural time differences (ITDs) (Carr and Konishi 1990; Moiseff and Konishi 1981; Peña et al. 1996), and its activity underlies the owls’ ability to differentiate between targets ≲10 μs apart (Bala et al. 2003). NL has a strong EFP termed the neurophonic, typically measured with electrodes with an impedance in the megaohm range. The neurophonic is characterized by high temporal precision (≲20 μs) (Wagner et al. 2005). We had previously shown that many (≳250) independent sources are needed for the generation of the neurophonic in NL (Kuokkanen et al. 2010). Furthermore, binaural neurophonic responses to ITD can be predicted with high precision by linear summation of the monaural neurophonic responses to ipsi- and contralateral stimulation (Kuokkanen et al. 2013). Both studies suggest that presynaptic inputs from the neurons in the ipsi- and contralateral nucleus magnocellularis (NM), i.e., afferent axon spikes and synaptic inputs, are the main sources of the neurophonic. These sources represent the input to NL rather than its output. Furthermore, our analyses showed that the sustained neurophonic response originates from a volume within 300 μm that includes hundreds of axonal nodes and synapses in contrast to only few NL neurons (Kuokkanen et al. 2010).

Although our analyses provided strong support for the neurophonic originating from input to NL, it seemed possible that the postsynaptic neurons in NL might also contribute to the EFP. To unmask this contribution, here we focus on EFP components that change with ITD. We had previously shown that ITD-dependent changes in the neurophonic were small (Kuokkanen et al. 2013) but hypothesized that their contribution would be detectable in the power spectral density (PSD) of the neurophonic. Evaluation of the differences between responses to stimulation at the best and worst ITD, and between spontaneous and driven activity, reveal which frequencies of the PSD reflected contributions from NL neurons’ activity and how large this contribution is. Comparisons to extra- and intracellularly recorded spikes in NL confirm the results. Thus, in this simple circuit, a comprehensive explanation of the sources of the EFP is almost complete.

MATERIALS AND METHODS

Experimental Paradigms

Tungsten-electrode recordings.

The experiments were conducted at the Departments of Biology of the University of Maryland and the University of Oldenburg. Fourteen adult barn owls of both sexes [11 Tyto furcata pratincola (American barn owl, formerly Tyto alba), and 3 Tyto alba (common barn owl)] were used to collect the data at 37 extracellular recording locations analyzed here. Most animals also supplied data to previous publications (Carr et al. 2015; Kuokkanen et al. 2010, 2013; McColgan et al. 2014; Wagner et al. 2005, 2009) and the experimental procedures have been described in detail there.

Procedures conformed to NIH Guidelines for Animal Research and were approved by the Animal Care and Use Committees of the Universities of Maryland and Oldenburg. Anesthesia was induced by intramuscular injections of 10–16 mg/kg ketamine hydrochloride and 3 mg/kg xylazine. Supplementary doses were administered to maintain a suitable plane of anesthesia. Alternatively, in some recordings, anesthesia was induced by urethane, and the drug was administered by intramuscular injection with a total of 8–10 ml/kg of 20% urethane divided into three to four injections over the course of 3 h, before recording from the brain. Body temperature was maintained at 39°C by a feedback-controlled heating blanket. More details may be found in Carr et al. (2015).

Recordings were made in a sound-attenuating chamber (IAC Acoustics, New York, NY). For extracellular recordings, tungsten electrodes with impedances between 2 and 20 MΩ were used. A grounded silver chloride pellet, placed under the animal’s skin around the incision, served as the reference electrode. Electrode signals were amplified, and the line noise was removed with a HumBug line noise eliminator (Quest Scientific, North Vancouver, BC, Canada), which only affects the signals at 60 Hz and its higher harmonics. Then the signals were band-pass filtered (1–13,000 Hz, 15 of 37 recordings; or 300–13,000 Hz, 2nd order Butterworth filter) by a custom-built headstage and amplifier or a WPI DAM 80 (World Precision Instruments, Sarasota, FL). Amplified electrode signals were passed to a threshold discriminator [SD1, Tucker-Davis Technologies (TDT), Gainesville, FL] and an analog-to-digital converter (DD1, TDT) connected to a personal computer via an optical interface (OI, TDT). Acoustic stimuli were digitally generated by custom-made software (“Xdphys” written in Dr. M. Konishi’s laboratory at Caltech) driving a signal-processing board (DSP2, TDT). Acoustic signals were fed to miniature earphones via D/A converters (DD1, TDT), anti-aliasing filters (FT6-2, TDT), and attenuators (PA4, TDT). Custom-made sound systems containing the earphones and miniature microphones were placed into the owl’s left and right ear canals. The sound systems were calibrated individually for both amplitude and phase before the recordings. At a given recording site, we measured frequency response curves and then tuning to ITD. In all experiments, voltage responses were recorded with a sampling frequency of 48,077 Hz, and saved for off-line analysis. The frequency-response curves were recorded to both monaural and binaural stimulation. For each recording location, an appropriate stimulus frequency near the location’s best frequency (BF, 3.0–7.3 kHz) was selected to record the ITD tuning curves and, based on them, to record 45 to 600 repetitions of the responses to 100-ms tone bursts at favorable and unfavorable ITDs at 40–60 dB sound-pressure level, dB re 20 μPa, stimulus level. These sound levels were used to ensure that firing rates were saturated (Köppl and Yates 1999).

Sharp-electrode recordings.

In addition, we reanalyzed previously published (Funabiki et al. 2011) extracellular spike waveforms from 36 NL neurons (as previously classified by Funabiki et al.) from twelve adult Tyto furcata pratincola of both sexes. Furthermore, we analyzed extracellular and intracellular recordings from 14 NM axons in NL from six adult Tyto furcata pratincola of both sexes. NM axonal data were collected as a by-product during the recordings by Funabiki et al. (2011), with identical methods and electrode. Altogether, data from fourteen barn owls were used.

Methods used for the recordings from NM axons and NL neurons in (Funabiki et al. 2011) differed from those used for recording extracellular neurophonics. In that study, a coaxial glass electrode containing a sharp microelectrode filled with 3 M potassium acetate was inserted into a patch electrode-type. Once within NL, the sharp electrode was advanced to record extracellular and intracellular responses from NL neurons.

Funabiki et al. (2011) distinguished the extracellular data from intracellular recordings by the DC drop at the start of the unit recordings. Stimuli were short binaural tone bursts (60 ms length) at the best frequencies, and ITD was varied. For the analysis of spike waveforms of NL neurons, we included only units with an ITD tuned firing rate (vector strength > 0.05 with significance P < 0.04, circular-linear correlation coefficient) in this analysis (28 of 36 units). The best frequencies of the units were in the range of 2.1–5.1 kHz.

Spikes were classified as originating from NM axons if their rate was insensitive to ITD and if the spontaneous rate was sufficiently high (>60 spikes/s). We included 14 such putative NM units in our further analyses. The best frequencies of the units ranged 3.3–5.3 kHz.

Data Analysis: Tungsten-Electrode Recordings of Neurophonic Potential

For the EFP recordings made with tungsten electrodes, we used the following procedures to analyze the obtained data: For each 100-ms tone burst, the voltage trace from 15 to 95 ms after the stimulus onset was analyzed. All the data analysis was done with MATLAB 7.6 or 9.0 (MathWorks, Natick, MA). We used the variance of the neurophonic response within the 80-ms segment as a simple measure to describe the spread of the voltage around its mean. The variance was averaged over trials for each stimulus condition. Only those recording sites at which we observed both frequency and ITD tuning of the variance were accepted for further analysis. Onset effects were excluded by windowing, and we averaged the spectra over several trials. For further details of this data analysis, see Kuokkanen et al. (2013).

Isolevel response curves of the variance of the voltage trace defined the best frequency (BF) at a recording site as follows (Kuokkanen et al. 2010): a line at half height of a tuning curve was derived from its peak value and the mean value of the spontaneous levels. The midpoint of the line at half height yielded the BF.

The ITD of the binaural stimulation ranged from −300 to 300 μs with 30- to 40-μs steps. The “favorable ITD” was a stimulus ITD close to the ITD at which the largest response variance was expected (circular-mean direction, i.e., mean phase, of the PSD peak amplitude at the stimulus frequency as a function of ITD). The unfavorable ITD was the favorable ITD plus half a period of the stimulus frequency.

Ratio of spectra.

To quantify spectral changes at frequency f, we used the ratio of PSDs (Henrie and Shapley 2005),

$$R(f)=\frac{P_{\text{driven}}(f)}{P_{\text{ref}}(f)},$$ (1)

where P_driven (f) is the PSD of the neurophonic in response to a stimulus (e.g., eliciting high activity), and P_ref (f) is the PSD of the reference activity (e.g., spontaneous activity or response to a stimulus eliciting low activity).

A value of the PSD ratio R(f₀) = 1 represents “no change in PSD at frequency f₀,” and values above one show “increase in the PSD.” Values between zero and one represent “decrease in the PSD.” In each PSD in response to stimulation, we excluded the contribution at the stimulus frequency as well as a margin of 150 Hz around it, to enable the comparison of the PSDs recorded at different stimulus frequencies. For spontaneous activity, exclusion of any frequencies was neither needed nor done.

Data Analysis: Sharp Electrode Recordings of Extra- and Intracellular Spikes

For the extracellular and intracellular single-unit recordings made with coaxial glass electrodes, we used the following procedures to analyze the data: For each tone burst, the voltage trace from the stimulus onset to the end of the stimulus was analyzed. All the data analysis was done with MATLAB 7.6 or 9.0 (MathWorks, Natick, MA).

Spike detection.

extracellular nl single-unit recordings.

We reanalyzed extracellular NL single-unit recordings (N = 28 units) published previously (Funabiki et al. 2011); half of these units were recorded close to NL neurons, i.e., just before intracellular recording. The other half (14 of 28) were recorded only extracellularly; the intracellular recording was not possible; presumably, the electrode either passed the soma at an unfavorable angle or the electrode was in the vicinity of the NL axon. The extracellular traces were recorded at multiple stimulus frequencies with a range of ITDs at each frequency. The traces were analyzed at the stimulus frequency corresponding to the BF of the intracellular recording, or if it was not available, at the BF of the extracellular recording. The BF of each neuron was defined online during the recording: the stimulus frequency that elicited the strongest response was determined with the help of an audio monitor, because the duration of recordings using sharp electrode did not allow for more precise measurements (Funabiki et al. 2011).

Putative spikes in extracellularly recorded voltage traces were detected by a combination of several methods. NL spike amplitudes were typically only two to five times larger than the amplitude of the neurophonic oscillation at the best stimulus frequency and best ITD. For the spike detection, the extracellular voltage traces were upsampled from 48,077 Hz to 50,000 Hz. Upsampling was done for associated analyses [see Kuokkanen et al. (2010)], to ensure an integer number of cycles of the stimulus frequency in each 60-ms segment analyzed. The upsampling did not affect our results. To select putative spikelike events, we used two methods: 1) thresholding [1.8 times the standard deviation (SD)] of the high-pass filtered (>200 Hz) voltage trace of all recordings done of that unit, and 2) a spike-detection method (Petrantonakis and Poirazi 2015) (window sizes 5, 11, and 15 samples, two of which were required to show a peak for a putative spike). Interspike intervals (ISIs) of <1 ms have been reported for both NL and NM neurons (Carr and Konishi 1990; Peña et al. 1996), especially NL spike doublets with ISIs ~0.2 ms (Carr and Konishi 1990). We however wanted to avoid distortions in the spike waveform by double peaks; thus, if there was more than one spike within 0.5 ms, we selected the one with the larger amplitude and omitted the other.

To calculate average spike waveforms, we aligned the putative spike waveforms to the peak of the first derivative (2-μs precision for spike waveforms upsampled to 500 kHz), i.e., to the steepest point of the waveform, and calculated repetition SDs of the spike width and height. To ensure that the spikes were from a single unit, we selected from these putative spikes those events that fulfilled a spike waveform criterion; we included spikes which were within 2 SD of the mean width of putative spikes and within 2 SD of their mean spike height. In the noisiest recordings from NL units (5 of 28) we furthermore increased the criterion for the minimum spike height such that the spontaneous firing rate was below 150 spikes/second, as reported in the literature. This increase did not have any effect on the driven firing rates. These criteria excluded some spikelike events. However, our main aim here was to extract a typical spike waveform from one neuron, and not to identify all spikes.

To calculate the PSD of the average spike waveform, we created a voltage trace V_s,ex(t) with an initial value of zero, and at each spike time t_i we added the average spike waveform k(τ) (for –2.3 ms ≤ τ ≤ +1.7 ms) of the selected spikes at that recording location (see also Fig. 3, B and F):

Fig. 3.

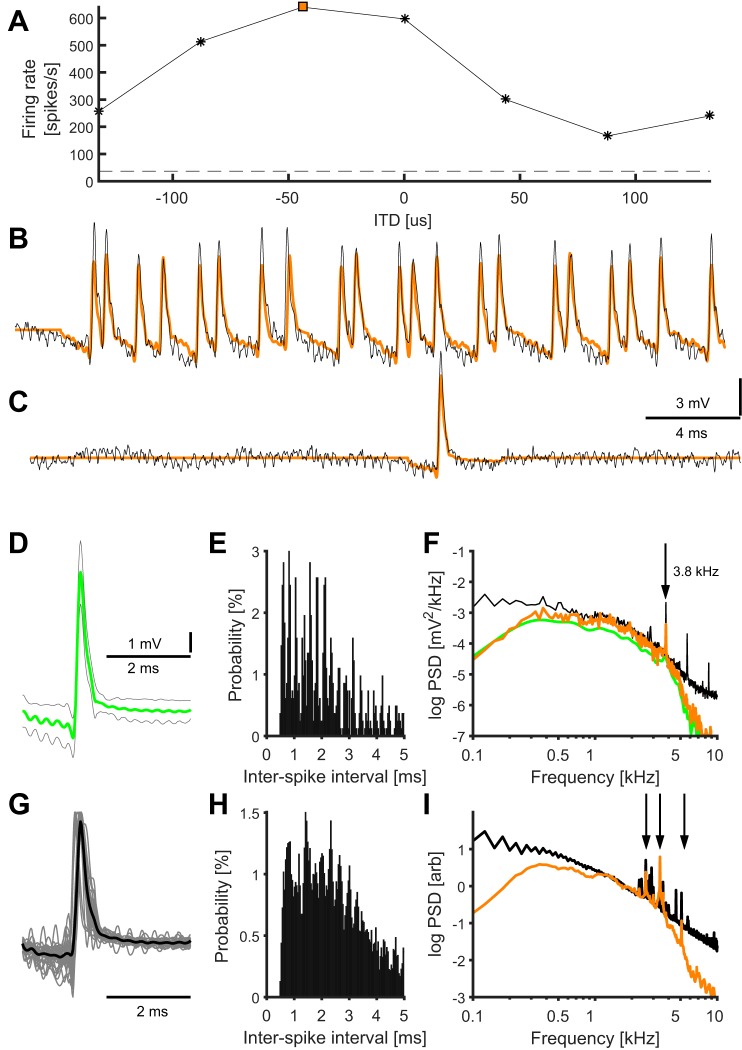
Extracellularly recorded activity of nucleus laminaris (NL) neurons in response to stimulation with binaural tones. A: ITD tuning of an NL neuron. Spontaneous rate: horizontal dashed line. Preferred ITD = −50 μs; orange square marks the favorable ITD (−44 μs) shown in B. Average of five stimulus repetitions. B and C: extracellular unfiltered voltage traces (black) and spike-replaced voltage traces (orange) where each detected spike was replaced with the mean spike waveform; voltage traces are shown for the favorable ITD = −44 μs (B) and for spontaneous activity (C). D: mean waveform of detected spikes in the example NL cell (green, N = 825 spikes), with an amplitude of 8.38 ± 2.14 mV (maximum–minimum of the spike waveform, mean ± SD), and an average half-peak width of 176 ± 105 μs. Gray lines indicate the SD around the mean spike waveform for each time point. The SE of the spike waveform was smaller than the width of the green line. E: interspike interval (ISI) distribution for the detected spikes in the example NL cell (bin size 40 μs). The probability of observing ISIs >5 ms was 7.3%. F: average PSD of the raw extracellular traces (black) of all recordings of the NL cell in A–E, the PSD of the single spike shown in D (scaled, green) and average PSD of all recordings at that site with detected spikes replaced by the average spike waveform (orange). The vertical arrow points to the stimulus frequency. G: mean spike waveforms of all analyzed neurons (N = 28, gray) with normalized peak values, and grand average of the mean spikes waveforms (black). H: ISI distribution (bin size 40 μs) for all recording sites. The probability of observing ISIs >5 ms was 14.9%. I: grand average of the normalized PSDs of all recording locations at each frequency (black), and grand average of all spike-replaced PSDs of all recording locations (orange). Vertical arrows point to the peaks in the PSDs that are related to the stimulus frequencies.

$$V_{s,ex}(t)={\displaystyle \sum _{i=1}^{N}k}(t-t_i)\mathrm{.}$$ (2)

The PSD of this spike-replaced trace was then calculated in the identical manner as for the neurophonic data. Because the spike amplitude varied typically ~20% through a recording, a single average waveform is determined to be a biased measure. We investigated this bias by generating surrogate data based on inhomogeneous Poisson spike times, a spike waveform as found in the extracellular data, and adding noise of ~5–15% of the spike waveform amplitude. There was a constant pink noise floor of 5% (at 25–25,000 Hz) and an ITD-dependent sinusoidal noise of 0–10% at 5-kHz oscillation frequency. The variation in the noise amplitude simulated the ITD dependency of the underlying neurophonic potential. We observed that the average spike waveform and its spectrum do capture the essence of the spikes in the trace, especially at 300–3,000 Hz frequency range.

In this study, we compared extracellular NL single-unit recordings made with coaxial glass electrodes (Fig. 3) with extracellular recording made with tungsten electrodes (Figs. 1 and 2). Based on this comparison, we revealed the typical contribution of a single NL neuron to the neurophonic; see also Data Analysis: Single-Neuron Contributions to the Extracellular Voltage. Such a quantitative argument requires that the signals recorded with the two different types of electrodes are of similar amplitude. We thus compared the average spectra recorded by the two types of electrodes. The low-frequency (<1 kHz) portions of the spectra were similar, which justifies our quantitative comparison of the contribution of NL spikes, which contributed mostly in the range 200–700 Hz. The spectra of the two electrode types were different for higher (>1 kHz) frequencies: the tungsten electrodes showed typically an order of magnitude more power at 5 kHz. Nevertheless, we could use coaxial glass electrodes to estimate NM axon spike waveforms (see next paragraph), which had large contributions at frequencies >1 kHz (Fig. 4), even though amplitudes of the estimated extracellular NM axon spike waveforms could not be related to the neurophonic recordings made with tungsten electrodes.

Fig. 1.

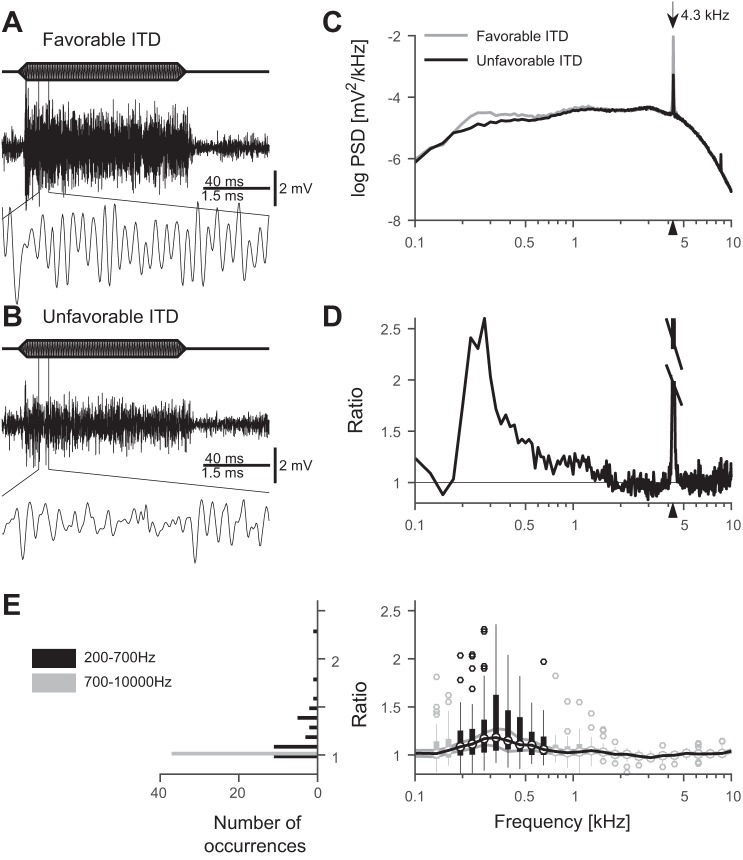
Neurophonics in response to binaural tone stimulation at frequencies close to the best frequency (BF). A: tonal stimulation at BF (4.3 kHz) at favorable interaural time difference (ITD) (8 μs). B: stimulation with unfavorable ITD (−108 μs). A and B: 100-ms stimulation (top), 160-ms segment of response (middle), and close-up of 22–28 ms of the response above (bottom). C: averaged power-spectral densities (PSDs, 500 trials) of the responses to stimulation with favorable and unfavorable ITDs in A and B (15–95 ms segments analyzed). Both axes are logarithmic to show differences more clearly. The arrow indicates the stimulus frequency (4.3 kHz), which is also marked by a triangle on the x-axis. D: ratio of PSDs in C. The peak value (23.7) at the stimulus frequency has been truncated. The triangle at the x-axis marks the stimulus frequency (4.3 kHz). E, right: in the population data, 25 of 37 recording sites show a significant change of >5% in the PSDs at frequencies 200–700 Hz, shown with logarithmic binning for illustration purposes. Vertical thick black and light gray bars show the 25–75 percentiles of the data. The black vertical bars (at 200–700 Hz) indicate at which frequency range the median (black horizontal line through the bars) was significantly different from one, whereas light gray (very small) vertical bars (<200 Hz and >700 Hz) indicate that median ratios were not significantly, or only by <5%, different from one. In some recording locations (circles), we observed ITD-sensitive changes of the PSD that are larger than 2.7 SDs (vertical thin lines, corresponding to 99% of the distribution) from the mean. The gray horizontal curves show 1 SE distance from the mean. Note that both the SD (thick bars) and the SE (gray horizontal line) of each frequency bin are shown to illustrate the variability as well as the reliability of the data. Left: histogram of the medians over the frequency ranges 200–700 Hz and 700–10,000 Hz for each recording location.

Fig. 2.

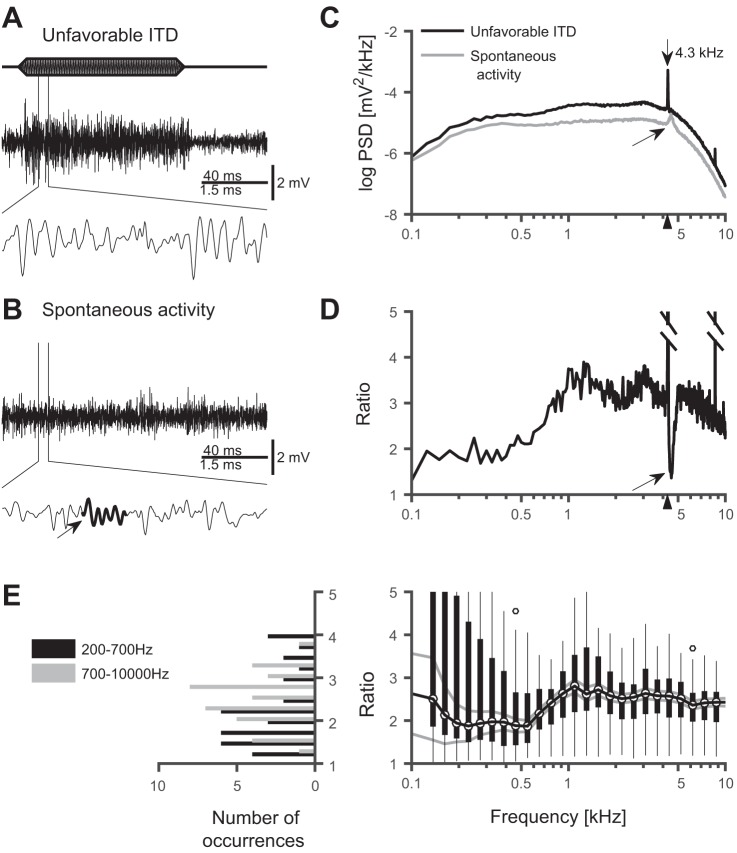
Driven and spontaneous extracellular potential. A: neurophonic in response to stimulation with a binaural tone at BF (4.3 kHz) at an unfavorable ITD (−108 μs), as shown in Fig. 1B. B: spontaneous activity at the same recording site. A and B: 100-ms stimulation (top bar), 160-ms segment of response (middle), and close-up of 22–28 ms of the response above (bottom). Arrow points to an oscillatory episode in spontaneous activity. C: averaged (500 trials) power-spectral densities (PSDs) of the responses to unfavorable ITD as in A (15–95 ms segments analyzed) and of 80-ms segments of spontaneous activity as in B. Arrow points to broad peak in the spontaneous PSD at ~4.5 kHz and a second arrow marks the stimulus frequency (4.3 kHz), which is also shown by a triangle on the x-axis. D: ratio of PSDs in C. The peak value (53.3) at the stimulus frequency has been truncated. Arrow shows a notch at ~4.5 kHz. The truncated peak at 8.6 kHz corresponds to the 2nd harmonic. The triangle at the x-axis marks the stimulus frequency (4.3 kHz). E, right: the population data of 37 recording sites shows a significant change in the spectra across all frequencies (all P < 4 ⋅ 10^{– 5}, t-test). In the spectra, the peaks at the stimulus frequency of each recording site were omitted. The largest changes are at frequencies ~0.9–1.4 kHz. Black vertical bars show the 25–75 percentiles of the data. The median is indicated by the black line and circles through the bars, and gray lines denote 1 SE distance from the mean. Vertical thin black lines mark 2.7 SDs (corresponding to 99% of the distribution) from the mean. In two recording locations (circles), we observed changes of the PSD larger than 2.7 SDs. At frequencies <400 Hz the 2.7 SD lines are truncated at the top. Left: histogram of the medians over the frequency ranges 200–700 Hz and 700–10,000 Hz for each recording location.

Fig. 4.

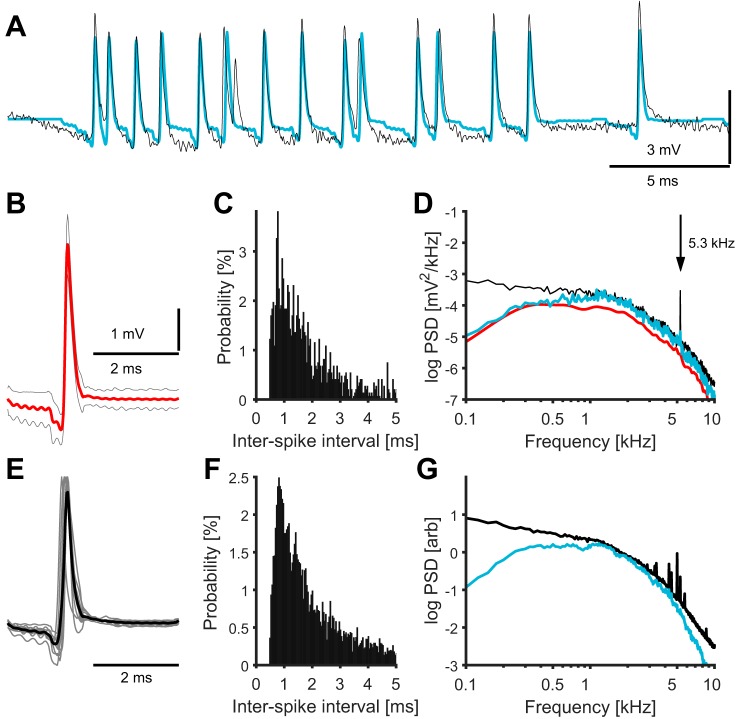
Extracellular recordings from nucleus magnocellularis axons in response to stimulation with tones. A: extracellular unfiltered voltage trace (black) and spike-replaced voltage trace (blue) where each detected spike was replaced with the mean spike waveform. The stimulus (60-ms tone burst) was turned on at the beginning of the shown trace. B: mean spike waveform of detected extracellular axonal spikes (red), ± SD for each time point (gray, N = 1,488 spikes). C: interspike interval (ISI) histogram for the detected spikes. The bin size was 40 μs, and the probability of ISIs >5 ms was 5.4%. D: average PSDs of all recordings of the example axon: PSD of the raw trace (black), the PSD of the single spike shown in B (scaled, red), and the PSD of the spike-replaced voltage trace (blue). The vertical arrow points to the stimulus frequency. E: grand average (black) of the extracellular mean spike waveforms (gray) of all 11 analyzed axons. The peak values were normalized to one. F: ISI histogram for all detected spikes in all axons. The bin size was 40 μs, and the probability of ISIs >5 ms was 12.1%. G: grand average PSD of raw traces of all recording locations at each frequency (black), and of all spike-replaced traces of all recording locations (blue). The sharp peaks at ~5 kHz are related to the stimulus frequencies used.

To estimate average PSDs at the population level (Figs. 3I and 4G), we normalized the peak of each units’s PSD to 1 before averaging across different recording locations. The average peak has a value <1 because the frequency to which the peak was normalized varied across recording locations. Around the stimulus frequencies of the population (Fig. 3I, arrows), the population average spectrum was somewhat increased because we did not exclude the peaks at the stimulus frequencies for this analysis.

nm axonal recordings.

We used the aforementioned procedure to detect spikes from 14 NM axons recorded in NL. The experimental protocols were identical to extracellular coaxial glass electrode recordings from NL neurons (Funabiki et al. 2011).

There were extracellular and intracellular recordings from NM axons. Recordings were classified as intracellular if the resting potential was <–55 mV, if the spike amplitude was >8 mV, and if the SNR at the stimulus frequency was <4 dB. Three of 14 units fulfilled these criteria, and in further analyses we focused on the 11 extracellular recordings from NM axons. The spike-detection algorithm was applied as described above for the NL single-unit recordings.

Data Analysis: Single-Neuron Contributions to the Extracellular Voltage

To test the hypothesis that at any recording location in NL spikes of at most only one single NL neuron contribute to the EFP, we used the variance as a basic measure of the EFP. As specified in detail below, we found that changes in the spiking activity of an NL neuron between favorable and unfavorable ITD stimuli were sufficient to explain changes in the low-frequency (<2 kHz) component of the spectra of the neurophonic. To do so, we associated these changes in the variance of the neurophonic (Fig. 1) with the waveforms in the single-cell data (Fig. 3) and the known changes in firing rates of NL neurons.

In general, the variance σ² of a voltage trace V(t) can be calculated either in the time domain or in the frequency domain. Calculated in the time domain, the variance includes all frequencies present in the trace. In the frequency domain, the integral over the whole spectrum equals the variance calculated in the time domain. The integral over a part of the spectrum from frequencies f_min to f_max equals the variance in the time domain for traces sharply band-pass filtered at these frequencies.

Utilizing this general statement for voltage traces V recorded in NL, we thus assume that the spectral contribution of the spikes of NL neurons is limited within some frequency range from f_min to f_max. Furthermore, we assume that the firing rate of the NL neurons is modulated specifically by ITD. Then, in the frequency domain, we can calculate the variance due to NL neurons’ activity (plus a constant baseline) as a function of ITD by integrating the PSD for a particular ITD over the assumed frequency range. Thus, the maximum change Δσ² in the variance that is assumed to be caused by an increase in NL neurons’ activity is equal to the area between the PSDs of the neurophonic to favorable and unfavorable ITD stimulation, i.e., PSD_f(f) and PSD_u(f), respectively (e.g., in Fig. 1C):

$$\Delta {\sigma }_{\text{NP}}^2={\displaystyle {\int }_{f_{\text{min}}}^{f_{\text{max}}}\left[{\text{PSD}}_f(f)-{\text{PSD}}_u(f)\right]}\text{d}f$$ (3)

where f_min = 50 Hz and f_max = 2,000 Hz. The large spectral peak at the stimulus frequency was not included. The spectral changes in the neurophonic at frequencies higher than the stimulus frequency were in the order of background noise and they were therefore neglected here.

In the time domain, we can calculate the variance of the voltage trace $V(t)={\displaystyle \sum _{t_i}k}(t-t_i)$ generated by spikes at times t_i with extracellular waveform k(t) of an NL neuron (e.g., Fig. 3) recorded with an electrode close to an NL neuron (Funabiki et al. 2011)

$${\sigma }_{\text{NL}}^2=\frac{1}{T}{\displaystyle {\int }_0^T{\left[V(t)-\overline{V}\right]}^2}\text{d}t=\left[\frac{1}{T}{\displaystyle {\int }_0^T{V}^2}(t)\text{d}t\right]-{\overline{V}}^2$$

where $\overline{V}=\frac{1}{T}{\displaystyle {\int }_0^{T}V}(t)\text{d}t$ is the mean voltage and T is the recording time. The change $\Delta {\sigma }_{\text{NL}}^2$ in variance due to changes Δλ of the firing rate λ of an NL neuron can then be derived as shown e.g., by Kuokkanen et al. (2010):

$$\Delta {\sigma }_{\text{NL}}^2=\left[\Delta \lambda {\displaystyle {\int }_{-\infty }^{+\infty }{k}^2}(t)\text{d}t\right]-\Delta ({\lambda }^2){\left[{\displaystyle {\int }_{-\infty }^{+\infty }k}(t)\text{d}t\right]}^2\mathrm{.}$$ (4)

The terms Δλ and Δ(λ²) describe changes in the firing rate and its squared value, respectively, between favorable and unfavorable ITDs, and we used mean values from Peña et al. (1996).

Having calculated the changes of the variances for the neurophonic in Eq. 3 and for the recordings close to NL neurons in Eq. 4, we can define the ratio

$$F=\sqrt{\frac{\Delta {\sigma }_{\text{NP}}^2}{\Delta {\sigma }_{\text{NL}}^2}\mathrm{.}}$$ (5)

We expect F ≪ 1 on average because the amplitude A of a spike waveform recorded at a random position in NL, at some distance r to the next NL neuron, is much smaller than the amplitude close to an NL neuron, i.e., at a distance that is approximately equal to the size of the soma of an NL neuron. The radius r_s of a typical NL cell is ~10 μm (Carr and Boudreau 1993; Kuokkanen et al. 2010).

To estimate the distance r, we compared two approaches. First, we followed the results from Pettersen and Einevoll (2008), who described the distance-dependent decay of spike waveforms. We parametrized their results (for r_s≤r≤120 μm) and used the following expression for spike amplitudes:

$$A(r)=A(r_s){\left(\frac{r_s}{r}\right)}^{(r+100\mu \text{m})/90\mu \text{m}},$$ (6)

assuming a frequency-independent decay for contributions at frequencies <2 kHz. For 10 μm ≲ r, the decay of the amplitude with distance is roughly proportional to r^–1.2, and for r≈80 μm, the decay is roughly proportional to r^–2. Furthermore, assuming F = A(r)/A(r_s), we can estimate the distance r of an electrode from the soma of the next NL neuron based on the changes in variance for the neurophonic and single-cell recordings.

As a second approach to estimate r, we numerically calculated the distance of randomly placed electrodes within NL to the next NL neuron. We thus distributed 6,804 neurons’ soma positions such that the mean and SD of the closest-neighbor distance corresponded to the distance measured in NL [mean ± SD: 100 ± 11 μm, Kuokkanen et al. (2010); shrinkage corrected from Carr and Boudreau (1993)]. As a simple model, we used a face-centered cubic (A3) lattice with a random jitter in x-, y-, and z-directions, each within (−20 μm, 20 μm). We then placed 6,804 electrode locations randomly into the model tissue and measured their distances to the nearest neighboring soma. The resulting electrode-to-soma distances were 58 ± 17 μm (mean ± SD). We did not include any structural inhomogeneities or differences due to several contributing sources with different tuning properties with respect to stimulus ITD or stimulus frequency.

RESULTS

To understand the contributions of all circuit elements to the EFP, and to further clarify the origin of the neurophonic potential in the NL of the barn owl, we analyzed extracellular recordings of the response to tonal stimuli. We had previously shown that the neurophonic could largely be explained by presynaptic sources (Kuokkanen et al. 2010, 2013; McColgan et al. 2017). Here we support the hypothesis that postsynaptic spikes of NL neurons can add a typically small contribution to the neurophonic that is sensitive to the ITD. Extracellular data were obtained with high-impedance tungsten microelectrodes, from 14 animals at 37 recording locations. We also analyzed extracellular coaxial glass-electrode recordings obtained from NL neurons just before recording intracellularly from them (Funabiki et al. 2011). Finally, we analyzed extracellular coaxial glass-electrode recordings from incoming axons of nucleus magnocellularis principal neurons, made within NL.

Output of NL: Comparison of Binaural Stimulation at Favorable and Unfavorable ITDs

The shape of the PSD of an EFP depends on contributions from various neuronal sources, and each source adds power proportional to its mean activity (Hohn and Burkitt 2001; Kuokkanen et al. 2010; Snyder and Miller 1991). The spectral component(s) of a particular type of source can be isolated if its mean activity can be changed selectively by varying a stimulus. We used this approach to estimate the spectral components of action potentials of NL neurons to the EFP. To achieve a selective change of the mean spiking activity of NL neurons, we exploited their selectivity to ITD, which arises in the auditory pathway for the first time in these neurons: Varying the ITD of a binaural tone leaves the mean spike rates of the inputs to the NL constant; only the relative phase of the inputs from the ipsi- and contralateral sides is changed. In contrast, varying the ITD affects the output rate of NL neurons, which act as coincidence detectors; the NL neurons fire ~180 spikes/s at an unfavorable ITD and ~400–500 spikes/s at a favorable ITD (Peña et al. 1996) (for definitions of favorable and unfavorable ITD, see materials and methods). A further advantage of NL is its tonotopic organization and that neurons are tuned to sound stimulus frequencies that are in the range of several kilohertz. In the PSDs, only a narrow frequency range around the stimulus frequency is affected when the relative phase of inputs changes, determining their overall phase locking to the tone. In what follows, we show that the stimulus frequencies we used were well separated from the spectral contributions of action potentials of NL neurons. We could thus isolate the spectral contribution of NL neurons’ action potentials to the PSD of the neurophonic.

To reveal contributions of the activity of NL neurons to the EFP, or neurophonic, we recorded responses to tonal stimuli at a favorable ITD (Fig. 1A) and an unfavorable ITD (Fig. 1B). Stimuli were at a constant frequency, close to the BF of the respective recording location (see materials and methods for a concise definition of the term “best frequency”). We observed an oscillatory neurophonic for stimulation with both favorable and unfavorable ITDs. The oscillation amplitude at the favorable ITD was notably larger than that at the unfavorable ITD (Fig. 1, A and B, bottom traces).

The PSDs in response to these binaural tones (Fig. 1C) had a stereotypical shape for both favorable and unfavorable ITDs, with a large peak at the stimulus frequency. Otherwise the PSDs weakly varied with frequency between 0.1 and 8 kHz. Changing the ITD from unfavorable to favorable affected the PSD in two ways: First, at frequencies between 200 and 700 Hz, the PSD for the favorable ITD (gray line) exceeded the PSD for the unfavorable ITD (black line), which we interpret as the contribution of action potentials of NL neurons. Second, the peak at the stimulus frequency 4.3 kHz was higher for the favorable ITD than for the unfavorable ITD, which can be fully explained by different relative phases of the ipsi- and contralateral inputs to NL (Kuokkanen et al. 2013). The change in relative phases could also be interpreted as a change in the average phase locking to the stimulus frequency in the population of inputs from both sides, which strongly affects the spectral peak height at the stimulus frequency.

To quantify changes in the PSD between stimulus conditions, we used the ratio of the two PSDs; see Eq. 1 in materials and methods. Here, the PSD at the favorable ITD was divided by the PSD at the unfavorable ITD (Fig. 1D). This ratio was large (≈23.7) at the stimulus frequency (4.3 kHz). We disregarded the peak at the stimulus frequency in our further analysis because we had shown that it originates from presynaptic spikes (Kuokkanen et al. 2013).

Interestingly, at frequencies ~300 Hz, in this example the PSD in response to a favorable ITD was more than twice as large as the PSD in response to unfavorable ITD stimuli (ratio: 2.6). We note that the frequency range (200–700 Hz) in which we observed marked changes was clearly distinct from the stimulus frequency (4.3 kHz). Moreover, the frequency range (200–700 Hz) was not related to the mean firing rate of the neurons, even if the values could be similar (see discussion).

To evaluate changes in the spectra in response to favorable and unfavorable ITDs across different stimulus frequencies and recording locations, we excluded the peak at the stimulus frequency from the PSDs in the population analysis (Fig. 1E). The median of the ratio of PSDs was significantly higher than one within the frequency range of 200–700 Hz (frequency resolution 25 Hz, all bins > 1.057 and P < 0.003; t-test, N = 37), and for individual recordings in 25 of 37 cases for the full 200–700 Hz range (all recordings P < 0.014, t-test, N = 20 frequency bins in each recording) even if the changes were typically very small (median ± SD ratio: 1.13 ± 0.06, N = 25, Fig. 1E, left-hand side, black bars). In the rest of the recordings the ratio was not significantly different from one. To further quantify this effect, we calculated the median PSD ratio in each frequency bin in the range 200–700 Hz (N = 37 recording locations). The highest median values (above 1.17) were found at 300–400 Hz (average 1.23 ± 0.03, 4 frequency bins). At other frequencies (<200 Hz and >700 Hz) the median of the ratio of PSDs was only occasionally significantly different from one (no continuous ranges of frequencies). These differences were also small, ratio being typically ≲1.04. The changes were independent of the type of anesthesia (ketamine hydrochloride with xylazine, or urethane).

To summarize, we found small (a few percent on average) changes in the PSD at ~300 Hz between the responses to the favorable ITD and unfavorable ITD. These changes were statistically significant and attributed to the NL neuronal spikes. The output of NL could therefore contribute to the spectrum at ~300 Hz.

Input to NL: Comparison of Spontaneous Activity and Binaural Stimulation at Unfavorable ITD

To disentangle the contributions of the input and the output of NL to the EFP, we analyzed the changes between spontaneous activity and driven activity at an unfavorable ITD. We hypothesized that these changes should selectively show the contribution of NM spiking activity, because NM input axons experience a significant increase in discharge rate (from spontaneous to driven rate) upon stimulation whereas NL neurons do not show as large an increase in firing rate (from spontaneous activity to driven at unfavorable ITD) (see discussion for a detailed derivation from published data). Figure 2 shows considerable changes between these conditions. The time course of the spontaneous activity in NL was not oscillatory and was much smaller in amplitude than the response to an unfavorable ITD (Fig. 2, A and B, same recording location as in Fig. 1, A–D). The PSD of the spontaneous activity was, accordingly, on average much lower than the PSD of the driven activity (Fig. 2C). Furthermore, the large peak in the PSD at the stimulus frequency was missing in the spontaneous activity (Fig. 2C, gray line). However, in this example the spontaneous activity exhibited some oscillatory episodes (arrow in Fig. 2B) and, due to these spontaneous oscillations, there was a broader peak at ~4.5 kHz (Fig. 2C, arrow), around the estimated best frequency of 4.3 kHz. Both the oscillatory episodes and the broad peak could originate from spontaneous population responses in the auditory nerve (Köppl 1997; Neubauer et al. 2009).

The ratio of PSDs (driven vs. spontaneous) was high (≳2) over the entire frequency range and largest for frequencies ≳1 kHz (Fig. 2D). A huge peak at the stimulus frequency was also observed (ratio: ≈53.3). Furthermore, there was a clear notch around the best frequency, which corresponds to the broad peak in the spontaneous activity (arrows in Fig. 2, C and D). The massive spectral changes related to the input, as seen in Fig. 2D for one recording location, were similar throughout the population (Fig. 2E). Note that in Fig. 2E the large peaks at the respective stimulus frequencies were omitted. In the population (N = 37 recording sites), at all analyzed frequencies (0.1–8 kHz), the medians of the ratios of PSDs were significantly greater than 1 (range: 1.8–3.1, bin size 25 Hz; all P < 4⋅10^{– 5}, t-test). The median of the ratio was highest (>2.6) at 925–1,375 Hz (2.83 ± 0.14, mean and SD of medians, 18 frequency bins) and lowest (<2.0) at 200–600 Hz (1.91 ± 0.06, mean and SD of medians, 15 frequency bins).

At low (<300 Hz) frequencies in Fig. 2E, the distribution of the PSD ratios was bimodal, with 15 of 37 recording locations showing a high PSD ratio (>3) and 18 of 37 recordings showing a low ratio (<2). The recording locations with the high PSD ratios were typically (in 11 of 15 recordings) recorded with a 1–13,000 Hz band-pass filter whereas the ones with a low PSD ratio were typically (in 14 of 18 recordings) recorded with a 300–13,000 Hz band-pass filter. The PSD ratios of the locations were significantly different for the two groups of filter settings (P value 0.05, t-test, N = 37). In contrast, in Fig. 1E there was no such bimodality for the PSD ratios between favorable and unfavorable ITDs, neither at frequencies < 300 Hz (P value 0.87), nor for the frequency range of 50–2,000 Hz (P value 0.59).

To summarize, we found considerable changes in the PSDs between responses to the unfavorable ITD and spontaneous activity. Changes ≳80% (ratio ≳1.8) were significant at all frequencies but strongest for frequencies in the range from 925 to 1375 Hz where the PSDs increased ≳160% (ratio ≳2.6). These changes were consistent with the large changes in the inputs to NL (i.e., NM axonal spikes and their synaptic currents onto NL neurons), and them being the dominating sources of the neurophonic over the entire range of frequencies examined.

Extracellular Waveforms of Action Potentials of NL Neurons

To further test whether the contribution to the PSD of the neurophonic in the frequency range 200–700 Hz could be due to NL spikes, we reanalyzed the extracellular spike waveforms of 28 NL neurons recorded by Funabiki et al. (2011). We used a strict criterion for selecting spikes (see materials and methods) to make sure that we included responses from only one NL neuron at each recording location. The criterion may have excluded some of the actual spikes, especially spike doublets (Carr and Konishi 1990) because of their different waveforms in comparison to isolated spikes. The firing rate of the neurons was modulated with ITD (example in Fig. 3A) and the rates (favorable ITD: 470 ± 136 spikes/s, mean ± SD, N = 28 neurons, range: 217–744 spikes/s; unfavorable ITD: 179 ± 109 spikes/s, range: 0–428 spikes/s) were similar to previously reported values (Peña et al. 1996; Funabiki et al. 2011). The rate at the unfavorable ITD was similar to or higher than the spontaneous firing rate (49 ± 51 spikes/s, range: 0–150 spikes/s).

In the extracellularly recorded voltage traces that were obtained close to an NL neuron, spikes were often clearly visible. Their amplitudes were typically several times larger than the neurophonic oscillation amplitude (example cell in Fig. 3, B and C). For high firing rates, spike waveforms may overlap (Fig. 3B). In this unit, we detected 825 spikes altogether across all stimulus conditions. The average waveform was obtained from all spikes of the respective unit (Fig. 3D; see also Eq. 2 in materials and methods). The ISIs (Fig. 3E) of the spikes of this unit showed a periodicity with the stimulus frequency (3.8 kHz) due to the phase locking. ISIs <0.5 ms were excluded by our spike detection algorithm.

The average PSD of the extracellular traces across all stimulus conditions at the example recording location showed a shoulder at ~400 Hz (Fig. 3F, black) overlaid on a larger low-frequency tail. There was also a small localized peak at the stimulus frequency (3.8 kHz, arrow in Fig. 3F), as reported previously by Ashida et al. (2012). To better assess the PSD of the average spike waveform and to increase its frequency resolution (a 4-ms voltage trace yields a maximum frequency resolution of only 250 Hz), we created voltage traces by replacing each detected spike with the average spike waveform (Fig. 3, B and C, orange) thus creating 80-ms segments with a frequency resolution of 12.5 Hz. We note that the spectrum of such an 80-ms segment with a given number of spikes (Fig. 3F, orange) is similar to the spectrum of a 80-ms segment with only one spike (Fig. 3F, green) because each spike makes the same contribution to the spectrum. However these two PSDs are different because correlations in the spike timing, for example preferred interspike intervals and phase locking to the stimulus frequency, add power to the spectrum. We also note that calculating PSDs from average spike waveforms suppresses power at frequencies to which spikes are not locked. This suppression has the strongest effect at <300 Hz and at >3,000 Hz. The PSDs of the single spike and of the spike-replaced trace showed a peak that coincided with the ~400-Hz shoulder of the full EFP (Fig. 3F, orange and green).

In the population of N = 28 neurons, we detected 1,030 ± 440 spikes (mean ± SD; range: 295–2,014). The amplitudes of the average spike waveforms (max-min) were 3.55 ± 2.16 mV (range 0.45–8.38 mV) with a half-peak width of 176 ± 39 μs (range 102–277 μs, Fig. 3G). The spike amplitudes and widths were not significantly different between the two groups of extracellular recordings that either was or was not followed by intracellular recordings (each group 14 recordings of 28, see materials and methods): The spike widths were 175 ± 44 μs and 177 ± 35 μs, respectively (P > 0.8, 2-sample t-test), and the amplitudes were 3.7 ± 2.5 mV and 3.35 ± 1.83 mV, respectively (P > 0.6, 2-sample t-test). The average spike waveforms sometimes included oscillatory components at the stimulus frequencies (range: 2.1–5.1 kHz). The range of ISIs in the population was typically 0.86–5.4 ms (10th and 90th percentiles), and median ISIs were in the range 1.4–4.7 ms (Fig. 3H). We note that spike doublets (ISI < 0.5 ms) were rejected by our spike selection algorithm because they had a different spike shape than isolated spikes. In the grand average ISI histogram the apparent phase locking is lost due to mixing of different stimulus frequencies.

In the population of 28 NL neurons, the grand average PSD of both extracellular traces and the spike-replaced traces (Fig. 3I) were similar to the example in Fig. 3F. The normalized population average PSD of the spike-replaced traces showed a large peak at ~400 Hz. A second, smaller peak at ~1.5 kHz was of unknown origin; a peak at a similar frequency was observed in the spectra of click responses in NL (Wagner et al. 2005, 2009).

To summarize, the peaks at ~400 Hz of the PSD of extracellularly recorded action potentials of NL neurons (Fig. 3, F and I) matched the frequency range 200–700 Hz in which the PSD of the neurophonic was ITD modulated (Fig. 1, C–E). This observation further supports our claim that NL neurons contribute to PSD of the EFP in this frequency range, although the overall contribution to the PSD is small.

ITD-Dependent Modulations of the PSD (<2 kHz) Are Consistent with Contributions of Single NL Neurons

We further investigated whether the small differences in the neurophonic spectra between responses to favorable and unfavorable ITDs could be explained by contributions of a single NL neuron. To test this, we first used the neurophonic to calculate the change of the variance (frequencies <2 kHz) and called this measure $\Delta {\sigma }_{\text{NP}}^2$. The variance, i.e., the area under the PSD curve, is proportional to the mean firing rate of the neuronal sources contributing to these frequencies. Then we used the spike waveforms from the single-unit recordings close to NL neurons and the ITD-dependent modulation of the firing rate of an NL neuron to obtain a second measure for the change of the variance, which we called $\Delta {\sigma }_{\text{NL}}^2$. Finally, we checked for the consistency of the two measures taking into account a model for the attenuation of the spike waveform amplitude with the distance from the NL neuron (for details, see materials and methods).

In the example shown in Fig. 1C, the neurophonic spectrum changed within the frequency range of 50–2,000 Hz by $\Delta {\sigma }_{\text{NP}}^2$ = 1.8·10⁻³ mV². In the population of 37 neurophonic recordings, the mean change was $\Delta {\sigma }_{\text{NP}}^2$ = 2.1 ± 2.5·10⁻³ mV² (range 0.002·10⁻³ mV²–11·10⁻³ mV², median 0.98·10⁻³ mV²). The distribution of changes in variance was skewed with a long tail toward the large variance changes. We note that the change in variance (as used above) is closely related to the ratio of the spectra (as used for example in Fig. 1E); they measure essentially the same changes. However, the change in variance measures the difference in an additive manner and its baseline is at zero whereas the ratio is a multiplicative measure and the baseline is at one. Thus, the distribution of the change in variance also closely resembled the distribution shown in Fig. 1E (left-hand side, black histogram) but had an even longer tail.

To estimate the change $\Delta {\sigma }_{\text{NL}}^2$ in the variance from the single-cell recordings, again comparing unfavorable and favorable ITD, we used Eq. 4. The equation calls for the change in firing rate λ as well as for the spike waveform k. For the firing rates at unfavorable and favorable ITD, we used the literature values because our spike detection method allowed for skipping spikes (for example spike doublets). Peña et al. (1996) provided a mean rate at favorable ITD (354 ± 168 spikes/s) and a mean rate at unfavorable ITD (180 ± 101 spikes/s), giving a difference in the firing rate of Δλ = 174 spikes/s and a squared difference of Δ(λ²) = 93,000 s⁻².

In the example shown in Fig. 3, A–F, the amplitude of the average spike waveform (max-min) was 8.38 mV. The integral over the spike waveform (Fig. 3D) was ∫k(t)dt = 0.11 μVs, and the integral over the squared spike waveform was ∫k²(t)dt = 7,500 μV²s. The predicted change in the variance was $\Delta {\sigma }_{\text{NL}}^2$=1.3 mV².

In the population of 28 NL single-cell recordings, the integral over the single spike waveform was ∫k(t)dt = 0.037 ± 0.077 μVs (range –0.15 to 0.25 μVs), and the integral over the squared spike waveform was ∫k²(t)dt = 1,690 ± 1,810 μV² (range 20 to 7,460 μV²s). Together, according to Eq. 4, this yielded a mean predicted change in variance of $\Delta {\sigma }_{\text{NL}}^2$= 0.29 ± 0.32 mV² (range 0.0027 to 1.3 mV², median 0.23 mV²).

The average change of the variance $\Delta {\sigma }_{\text{NP}}^2$ = 2.1·10⁻³ mV² of the extracellular voltage estimated from the neurophonic was more than two orders of magnitude smaller than the average change of the variance $\Delta {\sigma }_{\text{NL}}^2$ = 0.29 mV² estimated from NL spike waveforms. This small ratio was likely a function of the distance between neuron and recording electrode. We calculated the average conversion factor F that describes this average decrease of the spike amplitude, which is related to the decrease in the SD of the voltages (see also Eq. 5):

$$F=\sqrt{\frac{\Delta {\sigma }_{\text{NP}}^2}{\Delta {\sigma }_{\text{NL}}^2}}=\mathrm{0.084.}$$ (7)

Occasionally, our tungsten electrodes appeared to be close to an NL neuron. In these cases, the recorded contribution from NL neurons to $\Delta {\sigma }_{\text{NP}}^2$ assumed a relatively large value. The maximum value of $\Delta {\sigma }_{\text{NP}}^2$ we observed was 11·10⁻³ mV². This value should be similar to the lowest values obtained for extracellular recordings with sharp coaxial glass electrodes. Indeed, the smallest value for $\Delta {\sigma }_{\text{NL}}^2$ was 2.7·10⁻³ mV². In other words, as expected, the upper tail of distributions for $\Delta {\sigma }_{\text{NP}}^2$ overlapped with the lower tail of the distribution for $\Delta {\sigma }_{\text{NL}}^2$.

To further check the congruence of the two approaches to estimate the contribution of NL neurons to the EFPs in NL, we related the conversion factor F to the expected decrease of the spike waveform amplitude with distance from the NL neuron [see Eq. 6 and Pettersen and Einevoll (2008)]. Assuming that the mean value $\Delta {\sigma }_{\text{NL}}^2$ = 0.29 mV² explains the change of variance at ~10 μm distance from the soma (i.e., the radius of a soma), the measured values for $\Delta {\sigma }_{\text{NP}}^2$ resulted in a distribution of conversion factors F = 0.07 ± 0.05 (mean ± SD, range from 0.003 to 0.2). Using Eq. 6, this distribution for F predicted the mean distance r = 57 ± 22 μm (range: 31 to 117 μm) of the electrode to the nearest soma. The predicted distances from the electrophysiology were in line with a Monte Carlo simulation of an electrode tip placed randomly in NL tissue, which resulted in a distance of 58 ± 17 μm to the next NL neuron (for details see materials and methods).

To conclude, the small ITD-dependent modulation of the low-frequency (<2 kHz) component of the spectrum of the neurophonic can be explained by change of the firing rate of a single NL neuron. This contribution to the total variance of the EFP is, in general, quite small. Furthermore, its magnitude is highly variable because it is determined by the distance of the nearest NL neuron to the tip of the recording electrode.

Extracellular Voltage of NM Axonal Activity

What are the origins of the large contributions to the PSD of the neurophonic that are not modulated by ITD? We had previously shown that the PSD could largely be explained by NM spikes and synaptic currents (Kuokkanen et al. 2010, 2013; McColgan et al. 2017). We now show how NM axonal spike waveforms could contribute to the recorded PSD shapes. The extracellular fields due to synaptic currents from NM terminals onto NL neurons, another possible contributor, have not been quantified in barn owls, although Funabiki et al. (2011) and Ashida et al. (2012) have characterized and modeled these synaptic currents.

Extracellular spikes originating from single NM axons are presumably very small, except very close to an axonal node, in comparison to the neurophonic potential, which had amplitudes in the millivolt range. We were, however, able to measure their extracellular waveform in the same experiments described above (ITD-Dependent Modulations of the PSD (<2 kHz) Are Consistent with Contributions of Single NL Neurons). While searching for NL neurons in NL, Funabiki et al. (2011) occasionally recorded NM spike waveforms. We analyzed extracellular recordings from 11 of these NM axons within NL during tonal stimulation. We used the same spike detection method as for NL neurons (materials and methods). The firing rate of these NM axons did not depend on ITD but was modulated by the stimulus frequency.

Spikes were clearly visible in the extracellularly recorded voltage traces (Fig. 4A). In this example unit, we detected 1,488 spikes across all stimulus conditions. The average half-peak width of spikes was 135 ± 90 μs (Fig. 4B, red) and the average spike amplitude (max–min) was 4.3 ± 1.0 mV. The ISIs (Fig. 4C) were typically within the range 0.7–4.0 ms (10th and 90th percentiles, respectively; median: 1.5 ms) during tonal stimulation. The strong phase locking of the spikes of this unit showed a periodicity with the stimulus frequency (5.3 kHz) due to the phase locking. We note that ISIs <0.5 ms were excluded by our spike detection algorithm.

The average PSD of the extracellular traces across all stimulus conditions showed a wide plateau at <2,000 Hz (Fig. 4D, black). We also observed peaks at the stimulus frequency, consistent with the presence of the extracellular neurophonic population component in the signal. The spectrum of the example extracellular action potentials (Fig. 4D, blue/red) had a peak/shoulder at ~1,500 Hz.

In the population of N = 11 extracellular recordings from NM axons, we recorded 1280 ± 480 spikes per axon (mean ± SD, range: 372–1,980). The normalized average spike waveforms are shown in Fig. 4E. The half-peak width was 147 ± 37 μs (range: 99–224 μs) and the spike amplitude was 7.7 ± 5.8 mV (range: 1.0–18.3 mV). The firing rates in the population at the stimulus frequency (range: 3.3–5.3 kHz) were 450 ± 150 spikes/s (mean ± SD, range: 191–656 spikes/s), which were similar to those previously reported (Köppl 1997; Peña et al. 1996). The spontaneous firing rates were 121 ± 54 spikes/s (range: 63–261 spikes/s). The median interspike intervals in the population ranged 1.2–4.3 ms, similar to the example, and the population ISIs ranged 0.7–4.7 ms (10th and 90th percentiles, respectively, Fig. 4F). The distribution had a long, monotonically decreasing tail. The grand average spectrum of the extracellular voltage traces was also similar to the example, with strongest contributions <2,000 Hz (Fig. 4G, black). The spectrum of the extracellular action potentials (Fig. 4G, blue) had a peak at ~1,500 Hz. Note that the maximum height within 0.1–10 kHz of the PSDs of each axonal recording (excluding the peak at the stimulus frequency) was normalized to value one before averaging (Fig. 4G). Note also that the sharp peaks at ~5 kHz in Fig. 4G are related to the stimulus frequencies used.

We conclude that the large contributions to the PSD of the neurophonic at high frequencies (>1 kHz) derive from the activity of the input axons.

DISCUSSION

In many brain regions, identification of the sources of EFPs remains an open question, although the physical laws behind the phenomena are well understood (Buzsáki et al. 2012; Einevoll et al. 2013; Logothetis and Wandell 2004; Mitzdorf 1985; Nicholson and Freeman 1975). Here, we have made a significant step toward understanding the EFP in a relatively simple model system, the NL in the barn owl.

In the EFP there is often a large difference between the PSDs of the spontaneous activity and the driven activity (Burns et al. 2010b; Tokioka et al. 2000; Burns et al. 2010a). This difference corresponds to the altered relative contributions of many neuronal components (Henrie and Shapley 2005; Kuokkanen et al. 2010; Nikonov et al. 2002). Using the barn owl’s NL, we have developed a novel method of separating the spectral components of the activity representing the input (i.e., incoming axonal spikes) from the output (i.e., spikes of NL neurons). Similar approaches have been used for the EEG (Juergens et al. 1999) as well as for the LFP (Burns et al. 2010a; Henrie and Shapley 2005; Siegel and König 2003), mainly in the visual cortex.

What are the main components of the observed spectra of the EFP in NL of the barn owl? For sustained tonal stimulation, there is a high peak in the spectrum at the stimulus frequency, which is due to phase locking of the neural activity. Because sustained neuronal activity in NL can be well described by an inhomogeneous Poisson process (Kuokkanen et al. 2010), the shape of the spectrum of the EFP at frequencies that are different from the stimulus frequency is determined by the spectra of the spike waveforms associated with the sources (i.e., the waveforms of the extracellular spikes from these sources; see also Eqs. 3 and 4); the amplitude of the spectrum of the EFP at frequencies distinct from the stimulus frequency is proportional to the mean activity of the contributing neural sources, independent of their phase locking to the stimulus frequency (Hohn and Burkitt 2001; Kuokkanen et al. 2010; Lindén et al. 2011).

Extracellular waveforms are specific to the neuronal source, and have, for example, different widths: NM axonal extracellular spikes are narrow, with an estimated half-peak width of 147 ± 37 μs (mean ± SD). These narrow spikes are consistent with the observed changes at frequencies ≳0.5 kHz in the PSD (Fig. 4, D and G). Synaptic currents are estimated to have a half-peak width of ~100 μs (Ashida et al. 2013a; Funabiki et al. 2011) and contribute to the spectrum at even higher frequencies. For the extracellular spikes from NL neurons we observed a half-peak width of 176 ± 39 μs, which explains contributions in the spectrum at ≳0.3 kHz (Fig. 3F, I). Because NM axons, synapses, and NL neurons contribute to different frequency ranges, changing the relative activity of the different sources changes the shape of the resulting spectrum of the neurophonic.

By comparing spectra at favorable and unfavorable ITDs, which selectively affect the population activity of NL neurons, we found that NL neurons contributed to the spectrum of the neurophonic mainly at low frequencies (200–700 Hz) and that the contribution of NL neurons to the variance of the neurophonic was typically small, <5% (Fig. 1, C and D). In contrast, we observed large differences between the spectra of spontaneous activity and driven activity at an unfavorable ITD (typically ≳80% change in the area under the PSDs, i.e., the variance), and changes were most prominent at higher frequencies, i.e., >1 kHz (Fig. 2, C and D). We conclude that these large spectral changes are related to the input to NL, i.e., to the spiking activity of NM axons and synaptic currents.

Contribution of Laminaris Neurons to the Neurophonic Potential

The contribution from NL spikes to the neurophonic potential varied greatly between recording sites, consistent with the even spatial distribution of cell bodies in the nucleus (Fig. 1D–E). To quantify NL neurons’ contributions, we compared responses to favorable and unfavorable ITDs. PSDs did not depend on ITD for frequencies >1.5 kHz in any recording location. Therefore we used the median PSDs in the restricted frequency range 200–700 Hz and computed the ratio R for favorable and unfavorable ITD stimuli (see also Eq. 1 and Fig. 1E, left-hand side). In 19 of 37 recording sites, ratios were close to 1, that is 0.98 < R < 1.1. In 15 of 37 recording site the ratios were 1.1 ≤ R < 1.5, and only in 3 of 37 sites the ratios were >1.5; for these three recordings, we presume that the electrode was close to a neuron.

The large variability of the contribution of NL spikes to the neurophonic potential is in agreement with previous studies showing how the relative position of the recording electrode with respect to a neuron determines its extracellular spike amplitude (Gold et al. 2006; Lindén et al. 2010; Pettersen and Einevoll 2008). Moreover, we showed that the observed variability of the 200–700 Hz spectral component in the neurophonic can be explained by varied distances of recording electrodes to the nearest NL neuron and by the resulting decrease of the spike amplitude with distance.

All the extracellular single-unit recordings near NL neurons (Funabiki et al. 2011) that we reanalyzed showed a consistent NL extracellular spike waveform. The spike waveforms and widths were independent of whether or not an intracellular recording was achieved after the extracellular recording.

Extracellular spike waveforms always had a large positive peak. Such waveforms were reminiscent of the high-amplitude positive spikes observed by Gold et al. (2009) in the cat visual cortex. The extracellular waveforms we observed in NL are consistent with recordings close to a passive NL soma (Ashida et al. 2007) and action potentials being initiated in the axon: The resulting outward currents at the soma (capacitive and potassium currents) lead to a positive peak in the extracellular waveform. Because of a largely passive soma (Ashida et al. 2007) there should be no negative peak corresponding to inward sodium current. Since the membranes of NL neurons are extremely leaky [with a membrane resistance ~10.4 ± 8.2 MΩ in the 1–4 kHz frequency region (Funabiki et al. 2011), and higher frequencies having been modeled with even lower resistance (Ashida et al. 2007; Gerstner et al. 1996)], the capacitive current is of minor importance. During sustained tonal stimulation, the temporally variable membrane current may be roughly proportional to the deviation of the membrane voltage from its mean value. As a consequence, because membrane currents are also proportional to the extracellular voltage, the extra- and intracellular voltages should be approximately proportional to each other and show similar waveforms. Indeed, the extracellular NL spike waveform strongly resembles the intracellular NL spike waveform (Ashida et al. 2012; Funabiki et al. 2011); however, our extracellular waveforms were ~50% narrower. Furthermore, the spectra of the extracellular single-unit NL spikes had a peak at 200–700 Hz, which roughly agrees with the predictions made for currents produced by spiking activity in NL neurons (Ashida et al. 2007; Slee et al. 2010).

How does our spike-detection algorithm affect the estimate of the average spike waveform and its spectrum? Creating surrogate voltage traces with the same statistical properties as the measured traces and applying the same analysis to this surrogate data, we confirmed that the PSDs of average spike waveforms (colored spectra in Figs. 3 and 4) were slightly reduced at low (≲300 Hz) and high (≳3 kHz) frequencies. Averaging of spike waveforms suppressed low- and high-frequency signals that were uncorrelated to the spikes. This suppression did not affect our conclusions.

Previous results (Kuokkanen et al. 2010) showed that the magnitude of the large peak in the PSD at the stimulus frequency is proportional to the firing rate as well as to the synchronization index (vector strength) of the neuronal sources that provide significant power at this frequency. Spikes of NL neurons also phase-lock to the stimulating tone (Peña et al. 1996), but we nevertheless expect that their action potentials make only a minor contribution to the large peak in the PSD for two reasons: 1) The estimated overall contribution of action potentials of NL neurons to the PSD is rather small compared with the contribution of other sources (Figs. 1 and 2). 2) Spikes of NL neurons contribute to the spectral power mostly at frequencies 200–700 Hz (Fig. 1), and this frequency band is distinct from stimulus frequencies that are typically in the range of several kilohertz in our experiments. Together, the contribution of the NL output spikes to the PSD peak at the stimulus frequency should therefore be much smaller than that of the input-related activity. Similarly, for the cat medial superior olive (MSO) Goldwyn et al. (2014) suggested that spikes of MSO neurons do not contribute appreciably to the neurophonic.

The peak at the stimulus frequency in the PSD of the (extracellular) neurophonic is closely related to the large oscillation amplitude of the intracellularly recorded “sound analog potential” in NL neurons, and the oscillation amplitude determines the mean firing rate of an NL neuron (Ashida et al. 2012; Funabiki et al. 2011). This sound analog potential oscillates at the stimulus frequency because it is generated by the summed synaptic inputs, which are phase-locked to the stimulus frequency (Ashida et al. 2013a, 2013b). Thus both the neurophonic and the sound analog potential oscillate at the stimulus frequency because both are generated by the summed, phase-locked inputs that contribute to the respective potentials [see also Kuokkanen et al. (2010)]. Funabiki et al. (2011) also showed that the amplitude of the neurophonic is correlated to the amplitude of the sound analog potential. However, this correlation does not imply that NL neurons generate the neurophonic, even though their activity is good predictor for the neurophonic. Similarly, in the chicken NL, the neurophonic has been shown to be a good predictor of the response of neurons near the cell body layer (Köppl and Carr 2008; Palanca-Castan and Köppl 2015a), and the same conjecture has been made for the gerbil MSO (Goldwyn et al. 2014). In the gerbil, van der Heijden et al. (2013) demonstrated that inputs from both ears sum linearly in MSO neurons.

The small contribution of the NL spikes to the neurophonic and its very local modulation due to NL spikes have implications for information coding in NL. Importantly, the NL neurons are electrically isolated from each other in the sense that there is probably no ephaptic coupling across cells. In contrast, the EFP, which is generated by the inputs to the NL, could affect the spiking activity of NL neurons.

Contribution of the Input to NL to the Neurophonic Potential

In the neurophonic, how do the large differences in the PSDs between the spontaneous activity and the activity at the unfavorable ITD arise (Fig. 2)? We hypothesize that the extracellular field for spontaneous activity in NL is mainly shaped by the activity of the NM axons and synapses because the spontaneous (mean population) activity in NM is high (Köppl 1997; ~220 Hz) and because the number and density of NM axons in the recorded volume is also high (Kuokkanen et al. 2010). In contrast, NL neurons show low to moderate spontaneous spiking activity of (≤150 spikes/s) (Carr and Konishi 1990; Palanca-Castan and Köppl 2015a, 2015b; Peña et al. 1996), and the number and density of NL neurons is low.

The driven spectra are greatly influenced by the input (i.e., axonal spikes and synaptic contributions), particularly at high frequencies (>1 kHz, Fig. 2). Large differences in the PSDs (in particular outside the frequency range of 200–700 Hz) between the two conditions (spontaneous vs. unfavorable ITD) must be due to that input. This conclusion is further supported by estimates of the firing rate changes of NM and NL neurons: First, recordings from NM neurons show that the mean activity of the input to NL increases by ~90% (from ~220 spikes/s for spontaneous to ~420 spikes/s for sound-driven activity) (Köppl 1997; Peña et al. 1996. Second, the mean activity of NL neurons typically increases by only ~20% (from ~150 for spontaneous to ~180 spikes/s for unfavorable ITD) (Peña et al. 1996). Moreover, Fig. 1 demonstrated that even a >200% change in the mean activity of NL neurons (from unfavorable to favorable ITD) increased the PSD only by a few percent (typically <5% of the variance) and only within a narrow frequency range (200–700 Hz). Therefore, the ~20% change in the mean activity of NL neurons, which comprises the output of NL, should have only a small impact on the change in the PSD. Furthermore, contributions at low frequencies <1 kHz due to NL neurons’ activity can be assumed to be smaller than those from NM axons (McColgan et al. 2017) and synapses.

Here we reported that the input to NL contributes to frequencies mostly >1 kHz in the PSD. In contrast, many previous studies state that synaptic currents affect the local field potential at frequencies <500 Hz (Logothetis and Wandell 2004; Mitzdorf 1985; Nunez and Srinivasan 2006). In NL, however, these frequencies are affected the least by the “input” (including synaptic currents); it is unclear whether the synaptic currents can be seen at all in the neurophonic potential. However, our current study disregarded frequencies <100 Hz. It remains to be shown which spectral frequencies receive synaptic contributions.

In the spontaneous spectra, there was a broad peak at about the best frequency (arrows in Fig. 2C). Köppl (1997) reported so-called preferred intervals in the spontaneous discharge of NM units, which may explain this peak. The driven spectra at the unfavorable ITD did not show this broad peak, probably because the neural activity was locked strictly to the stimulus frequency. The spontaneous activity in the auditory nerve and in NM may also underlie oscillatory episodes observed in the spontaneous voltage traces (arrow in Fig. 2B). These oscillatory episodes were similar in shape to click-responses recorded in NL (Wagner et al. 2005, 2009; Fischer et al. 2011).

Synaptic Contributions and Inhibitory Activity in NL

A limitation of our approach to disentangle the sources of the EFP in NL is that the synaptic contributions, which in other systems have been suggested to be a substantial source of field potentials, cannot be differentiated here from incoming axonal spikes. Goldwyn et al. (2014) argued that in the cat MSO the neurophonic is generated mainly by synaptic currents.

To separate the synaptic contributions in NL from spikes in NM axons, a pharmacological approach is needed, possibly combined with quantitative modeling. Short-term synaptic plasticity might possibly contribute to frequencies ≲100 Hz of the spectra, since it has been suggested to occur in the birds’ auditory brainstem (MacLeod et al. 2007) with time constants on the order of 10–1,000 ms.

At low frequencies (≲100 Hz) of the spectra, there might also be an influence from the GABAergic inhibition to NL. GABAergic currents were observed in chick NM and NL (Funabiki et al. 1998; Monsivais et al. 2000), and they are much slower than the currents related to the NL spikes or NM spikes (Ashida et al. 2007; Carr and Konishi 1990; Funabiki et al. 2011; Köppl 1997). GABAergic activity also changes with ITD because the NL neurons project to the superior olivary nucleus, which provides inhibitory feedback and helps stabilize the NL neurons’ activity, allowing for representation of ITD independent of intensity [for review see Burger et al. (2011)]. To identify these GABAergic inputs, the spectra of responses to different stimulus levels should be analyzed.

Conclusions

EFP sources are generally incompletely understood. We analyzed a model EFP, the barn owl neurophonic driven by sustained tonal stimuli, and found that the contributions to the spectra of the neurophonic could be separated into components originating from the input to NL and others originating from the output of NL. The output NL spikes influenced the spectra to a small extent, mainly at low frequencies (200–700 Hz). In contrast, the input to NL, i.e., the NM axonal spikes and the synaptic input to NL neurons, affected the spectra to a greater extent and mostly at frequencies >1 kHz.

GRANTS

This research was sponsored by National Institute on Deafness and Other Communications Disorders (NIDCD) Grant DC-00436 to C. E. Carr; by NSF US-German Research Grant 1516357 to C. E. Carr; by NIDCD Training Grant T32-DC-000046 to A. Kraemer; by Kakenhi from Japan Society for the Promotion of Science (16K15727, 26280064 to K. Funabiki); by the German Research Foundation (DFG, Wa-606/12 to H. Wagner; CRC/TRR31 “Active Hearing” and Cluster of Excellence “Hearing4all” at the University of Oldenburg) and the Bundesministerium für Bildung und Forschung (BMBF, Bernstein Center for Computational Neuroscience Berlin, 01GQ1001A; German-US-American Collaboration in Computational Neuroscience “Field Potentials in the Auditory System” as part of the NSF/NIH/ANR/BMBF/BSF Collaborative Research in Computational Neuroscience Program, 01GQ1505A; Bernstein Focus “Neuronal Basis of Learning,” 01GQ0972).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

P.T.K., H.W., C.E.C., and R.K. conceived and designed research; P.T.K. analyzed data; P.T.K., T.M., C.E.C., and R.K. interpreted results of experiments; P.T.K. prepared figures; P.T.K. drafted manuscript; P.T.K., G.A., T.M., C.K., C.E.C., and R.K. edited and revised manuscript; P.T.K., G.A., A.K., T.M., K.F., H.W., C.K., C.E.C., and R.K. approved final version of manuscript; G.A., A.K., K.F., H.W., C.K., and C.E.C. performed experiments.