Modeling sources of interlaboratory variability in electrophysiological properties of mammalian neurons

Abstract

Patch-clamp electrophysiology is widely used to characterize neuronal electrical phenotypes. However, there are no standard experimental conditions for in vitro whole cell patch-clamp electrophysiology, complicating direct comparisons between data sets. In this study, we sought to understand how basic experimental conditions differ among laboratories and how these differences might impact measurements of electrophysiological parameters. We curated the compositions of external bath solutions (artificial cerebrospinal fluid), internal pipette solutions, and other methodological details such as animal strain and age from 509 published neurophysiology articles studying rodent neurons. We found that very few articles used the exact same experimental solutions as any other, and some solution differences stem from recipe inheritance from advisor to advisee as well as changing trends over the years. Next, we used statistical models to understand how the use of different experimental conditions impacts downstream electrophysiological measurements such as resting potential and action potential width. Although these experimental condition features could explain up to 43% of the study-to-study variance in electrophysiological parameters, the majority of the variability was left unexplained. Our results suggest that there are likely additional experimental factors that contribute to cross-laboratory electrophysiological variability, and identifying and addressing these will be important to future efforts to assemble consensus descriptions of neurophysiological phenotypes for mammalian cell types.

NEW & NOTEWORTHY This article describes how using different experimental methods during patch-clamp electrophysiology impacts downstream physiological measurements. We characterized how methodologies and experimental solutions differ across articles. We found that differences in methods can explain some, but not all, of the study-to-study variance in electrophysiological measurements. Explicitly accounting for methodological differences using statistical models can help correct downstream electrophysiological measurements for cross-laboratory methodology differences.

INTRODUCTION

Neurophysiological recordings form the basis for much of what is known about cellular electrophysiological function and dysfunction. This information is routinely reused, for example, in the comparison of new data with those from published experiments or in the development of computational models (Gleeson et al. 2010; Hines et al. 2004; Markram et al. 2015). Despite its importance, there have been few efforts to systematically compile and standardize data on electrophysiological characteristics of neurons (Teeters and Sommer 2009; Teeters et al. 2015; Tripathy et al. 2014). In this article, we consider the challenge of comparing and combining such data from the point of view of understanding sources of interlaboratory variance.

It is generally thought that subtle variation in experimental conditions introduces variation into the corresponding electrophysiological measurements, creating a challenge for data integration. However, there has been little effort to standardize basic experimental protocols such as in vitro patch-clamp electrophysiology across laboratories. As a result, differences in experimental protocols are often pointed to as the first culprit when results disagree between laboratories and investigators (Stuart et al. 1993; Yu et al. 2008). An aphorism reflects the conventional wisdom: an electrophysiologist would rather use another electrophysiologist’s toothbrush than use their data.

The impact of some experimental factors on electrophysiology has been previously reported, such as animal age (Okaty et al. 2009; Suter et al. 2013), strain (Moore et al. 2011), recording temperature (Grace and Onn 1989; Thompson et al. 1985), some solution components such as internal anions (Kaczorowski et al. 2007) or extracellular Ca²⁺ and Mg²⁺ (Aivar et al. 2014; Markram et al. 2015; Sanchez-Vives and McCormick 2000), and endogenous neuromodulator concentrations (Bjorefeldt et al. 2015). However, this direct experimental approach is typically limited to varying a single condition and studying effects in one or a few neuron types at a time within one laboratory. It is therefore unclear how these findings generalize to other neuron types, animal strains, and other confounding factors that typically remained fixed throughout each experiment.

Previously, we applied a meta-analysis approach to understand how variance in experimental conditions correlates with differences in electrophysiological measurements curated from published neuroscience studies (Tripathy et al. 2014, 2015). We found that electrode type (i.e., patch clamp vs. sharp electrode) and, to a lesser extent, animal age, strain, and recording temperature explain a portion of the observed study-to-study variance. However, a major unconsidered factor was the effect of experimental solutions.

In this work, we have expanded on our previous analysis to include the effects of recording and internal electrode solution composition. Given experimental and theoretical evidence suggesting that solution components are critical in defining cellular electrophysiological characteristics (Hille 2001), we reasoned that study-to-study electrophysiological variability could further be explained by differences in recording and pipette solution compositions. We developed a novel methodology that leverages both manual curation and text mining for extracting solution components from the Methods sections of published neurophysiological articles. Using these data, we provide the most comprehensive report on differences in experimental solutions used by laboratories to date. We next developed statistical models to rigorously quantify how solution composition differences, along with other basic experimental condition differences, contribute to electrophysiological variability. We find that this information increases the variability explained by the models, but the majority is left unexplained. This work suggests that there are additional factors contributing to electrophysiological variability, likely including ones not routinely reported within Methods sections.

MATERIALS AND METHODS

Description of the NeuroElectro database.

We used the NeuroElectro database (https://www.neuroelectro.org, RRID:SCR_006274) as a starting point for determining experimental condition factors that could influence electrophysiological measurements (Tripathy et al. 2014, 2015, 2017). Briefly, NeuroElectro was populated by curating published articles for summary data on neuronal electrophysiological measurements, such as resting membrane potential (V_rest) and input resistance (R_in). The electrophysiological values have been curated as the reported sample means, standard errors or deviations, and number of samples (e.g., V_rest: −56 ± 2.3 mV, n = 23). Neuron types were assigned by curators on the basis of an expert-defined listing of neuron types provided by NeuroLex.org (Hamilton et al. 2012; Larson and Martone 2013). Neuron instances within articles that could not be curated unambiguously to a single neuron type were assigned to the general neuron type “other.” Curators also annotated a set of relevant methodological information from Materials and Methods sections, including species, animal age, and electrode type (a full list of metadata features is shown in Fig. 3C and is available online at https://neuroelectro.org/). The database contains electrophysiological data reported under what were considered normal control conditions in the source publication. The database snapshot used in this study can be found on the UBC Dataverse (see endnote).

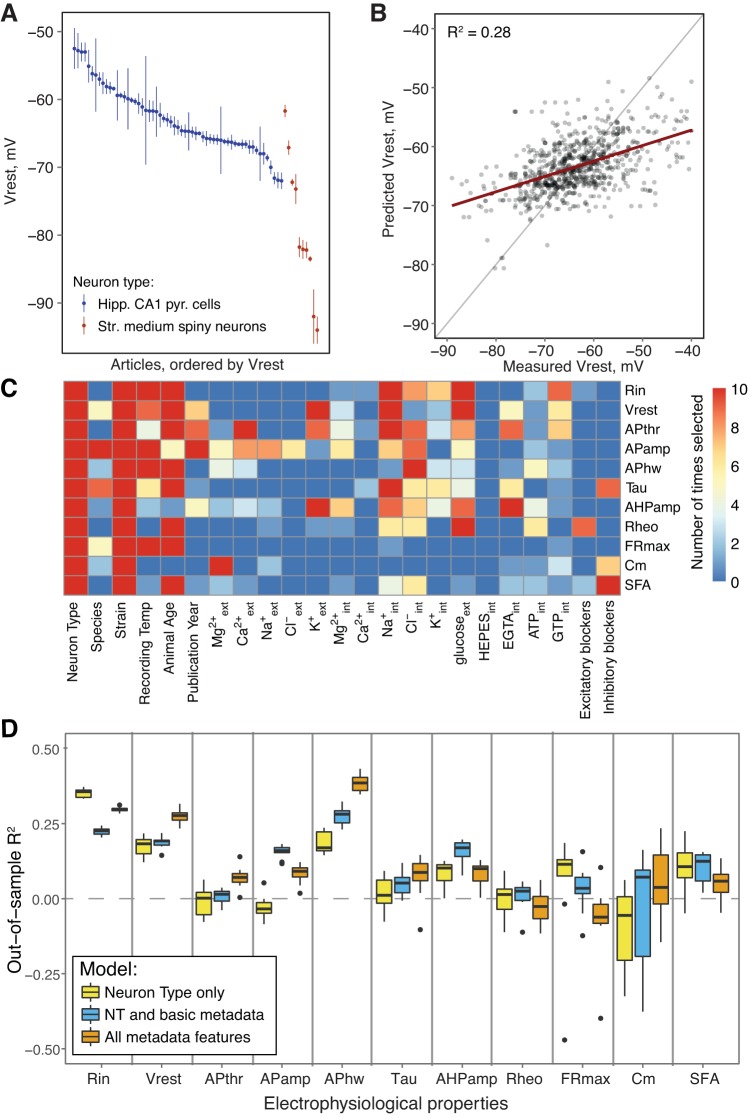
Fig. 3.

Experimental conditions can explain electrophysiological parameter variability. A: V_rest values curated from multiple articles. Data indicate means ± SE. B: use of multiple regression models for predicting electrophysiological parameters. x-axis indicates curated V_rest values, and y-axis shows predicted values (using data not used for model fitting). C: importance of specific features for explaining statistical variability in individual electrophysiological parameters. Heat map indicates selection frequency of individual features into the electrophysiological models across 10 separate cross-validation runs. D: out-of-sample (OOS) R² values for 3 models used to explain electrophysiological parameter variability: a model containing neuron type only (yellow), a model including neuron type plus basic experimental features (blue), and a final model including all experimental features (orange). Negative OOS R² values are an indication of model overfitting. Tau, membrane time constant; Rheo, rheobase; Cm, membrane capacitance; see text for other definitions.

Since publication of the original article describing the NeuroElectro database, we have implemented a number of improvements that are germane to the current work. Specifically, our curation and standardization efforts have yielded a greater number of electrophysiological properties for subsequent reanalysis, including afterhyperpolarization amplitude (AHP_amp), maximum spiking frequency (FR_max), and spike frequency adaptation (SFA).

Experimental solution curation and component extraction.

We developed a novel two-stage approach for extracting solution components and solute concentrations used during electrophysiological experiments that combines human curation with algorithmic text mining. First, curators identify sentences or sentence phrases from electrophysiological article Materials and Methods sections containing the composition of external and internal solutions. The assignment of the text spans describing internal or external solutions was verified by at least one additional senior curator. This manual step was required because our attempts at automated assignment were insufficiently accurate; the task of distinguishing between the various solutions used within an article (e.g., bath solution, incubation solution, PCR solution, etc.) was often difficult to quickly assign even for human curators.

Second, from the curated sentences, we used custom text-mining algorithms to extract the quantitative concentrations of ions and selected compounds of interest (ions: Ca²⁺, Mg²⁺, Na⁺, K⁺, Cl⁻, Cs⁺; selected compounds: glucose, ATP, GTP, HEPES, EGTA, EDTA, BAPTA). The algorithms make use of regular expressions and rule-based approaches to split the sentences into segments, each containing a chemical compound and its numeric concentration value. Next, for each compound, we extracted its chemical components (e.g., NaCl is recognized as Na⁺ and Cl⁻) and summed its concentrations to obtain the final concentration value. For example, a solution containing 126 mM NaCl and 25 mM NaHCO₃ would contain 151 mM Na⁺. When summing the concentrations of components, we assume complete chemical dissociation, because dissociation constants were unavailable for many chemical components at typical recording temperatures. Additionally, we extracted the concentrations of specific compounds that are commonly used to block synaptic activity: 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX), 6,7-dinitroquinoxaline-2,3-dione (DNQX), 2,3-dihydroxy-6-nitro-7-sulfamoyl-benzo[f]quinoxaline-2,3-dione (NBQX), bicuculline, picrotoxin, and gabazine.

Despite our reliance on automated text mining for extracting solution components from manually curated spans of solution-containing text, when we evaluated the algorithm’s accuracy using a set of manually curated solution concentrations from 100 articles, we found the solution component extraction algorithm to have a high accuracy: F₁ score of 0.97 for the major ions, 0.84 for selected compounds and 0.96 for strong synaptic blockers. The F₁ score is defined as the harmonic mean of precision and recall, scaled between 0 and 1. This evaluation consisted of the following criteria: correctly identifying each chemical compound used, the respective concentration values of each chemical constituent, and the total summed concentration value for each constituent.

Data preprocessing and filtering.

For the current study, we considered only data collected from experiments employing in vitro patch-clamp electrophysiology experiments performed on slices from mice, rats, or guinea pigs, providing a starting set of 532 articles. We also removed articles for which accompanying solution information was lacking, from either the article itself or through provided references (23 articles removed). After these filtering steps, we were left with a corpus of 509 articles for subsequent analysis.

We attempted to account for the correction of the liquid junction potential, where it had been applied. Only 46% of articles reported a junction potential value, and 24% reported having corrected for it. Therefore, it was easier to reverse the corrections than to impute unreported junction potentials based on solutions used. Specifically, when the junction offset value was reported, we added its absolute value to V_rest and action potential threshold (AP_thr) measurements. When junction offset was not mentioned but the junction potential was reported as corrected (28 articles), we imputed the offset value by taking a median of all reported junction offset absolute values (10 mV). We did not have sufficient information to calculate junction potential offsets post hoc (Barry 1994), since our solution curation did not extract every component of internal and external solutions.

In our data set, we found that very few articles reported making use of synaptic blockers in their external solutions. Of 509 articles, 40 reported use of at least one strong synaptic blocker that we targeted for extraction. To effectively capture the usage of synaptic blockers on electrophysiological properties, we grouped strong inhibitory blockers (bicuculline, picrotoxin, and gabazine: 32 articles) and strong excitatory blockers (CNQX, DNQX, and NBQX: 25 articles) in the downstream analysis.

Statistical comparisons.

We used the Bonferroni correction to correct P values for multiple comparisons, for example, when asking how individual solution component concentrations have changed over time.

Statistical models for explaining cross-laboratory electrophysiological variability.

We considered the 11 most commonly reported electrophysiological properties (in decreasing order of abundance: R_in, V_rest, AP_thr, AP amplitude (AP_amp), AP half-width (AP_hw), membrane time constant, spike AHP_amp, rheobase, FR_max, cell capacitance, and SFA ratio).

To model the data, we applied random forest regression. This nonlinear method improves on our previous linear regression-based approach (Tripathy et al. 2015) because it empirically better reduces statistical overfitting and can better capture nonlinear interactions between covariates (Breiman 2001). The electrophysiological models were implemented using the randomForest package in R (version 4.6-12; RRID:SCR_015718; Liaw and Wiener 2002). The model selection step was performed with cforest using the R package “party” (version 1.2-3; Strobl et al. 2008). cforest implements the randomForest algorithm using conditional decision trees, which addresses the decision trees bias toward continuous data during the feature selection process.

We used feature selection to first select specific experimental condition features that were informative in explaining variance specific to each electrophysiological property. First, we ranked the experimental features using the internal feature importance (varimp) algorithm of cforest. We then used the corrected Akaike Information Criterion (AICc) to determine how many experimental features (ordered from the most to the least informative) should be included into each electrophysiological property’s model (Hurvich and Tsai 1993). AICc assigns a score to each model based on its performance, adjusted for the number of features and the amount of data used for model fitting. We repeated this feature selection procedure 10 times, making use of 10-fold cross-validation (described below). We constructed an optimized model for each electrophysiological property using the experimental features that were selected as informative in at least 90% of the runs.

We evaluated model performance using 10 rounds of 10-fold cross-validation where all data were randomly split into training and testing folds. During cross-validation, we imposed several conditions on how data were segmented into training/testing splits to mitigate overfitting. First, we enforced that data from the same article could not be present in both training and testing splits (e.g., if an article contained 2 neuron types). Second, articles with rare neuron types that were only encountered once in the NeuroElectro database or assigned to the general neuron type “other” were not used for model testing and evaluation (i.e., they were never assigned to test folds).

We evaluated model performance by calculating R² values using only the “test” split (i.e., out-of-sample R²). We calculate model performance on unseen test data; therefore, a negative R² is possible and indicates that the model is overfitting to the training data.

After assessing model performance, we fit a final model for each electrophysiological property based on the full statistical model, after selecting individual experimental features using feature selection. This final model was trained using the total filtered corpus of the NeuroElectro data set containing 509 articles.

Advisor-advisee analysis using the NeuroTree database.

We made use of the NeuroTree database (https://neurotree.org, as of April 7, 2017; RRID:SCR_007383; David and Hayden 2012) containing user-entered advisor-advisee relationships. We used the NeuroTree API to associate the last authors of individual NeuroElectro articles to specific scientists in NeuroTree. We focused our analysis on selected electrophysiologists (Bert Sakmann, Roger Nicoll, David Prince, “advisors”) who have many former trainees with articles in NeuroElectro. Because NeuroElectro did not have many articles from the advisors, we manually curated the experimental solution contents from 10 randomly selected articles from their laboratories. We did not use these additionally curated articles elsewhere in this article.

Allen Institute for Brain Science validation data set.

For validation data unseen by the training procedures described above, we used the Allen Institute for Brain Science (AIBS) Cell Types data set. This data set reflects the intrinsic electrophysiological features from populations of mouse visual cortex neurons, collected using standardized protocols for in vitro patch-clamp electrophysiology. As described previously (Tripathy et al. 2017), for each cell in the AIBS Cell Types database (http://celltypes.brain-map.org/), representing 847 single cells as of December 2016, we downloaded its corresponding raw and summarized electrophysiological data (summary measurements included R_in and V_rest). For all spiking measurements except FR_max and SFA, we used the voltage trace corresponding to the first spike at rheobase stimulation level. A few electrophysiological properties were calculated from the raw traces, because these were not available in the precalculated summarized data (for example, AP_hw). Membrane capacitance was defined as the ratio of the membrane time constant to the membrane input resistance (R_in). FR_max and SFA were calculated using the voltage trace corresponding to the current injection eliciting the greatest number of spikes. SFA was defined as the ratio between the first and mean interspike intervals during this maximum spike-eliciting trace (i.e., neurons with greater SFA will show values closer to 0). We summarized single-cell electrophysiological data to the level of cell types by averaging measurements within the same Cre line (i.e., defining cell types by unique Cre lines).

For direct comparisons, we matched two NeuroElectro cell types to corresponding data from the AIBS Cell Types database: neocortical layer 2/3 pyramidal cells mapped to Cux2-Cre-labeled cells and neocortex basket cells mapped to Pvalb-Cre-labeled cells.

To perform the model-based adjustment of parameters for experimental conditions, we first used the final fit statistical models to predict and remove electrophysiological variance from the NeuroElectro data that could be explained by our models. We next added predicted electrophysiological variance introduced by the specific set experimental conditions used by AIBS. When adjusting data values from NeuroElectro to the experimental conditions employed by AIBS, we curated the following as AIBS-specific experimental conditions: animal age, 57.5 days; animal species/strain, C57BL mice; and recording temperature, 34°C. The internal solution contained (in mM) 20.3 Na⁺, 130 K⁺, 4 Cl⁻, 4 Mg²⁺, 10 HEPES, 4 ATP, 0.3 GTP, and 0.3 EGTA. The external solution contained (in mM) 153.25 Na⁺, 2.5 K⁺, 135 Cl⁻, 2 Ca²⁺, 1 Mg²⁺, and 12.5 glucose.

Univariate solution component: electrophysiological property relationships.

We used the Nernst equation to calculate reversal potentials given the curated recording temperature and external/internal ion concentrations (Hille 2001). To isolate the contribution of an individual ionic reversal potential to an electrophysiological property, we used the final fit statistical models to remove the explained variance due to all other parameters except those explicitly used in the reversal potential calculation. We used the median electrophysiological property value (calculated across all cell types) as a common baseline during this electrophysiological adjustment procedure.

Data and code availability.

The code used for text mining and preprocessing is incorporated into the NeuroElectro codebase and can be found online (https://github.com/neuroelectro/neuroelectro_org). The R files with the data processing, analysis, and statistical model creation are also available online (https://github.com/dtebaykin/InterLabEphysVar) along with the data files used.

RESULTS

Our goal was to understand how different experimental conditions impact the results of whole cell electrophysiology experiments conducted on acute brain slices. Our primary analysis is based on 509 published neurophysiology articles that met selection criteria (see materials and methods). We first conducted an exploratory analysis of experimental solution compositions. We then extended the analysis to include previously known sources of electrophysiological variability, such as animal species or age, and compare their relative impact. Finally, we developed models for several commonly reported electrophysiological properties that allow adjustment of the electrophysiological values from one set of experimental conditions to another. We validated these models using a novel, distinct intrinsic electrophysiology data set provided by The Allen Institute for Brain Science.

Analysis of experimental solution recipes.

Our curation efforts (see materials and methods) yielded detailed information on the concentrations of ions and selected compounds in external recording (artificial cerebrospinal fluid, ACSF) and internal patch-pipette solutions. Our general expectation was that there would be a consensus set of common ingredients and their concentrations (or at least concentration ranges) used in different whole cell current-clamp studies of mammalian neurons. This turned out to be the case, but we were also surprised at the degree of variability: very few articles reported the exact same conditions as any other.

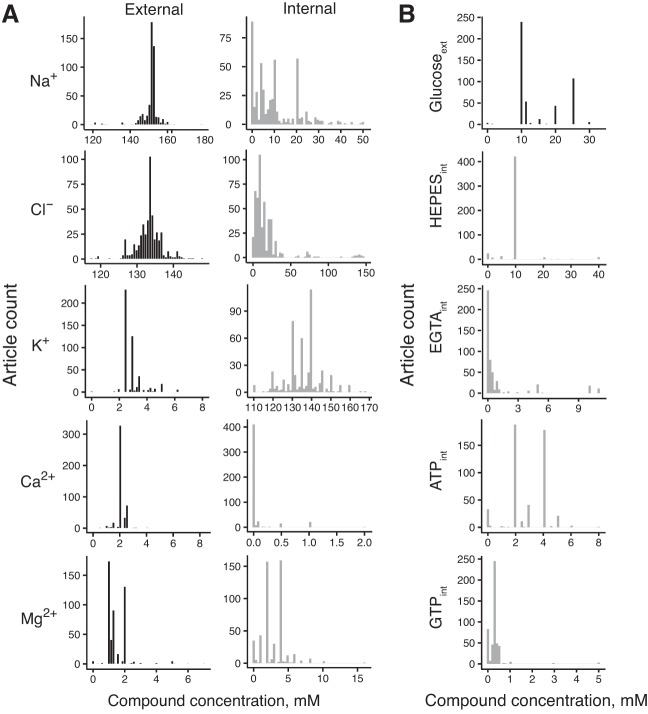
External solutions contained median values of the following components (in mM): 151.2 Na⁺, 2.8 K⁺, 2.0 Ca²⁺, 1.3 Mg²⁺, 133.5 Cl⁻, and 10.0 glucose (Fig. 1, A and B, and Table 1). These concentrations are similar to published values of cerebrospinal fluid compositions (human CSF, in mM): 142 Na⁺, 2.5 K⁺, 1.3 Ca²⁺, 0.8 Mg²⁺, 124 Cl⁻, and 3.9 glucose (Hall 2015). Internal solutions contained (in mM, median values) 8.0 Na⁺, 135.0 K⁺, 0 Ca²⁺, 3.0 Mg²⁺, 10.0 Cl⁻, 0 glucose, 10 HEPES, 0.1 EGTA, 3 ATP, and 0.3 GTP (Fig. 1, A and B, and Table 1). The recipes of internal solutions vary more than the compositions of external solutions. For example, the average of the median absolute deviations for the 5 major mono- and divalent ions was 0.87 mM for external solutions and 5.1 mM for internal solutions. Additionally, we calculated reversal potentials for the major ions by making use of the Nernst equation and the reported recording temperatures. The median reversal potentials for the major ions were as follows: E_Na = 75.4 mV, E_K = −101.7 mV, E_Cl = −68.2 mV, E_Ca = 190.1 mV, and E_Mg = −9.1 mV.

Fig. 1.

Chemical compositions of external and internal solutions. A: compositions of the major monovalent and divalent ions. B: compositions of selected compounds (int, internal; ext, external).

Table 1.

Summary of external and internal solution recipes for major ions and compounds

Chemical	External Solution, mM	Internal Solution, mM	Eion, mV
Na+	151.2 (151.0–153.0)	8.0 (2.35–18.35)	75.4 (55.5–109.0)
K+	2.8 (2.5–3.0)	135.0 (130.0–140.0)	−101.7 (−105.0–98.0)
Cl−	133.5 (131.9–135.0)	10.0 (6.0–20.0)	−68.2 (−81.5–50.0)
Mg2+	1.3 (1.0–2.0)	3.0 (2.0–4.0)	−9.1 (−17.6–0.0)
Ca2+	2.0 (2.0–2.0)	Q3 = 0.0 (max 2.0)	190.1 (184.5–192.0)
HEPES	0.0	10.0 (10.0–10.0)	N/A
EGTA	0.0	0.1 (0.0–0.5)	N/A
ATP	0.0	3.0 (2.0–4.0)	N/A
GTP	0.0	0.3 (0.2–0.3)	N/A
Glucose	10.0 (10.0–20.0)	0.0	N/A

Data are external and internal solution recipes for the major ions and compounds considered in the 509 articles used in this study. Values are given as medians (1st–3rd quartiles). For reversal potential (E_ion) calculations, ion concentrations that were effectively zero were assigned an arbitrary small concentration of 10⁻⁶ mM. Values for the internal solution Ca²⁺ concentration are shown as 3rd quartile (maximum value) due to sparsity of its values. N/A, not applicable.

We next analyzed how solution components covary. When only the 5 major ions (Na⁺, K⁺, Ca²⁺, Mg²⁺, Cl⁻) from 509 articles were considered, there were 269 (53%) unique external solutions and 390 (77%) unique internal solutions, with 442 (86%) articles using unique combinations of the two. We used principal component analysis supplemented by hierarchical clustering to further explore patterns in solution compositions. We found no obviously distinct clusters, suggesting that electrophysiologists use similar recipes with slight variations, within biologically reasonable concentration values. However, in external solutions, the greatest differentiator was Mg²⁺, with most articles using exactly 1, 1.3, or 2 mM Mg²⁺.

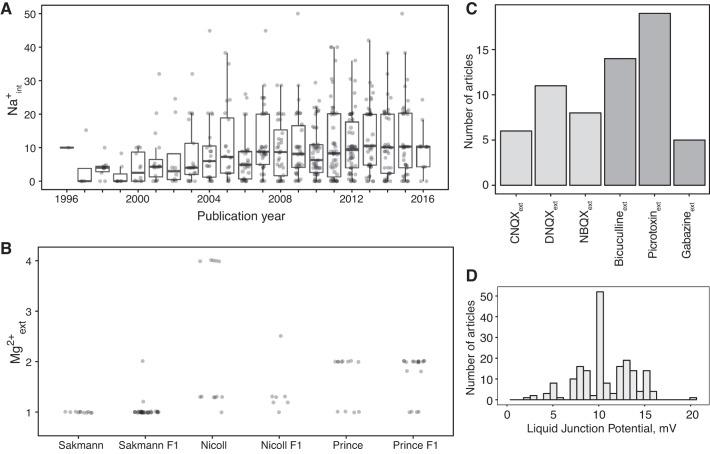
We analyzed linear trends in solution concentrations in the major ions over time, looking for trends in research practices over the years. We found that the concentration of internal Na⁺ has significantly increased from the 1990s (r = 0.22, β = 0.42 mM/year, Bonferroni P = 5.02 × 10⁻¹⁴; Fig. 2A). On further examination, this trend seems to be the result of the addition of 10–20 mM Na₂-phosphocreatine to internal solutions, which became popular during the mid 2000s. One immediate effect of increasing internal Na⁺ concentrations is to cause estimated Na⁺ reversal potentials (E_Na) to decrease. We also found significant but modest increases in external glucose concentrations (r = 0.08, β = 0.08 mM/year, Bonferroni P = 3.4 × 10⁻²) and internal Mg²⁺ (r = 0.12, β = 0.03 mM/year, Bonferroni P = 3.43 × 10⁻⁴).

Fig. 2.

Differences in experimental solutions are related to overall composition trends over the years and inheritance of solutions by advisees. A: trend of internal sodium concentration (Na⁺_int) as a function of publication year. Data points indicate individual articles and have been jittered for visual clarity. B: article-specific external magnesium concentration (Mg²⁺_ext; data points) subset by laboratory or advisor’s laboratory. x-axis indicates external Mg²⁺_ext values used in papers published by the laboratories of Bert Sakmann, Roger Nicoll, and David Prince or in articles published by the laboratories of their direct advisees (indicated by F1). C: histogram of commonly used strong synaptic blockers in external solutions for excitatory blockers (light gray) and inhibitory blockers (dark gray). D: histogram of absolute values of reported liquid junction potential measurements.

We hypothesized that some of the interlaboratory differences in experimental conditions might be explained by advisor-advisee relationships, in which practices learned during training are propagated to new laboratories. We were able to test this idea for external Mg²⁺, using data on advisor-advisee relationships from NeuroTree (David and Hayden 2012), and found evidence to support the inheritance hypothesis (Fig. 2B). We identified three electrophysiologists who had large numbers of trainees with articles in NeuroElectro (see materials and methods). For example, articles from Bert Sakmann’s laboratory tend to use 1 mM Mg²⁺, whereas articles from Roger Nicoll’s tend to use 1.3 or 4 mM. These differences were present in the papers of former advisees of these investigators.

Modeling variance in electrophysiological properties with experimental conditions.

Our next goal was to consider the extent to which experimental conditions explain variability in measured electrophysiological parameters across studies. This is of interest because the variability of the latter is very large compared with within-study variance. For example, hippocampal CA1 pyramidal cells are reported to have resting potentials ranging from −80.0 ± 1.0 to −55.1 ± 2.4 mV (means ± SE; Fig. 3A). These data are highly unlikely to be generated by different laboratories sampling from a single distribution. Although there might be bona fide biological differences due to factors such as species or strain, it is plausible that other experimental conditions contribute to the differences.

We therefore reasoned that we should be able to statistically model the influence of solution parameters on electrophysiological parameter variability. We built on the experimental condition-based regression approach, incorporating basic experimental factors such as animal species and age, that we have developed previously (Tripathy et al. 2015). Specifically, for each electrophysiological parameter (e.g., V_rest, AP_hw, etc.), we used a regression approach to model the relationship between experimental condition attributes and measured electrophysiological parameters (see materials and methods; Fig. 3B). Furthermore, our models incorporate approaches for reducing statistical overfitting, including incorporating feature selection to only use methodological features that are statistically explanatory for each electrophysiological property (see materials and methods).

To understand the contribution of individual experimental condition features for explaining cross-laboratory electrophysiological variability, a useful metric is how often individual features are selected for inclusion in our statistical models during the cross-validation process (Fig. 3C). We found that neuron type and animal strain features were almost always selected for modeling each electrophysiological property. Animal age and, to a lesser extent, recording temperature were also useful in explaining variance in some electrophysiological properties, consistent with our previous results (Tripathy et al. 2015). In modeling the effect of solution components, we elected to use the internal and external concentrations directly (as opposed to using the calculated reversal potentials). This provided us more specific information about the relative importance of solution features. We found that a few solution features were consistently informative for specific electrophysiological parameters, including external K⁺ concentration for V_rest and internal Na⁺ concentration for R_in, V_rest, and AP_thr.

On the other hand, many solution components were statistically noninformative (i.e., not selected in the model construction process). One reason why certain solution components tend not to be selected during feature selection might merely be that they tend not to vary much across studies. For example, because the concentration of external HEPES is 10 mM in most experiments (refer to Fig. 1B), its explanatory power for electrophysiological variance tends to be small.

In addition to fitting a full model relating each electrophysiological property to all the methodological information available (after performing feature selection), we fit two additional models to test the relative importance of different sets of experimental condition features (Fig. 3D). First, we fit a model containing information about only the neuron type used, serving as a reference or baseline model. Second, we fit a model containing neuron type plus basic, nonsolution experimental features, including animal age, species, strain, and recording temperature. This model provides a direct comparison to our previously published models (Tripathy et al. 2015). Furthermore, comparing this intermediate model to the full model containing neuron type, basic, and solution features can help quantify the explicit benefit for including solution information.

Comparing the predictive power of the different statistical models on out-of-sample (OOS) or “held-out” test data not used in model fitting (Fig. 3D), we found that there was generally little improvement between the neuron type-only model and a model containing both neuron type and basic experimental condition features (e.g., animal strain, recording temperature, etc.). For example, the neuron type-only model predicts V_rest values at accuracy comparable to a model considering neuron type plus basic condition features (OOS R² = 0.18 ± 0.03 vs. OOS R² = 0.19 ± 0.02; means ± SD). Although the basic experimental conditions contribute valuable information for predicting certain electrophysiological properties (AP_amp, AP_hw, AHP_amp), in most cases the benefit is relatively small (Fig. 3C). When comparing the full model containing solution component information with the two reduced-feature models, we found that for some electrophysiological properties, such as R_in, V_rest, AP_thr, and AP_hw, there was a considerable improvement (mean R² increase in performance relative to neuron type plus basic experimental conditions model, respectively: 0.06, 0.07, 0.05, 0.08). For electrophysiological properties where the model’s predictive performance degrades when additional experimental condition features (R_in, AP_amp, FR_max) are added, this likely reflects statistical overfitting.

In summary, these statistical models demonstrate that experimental condition features, and in particular, solution components, can explain some of the cross-laboratory electrophysiological variability. However, no model was anywhere near an OOS R² of 0.5, indicating that much of electrophysiological variability is left unexplained and is likely due to factors other than those we have explicitly considered in this report.

Comparison of experimental condition adjusted electrophysiological data to external data sets.

A motivation for modeling the effect of experimental conditions is to normalize data across laboratories. To this end, we compared NeuroElectro data to a corresponding electrophysiological data set collected by the Allen Institute for Brain Sciences (AIBS) (http://celltypes.brain-map.org/). Specifically, we used the experimental condition-based statistical models to quantitatively adjust the NeuroElectro measurements to that of the specific experimental conditions used by AIBS (see materials and methods). For example, given that there are multiple rodent species reflected within our data set and that the AIBS measurements were collected from adult mice, statistical normalization should help correct for such differences.

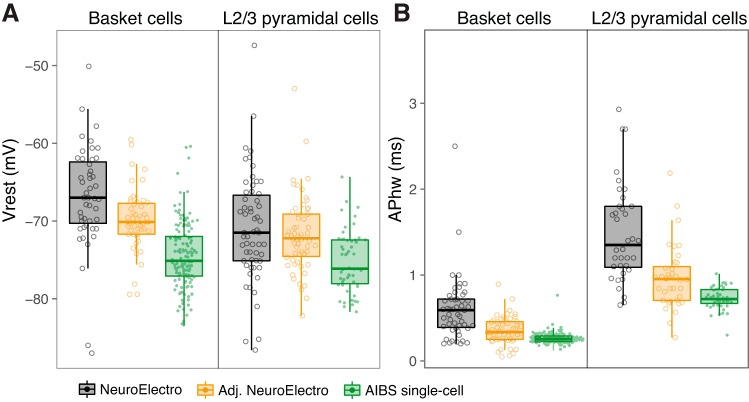
We found that after we performed the experimental condition-based adjustment, the NeuroElectro values were more consistent with the AIBS measurements. For example, the measured V_rest values for neocortical basket cells by AIBS were −74.7 ± 4.2 mV (mean ± SD), whereas the raw NeuroElectro values were −69.1 ± 7.1 mV and the adjusted values were −70.9 ± 4.6 mV (Fig. 4A). Similarly, for these same cells, the AP_hw values were 0.39 ± 0.22 ms, the uncorrected literature measurements were 0.97 ± 0.64 ms, and the adjusted values were 0.60 ± 0.43 ms (Fig. 4B). These examples illustrate that these experimental condition-based models can be used to help make electrophysiological data measurements collected in different laboratories more comparable. Furthermore, because the AIBS data were not used for model fitting, this comparison provides an external validation and check for statistical overfitting.

Fig. 4.

Accounting for experimental conditions makes cross-laboratory electrophysiological data more comparable. A and B: comparison of raw NeuroElectro data (black), experimental condition-adjusted NeuroElectro data (orange), and raw single-cell electrophysiological data collected by the Allen Institute for Brain Sciences (AIBS) Cell Types project (green). NeuroElectro values indicate article mean electrophysiological values (open circles), whereas AIBS values are from single cells (data points). Cell types are neocortical basket cells (left, labeled by Pvalb-Cre mouse line in AIBS) and neocortical layer 2/3 pyramidal cells (right, labeled by Cux2-Cre mouse line in AIBS).

Univariate relationships between electrophysiological properties and reversal potentials.

Last, we wanted to investigate individual relationships between experimental features and electrophysiological parameters captured by our statistical models. By statistically accounting for known sources of experimental variance (using an approach similar to that used in our comparison to the AIBS data set; see materials and methods), we could home in on interesting and potentially novel univariate relationships.

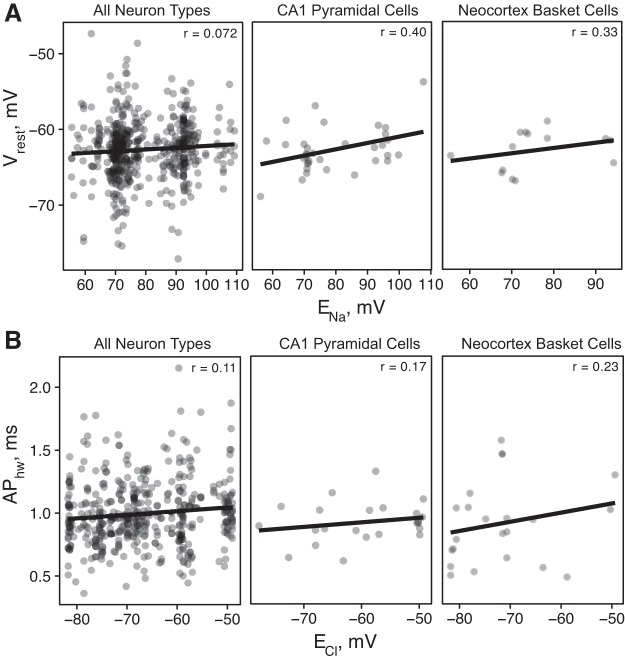
For example, in our analysis of solution compositions, we found that a major distinguishing factor among internal solutions was the use of Na₂-phosphocreatine, which has the effect of lowering the Na⁺ driving force, E_Na, from a typical value of ~100 mV to 50 mV. As expected through application of the Goldman-Hodgkin-Katz equation (Goldman 1943; Hille 2001), we found that cells recorded with the use of solutions with lower E_Na also tended to have more hyperpolarized resting potentials (Fig. 5A; r = 0.073 overall, 0.40 for CA1 pyramidal cells, and 0.31 for neocortex basket cells). As another example, we found a weak but consistent positive relationship between AP_hw and E_Cl (Fig. 5B; i.e., a stronger inward Cl⁻ driving force contributes to more rapid action potential repolarization). This relationship is consistent with a recent finding from hippocampal pyramidal cells that the opening of Ca²⁺-activated Cl⁻ channels during an action potential contributes to spike repolarization and spike width narrowing (Huang et al. 2012).

Fig. 5.

Ionic reversal potentials explain some of the observed differences in electrophysiological properties. A and B: each data point represents an experimental condition–electrophysiological property pair curated from an article, and lines show linear fit. x-axis shows the calculated reversal potentials using the Nernst equation (using external and internal concentrations and recording temperatures), and y-axis shows the experimental condition-adjusted electrophysiological data. Because of the difficulties in estimating true reversal potentials at very low concentrations, the x-axis has been filtered to only include data between the 1st and 3rd quartiles.

DISCUSSION

We have investigated the experimental sources of study-to-study variability in measurements of neuron electrophysiological parameters. One major conclusion from our exploratory analysis is that the external and internal solutions used by different laboratories tend to be similar in overall composition but are rarely identical. We used solution composition information in addition to other features such as animal strain, age, and recording temperature in an attempt to quantitatively explain study-to-study variability in electrophysiological parameters. Although we found that these features were statistically explanatory for some electrophysiological parameters, there was considerably much more variability left unexplained, typically greater than 50%. Our results suggest that there remain other experimental factors that are substantial contributors to electrophysiological variability.

Trends in experimental external and internal solutions.

Although external solutions (ACSF) tended to be very similar, there were a few notable areas of variation. One was the concentration of external Mg²⁺, with articles using either 1 or 2 mM concentrations. Our analysis using the NeuroTree database suggests that some of this difference might stem from the mentors with whom authors trained. For example, scientists who trained with Bert Sakmann tend to use 1 mM Mg²⁺, whereas those who trained with Roger Nicoll use 1.3 mM Mg²⁺ and those who trained with David Prince use 2 mM Mg²⁺. We are careful not to overinterpret this observation because academic lineage alone is far from the only source of methodological similarities. For example, similarity of experimental questions or paradigms, such as long-term potentiation or epilepsy, likely also influences methodological similarities. Internal patch-pipette solutions, on the other hand, were more variable. For example, the concentrations of internal Na⁺ and Cl⁻ were relatively uniformly distributed between 0 and 50 mM compared with external solution compositions. Delving deeper, around the mid 2000s, electrophysiologists began to consistently add some amount of phosphocreatine to their internal solutions. Because Na₂-phosphocreatine is a relatively inexpensive way to add phosphocreatine (almost 30 times cheaper compared with K₂-phosphocreatine: 14 vs. 400 Canadian dollars per gram; creatine phosphate, disodium salt, CAS 1933-65-4 vs. creatine phosphate, dipotassium salt, CAS 18838-38-5, Millipore Sigma), this could explain how the concentration of internal Na⁺ began to increase over time.

Successes and challenges in modeling study-to-study electrophysiological variability.

By curating experimental details from article Methods sections, we tried to relate electrophysiological parameter differences to underlying differences in how experiments were conducted using statistical models. For a small number of electrophysiological properties, such as resting potential and spike half-width, we found that there was positive, but modest, predictive power for methodological factors in explaining electrophysiological parameter variability.

Our modeling approach allowed us to statistically attribute electrophysiological variability to variance in specific methodological factors. This analysis confirmed a number of known relationships, for example, that Na⁺, K⁺, and Cl⁻ contribute to variance in resting potential, as expected through use of the Goldman-Hodgkin-Katz equation (Goldman 1943; Hille 2001). The analysis also suggested some potentially novel relationships. For example, internal GTP concentration was predictive of R_in variance, and this relationship is potentially plausible, although indirect, given that many K⁺ leak channels are G protein coupled (Sadja et al. 2003). Similarly, the relationship between internal EGTA and AHP_amp could be explained through the indirect effect of the EGTA’s calcium buffering effect on large-conductance (BK) and other Ca²⁺-activated K⁺ channels (Matthews et al. 2008; Springer et al. 2015).

We further demonstrated that these models could be used to aid in the cross-comparison of electrophysiological data collected in different laboratories by accounting for some of the effects of laboratory-specific methodologies. However, our key finding from this modeling work is that the vast majority of study-to-study electrophysiological parameter variability remains unexplained.

In considering possible sources of unexplained variance, we note several limitations in our solution analysis. Importantly, we did not account for every component. Some, such as major internal anions, including gluconate or methylsulfonate, have reported effects on electrophysiology (Kaczorowski et al. 2007). Similarly, we did not attempt to analyze the effects of slice cutting or incubation solutions (Jiang et al. 2015; Ting et al. 2014). It would be possible to extend our curation and text-mining pipeline to track the use of these methodological features in future work. Second, when quantifying solution components, we assumed complete dissociation of ionic species. Although we initially considered incorporating dissociation constants, because such constants remain unmeasured at typical recording temperatures in oxygenated solutions, we reasoned that including these would primarily contribute noise. However, we doubt these would fully explain the gap in explained variability, and there are reasons to suspect other sources of uncontrolled variability are contributing.

First, electrophysiological measurements often are not calculated using consistent and standardized protocols (Teeters et al. 2015; Tripathy et al. 2014, 2015). The solution would be to recalculate values from raw data, but such data (i.e., raw traces) is unavailable. Thus we cannot rule out that differences in how electrophysiological properties are calculated or defined (e.g., spike threshold measured using steps or ramps or the use of liquid junction potential correction) contribute to unaccounted electrophysiological variability (Higgs and Spain 2011; Neher 1992).

Second, unaccounted systematic biological effects likely contribute variability. For example, although we have curated electrophysiological reports to the level of major cell types (as present in NeuroLex; Hamilton et al. 2012; Larson and Martone 2013), it is possible that investigators are sampling different cellular subpopulations (for example, ventral vs. dorsal hippocampal CA1 pyramidal cells; Cembrowski et al. 2016; Malik et al. 2016). These distinctions might not be reported uniformly in articles, if at all. Along similar lines, our statistical modeling approach might be overly simplistic or too underpowered to capture biologically complex experimental condition-electrophysiological relationships. For example, although we have included the usage of strong synaptic blockers as an experimental feature in our analysis, they overall tend to be used too infrequently (~10% of articles) to show much of a considerable effect.

Last, there are several methodological factors that we could not include in our statistical models because they either were not mentioned or were inconsistently reported in Methods sections or would otherwise be difficult to precisely articulate. These factors include liquid junction potential correction, how recently electrodes are chlorinated, bridge balance and series resistance compensation, electrode resistance, seal quality, time elapsed since break-in, and criteria for how neurons were selected for characterization, among many others. Getting to the bottom of these differences would require considerable effort by laboratories to precisely replicate each other’s protocols. Although these issues are not specific to patch-clamp electrophysiology (Okaty et al. 2011; Vasilevsky et al. 2013), because patch-clamp electrophysiological data are so frequently reused yet remain labor intensive to collect, there are considerable benefits in addressing some of these technical differences.

Outlook.

This work has broad implications in the continued reuse of electrophysiological data collected across different laboratories using different conditions. Whereas explicitly correcting for experimental condition differences provides some value, at present such corrections only go so far. If electrophysiological data are to be pooled and compared across laboratories, the remaining major sources of variability need to be identified and accounted for. As more experimental metadata are reported and more raw electrophysiology data sets are made publicly available, for example, through efforts such as Neurodata Without Borders (Teeters et al. 2015), we envision that it will become easier to resolve these differences moving forward.

GRANTS

This work is supported by a NeuroDevNet grant (to P. Pavlidis), a University of British Columbia bioinformatics graduate training program grant (to D. Tebaykin), a Canadian Institutes of Health Research postdoctoral fellowship (to S. J. Tripathy), National Sciences and Engineering Research Council of Canada Discovery Grant RGPIN-2016-05991, National Institutes of Health (NIH) Grants MH106674 and EB021711 (to R. C. Gerkin), and NIH Grants MH111099 and GM076990 (to P. Pavlidis).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

ENDNOTE

At the request of the author(s), readers are herein alerted to the fact that additional materials related to this manuscript may be found at the institutional website of one of the authors, which at the time of publication they indicate is: http://hdl.handle.net/11272/10525; doi: 10.14288/1.0360719. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.

AUTHOR CONTRIBUTIONS

D.T., S.J.T., and P.P. conceived and designed research; D.T., N.B., and B.L. performed experiments; D.T., S.J.T., N.B., B.L., and R.C.G. analyzed data; D.T., S.J.T., N.B., R.C.G., and P.P. interpreted results of experiments; D.T., S.J.T., and N.B. prepared figures; D.T. drafted manuscript; D.T., S.J.T., N.B., B.L., R.C.G., and P.P. edited and revised manuscript; D.T., S.J.T., N.B., B.L., R.C.G., and P.P. approved final version of manuscript.