Abstract
Sequential change-point detection from time series data is a common problem in many neuroscience applications, such as seizure detection, anomaly detection, and pain detection. In our previous work (Chen Z, Zhang Q, Tong AP, Manders TR, Wang J. J Neural Eng 14: 036023, 2017), we developed a latent state-space model, known as the Poisson linear dynamical system, for detecting abrupt changes in neuronal ensemble spike activity. In online brain-machine interface (BMI) applications, a recursive filtering algorithm is used to track the changes in the latent variable. However, previous methods have been restricted to Gaussian dynamical noise and have used Gaussian approximation for the Poisson likelihood. To improve the detection speed, we introduce non-Gaussian dynamical noise for modeling a stochastic jump process in the latent state space. To efficiently estimate the state posterior that accommodates non-Gaussian noise and non-Gaussian likelihood, we propose particle filtering and smoothing algorithms for the change-point detection problem. To speed up the computation, we implement the proposed particle filtering algorithms using advanced graphics processing unit computing technology. We validate our algorithms, using both computer simulations and experimental data for acute pain detection. Finally, we discuss several important practical issues in the context of real-time closed-loop BMI applications.
NEW & NOTEWORTHY Sequential change-point detection is an important problem in closed-loop neuroscience experiments. This study proposes novel sequential Monte Carlo methods to quickly detect the onset and offset of a stochastic jump process that drives the population spike activity. This new approach is robust with respect to spike sorting noise and varying levels of signal-to-noise ratio. The GPU implementation of the computational algorithm allows for parallel processing in real time.
Keywords: acute pain, brain-machine interface, change-point detection, graphics processing unit, particle filtering, Poisson linear dynamical system, population codes, sequential Monte Carlo
INTRODUCTION
An important problem in closed-loop neuroscience experiments is to quickly identify abrupt changes in neural ensemble spike activity induced by external stimuli or internal change in brain states. Examples of applications include detection of acute pain signals (Chen et al. 2017a; Chen and Wang 2016), epileptic seizures (Malladi et al. 2013), and identification of reaction times (Mosqueiro et al. 2016) or changes in neuronal activity (Pillow et al. 2011). In the literature, many methods have been proposed for change-point detection, including the subspace method (Kawahara et al. 2007), the nonparametric density-ratio method (Kawahara and Sugiyama 2012; Liu et al. 2013), cumulative sum (CUSUM) (Koepcke et al. 2016), and model-free methods (Chen et al. 2017b). The central challenge in change-point detection is speed and accuracy. For speed, the objective of quickest detection is to detect changes as quickly as possible in an online fashion (Poor and Hadjiliadis 2009). In real-time brain-machine interface (BMI) applications, the requirement of time delay for closed-loop feedback is usually within tens of milliseconds. Therefore, many off-line algorithms are not suitable for BMI applications. To date, large-scale neural recordings (order of hundreds of recording channels) have become increasingly popular in systems neuroscience (Chen 2017; Stevenson and Kording 2011). This poses a great challenge in real-time neural signal processing, including spike detection, sorting, filtering, and feedback control. To scale up and speed up data flow, the designing of efficient or parallel computational algorithms has become a necessity in many closed-loop neuroscience experiments (Ciliberti and Kloosterman 2017).
Previously, we have developed model-based and model-free approaches for detecting abrupt changes of neuronal ensemble spike activity (Chen et al. 2017a, 2017b). Compared with model-based methods, the model-free method, such as the CUSUM algorithm (Koepcke et al. 2016; Page 1954), is operated directly on raw spike data and does not account for noise. Although the complexity of the CUSUM method is minimal, its performance is sensitive to the baseline statistics or the presence of noise (Chen et al. 2017b), which severely limits its applications in real-time BMI. In real-time BMI experiments, spikes are sorted online and may be corrupted by multiunit activity (MUA). Therefore, model-based methods are preferred in online applications. Our model-based approach to detecting abrupt changes of neuronal ensemble spike activity has broader applications in closed-loop neuroscience experiments. One of the noteworthy applications is closed-loop pain modulation.
Pain is an essential experience in life, but pain mechanisms in the brain remain poorly understood. To date, animal models of pain have been used to study pain mechanisms (Gregory et al. 2013). Consistent with human imaging studies of the anterior cingulate cortex (ACC) and primary somatosensory cortex (S1) (Bushnell et al. 2013; Perl 2007; Vierck et al. 2013; Vogt 2005), neurophysiological recordings of the ACC and S1 regions from rodent experiments have confirmed that subsets of neurons from these two brain regions respond to various pain stimuli (Chen et al. 2017a; Kuo and Yen 2005; Zhang et al. 2011, 2017).
From a treatment perspective, neuromodulation has emerged as a potential option for refractory pain. Demand-based neuromodulation, or closed-loop control for pain, depends critically on timely identification of pain signals and ultrafast neuromodulation. For instance, in closed-loop BMI applications, the desired detection latency should be within 50 ms or less. Optogenetic stimulations have provided a potential way for neuromoduation (Copits et al. 2016; Daou et al. 2013; Gu et al. 2015; Iyer et al. 2016; Lee et al. 2015). On the other hand, a BMI for closed-loop pain control also depends on timely and precise detection of pain signals—from either acute or chronic pain. This has motivated us to use animal models of acute and chronic pain to study the pathophysiology of pain (Xu and Brennan 2011; Zhang et al. 2017).
In our previous work (Chen et al. 2017a), we developed a statistical model and an associated algorithm for detecting pain signals. For computational tractability, the inference algorithm uses Gaussian assumptions in the prior distribution and Gaussian approximation in the likelihood model. However, these assumptions are simplistic and will affect detection accuracy or speed.
Particle filtering is a sequential Monte Carlo method that focuses on online state or parameter estimation (Chen 2003; Doucet et al. 2001). Particle filters have been used in neuroscience applications, such as population decoding (Brockwell et al. 2004; Ergün et al. 2007; Kelly and Lee 2003), parameter estimation (Meng et al. 2011), and synaptic input inference (Paninski et al. 2012). However, as a Monte Carlo sampling method, particle filtering is more computationally costly than the regular deterministic filter. Fortunately, particle filtering is built upon independent and parallel computational operations, which provide a great opportunity for graphics processing unit (GPU) implementation. Here we extend our previous work (Chen et al. 2017a) and develop real-time particle filtering and smoothing algorithms for detecting abrupt changes in neural ensemble spike activity. The contribution of this study is twofold. First, we introduce a dynamical noise mixture model to the latent state-space model to accommodate stochastic jump processes. Second, to account for the resulting non-Gaussian state noise and non-Gaussian likelihood, we propose three particle filtering algorithms (with gradually increasing complexity) to recursively estimate the latent state. We also derive a particle smoothing algorithm to allow semibatch or fixed-lag smoothing operations. In addition, to accommodate real-time processing in BMI applications, we implement the particle filtering algorithm with GPU computing technology.
In this report, we begin by reviewing previously developed state-space methods as well as new sequential Monte Carlo approaches for change-point detection. We then present results of extensive computer simulations. We further validate our approach in the application of detecting acute pain signals with experimental rodent recordings. We optimize the algorithmic performance and computational speed with GPU implementation. Finally, we conclude the report with some discussions in the context of closed-loop BMI applications.
METHODS
Poisson Linear Dynamical System
Throughout this report, the vector or matrix is represented by a boldface symbol, whereas the scalar represents a univariate variable. Let denote a C-dimensional population vector, with each element consisting of the neuronal spike count at the kth time bin (bin size Δ). Let the latent univariate variable represent an unobserved common input drawn from a stochastic process that drives neuronal ensemble spiking activity. Without loss of generality, let us assume that the latent state is univariate (i.e., m = 1). A general m-dimensional model can be easily extended (Chen et al. 2017a; Lawhern et al. 2010).
In contrast to the standard linear dynamical system (i.e., Kalman filter), the Poisson linear dynamical system (PLDS) is a state-space model that uses Poisson likelihood to estimate population spike count data (Buesing et al. 2012; Chen 2015; Chen et al. 2017a; Lawhern et al. 2010; Macke et al. 2012). The PLDS is a special case of the point-process dynamical system (Barbieri et al. 2004; Brown et al. 1998; Eden et al. 2004; Smith and Brown 2003). Let λk = [λ1,k,…,λC,k] = exp(ηk)Δ denote the Poisson firing rate vector for the observed C neurons. We assume that the Poisson spike data yk follow the following probability model:
| (1) |
| (2) |
| (3) |
where Eq. 1 describes a first-order autoregressive (AR) model (0 < |a| < 1) driven by a zero-mean Gaussian noise process . The parameters c, d, and ηk are unconstrained. The goal of statistical inference is to estimate the unknown state variable {zk} and parameters {a,c,d,σϵ} from observations y1:T. In practice, we can initialize exp(d) as the neuronal baseline firing rate and fix it for the model; in that case, only three parameters {a,c,σϵ} need to be estimated. It is found that this routine is more robust for the online filtering operation.
The joint state and parameter estimation can be tackled by the expectation-maximization (EM) algorithm (Chen et al. 2017a; Macke et al. 2015; Smith and Brown 2003). The basic operation of the EM algorithm is shown in algorithm 1 (appendix c). In the E step, we can run a forward-backward Kalman smoother based on variational or Laplacian approximation of the Poisson likelihood, from which we obtain the Gaussian sufficient statistics of latent state: . Alternatively, it can be solved efficiently by a convex optimization procedure (Paninski et al. 2010). In the M step, we directly optimize the likelihood function with respect to the unknown parameters. Specifically, we can set the baseline parameter c with the sample statistics: , where denotes the baseline firing rate. For the parameters a and d and , we have the closed-form solutions (Macke et al. 2015):
| (4) |
| (5) |
| (6) |
where (μk,Vk,l) denotes the posterior mean of zk and the posterior covariance of zk and zl, respectively, and Sk,l = Vk,l + μkμl.
Online Recursive Filtering
In online BMI applications, once the model parameters are identified, we can use a recursive (forward) filter to estimate the latent state variable for the PLDS (Chen et al. 2017a, 2017b):
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
where Qk|k−1 = Var[ẑk|k−1] and Qk|k−1 = Var[ẑk|k] denote the predicted and filtered state variance, respectively. Since the latent state variable z is unknown, we use ẑ to represent its estimate. This recursive filter updates the distribution of the latent state with an approximate Gaussian distribution: . We call this filter using Eqs. 7–11 the basic filter (Filter). This filter is an extension of the point process filter to spike count data (Eden et al. 2004; Smith and Brown 2003).
Change-Point Detection
From the online filtered estimate ẑk|k or smoothed estimated Zk|k+τ (τ > 0), we compute the Z score related to the baseline: and convert it to probability (Chen et al. 2017a; Chen and Wang 2016):
| (12) |
since the uncertainty of ẑk|k is assessed by its state posterior variance Qk|k. We can also compute the Z score’s confidence interval (CI) by twofold standard deviation:
| (13) |
Therefore, the criterion of Z-score change is determined by a critical threshold θ for reaching statistical significance. Using the 95% significance level [i.e., when θ = 1.65, P(Z score > θ) ≥ 0.95], it is concluded that a change point occurs when Z score – CI > 1.65 or Z score + CI < –1.65. A geometric illustration of Z score in a one-dimensional setting is shown in Fig. 1.
Fig. 1.
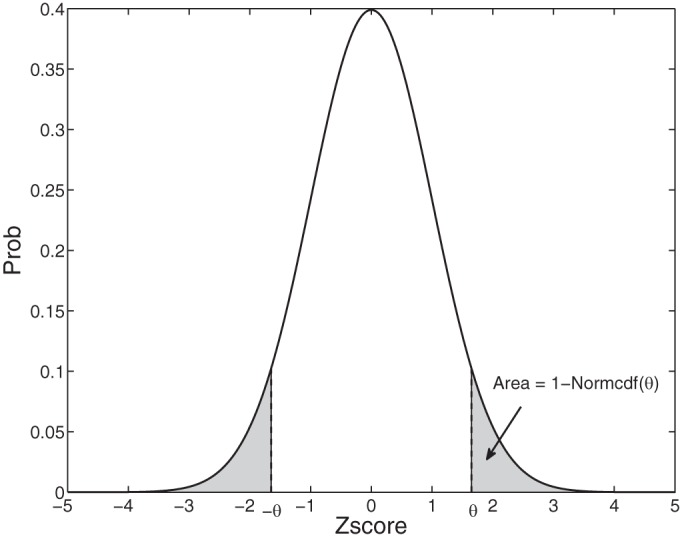
Geometrical illustration of Z score in 1-dimensional setting for assessing statistical significance. Plot shows a normal probability density function (zero mean, unit variance). Shaded areas on left and right represent the area represented by Eq. 12. Normcdf denotes the normal cumulative distribution function.
Particle Filtering
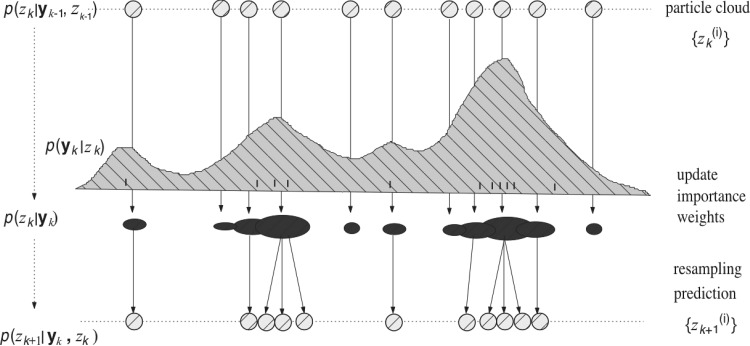
Particle filtering, also known as sequential Monte Carlo method, is a Bayesian filtering method that can track non-Gaussian nonlinear dynamical systems (Doucet et al. 2001). The core idea of all sequential Monte Carlo methods is sequential importance sampling (Fig. 2). Simply put, a particle filter uses a number of random samples called “particles,” sampled directly from the state space, to represent the posterior and updates the posterior by involving the new observations; the “particle system” is properly located, weighted, and propagated recursively, according to Bayes’ rule. Among many variations, one of the most popular methods is the sampling importance resampling (SIR) method that uses the importance sampling trick
| (14) |
where q(·) and p(·) are the proposal and target distributions, respectively. The probability density ratio is called the importance weight function. In Monte Carlo methods, assuming are Np-independent, identically distributed (i.i.d.) samples drawn from the proposal distribution q(θ), we can replace Eq. 14 with a point-mass approximation
Fig. 2.
Illustration of generic particle filter with importance sampling and resampling. In a generic operation, i.i.d. samples or particles (with equal weights) are first drawn from a proposal distribution. Ticks illustrate the neural spike observations overlaid on the conditional distribution p(y|z). Next, the particles are passed through the likelihood function p(yk|zk), weighted by their importance weights. More important particles are assigned greater weights (proportional to the size of the circles). The particles are further resampled to avoid the “weight degeneracy” problem, so that the importance weights are renormalized. Finally, the resampled particles are used for prediction in the next time step, producing the new particle set .
| (15) |
Theories of sequential Monte Carlo methods have been widely studied. Unlike methods based on Gaussian approximation, sequential Monte Carlo methods provide a theoretical guarantee of convergence or accuracy (Carvalho et al. 2010; Chopin 2004; Del Moral 2004).
SIR bootstrap filter.
The Bayesian bootstrap filter is the simplest version of the particle filter (Gordon et al. 1993), which is also very close in spirit to the SIR filter developed independently in statistics (Carpenter et al. 1999; Liu et al. 1998; Liu and Chen 1998; Pitt and Shephard 1999). The idea of the SIR filter is to approximate the proposal distribution q(zk|zk−1,y0:k) as a transition prior distribution p(zk|zk–1) (i.e., the Gaussian prior in light of Eq. 1), which yields
| (16) |
The derivation of the sequential update rule is given in appendix a. Therefore, in the SIR filter, at every time step we calculate the importance weight associated with the ith Monte Carlo sample as follows:
| (17) |
where denotes the ith predicted state estimate in light of Eq. 7 and the normalized importance weights: .
One well-known issue of particle filtering is the “weight degeneracy” problem. Namely, as time goes by, the importance weights of particles become skewed and concentrated on very few samples, creating a large variance. To alleviate the weight degeneracy problem at each particle filtering update, we can monitor the effective sample size (ESS) by an approximate estimate (Liu and Chen 1998):
| (18) |
When the importance weights are uniformly distributed, N̂eff achieves a maximum value Np, whereas when the importance weight distribution is a Dirac delta function (i.e., only one sample has the full mass, and the remaining samples have a zero weight), then N̂eff = 1. Intuitively, when the importance weights are highly skewed, it is inefficient to propagate the particles with low weights to the next iteration. A rule of thumb is that when N̂eff is below a predefined threshold (say Np/2), various resampling procedures can be performed, such as systematic resampling, stratified resampling, residual resampling, and multinomial resampling (Carpenter et al. 1999; Gordon et al. 1993; Liu and Chen 1998). If the threshold is set to be Np, then resampling will be implemented at every time step. Basically, resampling aims to diversify the Monte Carlo sample space. For instance, systematic resampling generates Np ordered numbers: [where u ∈ Uniform(0,1)] and then uses them to select particles based on a multinomial distribution. For detailed discussions of various resampling algorithms, see Doucet et al. (2001) and Hol et al. (2006).
Extension of proposal distribution.
The transition prior distribution used as the proposal distribution is Gaussian; therefore, it is incapable of capturing the discontinuity of abrupt change (i.e., jump) in the random variable. To accommodate the discontinuity or impulsive noise in latent state dynamics, we adapt the transition prior from Gaussian to a mixture of two Gaussian distributions
| (19) |
where 0 ≤ δ ≤ 1. The first term represents the standard Gaussian noise, and the second term represents the impulsive Gaussian noise subject to the variance constraint
| (20) |
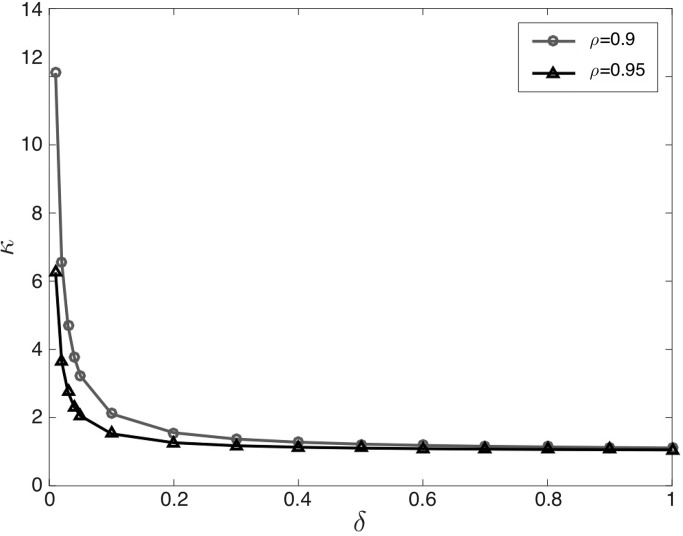
Note that the parameter κ controls the amplitude (variance) of the impulsive noise. The noise distribution of Eq. 19 is known as the Middleton Class A noise model (Haykin et al. 2004; Wang and Poor 1999). Let denote the noise variance ratio. We often set ρ = 0.9. Under the constant constraint, once ρ is fixed the parameters κ can be uniquely determined from δ (and vice versa) (see Fig. 3 for illustration). We often set δ ∈ [0.05,0.1].
Fig. 3.
Relationship between κ and δ in the Middleton Class A noise model (assuming ρ = 0.9 and ρ = 0.95).
To simulate the non-Gaussian dynamical noise (Eq. 19), we have
| (21) |
We call the particle filter using Eqs. 21 and 17 PFalgo1. This particle filter uses a mixture of Gaussians as proposal distribution.
Although the mixture of Gaussian proposal distribution has accommodated abrupt jumps in the state space, it is noted that the sampled particles have ignored the measurement yk in the optimal proposal distribution q(zk|zk−1,yk), which states that the optimal samples should be drawn conditional on previous states and current observations (Doucet et al. 2000). To further improve the efficiency of proposal distribution, motivated by some previous work (Chen et al. 2005; Ergün et al. 2007; Haykin et al. 2004), we propose an additional update for the particles
| (22) |
where ; and we use for computing the importance weights
| (23) |
We call the particle filter using Eqs. 22 and 23 PFalgo2.
Furthermore, we can directly draw samples from the proposal distribution with a mixture of Gaussian form:
| (24) |
where is a Gaussian with mean and variance obtained from Eqs. 11 and 10, respectively. Furthermore, the importance weights are updated as follows:
| (25) |
The evaluation of transition probability depends on which Gaussian distribution the ith particle is drawn from. We call the particle filter using Eqs. 24 and 25 PFalgo3. Note that the complexity of Eq. 25 is . Comparison of the three particle filtering algorithms is shown in Table 1.
Table 1.
Comparison of particle filtering and particle smoothing algorithms
Particle Smoothing
Next, we derive a fixed-interval particle smoothing algorithm (appendix a). Let us write p(zk|y0:T) in the following form (Doucet et al. 2000)
| (26) |
and the smoothing density p(zk|y0:T) is approximated by particle samples
| (27) |
where we have assumed that p̂(zk|y0:T) has the same support as the filtering density p̂(zk|y0:k) but with different importance weights. The smoothed importance weights are calculated as follows (Doucet et al. 2000): At time k = T, set ; for k = T − 1,…,0, update
| (28) |
In the end, we use the normalized smoothed importance weights to weigh the particles for computing the mean or variance statistics. In practice, we can adapt the fixed-interval smoothing to fixed-lag smoothing. We call the particle filter using Eqs. 26–28 PSmT. The algorithmic complexity of this particle smoothing algorithm is with memory requirement . If we implement a fixed-lag smoothing operation, say from k to k + τ, then the computational complexity is .
The particle filtering and smoothing algorithms are summarized in algorithms 2 and 3 (appendix c).
GPU Implementation
The complexity for implementing particle filtering or particle smoothing is computationally demanding (Table 1). However, particle filtering is amenable to distributed and parallel implementation, which fits well with a GPU application (Chitchian et al. 2013; Gelencsr-Horváth et al. 2013). In our first effort, we use GPU computing with MATLAB (MathWorks) through the Parallel Computing Toolbox P. Our custom computer programs were written in MATLAB (R2017a) and implemented in a PC with Windows 7 operating system. The PC is equipped with a CPU of Intel i7-4770 Quad Core Processor (3.4 GHz and 32 GB RAM). The embedded GPU is a NVIDIA (Santa Clara, CA) GTX 1060 6GB card.
RESULTS
Computer Simulations
Setup.
To compare the performance of different filtering algorithms, we generate synthetic population spike data that are driven by a latent state process reminiscent of the dynamic stimulus (i.e., ground truth). We call the units that significantly increase or decrease their firing rates in response to stimuli positive or negative responder units, respectively, and the units that do not significantly change their firing rates nonmodulated or neutral units. The neuronal population consists of C = 10 units, with each trial lasting 20 s (for multiple change points) or 10 s (for a single change point). With a bin size of 50 ms, this corresponds to 400 or 200 sample points in population spike count observations. The population spike counts are driven by a latent state model, where the random vector c consists of both positive and negative coefficients (large absolute value corresponds to a strongly modulated unit). The ground truth of latent process consists of two different levels of magnitude (high vs. low), with high and low amplitude (5 and 3, respectively, dimensionless) denoting the change from the baseline amplitude 0. Time 0 denotes the onset of the first change point. The offset is defined as the moment when the changed activity returns to baseline. Higher magnitude implies a greater level of stimuli intensity. The remaining 5-s period contains two change points with different magnitudes (Fig. 4).
Fig. 4.
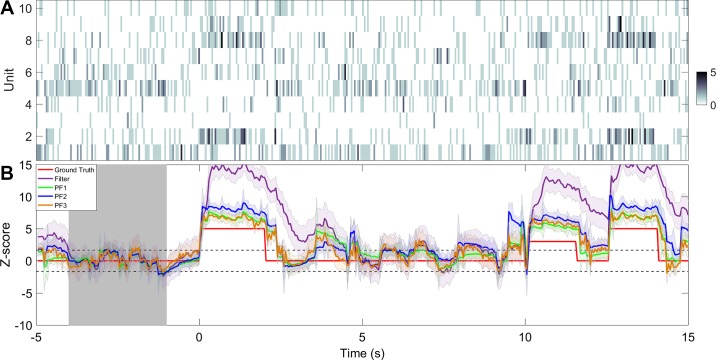
Comparison of different filtering algorithms on a single trial. A: spike count observations from C = 10 simulated units. Color bar denotes the spike count. B: inferred Z-score curves from inferred latent state variable with different filtering algorithms. Shaded areas denote 95% confidence intervals. All particle filters use 1,000 particles. Gray shaded area denotes the baseline period.
Some representative parameters for generating the PLDS model are
where the large positive (or negative) values (in boldface) in vector c correspond to the modulation coefficients of positively (or negatively) modulated units. The parameters are chosen in the way that population spike counts are bounded and there is a significant shift in response to the change points. Note that there are many choices of combinations of d and c that meet this criterion. In each Monte Carlo simulation, we also randomly perturb these two vectors by adding small Gaussian noise.
In all computer simulations, we use the first 10 s of individual single-trial data to estimate PLDS model parameters and then test the model parameters to run the filtering algorithms on the complete 10 s (single change point) or 20 s (multiple change points) of single-trial data. Initial parameters are set as a = 0.9, σϵ = 0.01, and c is initialized by linear factor analysis. Initial latent state is set as z0 = 0, Q0|0 = 0.01. However, the final performance is insensitive to all these initial conditions. Upon the EM inference (~400–500 iterations), the following suboptimal parameters are obtained:
As seen, the estimated parameters are quite accurate with only 200 sample points (10 s with 50-ms bin size). Note that there are algebraic sign and scale ambiguities in ĉ. For comparison, we rescale the parameters to obtain a similar scale.
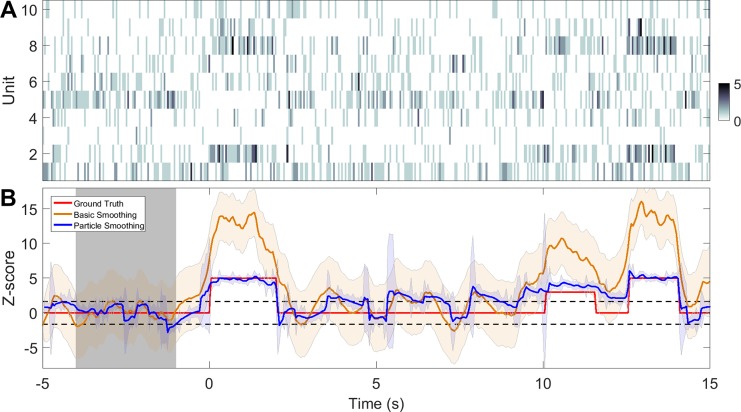
For online filtering, we compare four algorithms: Filter, PFalgo1, PFalgo2, and PFalgo3. Resampling is used at every iteration in all three particle filtering algorithms. We also compare the particle smoothing PSmT with the regular smoothing results obtained from the EM algorithm. Upon completion of inferring the latent state, we compute its Z-score trace from Eq. 12, where the period of [– 4,– 1] s is considered as the baseline. For comparison, we show single-trial examples of sequential change-point detection using filtering (Fig. 4) and smoothing (Fig. 5) algorithms. Compared with the regular filter, all particle filtering algorithms have faster rise and decay time for detecting the onset and offset of change points. In addition, the confidence intervals of Z scores derived from particle filtering are smaller. Similar observations also hold for smoothing.
Fig. 5.
Comparison of basic smoothing and particle smoothing (based on PFalgo2, 1,000 particles) on a single trial. A: spike count observations from C = 10 simulated units. Color bar denotes the spike count. B: inferred Z-score curves. Shaded areas denote the 95% confidence intervals. Gray shaded area denotes the baseline period.
Algorithmic comparison of tracking speed.
The most important question of our interest is the speed of detection on the onset and offset of the change points. We compare the performance of different filtering algorithms with respect to 1) the number of pain-modulated units and 2) the total number of units.
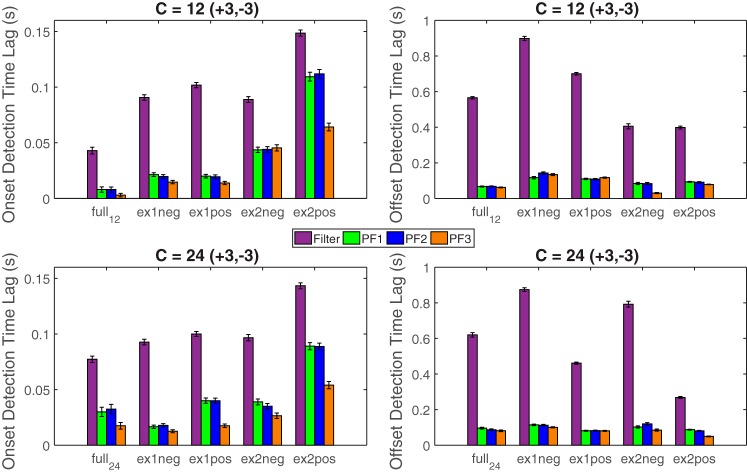
First, we start with a “full” model, which consists of C = 12 units (3 positively modulated, 3 negatively modulated, and 6 neutral units). We use 10-s data to identify the model parameters and then use the parameters to run four filtering algorithms. Next, we systematically and randomly remove positively or negatively modulated units and repeat the estimation and filtering procedure. Specifically, we test all combinations of positively and negatively modulated units and also remove nonmodulated units while keeping the ratio of modulated units unchanged. Each scenario is simulated with 100 independent trials; the mean ± SE statistics are reported in Fig. 6, top. Second, we increase the total number of units twofold (C = 24) while keeping the number of pain-modulated units unchanged. We repeat the procedure and obtain the Monte Carlo statistics from 100 independent trials (Fig. 6, bottom).
Fig. 6.
Comparison between different filtering algorithms for detecting the onset (left) and offset (right) of change points using different number of units (top: C = 12, bottom: C = 24). ex1neg, excluding 1 negatively modulated unit; ex1pos, excluding 1 positively modulated unit; ex2neg, excluding 2 negatively modulated units; ex2pos, excluding 2 positive modulated units. C = 12(+3,– 3) denotes that there are 3 positively and 3 negatively modulated units among 12 simulated units in the full model; similar notation holds for C = 24(+3,– 3).
In summary, two important observations are noteworthy: 1) In all cases, the proposed particle filtering algorithms outperform the basic filter algorithm. 2) In nearly all cases, PFalgo1 and PFalgo2 have similar performances, whereas PFalgo3 achieves better performance. 3) Removing negatively modulated units would affect PFalgo3 more than the other algorithms, whereas removing positively modulated units (especially ex2pos) would affect the onset detection latency of most algorithms except for PFalgo3. Compared with the onset detection, the offset detection latency is much worse for the regular filter, whereas all particle filtering algorithms have relatively stable performance. These observations can be due to the fact that the Gaussian noise assumption in the regular filter imposes a temporal smoothness constraint in the latent state update, whereas the incorporation of non-Gaussian noise can help improve the detection speed in all particle filtering algorithms. Under the same condition, PFalgo3 generally achieves slightly better performance than the other two particle filters because of its potentially more efficient sample selection and importance weight representation.
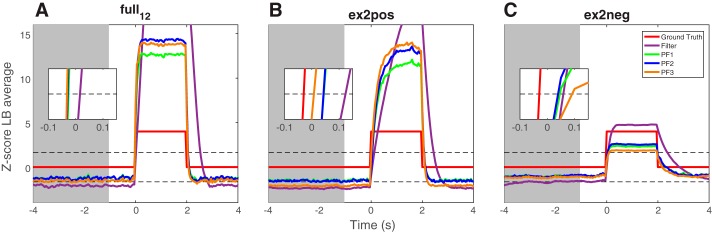
To further illustrate these points, we compute the averaged filtering trace based on 100 independent simulated trials, under three selected configurations (Fig. 7). A close examination of the averaged traces reveals several interesting findings. First, three particle filtering algorithms have similar performance in the full model (3 positively and 3 negatively modulated units), but all have faster detection speed than the basic filter. Second, when there are balanced or relatively more negatively modulated units (e.g., 3 negative vs. 1 positive), PFalgo3 achieves the best performance. Third, when there are insufficient negatively modulated units (e.g., 1 negative vs. 3 positive), the derived Z-score amplitudes from particle filtering algorithms are lower than that of the basic filter because of higher variability in the baseline period. Specifically, PFalgo3 has the lowest amplitude for the same reason. In addition, on average PFalgo3 has a slightly slower speed for detecting the onset of change points than the regular filter (Fig. 7C, inset). Therefore, there is a trade-off in choosing the optimal algorithm. Notably, negatively modulated units introduce a negative correlation between population spike activity in detection, thereby helping reduce the temporal variance of latent variables during the baseline period.
Fig. 7.
Comparison of averaged filtering traces in detecting the onset/offset of change point between different filters. A: full model of 12 units (3 positively and 3 negatively modulated units). B: ex2pos: 1 positively and 3 negatively modulated units. C: ex2neg: 3 positively and 1 negatively modulated units. Mean statistics are obtained from 100 independent simulated trials, Np = 1,000 particles. In each panel, inset shows the zoomed-in period of onset detection. Gray shaded area denotes the baseline period.
Finally, we compare the performance of change point detection by 1) varying the number of total units while keeping the ratio of the pain-modulated units unchanged (for instance, vs. vs. , setup C); 2) varying the number of modulated units while keeping C unchanged (setup B); and 3) changing the number of total units while keeping others unchanged (setup A). Different configurations reflect a similar signal-to-noise ratio (SNR) at the population level. The results derived from the PFalgo3 algorithm are summarized in Table 2. As seen, the performance is relatively robust with respect to various configurations; but when the number of modulated units is below a specific threshold the detection speed of onset will dramatically degrade. For instance, when there are only 1 positively modulated unit and 1 negatively modulated unit among C = 12 units, the detection latency of the onset and offset in the change point becomes equally poor. Overall, the detection speed depends on multiple factors: SNR, C, and the number of positively or negatively modulated units. As a general trend, the offset latency is slower than the onset latency. This is due to the asymmetry in the variance update (Eq. 10). However, adding negatively modulated units will help break the asymmetry.
Table 2.
Results of onset and offset latency derived from PFalgo3 under various setups
| Setup | No. of Total Units | No. of Positive Units | No. of Negative Units | Onset Latency, ms (mean ± SE) | Offset Latency, ms (mean ± SE) |
|---|---|---|---|---|---|
| A | 20 | 3 | 1 | 36.9 ± 4.6 | 72.7 ± 8.4 |
| 16 | 3 | 1 | 33.2 ± 4.9 | 153.6 ± 11.3 | |
| 12 | 3 | 1 | 35.4 ± 4.6 | 49.3 ± 5.7 | |
| 8 | 3 | 1 | 10.3 ± 2.3 | 158.8 ± 11.2 | |
| B | 12 | 5 | 1 | 41.0 ± 4.5 | 15.5 ± 3.1 |
| 12 | 2 | 1 | 42.4 ± 1.5 | 172.8 ± 3.7 | |
| 12 | 1 | 1 | 111.7 ± 3.0 | 163.1 ± 4.5 | |
| C | 20 | 3 | 2 | 12.6 ± 1.4 | 100.8 ± 3.1 |
| 16 | 3 | 1 | 26.6 ± 2.4 | 85.3 ± 5.7 | |
| 12 | 2 | 1 | 40.1 ± 1.5 | 146.3 ± 4.2 | |
| C | 20 | 2 | 3 | 17.5 ± 1.6 | 80.5 ± 2.8 |
| 16 | 2 | 2 | 16.0 ± 0.9 | 126.9 ± 2.7 | |
| 12 | 1 | 2 | 62.6 ± 2.0 | 91.9 ± 1.8 |
Setup A has constant numbers of positively and negatively modulated units. Setup B has constant numbers of total units and negatively modulated units. Setup C has a constant ratio (1/4) of total positively and negatively modulated units. Onset/offset latency is defined by time lag between the detected change and the on/off ground truth. Statistics are computed based on 100 independent simulations.
Impact of multiunit activity and non-Poisson noise.
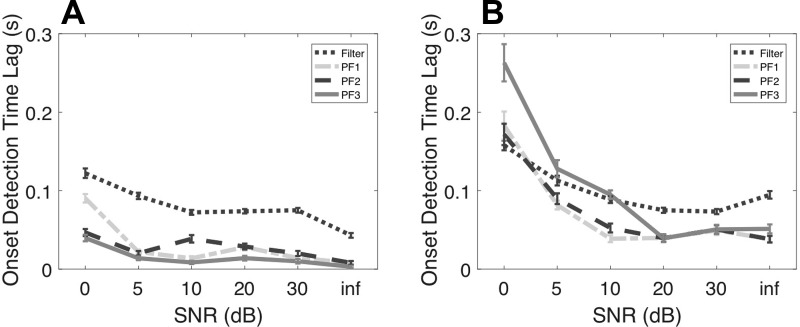
Spike sorting is an error-prone process and is inevitably subject to noise. First, we assume the presence of independent Poisson noise in spike sorting where the “units” contain MUA. We note that the sum of two independent Poisson variables is still Poisson, whereas the sum of two positively or negatively correlated Poisson variables is over- or underdispersed, respectively. We simulate independent Poisson noise according to varying SNR: (note that Poisson mean is equal to variance). For C = 12 units, we consider two scenarios: 3 positively modulated units and 3 negatively modulated units (A) and 3 positively modulated units and 1 negatively modulated unit (B). Results are shown in Fig. 8 (Fig. 8, A and B, correspond to scenarios A and B, respectively). As seen, in the ideal condition (scenario A), the algorithmic performance is robust with respect to various SNRs as low as 0 dB, in which PFalgo3 has the best performance. In a less ideal condition where there are fewer negatively than positively modulated units (scenario B), we see a reduction in performance at around 5–10 dB SNR, and PFalgo2 has the overall best performance. Overall, particle filtering algorithms are quite robust to MUA, and in nearly all cases PFalgo1 and PFalgo2 always outperform the regular filter.
Fig. 8.
Comparison of onset detection performance of different filters with independent Poisson noise under varying signal-to-noise ratio (SNR). Mean statistics are obtained from 100 independent simulated trials, Np = 1,000 particles. A: C = 12, with 3 positively modulated units and 3 negatively modulated units. B: C = 12, with 3 positively modulated units and 1 negatively modulated unit. All performances are derived from PFalgo3. SNR of infinity (inf) denotes a noiseless condition.
The performance drop of PFalgo3 in scenario B under a lower SNR (<20 dB) can be ascribed to the following reasoning. As we discussed above, the presence of negatively modulated units (i.e., negative correlation) helps reduce the temporal variance in the Z-score estimate during the baseline period. When the SNR is high, all particle filtering algorithms have similar performance. However, when the SNR is lower, this high variability issue in the baseline period unfavorably affects the detection speed and sensitivity of PFalgo3. In addition, the gap between the particle filtering algorithms and the basic filter becomes smaller with a decrease in SNR.
We also investigate the impact of non-Poisson noise, which introduces a model mismatch between the data and PLDS. Specifically, we generate correlated Gaussian noise (i.e., from a truncated Gaussian distribution to assure nonnegativity and integer observations), with the zero mean and covariance adjusted from the empirical covariance statistics of raw population spikes. We repeat the analysis and report the results in Fig. 9. As expected, the detection performance under the correlated Gaussian noise is worse than or comparable to the performance under the independent Poisson noise using a comparable SNR.
Fig. 9.
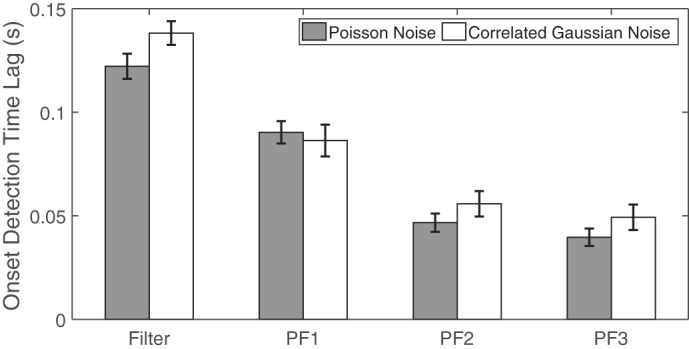
Comparison of onset detection performance of different filters with correlated Gaussian noise under SNR of 0 dB. In all simulations, we have C = 12 units, consisting of 3 positively modulated units and 3 negatively modulated units.
Note that our definition of SNR here is quite different from the coding criterion for a real neuron based on the likelihood principle (Czanner et al. 2015). Therefore, the SNR scale here is relative and may not reflect the actual nature of SNR of a single neuron, which can be very low (e.g., negative dB). In multitrial simulations, we have assumed a homogeneous SNR among all neurons and a perfect Poisson assumption (mean equal to variance), which implies that single-trial change-point detection depends on not only the neurons’ modulating coefficients but also the baseline firing rates. In addition, a low-SNR neuron (in our criterion) can be very informative if its modulation coefficient is negative. Therefore, an alternative SNR criterion may be the ratio of the number of modulated units to the number of nonmodulated units.
Comparison and guidelines for particle filtering algorithms.
In light of all computer simulations and empirical observations, we may draw a few comparisons between three particle filtering algorithms, from which we may provide a few practical guidelines on their use.
First, in terms of the number of modulated units (Figs. 6 and 7), in most conditions all particle filtering algorithms yield similar performance in the onset detection of change points, with PFalgo3 having slightly better overall performance. This observation also generally applies to offset detection.
Second, in terms of SNR (Fig. 8), when the SNR is low it is recommended to use PFalgo1 or PFalgo2 to achieve more robust performance, regardless of the tuning property of the pain-modulated units. However, when the SNR is high or there are sufficient negatively modulated units PFalgo3 is the preferred choice, for both Poisson and non-Poisson noise (Fig. 9).
Finally, it is also possible to combine different particle filters to achieve a more robust performance. A detailed discussion is presented in discussion.
Neuroscience Experiments for Detecting Acute Pain Signals
Experimental protocol and recordings.
All procedures in this study were performed according to protocols reviewed and approved by the New York University School of Medicine Institutional Animal Care and Use Committee and the National Institutes of Health Guide for the Care and Use of Laboratory Animals to ensure minimal animal use and discomfort. Male Sprague-Dawley rats were used in all experiments. Several types of noxious and nonnoxious stimuli are used in our investigations. One type of acute thermal pain stimulus is delivered by a blue (473-nm diode-pumped solid state) laser (Chen et al. 2017a; Zhang et al. 2017) with varying laser intensities (50–250 mW). Another type of acute mechanical pain stimulus is pinprick with a 28-gauge needle.
Animals are allowed to freely explore in a plastic chamber of size 38 × 20 × 25 cm3. One video camera (120 frames/s) is used to continuously record the animal behavior. A common characterization of an animal’s pain behavior is by the latency to paw withdrawal and the duration of paw licking (Cheppudira 2006). We construct custom microdrives (tetrodes or stereotrodes) to record neural activity from the rat ACC or S1 or simultaneously from both regions. With a Plexon (Dallas, TX) data acquisition system, the spikes are thresholded based on high-pass (>300 Hz) local field potentials. Similar to the real-time BMI setup, the spikes are further sorted on the basis of spike waveform features such as peak amplitude, energy, and principal components (Chen et al. 2017a; Zhang et al. 2017). In total, we have recorded >20 rats in the ACC or S1 or both regions simultaneously. For the purpose of illustration, we select two representative recording sessions from two rats to validate our proposed algorithms.
Result comparison.
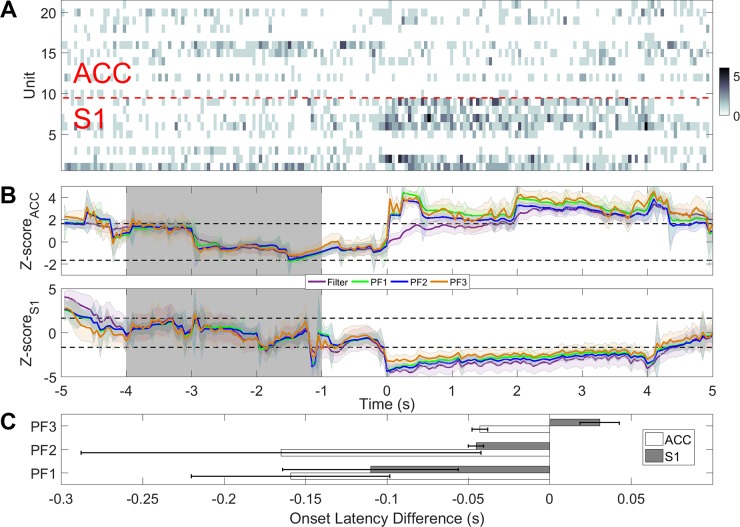
In the first example, we use a recording session with 12 ACC units and 9 S1 units (after online sorting), where mechanical pain stimuli (pinprick) were delivered to animals in a total of 26 trials, which were randomly mixed with nonpainful stimuli (2 g von Frey filament). In each trial, the onset of stimuli was recorded and marked as time 0. In each trial, we use 10-s data to estimate the model parameters. The PLDS converges after 1,000 iterations. Once the model is identified, we run four recursive filtering algorithms and compare their tracking or detection performance (Fig. 10B). We use 5,000 particles in all particle filtering algorithms. As shown in the averaged trial statistics (Fig. 10C), particle filters are able to detect the onset faster than the regular filter in the majority of trials, with a speed improvement ranging between 50 and 200 ms. The increase in speed is more pronounced in the ACC than in the S1 (Fig. 10C). In this case, PFalgo1 has an overall best performance in the ACC and S1, whereas PFalgo1 and PFalgo2 have similar performances in the ACC. In the S1, we observe a degraded performance in PFalgo3 compared with the basic filter. The most likely reason is the lack of sufficient negatively modulated units (e.g., see Fig. 7C, inset). This effect may become even more pronounced with a SNR lower than 10 dB (e.g., see Fig. 8B). In our empirical observations, we find that PFalgo3 is more sensitive to the very low firing rate condition during the baseline period (that is also why negatively modulated units with higher firing rates in baseline can help). The lower spike activity may cause a high variability in the latent state estimate for PFalgo3, and then further affect the amplitude of the Z score at the change point.
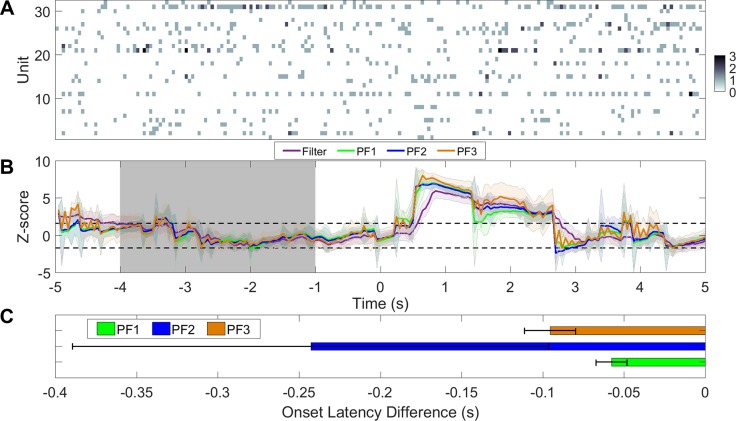
Fig. 10.
A: rat S1 and ACC population spike count observations (off-line sorted) with pinprick at time 0. B: Z-score curves derived from ACC (top) and S1 (bottom). C: comparison of onset detection latency between particle filters and the regular filter. Negative value means that the particle filter detects the onset faster than the regular filter.
In the second example, we use a single-region recording session with 32 ACC units (upon online sorting), during which two levels of laser stimulations were interleaved and delivered to the animal. The rat had hindpaw withdrawals among all 26 trials with 150-mW laser stimulation. As seen in Fig. 11, all particle filters detect the onset and offset faster than the regular filter, with a speed improvement ranging between 50 and 200 ms. On average, PFalgo2 has a slightly better performance among all trials, indicating its better robustness to noise or MUA induced by online sorting.
Fig. 11.
A: rat ACC population spike count observations of 32 units (online sorted) with 150-mW laser stimulation at time 0. B: Z-score curves derived from ACC. C: comparison of onset detection latency between particle filters and the regular filter. Negative value means that the particle filter detects the onset faster than the regular filter.
AUROC assessment.
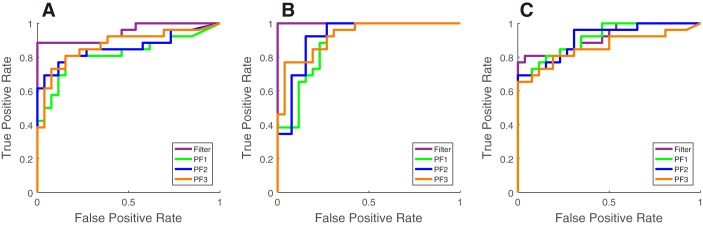
In any change-detection problem, it is important to define the detection sensitivity (i.e., true positive rate) and specificity (i.e., true negative rate). In other words, we need to determine the type I error (false positive, FP) and type II error (false negative, FN) of detection algorithms in relation to the detection threshold (i.e., Z score). Specifically, we compute the receiver operating characteristic (ROC) curve, which shows the trade-off of sensitivity and specificity at different thresholds, and the area under ROC (AUROC) indicates the overall detection performance (1 being perfect, 0.5 being a chance level).
For individual experimental trials, we use Z scores during [0, 1.5] s for identifying true positives and Z scores during the baseline period for identifying FPs. The results are summarized in Table 3 and Fig. 12. In the first example, the basic filter achieves the greatest AUROC statistic in both the S1 and ACC, followed by PFalgo3. In the second example, the basic filter and PFalgo1 obtain the best performance. Therefore, particle filters accelerate the detection speed of the change point from the basic filter, but their FPs or FNs also slightly increase partially because of the induced higher temporal variance during the baseline period (because of the impulsive noise). Finding an optimal trade-off between the detection speed and accuracy may depend on specific factors in each recording session, such as the SNR, MUA, and the ratio of pain-modulated units. It should be noted that our AUROC statistics for particle filters are derived from 5,000 particles. Increasing the number of particles may further improve the performance.
Table 3.
AUROC statistics of selected experimental sessions
| Area | No. of Units | Filter | PFalgo1 | PFalgo2 | PFalgo3 |
|---|---|---|---|---|---|
| ACC | 12 | 0.947 | 0.820 | 0.858 | 0.871 |
| S1 | 9 | 1 | 0.889 | 0.917 | 0.925 |
| ACC | 32 | 0.916 | 0.916 | 0.910 | 0.859 |
Fig. 12.
ROC curves. A: ACC population in the pinprick session (1st example). B: S1 population in the pinprick session (1st example). C: ACC population in the 150-mW laser stimulation session (2nd example).
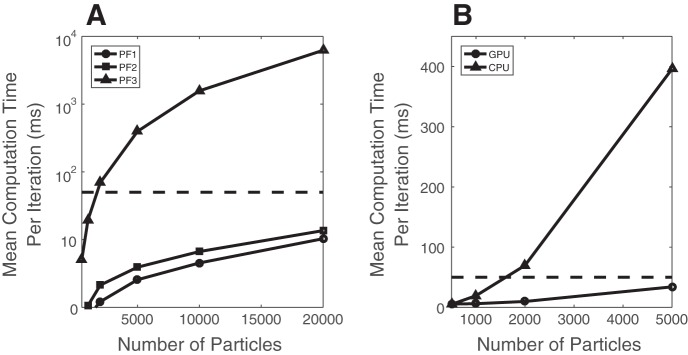
Computational complexity and speed.
For particle filtering, the computational cost comes from two sources: equation update and resampling. The computational complexity of update and resampling is linearly proportional to the number of particles Np, namely, per iteration. To investigate the computational speed, we vary Np from 500, 1,000, 2,000, 5,000, 10,000, and 20,000, using different filtering algorithms. We find that the resampling part takes ~50% of the time for PFalgo1 and PFalgo2 but only 2% for PFalgo3.
For the previous experimental example (32 online-sorted ACC units), we first compare the CPU run time for each particle filtering algorithm. As seen from Fig. 13A, PFalgo1 and PFalgo2 can easily meet the real-time requirement with a multicore CPU, but the computation time of PFalgo3 increases quadratically with increasing numbers of particles. Therefore, we further focus on optimizing the speed performance of PFalgo3.
Fig. 13.
A: comparison of CPU run time of 3 different particle filters per iteration with varying number of particles. Horizontal dashed line denotes 50 ms sampling time interval. B: comparison of CPU and GPU run time for PFalgo3 per iteration.
Specifically, we implement the PFalgo3 algorithm with an embedding GPU card (NVIDIA, 8 GB memory) and compare its computational time per iteration. The results are shown in Fig. 13B. As seen in the figure, the GPU results in a significant increase in computational speed over the CPU when Np is large, especially when Np > 2,000 and the CPU fails to meet the real-time processing requirement. When Np = 5,000, the GPU can achieve ~10-fold increase in speed over the CPU.
Currently, the standard resampling operation has not been parallelized for GPU implementation. However, the resampling operation has recently become feasible for GPU implementation with the use of a new parallel resampling algorithm (Murray et al. 2016a).
DISCUSSION
Connection to the Literature
Our proposed stochastic jump process model uses a random walk with a spike-and-slab prior to capture abrupt changes in the latent state sequence. Our work is closest to the idea of dynamic sparsity prior used in the state-space model (Ba et al. 2014). However, most of the work has focused on the maximum a posteriori mode (or maximum likelihood) estimation, instead of posterior distribution estimation. Specifically, we use variational or Laplace approximation for EM-based model identification and a sequential Monte Carlo-based Bayesian approach for state inference. In principle, it is possible to develop a fully Bayesian method for both model estimation and state inference within the sequential Monte Carlo framework, but the technical details are beyond the scope of the present report.
In addition to change-point detection, spike-and-slab priors have been applied in Bayesian feature or variable selection (Andersen et al. 2014; Hernandez-Lobato et al. 2013). It also came to our attention that there are some other fully Bayesian approaches combining particle Markov chain Monte Carlo (MCMC) methods with sparse Bayesian linear regression (Caron et al. 2012).
Presently, we have assumed the model is static once being identified. Alternatively, we can assume that the model is dynamic with uncertainties in parameters. There are also methods that apply sequential Monte Carlo or particle MCMC methods to estimate the model in time (Andrieu et al. 2010; Chopin et al. 2013).
Finally, there is an active research area that attempts to improve computational efficiency of sequential Monte Carlo or MCMC methods in online applications (Henriksen et al. 2005). Notably, Murray et al. (2016b) have recently proposed an anytime framework to address the computation issue using four billion particles distributed across a cluster of 128 GPUs, demonstrating the feasibility of large-scale Monte Carlo implementation in real-time processing.
Model Mismatch
In statistics, “all models are wrong, but some are useful.” Therefore, statistical models need to be adapted according to the purpose of interest (i.e., detection), which may or may not fully reflect the truth of the data generating process. Here we have implicitly assumed a model mismatch in our computer simulations. First, the ground truth of the latent process is deterministic and discontinuous at change points, but the state equation of the generalized PLDS is an AR(1) model with a driving noise process drawn from one mixture of two Gaussians. Our experimental observations have confirmed the robustness of PLDS and the associated particle filtering solutions. Second, our simulation examples have also confirmed that our model and method are robust with respect to various sources of noise.
Role of Negatively Modulated Neurons
Through computer simulations, we have found that the negatively modulated units (i.e., “OFF” units) play a critical role in detecting onset and offset of the change points. In addition, depending on the specific number of positive/negative units or SNR, different algorithms may achieve either quantitatively similar or different performance. For instance, where there are no negatively modulated units it is preferred to use PFalgo2; however, when negatively modulated units are present it is better to use PFalgo3. In addition, we find that the presence of negatively modulated units plays an important role in detecting the offset of change points. Actually, as a mirror image of firing rate change, the change-point onset for the positively modulated units (i.e., increase in firing rate) is equivalent to the change-point offset for the negatively modulated units (also increase in firing rate).
Experimentally, it has been known that in pain encoding a small percentage of negatively pain-modulated neurons are present in both the S1 and ACC regions (Chen et al. 2017a; Zhang et al. 2017). Functionally, those “negative responders” play a complementary role with “positive responders” in response to noxious stimuli. However, a full understanding of the neural mechanisms of those neurons requires further experimental investigations.
Practical Considerations
Our methods were motivated by designing efficient algorithms for detecting acute pain signals in freely behaving rodents. The neural ensemble spikes are sorted online. For closed-loop BMI applications, several practical considerations are noteworthy.
First, to accommodate real-time detection speed, we need to complete the filtering update per iteration within tens of milliseconds (<50 ms). In our naive MATLAB implementation it takes ~10−2 ms to process one-time iteration in the regular filter algorithm, yet the heavy computation of particle filters can be significantly improved by GPU parallel processing to meet the real-time processing demand (Fig. 13B). For an additional increase in speed, we can consider a CUDA implementation (CUDA is a parallel computing platform and programming model invented by NVIDIA). Furthermore, when the real-time processing is not mandatory, we can implement the fixed-lag particle smoothing algorithm PSmτ (when τ is small), using the GPU. In addition, we can consider a new parallel resampling method to further optimize the speed (Murray et al. 2016a).
Second, real-time BMI requires online spike sorting, which implies the presence of MUA and varying levels of SNR (compared with off-line spike sorting) among recorded units. We may need to adapt our particle filtering algorithmic parameters to accommodate various situations for optimized detection latency.
Third, to accommodate nonstationarity, we need to estimate model parameters regularly. One strategy is to relocate two parallel CPU threads (or one CPU and the other GPU), one for model estimation and the other for recursive filtering (Hu et al. 2017).
Finally, to accommodate large-scale neural recording technologies (e.g., simultaneous recording of hundreds of units), we can use a digital signal processing (DSP) board dedicated to model estimation, which may reallocate CPU memory and resources for multielectrode array data acquisition and processing.
Extension of Probabilistic Model
For the state equation, we may consider extending the AR(1) model to a higher AR(r) model to impose more temporal smoothness (except at the change point)
| (29) |
which can be rewritten as a vector AR model zk = Azk−1 + ϵk with a constrained matrix A. In general, a higher-order AR model implies a higher degree of temporal smoothness in latent state dynamics.1
Using a higher-order AR model will change the model complexity. As the dimensionality of unknown parameters increases, it will pose a greater challenge for the algorithmic convergence and model identifiability with a small sample size. In addition, when dim(zk) is large the particle filter will encounter the “curse of dimensionality,” or suffer from a more severe degeneracy issue. In our present application, we did not find a significant benefit in detection accuracy by using a higher-order AR model. Therefore, we have focused on using the AR(1) model in particle filtering. It is also possible to use a constrained AR model (with fewer unknown parameters) to reduce the variance of the Monte Carlo estimate while using particle filters.
For the measurement equation, we can consider a different link function f under the Poisson distribution. Other than using f(u) = exp(u), we can use f(u) = log[1 + exp(u)] or a custom function [e.g., f(u) = exp(u) for u ≤ 0 and f(u) = 1 + u + u2/2 for u > 0]. Derivation of the filtering update equations using a generic link function is shown in appendix b. In addition, we may consider a generalized probability model for spike count data, such as the negative binomial (Scott and Pillow 2012), the Conway-Maxwell-Poisson distribution (Stevenson 2016), and the generalized count model (Gao et al. 2016). Once the model parameters are identified by likelihood or Bayesian inference, implementation of particle filters for online filtering is straightforward.
Mixtures of Particle Filters
Depending on specific data observations (e.g., the number of negatively modulated neurons), we can run two or more different particle filtering algorithms in parallel (e.g., PFalgo2 and PFalgo3) and integrate their outcomes for decision making. For instance, one particle filter is good at detecting the onset of the change point, while the other may be good at tracking the offset (just as we have shown in computer simulations). As discussed earlier in simulation studies, a specific particle filtering algorithm may be employed for change-point detection, with a practical guideline depending on the specific conditions (e.g., SNR or properties of pain-modulated units). It is also possible to further improve PFalgo3 by designing case-dependent proposal distributions (e.g., to account for very low firing rate conditions during the baseline) to minimize the temporal variance of the latent state.
Thus far we have used the sequential Monte Carlo method to draw particles in parallel from one PLDS model. However, the concept of parallelization can be further generalized. Similar to the idea of a mixture of Kalman filters (Chen and Liu 2000), we can also develop mixtures of particle filters (Chen 2003), with each mixture running a distinct model that has a different link function or different likelihood function. The motivation is that each model may capture a slightly different aspect of the dynamics, for either the state equation or the measurement equation. Each particle filter will produce its estimated Z score or detection results, from which we will derive a decision rule by integrating the information from “ensembles of particle filters.”
Optimizing False Positives and False Negatives
In the application of detecting acute pain signals, it is important to find an optimal trade-off between sensitivity and specificity. Depending on the number of pain-modulated units in neural ensemble recordings, the level of SNR, or the property of MUA, we can choose a different particle filtering algorithm and optimize the free parameters in order to minimize the number of FPs and FNs. This is particularly important when simultaneous recordings from multiple brain regions (e.g., ACC, S1, and nucleus accumbens) become available. However, the design of an optimal decision rule from multiple brain areas requires further study.
In conclusion, we have developed novel particle filtering and smoothing algorithms for detecting abrupt changes in neural ensemble spike activity. By introducing a mixture of Gaussians in the dynamical noise, the abrupt changes in the latent state or measurement are better characterized by the generalized PLDS model. To accommodate online Bayesian inference for the non-Gaussian dynamical systems (in both state and measurement equations), we propose several particle filtering algorithms. With the use of powerful GPU technology, the computing bottleneck can be resolved for achieving online operations. Computer simulations have confirmed that our new algorithms outperform the previous method in both tracking speed and accuracy. We also demonstrate our method in a neuroscience application for detecting acute pain signals based on recorded ensemble spikes from freely behaving rats. Our method will be a powerful toolkit for implementing real-time BMI, used for closed-loop pain modulation and other neuroscience experiments.
GRANTS
The work was supported by National Science Foundation CRCNS Grant IIS-130764 (Z. Chen) and National Institutes of Health Grants R01-NS-100016 (Z. Chen, J. Wang) and R01-GM-115384 (J. Wang). S. Hu was partly supported by a Graduate Student Overseas Fellowship from Zhejiang University and China’s Fundamental Research Funds for the Central Universities.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
S.H. and Q.Z. performed experiments; S.H. and Z.C. analyzed data; S.H., J.W., and Z.C. interpreted results of experiments; S.H. and Z.C. prepared figures; S.H., Q.Z., J.W., and Z.C. approved final version of manuscript; J.W. and Z.C. conceived and designed research; Z.C. drafted manuscript; Z.C. edited and revised manuscript.
APPENDIX A: SEQUENTIAL BAYESIAN FILTERING AND SMOOTHING
Forward Filtering
Let us assume that the posterior p(z0:k|y0:k) can be factorized as
| (30) |
We further assume that the proposal distribution can be factorized as
| (31) |
Therefore, the importance weight function , defined as the ratio between the posterior and the proposal distribution, can be updated recursively in light of Eqs. 30 and 31 (Chen 2003; Doucet et al. 2001):
| (32) |
Backward Smoothing
In the forward step, we run a particle filter to obtain p(zk|y0:T) for all 0 < k < T; in the backward step, the smoothing process is recursively updated by
| (33) |
where the third step uses the assumption of first-order Markov dynamics. Here, p(zk:T|y0:T) denotes the current smoothed estimate, p(zk+1:T|y1:T) denotes the future smoothed estimate, p(zk|y0:k) is the current filtered estimate, and is the incremental ratio of modified dynamics.
APPENDIX B: DERIVATION OF RECURSIVE FILTERING FOR FLDS
We consider a fLDS with a generalized link function f, where f is a static nonlinear function. Namely, the PLDS is a special case of fLDS with an exponential link function. To derive a recursive filter, we simply replace Eqs. 10 and 11 with the following equations (whereas Eqs. 7 and 8 remain unchanged):
| (34) |
| (35) |
| (36) |
| (37) |
where .
APPENDIX C: PARTICLE FILTERING AND SMOOTHING ALGORITHMS
Algorithm 1: Summary of EM Algorithm for PLDS Identification
Input: Observations y1:T
Output: Latent state sequences and PLDS model parameters {a,c,d,σϵ}
Algorithm 2: Summary of Particle Filtering Operations
Initialization: set Np and initial conditions (z0,Q0|0)
While k < T do
Draw i.i.d. samples from the proposal distribution (Eq. 21, or Eq. 22, or Eq. 24)
Compute importance weights for i = 1,⋯,Np.
Normalize importance weights:
Resampling according to the prespecified criterion
- From , compute the statistics of filtered posterior distribution, such as the weighted sample mean and variance:
k = k + 1
End while
Algorithm 3: Summary of Particle Smoothing Operations
Input: for i = 1,…,Np
Set and .
While k ≥ 1 do
Update importance weights (Eq. 28)
From , recompute the statistics of smoothed posterior distribution
k = k − 1
End while
Footnotes
In the case of an AR(2) model, to ensure the stability the roots of the characteristic equation λ2 − a1λ − a2 = 0 must lie strictly inside the unit circle, namely |λ| < 1, where .
REFERENCES
- Andersen MR, Winther O, Hansen LK. Bayesian Inference for Structured Spike and Slab Priors, Advances in Neural Information Processing Systems New York: Curran, 2014, p. 1745–1753. [Google Scholar]
- Andrieu C, Doucet A, Holenstein R. Particle Markov chain Monte Carlo methods. J R Stat Soc Series B 72: 269–342, 2010. doi: 10.1111/j.1467-9868.2009.00736.x. [DOI] [Google Scholar]
- Ba D, Babadi B, Purdon PL, Brown EN. Robust spectrotemporal decomposition by iteratively reweighted least squares. Proc Natl Acad Sci USA 111: E5336–E5345, 2014. doi: 10.1073/pnas.1320637111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri R, Frank LM, Nguyen DP, Quirk MC, Solo V, Wilson MA, Brown EN. Dynamic analyses of information encoding in neural ensembles. Neural Comput 16: 277–307, 2004. doi: 10.1162/089976604322742038. [DOI] [PubMed] [Google Scholar]
- Brockwell AE, Rojas AL, Kass RE. Recursive bayesian decoding of motor cortical signals by particle filtering. J Neurophysiol 91: 1899–1907, 2004. doi: 10.1152/jn.00438.2003. [DOI] [PubMed] [Google Scholar]
- Brown EN, Frank LM, Tang D, Quirk MC, Wilson MA. A statistical paradigm for neural spike train decoding applied to position prediction from ensemble firing patterns of rat hippocampal place cells. J Neurosci 18: 7411–7425, 1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buesing L, Macke JH, Sahani M. Learning stable, regularised latent models of neural population dynamics. Network 23: 24–47, 2012. doi: 10.3109/0954898X.2012.677095. [DOI] [PubMed] [Google Scholar]
- Bushnell MC, Ceko M, Low LA. Cognitive and emotional control of pain and its disruption in chronic pain. Nat Rev Neurosci 14: 502–511, 2013. doi: 10.1038/nrn3516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caron F, Bornn L, Doucet A. Sparsity-Promoting Bayesian Dynamical Linear Models. Le Chesnay, France: INRIA, 2012, Technical Report No. 7895. [Google Scholar]
- Carpenter J, Clifford P, Fearnhead P. Improved particle filter for nonlinear problems. IEE Proc Radar Sonar Navig 146: 2–7, 1999. doi: 10.1049/ip-rsn:19990255. [DOI] [Google Scholar]
- Carvalho C, Johannes M, Lopes H, Polson N. Particle learning and smoothing. Stat Sci 25: 88–106, 2010. doi: 10.1214/10-STS325. [DOI] [Google Scholar]
- Chen R, Liu JS. Mixture Kalman filters. J R Stat Soc Series B 62: 493–508, 2000. doi: 10.1111/1467-9868.00246. [DOI] [Google Scholar]
- Chen Z. Bayesian Filtering: From Kalman Filters to Particle Filters, and Beyond (Technical Report). Hamilton, ON, Canada: McMaster University, 2003. [Google Scholar]
- Chen Z, editor Advanced State Space Methods in Neural and Clinical Data. Cambridge, UK: Cambridge University Press, 2015. doi: 10.1017/CBO9781139941433. [DOI] [Google Scholar]
- Chen Z. A primer on neural signal processing. IEEE Circuits Syst Mag 17: 33–50, 2017. doi: 10.1109/MCAS.2016.2642718. [DOI] [Google Scholar]
- Chen Z, Hu S, Zhang Q, Wang J. Quickest detection for abrupt changes in neuronal ensemble spiking activity using model-based and model-free approaches. In: Proceedings of 8th International IEEE/EMBS Conference on Neural Engineering (NER’17), 2017b, p. 481–484. [Google Scholar]
- Chen Z, Kirubarajan T, Morelande MR. Improved particle filtering schemes for target tracking. In: Proceedings of IEEE ICASSP, 2005, p. 145–148. [Google Scholar]
- Chen Z, Wang J. Statistical analysis of neuronal population codes for encoding acute pain. In: Proceedings of IEEE ICASSP, 2016, p. 829–833. [Google Scholar]
- Chen Z, Zhang Q, Tong AP, Manders TR, Wang J. Deciphering neuronal population codes for acute thermal pain. J Neural Eng 14: 036023, 2017a. doi: 10.1088/1741-2552/aa644d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheppudira BP. Characterization of hind paw licking and lifting to noxious radiant heat in the rat with and without chronic inflammation. J Neurosci Methods 155: 122–125, 2006. doi: 10.1016/j.jneumeth.2006.01.001. [DOI] [PubMed] [Google Scholar]
- Chitchian M, Simonetto A, van Amesfoort AS, Keviczky T. Distributed computation particle filters on GPU architectures for real-time control applications. IEEE Trans Contr Syst Technol 21: 2224–2238, 2013. doi: 10.1109/TCST.2012.2234749. [DOI] [Google Scholar]
- Chopin N. Central limit theorem for sequential Monte Carlo methods and its application to Bayesian inference. Ann Stat 32: 2385–2411, 2004. doi: 10.1214/009053604000000698. [DOI] [Google Scholar]
- Chopin N, Jacob PE, Papaspiliopoulos O. SMC2: an efficient algorithm for sequential analysis of state space models. J R Stat Soc Series B 75: 397–426, 2013. doi: 10.1111/j.1467-9868.2012.01046.x. [DOI] [Google Scholar]
- Ciliberti D, Kloosterman F. Falcon: a highly flexible open-source software for closed-loop neuroscience. J Neural Eng 14: 045004, 2017. doi: 10.1088/1741-2552/aa7526. [DOI] [PubMed] [Google Scholar]
- Copits BA, Pullen MY, Gereau RW 4th. Spotlight on pain: optogenetic approaches for interrogating somatosensory circuits. Pain 157: 2424–2433, 2016. doi: 10.1097/j.pain.0000000000000620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czanner G, Sarma SV, Ba D, Eden UT, Wu W, Eskandar E, Lim HH, Temereanca S, Suzuki WA, Brown EN. Measuring the signal-to-noise ratio of a neuron. Proc Natl Acad Sci USA 112: 7141–7146, 2015. doi: 10.1073/pnas.1505545112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daou I, Tuttle AH, Longo G, Wieskopf JS, Bonin RP, Ase AR, Wood JN, De Koninck Y, Ribeiro-da-Silva A, Mogil JS, Séguéla P. Remote optogenetic activation and sensitization of pain pathways in freely moving mice. J Neurosci 33: 18631–18640, 2013. doi: 10.1523/JNEUROSCI.2424-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Del Moral P. Feynman-Kac Formulae: Genealogical and Interacting Particle Systems with Applications. New York: Springer, 2004. doi: 10.1007/978-1-4684-9393-1. [DOI] [Google Scholar]
- Doucet A, de Freitas N, Gordon NJ, Sequential Monte Carlo Methods in Practice. New York: Springer, 2001. doi: 10.1007/978-1-4757-3437-9. [DOI] [Google Scholar]
- Doucet A, Godsill S, Andrieu C. On sequential Monte Carlo sampling methods for Bayesian filtering. Stat Comput 10: 197–208, 2000. doi: 10.1023/A:1008935410038. [DOI] [Google Scholar]
- Eden UT, Frank LM, Barbieri R, Solo V, Brown EN. Dynamic analysis of neural encoding by point process adaptive filtering. Neural Comput 16: 971–998, 2004. doi: 10.1162/089976604773135069. [DOI] [PubMed] [Google Scholar]
- Ergün A, Barbieri R, Eden UT, Wilson MA, Brown EN. Construction of point process adaptive filter algorithms for neural systems using sequential Monte Carlo methods. IEEE Trans Biomed Eng 54: 419–428, 2007. doi: 10.1109/TBME.2006.888821. [DOI] [PubMed] [Google Scholar]
- Gao Y, Archer E, Paninski L, Cunningham JP. Linear Dynamical Neural Population Models Through Nonlinear Embeddings, Advances in Neural Information Processing Systems. New York: Curran, 2016. [Google Scholar]
- Gelencsr-Horváth A, Tornai GJ, Horváth A, Cserey G. Fast, parallel implementation of particle filtering on the GPU architecture. EURASIP J Adv Signal Process 2013: 148, 2013. [Google Scholar]
- Gordon N, Salmond D, Smith AF. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc Radar Sonar Navig 140: 107–113, 1993. doi: 10.1049/ip-f-2.1993.0015. [DOI] [Google Scholar]
- Gregory NS, Harris AL, Robinson CR, Dougherty PM, Fuchs PN, Sluka KA. An overview of animal models of pain: disease models and outcome measures. J Pain 14: 1255–1269, 2013. doi: 10.1016/j.jpain.2013.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu L, Uhelski ML, Anand S, Romero-Ortega M, Kim YT, Fuchs PN, Mohanty SK. Pain inhibition by optogenetic activation of specific anterior cingulate cortical neurons. PLoS One 10: e0117746, 2015. doi: 10.1371/journal.pone.0117746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haykin S, Huber K, Chen Z. Bayesian sequential state estimation for MIMO wireless communications. Proc IEEE 92: 289–305, 2004. doi: 10.1109/JPROC.2003.823143. [DOI] [Google Scholar]
- Henriksen S, Wills A, Schon TB, Ninness B. Parallel implementation of particle MCMC methods on a GPU. In: Proceedings of 16th IFAC Symposium on System Identification, 2005, p. 1143–1148. [Google Scholar]
- Hernandez-Lobato D, Hernandez-Lobato J, Dupont P. Generalized spike-and-slab priors for Bayesian group feature selection using expectation propagation. J Mach Learn Res 14: 1891–1945, 2013. [Google Scholar]
- Hol JD, Schon TB, Gustafsson F. On resampling algorithms for particle filters. In: Proceedings of IEEE Nonlinear Statistical Signal Processing Workshop, 2006. [Google Scholar]
- Hu S, Zhang Q, Wang J, Chen Z. A real-time rodent neural interface for deciphering acute pain signals from neuronal ensemble spike activity. In: Proceedings of 51st Asilomar Conference on Signals, Systems, and Computers, 2017. [Google Scholar]
- Iyer SM, Vesuna S, Ramakrishnan C, Huynh K, Young S, Berndt A, Lee SY, Gorini CJ, Deisseroth K, Delp SL. Optogenetic and chemogenetic strategies for sustained inhibition of pain. Sci Rep 6: 30570, 2016. doi: 10.1038/srep30570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawahara Y, Sugiyama M. Sequential change-point detection based on direct density-ratio estimation. Stat Anal Data Min 5: 114–127, 2012. doi: 10.1002/sam.10124. [DOI] [Google Scholar]
- Kawahara Y, Yairi T, Machida K.. Change-point detection in time-series data based on subspace identification. In: Proc IEEE Conf Data Mining, 2007, p. 559–564. [Google Scholar]
- Kelly RC, Lee TS. Decoding V1 Neuronal Activity Using Particle Filtering with Volterra Kernels, Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2003. [Google Scholar]
- Koepcke L, Ashida G, Kretzberg J. Single and multiple change point detection in spike trains: comparison of different CUSUM methods. Front Syst Neurosci 10: 51, 2016. doi: 10.3389/fnsys.2016.00051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo CC, Yen CT. Comparison of anterior cingulate and primary somatosensory neuronal responses to noxious laser-heat stimuli in conscious, behaving rats. J Neurophysiol 94: 1825–1836, 2005. doi: 10.1152/jn.00294.2005. [DOI] [PubMed] [Google Scholar]
- Lawhern V, Wu W, Hatsopoulos N, Paninski L. Population decoding of motor cortical activity using a generalized linear model with hidden states. J Neurosci Methods 189: 267–280, 2010. doi: 10.1016/j.jneumeth.2010.03.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M, Manders TR, Eberle SE, Su C, D’amour J, Yang R, Lin HY, Deisseroth K, Froemke RC, Wang J. Activation of corticostriatal circuitry relieves chronic neuropathic pain. J Neurosci 35: 5247–5259, 2015. doi: 10.1523/JNEUROSCI.3494-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu JS, Chen R. Sequential Monte Carlo methods for dynamical systems. J Am Stat Assoc 93: 1032–1044, 1998. doi: 10.1080/01621459.1998.10473765. [DOI] [Google Scholar]
- Liu JS, Chen R, Wong WH. Rejection control and sequential importance sampling. J Am Stat Assoc 93: 1022–1031, 1998. doi: 10.1080/01621459.1998.10473764. [DOI] [Google Scholar]
- Liu S, Yamada M, Collier N, Sugiyama M. Change-point detection in time-series data by relative density-ratio estimation. Neural Netw 43: 72–83, 2013. doi: 10.1016/j.neunet.2013.01.012. [DOI] [PubMed] [Google Scholar]
- Macke JH, Buesing L, Cunningham JP, Yu BM, Shenoy KV, Sahani M. Empirical Models of Spiking in Neural Populations, Advances in Neural Information Processing Systems, vol. 24 New York: Curran, 2012. [Google Scholar]
- Macke JH, Buesing L, Sahani M. Estimating state and parameters in state space models of spike trains. In: Advanced State Space Methods in Neural and Clinical Data, edited by Chen Z Cambridge, UK: Cambridge Univ. Press, 2015. doi: 10.1017/CBO9781139941433.007 [DOI] [Google Scholar]
- Malladi R, Kalamangalam GP, Aazhang B. Online Bayesian change point detection algorithms for segmentation of epileptic activity. In: Proceedings of Asilomar Conference on Signals, Systems and Computers, p. 1833–1837, 2013. [Google Scholar]
- Meng L, Kramer MA, Eden UT. A sequential Monte Carlo approach to estimate biophysical neural models from spikes. J Neural Eng 8: 065006, 2011. doi: 10.1088/1741-2560/8/6/065006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mosqueiro T, Strube-Bloss M, Tuma R, Pinto R, Smith BH, Huerta R. Non-parametric change point detection for spike trains. In: Proc. Annual Conf. Info. Sci. Syst. (CISS), 2016. [Google Scholar]
- Murray LM, Lee A, Jacob PE. Parallel resampling in the particle filter. J Comput Graph Stat 25: 789–805, 2016a. doi: 10.1080/10618600.2015.1062015. [DOI] [Google Scholar]
- Murray LM, Singh S, Jacob PE, Lee A. Anytime Monte Carlo technical report (Preprint). arXiv 1612.03319v2, 2016b.
- Page ES. Continuous inspection schemes. Biometrika 41: 100–115, 1954. doi: 10.1093/biomet/41.1-2.100. [DOI] [Google Scholar]
- Paninski L, Ahmadian Y, Ferreira DG, Koyama S, Rahnama Rad K, Vidne M, Vogelstein J, Wu W. A new look at state-space models for neural data. J Comput Neurosci 29: 107–126, 2010. doi: 10.1007/s10827-009-0179-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paninski L, Vidne M, DePasquale B, Ferreira DG. Inferring synaptic inputs given a noisy voltage trace via sequential Monte Carlo methods. J Comput Neurosci 33: 1–19, 2012. doi: 10.1007/s10827-011-0371-7. [DOI] [PubMed] [Google Scholar]
- Perl ER. Ideas about pain, a historical view. Nat Rev Neurosci 8: 71–80, 2007. doi: 10.1038/nrn2042. [DOI] [PubMed] [Google Scholar]
- Pillow JW, Ahmadian Y, Paninski L. Model-based decoding, information estimation, and change-point detection techniques for multineuron spike trains. Neural Comput 23: 1–45, 2011. doi: 10.1162/NECO_a_00058. [DOI] [PubMed] [Google Scholar]
- Pitt M, Shephard N. Filtering via simulation: auxiliary particle filter. J Am Stat Assoc 94: 590–599, 1999. doi: 10.1080/01621459.1999.10474153. [DOI] [Google Scholar]
- Poor HV, Hadjiliadis O. Quickest Detection. Cambridge, UK: Cambridge Univ. Press, 2009. [Google Scholar]
- Scott J, Pillow JW. Fully Bayesian Inference for Neural Models with Negative-Binomial Spiking, Advances in Neural Information Processing Systems, vol. 25 New York: Curran, 2012, p. 1898–1906. [Google Scholar]
- Smith AC, Brown EN. Estimating a state-space model from point process observations. Neural Comput 15: 965–991, 2003. doi: 10.1162/089976603765202622. [DOI] [PubMed] [Google Scholar]
- Stevenson IH. Flexible models for spike count data with both over- and under- dispersion. J Comput Neurosci 41: 29–43, 2016. doi: 10.1007/s10827-016-0603-y. [DOI] [PubMed] [Google Scholar]
- Stevenson IH, Kording KP. How advances in neural recording affect data analysis. Nat Neurosci 14: 139–142, 2011. doi: 10.1038/nn.2731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vierck CJ, Whitsel BL, Favorov OV, Brown AW, Tommerdahl M. Role of primary somatosensory cortex in the coding of pain. Pain 154: 334–344, 2013. doi: 10.1016/j.pain.2012.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogt BA. Pain and emotion interactions in subregions of the cingulate gyrus. Nat Rev Neurosci 6: 533–544, 2005. doi: 10.1038/nrn1704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Poor V. Robust multiuser detection in non-Gaussian channels. IEEE Trans Signal Process 50: 289–305, 1999. doi: 10.1109/78.740103. [DOI] [Google Scholar]
- Xu J, Brennan TJ. The pathophysiology of acute pain: animal models. Curr Opin Anaesthesiol 24: 508–514, 2011. doi: 10.1097/ACO.0b013e32834a50d8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q, Manders T, Tong AP, Yang R, Garg A, Martinez E, Zhou H, Dale J, Goyal A, Urien L, Yang G, Chen Z, Wang J. Chronic pain induces generalized enhancement of aversion. eLife 6: e25302, 2017. doi: 10.7554/eLife.25302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Wang N, Wang JY, Chang JY, Woodward DJ, Luo F. Ensemble encoding of nociceptive stimulus intensity in the rat medial and lateral pain systems. Mol Pain 7: 64, 2011. doi: 10.1186/1744-8069-7-64. [DOI] [PMC free article] [PubMed] [Google Scholar]