A Bayesian Gene-Based Genome-Wide Association Study Analysis of Osteosarcoma Trio Data Using a Hierarchically Structured Prior

Abstract

Osteosarcoma is considered to be the most common primary malignant bone cancer among children and young adults. Previous studies suggest growth spurts and height to be risk factors for osteosarcoma. However, studies on the genetic cause are still limited given the rare occurrence of the disease. In this study, we investigated in a family trio data set that is composed of 209 patients and their unaffected parents and conducted a genome-wide association study (GWAS) to identify genetic risk factors for osteosarcoma. We performed a Bayesian gene-based GWAS based on the single-nucleotide polymorphism (SNP)-level summary statistics obtained from a likelihood ratio test of the trio data, which uses a hierarchically structured prior that incorporates the SNP-gene hierarchical structure. The Bayesian approach has higher power than SNP-level GWAS analysis due to the reduced number of tests and is robust by accounting for the correlations between SNPs so that it borrows information across SNPs within a gene. We identified 217 genes that achieved genome-wide significance. Ingenuity pathway analysis of the gene set indicated that osteosarcoma is potentially related to TP53, estrogen receptor signaling, xenobiotic metabolism signaling, and RANK signaling in osteoclasts.

Introduction

Osteosarcomas, with an incidence rate of 5 (95% confidence interval: 4.6-5.6) per million people per year in the age group of 0 to 19 years for all races and both sexes,¹ are considered to be the most common primary malignant bone cancer among children and young adults. The fact that osteosarcomas incidence reaches a primary peak during the age group of 0 to 24 years² suggests a close relationship between osteosarcomas and human growth. Hence, factors such as growth spurts and height have been investigated regarding their association with osteosarcomas. Case-control studies have provided evidence that tall stature and earlier pubertal growth spurts contribute to the occurrence of osteosarcomas during adolescence.^3–5

Some recent studies investigated the genetic cause of osteosarcoma via genome-wide association studies (GWAS) and identified several single-nucleotide polymorphisms (SNPs) as potential genetic risk factors for osteosarcoma. Savage et al⁶ conducted a large-scale multicenter GWAS that identified 2 susceptibility SNPs for osteosarcoma on human; a third potential susceptibility SNP is located in a gene that belongs to protein families associated with height, a known risk factor for for osteosarcomas. Another study suggested several SNPs in the human chromosome 8q24 may be associated with osteosarcoma.⁷ Several other pilot studies also found that some SNPs in the GRM4 gene⁸ and in the Fas gene⁹ are associated with a higher risk of osteosarcoma. One study noted that some SNPs in the COL1A1 gene are associated with a lower risk of osteosarcoma in the Chinese population.¹⁰ A GWAS done on dogs implicated that 33 SNPs related to bone growth account for more than 50% of the risk of osteosarcoma in 3 breeds of dogs.¹¹

These studies have revealed the importance of the role of genetic markers in osteosarcoma and suggested that those relevant to the development of height be of special interest to researchers. However, they primarily focused on the genetic risk factors at the SNP level. There has been an upward trend in the gene-based GWAS analyses because of some notable disadvantages of these SNP-level tests, such as constrained power due to large-scale multiple testing introduced by the tremendous number of SNPs, inability to account for the natural gene-SNP architecture, and indirect association with higher-order functions including biological pathways.

In this study, we performed a gene-based GWAS analysis on a family-based trio data set recently collected by Dr Logan Spector’s group at the University of Minnesota, which contains the genotypes of 697 110 SNPs for 209 patients with osteosarcoma and their unaffected biological parents. Our objective is to identify height-related genetic markers that are associated with osteosarcoma. We restricted the SNPs in our analysis only to those that are potentially associated with height with a screening step as height is identified as the major risk factor for osteosarcoma. Compared with the population-based case-control design, the family-based trio design has an advantage that it can control for confounding that might result from population stratification or mismatch between patients and controls by comparing the cases to the “controls” from the same mating type.^12,13 In addition, the family-based trio design is the basis of several well-developed association tests that are fundamental in a good number of GWAS analyses.

We performed a Bayesian gene-based GWAS analysis which is composed of 2 steps: We first conducted SNP-level association tests for the trio data using the likelihood ratio test (LRT) and obtained SNP level summary statistics and then conducted a gene-level GWAS on the summary statistics using a hierarchically structured prior that incorporates the SNP-gene hierarchical structure.

The LRT method was proposed by Weinberg et al¹⁴ for a likelihood-based association analysis of family trio data. Compared with the transmission disequilibrium test (TDT),¹⁵ a well-studied approach to test the linkage between SNPs and a trait, the LRT method can flexibly handle the situations where the genetic information of one parent is missing using the expectation-maximization algorithm,¹⁶ which satisfies the need in our data analysis as there is a nontrivial amount of missingness in our trio data. Specifically, among all of the 209 trio families, 106 (50.7%) of them are missing the SNP genotype information of either the father or the mother. Although several extensions of TDT, such as sib-TDT and sibship disequilibrium test, were proposed also to handle incomplete data with missing parents, they rely on the genetic information of the patients’ other unaffected siblings,^17–20 which is not available for most of the families in our trio data set.

In the second-stage analysis, we conducted a gene-based GWAS based on the SNP-level summary statistics obtained from the LRT association tests using the hierarchical structured variable selection (HSVS) method, a Bayesian approach that uses a prior proposed by Zhang et al²¹ for variable selection in presence of group structures among predictors in a linear regression problem. In the setting of the multiple testing problem as concerned in this article, the HSVS method uses a hierarchically structured prior that incorporates the SNP-gene hierarchical structure in the gene-level association study and accounts for serial correlations among SNPs so that it borrows information across SNPs within a gene. The Bayesian method generates posterior samples of the binary selection indicators and the posterior selection probability estimator for each gene, which can be used as a Bayesian-version P value to evaluate the significance of a gene. At the same time, posterior estimators for the association strength at the SNP level are obtained to evaluate the relative importance of SNPs within a gene. The gene-based Bayesian GWAS analysis is more sensitive to detect genes with consistent SNP-level effects as well as having reduced false positives by borrowing information across SNPs within each gene.

As a result, we identified 217 genes as significantly associated with osteosarcoma, all of which showed serial correlations among the SNPs and consistent SNP-disease associations within the gene. Ingenuity pathway analysis (IPA) of the gene set indicated that these genes are highly related to TP53, estrogen receptor signaling, xenobiotic metabolism signaling, and RANK signaling in osteoclasts, suggesting the association of these pathways with osteosarcoma. In comparison, we also conducted an SNP-level GWAS and a gene-level GWAS using the minimum P value method.²² With control of false discovery rates (FDRs) using the Benjamini-Hochberg procedure, the SNP-based GWAS and the minimum P value method identified 169 and 416 genes, respectively.

Methods

Prescreening of SNPs

Prior to the 2-stage analysis, we implemented a prescreening procedure with an objective of restricting the SNPs in our analysis only to those that are potentially associated with growth spurts and height. In particular, we used the height data from the Genetic Investigation of ANthropometric Traits (GIANT) consortium,²³ which contains the P values of 2 469 635 SNPs of association tests with height after a meta-analysis from 46 studies, to prescreen the SNPs in our data set. As a result, we included in our analysis 30 247 SNPs that have a P value less than .05 in the GIANT height studies.

LRT for univariate trio data analysis

We performed the expectation maximization LRT to determine the strength of association between each SNP and the disease. The original work of LRT proposed by Weinberg et al¹⁴ is based on a log-linear approach that models the expected number in each possible combination of the number of minor alleles within a trio for a particular SNP. On the basis of this log-linear model, Weinberg¹⁶ further extended this approach to impute the genotyped SNP information of the missing parents by employing the expectation-maximization algorithm.²⁴ The test statistic of LRT has a 2-df ${\chi }^2$ distribution under the null hypothesis that there is no association between an SNP and the disease; that is, for a particular SNP, the number of minor alleles in patients does not affect the risk of developing osteosarcoma.

We obtained the 2-df ${\chi }^2$ LRT statistics for the 30 247 SNPs by applying to our data the function “colEMlrt” from the R package “trio,”²⁵ an implementation of the expectation maximization LRT. We then converted the ${\chi }^2$ statistics to the standard normal z scores by the equation $z={\Phi }^{-1}(F_{{\chi }^2}(q))$, where $q$ is the realization of ${\chi }^2$ random variables, $z$ is the realization of standard normal random variables, and $F$ and $\Phi$ are the cumulative density functions. We solved this equation for the z scores by plugging in the obtained 2-df ${\chi }^2$ LRT statistics. The reason that we did this conversion is because of the normality assumption in our model that will be explicated in section “Gene-level association tests using the fused HSVS prior.”

Gene-level association tests using the fused HSVS prior

We now conduct gene-level association tests based on the SNP-level summary statistics obtained above. Let ${\mathbf{Z}}_{\mathbf{g}}={(Z_{g1},\dots ,Z_{g{k}_g})}^T$ denote the group of test statistics corresponding to the SNPs that belong to a single gene $g$, where $g$ indexes the gene, $k_g$ indicates the number of SNPs in the $g\mathrm{th}$ gene, and $Z_{gi}$ indicates the summary statistic of the LRT association test for the $i\mathrm{th}$ SNP within the $g\mathrm{th}$ gene. The order of SNPs reflects the relative relationship of their genomic location within the gene. We assume that ${\mathbf{Z}}_{\mathbf{g}}$ follows a multivariate normal distribution $N({\theta }_g,{\sigma }^2{\mathbf{I}}_{\mathbf{n}})$ and it can be expressed as follows:

$${\mathbf{Z}}_g={\mathbf{\theta }}_g+{\mathbf{ϵ}}_g$$

where the mean ${\theta }_g={({\theta }_{g1},\dots ,{\theta }_{g{k}_g})}^T$ and the error term ${ϵ}_g\sim N(\mathbf{0},{\sigma }^2{\mathbf{I}}_{\mathbf{n}})$. Our interest is to test the null hypothesis $H_0:{\theta }_g={({\theta }_{g1},\dots ,{\theta }_{g{k}_g})}^T=\mathbf{0}$; that is, there is no association between any of the SNPs in the $g\mathrm{th}$ gene and the disease status under $H_0$.

We tested the hypotheses in a Bayesian framework using a hierarchically structured prior, the HSVS prior, for each ${\theta }_g$, which was introduced by Zhang et al.²¹ Specifically, the HSVS prior is a discrete mixture distribution that can be expressed as follows:

$${\theta }_g|{\gamma }_g,{\sigma }^2,{\tau }_g^{\mathbf{2}},{\omega }_g^{\mathbf{2}}\sim (1-{\gamma }_g)I({\theta }_g=\mathbf{0})+{\gamma }_{g}N(\mathbf{0},{\sigma }^2{\Sigma }_{{\theta }_g})$$

The prior uses a binary indicator, ${\gamma }_g$, on the mean ${\theta }_g$ for gene-level selection so that when ${\gamma }_g=0$ we have ${\theta }_g=\mathbf{0}$ supporting the null hypothesis for the $g\mathrm{th}$ gene. However, ${\gamma }_g=1$ indicates that the null hypothesis is rejected and the $g\mathrm{th}$ gene is associated with the disease. We assume that under the alternative hypothesis, ${\theta }_g$ follows a normal distribution $N(\mathbf{0},{\sigma }^2{\Sigma }_{{\theta }_{\mathbf{g}}})$, where the matrix ${\Sigma }_{{\theta }_g}$ can be specified to accommodate the correlation among the strength of association between SNPs within the same gene and the disease of interest.

In the Bayesian framework, using such a mixture prior generates posterior samples of the binary selection indicator ${\gamma }_g$ that can be used to estimate the posterior probability $P({\theta }_{\mathbf{g}}=\mathbf{0})$ for each gene, which can be taken as a Bayesian-version P value to evaluate the significance of the gene. In this study, we specify the matrix ${\Sigma }_{{\theta }_g}$ as the one represented in the hierarchical prior for the Bayesian fused lasso²⁶ that can account for the serial correlation among SNPs within the gene region. That is, we set the covariance matrix such that

$${\Sigma }_{{\theta }_{\mathbf{g}}}^{-1}=\left[\begin{array}{ccccc}\frac{1}{{\tau }_{g1}^2}+\frac{1}{{\omega }_{g1}^2}& -\frac{1}{{\omega }_{g1}^2}& 0& \dots & 0\\ -\frac{1}{{\omega }_{g1}^2}& \frac{1}{{\tau }_{g2}^2}+\frac{1}{{\omega }_{g1}^2}+\frac{1}{{\omega }_{g2}^2}& -\frac{1}{{\omega }_{g2}^2}& \ddots & ⋮\\ 0& -\frac{1}{{\omega }_{g2}^2}& \frac{1}{{\tau }_{g3}^2}+\frac{1}{{\omega }_{g2}^2}+\frac{1}{{\omega }_{g3}^2}& \ddots & 0\\ ⋮& \ddots & \ddots & \ddots & -\frac{1}{{\omega }_{g(k_g-1)}^2}\\ 0& \dots & 0& -\frac{1}{{\omega }_{g(k_g-1)}^2}& \frac{1}{{\tau }_{g{k}_g}^2}+\frac{1}{{\omega }_{g(k_g-1)}^2}\end{array}\right]$$

Note that the off-diagonal elements in the inverse covariance matrix introduces positive correlations between neighboring SNPs. Such construction encourages similarity between the means ${\theta }_{gi}$ and ${\theta }_{gj}$ corresponding to each pair $(i,j)$ of neighboring SNPs. Following Zhang et al,²¹ we specify the hyperpriors for the parameters of the HSVS prior as follows:

$$\begin{array}{l}{\gamma }_g|p\sim Bernoulli(p),{\tau }_{gj}^2|{\lambda }_{1g}\sim \exp \left(\frac{{\lambda }_{1g}^2}{2}\right),\\ {\omega }_{gj}^2|{\lambda }_{2g}\sim \exp \left(\frac{{\lambda }_{2g}^2}{2}\right)\\ p\sim Beta(a,b),{\lambda }_{1g}^2\sim Gamma(r_1,{\delta }_1),\\ {\lambda }_{2g}^2\sim Gamma(r_2,{\delta }_2),{\sigma }^2\propto \frac{1}{{\sigma }^2}\end{array}$$

The specified hierarchical priors result in closed-form full conditionals for posterior sampling via the Gibbs algorithm. Jointing with parallel computing tools, the Bayesian construction leads to efficient computations that is scalable to the high-dimensional GWAS analysis. We will discuss the parallel computing in more detail in section “Discussion.”

Choice of hyperpriors

We set $(a,b)=(1,240)$ to introduce a sparse prior for $p$ with a purpose of controlling the average Bayesian FDR at 0.05. The value of b is estimated by $\tilde{b}$, the empirical Bayes estimate of b. Specifically, given that $E({\gamma }_g)=E_p(E_{{\gamma }_g|p}({\gamma }_g))=1/(b+1)$, the method of moments gives us $1/(\tilde{b}+1)=\widehat{P}({\gamma }_g=1|a=1,b))$ which yields $\tilde{b}={(\widehat{P}({\gamma }_g=1|a=1,b))}^{-1}-1$.²⁷ $\widehat{P}({\gamma }_g=1|a=1,b)$ is the estimated proportion of significant genes, and by considering a gene as significant if it has at least one significant SNP, we have $\widehat{P}({\gamma }_g=1|a=1,b)={\Sigma }_{g=1}^{G}I[{\Sigma }_{j=1}^{k_g}I(|z_{gj}|>4.59)>0]/G$ where 4.59 is the threshold that yields the adjusted 2-tailed P value after the Bonferroni correction for the number of genes $G$ (ie, 0.05/G) under the standard normal distribution. In addition, we set $(r_1,{\delta }_1)=(r_2,{\delta }_2)=(0.01,0.01)$ to impose a noninformative prior on ${\tau }_{gj}^2$ and ${\omega }_{gj}^2$.

Results

Selection of SNPs and genes

Prior to the prescreening procedure, our data set contains 697 110 SNPs; of which 30 247 SNPs were found to be potentially related to height in our prescreening procedure as detailed in section “Prescreening of SNPs.” Using the LRT method for the SNP-level association tests, we had the z scores for these 30 247 SNPs that entered our gene-based HSVS analysis and belong to 11 119 genes. We obtained the grouping information for the SNPs from Ensembl, a BioMart database^28,29 that contains the Ensembl stable IDs of the genes the SNPs belong to. By importing this data set into our MCMC sample generator in R, we obtained 6000 MCMC posterior samples of our fused HSVS model coefficients via Gibbs sampling in addition to 1000 burnin iterations.

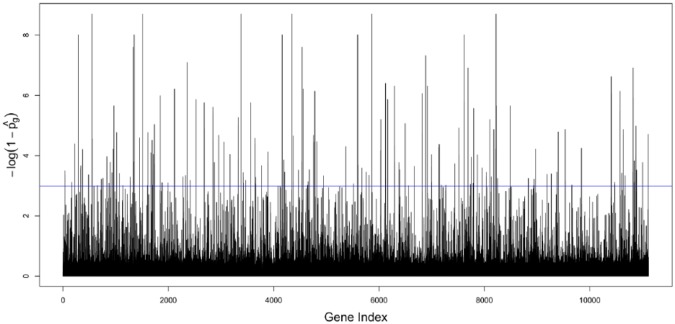
We denote the posterior selection probability for the $g\mathrm{th}$ gene by ${\widehat{p}}_g$. We note that ${\widehat{p}}_g=(1/N){\Sigma }_{i=1}^N{\gamma }_g^{(i)}$, where $N$ is the number of MCMC posterior samples, and ${\gamma }_g^{(i)}$ is the posterior sample of ${\gamma }_g$ in the $i\mathrm{th}$ MCMC iteration. We also note that $1-{\widehat{p}}_g$ can be interpreted as the Bayesian version of the P value,³⁰ indicating the significance of the genes. We calculated the ${\widehat{p}}_g$ for the 11 119 genes, 217 of which are greater than 0.95, which were identified as significantly associated with osteosarcomas. In Figure 1, we illustrate $-\log (1-{\widehat{p}}_g)$ for these 11 119 genes with a horizontal line at 3.0 $(\approx -\log (0.05))$ indicating the critical value for the selection of genes.

Figure 1.

$-\log (1-{\hat{P}}_g)$-log(1-Pˆg) for the 11 119 genes. The horizontal line at 3.0 $(\approx -\log (0.05))$) indicates the critical value for the selection of genes. Genes are indexed in order of their genomic locations.

We investigated the posterior estimates of the SNP effects for these identified significant genes. Our Bayesian association test uses the fused HSVS prior that incorporates a fused lasso formulation to account for the serial correlations between adjacent SNPs in the same gene. Thus, we expected that our fused HSVS model has more power to detect significant genes by borrowing strengths across the SNPs within a gene.

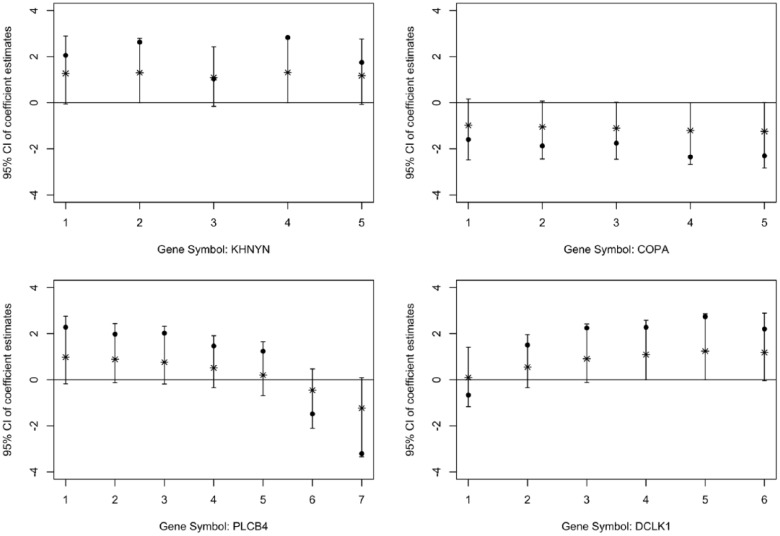
Figure 2 illustrates the posterior median estimates of the SNP effects with their 95% credible intervals for 4 of the 217 significant genes as an example; similar patterns were found in the rest of the 217 genes. The x-axis represents the SNPs in an order that reflects the relationship of their adjacent genomic positions in that gene. The original z scores were also shown for the SNPs in these 4 genes (as indicated by solid black dots). We notice in these plots that both the original z scores and the posterior estimates demonstrate the presence of serial correlation patterns and consistent effects among the SNPs within each gene, supporting the use of our fused HSVS method in the gene-based GWAS analysis, which is able to account for the serial correlations between adjacent SNPs in the same gene. Thus, although the SNPs within these genes do not necessarily stand out as significant by themselves, these genes were identified as significant in our Bayesian analysis by borrowing strengths across the SNPs within the gene.

Figure 2.

Examples of effect estimates for SNPs within 4 genes identified by the HSVS. The x-axis represents the index of SNPs in an order that reflects the relationship of their adjacent positions in that particular gene. The solid black dot indicates the z score of the association test. The asterisk indicates the posterior median. The vertical line indicates the 95% credible interval. The horizontal line indicates the marker for 0.

Ingenuity pathway analysis

We have the 217 selected genes analyzed through the core analysis of QIAGEN’s IPA (QIAGEN Redwood City; www.qiagen.com/ingenuity). Table 1 shows the results of the top 10 canonical pathways for the 217 genes. The P value indicates the likelihood that the association between genes and a pathway is due to random chance. The ratio indicates the number of genes that map to the pathway divided by the total number of genes that map to the canonical pathway. Table 2 shows the results of the selected upstream regulators. The list is filtered to keep only the upstream regulators with >5 target molecules, and P value of overlap <0.01. The P value of overlap indicates the likelihood that the overlap between the dataset genes and the genes that are regulated by a transcriptional regulator is due to random chance. The results of upstream regulators and canonical pathways have confirmed some previously known risk factors in osteosarcoma. For example, the estrogen receptor signaling pathway is known to play important roles in diverse physiological functions associated with the cardiovascular, central nervous, immune, and skeletal systems and is closely related to tumors in estrogen-regulated tissues. TP53, which stands out as the most significant upstream regulator of our set of identified genes, is a target of estrogen and is well known as a tumor suppressor gene whose mutation occurs in almost all human cancers including osteosarcoma with a high frequency.³¹ Several of the top identified canonical pathways as well as one selected upstream regulator, RARA, are related to retinoid X receptor (RXR), which is known to be important in vitamin D metabolism, function in bone development and control of cell growth, and be closely related to osteosarcoma.³² The pathways, xenobiotic metabolism signaling and RANK signaling, also have been identified in previous studies of osteosarcoma: the former involves genes functioning with the steroid and xenobiotic receptor (SXR), a nuclear hormone receptor that is expressed in osteosarcoma cell lines and modulates bone homeostasis,³³ whereas the latter increases cell motility and anchorage-independent growth of osteosarcoma cells and preosteoblasts.³⁴ For the other identified upstream regulators, the genes STAT6 and IL4 are important genes regulating the immune system, activities of which highly correlated with apoptosis and metastasis in various types of cancer.^35,36 The gene TGFB1 is a suggested risk factor for high-grade osteosarcoma,³⁷ LY294002 has been considered to be able to manage human osteosarcoma through affecting cancer stem-like cells,³⁸ and dexamethasone has been found to reduce type 4 cAMP-phosphodiesterase (PDE4), which affects the cAMP signaling pathway of human osteosarcoma.³⁹ These biological discoveries partially support our inferential results of the osteosarcoma trio data analysis based on the fused HSVS method.

Table 1.

The top 10 ingenuity pathway analysis (IPA) canonical pathways enriched with the 217 selected genes.

IPA canonical pathways	P value	Ratio
Xenobiotic metabolism signaling	.047	0.028
PXR/RXR activation	.051	0.062
Estrogen receptor signaling	.067	0.039
LPS/IL-1–mediated inhibition of RXR function	.095	0.027
TR/RXR activation	.098	0.041
Hepatic cholestasis	.100	0.031
RANK signaling in osteoclasts	.103	0.040
d-myo-inositol (1,4,5)-trisphosphate degradation	.114	0.111
Neuropathic pain signaling in dorsal horn neurons	.124	0.035
Autophagy	.125	0.05

Table 2.

The selected ingenuity pathway analysis (IPA) upstream regulators.

Upstream regulator	Molecule type	P value
TP53	Transcription regulator	8.27E−06
ERN1	Kinase	1.37E−04
STAT6	Transcription regulator	5.01E−04
IL4	Cytokine	5.14E−04
TGFB1	Growth factor	6.79E−04
Topotecan	Chemical drug	1.14E−03
LY294002	Chemical—kinase inhibitor	1.36E−03
Dexamethasone	Chemical drug	2.50E−03
RARA	Ligand-dependent nuclear receptor	3.81E−03
Camptothecin	Chemical drug	5.15E−03
NFYB	Transcription regulator	7.56E−03
CREB1	Transcription regulator	8.11E−03

Comparison with SNP-level GWAS and minimum P value

In addition to our HSVS approach that conducts the gene-level analysis, as comparisons we also conducted an SNP-level GWAS using the LRT method and a gene-level GWAS using the minimum P value method. The former identified 212 SNPs which belong to 169 genes, and the latter identified 416 genes with multiple adjustment by controlling the FDR using the Benjamini-Hochberg procedure.

In Figure 3, we compare the number of genes identified by the HSVS, in which we introduced a sparse prior to control the FDR, to the above 2 methods with the Benjamini-Hochberg procedure in a Venn diagram. Unsurprisingly, the SNP-level GWAS analysis identified the smallest number of genes due to the large number of tests. Most of the genes identified by the HSVS method was also identified by the other 2 methods. However, the HSVS method was able to identify 65 genes that were not identified by the other 2 methods; some of these genes turn out to have a close relationship with osteosarcoma. For example, the human BAG3 (Ensembl Gene ID ENSG00000151929) has an important role in the etiology of osteosarcoma by producing an impairment of basal cell survival.⁴⁰ A closer examination of their SNP-level effects suggests that the SNPs of these genes exhibit weak but consistent effects in the SNP-level analysis, which indicates that the HSVS method might be more sensitive to detect genes with consistent SNP-level effects by borrowing strength across SNPs within a gene.

Figure 3.

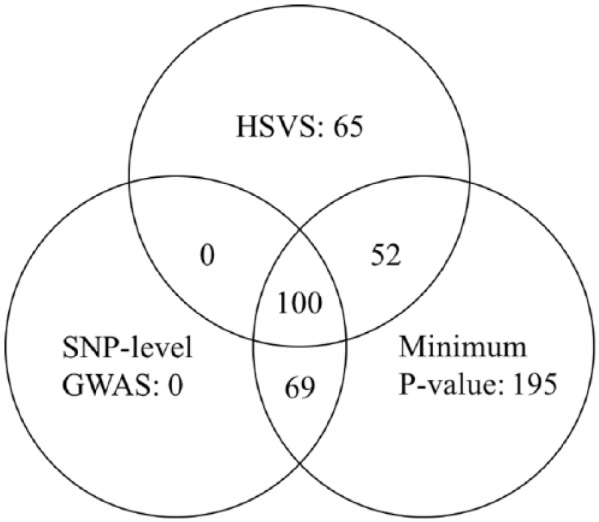
The Venn diagram that shows the number of significant genes identified by the HSVS method, the SNP-level GWAS with the Benjamini-Hochberg procedure, and the minimum P value method with with the Benjamini-Hochberg procedure. The number in each nonoverlapping region is the number of genes exclusively identified by that particular method. For example, the HSVS method was able to identify 65 genes not identifiable by the other 2 methods. GWAS indicates genome-wide association study; HSVS, hierarchical structured variable selection; SNP, single-nucleotide polymorphism.

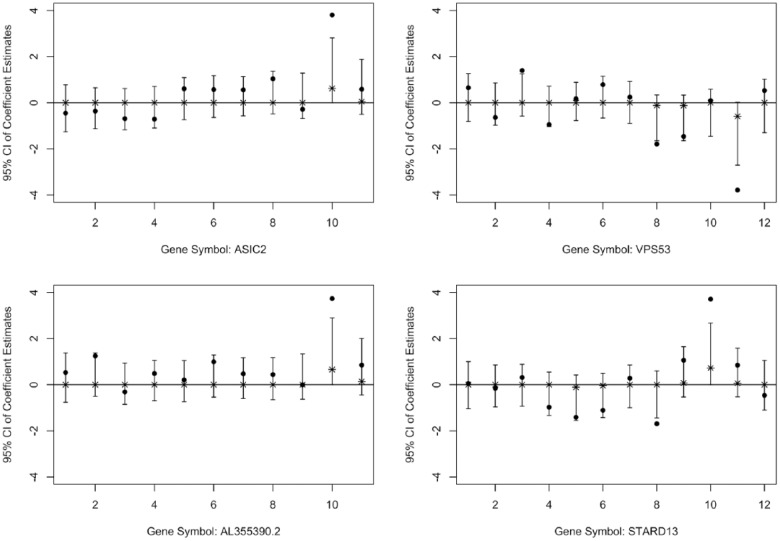
However, the minimum P value method with the Benjamini-Hochberg procedure identified 195 genes that were not identified by the other 2 methods. In Figure 4, we illustrate 4 of the 195 genes as an example; similar patterns were found in a considerable number of the 195 genes. Compared with the genes identified uniquely by our Bayesian method, these genes, instead of showing patterns of consistent SNP-level effects within a gene, usually have only 1 SNP that shows significant effect in the SNP-level analysis. We think a plausible reason that these genes were identified as significant by the minimum P value method is mostly because of a single SNP within the gene that has an outstanding effect, which are more likely to be false positives.

Figure 4.

Examples of effect estimates for SNPs within 4 genes exclusively identified by the minimum P value method with the Benjamini-Hochberg procedure. The x-axis represents the index of SNPs in an order that reflects the relationship of their adjacent positions in that particular gene. The solid black dot indicates the z score of the association test. The asterisk indicates the posterior median. The vertical line indicates the 95% credible interval. The horizontal line indicates the marker for 0.

Simulations

We included a simulation study to evaluate and compare the power and the type I error rate of the 3 methods. We specified the simulation setup that mimics our real data. In particular, we generated the z scores of SNPs for 11 000 genes, 200 of which are causal. Each gene randomly contains 1 to 10 SNPs with probabilities equal to the empirical distribution of the number of SNPs per gene in our real data. The distribution of simulated z scores also resembles that of the z scores in our real data. As shown in Table 3, averaging over 20 simulations with the same setup, the SNP-level GWAS analysis has a lower average power and the minimum P value method has a higher average type I error rate, compared with the HSVS method.

Table 3.

Comparison of the average power and type I error rate of 3 methods averaging over 20 simulations.

Method	Power	Type I error
HSVS	0.852	0.058
SNP-level GWAS	0.782	0.042
Minimum P value	0.836	0.070

Discussion

The data we analyzed in this study are family-based osteosarcoma trio data. This is different from previous osteosarcoma GWASs where the population-based case-control data were the primary sources of analysis.^6,7,11 We also note that our HSVS method identified susceptibility genetic markers that were not identified in previous studies. However, the susceptibility SNPs identified in several previous studies did not enter our final analysis as a result of the prescreening. This indicates that the prescreening, although it helped restrict the SNPs, has the risk of excluding potential susceptibility SNPs if the prescreening criterion is stringent.

Multiple testing is an important challenge in both SNP- and gene-level GWASs. In this study, we conducted a gene-level GWAS by applying the HSVS method to the SNP-level LRT statistics with their gene-SNP grouping information to implement the gene-level multiple testing. The specification of the covariance matrix in the HSVS model accounted for the serial correlation among adjacent SNPs. A natural extension of this application is to apply the HSVS method to a pathway-based GWAS with an objective of identifying significant pathways while accounting for the correlation among genes. For example, a gene-level common mean may be used in the sampling model for the SNP-level statistics so that we would be able to move the selection procedure up from the SNP-gene level to the gene-pathway level. Incorporating an extra binary selection indicator for pathways is also another potential solution.

The P value is a common issue in Bayesian multiple testing problems. The binary indicator for gene selection in the HSVS prior allowed us to obtain the posterior selection probability of each gene, and subtracting it from 1 yields the Bayesian-version P value. The specification of the covariance matrix in the “slab” part of the prior allowed us to borrow information and strength from the SNPs within a gene when calculating its P value. In this study, we used the fused lasso formulation for the covariance matrix to represent the serial correlation among SNPs. Other correlation structure may be used, such as exchangeable, AR-1, and M-dependent, with an inverse-Wishart⁴¹ or a G-Wishart⁴² prior.

The HSVS method provided a computationally scalable approach in the setting of high-dimensional data. The total computation time was 12.6 hours for the 7000 MCMC samples without parallel computation on the High Performance Computing System at the Minnesota Supercomputing Institute using 1 core of the Intel Haswell E5-2680v3 processors. Our experiment showed that parallel computing using 23 cores increased the efficiency of our MCMC sampler by 25.7%. Specifically, the parallel computing is built on the fact that the likelihood can be factorized given $p$, the overall selection probability. As a result, in each MCMC iteration, the posterior ${\theta }_g$, ${\gamma }_g$, ${\tau }_g$, ${\omega }_g$, ${\lambda }_{1g}$, and ${\lambda }_{2g}$ can be updated independently for each gene in our MCMC sampler. In practice, we used the “foreach” function with the %dopar% operator to distribute the posterior calculations into 23 cores. We experimented on the High Performance Computing System at the Minnesota Supercomputing Institute using 23 cores of the Intel Haswell E5-2680v3 processors. In the setting of 10 000 genes with 5 SNPs per gene, it took 6.25 minutes to complete 100 MCMC iterations without parallel computing and 4.64 minutes using parallel computing which is 25.7% fewer than the former.