Probability of Heat Intolerance: Standardized Interpretation of Heat-Tolerance Testing Results Versus Specialist Judgment

Abstract

Context: 

The heat-tolerance test (HTT) is a screening tool for secondary prevention of exertional heat illness by the Israel Defense Forces. To discern participant tolerance, recruits are exposed to intermediate environmental and exercise stresses, and their physiological responses, core temperature, and heart rate are monitored. When their physiological measures rise at a higher rate or exceed the upper levels of absolute values compared with other participants, heat intolerance (HI) is diagnosed.

Objective: 

To develop a mathematical model to interpret HTT results and provide a quantitative estimate of the probability of heat tolerance (PHT).

Design: 

Cross-sectional study.

Setting: 

Warrior Health Research Institute.

Patients or Other Participants: 

The HTT results of 175 random individuals tested after an episode of exertional heat illness were classified qualitatively and then divided into training (n = 112) and testing (n = 63) datasets. All individuals were male soldiers (age range = 18–22 years) who had sustained an episode of definitive or suspected exertional heat stroke.

Main Outcome Measure(s): 

Based on the decision algorithm used by the Israel Defense Forces for manual interpretation of the HTT, we designed a logistic regression model to predict the heat-tolerance state. The model used a time series of physiological measures (core temperature and heart rate) of individuals to predict the manually assigned diagnosis of HT or HI. It was initially fitted and then tested on 2 separate, random datasets. The model produced a single value, the PHT, and its predictive ability was demonstrated by prediction-density plots, receiver operating characteristic curve, contingency tables, and conventional screening test evaluation measures.

Results: 

According to prediction-density plots of the testing set, all HT patients had a PHT of 0.7 to 1. The receiver operating characteristic curve plot showed that PHT was an excellent predictor of the manual HT interpretations (area under the curve = 0.973). Using a cutoff probability of 0.5 for the diagnosis of HI, we found that PHT had sensitivity, specificity, and accuracy of 100%, 90%, and 92.06%, respectively.

Conclusions: 

The PHT has the potential to be substituted for manual interpretation of the HTT and to serve in a variety of clinical and research applications.

Key Points

• Unlike previous methods of interpreting heat-tolerance test (HTT) results, the probability-of-heat-tolerance (PHT) model incorporates previous experience and provides a standardized, repeatable output.

• In the PHT model, heat intolerance is defined on a continuous scale, which enables a more individualized approach to patients and can be used in secondary prevention of exertional heat illness and in thermoregulatory clinical research.

• In individuals with borderline HTT results, the PHT score must be the deciding factor for diagnosis and treatment recommendations and should determine how the HTT results are interpreted.

• People with a PHT between 0.5 and 0.9 should be classified as intermediately tolerant and should receive recommendations for supervised training and repeat testing.

• The PHT may help clinicians make return-to-competition decisions for athletes who have had exertional heat stroke during the season and particularly for those whose diagnosis of exertional heat stroke was uncertain.

The Israel Defense Forces (IDF) have used the heat-tolerance (HT) test (HTT) for the last 45 years as a screening tool for heat intolerance (HI) and secondary prevention of exertional heat illness (EHI) among soldiers after a single episode of EHI.^1,2 The test sets an intermediate-level thermoregulatory challenge, the physiological response to which varies among individuals. Records of 2 primary physiological measures, body core temperature (T_rec) and heart rate (HR), serve as the basis for inference about whether an individual accumulates body heat at a rate that is higher than expected; if so, HI is diagnosed.³ Individuals who have HI are unable to adapt to work or exercise in hot environments⁴ or at high workload intensities. The HI diagnosis is associated with an 11.4% rate of repeated EHI events despite the fact that individuals with HI are instructed to abstain from strenuous physical activity. Among individuals with HT, only 1.8% have reported experiencing repeated EHI after the HTT.⁵

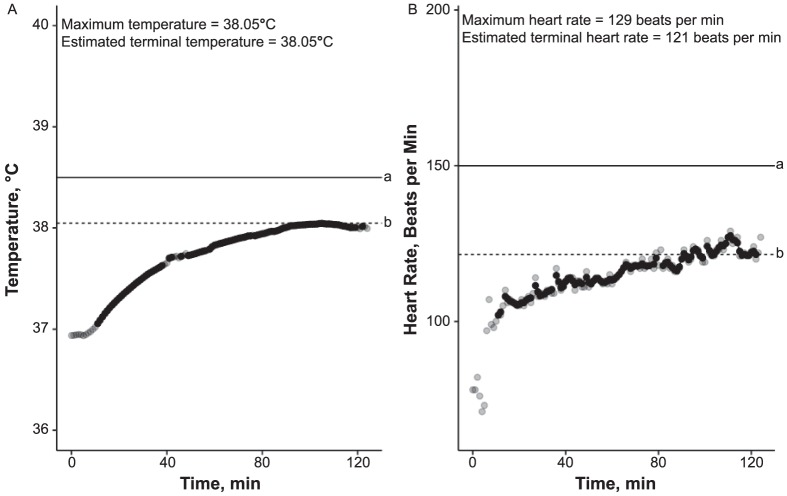
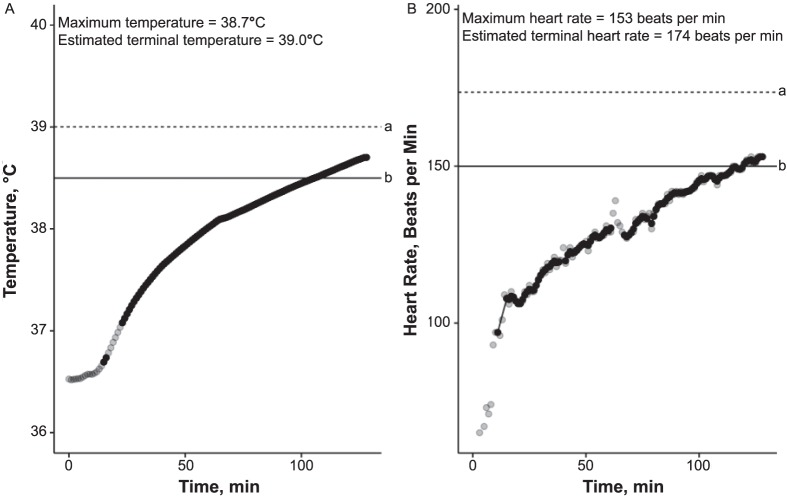
The test protocol consists of 120 minutes of walking at a speed of 5 km/h on an incline of 2% in a climate chamber with a relative humidity of 40% and a temperature of 40°C.³ An HT T_rec pattern is characterized by a slight increase in T_rec of 0.5°C to 1°C during the first hour and its stabilization (reaching a plateau or “tendency to plateau”) during the second hour.^3,6 This expected HT T_rec curve represents an individual who effectively activates cooling mechanisms (eg, vasodilation, sweating) and achieves an equilibrium between produced and dissipated heat at a T_rec of 37.7°C to 38.3°C³ (Figure 1). A representative T_rec curve indicating HI rises continuously throughout the test and exceeds a cutoff value of 38.5°C (Figure 2).

Figure 1.

Representative values for an individual with heat tolerance (probability of heat tolerance = 0.96): A, Temperature; B, Heart-rate curves. All points on each graph represent 1 measurement; points appear black when several overlap. ^a Indicates cutoff value. ^b Indicates estimated terminal value.

Figure 2.

Representative values for an individual with heat intolerance (probability of heat tolerance = 0): A, Temperature; B, Heart-rate curves. All points on each graph represent 1 measurement; points appear black when several overlap. ^a Indicates estimated terminal value. ^b Indicates cutoff value.

The HR reflects any increase in cardiac output caused by the physiological response of vasodilation, and the current HTT interpretation guidelines specify that a range of 105 to 135 beats/min is expected in most individuals with HT at the end of the second hour.³ Conversely, a sustained HR of 150 beats/min or greater indicates HI (Figure 3). However, some individuals show an intermediate pattern that may be classified as either HT or HI. Rigid cutoff values for final T_rec (38.5°C) and HR (150 beats/min) disregard all preceding information and are not useful or sufficient when interpreting these ambiguous results.

Figure 3.

Representative values for an individual with heat intolerance (probability of heat tolerance = 0): A, Temperature; B, Heart-rate curves. All points on each graph represent 1 measurement; points appear black when several overlap. ^a Indicates estimated terminal value. ^b Indicates cutoff value.

Recently, an indicator in the second hour, delta T_rec (dTC), which is calculated as T_rec on minute 120 (T_rec[120]) – T_rec on minute 60 (T_rec[60]), was suggested as reflective of HI or HT when it is equal to or less than 0.45°C,⁷ whereas dTC greater than 0.45°C invariably indicates HI. However, curves with dTC values of 0.25°C to 0.45°C do not appear to reach the heat equilibrium, especially when the final HR and T_rec values are submaximal (Figure 4). This greater reliance on subjective qualitative assessment of the test over rigid cutoff values of HR and T_rec leads to variability in diagnoses.

Figure 4.

Representative values for an individual with borderline heat tolerance (probability of heat tolerance = 0.64): A, Temperature; B, Heart-rate curves. All points on each graph represent 1 measurement; points appear black when several overlap. ^a Indicates cutoff value. ^b Indicates estimated terminal value.

When 2 experts were required to independently classify the results of the individuals in this study, they independently assessed both training and testing datasets (the dataset used for model fitting and the dataset used for model testing, respectively) and reached an interobserver agreement coefficient⁸ of κ = 0.67 (range, 0.55–0.8) in the training dataset and κ = 0.81 (range, 0.66–0.95) in the testing dataset. This evidence of the variability of clinical judgments highlights the need for an objective and repeatable decision tool. When addressing the ambiguous findings in our center, the most experienced professional is often asked to decide whether an individual has HI or HT. Consequently, an inconsistent decision-making process and difficulties in training new specialists and using HTT in other medical sites and facilities are likely. Therefore, the purpose of our study was to present a novel method for automated classification of the HTT. A logistic regression model was used to predict an individual's HT state on the basis of previous manual interpretations of the HTT. The process of model design was guided by the underlying physiology and current practice. For each test, the model provides a single number on a scale of 0.00 to 1.00: the probability of HT (PHT). Using this value and relying on predefined cutoff values, a clinician can consistently classify individuals with similar physiologic responses to HTT as either HT or HI.

METHODS

Model Design

To build a mathematical model, we reviewed the rationale for testing. The HTT was developed to elicit a faster and earlier rise in body temperature under heat and exercise stresses in individuals with HI³ and to observe the tendency of the person to reach the upper threshold of 40.5°C, which is a prerequisite for heat-stroke diagnosis.⁹ During the development of the HTT, testing time was shortened from 180 to 120 minutes after users observed that all individuals with HT achieved or tended to plateau at less than 38.5°C by minute 120. This implies that the HT state is determined by both the absolute final T_rec value and its change from minute 60; the former must be less than 38.5°C and the latter must display an exponential decay pattern. The HR is given less weight in the final interpretation of the HTT, and the range of 40 to 150 beats/min is considered normal.

Based on these principles, we designed an autoregressive model that may fit the T_rec and HR time-series data:

,

where observation is either T_rec or HR.

Using each test's data time series and after removing outlier observations, we fit model parameters μ and φ to minimize the sum of squares of residual (w) at each time (w[t]). This is a maximum-likelihood parameter-estimation approach.¹⁰ Namely, the given model with parameters obtained in this manner is more probabilistically likely to produce the observed data time series than with any other set of parameters.

A statistical interpretation of μ is a central tendency or, alternatively, an equilibrium value, for T_rec. Similarly, φ is a measure of how quickly T_rec would drift toward such equilibrium. Given that these values are computed for a single HTT data time series, they are specific to the particular HTT.

Consequently, we may interpret μ as a predicted maximal T_rec that the curve could achieve. This value is generally not the final observed T_rec value. It may be the plateau that could be achieved during the third testing hour or potential hyperthermia of 40°C and greater.

The HR time-series data from one person's HTT are then analyzed similarly to produce analogous values of μ and φ. Therefore, using our autoregressive models, we derived 4 statistical values (μ_Trec, φ_Trec, μ_HR, and φ_HR) for each HTT that we could use as factors to study the manual HTT classification process.

In the past, to standardize the HTT classification process, we formulated the following decision steps for HTT interpretation:

1. Assess T_rec and HR terminal values. These are generally readings taken at 120 minutes. If thresholds of T_rec > 38.5°C or HR > 150 beats/min are exceeded, classify as having HI.

2. Assess dTC = T_rec(120) − T_rec(60). If it exceeds 0.45, classify as having HI.

3. If 0.25 < dTC < 0.45, HR = 120 to 150 beats/min, and T_rec > 38.2°C, consider defining as having HI.

4. If dTC < 0.25, HR < 120 beats/min, and T_rec < 38.2°C, consider defining as having HT.

In our exploration of the training dataset and corresponding HTT classifications of expert physiologists, we found that the parameters φT_rec and φ_HR had little effect on HT or HI classification. However, both μ_Trec and μ_HR were strong and complementary explanatory variables. Furthermore, when either threshold (T_rec greater than 38.5°C or HR greater than 150 beats/min) was breached, we observed a much stronger tendency toward HI classification than could be explained by a combination of μ_Trec and μ_HR alone. This tendency is a byproduct of the outlined decision steps, with step 1 being the most important. Hence, we introduced a factor to μ_Trec and μ_HR that would serve as a penalty on breaches of these 2 thresholds. Our new factor, θ = max [0, maxT_rec − 38.5°C, (maxHR − 150) / 50], was incorporated in the model to reflect the described process, where max is maximum and θ equals zero unless maxT_rec − 38.5°C and (maxHR − 150) / 50 are not negative.

Study Population

The study dataset consisted of the sample results from 175 HTTs that were performed in the Warrior Health Research Institute. All participants were referred for testing by their unit physicians after an exertional collapse, classified either as exertional heat stroke (EHS; rectal temperature >40°C, return to consciousness within minutes to 1 hour, cooling within 15 minutes, mild laboratory abnormalities, and no sequelae) or suspected EHS, which was clinically defined as EHS except that measurement of rectal temperature was absent or delayed. A total of 152 (87%) tests were first or single tests performed within 45 to 60 days of the event. The remaining 23 (13%) tests were repeated results obtained about 6 months or more after the event. Use of the individuals' demographic and testing data for research was approved by The IDF Medical Corps Institutional Review Board.

Model Training and Testing

The dataset was divided into 2 parts: model training (n = 112) and testing (n = 63). Each test was independently reviewed by the institute's director (R.Y.) and physician (H.S.) and classified (ie, manually labeled) as either HT (coded as 1) or HI (coded as 0).

The dataset underwent reorganization and cleaning for subsequent analysis via the following steps: all data points within ±3 standard deviations of the rest of the series were removed as nonphysiological error values. The remaining time-series data were smoothed slightly to better estimate μ and φ. In addition, as a practical measure, φ was capped so the time-series half-life approached μ at no longer than 90 minutes.

In the next phase, we performed a logistic regression on 4 factors provided by the model (μ_Trec, φ_Trec, μ_HR, and φ_HR) to predict HT classification of the training group. The μ_Trec (P = .03) and μ_HR (P = .006) were predictors of HT. Whereas the logistic regression indicated θ was not different (P = .11), it is included in our model due to a noticeable reduction in the Akaike information criterion from 58.3 to 51.7. This estimator weighs the likelihood of a model against the number of parameters in the model. As such, it can be used to compare models and to measure the value added by a new parameter.

Model testing was performed on 63 individuals. Its predictive ability in the testing set was represented with a receiver operating characteristic curve, positive- and negative-predictions density plot, and contingency tables. All data manipulation, modeling, and graphical presentation were conducted using R (version 3.3.1; R Foundation for Statistical Computing, Vienna, Austria) open-source statistical software. The α level was set at .05.

RESULTS

The final algorithm that we developed for predicting HT in the testing set of our study and for subsequent clinical use consisted of 7 steps and was applied as follows:

For each HTT test dataset,

1. Remove outliers and smooth T_rec data;

2. Compute φT_rec and μT_rec;

3. Remove outliers and smooth HR data;

4. Compute φ_HR and μ_HR;

5. Compute θ using the formula θ = max [0, maxT_rec − 38.5°C, (maxHR − 150) / 50];

6. Compute Σ using the formula Σ = 0.2057 − 3.4398 × (μT_rec − 38.5°C) − 0.0496 × (μ_HR − 150) − 22.30 × θ; and

7. Compute PHT using the formula: prob = 1 / [1 + exp (−Σ)], where prob is probability.

For convenient calculation of this algorithm, we placed an open-access calculator at https://phtheller.shinyapps.io/HTTest/. The calculator requires only the input of a comma-separated values file with 3 columns of time-series data: time, HR, and T_rec. It then provides the HR and T_rec plots and the PHT value.

The testing-set predictions distribution (Figure 5A) demonstrated that most individuals with HT have a PHT greater than 0.8 and only a few individuals with HT have a PHT of 0.7 to 0.75. The receiver operating characteristic curve (Figure 5B) demonstrated a trade-off between sensitivity and specificity and excellent accuracy for classifying individuals as having HT or HI (area under the curve = 0.973). Using the given plots, one can select a cutoff PHT value, depending on the preference for maximum sensitivity or maximum specificity in identifying individuals who have the pathologic condition of HI.

Figure 5.

Diagnostic characteristics of the prediction model in the testing set. A, Distribution of predictions. B, Distribution of receiver operating characteristic curves. All points on each graph represent 1 measurement; points appear black when several overlap.

For the purpose of secondary prevention and return to duty post-EHI, we adopted the cutoff value of 0.5 (ie, defined such that individuals who have a model-predicted probability of 0.5 and lower for HT definitively have HI). A contingency table demonstrates the PHT sensitivity, specificity, and diagnostic accuracy in the training and testing sets using this cutoff value (Table 1). The sensitivity, specificity, and accuracy of HI diagnosis in the training set were 96.5%, 92.77%, and 93.75%, respectively, and in the testing set were 100%, 90%, and 92.06%, respectively.

Table 1.

Confusion Matrix for Calculation of the Model Diagnostic Ability of Heat Tolerance Using a Probability-of-Heat-Tolerance Cutoff Value of 0.5

Set	Training (n = 112)		Testing (n = 63)
	Prediction by Modela		Prediction by Modela
Manual labeling	Intolerance	Tolerance	Intolerance	Tolerance
Heat intolerance	28	1	13	0
Heat tolerance	6	77	5	45

^aIndicates cutoff of 0.5.

Alternatively, when using a cutoff PHT of 0.9, the sensitivity was low (59.26%), but the specificity (96.55%) and accuracy (94.12%) were high in the training set (Table 2). In the testing set, sensitivity was 85%, specificity was 97.67%, and diagnostic accuracy was 93.65%. This implies that individuals who have more HI and a PHT of 0.5 to 0.9 can be misclassified as having HT, but those with a PHT greater than 0.9 almost definitely have HT.

Table 2.

Confusion Matrix for Calculation of the Model Diagnostic Ability of Heat Tolerance Using a Probability-of-Heat-Tolerance Cutoff Value of 0.9

Set	Training (n = 112)		Testing (n = 63)
	Prediction by Modela		Prediction by Modela
Manual labeling	Intolerance	Tolerance	Intolerance	Tolerance
Heat intolerance	32	22	17	3
Heat tolerance	2	56	1	42

^aIndicates cutoff of 0.9.

DISCUSSION

In general, the HTT is used in industrial, military, and sport settings.^4,11–13 These population cohorts, although considered healthy and fit, are exposed to an increased risk of EHS due to strenuous activity because they are required to perform in a wide range of ambient conditions.^14,15 During exertion, the rise in body core temperature may initiate several pathophysiological processes, including systemic inflammatory reaction and cardiovascular failure, that eventually result in functional physiological decline.¹⁶

Clinical indices typically include elevated body core temperature, neurologic dysfunction (eg, delirium, convulsions, and coma), and multiorgan damage.¹⁷ In most cases of EHS, the body core temperature exceeds 40°C to 40.5°C. However, lower core temperatures may not rule out the diagnosis of EHS, which relies primarily on neurologic symptoms. Classifying EHS as mild or severe at the initial point of care would not be correct because treatment by immediate and aggressive cooling may reverse the ongoing pathophysiological processes and improve the final outcome.¹⁸ Conversely, delaying cooling by 30 minutes results in higher complication rates.¹¹ Survivors of EHS may have residual damage, including neurologic dysfunction and HI.

In military settings, the decision about whether an individual should return to duty or training can be complicated. The US Army⁹ and American College of Sports Medicine¹⁸ guidelines highlight the importance of clinical recovery before returning to activity. In our previous work,⁵ we demonstrated that symptoms of headache and dizziness on exertion predict repeated episodes of EHI. However, these symptoms are subjective, and their predictive ability has not been assessed prospectively. The HTT provides an objective measure of HT, which may be applied repeatedly, such as after recovery from an episode of EHI.

We believe that the model we have proposed is an accurate tool for interpreting HTT. For the HTT to become a standardized test, clear descriptions of the indications, testing process, and interpretation of results are needed. Whereas the indications and testing protocol have long been defined, HTT interpretation has remained relatively subjective and overwhelmed by the multiplicity of measures that may be considered when diagnosing HI,¹⁹ especially in borderline cases. The suggested model incorporates several measures and produces a single score as the HTT result: PHT. Researchers and clinicians may use this score for a variety of applications, which we will discuss.

The primary purpose of the HTT is to screen individuals who have experienced EHS and individuals with suspected HI to prevent recurrent EHI. An example of successful implementation of HTT in industry, screening for HI, and a heat-acclimatization program was reported to reduce mortality among gold miners in South Africa.⁴ The American College of Sports Medicine¹¹ has recommended using HTT in the evaluation of athletes who have difficulty returning to competition after an episode of EHS. Prevention policies may necessitate a more conservative assessment, and our model will easily adapt to these changes. We used contingency tables to demonstrate how changing the cutoff value influences model sensitivity and specificity. By defining the PHT score of 0.9 or 0.95 as the minimal requirement for combat service, the IDF and other organizations may identify individuals who have HT and probably reduce the incidence of EHI.

Similarly, we can use the PHT in civilian settings where the HTT is applicable, such as industry and sports. We suggest that individuals with a PHT between 0.5 and 0.9 are not simply at risk of being misclassified as HT or HI but actually represent a population whose HT status is uncertain or modifiable. Therefore, we recommend that those individuals be classified as intermediately tolerant and receive guidelines for supervised training and probably repeat testing. To facilitate clinical application of the new model, we have built the open-access PHT calculator, as shown in the “Results” section, and summarized our recommendations for people with different PHT values in Table 3.

Table 3.

Suggested Clinical Recommendations According to Probability-of-Heat-Tolerance Results

Probability of Heat Tolerance	Diagnosis	Recommendations
0–0.49	Heat intolerance	Weight reduction, walking, swimming, indoor cycling at 50% of maximum pulse
		Repeat testing after 3 mo
0.5–0.89	Borderline heat tolerance	Supervised gradual return to running
		Repeat testing if symptomatic and before performing sprints, medium-distance running, or walking with >30% body weight
0.90–100	Heat tolerance	Return to unrestricted activity. If symptomatic, consider neurologic or ear, nose, and throat assessment.

Heat-tolerance testing may be proposed to symptomatic individuals who have been unable to return to previous activity since the episode of EHS but strongly wish to do so. A graded fitness program intended to help the individual acquire HT via acclimatization and improved aerobic capacity may be followed by serial evaluations of PHT. In sports, PHT may help the clinician decide whether an athlete can return to competition after an EHS during the same season, especially when the diagnosis of EHS is uncertain.

Last, we have addressed several cases of disability claims by soldiers who sustained EHS during their service. The HTT was proposed to evaluate the individuals for HI, presumably as a residual of the EHS. Most claims were issued several years after the event, so the individuals were older, making it impossible to distinguish the lasting effects of EHS from the effects of age, weight gain, and reduced fitness. As a continuous measure, PHT can be used to develop tables of normal PHT ranges for different age, weight, and aerobic capacity groups. These can be helpful for the purposes described earlier.

Another important consideration is that, whereas the binary outcome of HI or HT is used for screening and prevention, the PHT could be advantageous for research. Given that it is a continuous score, it facilitates a more accurate use of regression models in evaluating physiological factors and exposures that might influence the HT state (eg, food additives, protective garments, acclimatization, sleep deprivation). It also provides an absolute measure of HT that enables comparisons among individuals and generalization of each investigation's results. One can use the PHT to create any number of different cohorts, for example, on a scale of HT: probably heat tolerant, borderline heat tolerant, probably heat intolerant, or heat intolerant.

Our study had several limitations. First, the applicability of the PHT index is confined to improved interpretation of the HTT results and not to clinical outcomes. Second, PHT was developed to predict HTT interpretation by experts, which itself is subject to interobserver disagreement. In the training set, 2 physicians agreed on 96 of 117 HTTs (agreement = 82%). Third, as mentioned, all individuals were male soldiers of the IDF and were 18 to 22 years of age. Therefore, our results may not be applicable to other population cohorts. Fourth, this model may be applied only to individuals who undergo the specific HTT protocol used by the IDF.

CONCLUSIONS

We presented a novel approach to HTT analysis. Because the decision of whether an individual has HT or HI has a crucial effect on the individual's future physical behavior, we believe that, with borderline HTT results, the PHT score must serve as the deciding factor for diagnosis and treatment recommendations. Moreover, as such, it would be the final decision as to how an expert should interpret the HTT. The PHT score does not make other physiological measures and the specialist interpretation of the HTT redundant. Instead, it adds to the consistency of the final decision and enhances the accuracy of the HTT result.

Future researchers should use the PHT and a time-series analysis to build a real-time analytic tool that would enable individualization of the HTT for very fit individuals (ie, adjustment of exercise difficulty to an individual's cardiovascular capacity during the second hour of testing based on the information collected during the first hour of HTT). The HTT was initially proposed as a standardized test, with exercise difficulty corresponding to 30% of the maximal oxygen uptake of an average individual. However, average exercise and HT could have changed since the 1970s, and the test also may be too easy for highly fit individuals who sustained an EHS during long-distance running.